1. Introduction
Coronavirus disease (COVID-19) is an infectious disease caused by the novel coronavirus SARS-CoV-2 virus [
1], characterized as a pandemic in March 2020 by the World Health Organization [
2]. Since the first case detected in Wuhan, dated December 2019, COVID-19 has caused 275 million cases and over 5 million deaths up to December 2021 [
3]. Health systems have been significantly challenged by the spread of COVID-19, especially Italy, which was the first European country to be affected by COVID-19 [
4] and which faced an overwhelming increase in COVID-19 patients who needed hospitalization at the beginning of the pandemic, risking the collapse of the system [
5]. The COVID-19 pandemic highlighted the need for a management strategy to predict the demand for hospital services so that healthcare facilities can efficiently make resources available when needed.
The length of stay (LoS) is a key indicator of how efficiently hospitals are being managed and is used to assess the efficiency of hospital management and patient quality of care, and for functional evaluations. A shorter stay means that more beds are available for more patients and reduces hospital resource consumption; thus, it corresponds to a decrease in health-related expenditure [
6]. Reducing LoS has been linked to lower risks of opportunistic infections and medication side effects [
7], and improved treatment outcomes and lower mortality rates. In addition, a shorter hospital stay reduces the burden of medical fees and increases bed turnover, and thus increases hospitals’ profit margins [
7] while lowering the overall social costs [
8,
9,
10]. Researchers must determine which characteristics are associated with longer or shorter hospital stays in patients [
11].
A recent systematic review and meta-analysis [
12] research compared the LoS of COVID-19 patients in China versus the rest of the world (Europe, the U.S., and the UK) using 52 studies. By combining information from different studies, a substantial difference in LoS between China (longer LoS) and other locations (shorter LoS) was found. There is also little evidence concerning the impact of the study period, age, and disease severity on LoS. Another retrospective study in Vietnam found that age was significantly associated with a long hospital stay in COVID-19 patients [
13]; other studies in China found that the average age of patients with a prolonged LoS was higher than that of patients with an average LoS [
14]. A better understanding of the COVID-19 pandemic’s spillover effects between waves might help healthcare professionals better support at-risk persons during the pandemic. Study results have indicated that there is a minor difference in overall LoS before and after the years of the COVID-19 pandemic according to a territory-wide retrospective cohort study conducted in Hong Kong on 28-day in-hospital mortality and LoS. In 2020, patients triaged as critical in the emergency department (ED) had a 2.71-day shorter LoS than those in 2019. LoS declined significantly for patients who died in 2020, when their hospital stay was 2.31 days shorter on average than in 2019 [
15].
Through univariate and multivariate logistic regressions models, a retrospective analysis of patients hospitalized with COVID-19 from a single hospital in Hefei, China, was carried out to explore the risk variables associated with a prolonged hospital LoS. The findings revealed that patients with a prolonged LoS had a higher average age than those with a median LoS [
13]. A time-to-event analysis implementing a Cox proportional hazard model was applied to identify the factors associated with the LoS. Factors linked to a longer hospital stay should be considered when arranging bed strength on a contingency basis, and the estimated LoS of patients was required in order to model bed occupancy and make contingency plans. Artificial Intelligence (AI) researchers developed algorithms in order to model bed occupancy and make contingency plans [
16]. Another study in South Korea used multivariate negative binomial and gamma regression models to determine the influencing factors of LoS [
17]. The results showed that the average LoS in hospitals for COVID-19 patients was 5.5 days, and the average LoS also tended to be higher for older patients, except for the group aged 65 years or older, who had a shorter hospital stay than the others. A study in the UK used an Accelerated Failure Time (AFT) survival model, a truncation corrected (TC) method, both with underlying Weibull distributions, and a multi-state (MS) survival model to analyze LoS data [
18]. The results showed that all methods produced similar estimates of LoS for the overall hospital stay, considering ordinary hospitalization only: 8.4, 9.1, and 8.0 days for AFT, TC, and MS, respectively. This study also tried to mention the complexities and partiality of many data sources, as well as the continuously developing nature of the COVID-19 pandemic that suggests approaches should be based on a variety of analytical methodologies across multiple datasets. From a management point of view, research in Dubai used AI-based modeling by using Decision Tree prediction models to forecast the LoS and risk of mortality accurately. In principle, these smart models might equip front-line clinicians with the tools they need to improve management techniques and save lives [
19].
Researchers have been focusing on modeling count data due to observed problems with the commonly used analytic methods. For example, ordinary least squares (OLS) regression is often inappropriate because the count data violate the underlying assumptions of OLS regression (i.e., the normality of the residuals), resulting inaccurate coefficient estimates and standard errors, and misleading
p-values and consequent confidence intervals [
20,
21].
Only recently, several studies have examined the effective management of LoS, and several statistical models have been proposed to analyze the data with count-type outcomes (such as LoS in the hospital, number of antenatal care visits, number of purchases made, and many more) with different settings and predictors [
22,
23]. There are, however, different characteristics in different count data; therefore, certain count data models cannot be used with them. Often, the first model used to analyze count outcomes is the Poisson model [
10,
20] but, in practice, these two assumptions (i.e., the variance being equal to mean, and independent events) [
10,
20] are typically violated. Overdispersion is generally always the result of any assumptions being violated [
20,
24,
25], and alternate strategies for modeling count data, such as negative binomial regression [
20,
24,
25], should be considered. Aside from overdispersion, many empirical counts contain a large number of zero observations, which can be modeled using Hurdle models [
26]. A Hurdle model combines a binary count outcome (LoS = 0 vs. LoS > 0) with a truncated model for results above the hurdle (LoS > 0). Excess zeros are modeled using the Hurdle model. In some cases, these zeros cannot be ignored, since they are critical and meaningful. To assess the fitted count regression model, researchers have used a graphical approach called Rootograms [
27,
28].
Another statistical method used to characterize the effects of covariates on a given phenomenon is to study the quantiles’ distribution instead of modeling the mean. Quantile regression models estimate the relationship between the qth quantile of the response
y and the covariate
x [
29]. Quantile regression models at multiple percentiles can help compare the changes associated with covariates across the distribution of the phenomenon under study [
30]. Machado et al. [
31] extended quantile regression models for count data. This approach has already been applied in a study [
32] to evaluate the LoS of diabetes patients.
This study aimed to identify and explore the hospital admission risk factors associated with LoS in COVID-19 patients in Bologna, Italy, by applying a relatively novel statistical method (i.e., count regression and quantile regression models) using the currently available predictors. The second goal of this study was to model the LoS of COVID patients in Bologna hospitals from 1 February to 10 May 2021 in order to determine which covariates had a significant impact on it and to discover the potential risk factors linked with LoS.
2. Materials and Methods
2.1. Population
This study obtained data with permission from the local health authority (AUSL) of Bologna. Data were retrieved from 1 February 2020 to 10 May 2021. Our dataset referred to COVID-19 patients both in the ICU (intensive plus sub-intensive) and ordinary settings in 7 Bolognese hospitals. We also categorized the hospital stays as “regular” for 5 hospitals, and “long-term” for 2 hospitals. This distinction is important because hospitals providing extended hospitalization have mainly rehabilitation purposes.
2.2. Database Preprocessing
Individual patients were considered on the basis of their unique ID, and we merged the repeated IDs (patients who went to the hospital more than one time) via the following procedure:
- -
Detect repeated ID;
- -
Order rows referring to the same ID chronologically;
- -
Check if two consecutive rows differ for >3 days
- -
If they differed for >3 days, the two rows were treated as two different stays. The second stay was removed from further analysis;
- -
If they did not differ for >3 days, merge multiple rows by using:
- -
Hospital: prevalent hospital
- -
Setting: add a variable with two levels: “low-intensity” if the patient was only hospitalized in the low-intensity setting and “ICU” if the patient was in the intensive care unit at least one time.
We categorized the hospital stay information as regular hospitalization and long-term hospitalization based on the prevalent hospital.
2.3. Outcome and Covariates
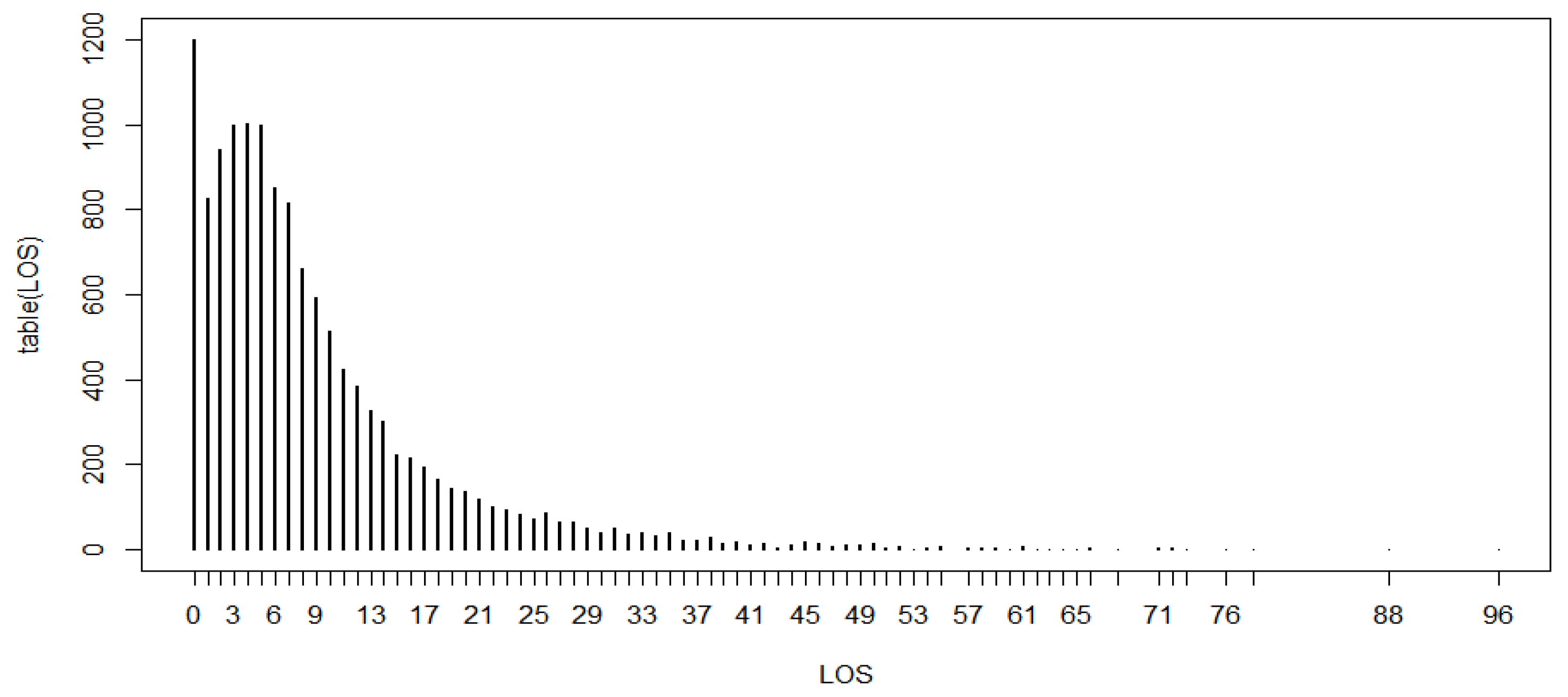
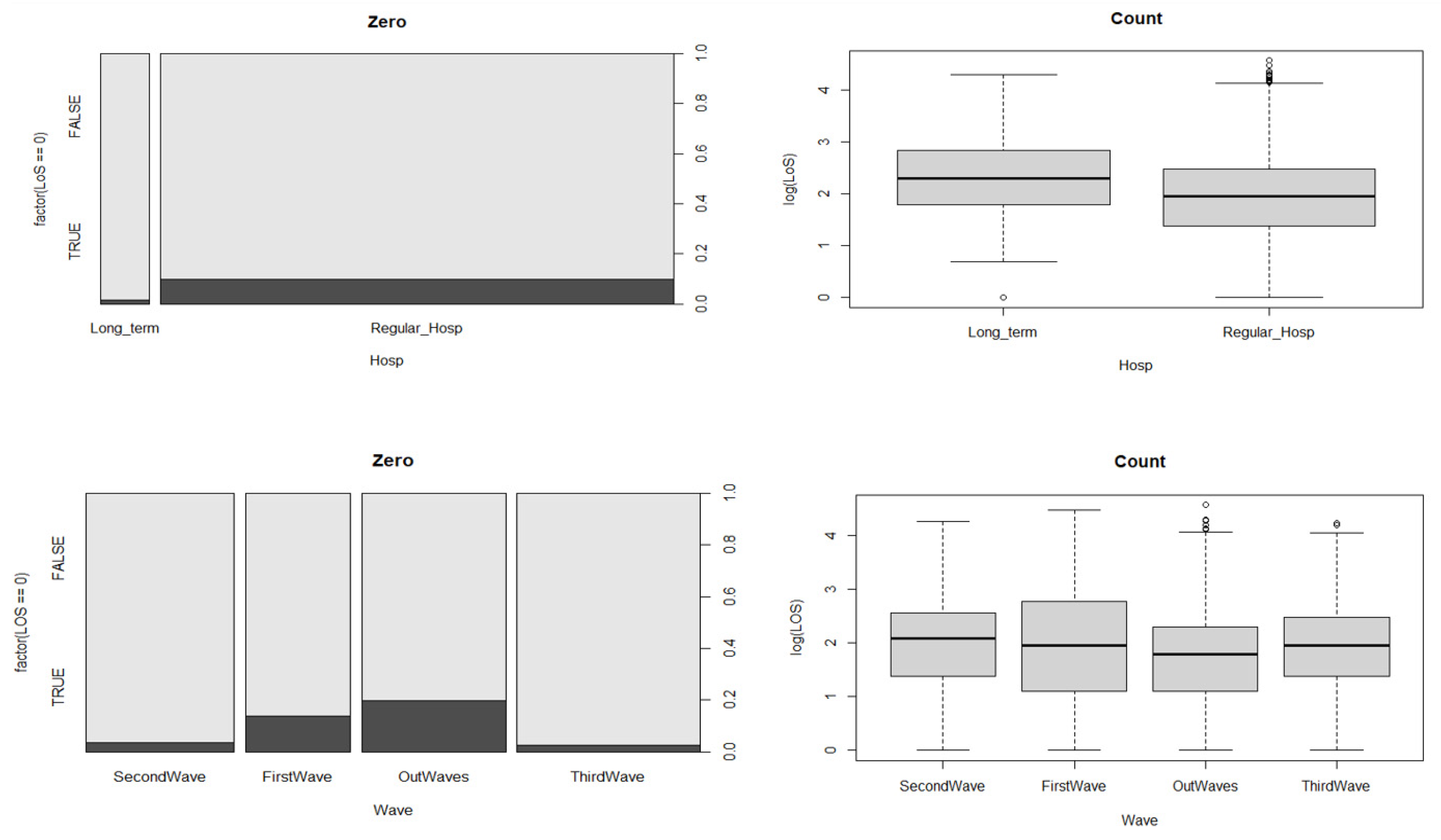
The study’s main outcome was the LoS (a non-negative integer), defined as the number of days between inpatient admission and hospital exit or discharge, and it was the target outcome variable for which this study aimed to identify a proper count regression model. The explanatory variables were:
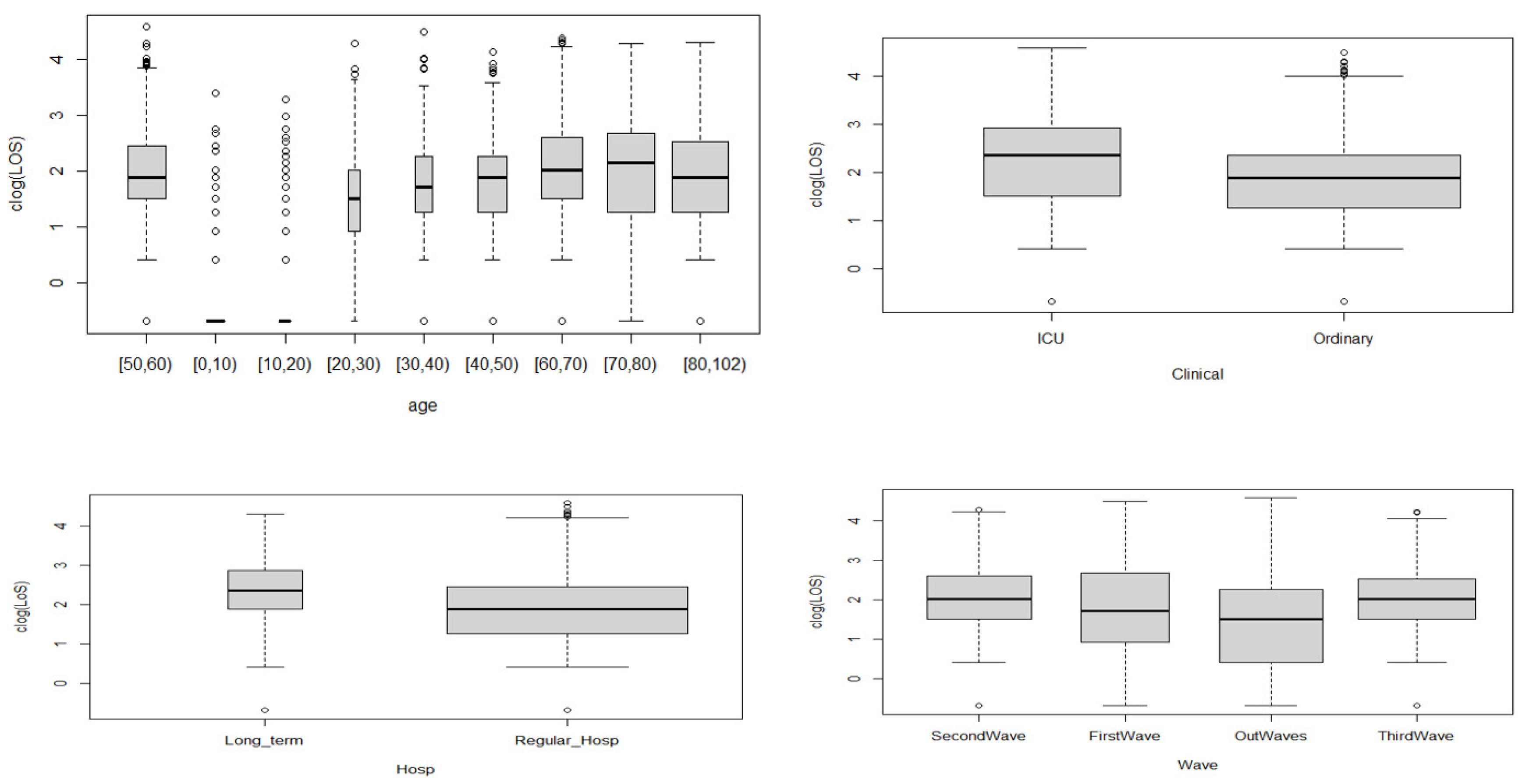
Clinical setting: ICU setting (intensive care + sub-intensive) of COVID-19 patients, and ordinary and low-intensity COVID-19 stays.
Age: An integer representing patient age in years, grouped in 10-year categories: [0, 10), [10, 20), [20, 30), [30, 40), [40, 50), [50, 60), [60, 70), [70, 80), and [80, 102).
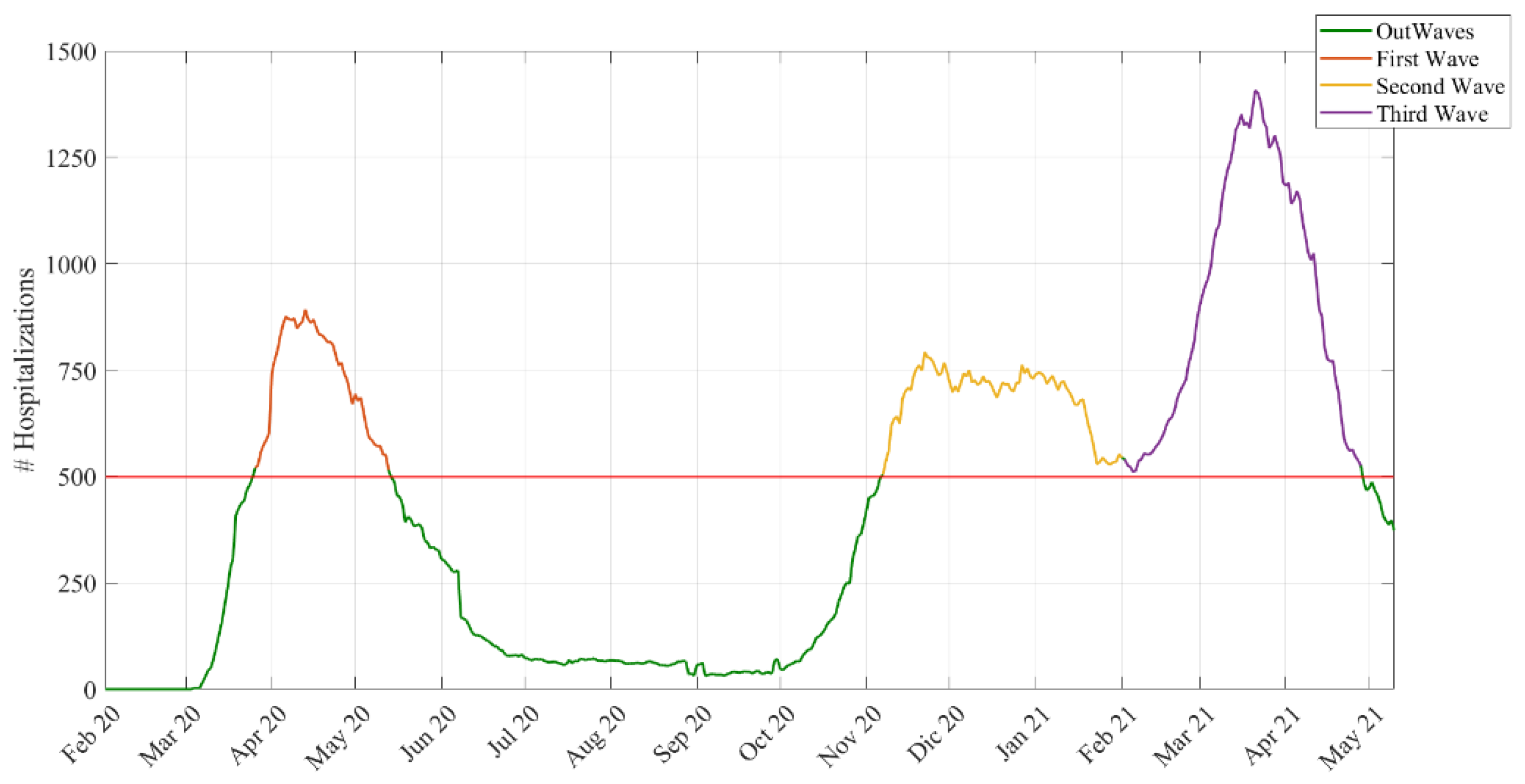
Waves: We defined waves based on an empirical approach.
We assumed that a wave started with more than 500 total hospitalizations and ended when the hospitalizations dropped below 500 (see
Figure 1). Using this cut-off, we chose a day in the stationary phase between the second and the third wave located in the middle of this period. We chose a middle point to divide the second from the third wave, since hospitalization in that period never dropped to less than 500. Using this criterion, these were the dates and durations of the waves:
First wave → 26 March 2020–13 May 2020 (48 days)
Second wave → 7 November 2020–1 February 2021 (86 days)
Third wave → 2 February 2021–28 April 2021 (85 days)
Out-waves → other periods.
Hospital stay: A factor containing hospital name and categorized as long-term or regular hospitalization.
2.4. Ethical Considerations
Ethical approval for the study was obtained from the University of Bologna’s Ethical Committee (approval number 283066, 5 October 2021).
2.5. Statistical Analysis
2.5.1. Poisson and Hurdle Models
The generalized linear model (GLM) is a framework for regression models with a wide range of outcome variable types [
33]. A
p-value of ≤ 0.05 was deemed to be significant. The outcome variable, LoS, is a count type, and Poisson regression is the most common type used to analyze this kind of data. However, in practice, the Poisson assumptions are usually violated (there is overdispersion), and it was revealed that the Poisson model did not fit the data, so alternative models such as the negative binomial model were considered [
20,
24,
25]. Both the Poisson and NB models were implemented in R Studio with R version 4.0.4. [
34] by the glm function in the stats package and the glm.nb function in the MASS package.
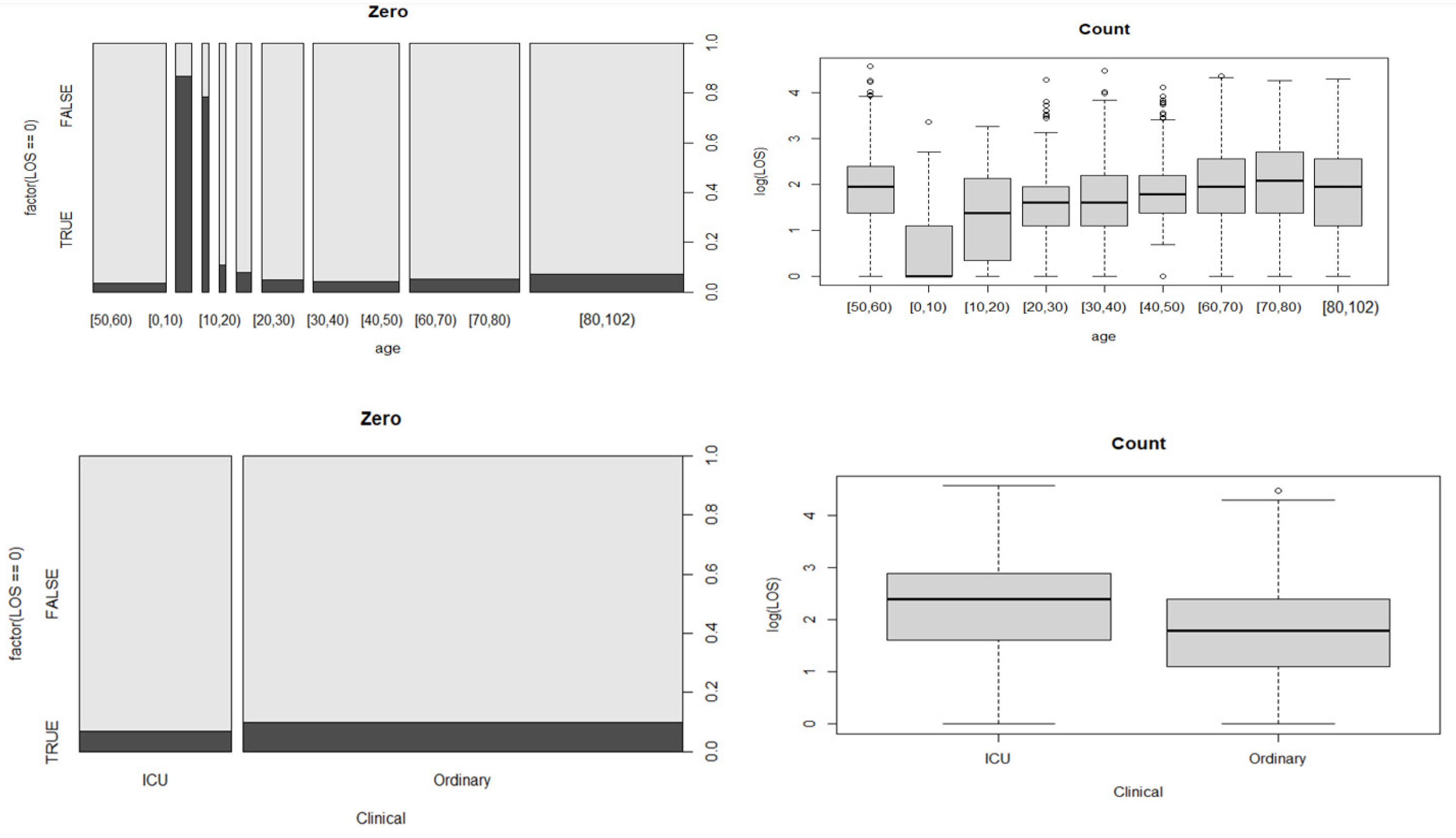
In addition to overdispersion, many count data have more zero observations. As a result, if the proportion of zeros in the response variable is not high, the Hurdle model would be a preferable option [
26].
This is a two-stage model:
It combines a count data model
(left-truncated at
and a zero Hurdle model
(right-censored at
):
where
is the value of the dependent variable,
is a vector denoting the predictor variable in the zero Hurdle model,
represents a vector denoting the predictor variable in the count data model,
is a vector of the coefficients related to
, and
denotes a vector of coefficients related to
.
is a probability density function of
, typically modeled with binary logistic regression, where all counts greater than 0 are given a value of 1 and 0 otherwise [
26]. In R Studio (R version 4.0.4), Hurdle count data models are fitted with the hurdle function of the pscl package [
35].
2.5.2. Model Selection and Comparison
We compared the performance of various count models to determine which one was the best based on the following criteria:
1. Akaike Information Criterion (AIC):
For non-nested models, the standard approach is to use information criteria such as the AIC [
36,
37] and the Bayesian Information Criteria (BIC) [
37]. The AIC estimates the quality of each model based on the formula:
, where
is the maximized likelihood function for the estimated model and
is the number of parameters in the model. Given a set of candidate models for the data, the preferred model has the minimum AIC value [
36].
2. Vuong test:
The purpose of the Vuong test [
38] is to compare two models (that are not nested) fitted to the same data by maximum likelihood, and it is based on a comparison of the predicted probabilities of two models that are not nested. Specifically, it tests the null hypothesis that the two models fit the data equally well. A large positive test statistic provides evidence of the superiority of Model 1 over Model 2, while a large negative test statistic is evidence of the superiority of Model 2 over Model 1, under the null hypothesis that the models are indistinguishable.
Let
be the predicted probabilities from Model 1, evaluated conditionally on the estimated MLEs. Let
be the corresponding probabilities from Model 2. The Vuong statistic is:
where
,
is the sample standard deviation of
, and
N is the sample size [
9]. We compared all the count models in R Studio with R version 4.0.4. using the pscl package [
35].
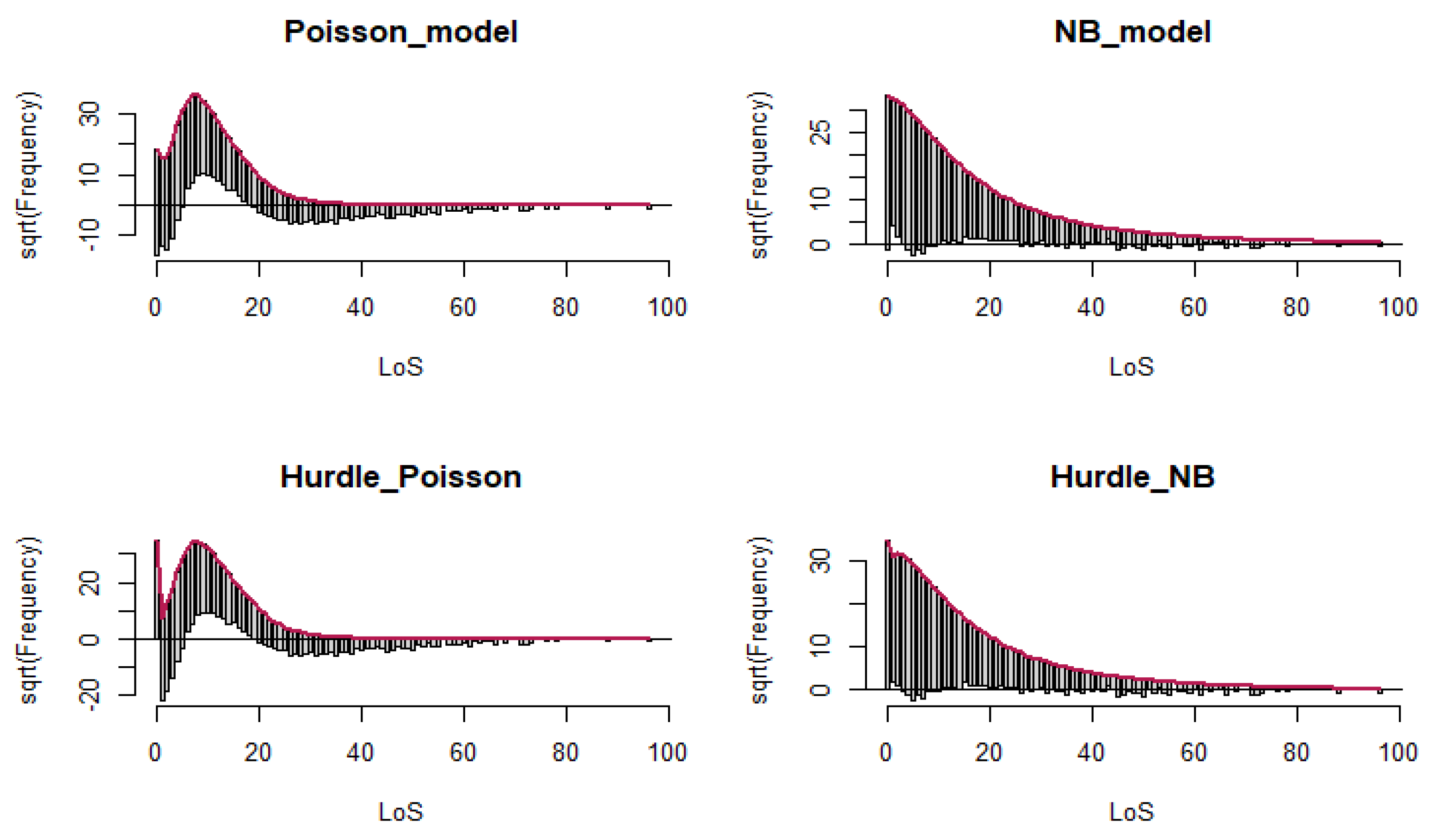
3. Rootograms:
Rootograms is a graphical approach used to assess the fit of a count regression model. It is useful for diagnosing and treating issues such as overdispersion and/or excess zeros in count data models [
27,
28]. We visualized the plot in R Studio with R version 4.0.4. using the countreg package [
27,
28].
2.5.3. Quantile Regression Model
A quantile regression model can be used to explore the relationships between the quantiles of the response distribution and the available covariates. By comparing such quantiles, we can obtain a more complete picture of the conditional distribution than we can with regression models that consider the mean. In addition, quantile regression allows researchers to explore a range of conditional quantile functions, thereby exposing various forms of conditional heterogeneity and controlling for unobserved individual characteristics.
With a Poisson distribution, quantile regression models were used to model the effects of covariates on the quantile values of the response variable, LoS. A linear quantile regression model was fitted to the log-transformed response. The modeled quantiles were 0.25, 0.5, 0.75, 0.8, 0.9, and 0.95. We used the quantreg package in R [
39].
4. Discussion
Researchers in the medical field are currently working to improve the quality and efficiency of health care systems and services in various ways, with LoS [
26] being one of the efficiency and quality indicators. To the best of our knowledge, no previous study has examined the LoS in Bologna, Italy, among COVID-19 patients, and this is the first study to consider analyzing LoS using the best count fit model and comparing several models. This study also aimed to explore the hospital admission risk factors associated with LoS and presents a relatively novel method for modeling LoS using predictors.
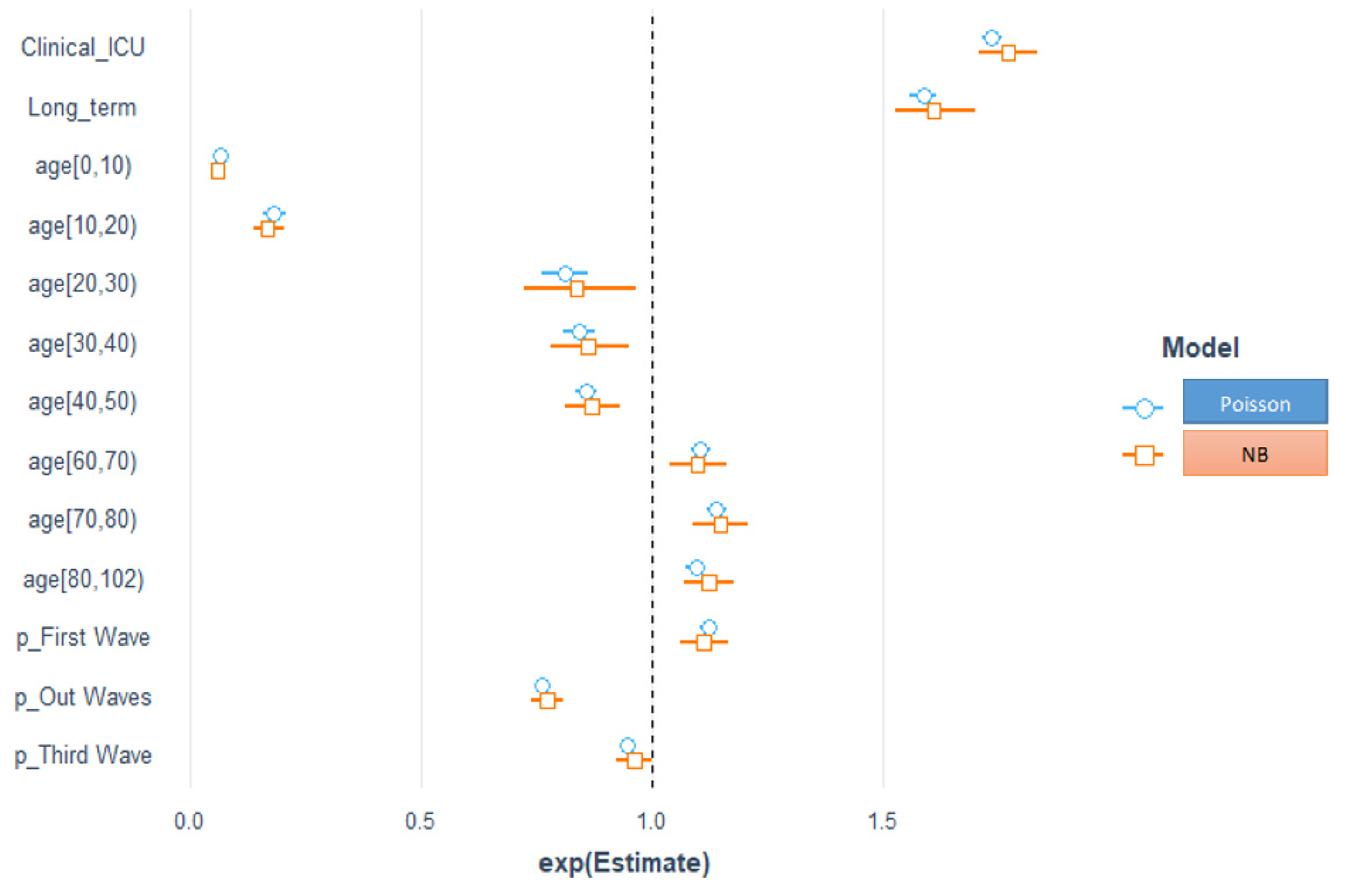
The necessity of carefully picking a model that effectively describes the observed count data is demonstrated by the fact that the different statistical techniques produce mixed findings. First, we used the Poisson, negative binomial, Hurdle–Poisson, and Hurdle–NB regression models to model the effects of covariates on LoS. Second, we used quantile regression to model the impact of the variables on the quantile values of the response variable LoS. Compared with Poisson regression, the fit of the NB regression better tolerated the overdispersion in the data [
20,
24,
25]. In addition to the overdispersion, the Hurdle models accounted for zero LoS more thoroughly [
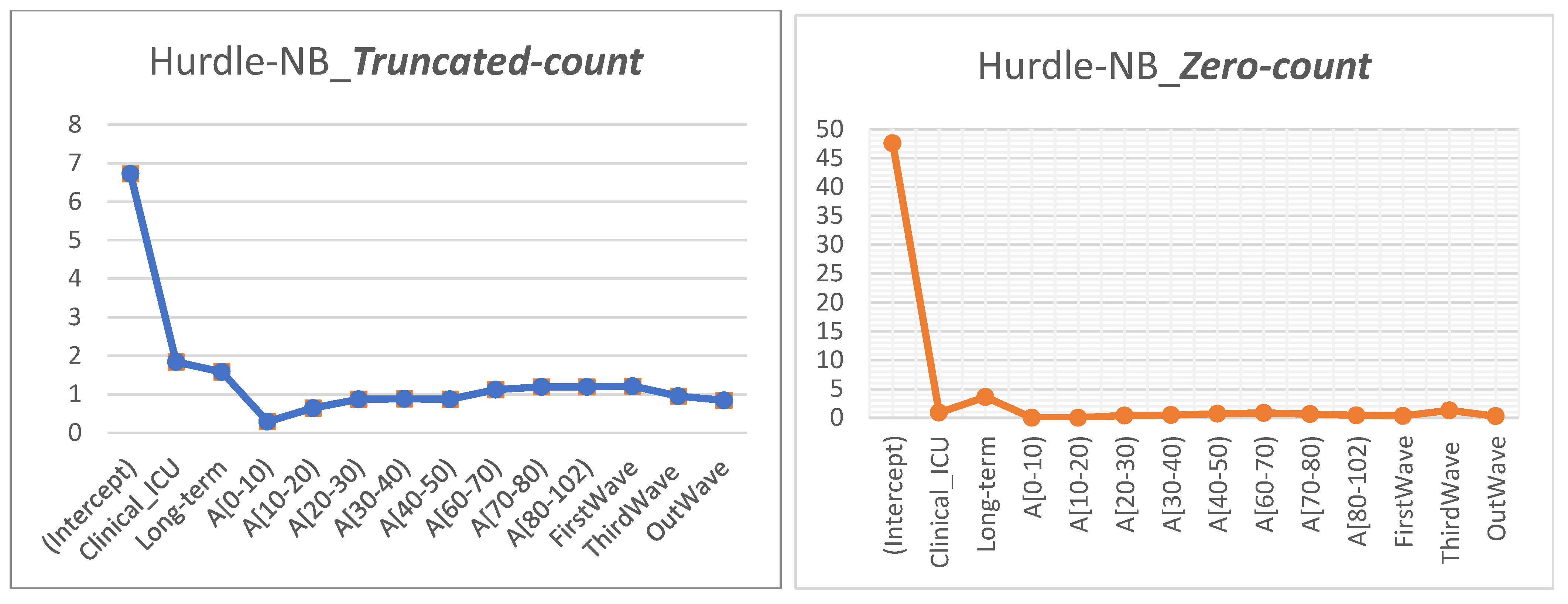
26]. The Hurdle–NB model was finally chosen on the basis of three criteria, including the AIC, the Vuong test, and Rootograms to understand the impacts of the predictors on the average LoS.
In our analysis, the median LoS was 6 days, which is comparable with the value reported in a similar study in Europe, USA, and the UK, but shorter than one in a study on China [
12]. In this systematic review, the median hospital LoS ranged from 4 to 53 days within China (45 studies surveyed), and from 4 to 21 days outside China (eight studies surveyed). Similarly, a shorter LoS was also documented by the ISARIC (International Severe Acute Respiratory and Emerging Infections Consortium) report [
40]. This report (which included data from 25 countries) described a median and IQR LoS of 4 and 1–9 days, respectively, which are substantially lower than in our study. Differences in LoS duration between nations can be explained by the different policies or strategies applied to control COVID-19 infection, or by the different population samples involved in the studies. Knowing the LoS or other adverse events in advance can help te health care systems organize the allocation of limited resources more efficiently.
Our results in Bologna are entirely consistent with those from studies which observed that older age (≥60 years) was associated with prolonged LoS [
41,
42,
43]. Patients with ICU admissions had a longer LoS than those with only ordinary hospitalization, as these patients might need additional treatment or time when their disease reaches severe stages and they need more complex treatments. Staying in a long-term hospital was another contributing factor for a LoS longer than that in regular hospitals. This might be explained by the higher percentage of surgical operations and transfer rates, as well as restricted antibiotic use compared with other patients.
Usually, public hospitals manage acute patients’ LoS efficiently [
44] in Italy. However, due to the new variants of the virus that causes COVID-19, the ability to assess or predict LoS will be more and more crucial in the future as a higher LoS is also associated with higher costs [
45] and reduced capacity for other sanitary needs [
46]. From this perspective, it is worth noting that we found that the LoS in Bologna was higher during the first wave—when the government proclaimed a state of emergency in response to an increase in the number of infection cases—and peaked around April 2021. However, during the third wave and out-wave, there was a drop, indicating that the chosen policies and strategies of the government and the health department, together with better clinical knowledge of the disease, have had a positive impact on the management of the patients.
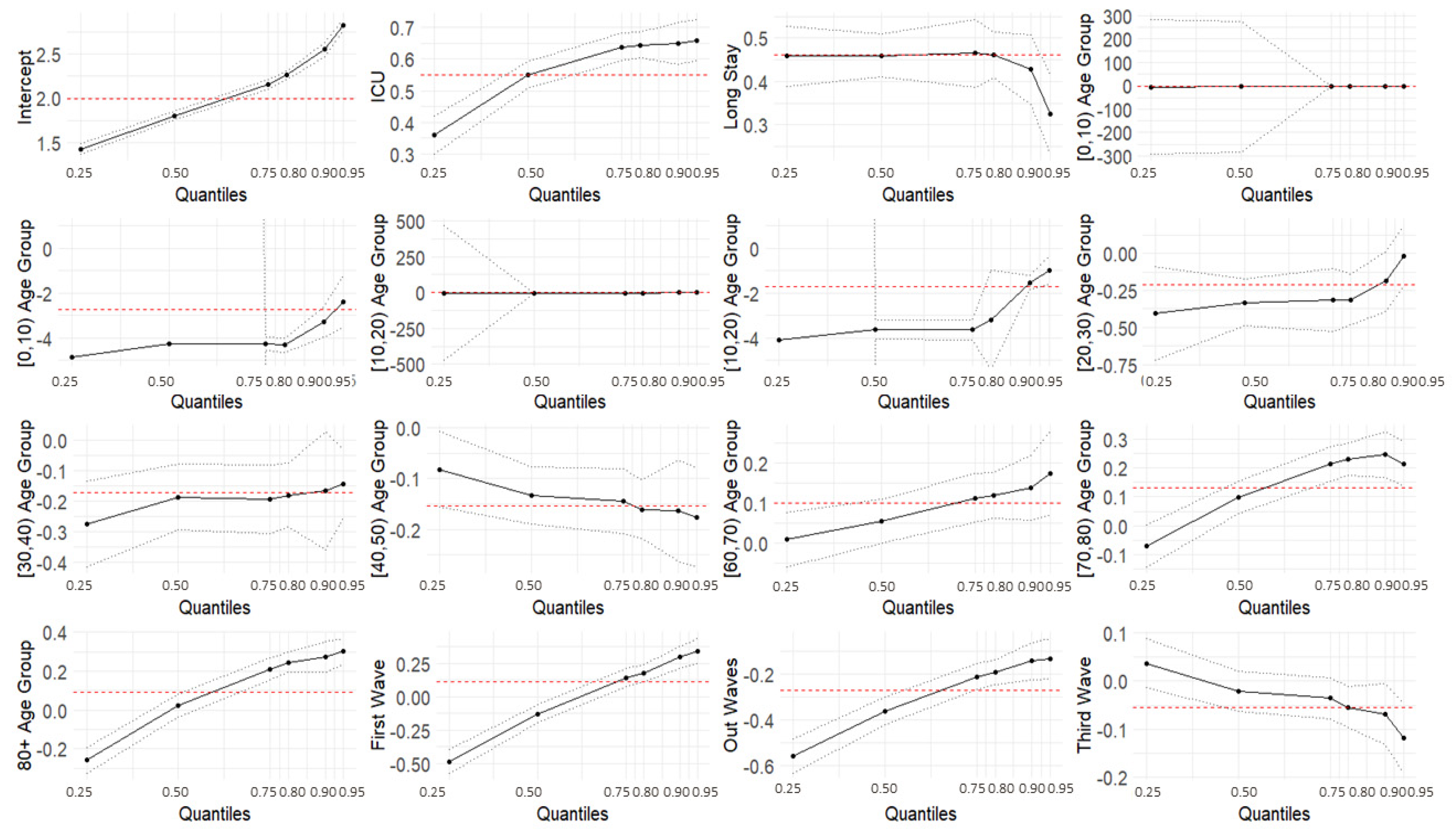
We also used quantile regression to model the effects of the covariates on the quantile values of the response variable LoS, using a Poisson distribution, and to explore a range of conditional quantile functions, thereby exposing various forms of conditional heterogeneity and controlling for unobserved individual characteristics. The results from the quantile regression showed that the covariates related to the ICU setting, long-term hospitals, age groups, the first wave, and the out-waves were statistically significant for all the modeled quantiles. Specifically, for the ICU setting, the coefficients were higher for higher quantile values than ordinary hospitalization, meaning a longer LoS, and the effect was more pronounced for the higher quantiles. All the age groups, except for the [40, 50) group, showed an increasing trend with the quantiles. The wave also played a role: during the first wave, short LoSs were shorter (negative coefficients) and long LoSs were longer (positive coefficients) compared with those of the second wave. LoSs recorded in the out-wave period were shorter for all the quantiles (negative coefficients), and for the third wave, longer LoSs shortened (negative coefficients). The coefficients for long-term hospitalization became closer to zero as the quantile values increased, representing a less marked difference with respect to regular hospitalization.
The quantile regression models provided a more comprehensive overview of the effect of the covariates on a given phenomenon. As appears evident from this work, the same covariate can have a non-constant effect on different quantiles. This is valuable information for better modeling the LoS, which would not be controlled by simply evaluating the effect of the covariates on the mean values.
One limitation of our study is the absence of information on additional demographic and socio-economic variables, clinical characteristics, medical conditions, and laboratory tests for the patients, which might be among the most important factors that tend to increase the LoS. However, we have now started to analyze an extended, non-aggregated version of this dataset including all these variables.
COVID-19 cases are complex and still increasing worldwide, and it is difficult to predict when it will stop completely. Countries should plan and prepare for the worst-case scenarios, such as when different variants come into play (as in the case of Omicron at this time). In Italy, we have now entered into a fourth wave, so the wise use of limited health care resources is one of the most important priorities. Studies such as the present one might help health policymakers and managers to better plan the logistics of hospital settings, define priorities, and carry out a more accurate cost analysis. In addition, the information we have obtained and the method we used might serve as a tool or as a reference in the case of similar epidemics in the future.