A Scoping Review of Drug Epidemic Models
Abstract
:1. Introduction
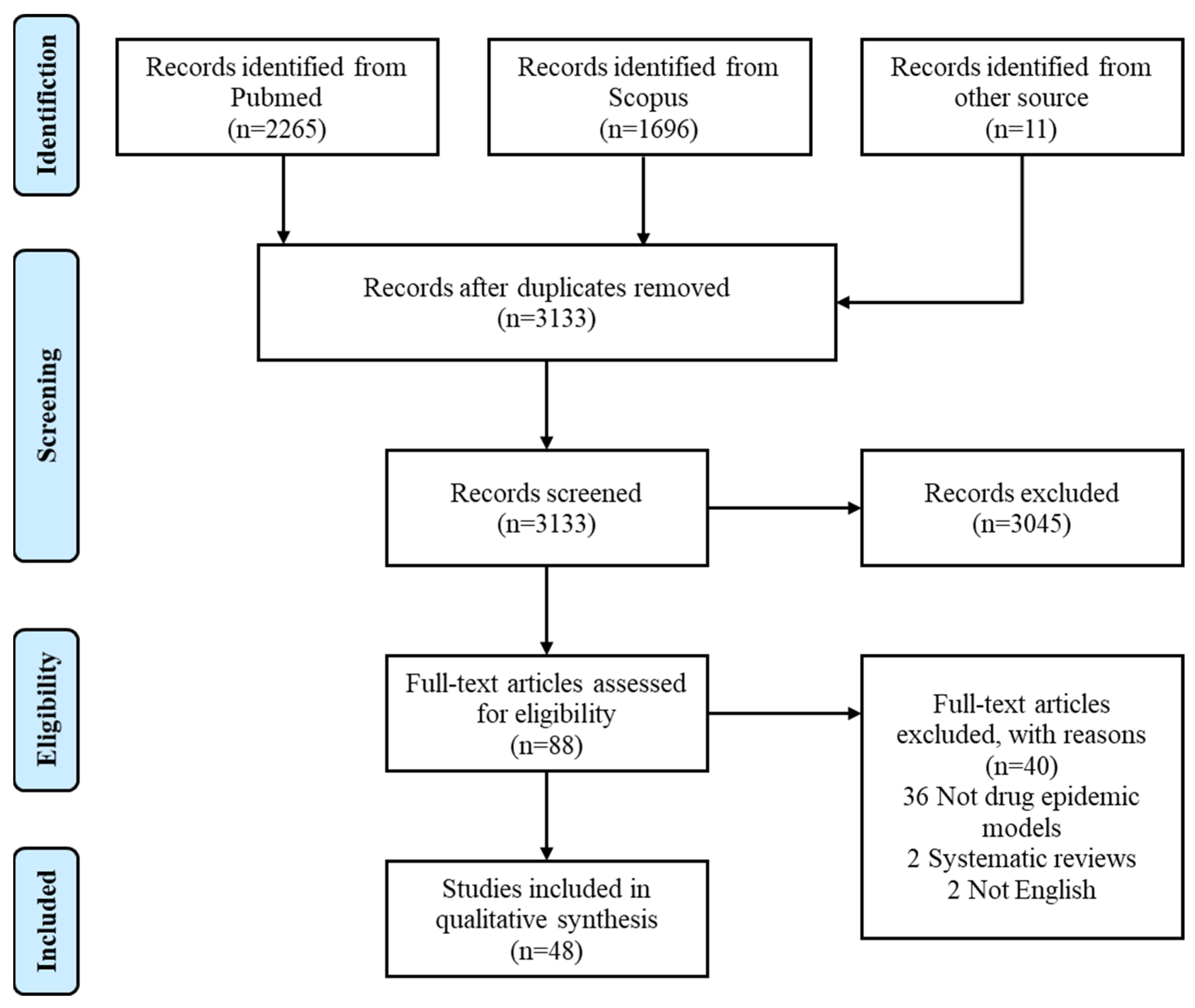
2. Methods
2.1. Search Strategy
- (“Heroin” OR “Synthetic drug” OR “Methamphetamine”) AND
- (“Epidemic model” OR “Transmission model”)
2.2. Article Selection
- Drug epidemic modelling studies based on compartmental dynamic models;
- Models based on mathematical tools including ordinary differential equations (ODE), partial differential equations (PDE), delayed differential equations (DDE), stochastic differential equations (SDE) and difference equations (DE) were all considered eligible;
- Models simply investigating HIV epidemic among populations including drug users, without any focus on drug epidemic, were excluded;
- Systematic reviews and articles not in English were excluded.
2.3. Data Extraction
3. Results
3.1. Characteristics of Studies
3.2. Early Attempts of Drug Epidemic Model
3.3. The White–Comiskey Model
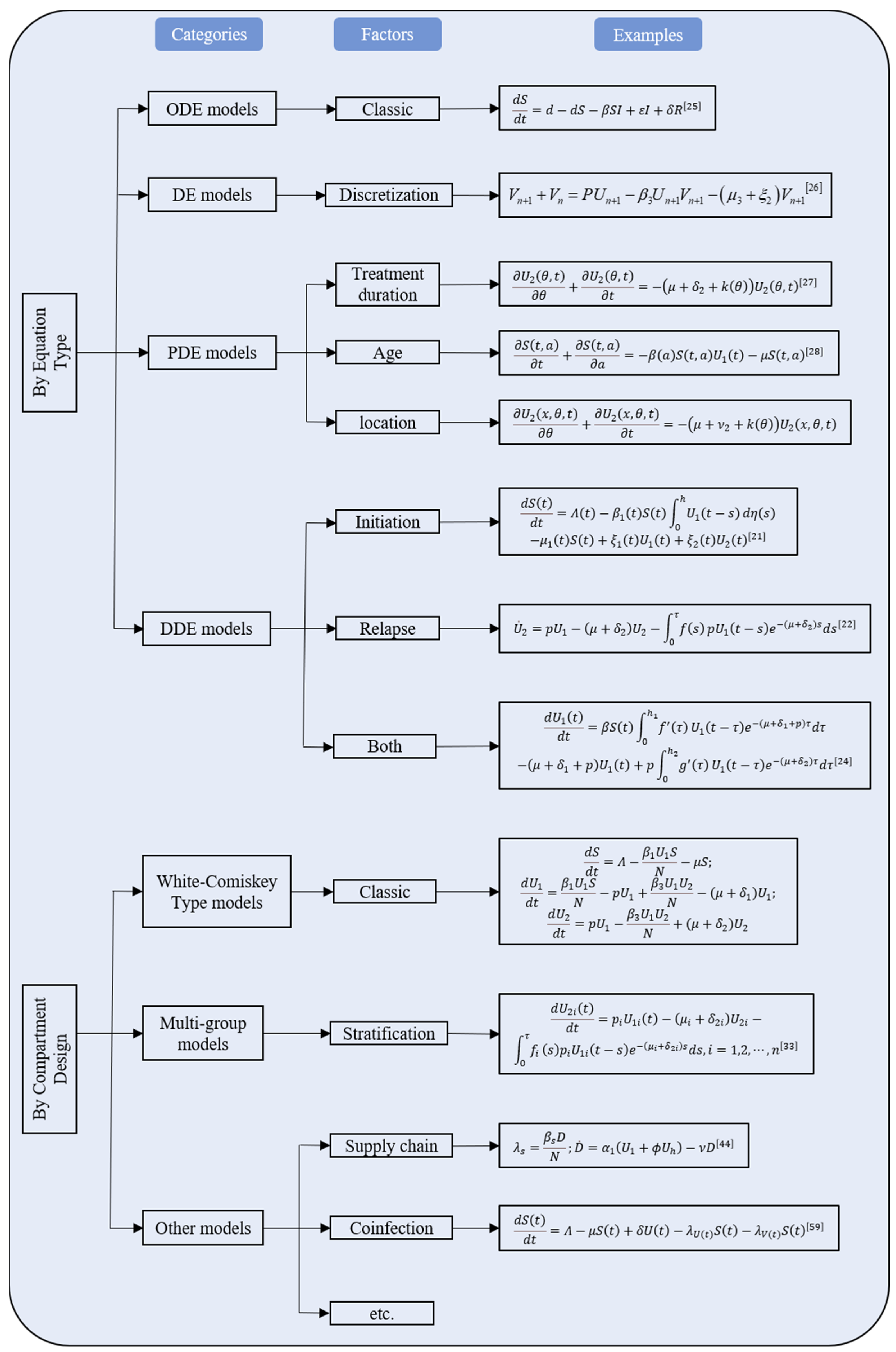
3.4. Modifications of the White–Comiskey Model
3.4.1. Models Based on DDE
3.4.2. Models Based on ODE or DE
3.4.3. Models Based on PDE
3.4.4. Multi–Group Models
3.4.5. Models Based on SDE
3.5. South Africa’s Methamphetamine Models
3.6. Other Drug Epidemic Models
3.6.1. Heroin Epidemic Models
3.6.2. Synthetic Drug Epidemic Model
3.6.3. Other Modeling Attempts
4. Discussion
4.1. Overall Features
4.2. Utilization of Mathematical Tools
4.3. Knowledge Gaps
4.4. Perspectives
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- UNODC. World Drug Report 2019; United Nations Publication: New York, NY, USA, 2019; Available online: https://wdr.unodc.org/wdr2019/prelaunch/WDR19_Booklet_1_EXECUTIVE_SUMMARY.pdf (accessed on 9 December 2021).
- UNODC. World Drug Report 2010; United Nations Publication: New York, NY, USA, 2010; Available online: https://www.unodc.org/documents/wdr/WDR_2010/World_Drug_Report_2010_lo-res.pdf (accessed on 9 December 2021).
- Greene, M.H. An Epidemiologic Assessment of Heroin Use. Am. J. Public Health 1974, 64 (Suppl. S12), 1–10. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jacobs, P.E. Epidemiology Abuse: Epidemiological and Psychosocial Models of Drug Abuse. J. Drug Educ. 1976, 6, 259–271. [Google Scholar] [CrossRef]
- Mackintosh, D.R.; Stewart, G.T. A mathematical model of a heroin epidemic: Implications for control policies. J. Epidemiol. Community Health 1979, 33, 299. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kermack, W.O.; McKendrick, A.G. Contributions to the mathematical theory of epidemics IV. Analysis of experimental epidemics of the virus disease mouse ectromelia. J. Hyg. 1937, 37, 172–187. [Google Scholar] [CrossRef] [Green Version]
- Rossi, C. Operational models for epidemics of problematic drug use: The Mover–Stayer approach to heterogeneity. Socio-Econ. Plan. Sci. 2004, 38, 73–90. [Google Scholar] [CrossRef] [Green Version]
- White, E.; Comiskey, C. Heroin epidemics, treatment and ODE modelling. Math. Biosci. 2007, 208, 312–324. [Google Scholar] [CrossRef]
- Ma, Z.E.; Zhou, Y.C.; Wang, W.D. Mathematical Models and Dynamics of Infectious Disease, 1st ed.; China Science Press: Beijing, China, 2004. [Google Scholar]
- Sharareh, N.; Sabounchi, S.S.; McFarland, M.; Hess, R. Evidence of Modeling Impact in Development of Policies for Controlling the Opioid Epidemic and Improving Public Health: A Scoping Review. Subst. Abus. Res. Treat. 2019, 13, 1178221819866211. [Google Scholar] [CrossRef] [Green Version]
- Arksey, H.; O’Malley, L. Scoping studies: Towards a methodological framework. Int. J. Soc. Res. Methodol. 2005, 8, 19–32. [Google Scholar] [CrossRef] [Green Version]
- Moher, D.; Shamseer, L.; Clarke, M.; Ghersi, D.; Liberati, A.; Petticrew, M.; Shekelle, P.; Stewart, L.A. Preferred reporting items for systematic review and meta-analysis protocols (PRISMA-P) 2015 statement. Syst. Rev. 2015, 4, 1. [Google Scholar] [CrossRef] [Green Version]
- Hoppensteadt, F.C.; Murray, J.D. Threshold analysis of a drug use epidemic model. Math. Biosci. 1981, 53, 79–87. [Google Scholar] [CrossRef]
- Knolle, H. Incidence and prevalence of illegal drug use in Switzerland in the 1980s and early 1990s: An analytical study. Subst. Use Misuse 1997, 32, 1349–1368. [Google Scholar] [CrossRef] [PubMed]
- Almeder, C.; Caulkins, J.P.; Feichtinger, G.; Tragler, G. An age-structured single-state drug initiation model—Cycles of drug epidemics and optimal prevention programs. Socio-Econ. Plan. Sci. 2004, 38, 91–109. [Google Scholar] [CrossRef]
- Caulkins, J.P.; Dietze, P.; Ritter, A. Dynamic compartmental model of trends in Australian drug use. Health Care Manag. Sci. 2007, 10, 151–162. [Google Scholar] [CrossRef] [PubMed]
- Caulkins, J.P.; Tragler, G.; Wallner, D. Optimal timing of use reduction vs. harm reduction in a drug epidemic model. Int. J. Drug Policy 2009, 20, 480–487. [Google Scholar] [CrossRef]
- Caulkins, J.P.; Feichtinger, G.; Tragler, G.; Wallner, D. When in a drug epidemic should the policy objective switch from use reduction to harm reduction? Eur. J. Oper. Res. 2010, 201, 308–318. [Google Scholar] [CrossRef]
- Mulone, G.; Straughan, B. A note on heroin epidemics. Math. Biosci. 2009, 218, 138–141. [Google Scholar] [CrossRef]
- Wang, X.Y.; Yang, J.Y.; Li, X.Z. Dynamics of a Heroin Epidemic Model with Very Population. Appl. Math. 2011, 2, 732–738. [Google Scholar] [CrossRef] [Green Version]
- Samanta, G.P. Dynamic behaviour for a nonautonomous heroin epidemic model with time delay. J. Appl. Math. Comp. 2011, 35, 161–178. [Google Scholar] [CrossRef]
- Liu, J.L.; Zhang, T.L. Global behaviour of a heroin epidemic model with distributed delays. Appl. Math. Lett. 2011, 24, 1685–1692. [Google Scholar] [CrossRef] [Green Version]
- Huang, G.; Liu, A.P. A note on global stability for a heroin epidemic model with distributed delay. Appl. Math. Lett. 2013, 26, 687–691. [Google Scholar] [CrossRef]
- Fang, B.; Li, X.Z.; Martcheva, M.; Cai, L. Global stability for a heroin model with two distributed delays. Discret. Contin. Dyn. Syst. B 2014, 19, 715–733. [Google Scholar] [CrossRef]
- Muroya, Y.; Li, H.X.; Kuniya, T. Complete global analysis of an SIRS epidemic model with graded cure and incomplete recovery rates. J. Math. Anal. Appl. 2014, 410, 719–732. [Google Scholar] [CrossRef]
- Abdurahman, X.; Zhang, L.; Teng, Z.D. Global dynamics of a discretized heroin epidemic model with time delay. Abstr. Appl. Anal. 2014, 2014, 742385. [Google Scholar] [CrossRef] [Green Version]
- Fang, B.; Li, X.Z.; Martcheva, M.; Cai, L. Global asymptotic properties of a heroin epidemic model with treat-age. Appl. Math. Comput. 2015, 263, 315–331. [Google Scholar] [CrossRef]
- Fang, B.; Li, X.Z.; Martcheva, M.; Cai, L. Global stability for a heroin model with age-dependent susceptibility. J. Syst. Sci. Complex. 2015, 28, 1243–1257. [Google Scholar] [CrossRef]
- Yang, J.Y.; Li, X.X.; Zhang, F.Q. Global dynamics of a heroin epidemic model with age structure and nonlinear incidence. Int. J. Biomath. 2016, 9, 1650033. [Google Scholar] [CrossRef]
- Djilali, S.; Touaoula, T.M.; Miri, S.E.H. A Heroin Epidemic Model: Very General Non Linear Incidence, Treat-Age, and Global Stability. Acta Appl. Math. 2017, 152, 171–194. [Google Scholar] [CrossRef]
- Liu, L.L.; Liu, X.N. Mathematical Analysis for an Age-Structured Heroin Epidemic Model. Acta Appl. Math. 2019, 164, 193–217. [Google Scholar] [CrossRef]
- Duan, X.C.; Li, X.Z.; Martcheva, M. Qualitative analysis on a diffusive age-structured heroin transmission model. Nonlinear Anal. Real World Appl. 2020, 54, 103105. [Google Scholar] [CrossRef]
- Liu, X.N.; Wang, J.L. Epidemic dynamics on a delayed multi-group heroin epidemic model with nonlinear incidence rate. J. Nonlinear Sci. Appl. 2016, 9, 2149–2160. [Google Scholar] [CrossRef]
- Yang, J.Y.; Wang, L.H.; Li, X.X.; Zhang, F.Q. Global dynamical analysis of a heroin epidemic model on complex networks. J. Appl. Anal. Comput. 2016, 6, 429–442. [Google Scholar]
- Liu, L.L.; Liu, X.N.; Wang, J.L. Threshold dynamics of a delayed multi-group heroin epidemic model in heterogeneous populations. Discrete Contin. Dyn. Syst. Ser. B 2016, 21, 2615–2630. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.L.; Wang, J.; Kuniya, T. Analysis of an age-structured multi-group heroin epidemic model. Appl. Math. Comput. 2019, 347, 78–100. [Google Scholar] [CrossRef]
- Li, G.J.; Yang, Q.G.; Wei, Y.C. Dynamics of stochastic heroin epidemic model with lévy jumps. J. Appl. Anal. Comput. 2018, 8, 998–1010. [Google Scholar]
- Liu, S.T.; Zhang, L.; Xing, Y.F. Dynamics of a stochastic heroin epidemic model. J. Comput. Appl. Math. 2019, 351, 260–269. [Google Scholar] [CrossRef]
- Liu, S.T.; Zhang, L.; Zhang, X.B.; Li, A. Dynamics of a stochastic heroin epidemic model with bilinear incidence and varying population size. Int. J. Biomath. 2019, 12, 1950005. [Google Scholar] [CrossRef]
- Wei, Y.C.; Yang, Q.G.; Li, G.J. Dynamics of the stochastically perturbed Heroin epidemic model under non-degenerate noises. Phys. A Stat. Mech. Appl. 2019, 526, 120914. [Google Scholar] [CrossRef]
- Rafiq, M.; Raza, A.; Iqbal, M.U.; Butt, Z.; Azam, S. Numerical treatment of stochastic heroin epidemic model. Adv. Differ. Equ. 2019, 2019, 434. [Google Scholar] [CrossRef] [Green Version]
- Nyabadza, F.; Hove-Musekwa, S.D. From heroin epidemics to methamphetamine epidemics: Modelling substance abuse in a South African province. Math. Biosci. 2010, 225, 132–140. [Google Scholar] [CrossRef]
- Nyabadza, F.; Njagarah, J.B.; Smith, R.J. Modelling the dynamics of crystal meth (‘tik’) abuse in the presence of drug-supply chains in South Africa. Bull. Math. Biol. 2013, 75, 24–48. [Google Scholar] [CrossRef]
- Kalula, A.S.; Nyabadza, F. A theoretical model for substance abuse in the presence of treatment. S. Afr. J. Sci. 2012, 108, 1–2. [Google Scholar]
- Mushanyu, J.; Nyabadza, F.; Stewart, A.G. Modelling the trends of inpatient and outpatient rehabilitation for methamphetamine in the Western Cape province of South Africa. BMC Res. Notes 2015, 8, 797. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mushanyu, J.; Nyabadza, F.; Muchatibaya, G. Modelling Drug Abuse Epidemics in the Presence of Limited Rehabilitation Capacity. Bull. Math. Biol. 2016, 78, 2364–2389. [Google Scholar] [CrossRef] [PubMed]
- Mushanyu, J.; Nyabadza, F.; Muchatibaya, G.; Stewart, A.G.R. On the Role of Imitation on Adolescence Methamphetamine Abuse Dynamics. Acta Biotheor. 2017, 65, 37–61. [Google Scholar] [CrossRef] [PubMed]
- Wangari, I.M.; Stone, L. Analysis of a Heroin Epidemic Model with Saturated Treatment Function. J. Appl. Math. 2017, 2017, 1953036. [Google Scholar] [CrossRef] [Green Version]
- Duan, X.C.; Li, X.Z.; Martcheva, M. Dynamics of an age-structured heroin transmission model with vaccination and treatment. Math. Biosci. Eng. 2019, 16, 397–420. [Google Scholar] [CrossRef]
- Memarbashi, R.; Pourhossieni, M. Global dynamic of a heroin epidemic model. UPB Sci. Bull. Ser. A 2019, 81, 115–126. [Google Scholar]
- Abdurahman, X.; Teng, Z.; Zhang, L. Global dynamics in a heroin epidemic model with different conscious stages and two distributed delays. Int. J. Biomath. 2019, 12, 1950038. [Google Scholar] [CrossRef]
- Ma, M.J.; Liu, S.Y.; Xiang, H.; Li, J. Dynamics of synthetic drugs transmission model with psychological addicts and general incidence rate. Phys. A Stat. Mech. Appl. 2018, 491, 641–649. [Google Scholar] [CrossRef]
- Naowarat, S.; Kumat, N. The Role of Family on the Transmission Model of Methamphetamine. J. Phys. Conf. Ser. 2018, 1039, 012036. [Google Scholar] [CrossRef]
- Saha, S.; Samanta, G.P. Synthetic drugs transmission: Stability analysis and optimal control. Lett. Biomath. 2019, 6, 1–31. [Google Scholar] [CrossRef]
- Liu, P.Y.; Zhang, L.; Xing, Y.F. Modelling and stability of a synthetic drugs transmission model with relapse and treatment. J. Appl. Math. Comp. 2019, 60, 465–484. [Google Scholar] [CrossRef]
- Zhang, Z.Z.; Yang, F.F.; Xia, W.J. Hopf Bifurcation Analysis of a Synthetic Drug Transmission Model with Time Delays. Complexity 2019, 2019, 3492589. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Ma, M.J. The analysis of a drug transmission model with family education and public health education. Infect. Dis. Model. 2018, 3, 74–84. [Google Scholar] [CrossRef]
- Su, S.; Fairley, C.K.; Mao, L.M.; Nicholas, A.M.; Jing, J.; Cheng, F.; Zhang, L. Estimates of the national trend of drugs use during 2000–2030 in China: A population-based mathematical model. Addict. Behav. 2019, 93, 65–71. [Google Scholar] [CrossRef]
- Duan, X.C.; Li, X.Z.; Martcheva, M. Coinfection dynamics of heroin transmission and HIV infection in a single population. J. Biol. Dyn. 2020, 14, 116–142. [Google Scholar] [CrossRef] [Green Version]
- Arriola, L.; Hyman, J. Lecture Notes, Forward and Adjoint Sensitivity Analysis: With Applications in Dynamical Systems, Linear Algebra and Optimisation; Mathematical and Theoretical Biology Institute: Tempe, AZ, USA, 2005. [Google Scholar]
- Jia, Z.; Liu, Z.; Chu, P.; Jennifer, M.M.; Cong, M.; Shi, J.; Lu, L. Tracking the evolution of drug abuse in China, 2003–2010: A retrospective, self-controlled study. Addiction 2015, 110 (Suppl. S1), 4–10. [Google Scholar] [CrossRef] [Green Version]
- Franken, I.H.A. Drug craving and addiction: Integrating psychological and neuropsychopharmacological approaches. Prog. Neuro-Psychopharmacol. Biol. Psychiatry 2003, 27, 563–579. [Google Scholar] [CrossRef]
- Volkow, N.D.; Li, T.-K. Drug addiction: The neurobiology of behaviour gone awry. Nat. Rev. Neurosci. 2004, 5, 963–970. [Google Scholar] [CrossRef]
- Baler, R.D.; Volkow, N.D. Drug addiction: The neurobiology of disrupted self-control. Trends Mol. Med. 2006, 12, 559–566. [Google Scholar] [CrossRef]
- Hyman, S.E.; Malenka, R.C.; Nestler, E.J. Neural Mechanisms of Addiction: The Role of Reward-Related Learning and Memory. Annu. Rev. Neurosci. 2006, 29, 565–598. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Everitt, B.J. Neural and psychological mechanisms underlying compulsive drug seeking habits and drug memories—indications for novel treatments of addiction. Eur. J. Neurosci. 2014, 40, 2163–2182. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Volkow Nora, D.; Morales, M. The Brain on Drugs: From Reward to Addiction. Cell 2015, 162, 712–725. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shen, X.Y.; Orson, F.M.; Kosten, T.R. Vaccines Against Drug Abuse. Clin. Pharmacol. Ther. 2012, 91, 60–70. [Google Scholar] [CrossRef] [PubMed]
- Ozgen, M.H.; Blume, S. The continuing search for an addiction vaccine. Vaccine 2019, 37, 5485–5490. [Google Scholar] [CrossRef] [PubMed]
- Pravetoni, M.; Comer, S.D. Development of vaccines to treat opioid use disorders and reduce incidence of overdose. Neuropharmacology 2019, 158, 107662. [Google Scholar] [CrossRef]
- Anton, B.; Leff, P. A novel bivalent morphine/heroin vaccine that prevents relapse to heroin addiction in rodents. Vaccine 2006, 24, 3232–3240. [Google Scholar] [CrossRef]
- Gentry, W.B.; Rüedi-Bettschen, D.; Owens, S.M. Development of active and passive human vaccines to treat methamphetamine addiction. Hum. Vaccines 2009, 5, 206–213. [Google Scholar] [CrossRef] [Green Version]
- Zgierska, A.; Rabago, D.; Chawla, N.; Kushner, K.; Koehler, R.; Marlatt, A. Mindfulness Meditation for Substance Use Disorders: A Systematic Review. Subst. Abus. 2009, 30, 266–294. [Google Scholar] [CrossRef] [Green Version]
- Sofuoglu, M.; DeVito, E.E.; Waters, A.J.; Carroll, K.M. Cognitive enhancement as a treatment for drug addictions. Neuropharmacology 2013, 64, 452–463. [Google Scholar] [CrossRef] [Green Version]
- Noble, A.; Best, D.; Man, L.-H.; Gossop, M.; Strang, J. Self-detoxification attempts among methadone maintenance patients: What methods and what success? Addict. Behav. 2002, 27, 575–584. [Google Scholar] [CrossRef]
- Day, E.; Eggen, J.; Ison, J.; Copello, A.; Fazil, Q. Ethnicity and attempts at self-detoxification from opioid drugs. Drugs Educ. Prev. Policy 2006, 13, 93–103. [Google Scholar] [CrossRef]
- Ison, J.; Day, E.; Fisher, K.; Pratt, M.; Hull, M.; Copello, A. Self-detoxification from opioid drugs. J. Subst. Use 2006, 11, 81–88. [Google Scholar] [CrossRef]
- Kenney, S.R.; Bailey, G.L.; Anderson, B.J.; Stein, M.D. Heroin refusal self-efficacy and preference for medication-assisted treatment after inpatient detoxification. Addict. Behav. 2017, 73, 124–128. [Google Scholar] [CrossRef]
- Blyuss, K.B.; Kyrychko, Y.N. On a basic model of a two-disease epidemic. Appl. Math. Comput. 2005, 160, 177–187. [Google Scholar] [CrossRef]
- Abu-Raddad, L.J.; Patnaik, P.; Kublin, J.G. Dual infection with HIV and malaria fuels the spread of both diseases in Sub-Saharan Africa. Science 2006, 314, 1603–1606. [Google Scholar] [CrossRef]
- Sharomi, O.; Podder, C.N.; Gumel, A.B.; Song, B. Mathematical analysis of the transmission dynamics of HIV/TB coinfection in the presence of treatment. Math. Biosci. Eng. 2008, 5, 145–174. [Google Scholar]
- Roeger, L.I.W.; Feng, Z.; Castillo-Chavez, C. Modeling TB and HIV co-infections. Math. Biosci. Eng. 2009, 6, 815–837. [Google Scholar]
- Keeling, M.J.; Rohani, P. Modeling Infectious Diseases in Humans and Animals; Princeton University Press: Princeton, NJ, USA, 2011; pp. 1–368. [Google Scholar]
- Lawi, G.O.; Mugisha, J.Y.T.; Omolo-Ongati, N. Mathematical model for malaria and meningitis co-infection among children. Appl. Math. Sci. 2011, 5, 2337–2359. [Google Scholar]
- Mushayabasa, S.; Tchuenche, J.M.; Bhunu, C.P.; Ngarakana-Gwasira, E. Modeling gonorrhea and HIV co-interaction. Biosystems 2011, 103, 27–37. [Google Scholar] [CrossRef]
- Alizon, S. Co-infection and super-infection models in evolutionary epidemiology. Interface Focus 2013, 3, 20130031. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mallela, A.; Lenhart, S.; Vaidya, N.K. HIV–TB co-infection treatment: Modeling and optimal control theory perspectives. J. Comput. Appl. Math. 2016, 307, 143–161. [Google Scholar] [CrossRef] [Green Version]
- Golichenko, M.; Chu, S.K.H. Human rights in patient care: Drug treatment and punishment in Russia. Public Health Rev. 2018, 39, 12. [Google Scholar] [CrossRef] [PubMed]
- Feng, X.M.; Teng, Z.D.; Zhang, F.Q. Global dynamics of a general class of multi-group epidemic models with latency and relapse. Math. Biosci. Eng. 2015, 12, 99–115. [Google Scholar] [CrossRef] [PubMed]
- Li, M.-T.; Jin, Z.; Sun, G.-Q.; Zhang, J. Modeling direct and indirect disease transmission using multi-group model. J. Math. Anal. Appl. 2017, 446, 1292–1309. [Google Scholar] [CrossRef]
| Study | Number of Compartment a | Equation Type b | Incidence Function | Intervention | Drug Type | Scenario |
|---|---|---|---|---|---|---|
| Hoppensteadt 1981 | 2 | PDE | bilinear | parameter | - | - |
| Knolle 1997 | 2 | ODE | linear | - | multiple | Switzerland, 1979–1995 |
| Almeder 2004 | 2 | PDE | complex | parameter | - | - |
| Caulkins 2007 | 5 | DE | linear | parameter | illicit drug | Australia, 1960–2010 |
| Caulkins 2009 | 2 | ODE | complex | - | - | Australian IDU and US cocaine |
| Caulkins 2010 | 2 | ODE | complex | - | - | Australian IDU and US cocaine |
| White 2007 | 3 | ODE | standard | both | heroin | - |
| Mulone 2009 | 3 | ODE | standard | compartment | heroin | - |
| Nyabadza 2010 | 5 | ODE | complex | both | methamphetamine | South Africa, 1996–2008 |
| Samanta 2011 | 3 | DDE | bilinear | both | heroin | - |
| Wang 2011 | 3 | ODE | standard | compartment | heroin | - |
| Liu 2011 | 3 | DDE | bilinear | both | heroin | - |
| Kalula 2012 | 6 | ODE | complex | both | methamphetamine | South Africa, 1996–2009 |
| Huang 2013 | 3 | DDE | bilinear | compartment | heroin | - |
| Nyabadza 2013 | 6 | ODE | complex | both | methamphetamine | South Africa, 1997–2010 |
| Muroya 2014 | 3 | ODE | bilinear | compartment | light drug | - |
| Abdurahman 2014 | 3 | DE | bilinear | both | heroin | - |
| Fang 2014 | 3 | DDE | bilinear | both | heroin | - |
| Fang 2015 a | 3 | PDE | bilinear | both | heroin | - |
| Fang 2015 b | 3 | PDE | bilinear | both | heroin | - |
| Mushanyu 2015 | 4 | ODE | complex | compartment | methamphetamine | South Africa, 1999–2013 |
| Liu 2016 | 3n | DDE | complex | compartment | heroin | - |
| Yang 2016 | 3n | ODE | complex | both | heroin | - |
| Yang 2016 | 3 | PDE | complex | both | heroin | - |
| Mushanyu 2016 | 5 | ODE | complex | both | - | South Africa |
| Liu 2016 | 3n | DDE | complex | both | heroin | - |
| Djilali 2017 | 3 | PDE | complex | both | heroin | - |
| Wangari 2017 | 4 | ODE | bilinear | both | heroin | - |
| Mushanyu 2017 | 4 | ODE | complex | both | methamphetamine | South Africa, 2000–2013 |
| Li 2018 a | 3 | SDE | bilinear | compartment | heroin | - |
| Ma 2018 | 4 | ODE | complex | both | synthetic drug | - |
| Li 2018b | 6 | ODE | bilinear | both | - | - |
| Naowarat 2018 | 5 | ODE | complex | compartment | methamphetamine | - |
| Wang 2019 | 3n | PDE | bilinear | both | heroin | - |
| Liu 2019 | 3 | SDE | bilinear | both | heroin | - |
| Liu 2019 | 3 | SDE | standard | both | heroin | - |
| Duan 2019 | 4 | PDE | bilinear | compartment | heroin | - |
| Wei 2019 | 3 | SDE | standard | compartment | heroin | - |
| Su 2019 | 3 | ODE | linear | - | multiple | China, 2000–2030 |
| Memarbashi 2019 | 5 | ODE | standard | compartment | heroin | - |
| Abdurahman 2019 | 4 | DDE | complex | compartment | heroin | - |
| Zhang 2019 | 4 | DDE | bilinear | compartment | synthetic drug | - |
| Liu 2019 | 3 | PDE | bilinear | both | heroin | - |
| Liu 2019 | 4 | ODE | bilinear | both | synthetic drug | - |
| Rafiq 2019 | 3 | SDE | bilinear | compartment | heroin | - |
| Saha 2019 | 4 | ODE | complex | both | synthetic drug | South Africa |
| Duan 2020 | 5 | ODE | standard | parameter | heroin and HIV | USA, 2005–2017 |
| Duan 2020 | 3 | PDE | bilinear | compartment | heroin | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, W.; Lu, S.; Tang, H.; Wang, B.; Sun, C.; Zheng, P.; Bai, Y.; Lu, Z.; Kang, Y. A Scoping Review of Drug Epidemic Models. Int. J. Environ. Res. Public Health 2022, 19, 2017. https://doi.org/10.3390/ijerph19042017
Wang W, Lu S, Tang H, Wang B, Sun C, Zheng P, Bai Y, Lu Z, Kang Y. A Scoping Review of Drug Epidemic Models. International Journal of Environmental Research and Public Health. 2022; 19(4):2017. https://doi.org/10.3390/ijerph19042017
Chicago/Turabian StyleWang, Wei, Sifen Lu, Haoxiang Tang, Biao Wang, Caiping Sun, Pai Zheng, Yi Bai, Zuhong Lu, and Yulin Kang. 2022. "A Scoping Review of Drug Epidemic Models" International Journal of Environmental Research and Public Health 19, no. 4: 2017. https://doi.org/10.3390/ijerph19042017
APA StyleWang, W., Lu, S., Tang, H., Wang, B., Sun, C., Zheng, P., Bai, Y., Lu, Z., & Kang, Y. (2022). A Scoping Review of Drug Epidemic Models. International Journal of Environmental Research and Public Health, 19(4), 2017. https://doi.org/10.3390/ijerph19042017






