Analysing Interlinked Frequency Dynamics of the Urban Acoustic Environment
Abstract
1. Introduction
2. Data
2.1. Recording Methods
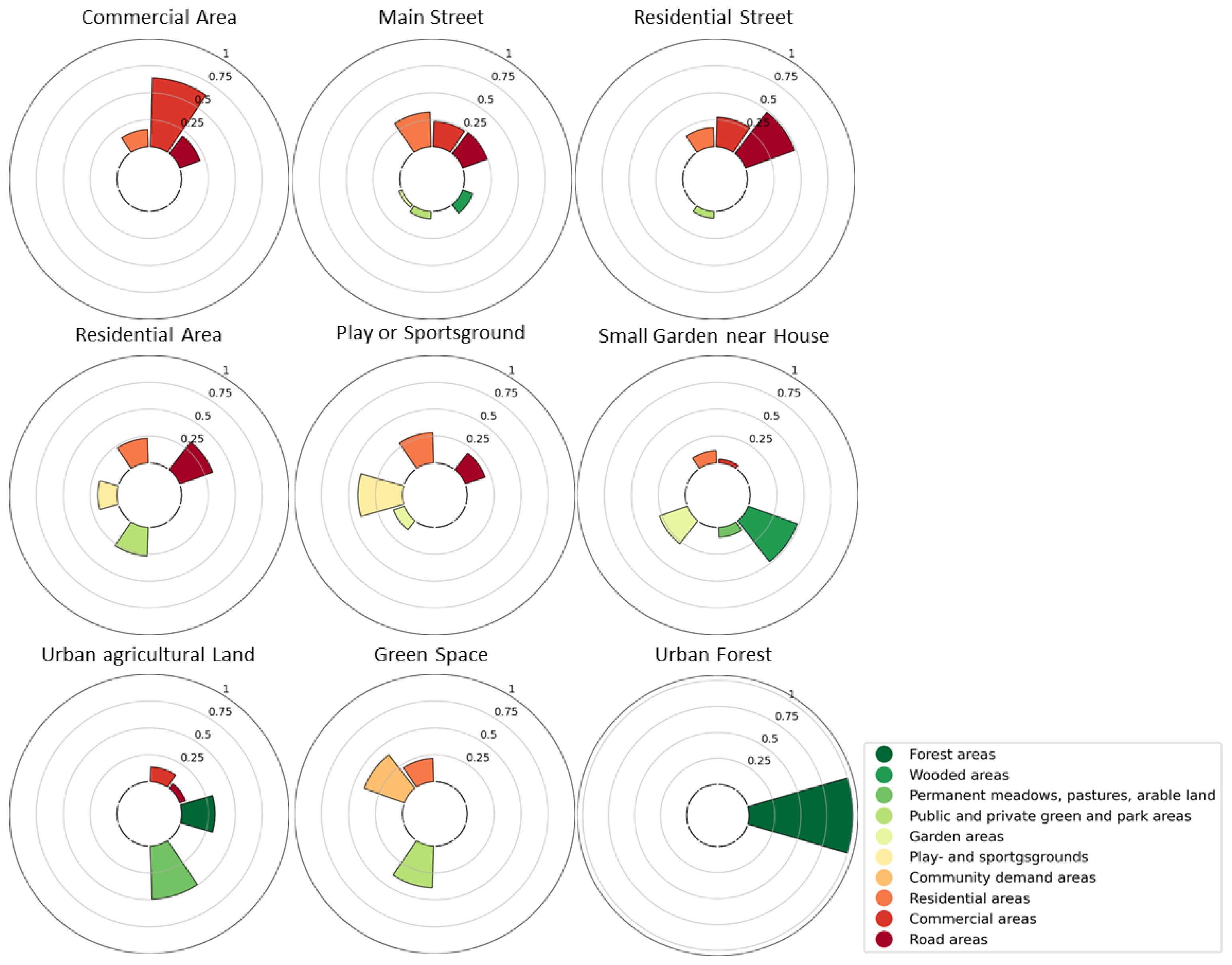
2.2. Land Use Types
3. Materials and Methods
3.1. Pre-Processing
3.1.1. Plausibility Check
3.1.2. Calculation of Power Spectra
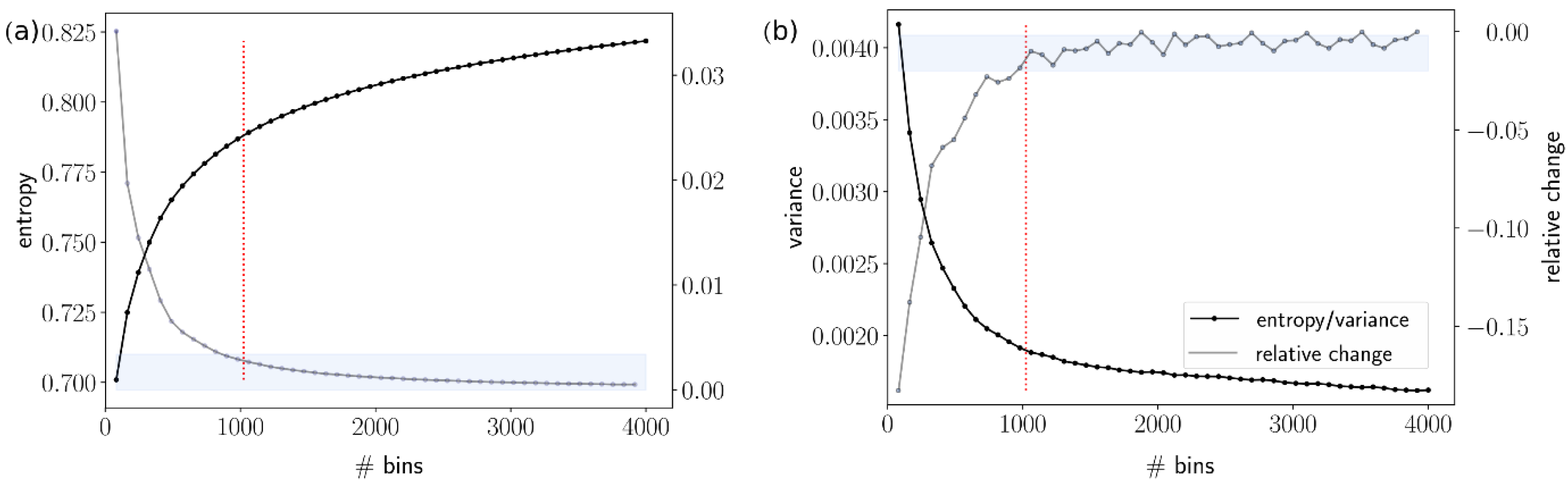
3.1.3. De-Noising and Outlier Removal
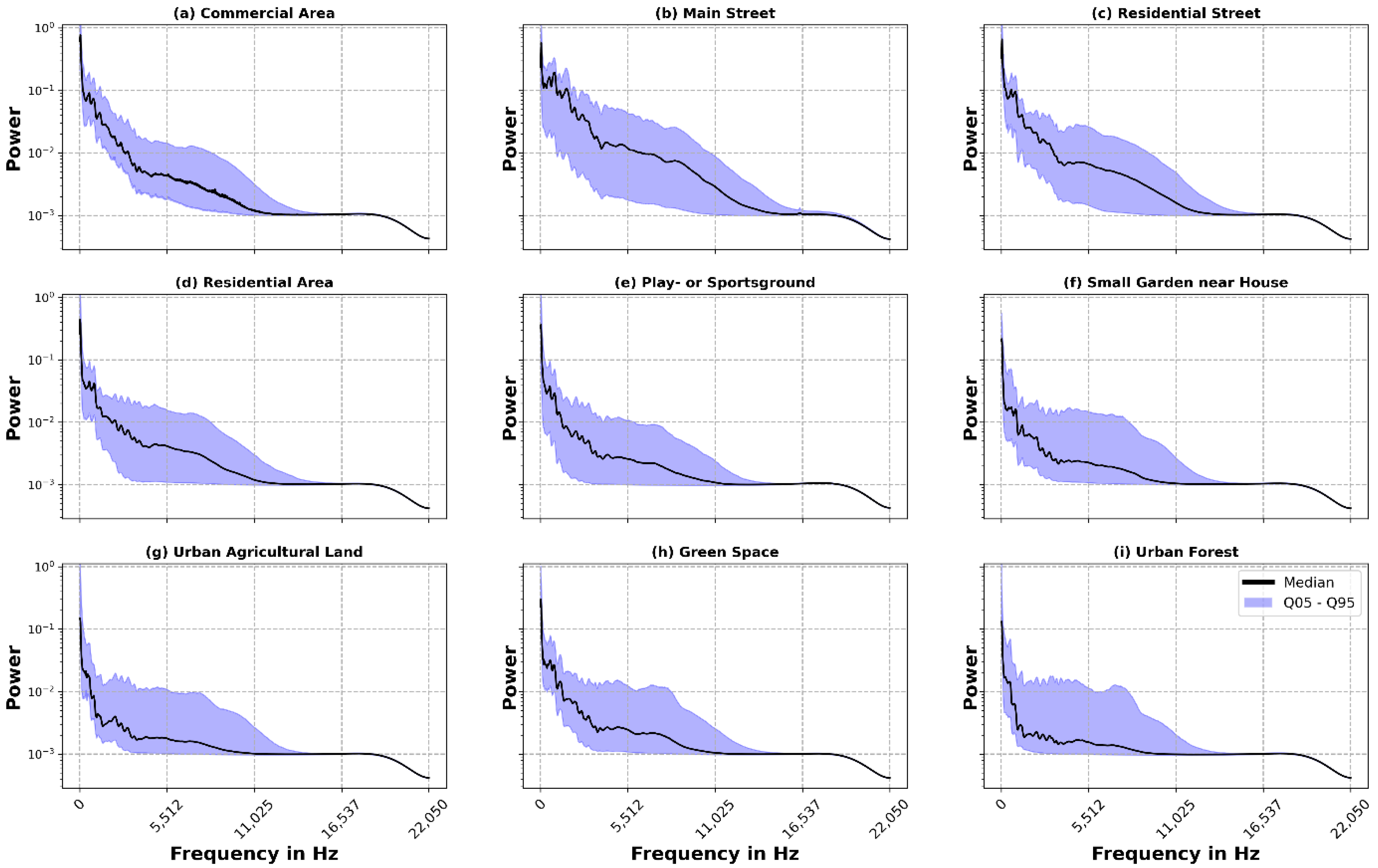
3.2. Median Power Spectrum
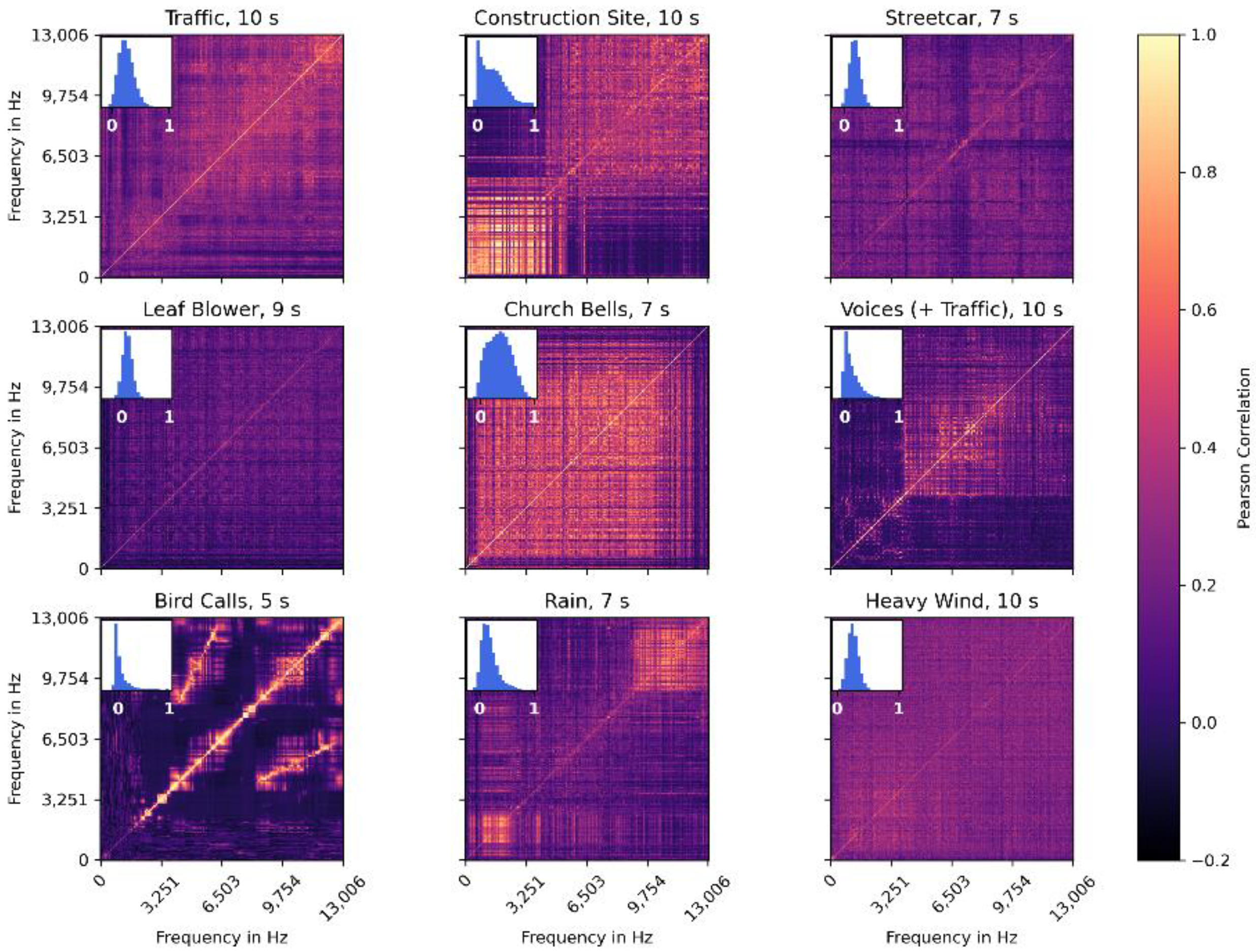
3.3. Normalised Spectrograms
3.4. Correlation Matrices
4. Results
4.1. Median Power Spectrum
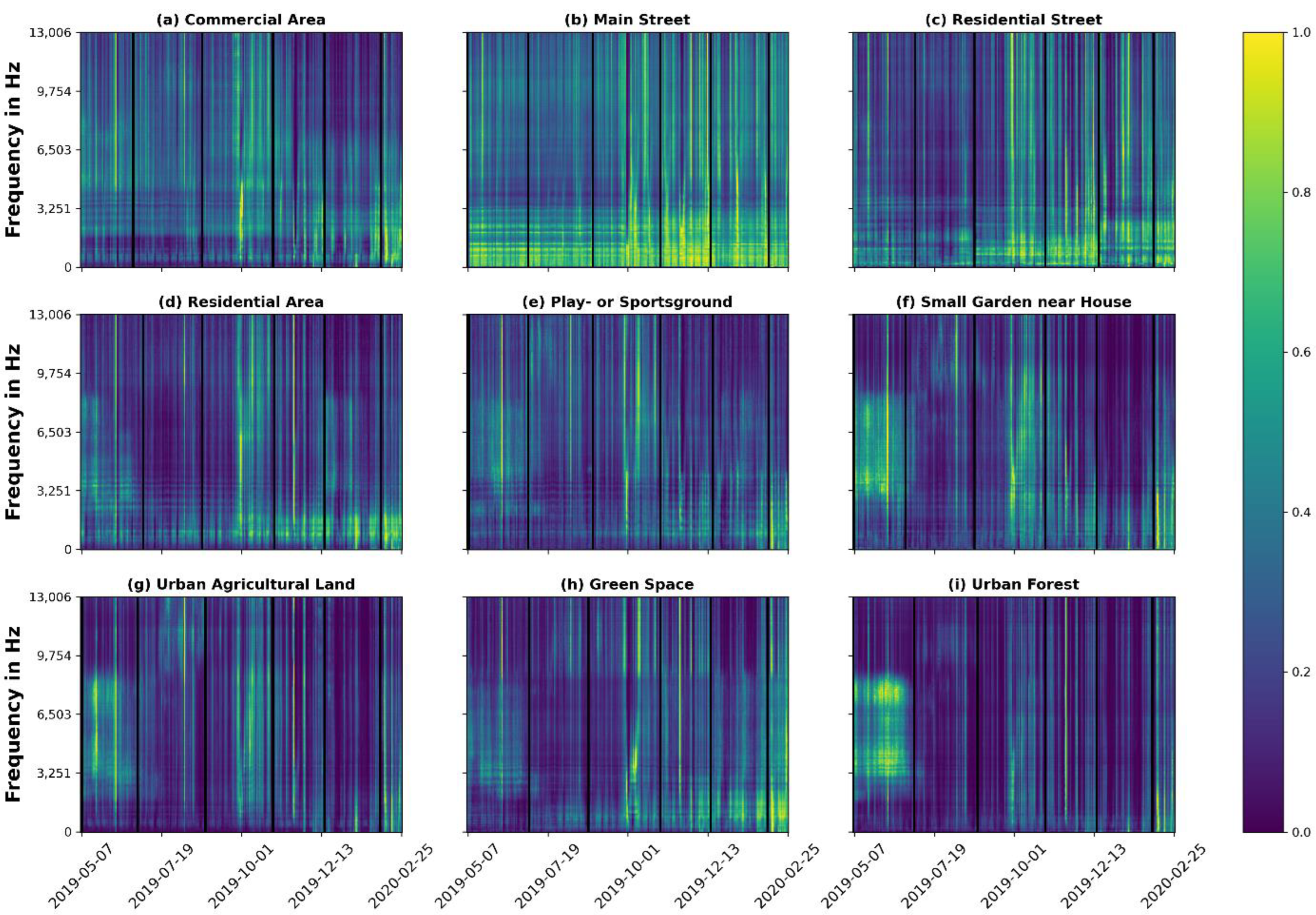
4.2. Normalised Spectrograms
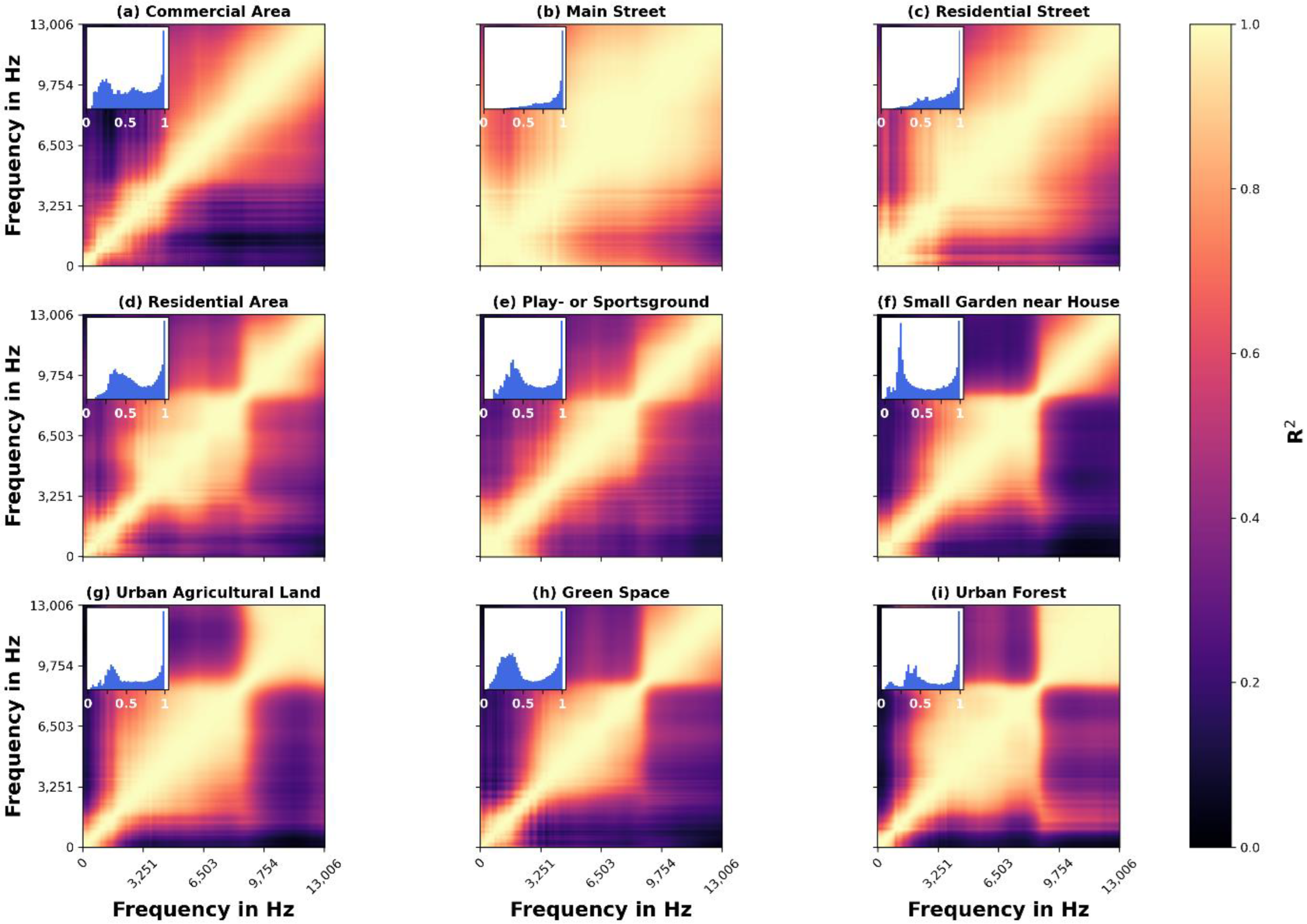
4.3. Correlation Matrices
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Van Kempen, E.; Casas, M.; Pershagen, G.; Foraster, M. WHO Environmental Noise Guidelines for the European Region: A systematic review on environmental noise and cardiovascular and metabolic effects: A summary. Int. J. Environ. Res. Public Health 2018, 15, 379. [Google Scholar] [CrossRef] [PubMed]
- Babisch, W.; Beule, B.; Schust, M.; Kersten, N.; Ising, H. Traffic noise and risk of myocardial infarction. Epidemiology 2005, 16, 33–40. [Google Scholar] [CrossRef]
- Barregard, L.; Bonde, E.; Ohrstrom, E. Risk of hypertension from exposure to road traffic noise in a population-based sample. Occup. Environ. Med. 2009, 66, 410–415. [Google Scholar] [CrossRef] [PubMed]
- Fuks, K.; Moebus, S.; Hertel, S.; Viehmann, A.; Nonnemacher, M.; Dragano, N.; Mohlenkamp, S.; Jakobs, H.; Kessler, C.; Erbel, R.; et al. Long-term urban particulate air pollution, traffic noise, and arterial blood pressure. Environ. Health Perspect. 2011, 119, 1706–1711. [Google Scholar] [CrossRef] [PubMed]
- Kälsch, H.; Hennig, F.; Moebus, S.; Möhlenkamp, S.; Dragano, N.; Jakobs, H.; Memmesheimer, M.; Erbel, R.; Jöckel, K.-H.; Hoffmann, B. Are air pollution and traffic noise independently associated with atherosclerosis: The Heinz Nixdorf Recall Study. Eur. Heart J. 2014, 35, 853–860. [Google Scholar] [CrossRef]
- Orban, E.; McDonald, K.; Sutcliffe, R.; Hoffmann, B.; Fuks, K.B.; Dragano, N.; Viehmann, A.; Erbel, R.; Jöckel, K.-H.; Pundt, N. Residential road traffic noise and high depressive symptoms after five years of follow-up: Results from the Heinz Nixdorf recall study. Environ. Health Perspect. 2016, 124, 578–585. [Google Scholar] [CrossRef]
- Selander, J.; Nilsson, M.E.; Bluhm, G.; Rosenlund, M.; Lindqvist, M.; Nise, G.; Pershagen, G. Long-term exposure to road traffic noise and myocardial infarction. Epidemiology 2009, 20, 272–279. [Google Scholar] [CrossRef]
- Sørensen, M.; Andersen, Z.J.; Nordsborg, R.B.; Becker, T.; Tjønneland, A.; Overvad, K.; Raaschou-Nielsen, O. Long-Term exposure to road traffic noise and incident diabetes: A cohort study. Environ. Health Perspect. 2013, 121, 217–222. [Google Scholar] [CrossRef]
- Sørensen, M.; Hvidberg, M.; Andersen, Z.J.; Nordsborg, R.B.; Lillelund, K.G.; Jakobsen, J.; Tjønneland, A.; Overvad, K.; Raaschou-Nielsen, O. Road traffic noise and stroke: A prospective cohort study. Eur. Heart J. 2011, 32, 737–744. [Google Scholar] [CrossRef]
- Kang, J.; Aletta, F.; Gjestland, T.T.; Brown, L.A.; Botteldooren, D.; Schulte-Fortkamp, B.; Lercher, P.; van Kamp, I.; Genuit, K.; Fiebig, A. Ten questions on the soundscapes of the built environment. Build. Environ. 2016, 108, 284–294. [Google Scholar] [CrossRef]
- Araújo Alves, J.; Neto Paiva, F.; Torres Silva, L.; Remoaldo, P. Low-Frequency Noise and Its Main Effects on Human Health—A Review of the Literature between 2016 and 2019. Appl. Sci. 2020, 10, 5205. [Google Scholar] [CrossRef]
- Baliatsas, C.; van Kamp, I.; van Poll, R.; Yzermans, J. Health effects from low-frequency noise and infrasound in the general population: Is it time to listen? A systematic review of observational studies. Sci. Total Environ. 2016, 557, 163–169. [Google Scholar] [CrossRef] [PubMed]
- van Kamp, I.; van den Berg, F. Health Effects Related to Wind Turbine Sound, Including Low-Frequency Sound and Infrasound. Acoust. Aust. 2018, 46, 31–57. [Google Scholar] [CrossRef]
- Aletta, F.; Oberman, T.; Kang, J. Associations between positive health-related effects and soundscapes perceptual constructs: A systematic review. Int. J. Environ. Res. Public Health 2018, 15, 2392. [Google Scholar] [CrossRef]
- Alvarsson, J.J.; Wiens, S.; Nilsson, M.E. Stress Recovery during Exposure to Nature Sound and Environmental Noise. Int. J. Environ. Res. Public Health 2010, 7, 1036–1046. [Google Scholar] [CrossRef]
- Medvedev, O.; Shepherd, D.; Hautus, M.J. The restorative potential of soundscapes: A physiological investigation. Appl. Acoust. 2015, 96, 20–26. [Google Scholar] [CrossRef]
- Öhrström, E.; Skånberg, A.; Svensson, H.; Gidlöf-Gunnarsson, A. Effects of road traffic noise and the benefit of access to quietness. J. Sound Vib. 2006, 295, 40–59. [Google Scholar] [CrossRef]
- Jiang, L.; Bristow, A.; Kang, J.; Aletta, F.; Thomas, R.; Notley, H.; Thomas, A.; Nellthorp, J. Ten questions concerning soundscape valuation. Build. Environ. 2022, 219, 109231. [Google Scholar] [CrossRef]
- Wang, V.-S.; Lo, E.-W.; Liang, C.-H.; Chao, K.-P.; Bao, B.-Y.; Chang, T.-Y. Temporal and spatial variations in road traffic noise for different frequency components in metropolitan Taichung, Taiwan. Environ. Pollut. 2016, 219, 174–181. [Google Scholar] [CrossRef]
- Farina, A. Soundscape Ecology: Principles, Patterns, Methods and Applications; Springer: Dordrecht, The Netherlands, 2013. [Google Scholar]
- Kasten, E.P.; Gage, S.H.; Fox, J.; Joo, W. The remote environmental assessment laboratory’s acoustic library: An archive for studying soundscape ecology. Ecol. Inform. 2012, 12, 50–67. [Google Scholar] [CrossRef]
- Krause, B.; Farina, A. Using ecoacoustic methods to survey the impacts of climate change on biodiversity. Biol. Conserv. 2016, 195, 245–254. [Google Scholar] [CrossRef]
- Pijanowski, B.C.; Farina, A.; Gage, S.H.; Dumyahn, S.L.; Krause, B.L. What is soundscape ecology? An introduction and overview of an emerging new science. Landsc. Ecol. 2011, 26, 1213–1232. [Google Scholar] [CrossRef]
- Sueur, J. Sound Analysis and Synthesis with R; Springer: Culemborg, The Netherlands, 2018. [Google Scholar]
- Sueur, J.; Farina, A. Ecoacoustics: The ecological investigation and interpretation of environmental sound. Biosemiotics 2015, 8, 493–502. [Google Scholar] [CrossRef]
- Bradfer-Lawrence, T.; Gardner, N.; Bunnefeld, L.; Bunnefeld, N.; Willis, S.G.; Dent, D.H. Guidelines for the use of acoustic indices in environmental research. Methods Ecol. Evol. 2019, 10, 1796–1807. [Google Scholar] [CrossRef]
- Fairbrass, A.J.; Rennert, P.; Williams, C.; Titheridge, H.; Jones, K.E. Biases of acoustic indices measuring biodiversity in urban areas. Ecol. Indic. 2017, 83, 169–177. [Google Scholar] [CrossRef]
- Haselhoff, T.; Hornberg, J.; Fischer, J.L.; Lawrence, B.T.; Ahmed, S.; Gruehn, D.; Moebus, S. The acoustic environment before and during the SARS-CoV-2 lockdown in a major German city as measured by ecoacoustic indices. J. Acoust. Soc. Am. 2022, 152, 1192–1200. [Google Scholar] [CrossRef] [PubMed]
- Gibb, R.; Browning, E.; Glover-Kapfer, P.; Jones, K.E. Emerging opportunities and challenges for passive acoustics in ecological assessment and monitoring. Methods Ecol. Evol. 2019, 10, 169–185. [Google Scholar] [CrossRef]
- Haselhoff, T.; Lawrence, B.; Hornberg, J.; Ahmed, S.; Sutcliffe, R.; Gruehn, D.; Moebus, S. The acoustic quality and health in urban environments (SALVE) project: Study design, rationale and methodology. Appl. Acoust. 2022, 188, 108538. [Google Scholar] [CrossRef]
- Gage, S.H.; Towsey, M.; Kasten, E.P. Analytical Methods in Ecoacoustics. Ecoacoustics. 2017, 16, 273–296. [Google Scholar] [CrossRef]
- Achard, S.; Salvador, R.; Whitcher, B.; Suckling, J.; Bullmore, E. A Resilient, Low-Frequency, Small-World Human Brain Functional Network with Highly Connected Association Cortical Hubs. J. Neurosci. 2006, 26, 63–72. [Google Scholar] [CrossRef]
- Donges, J.F.; Zou, Y.; Marwan, N.; Kurths, J. Complex networks in climate dynamics. Eur. Phys. J. Spec. Top. 2009, 174, 157–179. [Google Scholar] [CrossRef]
- Miksis-Olds, J.L.; Nichols, S.M. Is low frequency ocean sound increasing globally? J. Acoust. Soc. Am. 2016, 139, 501–511. [Google Scholar] [CrossRef]
- Nichols, S.M.; Bradley, D.L. Use of noise correlation matrices to interpret ocean ambient noise. J. Acoust. Soc. Am. 2019, 145, 2337–2349. [Google Scholar] [CrossRef] [PubMed]
- Asensio, C.; Pavón, I.; de Arcas, G. Changes in noise levels in the city of Madrid during COVID-19 lockdown in 2020. J. Acoust. Soc. Am. 2020, 148, 1748–1755. [Google Scholar] [CrossRef]
- Hornberg, J.; Haselhoff, T.; Lawrence, B.T.; Fischer, J.L.; Ahmed, S.; Gruehn, D.; Moebus, S. Impact of the COVID-19 Lockdown Measures on Noise Levels in Urban Areas—A Pre/during Comparison of Long-Term Sound Pressure Measurements in the Ruhr Area, Germany. Int. J. Environ. Res. Public Health 2021, 18, 4653. [Google Scholar] [CrossRef] [PubMed]
- Basu, B.; Murphy, E.; Molter, A.; Sarkar Basu, A.; Sannigrahi, S.; Belmonte, M.; Pilla, F. Investigating changes in noise pollution due to the COVID-19 lockdown: The case of Dublin, Ireland. Sustain. Cities Soc. 2021, 65, 102597. [Google Scholar] [CrossRef]
- Acoustics, W. Song Meter SM4 Acoustic Recorder. Available online: https://www.wildlifeacoustics.com/products/song-meter-sm4 (accessed on 10 November 2022).
- ISO/TS 12913-2:2018; Acoustics—Soundscape—Part 2: Data Collection and Reporting Requirements. ISO: Geneva, Switzerland, 2014.
- Regionalverband Ruhr. Flächennutzungskartierung. Daten Für Die Stadt- Und Regionalplanung. Available online: https://www.rvr.ruhr/daten-digitales/geodaten/flaechennutzungskartierung/ (accessed on 10 November 2022).
- Sueur, J.; Aubin, T.; Simonis, C. Seewave, a free modular tool for sound analysis and synthesis. Bioacoustics 2008, 18, 213–226. [Google Scholar] [CrossRef]
- Villanueva-Rivera, L.J.; Pijanowski, B.C.; Villanueva-Rivera, M.L.J. Package ‘soundecology’. R Package Version 2018, 1, 3. [Google Scholar]
- Israel, G.D. Determining Sample Size; University of Florida: Gainesville, FL, USA, 1992. [Google Scholar]
- Cooley, J.W.; Tukey, J.W. An Algorithm for the Machine Calculation of Complex Fourier Series. Math. Comput. 1965, 19, 297–301. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Hotelling, H. Analysis of a complex of statistical variables into principal components. J. Educ. Psychol. 1933, 24, 417. [Google Scholar] [CrossRef]
- Abdi, H.; Williams, L.J. Principal component analysis. Wiley Interdiscip. Rev. Comput. Stat. 2010, 2, 433–459. [Google Scholar] [CrossRef]
- Wilcox, R.R. Introduction to Robust Estimation and Hypothesis Testing, 2nd ed.; Academic Press: San Diego, CA, USA, 2011. [Google Scholar]
- Benesty, J.; Chen, J.; Huang, Y.; Cohen, I. Pearson correlation coefficient. In Noise Reduction in Speech Processing; Springer: Berlin/Heidelberg, Germany, 2009; pp. 1–4. [Google Scholar]
- McLachlan, G.J.; Lee, S.X.; Rathnayake, S.I. Finite mixture models. Annu. Rev. Stat. Its Appl. 2019, 6, 355–378. [Google Scholar] [CrossRef]
- Boelman, N.T.; Asner, G.P.; Hart, P.J.; Martin, R.E. Multi-Trophic Invasion Resistance in Hawaii: Bioacoustics, Field Surveys, and Airborne Remote Sensing. Ecol. Appl. 2007, 17, 2137–2144. [Google Scholar] [CrossRef] [PubMed]
- Ma, X.; Wu, Z.; Jia, J.; Xu, M.; Meng, H.; Cai, L. Emotion Recognition from Variable-Length Speech Segments Using Deep Learning on Spectrograms. In Proceedings of the Interspeech, Hyderabad, India, 2–3 September 2018; pp. 3683–3687. [Google Scholar]
- Towsey, M.W.; Truskinger, A.M.; Roe, P. The Navigation and Visualisation of Environmental Audio Using Zooming Spectrograms. In Proceedings of the 2015 IEEE International Conference on Data Mining Workshop (ICDMW), Atlantic City, NJ, USA, 14–17 November 2015; pp. 788–797. [Google Scholar]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Haselhoff, T.; Braun, T.; Hornberg, J.; Lawrence, B.T.; Ahmed, S.; Gruehn, D.; Moebus, S. Analysing Interlinked Frequency Dynamics of the Urban Acoustic Environment. Int. J. Environ. Res. Public Health 2022, 19, 15014. https://doi.org/10.3390/ijerph192215014
Haselhoff T, Braun T, Hornberg J, Lawrence BT, Ahmed S, Gruehn D, Moebus S. Analysing Interlinked Frequency Dynamics of the Urban Acoustic Environment. International Journal of Environmental Research and Public Health. 2022; 19(22):15014. https://doi.org/10.3390/ijerph192215014
Chicago/Turabian StyleHaselhoff, Timo, Tobias Braun, Jonas Hornberg, Bryce T. Lawrence, Salman Ahmed, Dietwald Gruehn, and Susanne Moebus. 2022. "Analysing Interlinked Frequency Dynamics of the Urban Acoustic Environment" International Journal of Environmental Research and Public Health 19, no. 22: 15014. https://doi.org/10.3390/ijerph192215014
APA StyleHaselhoff, T., Braun, T., Hornberg, J., Lawrence, B. T., Ahmed, S., Gruehn, D., & Moebus, S. (2022). Analysing Interlinked Frequency Dynamics of the Urban Acoustic Environment. International Journal of Environmental Research and Public Health, 19(22), 15014. https://doi.org/10.3390/ijerph192215014






