Using Random Effect Models to Produce Robust Estimates of Death Rates in COVID-19 Data
Abstract
1. Introduction
2. Methodology
3. Technical Details
3.1. Choice of Lag
3.2. Choice of Number of Mass Points
3.3. Clustering and MAP Rule
4. Results
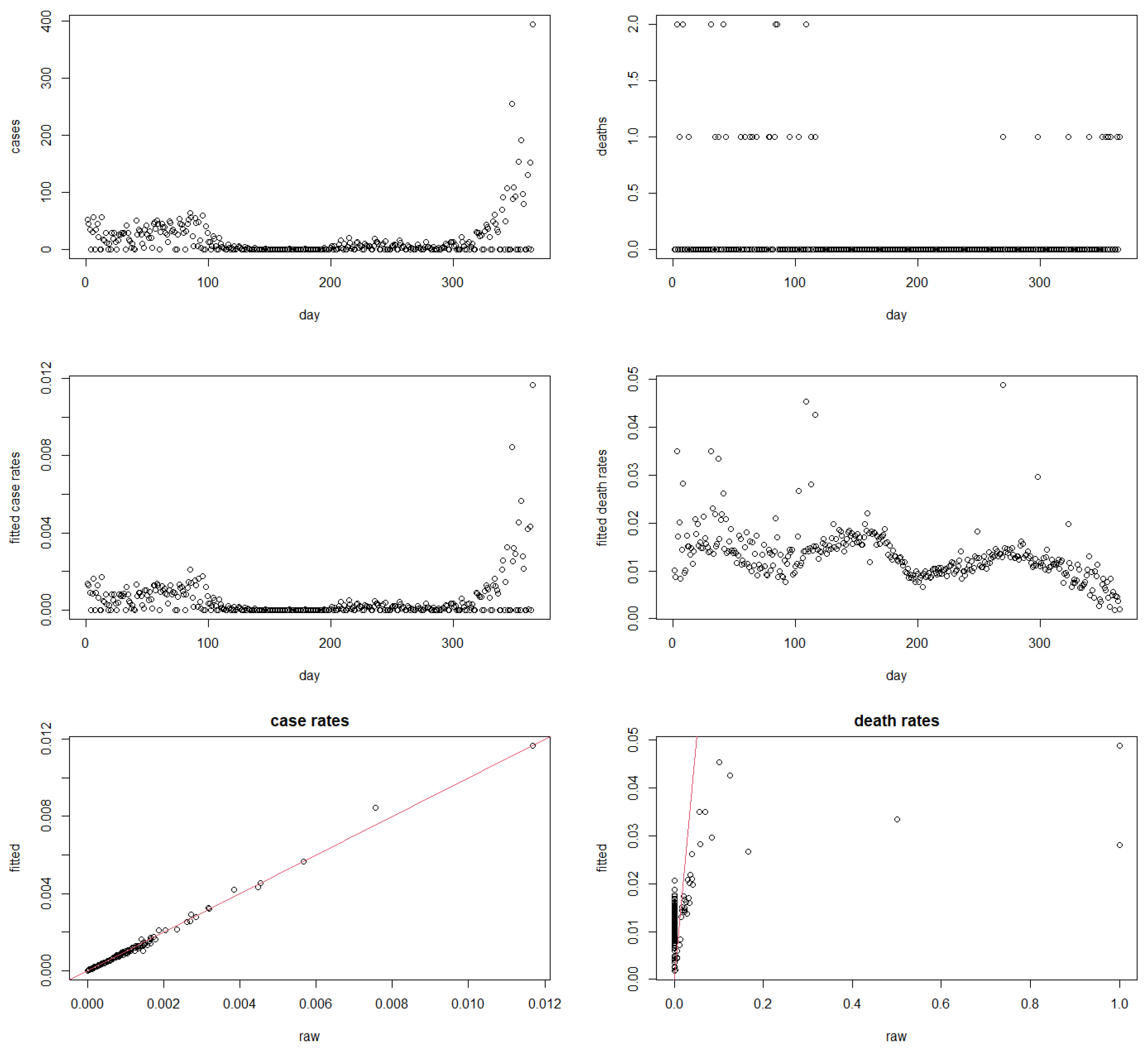
4.1. Robust Rates for All Countries
4.2. Finding Clusters of Countries
4.3. Case Study 1: San Marino Data in 2021
4.4. Case Study 2: Saudi Arabia Data in 2021
5. Discussion
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| BIC | Bayesian Information Criterion |
| EM | Expectation-Maximization |
| MAP | Maximum a posteriori |
| NaN | Not a Number |
| NPML | Nonparametric maximum likelihood |
References
- Verity, R.; Okell, L.C.; Dorigatti, I.; Winskill, P.; Whittaker, C.; Imai, N.; Cuomo-Dannenburg, G.; Thompson, H.; Walker, P.G.; Fu, H.; et al. Estimates of the severity of coronavirus disease 2019: A model-based analysis. Lancet Infect. Dis. 2020, 20, 669–677. [Google Scholar] [CrossRef]
- Molenberghs, G.; Faes, C.; Verbeeck, J.; Deboosere, P.; Abrams, S.; Willem, L.; Aerts, J.; Theeten, H.; Devleesschauwer, B.; Bustos Sierra, N.; et al. COVID-19 mortality, excess mortality, deaths per million and infection fatality ratio, Belgium, 9 March 2020 to 28 June 2020. Eurosurveillance 2022, 27, 2002060. [Google Scholar] [CrossRef] [PubMed]
- COVID-19 Coronavirus Pandemic. Available online: https://www.worldometers.info/coronavirus/ (accessed on 1 July 2022).
- Flaxman, S.; Mishra, S.; Gandy, A.; Unwin, H.J.T.; Mellan, T.A.; Coupland, H.; Whittaker, C.; Zhu, H.; Berah, T.; Eaton, J.W.; et al. Estimating the number of infections and the impact of non-pharmaceutical interventions on COVID-19 in European. Nature 2020, 584, 257–261. [Google Scholar] [CrossRef]
- Gelfand, M.J.; Jackson, J.C.; Pan, X.; Nau, D.; Pieper, D.; Denison, E.; Van Lange, P.A.; Chiu, C.Y.; Wang, M. The relationship between cultural tightness–looseness and COVID-19 cases and deaths: A global analysis. Lancet Planet. Health 2021, 5, e135–e144. [Google Scholar] [CrossRef]
- Tuan, N.H.; Mohammadi, H.; Rezapour, S. A mathematical model for COVID-19 transmission by using the Caputo fractional derivative. Chaos Solitons Fractals 2020, 140, 110107. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2021. [Google Scholar]
- Tsutakawa, R. Estimation of cancer mortality rates: A Bayesian analysis of small frequencies. Biometrics 1985, 41, 69–79. [Google Scholar] [CrossRef] [PubMed]
- Dobson, A.J.; Barnett, A.G. An Introduction to Generalized Linear Models, 4th ed.; Chapman and Hall: London, UK; CRC: London, UK, 2018. [Google Scholar] [CrossRef]
- Aitkin, M. A general maximum likelihood analysis of overdispersion in generalized linear models. Stat. Comput. 1996, 6, 251–262. [Google Scholar] [CrossRef]
- Aitkin, M. Empirical Bayes shrinkage using posterior random effect means from nonparametric maximum likelihood estimation in general random effect models. In Proceedings of the 11th International Workshop on Statistical Modelling, Orvieto, Italy, 15–19 July 1996; pp. 87–94. [Google Scholar]
- Sofroniou, N.; Einbeck, J.; Hinde, J. Analyzing Irish suicide rates with mixture models. In Proceedings of the 21st International Workshop on Statistical Modelling, Galway, Ireland, 3–7 July 2006; pp. 474–481. [Google Scholar]
- Einbeck, J.; Gray, E.; Sofroniou, N.; Marques da Silva Junior, A.H.; Gledhill, J. Confidence intervals for posterior intercepts, with application to the PIAAC literacy survey. In Proceedings of the 32nd International Workshop on Statistical Modelling, Groningen, The Netherlands, 3–7 July 2017; pp. 217–222. [Google Scholar]
- Sofroniou, N.; Hoad, D.; Einbeck, J. League tables for literacy survey data based on random effect models. In Proceedings of the 23rd International Workshop on Statistical Modelling, Utrecht, The Netherlands, 7–11 July 2008; pp. 402–405. [Google Scholar]
- Ward, T.; Johnsen, A. Understanding an evolving pandemic: An analysis of the clinical time delay distributions of COVID-19 in the United Kingdom. PLoS ONE 2021, 16, e0257978. [Google Scholar] [CrossRef]
- Fritz, M.K. Wave after wave–Determining the temporal lag in COVID-19 infections and deaths using spatial panel data from Germany. J. Spat. Econom. 2021, 3, 1–30. [Google Scholar] [CrossRef]
- Zhou, F.; Yu, T.; Du, R.; Fan, G.; Liu, Y.; Liu, Z.; Xiang, J.; Wang, Y.; Song, B.; Gu, X.; et al. Clinical course and risk factors for mortality of adult inpatients with COVID-19 in Wuhan, China: A retrospective cohort study. Lancet 2020, 395, 1054–1062. [Google Scholar] [CrossRef]
- Ruan, Q.; Yang, K.; Wang, W.; Jiang, L.; Song, J. Clinical predictors of mortality due to COVID-19 based on an analysis of data of 150 patients from Wuhan, China. Intensive Care Med. 2020, 46, 846–848. [Google Scholar] [CrossRef] [PubMed]
- Jin, J.M.; Bai, P.; He, W.; Wu, F.; Liu, X.F.; Han, D.M.; Liu, S.; Yang, J.K. Gender differences in patients with COVID-19: Focus on severity and mortality. Front. Public Health 2020, 8, 152. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Li, T.; Ye, Y.; Chen, Y.; Pan, J. Impact of fundamental diseases on patients with COVID-19. Disaster Med. Public Health Prep. 2020, 14, 776–781. [Google Scholar] [CrossRef] [PubMed]
- Harrison, E.; Docherty, A.; Semple, C. COVID-19: Time from Symptom Onset Until Death in UK Hospitalised Patients. 2020. Available online: https://assets.publishing.service.gov.uk/government/uploads/system/uploads/attachment_data/file/928729/S0803_CO-CIN_-_Time_from_symptom_onset_until_death.pdf (accessed on 1 September 2022).
- Harrison, R.F.; Forte, K.; Buscher, M.G., Jr.; Chess, A.; Patel, A.; Moylan, T.; Mize, C.H.; Werdmann, M.; Ferrigno, R. The association of preinfection daily oral anticoagulation use and all-cause in hospital mortality from novel coronavirus 2019 at 21 days: A retrospective cohort study. Crit. Care Explor. 2021, 3, e0324. [Google Scholar] [CrossRef]
- Faes, C.; Abrams, S.; Van Beckhoven, D.; Meyfroidt, G.; Vlieghe, E.; Hens, N. Time between symptom onset, hospitalisation and recovery or death: Statistical analysis of Belgian COVID-19 patients. Int. J. Environ. Res. Public Health 2020, 17, 7560. [Google Scholar] [CrossRef]
- Hawryluk, I.; Mellan, T.A.; Hoeltgebaum, H.; Mishra, S.; Schnekenberg, R.P.; Whittaker, C.; Zhu, H.; Gandy, A.; Donnelly, C.A.; Flaxman, S.; et al. Inference of COVID-19 epidemiological distributions from Brazilian hospital data. J. R. Soc. Interface 2020, 17, 20200596. [Google Scholar] [CrossRef]
- Marschner, I.C. Estimating age-specific COVID-19 fatality risk and time to death by comparing population diagnosis and death patterns: Australian data. BMC Med. Res. Methodol. 2021, 21, 1–10. [Google Scholar] [CrossRef]
- Lefrancq, N.; Paireau, J.; Hozé, N.; Courtejoie, N.; Yazdanpanah, Y.; Bouadma, L.; Boëlle, P.Y.; Chereau, F.; Salje, H.; Cauchemez, S. Evolution of outcomes for patients hospitalised during the first 9 months of the SARS-CoV-2 pandemic in France: A retrospective national surveillance data analysis. Lancet Reg.-Health-Eur. 2021, 5, 100087. [Google Scholar] [CrossRef]
- Asirvatham, E.S.; Sarman, C.J.; Saravanamurthy, S.P.; Mahalingam, P.; Maduraipandian, S.; Lakshmanan, J. Who is dying from COVID-19 and when? An Analysis of fatalities in Tamil Nadu, India. Clin. Epidemiol. Glob. Health 2021, 9, 275–279. [Google Scholar] [CrossRef]
- Mehta, R.M.; Bansal, S.; Bysani, S.; Kalpakam, H. A shorter symptom onset to remdesivir treatment (SORT) interval is associated with a lower mortality in moderate-to-severe COVID-19: A real-world analysis. Int. J. Infect. Dis. 2021, 106, 71–77. [Google Scholar] [CrossRef]
- Aitkin, M.; Francis, B.; Hinde, J.; Darnell, R. Statistical Modelling in R; Oxford University Press: Oxford, UK, 2009. [Google Scholar]
- Our World in Data: Owid/COVID-19-Data. Available online: https://covid.ourworldindata.org/data/owid-covid-data.csv (accessed on 1 September 2022).
- de Groot, M.H.; Schervish, M.J. Probability and Statistics, 4th ed.; Pearson: Harlow, UK, 2014. [Google Scholar]
- Holt, C.C. Forecasting seasonals and trends by exponentially weighted moving averages [reprinted]. Int. J. Forecast. 2004, 20, 5–10. [Google Scholar] [CrossRef]
- Qarmalah, N.M.; Einbeck, J.; Coolen, F.P.A. Mixture Models for Prediction from Time Series, with Application to Energy Use Data. Arch. Data Sci. Ser. 2017, 2, 1–15. [Google Scholar]

| Study ID | Region | Sample Size | Lag (Days) | Deaths (Count) |
|---|---|---|---|---|
| Zhou et al. (2020) [17] | China, Wuhan | 191 | 18.5 | 53 |
| Ruan et al. (2020) [18] | China, Wuhan | 150 | 18.0 | 68 |
| Jin et al. (2020) [19] | China, Wuhan | 1056 | 13.0 | 37 |
| Chen et al. (2020) [20] | China, Wuhan | 50 | 13.0 | 50 |
| Verity et al.(2020) [1] | China, mainland | 3665 | 17.8 | NA |
| Harrison et al. (2020) [21] | UK | 7802 | 7 | 7802 |
| Harrison et al. (2021) [22] | UK | 1026 | 21 | 236 |
| Faes et al. (2020) [23] | Belgium | 14,618 | 9 | 1534 |
| Hawryluk et al. (2020) [24] | Brazil | 1,557,000 | 15.2 | NA |
| Marschner (2021) [25] | Australia | 6235 | 18.1 | 816 |
| Lefrancq et al. (2021) [26] | France | 198,846 | 19.0 | 33,269 |
| Asirvatham et al. (2021) [27] | India | 1761 | 4.0 | 1710 |
| Mehta et al. (2021) [28] | India | 346 | 9.0 | 76 |
| Location | Population | Cases | Fitted | Raw | Fitted | Deaths | Fitted | Raw | Fitted |
|---|---|---|---|---|---|---|---|---|---|
| Cases | Case Rate | Case Rate | Deaths | Death Rate | Death Rate | ||||
| Afghanistan | 40,099,462 | 83 | 91.839 | 0.0000021 | 0.0000023 | 1 | 0.359 | 0.0120482 | 0.0039064 |
| Albania | 2,854,710 | 219 | 229.240 | 0.0000767 | 0.0000803 | 0 | 0.251 | 0.0000000 | 0.0010937 |
| Algeria | 44,177,969 | 8 | 2.766 | 0.0000002 | 0.0000001 | 0 | 0.005 | 0.0000000 | 0.0019397 |
| Andorra | 79,034 | 0 | 0.013 | 0.0000000 | 0.0000002 | 0 | 0.000 | NaN | 0.0019828 |
| Angola | 34,503,774 | 0 | 2.160 | 0.0000000 | 0.0000001 | 0 | 0.004 | NaN | 0.0019489 |
| Anguilla | 15,753 | 0 | 0.005 | 0.0000000 | 0.0000003 | 0 | 0.000 | NaN | 0.0019829 |
| Antigua/Barbuda | 93,220 | 0 | 0.014 | 0.0000000 | 0.0000002 | 0 | 0.000 | NaN | 0.0019828 |
| Argentina | 45,276,780 | 0 | 2.835 | 0.0000000 | 0.0000001 | 0 | 0.005 | NaN | 0.0019386 |
| Armenia | 2,790,974 | 0 | 0.183 | 0.0000000 | 0.0000001 | 0 | 0.000 | NaN | 0.0019801 |
| Aruba | 106,536 | 0 | 0.016 | 0.0000000 | 0.0000001 | 0 | 0.000 | NaN | 0.0019828 |
| Australia | 25,921,089 | 32,895 | 36,211.746 | 0.0012690 | 0.0013970 | 62 | 75.118 | 0.0018848 | 0.0020744 |
| Austria | 8,922,082 | 5233 | 5305.067 | 0.0005865 | 0.0005946 | 5 | 4.154 | 0.0009555 | 0.0007830 |
| Azerbaijan | 10,312,992 | 21 | 23.619 | 0.0000020 | 0.0000023 | 0 | 0.040 | 0.0000000 | 0.0016807 |
| Bahamas | 407,906 | 34 | 33.705 | 0.0000834 | 0.0000826 | 0 | 0.054 | 0.0000000 | 0.0015891 |
| Bahrain | 1,463,265 | 2078 | 2044.180 | 0.0014201 | 0.0013970 | 0 | 1.553 | 0.0000000 | 0.0007595 |
| Bangladesh | 169,356,251 | 874 | 973.659 | 0.0000052 | 0.0000057 | 2 | 1.425 | 0.0022883 | 0.0014636 |
| Barbados | 281,200 | 145 | 146.826 | 0.0005156 | 0.0005221 | 0 | 0.173 | 0.0000000 | 0.0011807 |
| Belarus | 9,578,168 | 0 | 0.600 | 0.0000000 | 0.0000001 | 0 | 0.001 | NaN | 0.0019734 |
| Belgium | 11,611,420 | 0 | 0.727 | 0.0000000 | 0.0000001 | 0 | 0.001 | NaN | 0.0019714 |
| Belize | 400,031 | 277 | 238.169 | 0.0006924 | 0.0005954 | 1 | 0.433 | 0.0036101 | 0.0018169 |
| Location | Cases | Fitted Cases | Raw CASE Rate | Fitted Case Rate | Fitted Deaths | Raw Death Rate | Fitted Death Rate |
|---|---|---|---|---|---|---|---|
| Afghanistan | 53 | 65.833 | 0.0000013 | 0.0000016 | 0.439 | 0.0120482 | 0.0066713 |
| Albania | 53 | 54.046 | 0.0000186 | 0.0000189 | 0.070 | 0.0000000 | 0.0012918 |
| Algeria | 4 | 3.914 | 0.0000001 | 0.0000001 | 0.007 | 0.0000000 | 0.0018068 |
| Andorra | 0 | 0.017 | 0.0000000 | 0.0000002 | 0.000 | NaN | 0.0018613 |
| Angola | 0 | 3.056 | 0.0000000 | 0.0000001 | 0.006 | NaN | 0.0018185 |
| Anguilla | 0 | 0.007 | 0.0000000 | 0.0000004 | 0.000 | NaN | 0.0018614 |
| Antigua and Barbuda | 0 | 0.019 | 0.0000000 | 0.0000002 | 0.000 | NaN | 0.0018612 |
| Argentina | 0 | 4.010 | 0.0000000 | 0.0000001 | 0.007 | NaN | 0.0018054 |
| Armenia | 0 | 0.273 | 0.0000000 | 0.0000001 | 0.001 | NaN | 0.0018576 |
| Aruba | 0 | 0.021 | 0.0000000 | 0.0000002 | 0.000 | NaN | 0.0018612 |
| Australia | 33,223 | 33,031.390 | 0.0012817 | 0.0012743 | 48.139 | 0.0018848 | 0.0014574 |
| Austria | 2183 | 2284.134 | 0.0002447 | 0.0002560 | 3.953 | 0.0009555 | 0.0017305 |
| Azerbaijan | 0 | 0.925 | 0.0000000 | 0.0000001 | 0.002 | 0.0000000 | 0.0018483 |
| Bahamas | 20 | 19.675 | 0.0000490 | 0.0000482 | 0.032 | 0.0000000 | 0.0016104 |
| Bahrain | 997 | 1054.167 | 0.0006814 | 0.0007204 | 0.340 | 0.0000000 | 0.0003224 |
| Bangladesh | 54 | 60.609 | 0.0000003 | 0.0000004 | 0.722 | 0.0022883 | 0.0119116 |
| Barbados | 104 | 93.738 | 0.0003698 | 0.0003334 | 0.099 | 0.0000000 | 0.0010537 |
| Belarus | 0 | 0.861 | 0.0000000 | 0.0000001 | 0.002 | NaN | 0.0018492 |
| Belgium | 5944 | 6189.447 | 0.0005119 | 0.0005330 | 1.182 | NaN | 0.0001910 |
| Belize | 224 | 212.846 | 0.0005600 | 0.0005321 | 0.638 | 0.0036101 | 0.0029986 |
| ℓ | 1 | 2 | 3 | 4 | |
|---|---|---|---|---|---|
| Afghanistan | 0.020 | 0.174 | 0.230 | 0.577 | 4 |
| Albania | 0.313 | 0.369 | 0.172 | 0.145 | 2 |
| Algeria | 0.259 | 0.324 | 0.174 | 0.243 | 2 |
| Andorra | 0.254 | 0.320 | 0.174 | 0.252 | 2 |
| Angola | 0.258 | 0.323 | 0.174 | 0.245 | 2 |
| Anguilla | 0.254 | 0.320 | 0.174 | 0.252 | 2 |
| Antigua and Barbuda | 0.254 | 0.320 | 0.174 | 0.252 | 2 |
| Argentina | 0.259 | 0.324 | 0.174 | 0.243 | 2 |
| Armenia | 0.254 | 0.320 | 0.174 | 0.251 | 2 |
| Aruba | 0.254 | 0.320 | 0.174 | 0.252 | 2 |
| Australia | 0.000 | 1.000 | 0.000 | 0.000 | 2 |
| Austria | 0.000 | 0.839 | 0.161 | 0.000 | 2 |
| Azerbaijan | 0.255 | 0.321 | 0.174 | 0.250 | 2 |
| Bahamas | 0.277 | 0.340 | 0.175 | 0.208 | 2 |
| Bahrain | 0.746 | 0.247 | 0.007 | 0.000 | 1 |
| Bangladesh | 0.000 | 0.025 | 0.099 | 0.875 | 4 |
| Barbados | 0.351 | 0.392 | 0.164 | 0.093 | 2 |
| Belarus | 0.255 | 0.321 | 0.174 | 0.250 | 2 |
| Belgium | 1.000 | 0.000 | 0.000 | 0.000 | 1 |
| Belize | 0.054 | 0.397 | 0.348 | 0.201 | 2 |
| −8.564 | −6.531 | −5.458 | −4.251 | ||
| 0.254 | 0.320 | 0.174 | 0.252 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Almohaimeed, A.; Einbeck, J.; Qarmalah, N.; Alkhidhr, H. Using Random Effect Models to Produce Robust Estimates of Death Rates in COVID-19 Data. Int. J. Environ. Res. Public Health 2022, 19, 14960. https://doi.org/10.3390/ijerph192214960
Almohaimeed A, Einbeck J, Qarmalah N, Alkhidhr H. Using Random Effect Models to Produce Robust Estimates of Death Rates in COVID-19 Data. International Journal of Environmental Research and Public Health. 2022; 19(22):14960. https://doi.org/10.3390/ijerph192214960
Chicago/Turabian StyleAlmohaimeed, Amani, Jochen Einbeck, Najla Qarmalah, and Hanan Alkhidhr. 2022. "Using Random Effect Models to Produce Robust Estimates of Death Rates in COVID-19 Data" International Journal of Environmental Research and Public Health 19, no. 22: 14960. https://doi.org/10.3390/ijerph192214960
APA StyleAlmohaimeed, A., Einbeck, J., Qarmalah, N., & Alkhidhr, H. (2022). Using Random Effect Models to Produce Robust Estimates of Death Rates in COVID-19 Data. International Journal of Environmental Research and Public Health, 19(22), 14960. https://doi.org/10.3390/ijerph192214960






