Development of 222Rn Emanation Sources with Integrated Quasi 2π Active Monitoring
Abstract
1. Introduction
1.1. Background and Motivation
1.2. Theoretical Considerations for 222Rn Emanation Standards for Outdoor Activity Concentrations
2. Materials and Methods
2.1. Construction of 226Ra Modified Ion-Implanted Si-Diode Detectors
2.2. Operation of Integrated 222Rn Sources/Detectors
2.3. Autoradiography
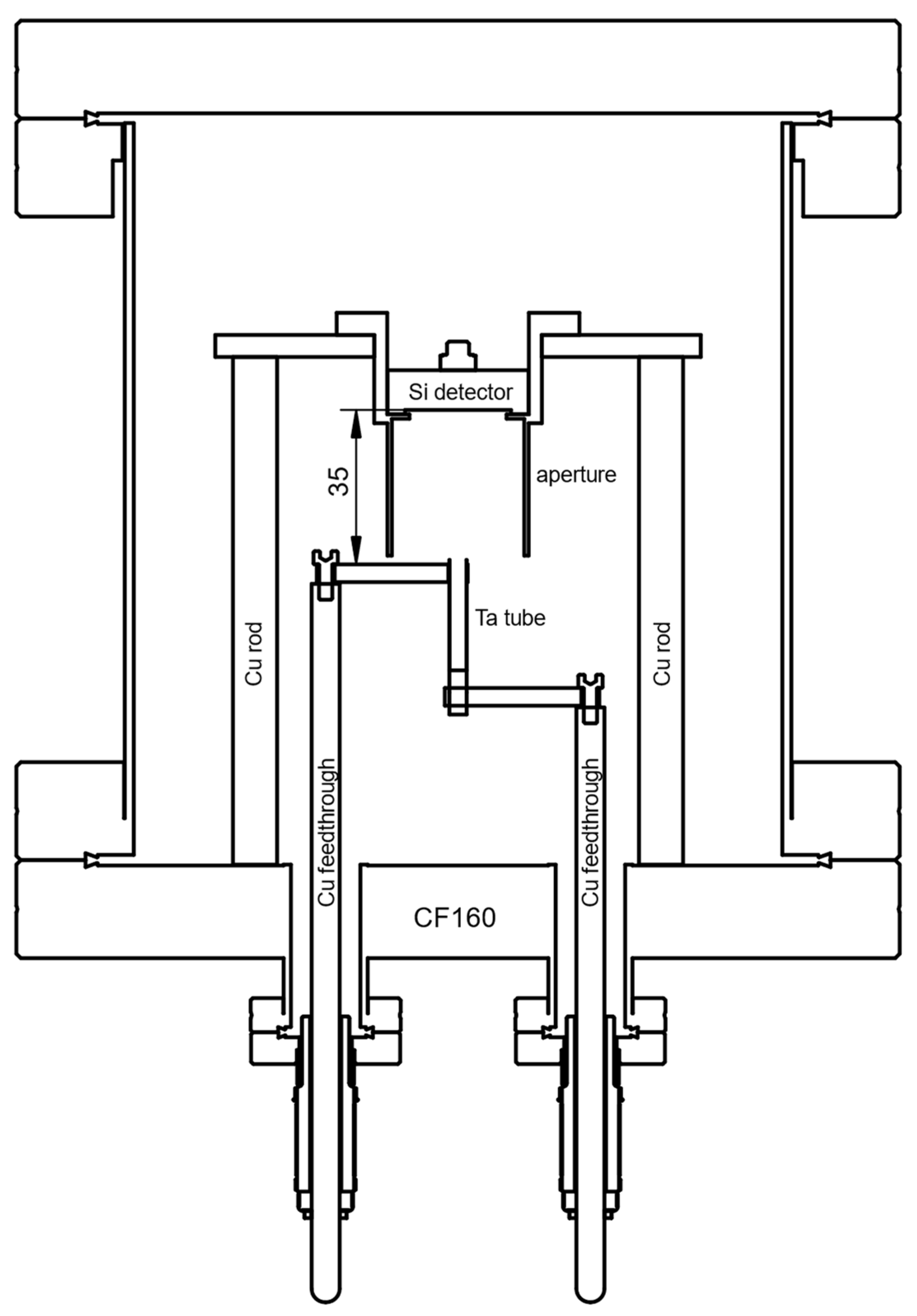
2.4. Alpha-Particle Spectrometry under Defined Solid-Angle
2.4.1. General Defined Solid-Angle Setup
2.4.2. Calculation of Geometrical Efficiency
2.4.3. Peak Area Analysis
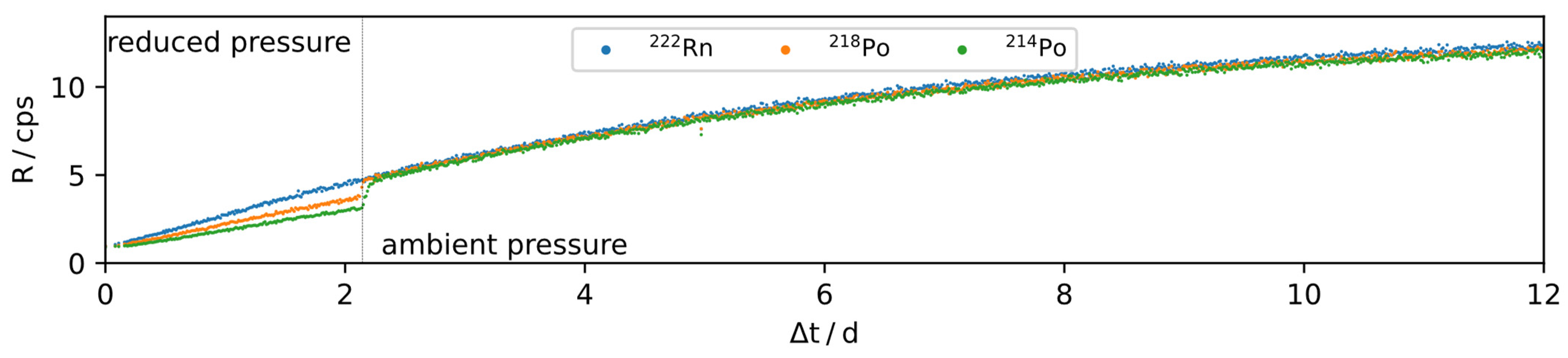
2.5. Estimation of 222Rn Emanation from Spectral Time-Series
3. Results and Discussion
3.1. Morphological Characterization
3.2. Typical α-Particle Spectrum Features of the IRSD
3.3. Efficiency Calibration
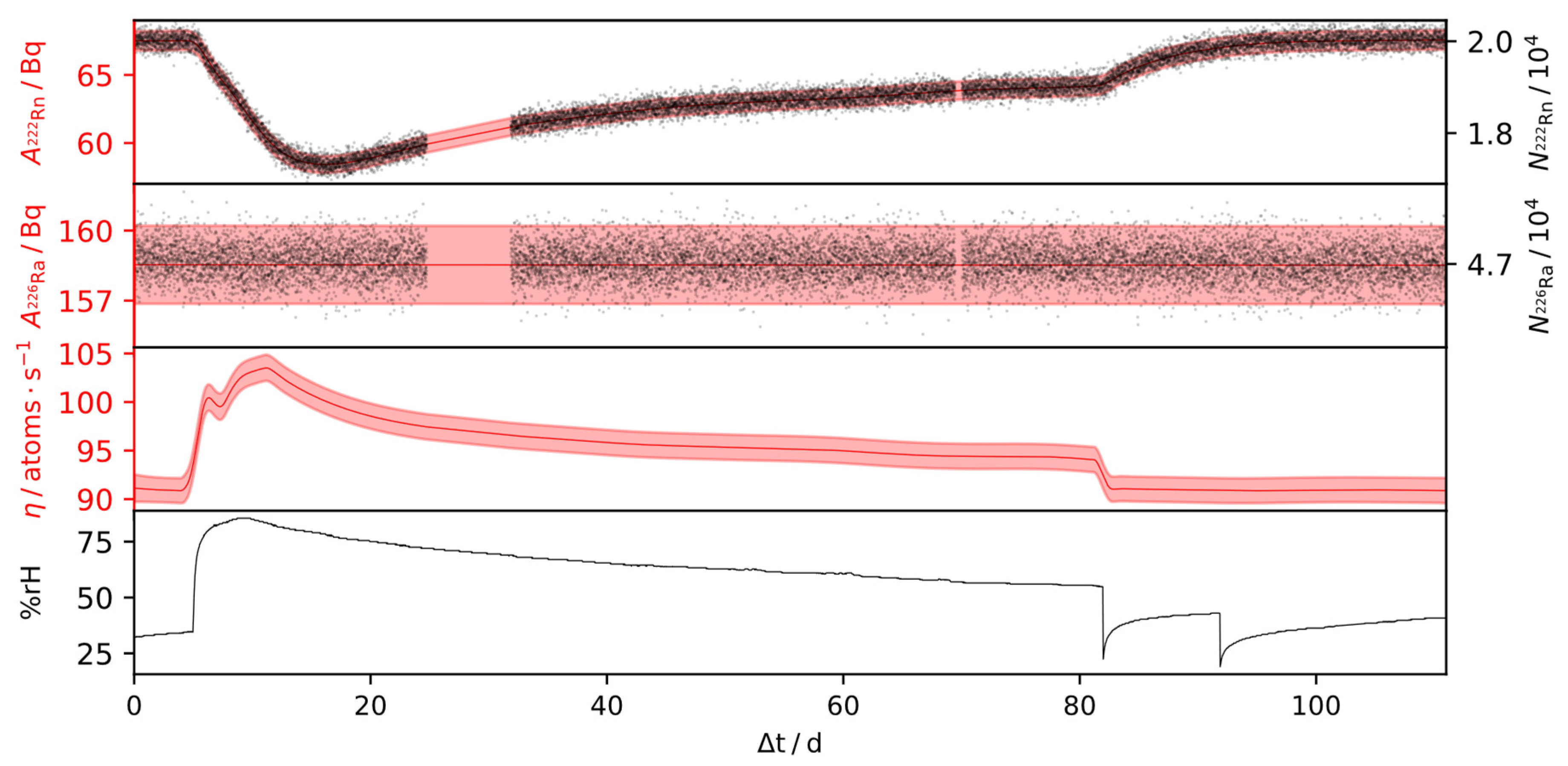
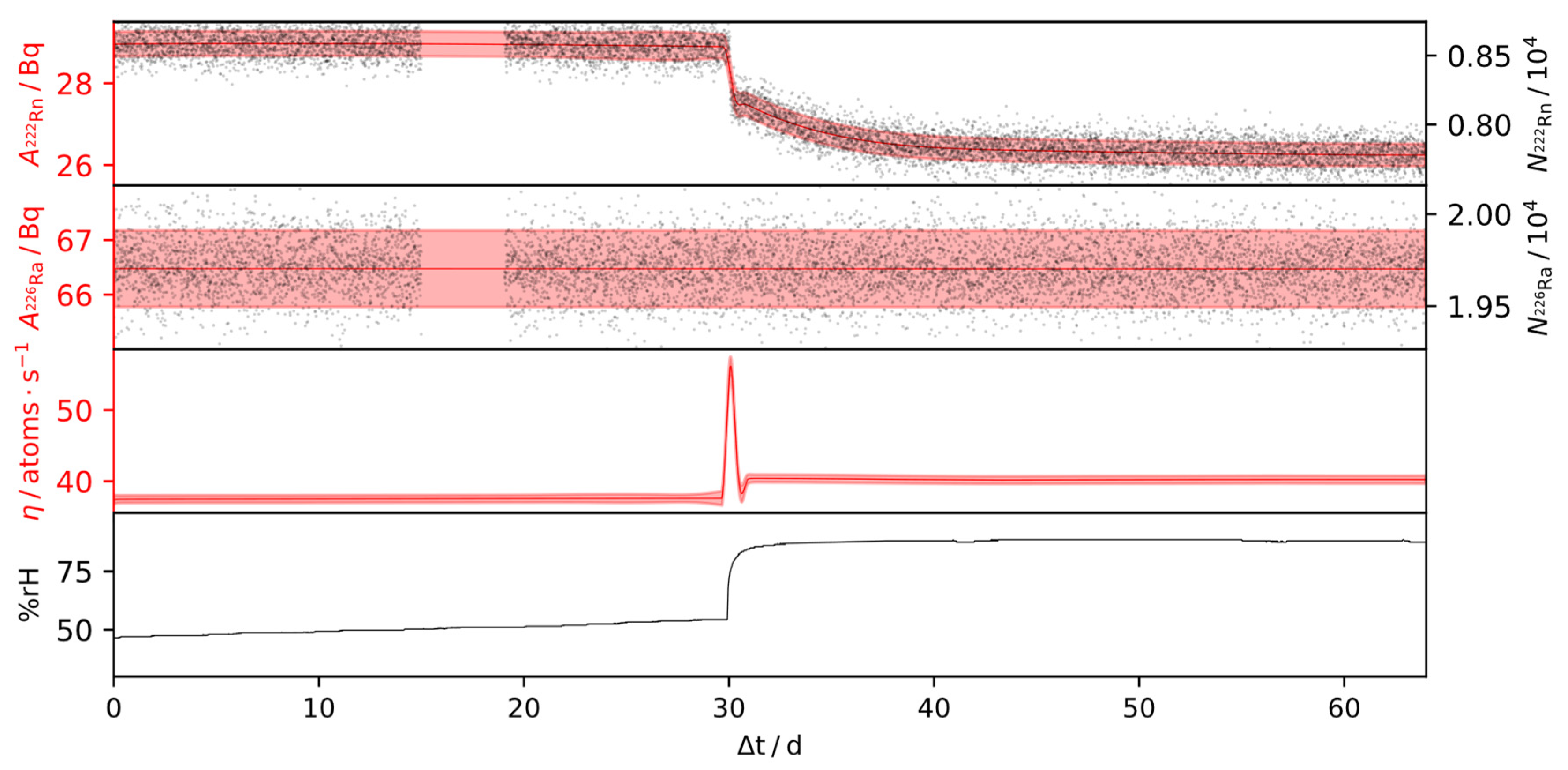
3.4. Estimation of 222Rn Emanation from IRSD Time-Series and its Humidity Dependence
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
References
- ICRP. Lung Cancer Risk from Radon and Progeny & Statement on Radon; ICRP Publication 115; ICRP: Stockholm, Sweden, 2010; Volume 40, p. 1. [Google Scholar]
- ICRP. Radiological Protection Against Radon Exposure; ICRP Publication 126; ICRP: Stockholm, Sweden, 2010; Volume 43, p. 3. [Google Scholar]
- Darby, S.; Hill, D.; Auvinen, A.; Barros-Dios, J.M.; Baysson, H.; Bochicchio, F.; Deo, H.; Falk, R.; Forastiere, F.; Hakama, M.; et al. Radon in homes and risk of lung cancer: Collaborative analysis of individual data from 13 European case-control studies. BMJ 2005, 330, 223. [Google Scholar] [CrossRef]
- Williams, A.G.; Chambers, S.D.; Conen, F.; Reimann, S.; Hill, M.; Griffiths, A.D.; Crawford, J. Radon as a tracer of atmospheric influences on traffic-related air pollution in a small inland city. Tellus B Chem. Phys. Meteorol. 2016, 68, 30967. [Google Scholar] [CrossRef]
- Chambers, S.D.; Preunkert, S.; Weller, R.; Hong, S.-B.; Humphries, R.S.; Tositti, L.; Angot, H.; Legrand, M.; Williams, A.G.; Griffiths, A.D.; et al. Characterizing Atmospheric Transport Pathways to Antarctica and the Remote Southern Ocean Using Radon-222. Front. Earth Sci. 2018, 6, 190. [Google Scholar] [CrossRef]
- Chambers, S.; Guérette, E.-A.; Monk, K.; Griffiths, A.; Zhang, Y.; Duc, H.; Cope, M.; Emmerson, K.; Chang, L.; Silver, J.; et al. Skill-Testing Chemical Transport Models across Contrasting Atmospheric Mixing States Using Radon-222. Atmosphere 2019, 10, 25. [Google Scholar] [CrossRef]
- Chambers, S.D.; Williams, A.G.; Conen, F.; Griffiths, A.D.; Reimann, S.; Steinbacher, M.; Krummel, P.B.; Steele, L.P.; van der Schoot, M.V.; Galbally, I.E.; et al. Towards a Universal “Baseline” Characterisation of Air Masses for High- and Low-Altitude Observing Stations Using Radon-222. Aerosol. Air Qual. Res. 2016, 16, 885–899. [Google Scholar] [CrossRef]
- Williams, A.G.; Chambers, S.; Griffiths, A. Bulk Mixing and Decoupling of the Nocturnal Stable Boundary Layer Characterized Using a Ubiquitous Natural Tracer. Bound. Layer Meteorol. 2013, 149, 381–402. [Google Scholar] [CrossRef]
- Levin, I.; Karstens, U.; Hammer, S.; DellaColetta, J.; Maier, F.; Gachkivskyi, M. Limitations of the Radon Tracer Method (RTM) to estimate regional Greenhouse Gases (GHG) emissions—A case study for methane in Heidelberg. Atmos. Chem. Phys. Discuss. 2021, preprint. [Google Scholar] [CrossRef]
- Levin, I.; Hammer, S.; Eichelmann, E.; Vogel, F.R. Verification of greenhouse gas emission reductions: The prospect of atmospheric monitoring in polluted areas. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2011, 369, 1906–1924. [Google Scholar] [CrossRef]
- Der Laan, V.; Karstens, U.; Neubert, R.E.; Der Laan-Luijkx, V.; Meijer, H.A.J. Observation-based estimates of fossil fuel-derived CO 2 emissions in the Netherlands using Δ14C, CO and 222 Radon. Tellus. B Chem. Phys. Meteorol. 2010, 62, 389–402. [Google Scholar] [CrossRef]
- Biraud, S.; Ciais, P.; Ramonet, M.; Simmonds, P.; Kazan, V.; Monfray, P.; O’doherty, S.; Spain, G.; Jennings, S.G. Quantification of carbon dioxide, methane, nitrous oxide and chloroform emissions over Ireland from atmospheric observations at Mace Head. Tellus B Chem. Phys. Meteorol. 2002, 54, 41–60. [Google Scholar] [CrossRef]
- Perrino, C.; Pietrodangelo, A.; Febo, A. An atmospheric stability index based on radon progeny measurements for the evaluation of primary urban pollution. Atmos. Environ. 2001, 35, 5235–5244. [Google Scholar] [CrossRef]
- Röttger, A.; Röttger, S.; Grossi, C.; Vargas, A.; Curcoll, R.; Otáhal, P.; Hernández-Ceballos, M.Á.; Cinelli, G.; Chambers, S.; Barbosa, S.A.; et al. New metrology for radon at the environmental level. Meas. Sci. Technol. 2021, 32, 124008. [Google Scholar] [CrossRef]
- Picolo, J.L. Absolute measurement of radon 222 activity. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrom. Detect. Assoc. Equip. 1996, 369, 452–457. [Google Scholar] [CrossRef]
- Mertes, F.; Röttger, S.; Röttger, A. A new primary emanation standard for Radon-222. Appl. Radiat. Isot. 2020, 156, 108928. [Google Scholar] [CrossRef]
- Röttger, A.; Honig, A.; Linzmaier, D. Calibration of commercial radon and thoron monitors at stable activtiy concentrations. Appl. Radiat. Isot. 2014, 87, 44–47. [Google Scholar] [CrossRef]
- Linzmaier, D.; Röttger, A. Development of a low-level radon reference atmosphere. Appl. Radiat. Isot. 2013, 81, 208–211. [Google Scholar] [CrossRef] [PubMed]
- Janik, M.; Omori, Y.; Yonehara, H. Influence of humidity on radon and thoron exhalation rates from building materials. Appl. Radiat. Isot. 2015, 95, 102–107. [Google Scholar] [CrossRef]
- Zhou, Q.; Shubayr, N.; Carmona, M.; Standen, T.M.; Kearfott, K.J. Experimental study of dependence on humidity and flow rate for a modified flowthrough radon source. J. Radioanal. Nucl. Chem. 2020, 324, 673–680. [Google Scholar] [CrossRef]
- Stranden, E.; Kolstad, A.K.; Lind, B. The Influence of Moisture and Temperature on Radon Exhalation. Radiat. Prot. Dosim. 1984, 7, 55–58. [Google Scholar] [CrossRef]
- Fialova, E.; Otahal, P.P.S.; Vosahlik, J.; Mazanova, M. Equipment for Testing Measuring Devices at a Low-Level Radon Activity Concentration. Int. J. Environ. Res. Public Health 2020, 17, 1904. [Google Scholar] [CrossRef] [PubMed]
- Mertes, F.; Kneip, N.; Heinke, R.; Kieck, T.; Studer, D.; Weber, F.; Röttger, S.; Röttger, A.; Wendt, K.; Walther, C. Ion implantation of 226Ra for a primary 222Rn emanation standard. Appl. Radiat. Isot. 2021, 181, 11093. [Google Scholar] [CrossRef] [PubMed]
- Ziegler, J.F.; Ziegler, M.D.; Biersack, J.P. SRIM—The stopping and range of ions in matter (2010). Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. At. 2010, 268, 1818–1823. [Google Scholar] [CrossRef]
- Maier, C.G. Vapor Pressure of the Common Metallic Chlorides and a Static Method and High Temperatures; Department of the Interior, Bureau of Mines: Washington, DC, USA, 1925. [Google Scholar]
- Van Westenburg, J.A. Activitees of Alkaline Earth Metals in Their Molten Chlorides; Iowa State University: Ames, IA, USA, 1964. [Google Scholar]
- Garcia Ruiz, R.F.; Berger, R.; Billowes, J.; Binnersley, C.L.; Bissell, M.L.; Breier, A.A.; Brinson, A.J.; Chrysalidis, K.; Cocolios, T.E.; Cooper, B.S.; et al. Spectroscopy of short-lived radioactive molecules. Nature 2020, 581, 396–400. [Google Scholar] [CrossRef] [PubMed]
- Philip Horwitz, E.; Chiarizia, R.; Dietz, M.L. A Novel Strontium-Selective Extraction Chromatographic Resin. Solvent. Extr. Ion. Exch. 2007, 10, 313–336. [Google Scholar] [CrossRef]
- Marx, S. Purification of Radium-226 for the Manufacturing of Actinium-225 in a Cyclotron for Alpha-Immunotherapy; Technical University Munich: Munich, Germany, 2014. [Google Scholar]
- Pommé, S. Methods for primary standardization of activity. Metrologia 2007, 44, S17–S26. [Google Scholar] [CrossRef]
- Stefaan, P.; Goedele, S. Alpha-Particle Counting and Spectrometry in a Primary Standardisation Laboratory. ACTA Chim. Slov. 2008, 55, 111–119. [Google Scholar]
- Arinc, A.; Parfitt, M.J.; Keightley, J.D.; Wilson, A. Defined solid angle alpha counting at NPL. Appl. Radiat. Isot. 2016, 109, 198–204. [Google Scholar] [CrossRef]
- Bortels, G.; Collaers, P. Analytical function for fitting peaks in alpha-particle spectra from Si detectors. Int. J. Radiat. Appl. Instrum. Part 1987, 38, 831–837. [Google Scholar] [CrossRef]
- Pommé, S.; Caro Marroyo, B. Improved peak shape fitting in alpha spectra. Appl. Radiat. Isot. 2015, 96, 148–153. [Google Scholar] [CrossRef]
- Mertes, F.; Röttger, S.; Röttger, A. D3.3 Approximate Sequential Bayesian Filtering to Estimate Rn-222 Emanation from Ra-226 Sources from Spectra. In Proceedings of the SMSI 2021—Measurement Science, Wenstorf, Germany, 3–6 May 2021; pp. 256–257. [Google Scholar]
- Mertes, F.; Röttger, S.; Röttger, A. Approximate sequential Bayesian filtering to estimate 222Rn emanation from 226Ra sources using spectral time-series. J. Sens. Sens. Syst. 2021; under review. [Google Scholar]
- Pommé, S. The uncertainty of counting at a defined solid angle. Metrologia 2015, 52, S73–S85. [Google Scholar] [CrossRef]
- Shepherd, M.M.; Laframboise, J.G. Chebyshev approximation of (1 + 2x) exp(x2) erfc(x) in 0 ≤ x < ∞. Math. Comput. 1981, 36, 249–253. [Google Scholar] [CrossRef][Green Version]
- Egozcue, J.J.; Pawlowsky-Glahn, V.; Mateu-Figueras, G.; Barceló-Vidal, C. Isometric Logratio Transformations for Compositional Data Analysis. Math. Geol. 2003, 35, 279–300. [Google Scholar] [CrossRef]
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0: Fundamental algorithms for scientific computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef]
- Bradburry, J.; Frostig, R.; Hawkins, P.; Johnson, M.J.; Maclaurin, D.; Necula, G.; Paszke, A.; van der Plas, J.; Wanderman-Milne, S.; Zhang, Q. JAX: Composable Transformations of Python + Numpy Programs. 2018. Available online: https://github.com/google/jax (accessed on 1 November 2021).
- Marouli, M.; Pommé, S.; Van Ammel, R.; García-Toraño, E.; Crespo, T.; Pierre, S. Direct measurement of alpha emission probabilities in the decay of 226 Ra. Appl. Radiat. Isot. 2017, 125, 196–202. [Google Scholar] [CrossRef] [PubMed]
- Kalman, R.E. A New Approach to Linear Filtering and Prediction Problems. J. Basic Eng. 1960, 82, 35–45. [Google Scholar] [CrossRef]
- Barber, D. Expectation Correction for Smoothed Inference in Switching Linear Dynamical Systems. J. Mach. Learn. Res. 2006, 7, 2515–2540. [Google Scholar]
- Ebeigbe, D.; Berry, T.; Schiff, S.J.; Sauer, T. Poisson Kalman filter for disease surveillance. Phys. Rev. Res. 2020, 2, 043028. [Google Scholar] [CrossRef]




| Detector Type | Active Area/Depletion Depth | A(226Ra)/Bq | ||
|---|---|---|---|---|
| Mirion PIPS® | 450 mm2/300 μm | 1.91 ± 0.02 | 0.502 ± 0.006 | 0.999 ± 0.017 |
| Ametek Ortec ULTRA® | 450 mm2/300 μm | 66.4 ± 0.5 | 0.494 ± 0.004 | Figure 8 |
| Mirion PIPS® | 450 mm2/300 μm | 158.6 ± 1.7 | 0.494 ± 0.005 | Figure 7 |
| Mirion PIPS® | 450 mm2/100 μm | 442 ± 4 | 0.492 ± 0.005 | 209 ± 4 |
| Description and Type | Value and Uncertainty | Rel. Uncertainty | Rel. Contribution |
|---|---|---|---|
| Solid angle (systematic) | sr | 0.6% | 28.4% |
| BackscatteringDSA (systematic) | 1 ± 0.002 | 0.2% | 3% |
| TailingDSA (systematic) | 1 ± 0.003 | 0.3% | 6.7% |
| TailingSi (systematic) | 1 ± 0.003 | 0.3% | 6.7% |
| 226Ra rateDSA (stochastic) | 0.8% | 55.1% | |
| 226Ra rateSi (stochastic) | 0.04% | 0.1% | |
| 0.502 ± 0.006 | 1.2% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mertes, F.; Röttger, S.; Röttger, A. Development of 222Rn Emanation Sources with Integrated Quasi 2π Active Monitoring. Int. J. Environ. Res. Public Health 2022, 19, 840. https://doi.org/10.3390/ijerph19020840
Mertes F, Röttger S, Röttger A. Development of 222Rn Emanation Sources with Integrated Quasi 2π Active Monitoring. International Journal of Environmental Research and Public Health. 2022; 19(2):840. https://doi.org/10.3390/ijerph19020840
Chicago/Turabian StyleMertes, Florian, Stefan Röttger, and Annette Röttger. 2022. "Development of 222Rn Emanation Sources with Integrated Quasi 2π Active Monitoring" International Journal of Environmental Research and Public Health 19, no. 2: 840. https://doi.org/10.3390/ijerph19020840
APA StyleMertes, F., Röttger, S., & Röttger, A. (2022). Development of 222Rn Emanation Sources with Integrated Quasi 2π Active Monitoring. International Journal of Environmental Research and Public Health, 19(2), 840. https://doi.org/10.3390/ijerph19020840






