Two-Dimensional Decoupling and Decomposition Analysis of CO2 Emissions from Economic Growth: A Case Study of 57 Cities in the Yellow River Basin
Abstract
1. Introduction
2. Literature Review
3. Material and Methods
3.1. CO2 Emission Accounting Model
3.2. Two-Dimensional Decoupling Model
3.2.1. Environmental Kuznets Curve
3.2.2. Basic Decoupling Model
3.2.3. Two-Dimensional Decoupling Model
3.3. Decomposition Model of Decoupling Index
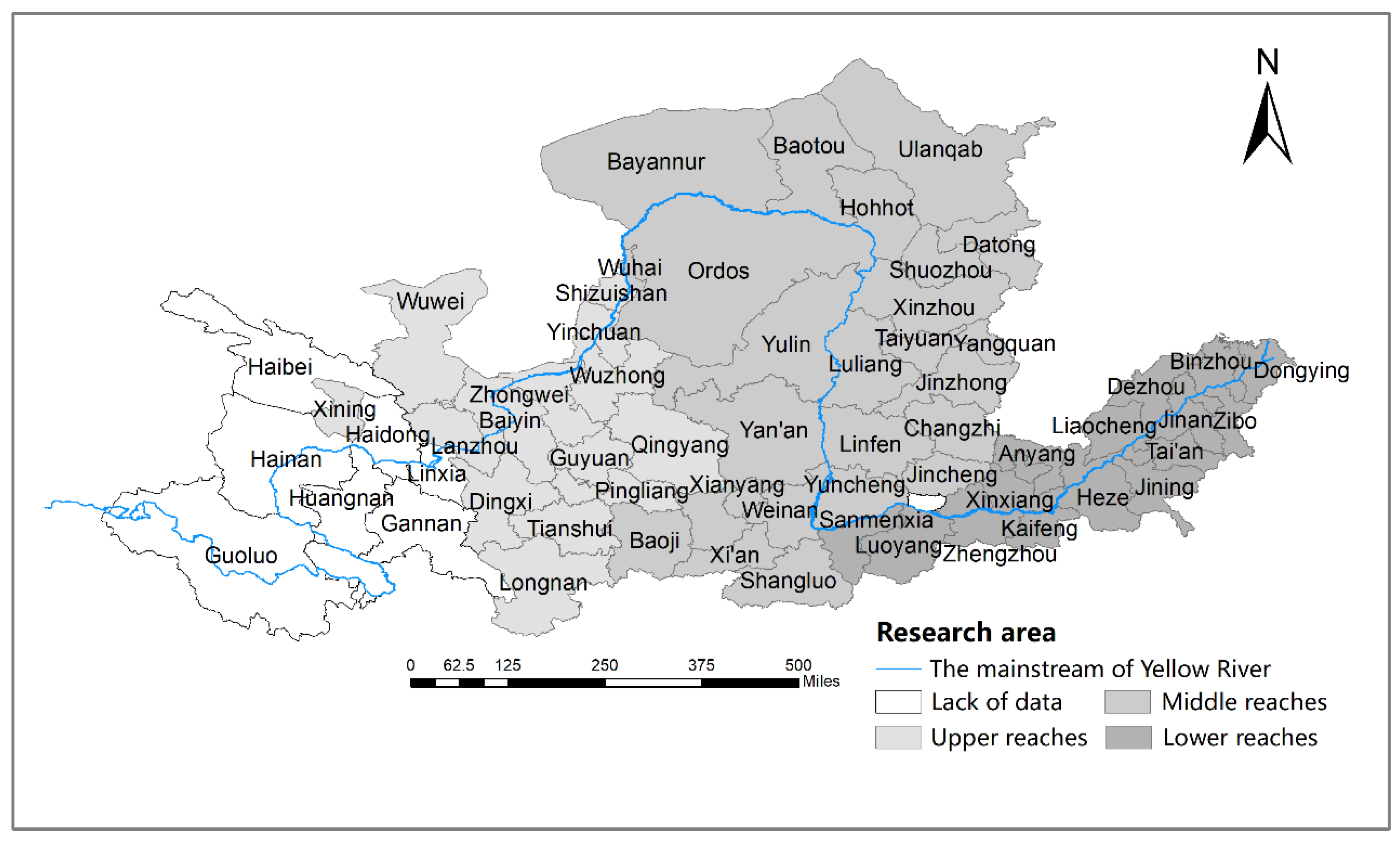
3.4. Research Area and Data Source
4. Results
4.1. Decoupling Analysis
4.1.1. Basic Decoupling Analysis
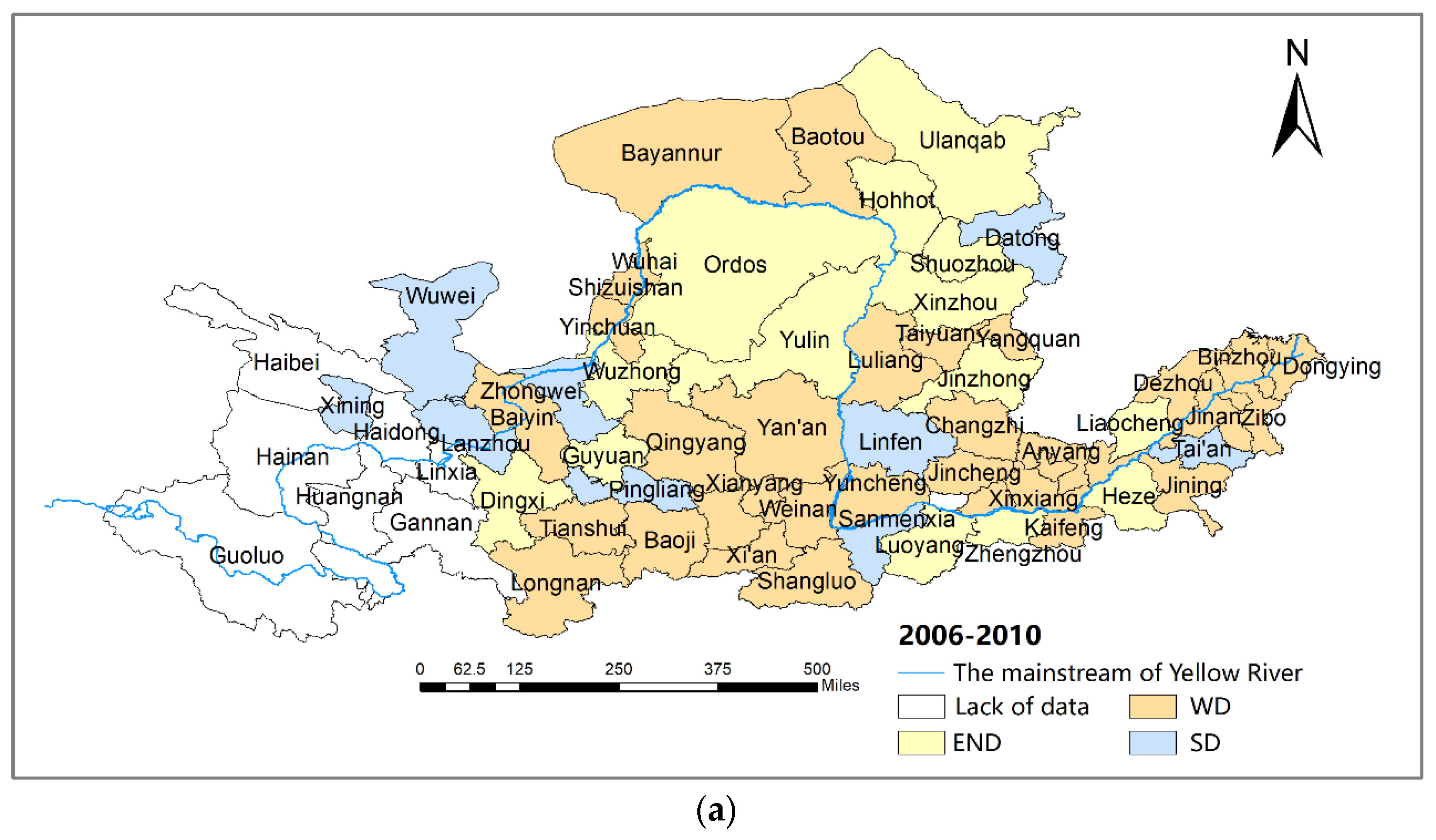
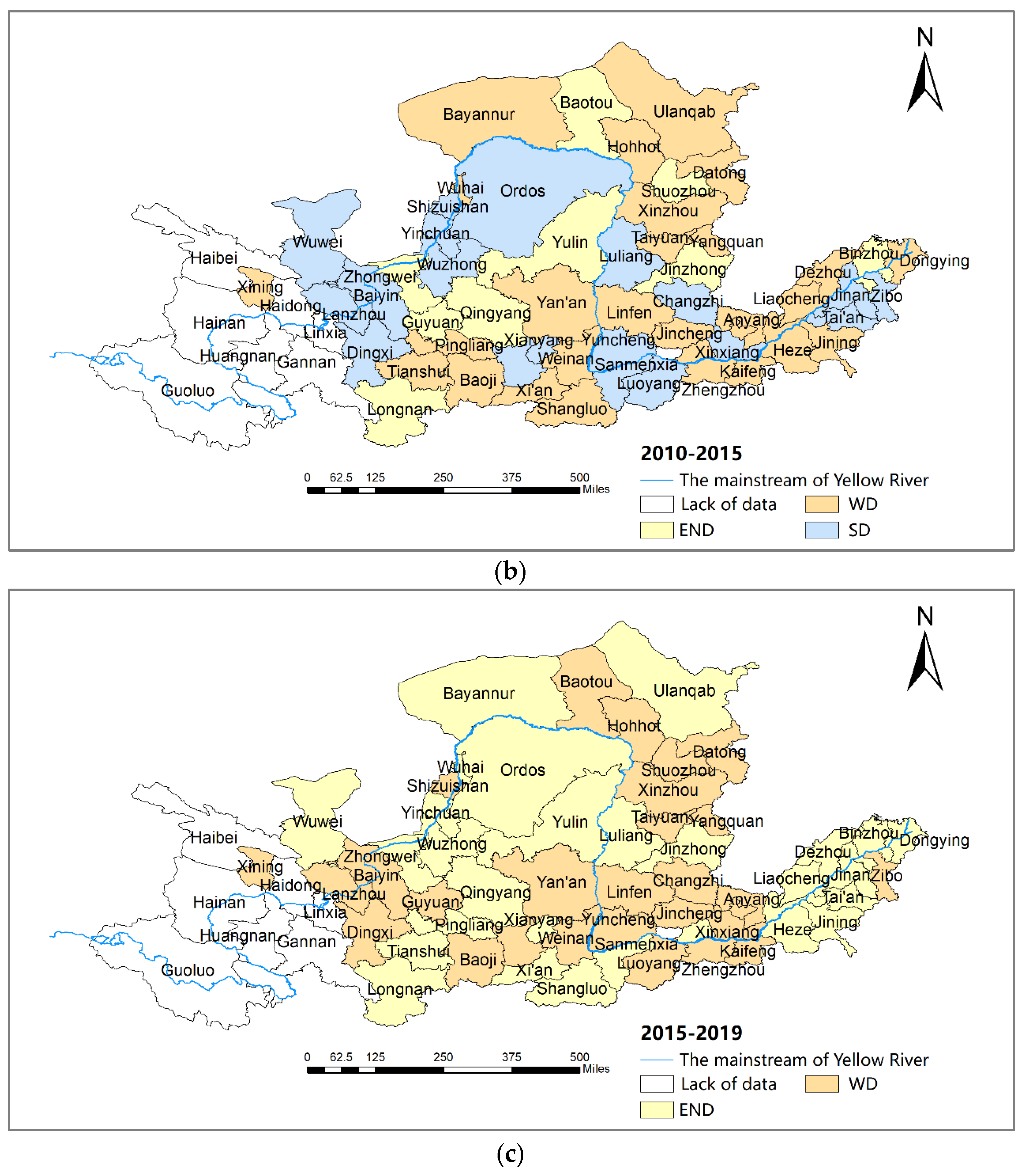
4.1.2. Two-Dimensional Decoupling Analysis
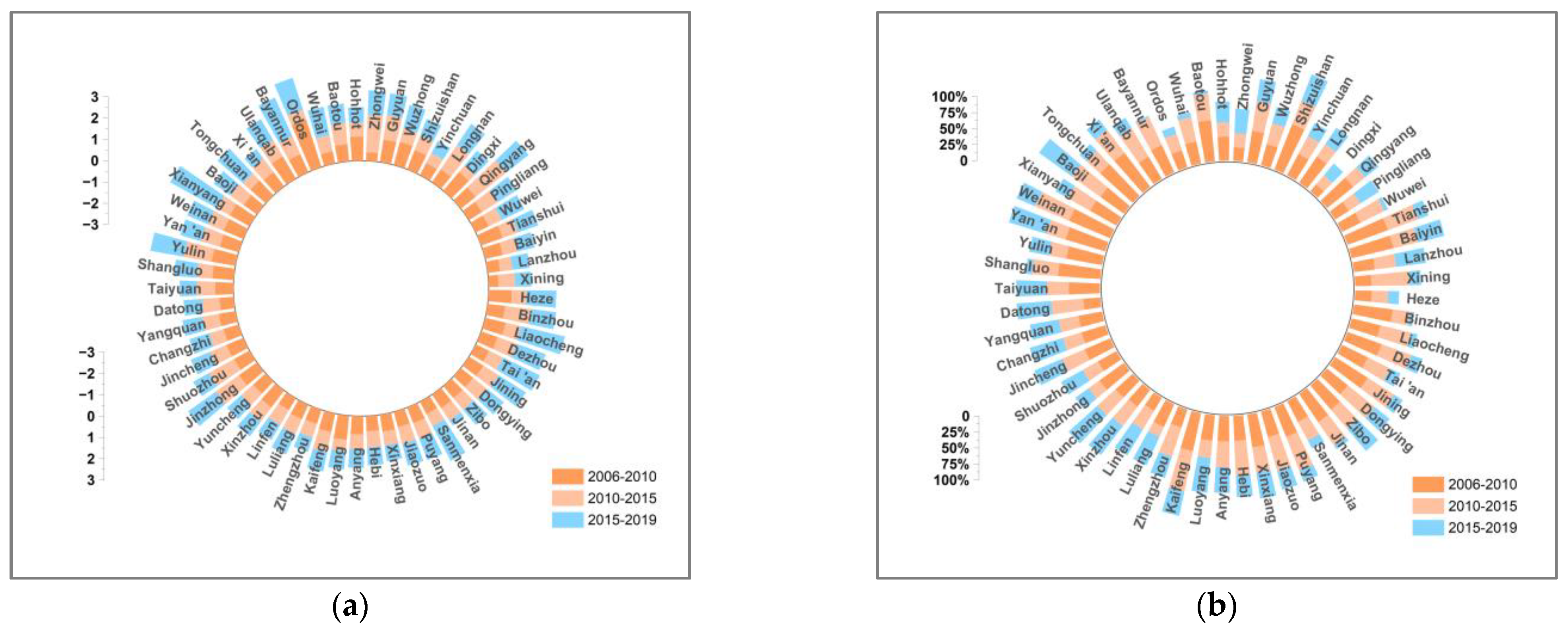
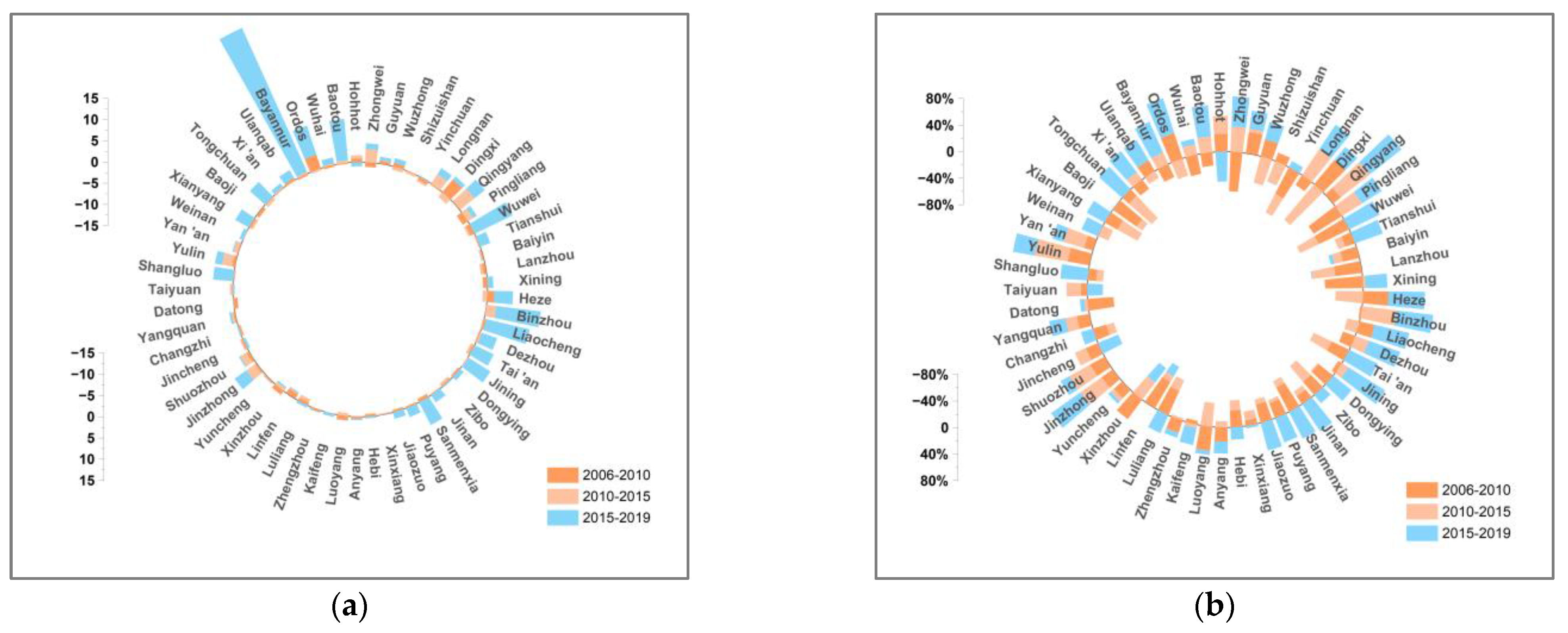
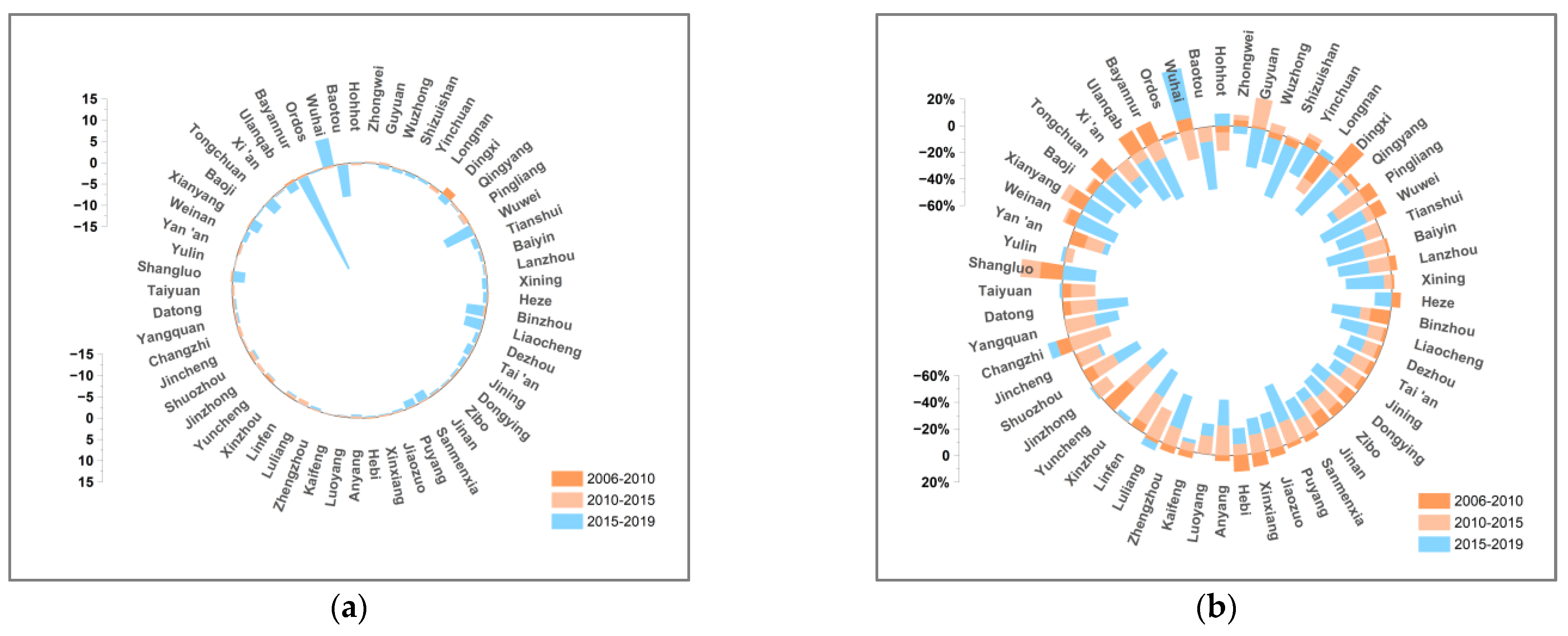
4.2. Driving Factors Analysis
4.2.1. Economic-Output Factor
4.2.2. Energy-Intensity Factor
4.2.3. Industrial-Structure Factor
4.2.4. Carbon-Emission-Coefficient Factor
4.2.5. Population-Scale Factor
4.2.6. Energy-Structure Factor
5. Discussions
5.1. Revisiting Decoupling and Decomposition Analysis of Cities in the YRB
5.2. Limitations and Potential Solutions
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, Y.J. The Impact of Financial Development on Carbon Emissions: An Empirical Analysis in China. Energy Policy 2011, 39, 2197–2203. [Google Scholar] [CrossRef]
- China State Council. The 13th Five-Year Plan for Controlling Greenhouse Gas Emissions [EB/OL]. Available online: http://www.gov.cn/zhengce/content/2016-11/04/content_5128619.htm (accessed on 27 October 2016).
- Osaki, M. 2013 Supplement to the 2006 IPCC Guidelines for National Greenhouse Gas Inventories: Wetlands Methodological Guidance on Lands with Wet and Drained Soils, and Construct ed Wetlands; IPCC: Geneva, Switzerland, 2014. [Google Scholar]
- Jin, F.J. Coordinated Promotion Strategy of Ecological Protection and High-quality Development in the Yellow River Basin. Reform 2019, 11, 33–39. [Google Scholar]
- Lu, D.D. Understanding and suggestions on the high quality development of the Yellow River Basin. China Science Daily, 10 December 2019. [Google Scholar]
- Lu, D.D.; Sun, D.Q. Development and management tasks of the Yellow River Basin: A preliminary understanding and suggestion. Acta Geogr. Sin. 2019, 74, 2431–2436. [Google Scholar]
- Zhu, X.M.; Wang, Z.S. Study on the assessment of carbon and water footprint and its spatial-temporal pattern in the Yellow River Basin. Environ. Sci. Technol. 2020, 43, 200–211. [Google Scholar]
- Wang, J.; Xu, D.Q.; Ma, B.B. Carbon emission and factor decomposition of energy consumption in Xi’an City based on GFI model. Arid Land Geogr. 2018, 41, 1388–1395. [Google Scholar]
- Wang, L.Y.; Chen, X.P.; Pang, J.X.; Duan, J.J. Decomposition and Scenario Analysis of Carbon Emission from Energy Consumption Based on LMDI Method: Taking Lanzhou as an Example. Ecol. Econ. 2019, 35, 38–44. [Google Scholar]
- Yang, M.; Lu, X.; Duan, H.B. Analysis on the determinants and peaking paths of CO2 emissions in China’s high energy-consuming industries. Syst. Eng. Theory Pract. 2018, 38, 11. [Google Scholar]
- Yu, W.M.; Zhang, T.T.; Shen, D.J. County-level spatial pattern and influencing factors evolution of carbon emission intensity in China: A random forest model analysis. China Environ. Sci. 2022, 42, 2788–2798. [Google Scholar]
- Wang, S.J.; Xie, Z.H.; Wang, Z.H. The spatiotemporal pattern evolution and influencing factors of CO2 emissions at the county level of China. Acta Geogr. Sin. 2021, 76, 3103–3118. [Google Scholar]
- Martinez-Zarzoso, I.; Bengochea-Morancho, A. Pooled Mean Group Estimation for an Environmental Kuznets Curve for CO2. Econ. Lett. 2004, 82, 121–126. [Google Scholar] [CrossRef]
- Tapio, P. Towards a theory of decoupling: Degrees of decoupling in the EU and the case of road traffic in Finland between 1970 and 2001. Transp. Policy 2005, 12, 137–151. [Google Scholar] [CrossRef]
- Zhou, Y.N.; Yang, Y.; Cheng, B.; Huang, J. Regional differences in the coupling relationship between Chinese economic growth and carbon emissions based on decoupling index and LMDI. J. Univ. Chin. Acad. Sci. 2020, 37, 295–307. [Google Scholar]
- Chen, Z.M.; Wu, S.M.; Ma, W.B.; Liu, X. Driving forces of carbon dioxide emission for China’s cities: Empirical analysis based on extended STIRPAT Model. China Popul. Resour. Environ. 2018, 28, 45–54. [Google Scholar]
- Hu, C.; Ding, Z.S.; Mu, X.Q.; Guo, X.Y.; Du, Z.J. The Spatio-Temporal Evolution and Driving Factors of Carbon Dioxide Emissions From Tourism Transportation in the Yangtze River Economic Belt. J. Nanjing Norm. Univ. 2021, 30, 1–11. [Google Scholar]
- Kuznets, S. Economic Growth and Income Equality. Am. Econ. Rev. 1955, 45, 1–28. [Google Scholar]
- Grossman, G.; Krueger, A. Environmental Impacts of the North American Free Trade Agreement. Q. J. Econ. 1995, 110, 13–56. [Google Scholar]
- Selden, T.M.; Song, D. Environmental Quality and Development: Is There a Kuznets Curve for Air Pollution Emissions? J. Environ. Econ. Manag. 1994, 27, 147–162. [Google Scholar] [CrossRef]
- Friedl, B.; Getzner, M. Determinants of CO2 Emissions in a Small Open Economy. Ecol. Econ. 2003, 45, 133–148. [Google Scholar] [CrossRef]
- Zhu, Y. Modeling Economic Growth and Water Environmental Degradation in the Circum-Bohai-Sea Zone of Liaoning Province. China Popul. Resour. Environ. 2014, 24, 65–68. [Google Scholar]
- Churchill, S.A.; Inekwe, J.; Ivanovski, K.; Smyth, R. The Environmental Kuznets Curve in the OECD: 1870–2014. Energy Econ. 2018, 75, 389–399. [Google Scholar] [CrossRef]
- Wang, Q.; Su, M. Drivers of decoupling economic growth from carbon emission—An empirical analysis of 192 countries using decoupling model and decomposition method. Environmental Impact Assess. Rev. 2020, 81, 106356. [Google Scholar] [CrossRef]
- Zhang, H.M.; Yuan, P.F.; Zhu, Z.S. Decoupling effects of carbon emissions and reduction path in the Yellow River Basin. Resour. Sci. 2022, 44, 59–69. [Google Scholar] [CrossRef]
- Li, H.; Zhao, Y.; Qiao, X.; Liu, Y.; Cao, Y.; Li, Y.; Wang, S.; Zhang, Z.; Zhang, Y.; Weng, J. Identifying the driving forces of national and regional CO2 emissions in China: Based on temporal and spatial decomposition analysis models. Energy Econ. 2017, 68, 522–538. [Google Scholar] [CrossRef]
- Wang, Q.; Wang, S.; Li, R. Determinants of Decoupling Economic Output from Carbon Emission in the Transport Sector: A Comparison Study of Four Municipalities in China. Int. J. Environ. Res. Public Health 2019, 16, 3729. [Google Scholar] [CrossRef] [PubMed]
- Ning, Y.D.; Zhang, B.Y.; Ding, T. Study of decoupling states of CO2 emission and its driving factors in Yangtze River economic belt. J. Dalian Univ. Technol. 2017, 57, 459–466. [Google Scholar]
- Zhao, M.M.; Li, R.R. Decoupling and decomposition analysis of carbon emissions from economic output in Chinese Guangdong Province: A sector perspective. Energy Environ. 2018, 29, 543–555. [Google Scholar] [CrossRef]
- Song, Y.; Zhang, M.; Zhou, M. Study on the decoupling relationship between CO2 emissions and economic development based on two-dimensional decoupling theory: A case between China and the United States. Ecol. Indic. 2019, 102, 230–236. [Google Scholar] [CrossRef]
- Song, Y.; Sun, J.J.; Zhang, M.; Su, B. Using the Tapio-Z decoupling model to evaluate the decoupling status of China’s CO2 emissions at provincial level and its dynamic trend. Struct. Change Econ. Dyn. 2020, 52, 120–129. [Google Scholar] [CrossRef]
- Xin, L.L.; Jia, J.S.; Hu, W.H.; Zeng, H.; Chen, C.; Wu, B. Decomposition and Decoupling Analysis of CO2 Emissions Based on LMDI and Two-Dimensional Decoupling Model in Gansu Province, China. Int. J. Environ. Res. Public Health 2021, 18, 6013. [Google Scholar] [CrossRef]
- Glaeser, L.E.; Kahn, E.M. The greenness of cities: Carbon dioxide emissions and urban development. J. Urban Econ. 2010, 67, 404–418. [Google Scholar] [CrossRef]
- Wu, J.X.; Guo, Z.Y. Research on the Convergence of Carbon Dioxide Emissions in China: A Continuous Dynamic Distribution Approach. Stat. Res. 2016, 33, 54–60. [Google Scholar]
- Zhang, H.; Feng, F. Can Informal environmental Regulation Reduce Carbon Emission?—Quasi-natural experiments from environmental disclosure. Res. Econ. Manag. 2020, 41, 62–80. [Google Scholar]
- Ren, X.S.; Liu, Y.J.; Zhao, G.H. The impact and transmission mechanism of economic agglomeration on carbon intensity. China Popul. Resour. Environ. 2020, 30, 95–106. [Google Scholar]
- Liu, X.P.; Sheng, S.H.; Wang, K.Y. Whether Economic Spatial Agglomeration Can Increase Carbon Productivity or Not? Econ. Rev. 2017, 6, 107–121. [Google Scholar]
- Nguyen, T.T.; Pham, T.A.T.; Tram, H.T.X. Role of information and communication technologies and innovation in driving carbon emissions and economic growth in selected G-20 countries. J. Environ. Manag. 2020, 261, 110162. [Google Scholar] [CrossRef] [PubMed]
- Grossman, G.M.; Krueger, A.B. Environmental Impacts of a North American Free Trade Agreement; National Bureau of Economic Research: Cambridge, MA, USA, 1991. [Google Scholar]
- Pal, D.; Mitra, S.K. The environmental Kuznets curve for carbon dioxide in India and China: Growth and pollution at crossroad. J. Policy Modeling 2017, 39, 371–385. [Google Scholar] [CrossRef]
- Kaya, Y. Impact of Carbon Dioxide Emission Control on GNP Growth: Interpretation of Proposed Scenarios; Intergovernmental Panel on Climate Change/Response Strategies Working Group; IPCC: Paris, France, 1989. [Google Scholar]
- Yue, S.J. Factor decomposition and scenario prediction of carbon peak in Yangtze River Delta urban agglomeration. Guizhou Soc. Sci. 2021, 9, 115–124. [Google Scholar]
- Ang, B.W. The LMDI approach to decomposition analysis: A practical guide. Energy Policy 2005, 33, 867–871. [Google Scholar] [CrossRef]
- Wang, Q.W.; Zhou, D.Q. Improved Model for Evaluating Rebound Effect of Energy Resource and Its Empirical Research. Chin. J. Manag. 2008, 5, 688–691. [Google Scholar]
- Li, G.Z.; Li, Z.Z. Analysis of demographic, economic and technological impacts on CO2 emissions: Based on dynamic panel models. Popul. Res. 2010, 34, 32–39. [Google Scholar]
- Zhang, W.Y.; Duan, X.J. The Research Progress in the Relationship among Economic Growth, Industrial Structure, and Carbon Emissions. Prog. Geogr. 2012, 31, 442–450. [Google Scholar]
- Guo, H.; Ren, B.P. Spatial Governance of High-quality Development in the Yellow River Basin: Mechanism Interpretation and Practical Strategies. Reform 2020, 4, 74–85. [Google Scholar]
- Xu, Y.; Wang, C.S. Ecological Protection and High-quality Development in the Yellow River Basin: Framework, Path, and Countermeasure. Bull. Chin. Acad. Sci. 2020, 35, 875–883. [Google Scholar]
- Huang, R.; Wang, Z.; Ding, G.Q.; Gong, Y.; Liu, C. Trend prediction and analysis of influencing factors of carbon emissions from energy consumption in Jiangsu province based on STIRPAT mode. Geogr. Res. 2016, 35, 781–789. [Google Scholar]
- Sun, Y.F.; Zhou, M. Decoupling and Driving Factors Analysis between the Energy Carbon Emissions and Economic Growth in China. Rev. Econ. Manag. 2017, 33, 21–30. [Google Scholar]
- Zhang, X.H.; Dong, H.Z. Study on Spatial-temporal Evolution of Carbon Emissions in “2 + 26” Cities and Its Driving Factors. Resour. Dev. Mark. 2021, 37, 1448–1456. [Google Scholar]
- Zhao, X.; Zhang, X.; Li, N.; Shao, S.; Geng, Y. Decoupling economic growth from carbon dioxide emissions in China: A sectoral factor decomposition analysis. J. Clean. Prod. 2017, 142, 3500–3516. [Google Scholar] [CrossRef]
- Ren, B.P.; Zhang, Q. The strategic design and support system construction of high-quality development in the Yellow River Basin. Reform 2019, 10, 26–34. [Google Scholar]
- Zhang, M.; Li, H.; Su, B.; Yang, X. Using a new two-dimensional decoupling model to evaluate the decoupling state of global energy footprint. Sustain. Cities Soc. 2020, 63, e102461. [Google Scholar] [CrossRef]
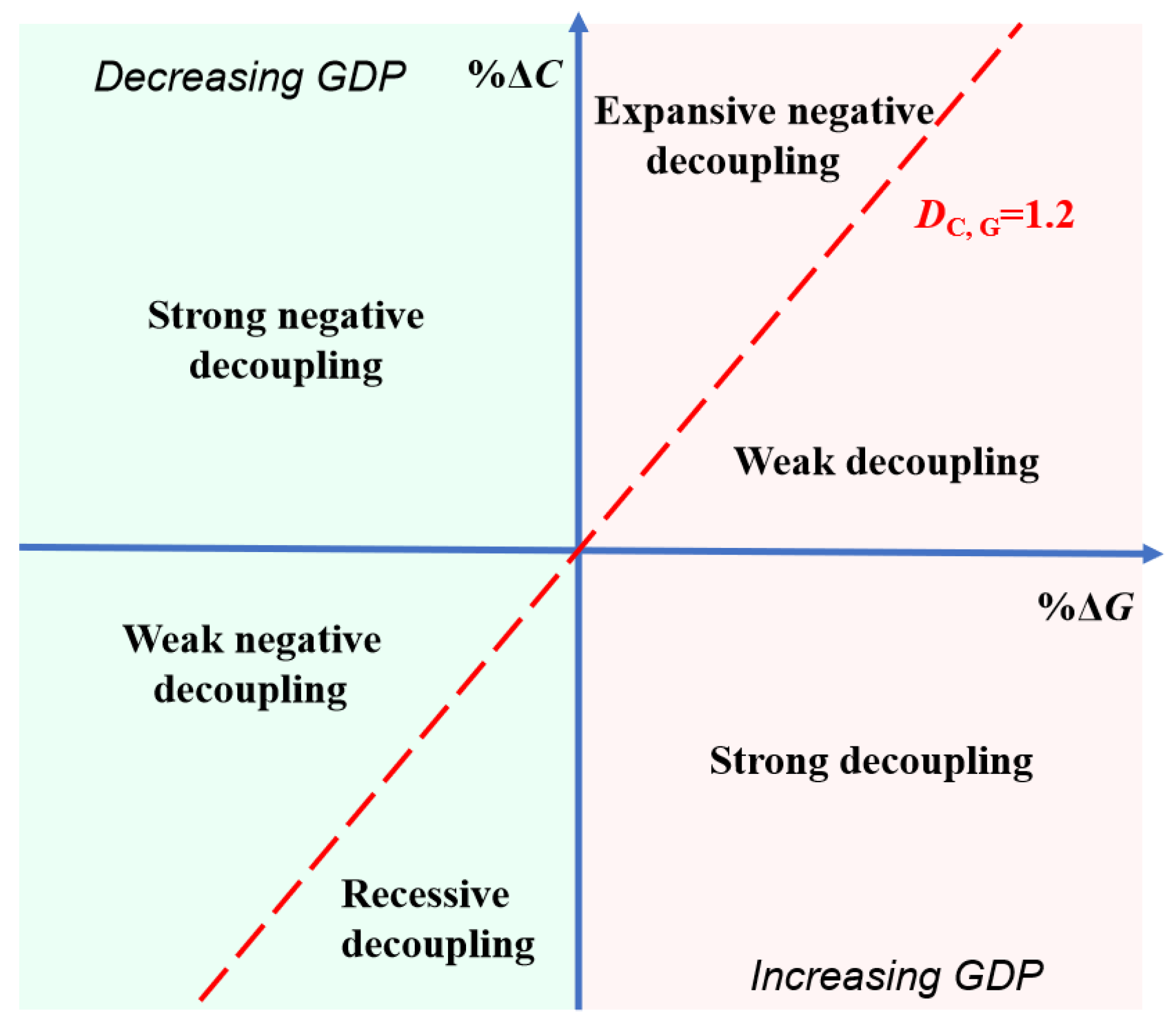
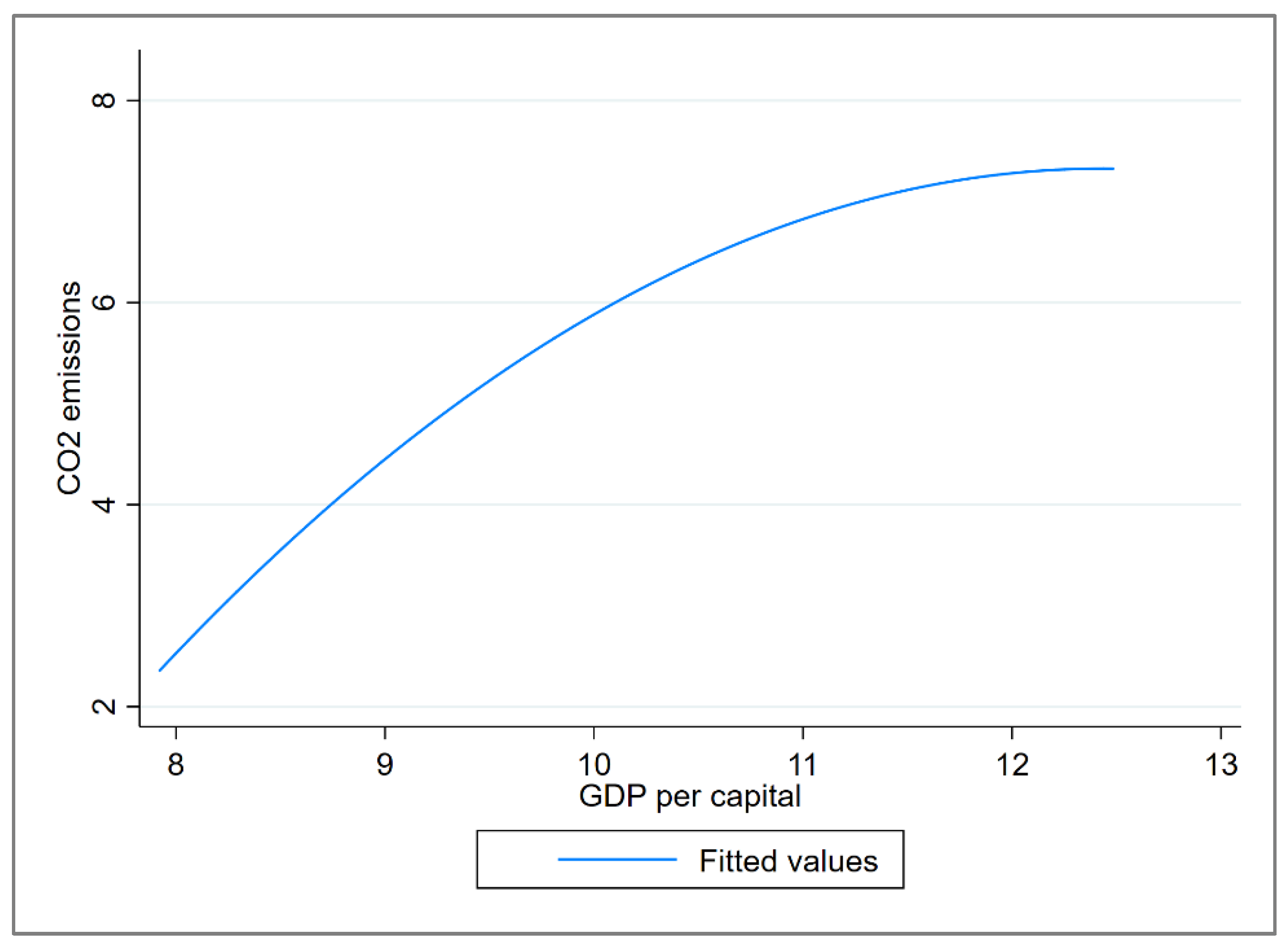
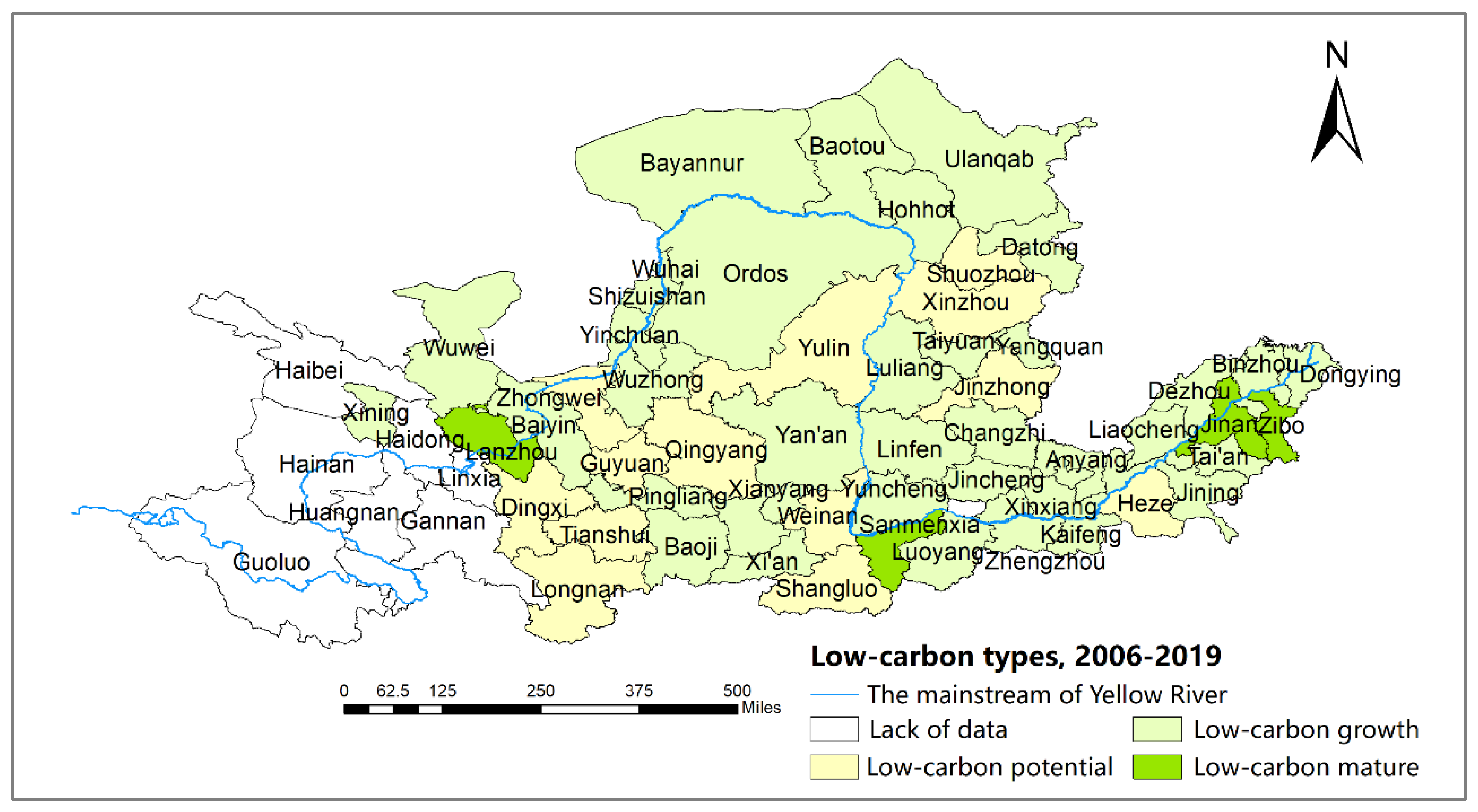
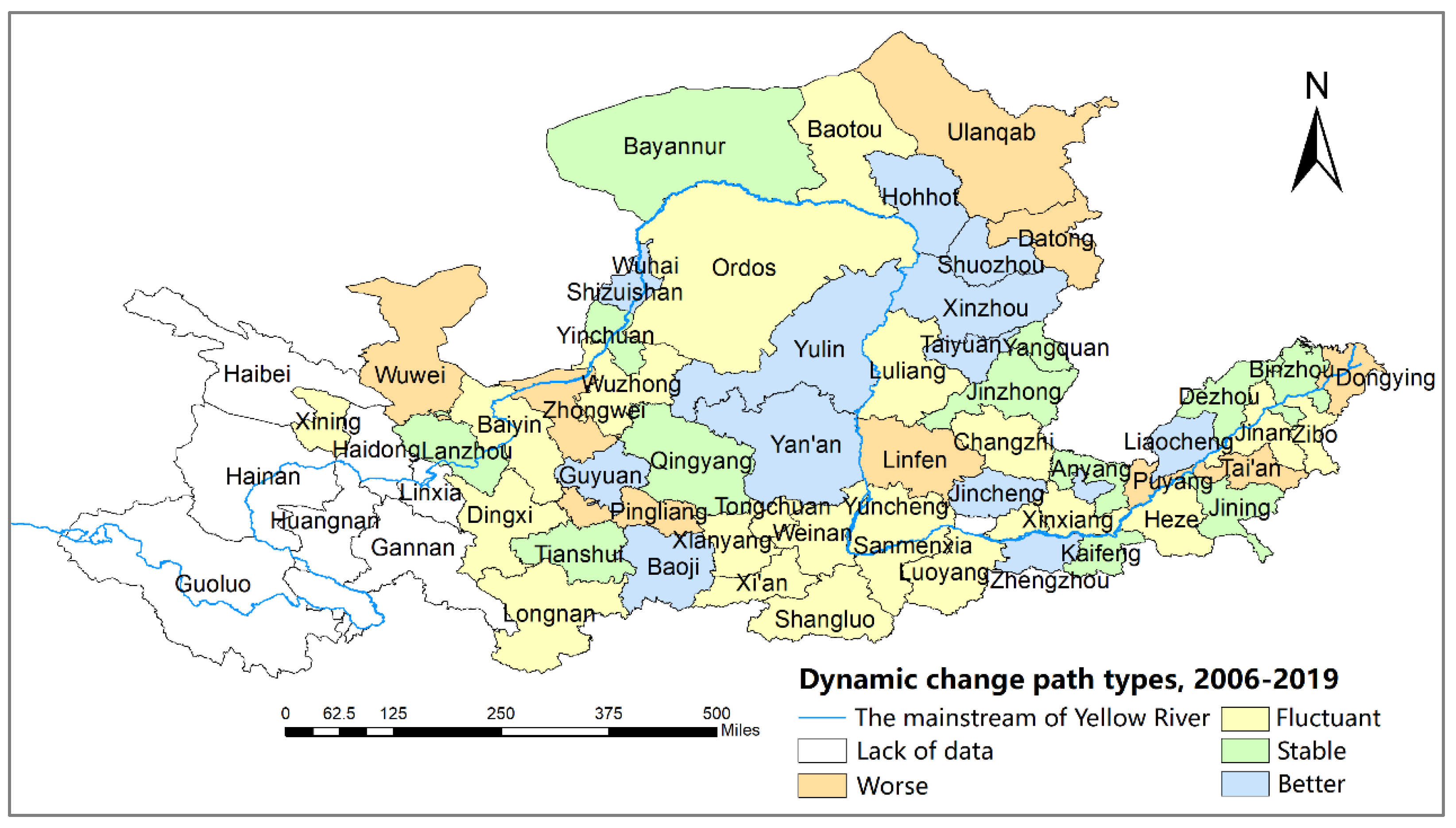
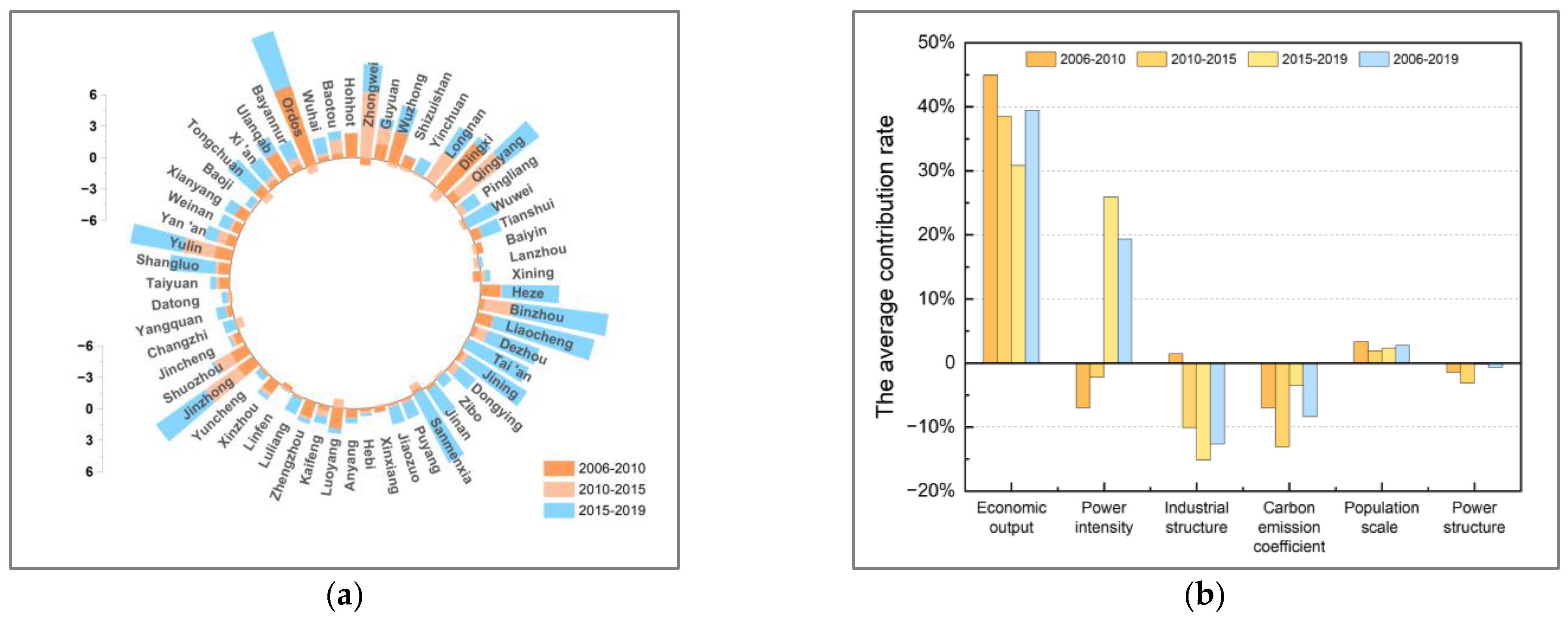



| Primary Term | Secondary Term | Tertiary Term | Type |
|---|---|---|---|
| U-shaped | |||
| Inverted U-shaped | |||
| N-shaped | |||
| Inverted N-shaped |
| Curve Types | Per Capita GDP | Two-Dimensional Decoupling Analysis Framework | |
|---|---|---|---|
| U-shaped | 0 |  (a) (b) (a) (b) | |
| 1.2 | |||
| Inverted U-shaped | 0 |  (c) (d) (c) (d) | |
| 1.2 | |||
| N-shaped | 0 | 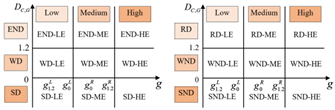 (e) (f) (e) (f) | |
| 1.2 | |||
| Inverted N-shaped | 0 | 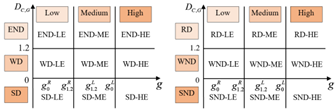 (g) (h) (g) (h) | |
| 1.2 |
| Variables | Indicator Explanation | Symbol |
|---|---|---|
| Population scale | Resident population at year-end | |
| Economic output | GDP per capita | |
| Industrial structure | Ratio of the second industrial increment to GDP | |
| Power intensity | Ratio of the total energy consumption to the second industrial increment | |
| Power structure | The proportion of consumption of energy in total energy consumption | |
| Carbon emission coefficient | Ratio of CO2 emission emitted by energy to consumption of energy |
| Energy Types | Average Low Calorific Capacity (kJ/kg) | Conversion Factor of Standard Coal (kgce/kg, m3) | CO2 Content per Unit Calorific Value (t CO2/TJ) | Oxidation Rate of CO2 | CO2 Emission Factor (kgCO2/kg) |
|---|---|---|---|---|---|
| Raw coal | 20,908 | 0.7143 | 26.37 | 0.94 | 1.9003 |
| Natural gas | 38,931 | 12.143 | 17.20 | 0.99 | 2.1622 |
| Liquefied petroleum gas | 50,179 | 1.7143 | 15.30 | 0.98 | 3.1013 |
| Region | Provinces and Cities |
|---|---|
| Northern China | Beiijng City, Tianjin City, Hebei Province, Shanxi Province, Shandong Province, Inner Mongolia Autonomous Region |
| Northeast China | Liaoning Province, Jilin Province, Heilongjiang Province |
| Eastern China | Shanghai City, Jiangsu Province, Zhejiang Province, Anhui Province, Fujian Province |
| Central China | Henan Province, Hubei Province, Hunan Province, Jiangxi Province, Sichuan Province, Chongqing City |
| Northwest China | Shaanxi Province, Gansu Province, Qinghai Province, Ningxia Autonomous Region, Xinjiang Autonomous Region |
| Southern Region | Guangdong Province, Guangxi Zhuang Autonomous Region, Yunnan Province, Guizhou Province, Hainan Province |
| Year | CO2 Emission Factors (kgCO2/Kwh) | |||||
|---|---|---|---|---|---|---|
| Northern China | Northeast China | Eastern China | Central China | Northwest China | Southern Region | |
| 2006 | 0.9825 | 1.0045 | 0.8640 | 0.9445 | 0.8410 | 0.7784 |
| 2007 | 1.0302 | 1.0517 | 0.9047 | 0.9746 | 0.8498 | 0.8434 |
| 2008 | 0.9928 | 1.0314 | 0.8888 | 0.9735 | 0.8712 | 0.8712 |
| 2009 | 0.8935 | 0.9267 | 0.7826 | 0.8529 | 0.8340 | 0.7880 |
| 2010 | 0.8704 | 0.9097 | 0.7691 | 0.7707 | 0.8413 | 0.7134 |
| 2011 | 0.8114 | 0.8420 | 0.7495 | 0.7244 | 0.7926 | 0.6323 |
| 2012 | 0.7980 | 0.8520 | 0.7567 | 0.7339 | 0.7656 | 0.6568 |
| 2013 | 0.8039 | 0.8619 | 0.7613 | 0.7385 | 0.7418 | 0.6496 |
| 2014 | 0.7995 | 0.8409 | 0.7478 | 0.7231 | 0.7045 | 0.6775 |
| 2015 | 0.7598 | 0.7803 | 0.7029 | 0.6508 | 0.6310 | 0.6304 |
| 2016 | 0.7253 | 0.7798 | 0.6785 | 0.6150 | 0.6392 | 0.5874 |
| 2017 | 0.7129 | 0.7196 | 0.6485 | 0.6063 | 0.6194 | 0.5422 |
| 2018 | 0.7080 | 0.6778 | 0.5886 | 0.5714 | 0.6430 | 0.5029 |
| 2019 | 0.7119 | 0.6613 | 0.5896 | 0.5721 | 0.6665 | 0.5089 |
| Variable | Coefficients | z-Statistic | Prob. |
|---|---|---|---|
| lng | 3.032 | 6.40 | 0.000 |
| lng2 | −0.651 | −4.38 | 0.000 |
| City | Decoupling State | Dynamic Path | Total Score | Rank | Type | ||
|---|---|---|---|---|---|---|---|
| 2006–2010 | 2010–2015 | 2015–2019 | |||||
| Zibo | WD-HE | SD-HE | WD-HE | 3-4-3 | 10 | 1 | I |
| Lanzhou | SD-ME | SD-ME | WD-HE | 3-3-3 | 9 | 2 | I |
| Sanmenxia | SD-ME | SD-HE | END-HE | 3-4-2 | 9 | 3 | I |
| Jinan | WD-HE | SD-HE | END-HE | 3-4-2 | 9 | 4 | I |
| Xining | SD-ME | WD-ME | WD-HE | 3-2-3 | 8 | 5 | II |
| Shizuishan | WD-ME | SD-ME | WD-HE | 2-3-3 | 8 | 6 | II |
| Hohhot | END-HE | WD-HE | WD-HE | 2-3-3 | 8 | 7 | II |
| Baotou | WD-HE | END-HE | WD-HE | 3-2-3 | 8 | 8 | II |
| Wuhai | WD-HE | WD-HE | END-HE | 3-3-2 | 8 | 9 | II |
| Ordos | END-HE | SD-HE | END-HE | 2-4-2 | 8 | 10 | II |
| Taiyuan | WD-ME | WD-HE | WD-HE | 2-3-3 | 8 | 11 | II |
| Luoyang | END-ME | SD-HE | WD-HE | 1-4-3 | 8 | 12 | II |
| Dongying | WD-HE | WD-HE | END-HE | 3-3-2 | 8 | 13 | II |
| Taian | SD-ME | SD-ME | END-HE | 3-3-2 | 8 | 14 | II |
| Baiyin | WD-ME | SD-ME | WD-ME | 2-3-2 | 7 | 15 | II |
| Wuwei | SD-ME | SD-ME | END-ME | 3-3-1 | 7 | 16 | II |
| Datong | SD-ME | WD-ME | WD-ME | 3-2-2 | 7 | 17 | II |
| Changzhi | WD-ME | SD-ME | WD-ME | 2-3-2 | 7 | 18 | II |
| Jincheng | WD-ME | WD-ME | WD-HE | 2-2-3 | 7 | 19 | II |
| Yuncheng | WD-ME | SD-ME | WD-ME | 2-3-2 | 7 | 20 | II |
| Linfen | SD-ME | WD-ME | WD-ME | 3-2-2 | 7 | 21 | II |
| Xi’an | WD-ME | WD-HE | END-HE | 2-3-2 | 7 | 22 | II |
| Baoji | WD-ME | WD-ME | WD-HE | 2-2-3 | 7 | 23 | II |
| Xianyang | WD-ME | SD-ME | WD-ME | 2-3-2 | 7 | 24 | II |
| Yan’an | WD-ME | WD-ME | WD-HE | 2-2-3 | 7 | 25 | II |
| Zhengzhou | END-ME | WD-HE | WD-HE | 1-3-3 | 7 | 26 | II |
| Hebi | WD-ME | WD-ME | WD-HE | 2-2-3 | 7 | 27 | II |
| Xinxiang | WD-ME | SD-ME | WD-ME | 2-3-2 | 7 | 28 | II |
| Jiaozuo | WD-ME | WD-HE | END-HE | 2-3-2 | 7 | 29 | II |
| Yinchuan | WD-ME | SD-HE | END-HE | 2-2-2 | 6 | 30 | II |
| Bayannao | WD-ME | WD-ME | END-HE | 2-2-2 | 6 | 31 | II |
| Yangquan | WD-ME | WD-ME | WD-ME | 2-2-2 | 6 | 32 | II |
| Luliang | WD-ME | SD-ME | END-ME | 2-3-1 | 6 | 33 | II |
| Tongchuan | WD-ME | SD-ME | END-ME | 2-3-1 | 6 | 34 | II |
| Kaifeng | WD-ME | WD-ME | WD-ME | 2-2-2 | 6 | 35 | II |
| Anyang | WD-ME | WD-ME | WD-ME | 2-2-2 | 6 | 36 | II |
| Jining | WD-ME | WD-ME | END-HE | 2-2-2 | 6 | 37 | II |
| Dezhou | WD-ME | WD-ME | END-HE | 2-2-2 | 6 | 38 | II |
| Binzhou | WD-ME | END-HE | END-HE | 2-2-2 | 6 | 39 | II |
| Pingliang | SD-LE | WD-ME | END-ME | 2-2-1 | 5 | 40 | II |
| Wuzhong | END-ME | SD-ME | END-ME | 1-3-1 | 5 | 41 | II |
| Weinan | WD-LE | WD-ME | WD-ME | 1-2-2 | 5 | 42 | II |
| Puyang | WD-ME | WD-ME | END-ME | 2-2-1 | 5 | 43 | II |
| Liaocheng | END-ME | WD-ME | END-HE | 1-2-2 | 5 | 44 | II |
| Zhongwei | SD-LE | END-ME | END-ME | 2-1-1 | 4 | 45 | III |
| Ulanqab | END-ME | WD-ME | END-ME | 1-2-1 | 4 | 46 | III |
| Shuozhou | END-ME | END-ME | WD-ME | 1-1-2 | 4 | 47 | III |
| Xinzhou | END-LE | WD-ME | WD-ME | 0-2-2 | 4 | 48 | III |
| Yulin | END-ME | END-ME | END-HE | 1-1-2 | 4 | 49 | III |
| Shangluo | WD-LE | WD-ME | END-ME | 1-2-1 | 4 | 50 | III |
| Tianshui | WD-LE | WD-LE | END-ME | 1-1-1 | 3 | 51 | III |
| Qingyang | WD-LE | END-ME | END-ME | 1-1-1 | 3 | 52 | III |
| Dingxi | END-LE | SD-LE | WD-LE | 0-2-1 | 3 | 53 | III |
| Jinzhong | END-ME | END-ME | END-ME | 1-1-1 | 3 | 54 | III |
| Heze | END-LE | WD-ME | END-ME | 0-2-1 | 3 | 55 | III |
| Longnan | WD-LE | END-LE | END-ME | 1-0-1 | 2 | 56 | III |
| Guyuan | END-LE | END-LE | WD-ME | 0-0-2 | 2 | 57 | III |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kong, Y.; Liu, C.; Liu, S.; Feng, S.; Zhou, H. Two-Dimensional Decoupling and Decomposition Analysis of CO2 Emissions from Economic Growth: A Case Study of 57 Cities in the Yellow River Basin. Int. J. Environ. Res. Public Health 2022, 19, 12503. https://doi.org/10.3390/ijerph191912503
Kong Y, Liu C, Liu S, Feng S, Zhou H. Two-Dimensional Decoupling and Decomposition Analysis of CO2 Emissions from Economic Growth: A Case Study of 57 Cities in the Yellow River Basin. International Journal of Environmental Research and Public Health. 2022; 19(19):12503. https://doi.org/10.3390/ijerph191912503
Chicago/Turabian StyleKong, Yawen, Chunyu Liu, Shuguang Liu, Shan Feng, and Hongwei Zhou. 2022. "Two-Dimensional Decoupling and Decomposition Analysis of CO2 Emissions from Economic Growth: A Case Study of 57 Cities in the Yellow River Basin" International Journal of Environmental Research and Public Health 19, no. 19: 12503. https://doi.org/10.3390/ijerph191912503
APA StyleKong, Y., Liu, C., Liu, S., Feng, S., & Zhou, H. (2022). Two-Dimensional Decoupling and Decomposition Analysis of CO2 Emissions from Economic Growth: A Case Study of 57 Cities in the Yellow River Basin. International Journal of Environmental Research and Public Health, 19(19), 12503. https://doi.org/10.3390/ijerph191912503





