Spatial Pattern and Fairness Measurement of Educational Resources in Primary and Middle Schools: A Case Study of Chengdu–Chongqing Economic Circle
Abstract
1. Introduction
2. Study Area and Materials
3. Methodology
3.1. Standard Deviation Ellipse
3.2. Kernel Density Estimation
3.3. Spatial Autocorrelation Analysis
- Global spatial autocorrelation analysis
- Local spatial autocorrelation analysis
3.4. Index of Dissimilarity
3.5. Agglomeration Degree
4. Results
4.1. Analysis on the Spatial Pattern of PMSs
4.1.1. Spatial Distribution of PMSs
4.1.2. Agglomeration Characteristics of PMSs
4.2. Analysis on the Fairness of Educational Resources
4.2.1. Temporal Variation Characteristics of Fairness on a Global Scale
4.2.2. Temporal Variation Characteristics of Fairness on a Local Scale
5. Discussion
5.1. Advantages of Proposed Method over Conventional Methods
5.2. Factors Affecting the Fairness of Educational Resources
5.3. Limitations and Future Research Directions
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Region | Type | Center-x | Center-y | StdDist-x | StdDist-y | Rotation |
|---|---|---|---|---|---|---|
| Chengdu | Primary school | 104.05 | 30.65 | 0.46 | 0.26 | 86.30 |
| Middle school | 104.04 | 30.64 | 0.45 | 0.28 | 89.98 | |
| Mianyang | Primary school | 104.97 | 31.40 | 0.48 | 0.34 | 128.84 |
| Middle school | 104.88 | 31.41 | 0.46 | 0.29 | 129.66 | |
| Dazhou | Primary school | 107.40 | 31.07 | 0.53 | 0.29 | 59.04 |
| Middle school | 107.45 | 31.13 | 0.54 | 0.27 | 57.52 | |
| Deyang | Primary school | 104.43 | 31.10 | 0.43 | 0.18 | 123.37 |
| Middle school | 104.43 | 31.09 | 0.40 | 0.18 | 123.39 | |
| Guang’an | Primary school | 106.63 | 30.45 | 0.40 | 0.22 | 100.04 |
| Middle school | 106.64 | 30.41 | 0.43 | 0.19 | 95.11 | |
| Leshan | Primary school | 103.69 | 29.41 | 0.35 | 0.39 | 29.69 |
| Middle school | 103.73 | 29.46 | 0.32 | 0.39 | 13.74 | |
| Luzhou | Primary school | 105.59 | 28.59 | 0.32 | 0.68 | 164.14 |
| Middle school | 105.56 | 28.68 | 0.30 | 0.62 | 160.58 | |
| Meishan | Primary school | 103.89 | 30.02 | 0.47 | 0.22 | 85.97 |
| Middle school | 103.92 | 30.01 | 0.48 | 0.21 | 86.24 | |
| Nanchong | Primary school | 106.19 | 31.14 | 0.46 | 0.40 | 59.25 |
| Middle school | 106.19 | 31.10 | 0.38 | 0.44 | 39.03 | |
| Neijiang | Primary school | 104.96 | 29.60 | 0.37 | 0.21 | 113.09 |
| Middle school | 104.96 | 29.61 | 0.35 | 0.20 | 115.73 | |
| Suining | Primary school | 105.47 | 30.63 | 0.25 | 0.32 | 152.92 |
| Middle school | 105.45 | 30.63 | 0.23 | 0.32 | 158.97 | |
| Ya’an | Primary school | 102.93 | 29.88 | 0.15 | 0.57 | 39.91 |
| Middle school | 102.95 | 29.91 | 0.16 | 0.56 | 39.54 | |
| Yibin | Primary school | 104.73 | 28.59 | 0.48 | 0.39 | 134.41 |
| Middle school | 104.70 | 28.62 | 0.47 | 0.37 | 125.84 | |
| Ziyang | Primary school | 105.07 | 30.12 | 0.46 | 0.21 | 100.74 |
| Middle school | 105.08 | 30.09 | 0.46 | 0.22 | 102.70 | |
| Zigong | Primary school | 104.85 | 29.26 | 0.39 | 0.14 | 113.14 |
| Middle school | 104.81 | 29.27 | 0.38 | 0.13 | 112.66 | |
| MUAC | Primary school | 106.55 | 29.59 | 0.18 | 0.22 | 31.93 |
| Middle school | 106.54 | 29.59 | 0.17 | 0.22 | 31.29 | |
| Bishan | Primary school | 106.19 | 29.53 | 0.05 | 0.20 | 17.18 |
| Middle school | 106.20 | 29.56 | 0.05 | 0.19 | 16.08 | |
| Dazu | Primary school | 105.76 | 29.65 | 0.16 | 0.13 | 83.13 |
| Middle school | 105.74 | 29.64 | 0.11 | 0.13 | 150.80 | |
| Dianjiang | Primary school | 107.40 | 30.27 | 0.11 | 0.18 | 22.00 |
| Middle school | 107.39 | 30.27 | 0.11 | 0.17 | 7.20 | |
| Fengdu | Primary school | 107.79 | 29.94 | 0.15 | 0.25 | 144.09 |
| Middle school | 107.77 | 29.96 | 0.15 | 0.20 | 149.76 | |
| Fuling | Primary school | 107.34 | 29.70 | 0.23 | 0.13 | 61.32 |
| Middle school | 107.32 | 29.68 | 0.22 | 0.10 | 57.93 | |
| Hechuan | Primary school | 106.33 | 30.11 | 0.25 | 0.16 | 98.19 |
| Middle school | 106.31 | 30.08 | 0.24 | 0.14 | 110.64 | |
| Jiangjin | Primary school | 106.25 | 29.16 | 0.21 | 0.23 | 4.85 |
| Middle school | 106.27 | 29.12 | 0.20 | 0.25 | 176.10 | |
| Kaizhou | Primary school | 108.37 | 31.11 | 0.05 | 0.18 | 39.26 |
| Middle school | 108.39 | 31.14 | 0.05 | 0.13 | 39.65 | |
| Liangping | Primary school | 107.73 | 30.66 | 0.22 | 0.11 | 83.30 |
| Middle school | 107.72 | 30.66 | 0.21 | 0.11 | 88.18 | |
| Nanchuan | Primary school | 107.15 | 29.17 | 0.13 | 0.22 | 148.49 |
| Middle school | 107.11 | 29.20 | 0.12 | 0.08 | 65.35 | |
| Pengshui | Primary school | 108.34 | 29.62 | 0.09 | 0.06 | 85.71 |
| Middle school | 108.36 | 29.61 | 0.08 | 0.05 | 106.93 | |
| Qijiang | Primary school | 106.74 | 28.91 | 0.17 | 0.20 | 14.23 |
| Middle school | 106.72 | 28.93 | 0.17 | 0.21 | 5.27 | |
| Qianjiang | Primary school | 108.71 | 29.53 | 0.11 | 0.23 | 152.02 |
| Middle school | 108.75 | 29.47 | 0.10 | 0.19 | 160.28 | |
| Rongchang | Primary school | 105.52 | 29.44 | 0.16 | 0.10 | 125.55 |
| Middle school | 105.51 | 29.44 | 0.10 | 0.16 | 136.69 | |
| Shizhu | Primary school | 108.20 | 29.73 | 0.01 | 0.05 | 28.25 |
| Middle school | 108.19 | 29.72 | 0.01 | 0.04 | 25.81 | |
| Tongliang | Primary school | 106.03 | 29.83 | 0.13 | 0.17 | 177.95 |
| Middle school | 106.03 | 29.79 | 0.11 | 0.17 | 165.65 | |
| Tongnan | Primary school | 105.81 | 30.14 | 0.11 | 0.19 | 6.00 |
| Middle school | 105.80 | 30.16 | 0.11 | 0.14 | 5.93 | |
| Wanzhou | Primary school | 108.40 | 30.77 | 0.23 | 0.13 | 89.88 |
| Middle school | 108.35 | 30.77 | 0.21 | 0.12 | 82.90 | |
| Yongchuan | Primary school | 105.88 | 29.30 | 0.10 | 0.19 | 25.27 |
| Middle school | 105.87 | 29.28 | 0.10 | 0.20 | 24.94 | |
| Yunyang | Primary school | 108.71 | 31.00 | 0.12 | 0.18 | 7.41 |
| Middle school | 108.72 | 31.03 | 0.11 | 0.18 | 20.84 | |
| Changshou | Primary school | 107.12 | 29.96 | 0.11 | 0.17 | 34.30 |
| Middle school | 107.11 | 29.92 | 0.12 | 0.14 | 42.38 | |
| Zhongxian | Primary school | 107.93 | 30.33 | 0.23 | 0.14 | 74.30 |
| Middle school | 107.91 | 30.31 | 0.23 | 0.13 | 83.23 |

References
- Dadon-Golan, Z.; BenDavid-Hadar, I.; Klein, J. Revisiting educational (in)equity: Measuring educational Gini coefficients for Israeli high schools during the years 2001–2011. Int. J. Educ. Dev. 2019, 70, 102091. [Google Scholar] [CrossRef]
- Tarabini, A. Education and poverty in the global development agenda: Emergence, evolution and consolidation. Int. J. Educ. Dev. 2010, 30, 204–212. [Google Scholar] [CrossRef]
- Yang, J.; Huang, X.; Liu, X. An analysis of education inequality in China. Int. J. Educ. Dev. 2014, 37, 2–10. [Google Scholar] [CrossRef]
- Xiang, L.; Stillwell, J.; Burns, L.; Heppenstall, A.J.; Norman, P. A geodemographic classification of sub-districts to identify education inequality in Central Beijing. Comput. Environ. Urban Syst. 2018, 70, 59–70. [Google Scholar] [CrossRef]
- Burger, K. The socio-spatial dimension of educational inequality: A comparative European analysis. Stud. Educ. Eval. 2019, 62, 171–186. [Google Scholar] [CrossRef]
- Hu, L.; He, S.; Luo, Y.; Su, S.; Xin, J.; Weng, M. A social-media-based approach to assessing the effectiveness of equitable housing policy in mitigating education accessibility induced social inequalities in Shanghai, China. Land Use Policy 2020, 94, 104513. [Google Scholar] [CrossRef]
- Li, G.; Jiang, G.; Jiang, C.; Bai, J. Differentiation of spatial morphology of rural settlements from an ethnic cultural perspective on the Northeast Tibetan Plateau, China. Habitat Int. 2018, 79, 1–9. [Google Scholar] [CrossRef]
- Yan, Q.; Li, C.; Jing, Z.; Luo, F. Uneven distribution of primary and middle schools: A case study of Changchun, China. Front. Educ. China 2018, 13, 633–655. [Google Scholar] [CrossRef]
- Guo, M.; Hu, B. Assessing the spatial layout efficiency of basic educational resources by an improved coverage model: A case study of Nanchang City, China. J. Geo-Inf. Sci. 2019, 21, 875–886. [Google Scholar] [CrossRef]
- Zhao, D.; Parolin, B. Merged or unmerged school? School preferences in the context of school mapping restructure in rural China. Asia-Pac. Educ. Res. 2013, 23, 547–563. [Google Scholar] [CrossRef]
- Knight, D. Are school districts allocating resources equitably? The every student succeeds act, teacher experience gaps, and equitable resource allocation. Educ. Policy 2017, 33, 615–649. [Google Scholar] [CrossRef]
- Halai, A. Equality or equity: Gender awareness issues in secondary schools in Pakistan. Int. J. Educ. Dev. 2011, 31, 44–49. [Google Scholar] [CrossRef]
- Meschi, E.; Scervini, F. A new dataset on educational inequality. Empir. Econ. 2014, 47, 695–716. [Google Scholar] [CrossRef]
- Kyriakides, L.; Creemers, B.; Charalambous, E. Searching for differential teacher and school effectiveness in terms of student socioeconomic status and gender: Implications for promoting equity. Sch. Eff. Sch. Improv. 2018, 30, 286–308. [Google Scholar] [CrossRef]
- Luo, Y.; Zhou, R.; Mizunoya, S.; Amaro, D. How various types of disabilities impact children’s school attendance and completion—Lessons learned from censuses in eight developing countries. Int. J. Educ. Dev. 2020, 77, 102222. [Google Scholar] [CrossRef]
- Birdsall, N.; Londono, J. Asset inequality matters: An assessment of the world bank’s approach to poverty reduction. Am. Econ. Rev. 1997, 87, 32–37. [Google Scholar] [CrossRef]
- Lam, D.; Levison, D. Declining inequality in schooling in Brazil and its effects on inequality in earnings. J. Dev. Econ. 1991, 37, 199–225. [Google Scholar] [CrossRef]
- Tomul, E. Educational inequality in Turkey: An evaluation by Gini Index. Eğitim Ve Bilim 2011, 36, 133–143. [Google Scholar]
- Saeed, N.; Fatima, A. Educational inequality in rural and urban Sindh. Pak. Dev. Rev. 2015, 54, 767–777. [Google Scholar] [CrossRef]
- Yu, Y.; Han, Z.; Du, P. Study on equality and distribution optimization of educational resources in primary schools: A case study of Dazheng Town. J. Liaoning Norm. Univ. 2017, 40, 95–103. [Google Scholar] [CrossRef]
- Omoeva, C.; Menezes Cunha, N.; Moussa, W. Measuring equity of education resource allocation: An output-based approach. Int. J. Educ. Dev. 2021, 87, 102492. [Google Scholar] [CrossRef]
- Adams, D. Educational planning. Science 1973, 179, 1254–1255. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Stone, R. Input-output and demographic accounting: A tool for educational planning. Minerva 1966, 4, 365–380. [Google Scholar] [CrossRef]
- Hones, G.; Ryba, R. Why not a geography of education? J. Geogr. 1972, 71, 135–139. [Google Scholar] [CrossRef]
- Pacione, M. The geography of educational disadvantage in Glasgow. Appl. Geogr. 1997, 17, 169–192. [Google Scholar] [CrossRef]
- Mulaku, G.; Nyadimo, E. Gis in education planning: The kenyan school mapping project. Surv. Rev. 2011, 43, 567–578. [Google Scholar] [CrossRef]
- Sohoni, D.; Saporito, S. Mapping school segregation: Using GIS to explore racial segregation between schools and their corresponding attendance areas. Am. J. Educ. 2009, 115, 569–600. [Google Scholar] [CrossRef]
- Butler, T.; Robson, G. Social capital, gentrification and neighbourhood change in London: A comparison of three south london neighbourhoods. Urban Stud. 2001, 38, 2145–2162. [Google Scholar] [CrossRef]
- Lubienski, C.; Lee, J. Geo-spatial analyses in education research: The critical challenge and methodological possibilities. Geogr. Res. 2017, 55, 89–99. [Google Scholar] [CrossRef]
- Thrupp, M. School admissions and the segregation of school intakes in New Zealand cities. Urban Stud. 2007, 44, 1393–1404. [Google Scholar] [CrossRef]
- Fincher, R.; Shaw, K. The unintended segregation of transnational students in central Melbourne. Environ. Plan. A 2009, 41, 1884–1902. [Google Scholar] [CrossRef]
- Hubbard, P. Geographies of studentification and purpose-built student accommodation: Leading separate lives? Environ. Plan. A 2009, 41, 1903–1923. [Google Scholar] [CrossRef]
- Witten, K.; Kearns, R.; Lewis, N.; Coster, H.; McCreanor, T. Educational restructuring from a community viewpoint: A case study of school closure from Invercargill, New Zealand. Environ. Plan. C Gov. Policy 2003, 21, 203–223. [Google Scholar] [CrossRef]
- Pizzol, B.; Giannotti, M.; Tomasiello, D.B. Qualifying accessibility to education to investigate spatial equity. J. Transp. Geogr. 2021, 96, 103199. [Google Scholar] [CrossRef]
- Romanillos, G.; García-Palomares, J. Accessibility to schools: Spatial and social imbalances and the impact of population density in four European cities. J. Urban Plan. Dev. 2018, 144, 04018044. [Google Scholar] [CrossRef]
- Chen, Z.; Zhou, X.; Yeh, A. Spatial accessibility to kindergartens using a spectrum combinational approach: Case study of Shanghai using cellphone data. Environ. Plan. B Urban Anal. City Sci. 2020, 48, 1390. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, Y.; Xing, L.; Zhang, Z. An improved accessibility-based model to evaluate educational equity: A case study in the city of Wuhan. ISPRS Int. J. Geo-Inf. 2021, 10, 458. [Google Scholar] [CrossRef]
- Chen, S.; Qi, X.; Lin, H.; Jin, X.; Li, D. The improvement and application of two-step floating catchment area method in measuring accessibility to education public service: A case study of kindergartens in Fuzhou. Hum. Geogr. 2017, 32, 53–60. [Google Scholar] [CrossRef]
- Yuan, Z.; Guo, J.; Yang, Y.; Zhu, H. Analysis of the spatial structure, mechanism and social-political effects of the high-quality basic educational resources in China. Acta Geogr. Sin. 2020, 75, 318–331. [Google Scholar] [CrossRef]
- Luo, Z.; Gao, X.; Zhang, Y.; Li, L. Research on the spatial pattern and influencing factors of urban shadow education institutions based on POI data : A case of Lanzhou. Hum. Geogr. 2020, 35, 95–105. [Google Scholar] [CrossRef]
- Wang, M.; Guo, Y.; Xie, Y.; Yang, X.; Huang, Y. Evaluation and analysis of spatial equity measure of public education resources. Sci. Surv. Mapp. 2020, 45, 191–196. [Google Scholar] [CrossRef]
- Lu, W.; Li, Y.; Zhao, R.; Wang, Y. Using remote sensing to identify urban fringe areas and their spatial pattern of educational resources: A case study of the Chengdu-Chongqing economic circle. Remote Sens. 2022, 14, 3148. [Google Scholar] [CrossRef]
- Williams, S.; Wang, F. Disparities in accessibility of public high schools, in metropolitan Baton Rouge, Louisiana 1990–2010. Urban Geogr. 2014, 35, 1066–1083. [Google Scholar] [CrossRef]
- Boussauw, K.; van Meeteren, M.; Witlox, F. Short trips and central places: The home-school distances in the Flemish primary education system (Belgium). Appl. Geogr. 2014, 53, 311–322. [Google Scholar] [CrossRef]
- Talen, E. School, community, and spatial equity: An empirical investigation of access to elementary schools in West Virginia. Ann. Assoc. Am. Geogr. 2001, 91, 465–486. [Google Scholar] [CrossRef]
- Zhao, W.; Zou, X.; Pu, H. Construction of ecological security pattern in Chengdu-Chongqing twin-city economic circle. China Environ. Sci. 2021, 41, 2423–2433. [Google Scholar] [CrossRef]
- He, W.; Lan, G.; Yang, K. The layout and structure optimization of higher education in Chengdu-Chongqing main axis. ChongQing High. Educ. Res. 2020, 8, 23–33. [Google Scholar] [CrossRef]
- Lefever, D. Measuring geographic concentration by means of the standard deviational ellipse. Am. J. Sociol. 1926, 32, 88–94. [Google Scholar] [CrossRef]
- Silverman, B. Density estimation for statistics and data analysis chapman and hall. J. Am. Stat. Assoc. 1988, 83, 269–270. [Google Scholar] [CrossRef]
- Di, Q.; Wang, L.; Qiu, Y. Spatial correlation analysis of urban development level of prefecture-cities in China’s coastal provinces. Resour. Dev. Mark. 2018, 34, 649–653. [Google Scholar] [CrossRef]
- Zang, L.; Zhang, C.; Hao, J. Research on spatial distribution of under-forest economic development in China. Probl. For. Econ. 2014, 34, 442–446. [Google Scholar] [CrossRef]
- Li, E. Analysis on comprehensive benefit evaluation of land use: Taking Liuzhou City as an example. Rural. Econ. Sci. Technol. 2011, 22, 5–8. [Google Scholar] [CrossRef]
- Zhang, S.; Wang, Y.; Li, Y.; Zhang, P. Spatial distribution of haze pollution and its influencing factors. China Popul. Resour. Environ. 2017, 27, 15–22. [Google Scholar] [CrossRef]
- Yao, K.; Yue, S. Study on spatial distribution of modern sweet diet and its impact factors in China based on big data from internet. J. Geo-Inf. Sci. 2020, 22, 1202–1215. [Google Scholar] [CrossRef]
- Li, X.; Zhang, Q. Analysis on the equity of health resources allocation based on Gini coefficient and index of dissimilarity in Guangdong. Mod. Prev. Med. 2019, 46, 658–662+686. [Google Scholar]
- Zhou, M.; Tan, H.; He, S.; Shao, M.; Feng, X. Equity of primary medical and health resources based on the difference index and the agglomeration degree, Sichuan. Mod. Prev. Med. 2021, 48, 469–472+490. [Google Scholar]
- Zhou, M.; Tan, H.; Feng, Y. Fairness of health resource allocation in Guizhou based on concentration index and agglomeration degree. Mod. Prev. Med. 2020, 47, 3148–3150+3157. [Google Scholar]
- Bongiorno, C.; Santucci, D.; Kon, F.; Santi, P.; Ratti, C. Comparing bicycling and pedestrian mobility: Patterns of non-motorized human mobility in Greater Boston. J. Transp. Geogr. 2019, 80, 102501. [Google Scholar] [CrossRef]
- Bantis, T.; Haworth, J. Assessing transport related social exclusion using a capabilities approach to accessibility framework: A dynamic Bayesian network approach. J. Transp. Geogr. 2020, 84, 102673. [Google Scholar] [CrossRef]
- Jiang, Y.; Zhen, F.; Sun, H. Spatial characteristics of urban health resources at block scale: A case study of central urban area of Nanjing. Econ. Geogr. 2018, 38, 85–94. [Google Scholar] [CrossRef]
- Yuan, M.; Liu, T.; Yang, C. Exploring the relationship among human activities, COVID-19 morbidity, and at-risk areas using location-based social media data: Knowledge about the early pandemic stage in Wuhan. Int. J. Environ. Res. Public Health 2022, 19, 6523. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, Y.; Chen, Y.; Liu, S.; Yang, Q. Spatiotemporal heterogeneity of urban land expansion and urban population growth under new urbanization: A case study of Chongqing. Int. J. Environ. Res. Public Health 2022, 19, 7792. [Google Scholar] [CrossRef] [PubMed]
- Liu, H.; Chen, W. A review of research on the distribution of basic education resources in China. Prog. Geogr. 2017, 36, 557–568. [Google Scholar] [CrossRef]
- Zhang, H. Opportunity or new poverty trap: Rural-urban education disparity and internal migration in China. China Econ. Rev. 2017, 44, 112–124. [Google Scholar] [CrossRef]
- Yu, N.; Yu, B.; de Jong, M.; Storm, S. Does inequality in educational attainment matter for China’s economic growth? Int. J. Educ. Dev. 2015, 41, 164–173. [Google Scholar] [CrossRef]
- Xie, T.; Feng, C.; Yang, Y. Spatial analysis on education facilities of a typical valley-basin city: A case of middle school in Lanzhou Center Town. Urban Dev. Stud. 2014, 21, 29–32. [Google Scholar] [CrossRef]


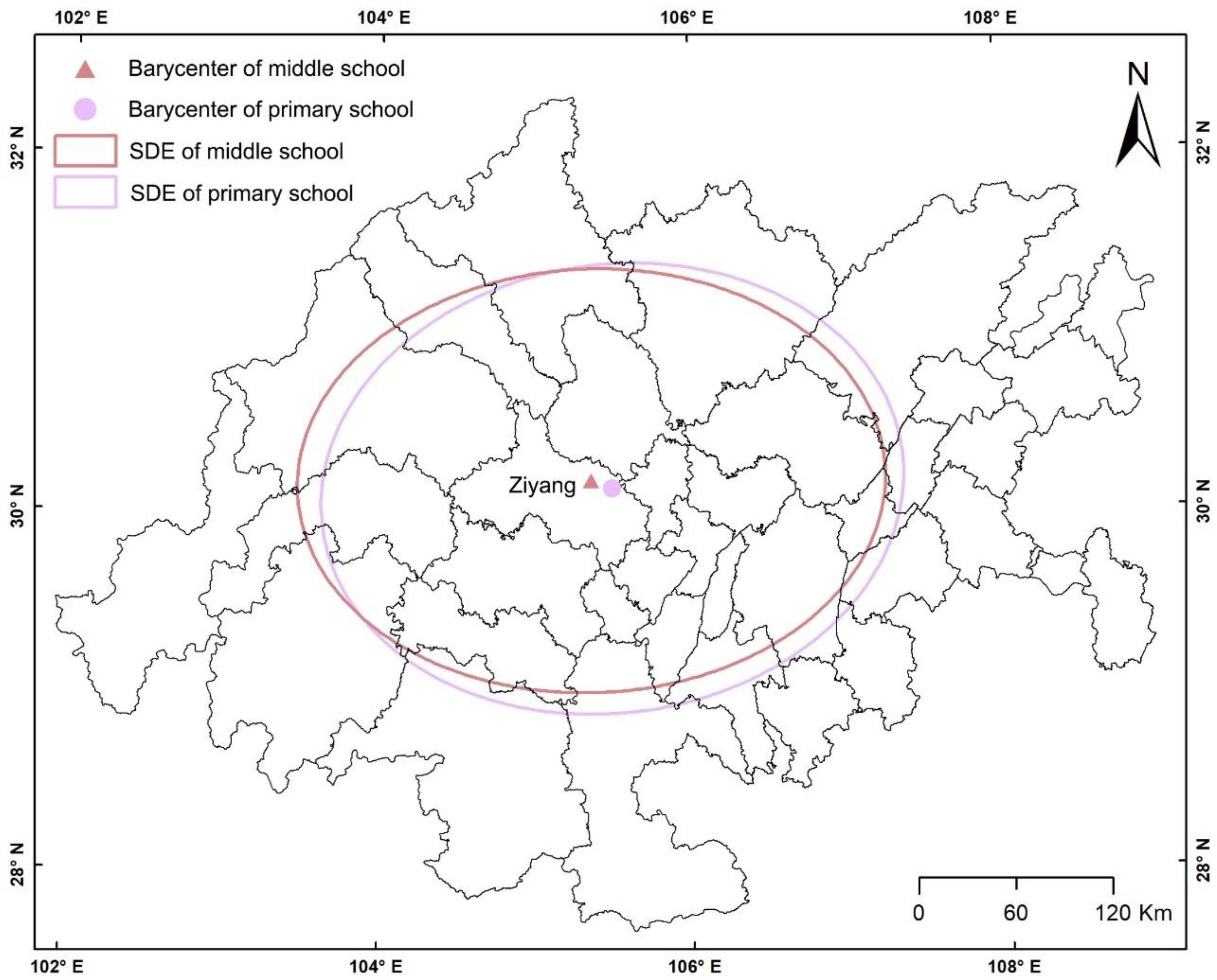





| Type | Center-x | Center-y | StdDist-x | StdDist-y | Rotation |
|---|---|---|---|---|---|
| Primary school | 105.49 | 30.14 | 1.87 | 1.25 | 85.20 |
| Middle school | 105.36 | 30.18 | 1.89 | 1.18 | 88.64 |
| Type | Moran’s I | Z-Score | p-Value |
|---|---|---|---|
| Primary school | 0.28 | 5.64 | 0 |
| Middle school | 0.24 | 4.85 | 0.000001 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, W.; Li, Y.; Zhao, R.; He, B.; Qian, Z. Spatial Pattern and Fairness Measurement of Educational Resources in Primary and Middle Schools: A Case Study of Chengdu–Chongqing Economic Circle. Int. J. Environ. Res. Public Health 2022, 19, 10840. https://doi.org/10.3390/ijerph191710840
Lu W, Li Y, Zhao R, He B, Qian Z. Spatial Pattern and Fairness Measurement of Educational Resources in Primary and Middle Schools: A Case Study of Chengdu–Chongqing Economic Circle. International Journal of Environmental Research and Public Health. 2022; 19(17):10840. https://doi.org/10.3390/ijerph191710840
Chicago/Turabian StyleLu, Wei, Yuechen Li, Rongkun Zhao, Bo He, and Zihua Qian. 2022. "Spatial Pattern and Fairness Measurement of Educational Resources in Primary and Middle Schools: A Case Study of Chengdu–Chongqing Economic Circle" International Journal of Environmental Research and Public Health 19, no. 17: 10840. https://doi.org/10.3390/ijerph191710840
APA StyleLu, W., Li, Y., Zhao, R., He, B., & Qian, Z. (2022). Spatial Pattern and Fairness Measurement of Educational Resources in Primary and Middle Schools: A Case Study of Chengdu–Chongqing Economic Circle. International Journal of Environmental Research and Public Health, 19(17), 10840. https://doi.org/10.3390/ijerph191710840






