Simulation on the Evolution Trend of the Urban Sprawl Spatial Pattern in the Upper Reaches of the Yangtze River, China
Abstract
:1. Introduction
2. Study Area and Data Sources
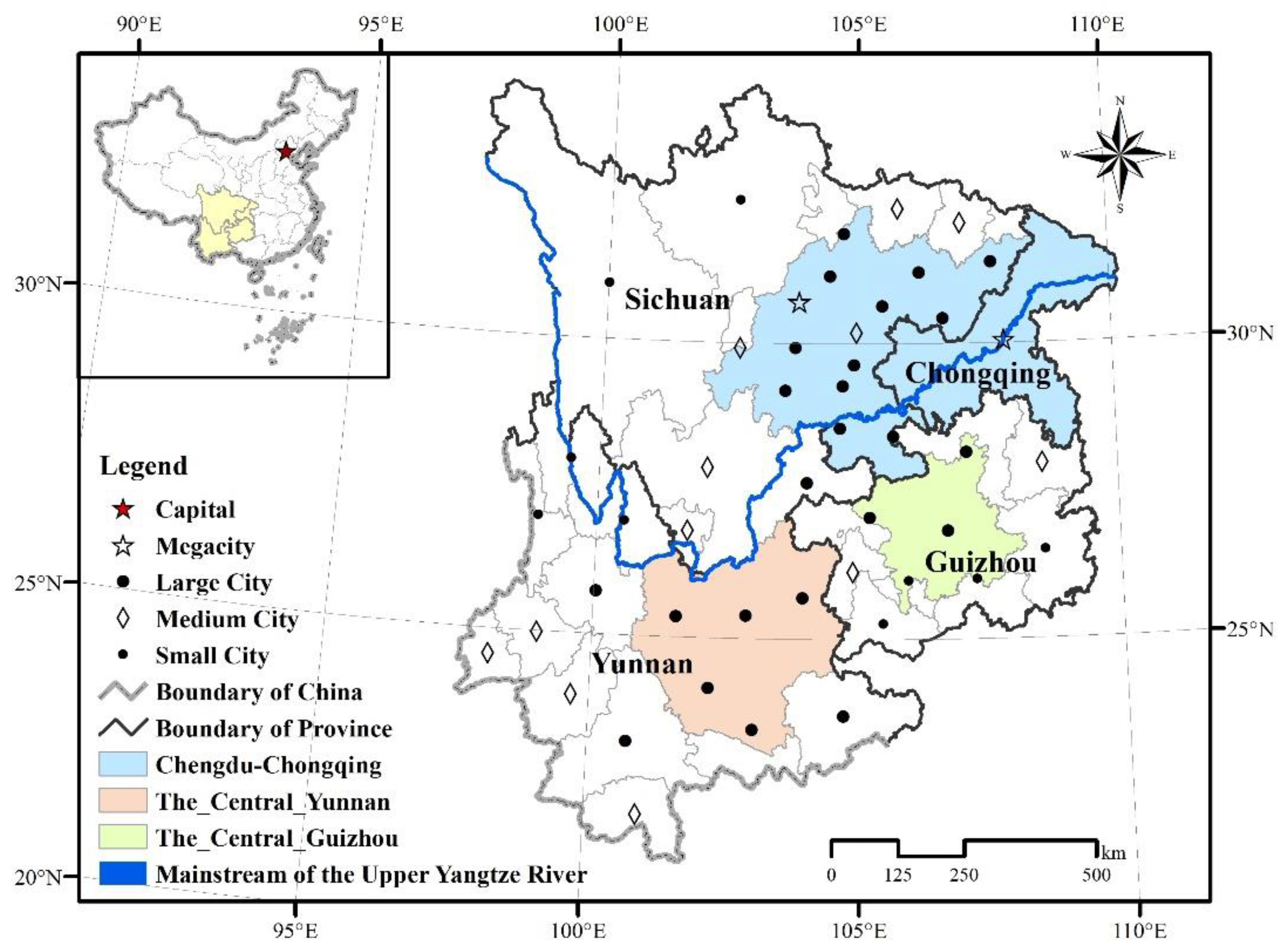
2.1. Study Area
2.2. Data Sources
3. Methods
3.1. Urban Sprawl Index
3.2. Spatial Autocorrelation Model
3.3. Urban Sprawl Scenario Analysis Model
3.4. Urban Sprawl Influence Factor Model
3.4.1. Geodetector
3.4.2. Urban Sprawl Influence Indicator System Construction
4. Results
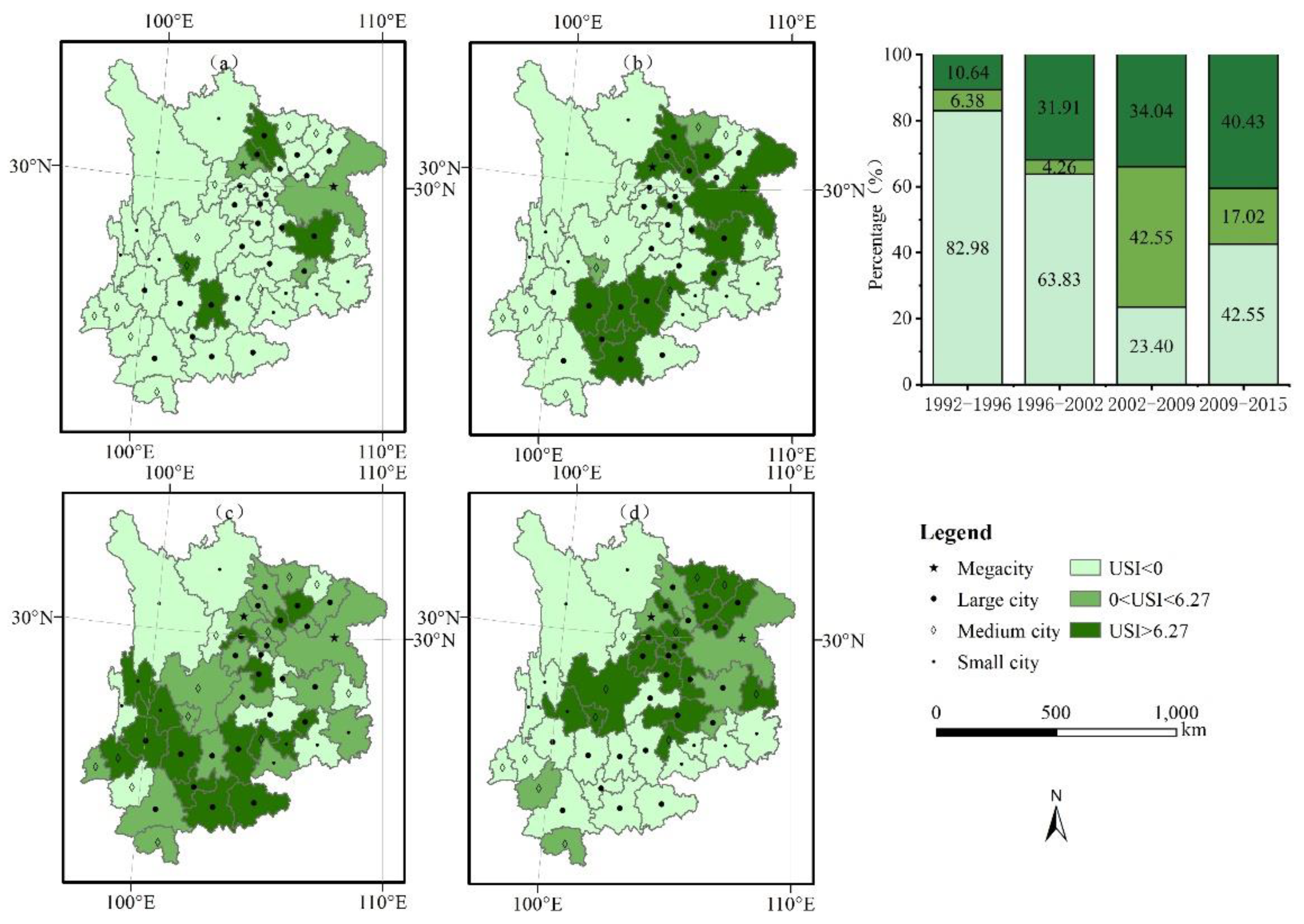
4.1. Recognition of the Spatial Features of Urban Sprawl
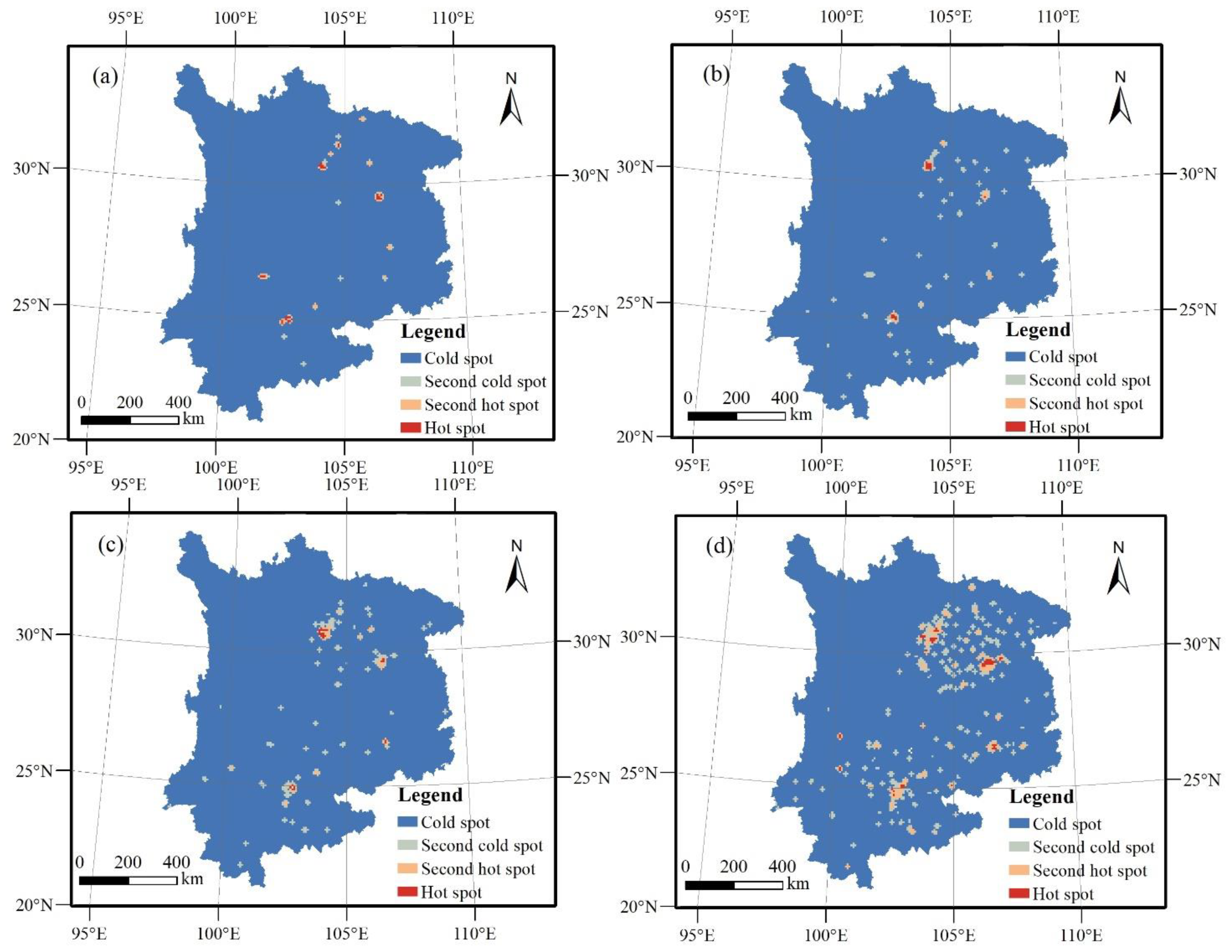
4.2. The Pattern and Evolution of the Urban Sprawl Cold and Hot Spots
4.3. The Simulation Results of the Different Urban Sprawl Scenarios
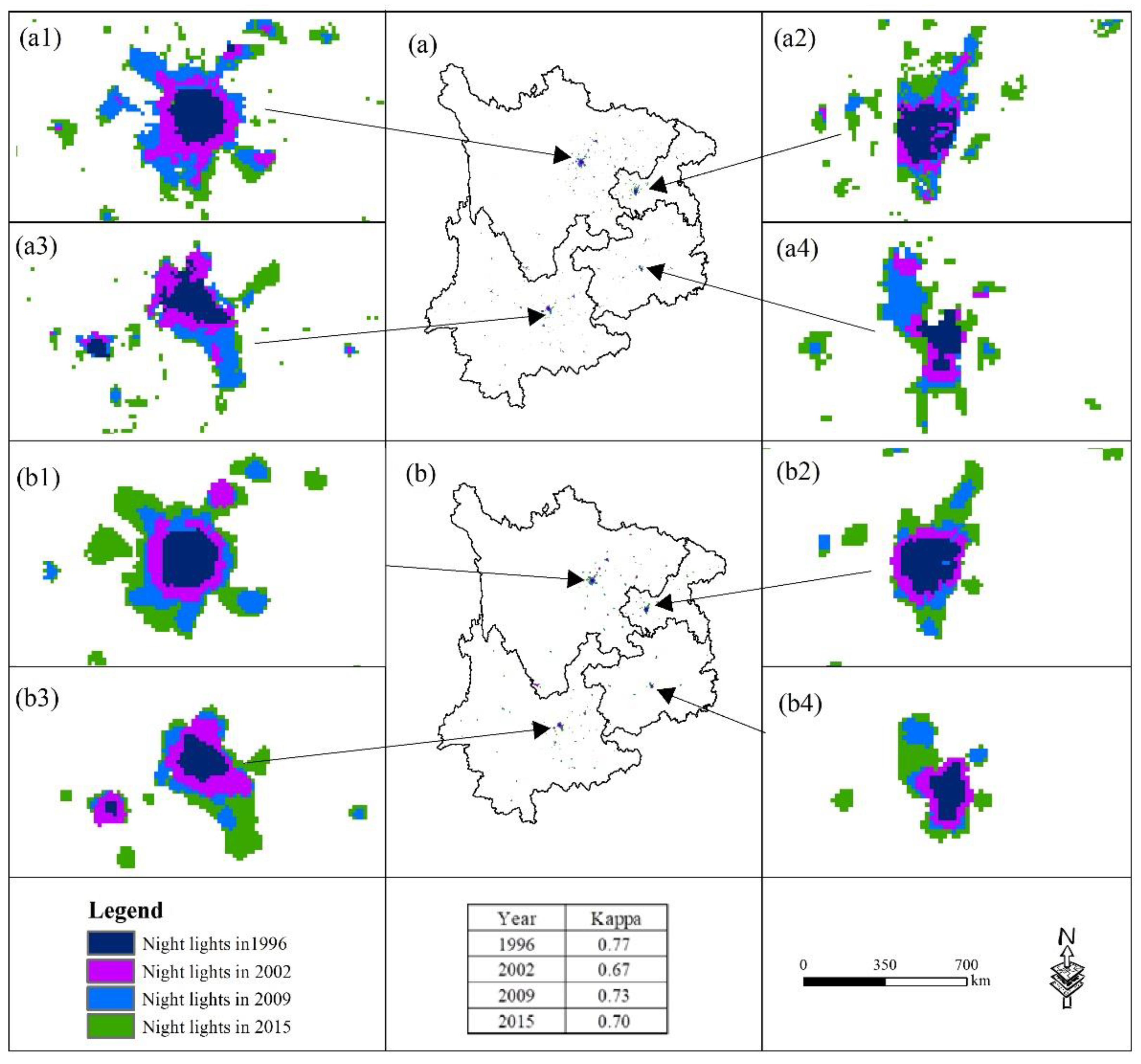
4.3.1. Test of the Urban Sprawl Scenario Analysis Model
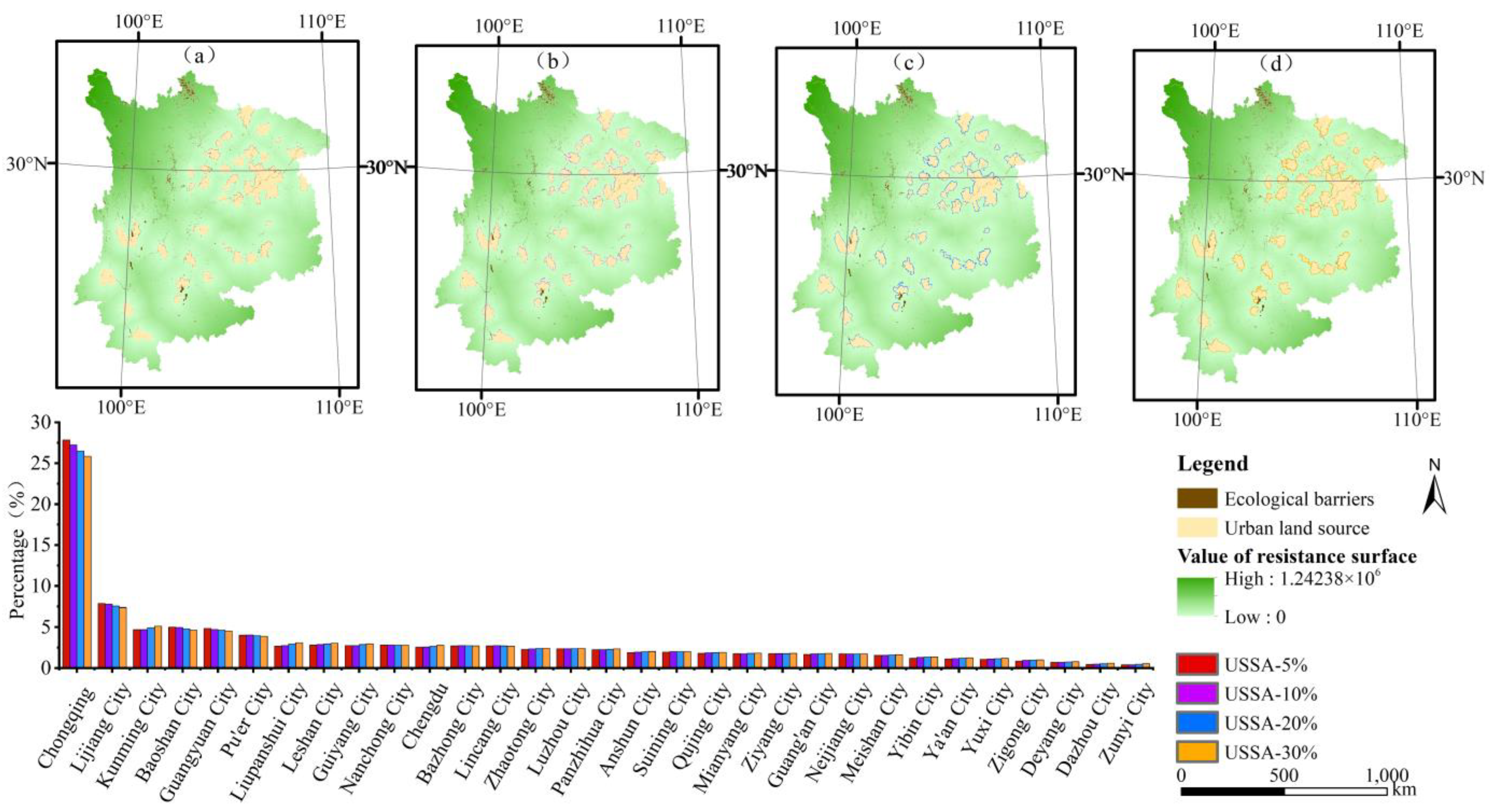
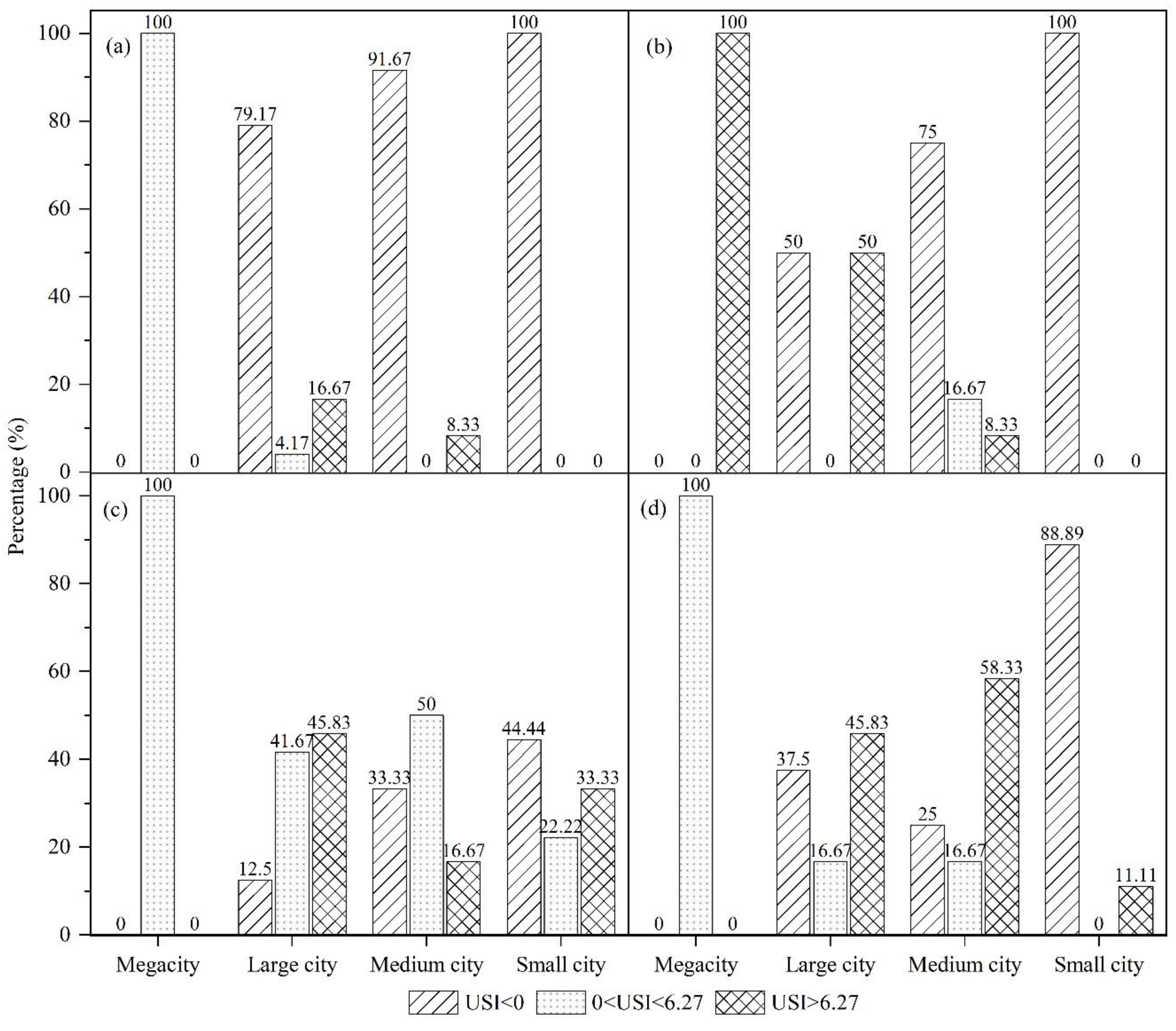
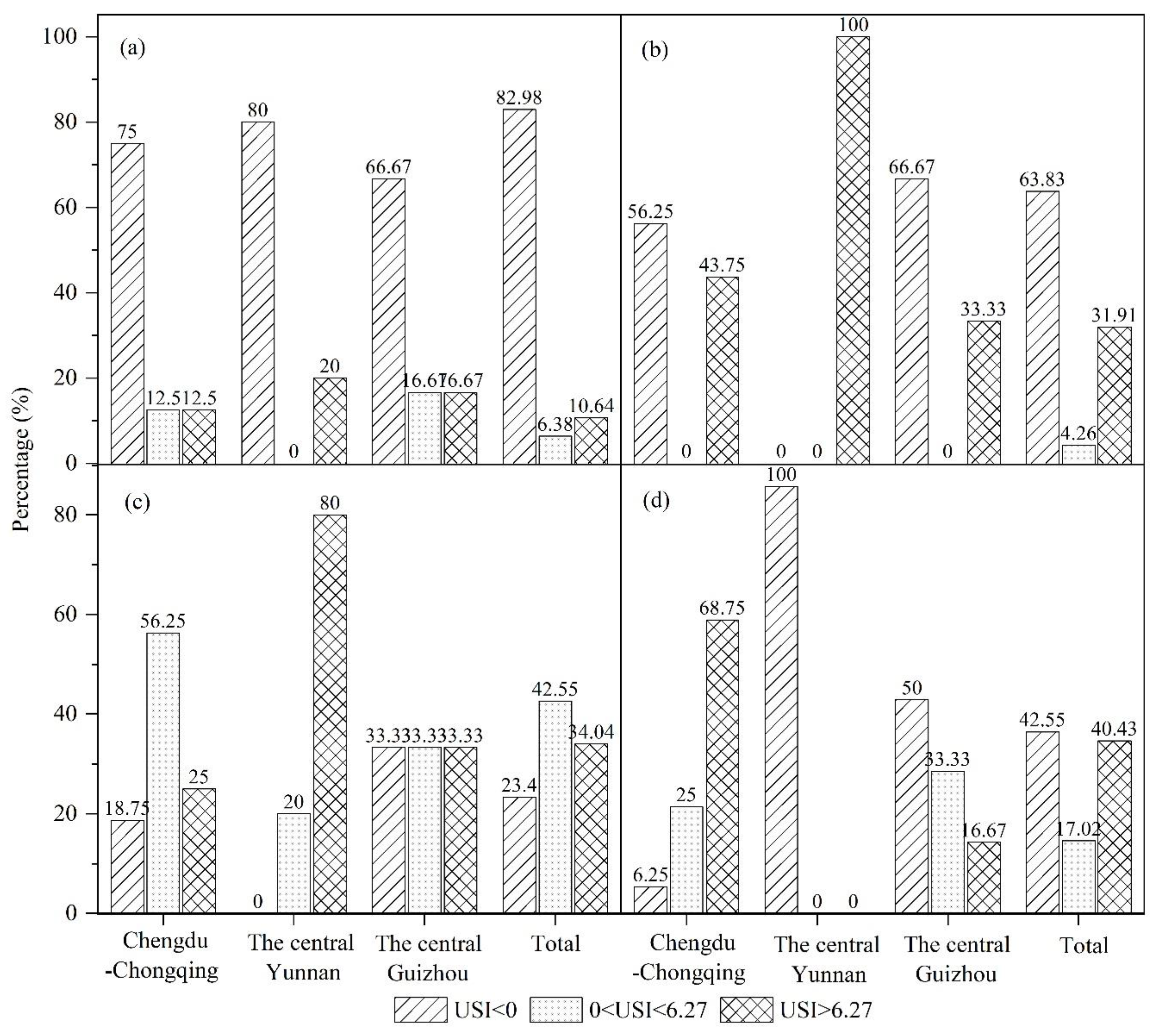
4.3.2. Scenario Simulation of the Different Scales of Urban Sprawl
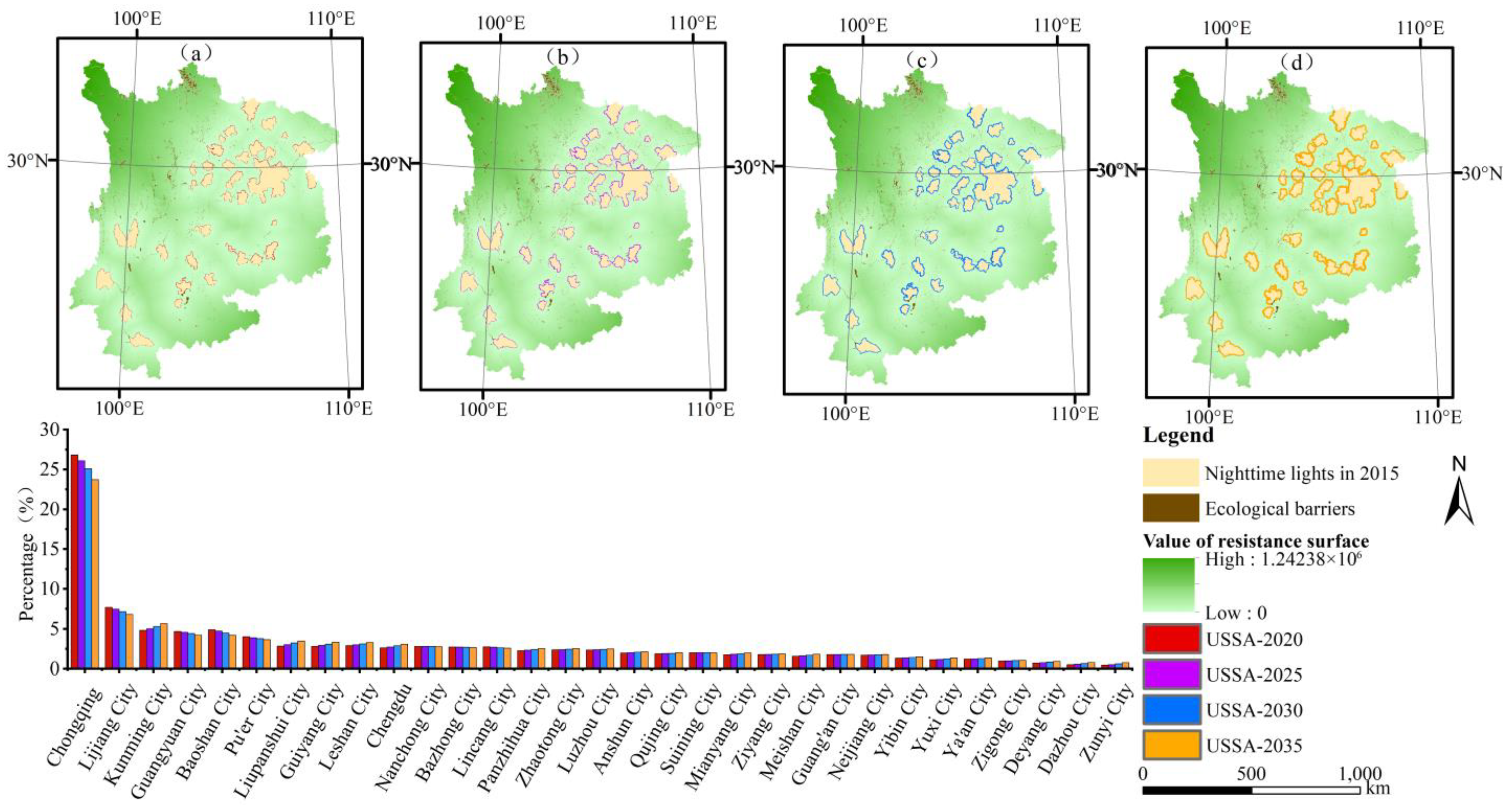
4.3.3. Scenario Simulation of the Urban Sprawl at Different Times
4.4. Analysis of Urban Sprawl Influencing Factors
4.4.1. Analysis of Urban Sprawl Influence Factor Detectors
4.4.2. Analysis of Urban Sprawl Influence Factor Interaction Detectors
5. Discussion
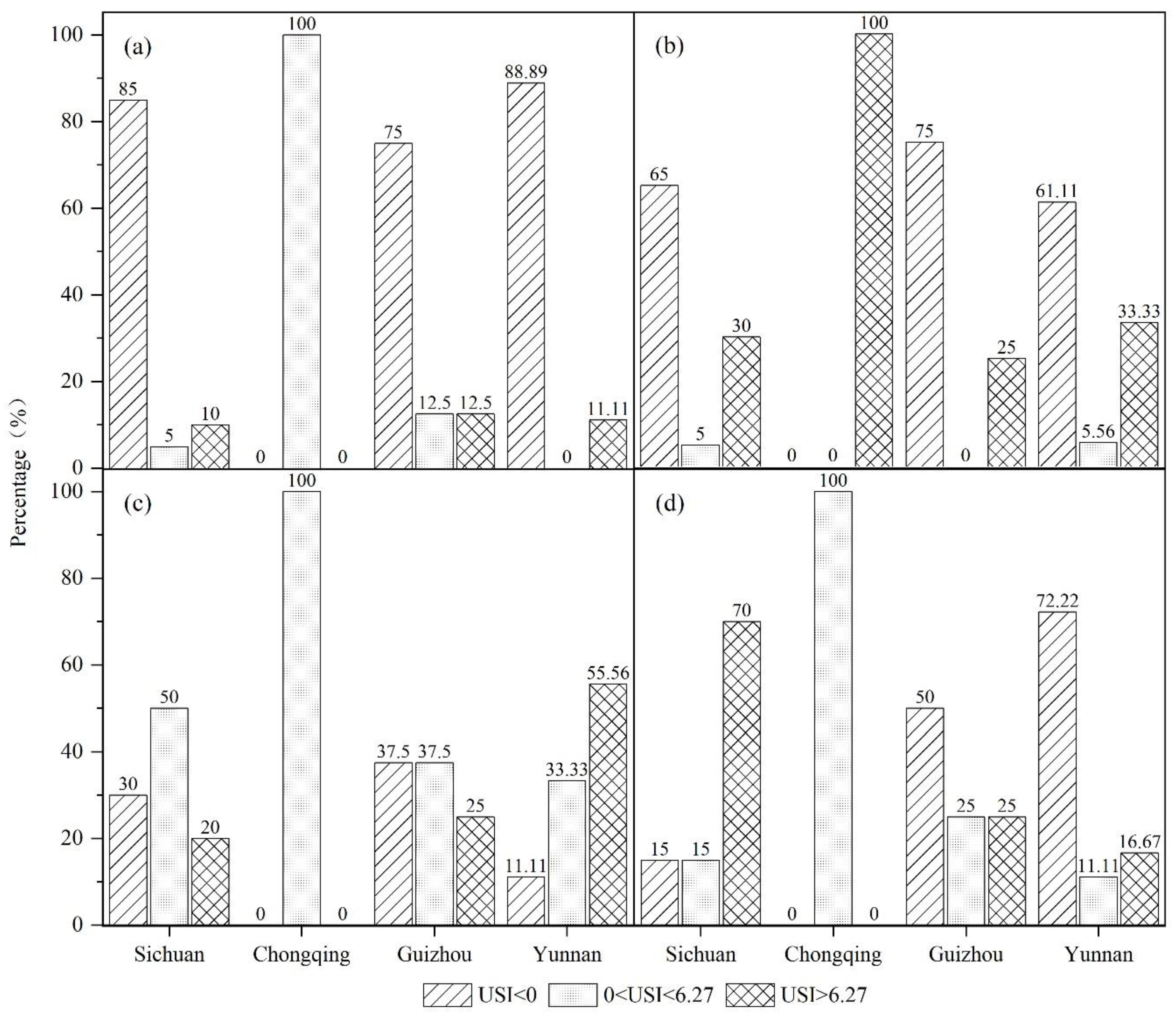
5.1. The Scale Effect of Urban Sprawl Spatial Pattern Evolution
5.2. The Scale Effect of the Urban Sprawl under Different Time Scenarios
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bhatta, B.; Saraswati, S.; Bandyopadhyay, D. Urban sprawl measurement from remote sensing data. Appl. Geogr. 2010, 30, 731–740. [Google Scholar] [CrossRef]
- Chen, D.; Lu, X.; Hu, W.; Zhang, C.; Lin, Y. How urban sprawl influences eco-environmental quality: Empirical research in China by using the Spatial Durbin model. Ecol. Indic. 2021, 131, 108113. [Google Scholar] [CrossRef]
- Han, J. Can urban sprawl be the cause of environmental deterioration? Based on the provincial panel data in China. Environ. Res. 2020, 189, 109954. [Google Scholar] [CrossRef] [PubMed]
- Feng, Y.; Wang, X. Effects of urban sprawl on haze pollution in China based on dynamic spatial Durbin model during 2003–2016. J. Cleaner Prod. 2020, 242, 118368. [Google Scholar] [CrossRef]
- Jia, M.; Zhang, H.; Yang, Z. Compactness or sprawl: Multi-dimensional approach to understanding the urban growth patterns in Beijing-Tianjin-Hebei region, China. Ecol. Indic. 2022, 138, 108816. [Google Scholar] [CrossRef]
- Feng, Y.; Wang, X.; Du, W.; Liu, J.; Li, Y. Spatiotemporal characteristics and driving forces of urban sprawl in China during 2003–2017. J. Cleaner Prod. 2019, 241, 118061. [Google Scholar] [CrossRef]
- Burchfield, M.; Overman, H.G.; Puga, D.; Turner, M.A. Causes of Sprawl: A Portrait from Space. Q. J. Econ. 2006, 121, 587–633. [Google Scholar] [CrossRef]
- Whyte, W.H. The Exploding Metropolis; Doubleday: Garden City, NY, USA, 1958. [Google Scholar]
- Bauer, G.; Roux, J.-M. La Rurbanisation ou la ville éparpillée. Rev. Française De Sociol. 1977, 18, 147. [Google Scholar] [CrossRef]
- Indovina, F. La Città Diffusa: Cos’è e Come Si Governa; Daest-IUAV: Venècia, Italy, 1989; pp. 47–58. [Google Scholar]
- Carruthers, J.I. The Impacts of State Growth Management Programmes: A Comparative Analysis. Urban Stud. 2002, 39, 1959–1982. [Google Scholar] [CrossRef]
- Brueckner, J.K. Urban Sprawl: Diagnosis and Remedies. Int. Reg. Sci. Rev. 2000, 23, 160–171. [Google Scholar] [CrossRef]
- Gottmann, J. The Growing City as a Political Process. Southeast. Geogr. 1969, 9, 4–16. [Google Scholar] [CrossRef]
- Anderson, W.P.; Kanaroglou, P.S.; Miller, E.J. Urban Form, Energy and the Environment: A Review of Issues, Evidence and Policy. Urban Stud. 1996, 33, 7–35. [Google Scholar] [CrossRef]
- Lopez, R.; Hynes, H.P. Sprawl in the 1990s: Measurement, Distribution and Trends. Urban Aff. Rev. 2003, 38, 325–355. [Google Scholar] [CrossRef]
- Ewing, R.S.R.; Zegeer, C.V. Urban sprawl as a risk factor in motor vehicle occupant and pedestrian fatalities. Am. J. Public Health 2003, 93, 1541–1545. [Google Scholar] [CrossRef] [PubMed]
- Ewing, R.; Pendall, R.; Chen, D. Measuring Sprawl and Its Impact; Smart Growth America: Washington, DC, USA, 2002. [Google Scholar]
- Torrens, P.M. A Toolkit for Measuring Sprawl. Appl. Spat. Anal. Policy 2008, 1, 5–36. [Google Scholar] [CrossRef] [Green Version]
- Zhou, D.; Li, Z.; Wang, S.; Tian, Y.; Zhang, Y.; Jiang, G. How does the newly urban residential built-up density differ across Chinese cities under rapid urban expansion? Evidence from residential FAR and statistical data from 2007 to 2016. Land Use Policy 2021, 104, 105365. [Google Scholar] [CrossRef]
- Das, S.; Angadi, D.P. Assessment of urban sprawl using landscape metrics and Shannon’s entropy model approach in town level of Barrackpore sub-divisional region, India. Modeling Earth Syst. Environ. 2021, 7, 1071–1095. [Google Scholar] [CrossRef]
- Wang, X.; Shi, R.; Zhou, Y. Dynamics of urban sprawl and sustainable development in China. Socio-Econ. Plan. Sci. 2020, 70, 100736. [Google Scholar] [CrossRef]
- Mansour, S.; Al-Belushi, M.; Al-Awadhi, T. Monitoring land use and land cover changes in the mountainous cities of Oman using GIS and CA-Markov modelling techniques. Land Use Policy 2020, 91, 104414. [Google Scholar] [CrossRef]
- Fan, J.; Zhou, L. Three-dimensional intergovernmental competition and urban sprawl: Evidence from Chinese prefectural-level cities. Land Use Policy 2019, 87, 104035. [Google Scholar] [CrossRef]
- Guite, L.T.S. Assessment of urban sprawl in Bathinda city, India. J. Urban Manag. 2019, 8, 195–205. [Google Scholar] [CrossRef]
- Domingo, D.; Palka, G.; Hersperger, A.M. Effect of zoning plans on urban land-use change: A multi-scenario simulation for supporting sustainable urban growth. Sustain. Cities Soc. 2021, 69, 102833. [Google Scholar] [CrossRef]
- Koprowska, K.; Łaszkiewicz, E.; Kronenberg, J. Is urban sprawl linked to green space availability? Ecol. Indic. 2020, 108, 105723. [Google Scholar] [CrossRef]
- Guan, D.; He, X.; He, C.; Cheng, L.; Qu, S. Does the urban sprawl matter in Yangtze River Economic Belt, China? An integrated analysis with urban sprawl index and one scenario analysis model. Cities 2020, 99, 102611. [Google Scholar] [CrossRef]
- Li, W.; Zhou, W.; Han, L.; Qian, Y. Uneven urban-region sprawl of China’s megaregions and the spatial relevancy in a multi-scale approach. Ecol. Indic. 2019, 97, 194–203. [Google Scholar] [CrossRef]
- Gavrilidis, A.A.; Niță, M.R.; Onose, D.A.; Badiu, D.L.; Năstase, I.I. Methodological framework for urban sprawl control through sustainable planning of urban green infrastructure. Ecol. Indic. 2019, 96, 67–78. [Google Scholar] [CrossRef]
- Menzori, I.D.; Sousa, I.C.N.d.; Gonçalves, L.M. Urban growth management and territorial governance approaches: A master plans conformance analysis. Land Use Policy 2021, 105, 105436. [Google Scholar] [CrossRef]
- Tan, R.; Zhang, T.; Liu, D.; Xu, H. How will innovation-driven development policy affect sustainable urban land use: Evidence from 230 Chinese cities. Sustain. Cities Soc. 2021, 72, 103021. [Google Scholar] [CrossRef]
- Yang, X.; Bai, Y.; Che, L.; Qiao, F.; Xie, L. Incorporating ecological constraints into urban growth boundaries: A case study of ecologically fragile areas in the Upper Yellow River. Ecol. Indic. 2021, 124, 107436. [Google Scholar] [CrossRef]
- Okwuashi, O.; Ndehedehe, C.E. Integrating machine learning with Markov chain and cellular automata models for modelling urban land use change. Remote. Sens. Appl. Soc. Environ. 2021, 21, 100461. [Google Scholar] [CrossRef]
- Liao, J.; Shao, G.; Wang, C.; Tang, L.; Huang, Q.; Qiu, Q. Urban sprawl scenario simulations based on cellular automata and ordered weighted averaging ecological constraints. Ecol. Indic. 2019, 107, 105572. [Google Scholar] [CrossRef]
- Li, N.; Miao, S.; Wang, Y. The future urban growth under policies and its ecological effect in the Jing-Jin-Ji area, China. Heliyon 2021, 7, e06786. [Google Scholar] [CrossRef]
- Huang, D.; Huang, J.; Liu, T. Delimiting urban growth boundaries using the CLUE-S model with village administrative boundaries. Land Use Policy 2019, 82, 422–435. [Google Scholar] [CrossRef]
- Chen, D.; Jiang, P.; Li, M. Assessing potential ecosystem service dynamics driven by urbanization in the Yangtze River Economic Belt, China. J. Environ. Manage. 2021, 292, 112734. [Google Scholar] [CrossRef]
- Abedini, A.; Khalili, A.; Asadi, N. Urban Sprawl Evaluation Using Landscape Metrics and Black-and-White Hypothesis (Case Study: Urmia City). J. Indian Soc. Remote. Sens. 2020, 48, 1021–1034. [Google Scholar] [CrossRef]
- Delgado Blasco, J.M.; Cian, F.; Hanssen, R.F.; Verstraeten, G. Mapping and Quantifying the Human-Environment Interactions in Middle Egypt Using Machine Learning and Satellite Data Fusion Techniques. Remote. Sens. 2020, 12, 584. [Google Scholar] [CrossRef] [Green Version]
- Lan, H.; Zheng, P.; Li, Z. Constructing urban sprawl measurement system of the Yangtze River economic belt zone for healthier lives and social changes in sustainable cities. Technol. Forecast. Soc. Chang. 2021, 165, 120569. [Google Scholar] [CrossRef]
- Boulila, W.; Ghandorh, H.; Khan, M.A.; Ahmed, F.; Ahmad, J. A novel CNN-LSTM-based approach to predict urban expansion. Ecol. Inf. 2021, 64, 101325. [Google Scholar] [CrossRef]
- Devendran, A.A.; Lakshmanan, G. Analysis and Prediction of Urban Growth Using Neural-Network-Coupled Agent-Based Cellular Automata Model for Chennai Metropolitan Area, Tamil Nadu, India. J. Indian Soc. Remote. Sens. 2019, 47, 1515–1526. [Google Scholar] [CrossRef]
- Zhang, X.R.; Zhou, J.; Song, W. Simulating Urban Sprawl in China Based on the Artificial Neural Network-Cellular Automata-Markov Model. Sustainability 2020, 12, 4341. [Google Scholar] [CrossRef]
- Gao, B.; Huang, Q.; He, C.; Sun, Z.; Zhang, D. How does sprawl differ across cities in China? A multi-scale investigation using nighttime light and census data. Landsc. Urban Plann. 2016, 148, 89–98. [Google Scholar] [CrossRef]
- Ma, R.; Chen, W.; Chen, X.; Duan, X. Town and constrution land growth of Changshu City. Acta Geogr. Sin. 2004, 3, 418–426. (In Chinese) [Google Scholar]
- Wang, J.F.; Xu, C.D. Geodetector: Principle and prospective. Acta Geogr. Sin. 2017, 72, 116–134. (In Chinese) [Google Scholar] [CrossRef]
- Zhang, X.; Lu, L.; Ren, Y.; Xu, Y.; Zhang, H. Spatiotemporal Evolution Pattern of Urban Sprawl in China and Its Influencing Factors. Econ. Geogr. 2021, 41, 77–85. (In Chinese) [Google Scholar] [CrossRef]
- Wang, J.F.; Zhang, T.L.; Fu, B.J. A measure of spatial stratified heterogeneity. Ecol. Indic. 2016, 67, 250–256. [Google Scholar] [CrossRef]
- Xu, Q.; Zheng, X.; Zhang, C. Quantitative Analysis of the Determinants Influencing Urban Expansion: A Case Study in Beijing, China. Sustainability 2018, 10, 1630. [Google Scholar] [CrossRef] [Green Version]
- Chen, L.; Ren, C.; Zhang, B.; Wang, Z.; Liu, M. Quantifying Urban Land Sprawl and its Driving Forces in Northeast China from 1990 to 2015. Sustainability 2018, 10, 188. [Google Scholar] [CrossRef] [Green Version]
- Liu, J.; Xu, Q.; Yi, J.; Huang, X. Analysis of the heterogeneity of urban expansion landscape patterns and driving factors based on a combined Multi-Order Adjacency Index and Geodetector model. Ecol. Indic. 2022, 136, 108655. [Google Scholar] [CrossRef]

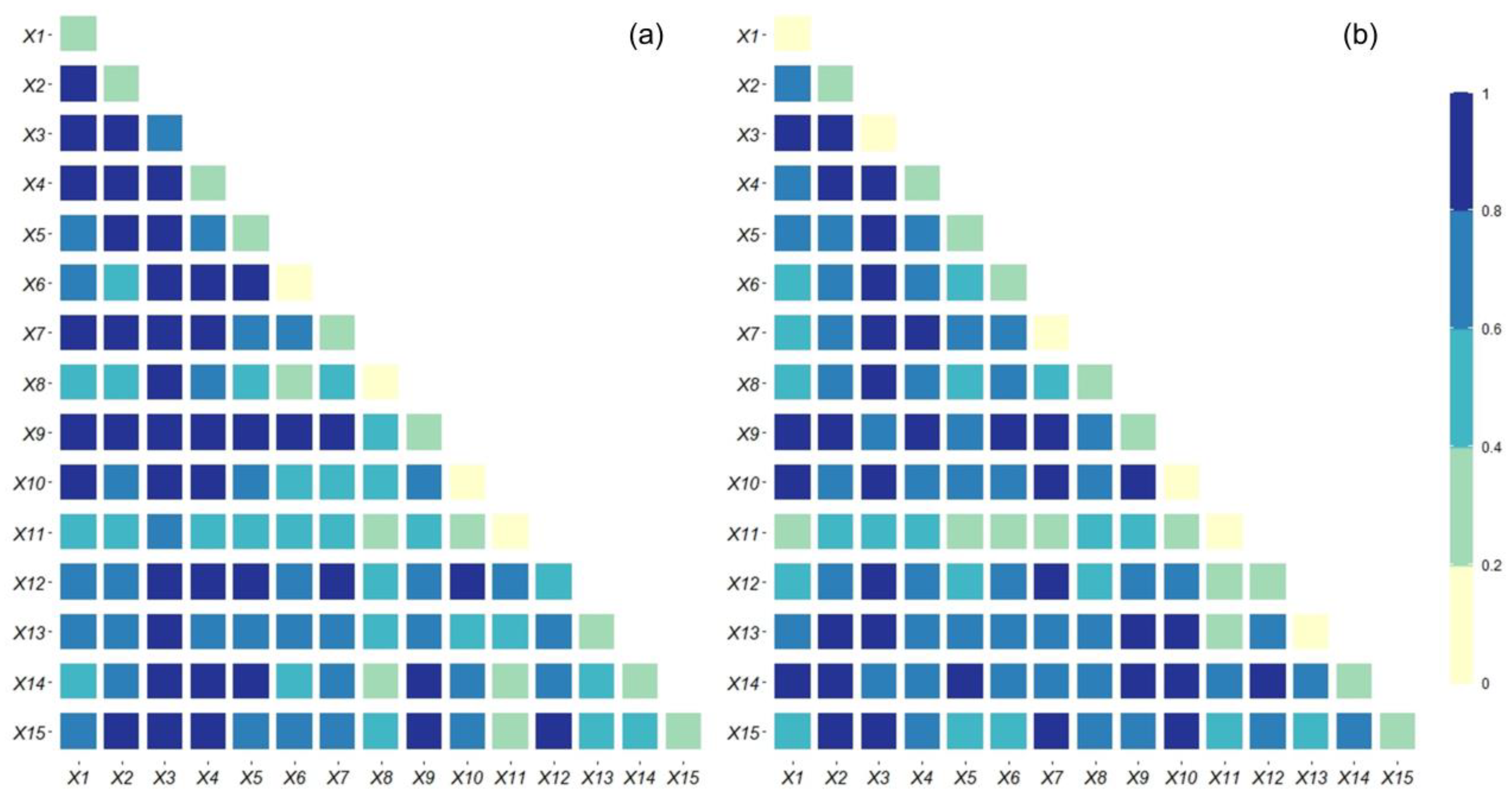
| Judgment Conditions | Interaction |
|---|---|
| q(X1∩X2) < Min(q(X1),q(X2)) | Non-linear reduction |
| Min(q(X1),q(X2)) < q(X1∩X2) < Max(q(X1),q(X2)) | Single-factor nonlinearity reduction |
| q(X1∩X2) > Max(q(X1),q(X2)) | Two-factor enhancement |
| q(X1∩X2) = q(X1) + q(X2) | Independent |
| q(X1∩X2) > q(X1) + q(X2) | Non-linear enhancement |
| Dimensions | Factors | Code | Unit |
|---|---|---|---|
| Economic development | GDP | X1 | Billion CNY |
| Urban disposable income per capita | X2 | CNY | |
| Secondary industry share of GDP | X3 | % | |
| Tertiary industry share of GDP | X4 | % | |
| Investment in real estate development | X5 | Billion CNY | |
| Social culture | Population | X6 | Million |
| Urbanization rate | X7 | % | |
| Number of high schools | X8 | - | |
| Urban green space per capita | X9 | m2 | |
| Transportation | Urban road area per capita | X10 | m2 |
| Distance from major railroads | X11 | m | |
| Private car ownership | X12 | - | |
| Highway mileage | X13 | km | |
| Government regulation | Public finance expenditure | X14 | Billion CNY |
| Fixed assets input | X15 | Billion CNY |
| Scale Type | 2020 | 2025 | 2030 | 2035 | |
|---|---|---|---|---|---|
| Urban size | Megacity | 3001.275 | 5204.275 | 8927.358 | 15,101.67 |
| 21.88% | 22.13% | 22.09% | 21.78% | ||
| Large city | 6580.468 | 11,244.46 | 19,326.38 | 33,389.08 | |
| 47.98% | 47.81% | 47.83% | 48.16% | ||
| Medium city | 3101.561 | 5298.561 | 9081.561 | 15,606.56 | |
| 22.61% | 22.53% | 22.47% | 22.51% | ||
| Small city | 1031.342 | 1772.342 | 3072.342 | 5230.342 | |
| 7.52% | 7.54% | 7.60% | 7.54% | ||
| Urban agglomeration | Chengdu-Chongqing | 6987.412 | 12,089.41 | 20,684.41 | 35,299.41 |
| 50.95% | 51.40% | 51.19% | 50.92% | ||
| The central Yunnan | 1550.725 | 2652.725 | 4549.725 | 7858.725 | |
| 11.31% | 11.28% | 11.26% | 11.34% | ||
| The central Guizhou | 1165.393 | 1921.393 | 3275.393 | 5648.393 | |
| 8.50% | 8.17% | 8.11% | 8.15% | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Guan, D.; He, X.; Yin, B. Simulation on the Evolution Trend of the Urban Sprawl Spatial Pattern in the Upper Reaches of the Yangtze River, China. Int. J. Environ. Res. Public Health 2022, 19, 9190. https://doi.org/10.3390/ijerph19159190
Zhang Y, Guan D, He X, Yin B. Simulation on the Evolution Trend of the Urban Sprawl Spatial Pattern in the Upper Reaches of the Yangtze River, China. International Journal of Environmental Research and Public Health. 2022; 19(15):9190. https://doi.org/10.3390/ijerph19159190
Chicago/Turabian StyleZhang, Yuxiang, Dongjie Guan, Xiujuan He, and Boling Yin. 2022. "Simulation on the Evolution Trend of the Urban Sprawl Spatial Pattern in the Upper Reaches of the Yangtze River, China" International Journal of Environmental Research and Public Health 19, no. 15: 9190. https://doi.org/10.3390/ijerph19159190
APA StyleZhang, Y., Guan, D., He, X., & Yin, B. (2022). Simulation on the Evolution Trend of the Urban Sprawl Spatial Pattern in the Upper Reaches of the Yangtze River, China. International Journal of Environmental Research and Public Health, 19(15), 9190. https://doi.org/10.3390/ijerph19159190






