Solar Ultraviolet Radiation Risk Estimates—A Comparison of Different Action Spectra and Detector Responsivities
Abstract
1. Introduction
2. Materials and Methods
2.1. Solar Spectral Irradiance
2.2. Analysis Routine
2.3. Literature Solar Spectra
2.4. Action Spectra
2.5. Detector Responsivities
3. Results
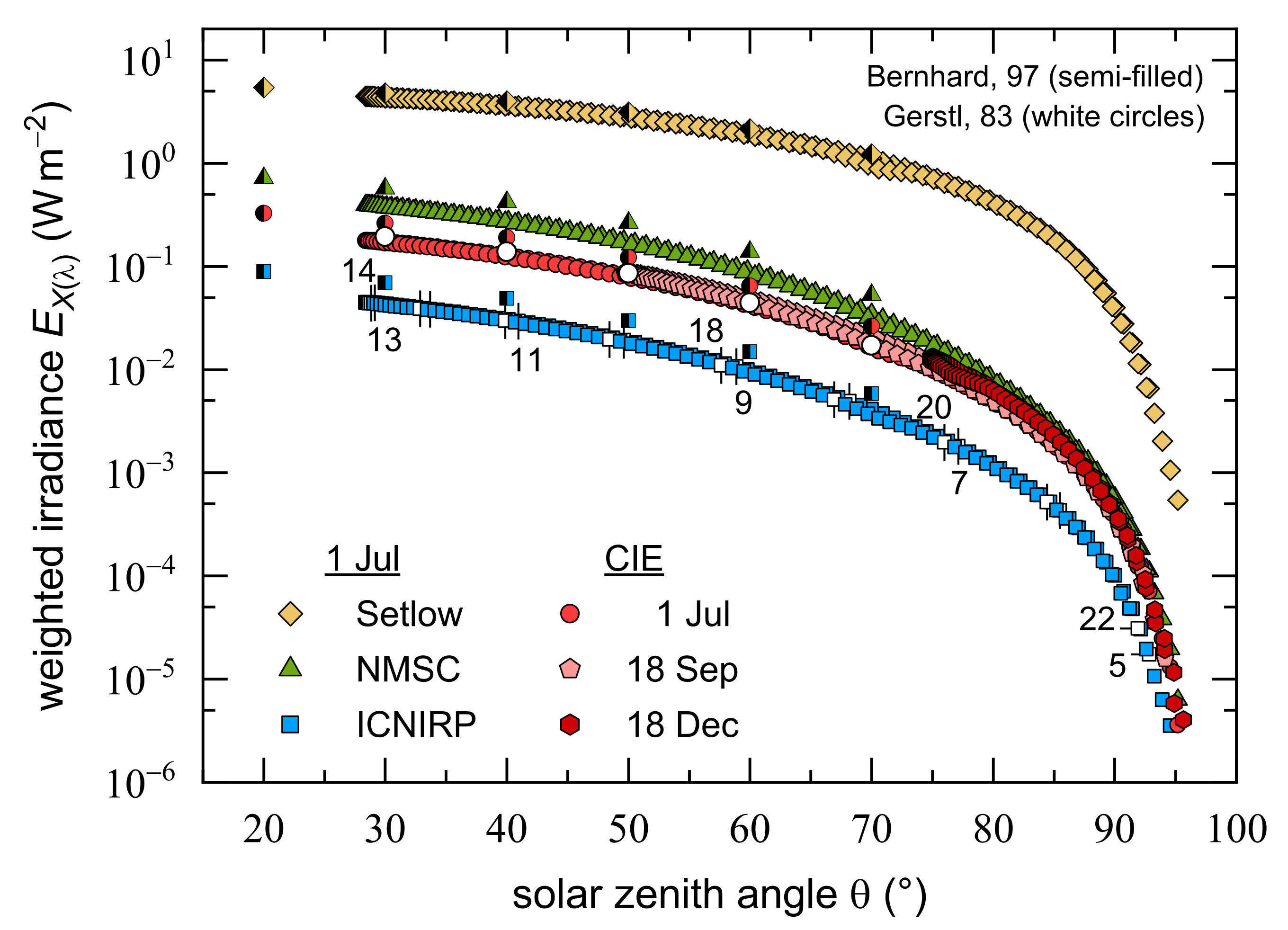
3.1. Weighted UV Irradiances as a Function of the Solar Zenith Angle
3.2. Annual Course of Cumulative Weighted UV Doses
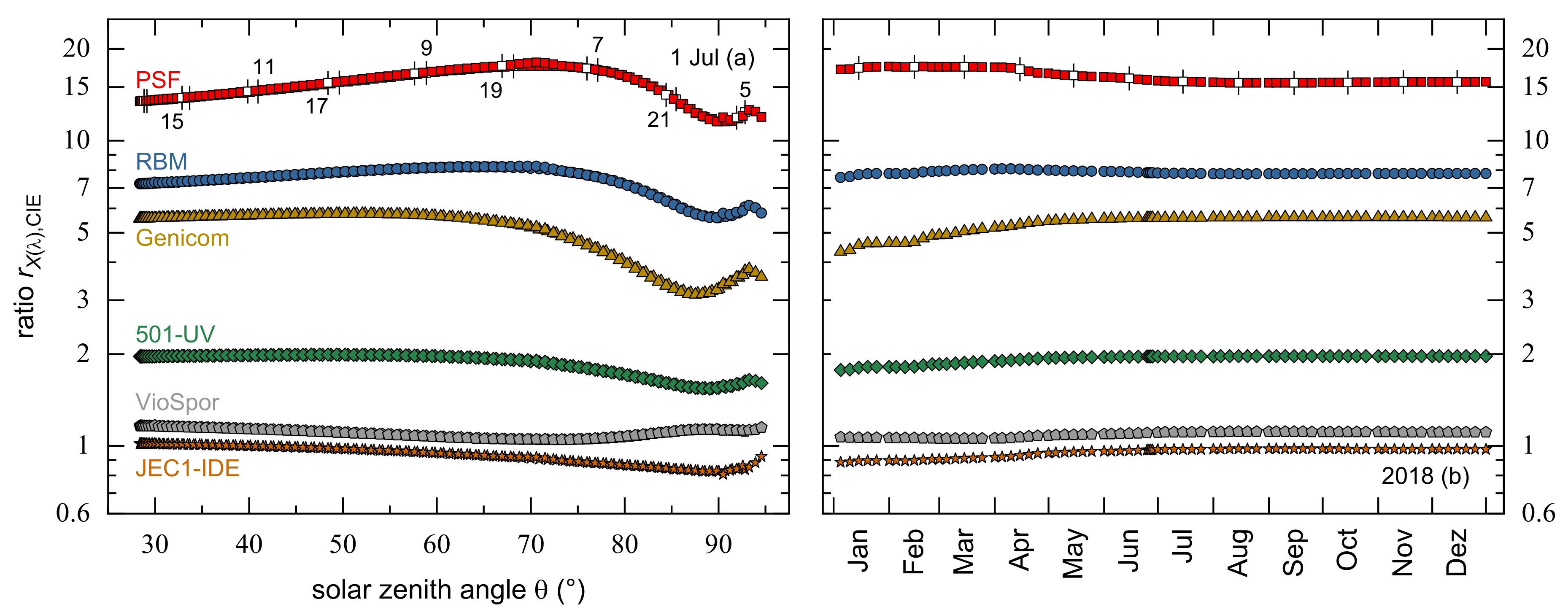
3.3. UV Doses Measured by Detectors Mimicking Erythema Sensitivity
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- De Gruijl, F.R. Skin cancer and solar UV radiation. Eur. J. Cancer 1999, 35, 2003–2009. [Google Scholar] [CrossRef]
- Reeve, V.E.; Ley, R.D. Animal models of ultraviolet radiation-induced skin cancer. In Prevention of Skin Cancer—Cancer Causes; Hill, D., Elwood, J.M., English, D.R., Eds.; Springer: Dordrecht, The Netherlands, 2004; Volume 3, pp. 177–194. [Google Scholar]
- National Research Council (NRC). Causes and Effects of Changes in Stratospheric Ozone: Update 1983; National Academy Press: Washington, DC, USA, 1984. [Google Scholar]
- Qureshi, A.A.; Laden, F.; Colditz, G.A.; Hunter, D.J. Geographic variation and risk of skin cancer in US women. Differences between melanoma, squamous cell carcinoma, and basal cell carcinoma. Arch. Intern. Med. 2008, 168, 501–517. [Google Scholar] [CrossRef] [PubMed]
- Moan, J.; Grigalavicius, M.; Baturaite, Z.; Juzeniene, A.; Dahlback, A. North-South gradients of melanomas and non-melanomas: A role of vitamin D? Dermatoendocrinology 2013, 5, 186–191. [Google Scholar] [CrossRef] [PubMed]
- Rivas, M.; Rojas, E.; Calaf, G.M.; Barberán, M.; Liberman, C.; De Paula Correa, M. Association between non-melanoma and melanoma skin cancer rates, vitamin D and latitude. Oncol. Lett. 2017, 13, 3787–3792. [Google Scholar] [CrossRef]
- Bauer, A.; Diepgen, T.L.; Schmitt, J. Is occupational solar ultraviolet irradiation a relevant risk factor for basal cell carcinoma? A systematic review and meta-analysis of the epidemiological literature. Br. J. Dermatol. 2011, 165, 612–625. [Google Scholar] [CrossRef]
- Modenese, A.; Korpinen, L.; Gobba, F. Solar Radiation Exposure and Outdoor Work: An Underestimated Occupational Risk. Int. J. Environ. Res. Public Health 2018, 15, 2063. [Google Scholar] [CrossRef]
- Paulo, M.S.; Adam, B.; Akagwu, C.; Akparibo, I.; Al-Rifai, R.H.; Bazrafshan, S.; Gobba, F.; Green, A.C.; Ivanov, I.; Kezic, S.; et al. WHO/ILO work-related burden of disease and injury: Protocol for systematic reviews of occupational exposure to solar ultraviolet radiation and of the effect of occupational exposure to solar ultraviolet radiation on melanoma and non-melanoma skin cancer. Environ. Int. 2019, 126, 804–815. [Google Scholar] [CrossRef]
- Moehrle, M. Outdoor sports and skin cancer. Clin. Dermatol. 2008, 26, 12–15. [Google Scholar] [CrossRef]
- Li, J.; Uter, W.; Pfahlberg, A.; Gefeller, O. A comparison of patterns of sun protection during beach holidays and everyday outdoor activities in a population sample of young German children. Br. J. Dermatol. 2012, 166, 803–810. [Google Scholar] [CrossRef]
- Diffey, B.L. Time and Place as Modifiers of Personal UV Exposure. Int. J. Environ. Res. Public Health. 2018, 15, 1112. [Google Scholar] [CrossRef]
- Gandini, S.; Sera, F.; Cattaruzza, M.S.; Pasquini, P.; Picconi, O.; Boyle, P.; Melchi, C.F. Meta-analysis of risk factors for cutaneous melanoma: II. Sun exposure. Eur. J. Cancer. 2005, 41, 45–60. [Google Scholar] [CrossRef]
- Xiang, F.; Lucas, R.; Hales, S.; Neale, R. Incidence of nonmelanoma skin cancer in relation to ambient UV radiation in white populations, 1978–2012: Empirical relationships. JAMA Dermatol. 2014, 150, 1063–1071. [Google Scholar] [CrossRef]
- Wu, S.; Han, J.; Vleugels, R.A.; Puett, R.; Laden, F.; Hunter, D.J.; Qureshi, A.A. Cumulative ultraviolet radiation flux in adulthood and risk of incident skin cancers in women. Br. J. Cancer. 2014, 110, 1855–1861. [Google Scholar] [CrossRef]
- Zhu, G.A.; Raber, I.; Sakshuwong, S.; Li, S.; Li, A.S.; Tan, C.; Chang, A.L. Estimation of individual cumulative ultraviolet exposure using a geographically-adjusted, openly-accessible tool. BMC Dermatol. 2016, 16, 1. [Google Scholar] [CrossRef]
- Liu-Smith, F.; Farhat, A.M.; Arce, A.; Ziogas, A.; Taylor, T.; Wang, Z.; Yourk, V.; Liu, J.; Wu, J.; McEligot, A.J.; et al. Gender differences in the association of cutaneous melanoma incidence rates and geographic ultraviolet light exposure. J. Am. Acad. Dermatol. 2017, 76, 499–505. [Google Scholar] [CrossRef]
- Vernez, D.; Milon, A.; Vuilleumier, L.; Bulliard, J.L. Anatomical exposure patterns of skin to sunlight: Relative contributions of direct, diffuse and reflected ultraviolet radiation. Br. J. Dermatol. 2012, 167, 383–390. [Google Scholar] [CrossRef]
- Weihs, P.; Schmalwieser, A.W.; Reinisch, C.; Meraner, E.; Walisch, S.; Harald, M. Measurements of personal UV exposure on different parts of the body during various activities. Photochem. Photobiol. 2013, 89, 1004–1007. [Google Scholar] [CrossRef]
- Casale, G.R.; Siani, A.M.; Diémoz, H.; Kimlin, M.G.; Colosimo, A. Applicability of the polysulphone horizontal calibration to differently inclined dosimeters. Photochem. Photobiol. 2012, 88, 207–214. [Google Scholar] [CrossRef]
- Schmalwieser, A.W.; Casale, G.R.; Colosimo, A.; Schmalwieser, S.S.; Siani, A.M. Review on Occupational Personal Solar UV Exposure Measurements. Atmosphere 2021, 12, 142. [Google Scholar] [CrossRef]
- Schmalwieser, A.W.; Siani, A.M. Review on Nonoccupational Personal Solar UV Exposure Measurements. Photochem. Photobiol. 2018, 94, 900–915. [Google Scholar] [CrossRef]
- de Gruijl, F.R.; Van der Leun, J.C. Estimate of the Wavelength Dependency of Ultraviolet Carcinogenesis in Humans and Its Relevance to the Risk Assessment of a Stratospheric Ozone Depletion. Health Phys. 1994, 67, 319–325. [Google Scholar] [CrossRef]
- International Organization for Standardization/International Commission on Illumination. ISO/CIE 17166:2019 Erythema Reference Action Spectrum and Standard Erythema Dose. 2019. Available online: https://www.iso.org/standard/74167.html (accessed on 8 April 2021).
- International Organization for Standardization/International Commission on Illumination. ISO/CIE 28077:2016 Photocarcinogenesis Action Spectrum. 2016. Available online: https://www.iso.org/standard/69651.html (accessed on 8 April 2021).
- Parisi, A.V.; Wong, J.C. Erythemal irradiances of filtered ultraviolet radiation. Phys. Med. Biol. 1997, 42, 1263–1275. [Google Scholar] [CrossRef][Green Version]
- Setlow, R.B. Spectral Regions Contributing to Melanoma: A Personal View. J. Investig. Derm. Symp. Proc. 1999, 4, 46–49. [Google Scholar] [CrossRef]
- Madronich, S. The Atmosphere and UV-B Radiation at Ground Level. In Environmental UV Photobiology, 1st ed.; Young, R.A., Björn, L.O., Moan, J., Nultsch, W., Eds.; Plenum Press: New York, NY, USA, 1993; pp. 1–39. [Google Scholar]
- Bernhard, G.; Mayer, B.; Seckmeyer, G.; Moise, A. Measurements of spectral solar UV irradiance in tropical Australia. J. Geophys. Res. 1997, 102, 8719–8730. [Google Scholar] [CrossRef]
- Gerstl, S.A.W.; Zardecki, A.; Wiser, H.L. UV-B Handbook, Vol. I; Document LAIR83728; National Laboratory: Los Alamos, NM, USA, 1983. [Google Scholar]
- International Commission on Non-Ionizing Radiation Protection (ICNIRP). Guidelines on Limits of Exposure to Ultraviolet Radiation of Wavelengths between 180 nm and 400 nm (Incoherent Optical Radiation). Health Phys. 2004, 87, 171–186. [Google Scholar] [CrossRef]
- McKinlay, A.F.; Diffey, B.L. A reference action spectrum for ultraviolet induced erythemal in human skin. CIE J. 1987, 6, 17–22. [Google Scholar]
- Webb, A.R.; Slaper, H.; Koepke, P.; Schmalwieser, A.W. Know your standard: Clarifying the CIE erythema action spectrum. Photochem. Photobiol. 2011, 87, 483–486. [Google Scholar] [CrossRef]
- Schmalwieser, A.W.; Wallisch, S.; Diffey, B. A Library of Action Spectra for Erythema and Pigmentation. Photochem. Photobiol. Sci. 2012, 11, 251–268. [Google Scholar] [CrossRef]
- International Commission on Illumination. CIE S 013/E:2003 International Standard Global Solar UV Index. 2003. Available online: https://cie.co.at/publications/international-standard-global-solar-uv-index (accessed on 8 April 2021).
- Setlow, R.B.; Grist, E.; Thompson, K.; Woodhead, A.D. Wavelengths effective in induction of malignant melanoma. Proc. Natl. Acad. Sci. USA 1993, 90, 6666–6670. [Google Scholar] [CrossRef]
- Anderson, R.R.; Parrish, J.A. The Optics of Human Skin. J. Investig. Dermat. 1981, 77, 13–19. [Google Scholar] [CrossRef]
- Bruls, W.A.; Slaper, H.; van der Leun, J.C.; Berrens, L. Transmission of human epidermis and stratum corneum as a function of thickness in the ultraviolet and visible wavelengths. Photochem. Photobiol. 1984, 40, 485–494. [Google Scholar] [CrossRef] [PubMed]
- Meinhardt, M.; Krebs, R.; Anders, A.; Heinrich, U.; Tronnier, H. Effect of ultraviolet adaptation on the ultraviolet absorption spectra of human skin in vivo. Photodermatol. Photoimmunol. Photomed. 2008, 24, 76–82. [Google Scholar] [CrossRef] [PubMed]
- Berger, D.S. The sunburning ultraviolet meter: Design and performance. Photochem. Photobiol. 1976, 24, 587–593. [Google Scholar] [CrossRef] [PubMed]
- De Luisi, J.; Wendell, J.; Kreiner, F. An Examination of the Spectral Response Characteristics of Seven Robertson-Berger Meters After Long-Term Field Use. Photochem. Photobiol. 1992, 56, 115–122. [Google Scholar] [CrossRef]
- Solar Light. User Manual Model 501-DA Analog UV Biometer Sensor. Available online: https://solarlight.com/wp-content/uploads/Model-501-DA-Analog-UV-Biometer-User.pdf (accessed on 5 January 2021).
- Heydenreich, J.; Wulf, H.C. Personal UVR Dosimeter Measurements: Specific and General Uncertainties. Photochem. Photobiol. Sci. 2019, 18, 1461–1470. [Google Scholar] [CrossRef]
- Grandahl, K.; Erikson, P.; Ibler, K.S.; Bonde, J.P.; Mortensen, O.S. Supporting Information Measurements of Solar Ultraviolet Radiation Exposure at Work and at Leisure in Danish Workers. Photochem. Photobiol. 2018, 94, 807–814. [Google Scholar] [CrossRef]
- International Commission on Illumination (CIE). Technical Report—Personal Dosimetry of UV Radiation, CIE 98. 1992. Available online: https://cie.co.at/publications/personal-dosimetry-uv-radiation (accessed on 8 April 2021).
- Quintern, L.E.; Furusawa, Y.; Fukutsu, K.; Holtschmidt, H. Characterization and Application of UV Detector Spore Films: The Sensitivity Curve of a New Detector System Provides Good Similarity to the Action Spectrum for UV-Induced Erythema in Human Skin. J. Photochem. Photobiol. B 1997, 37, 158–166. [Google Scholar] [CrossRef]
- Morys, M.; Berger, D.S. The accurate measurements of biologically effective ultraviolet radiation. In Atmospheric Radiation; Stamnes, K.H., Ed.; Proc. SPIE: Bellingham, WA, USA, 1993; Volume 2049, pp. 152–161. [Google Scholar]
- Grandahl, K.; Mortensen, O.S.; Sherman, D.Z.; Køster, B.; Lund, P.A.; Ibler, K.S.; Eriksen, P. Solar UV exposure among outdoor workers in Denmark measured with personal UV-B dosimeters: Technical and practical feasibility. Biomed. Eng. Online 2017, 16, 119. [Google Scholar] [CrossRef]
- Davis, A.; Deane, G.H.; Diffey, B.L. Possible dosimeter for ultraviolet radiation. Nature 1976, 261, 169–170. [Google Scholar] [CrossRef]
- Knuschke, P.; Barth, J. Biologically weighted personal UV dosimetry. J. Photochem. Photobiol. B 1996, 36, 77–83. [Google Scholar] [CrossRef]
- Casale, G.R.; Siani, A.M.; Colosimo, A. Polysulphone dosimetry as a tool for personal exposure studies. Biophys. Bioeng. Lett. 2009, 2, 1–14. [Google Scholar]
- Kimlin, M.G.; Martinez, N.; Green, A.C.; Whiteman, D.C. Anatomical distribution of solar ultraviolet exposures among cyclists. J. Photochem. Photobiol. B 2006, 85, 23–27. [Google Scholar] [CrossRef]
- Downs, N.; Parisi, A. Mean exposure fractions of human body solar UV exposure patterns for application in different ambient climates. Photochem. Photobiol. 2012, 88, 223–226. [Google Scholar] [CrossRef]
- Seckmeyer, G.; Klingebiel, M.; Riechelmann, S.; Lohse, I.; McKenzie, R.L.; Liley, J.B.; Allen, M.W.; Siani, A.M.; Casale, G.R. A critical assessment of two types of personal UV dosimeters. Photochem. Photobiol. 2012, 88, 215–222. [Google Scholar] [CrossRef]
- Siani, A.M.; Casale, G.R.; Modesti, S.; Parisi, A.V.; Colosimo, A. Investigation on the capability of polysulphone for measuring biologically effective solar UV exposures. Photochem. Photobiol. Sci. 2014, 13, 521–530. [Google Scholar] [CrossRef]
- Bais, A.F.; McKenzie, R.L.; Bernhard, G.; Aucamp, P.J.; Ilyas, M.; Madronich, S.; Tourpali, K. Ozone depletion and climate change: Impacts on UV radiation. Photochem. Photobiol. Sci. 2015, 14, 19–52. [Google Scholar] [CrossRef]
- Bais, A.F.; Bernhard, G.; McKenzie, R.L.; Aucamp, P.J.; Young, P.J.; Ilyas, M.; Jöckel, P.; Deushi, M. Ozone-climate interactions and effects on solar ultraviolet radiation. Photochem. Photobiol. Sci. 2019, 18, 602–640. [Google Scholar] [CrossRef]
- Aun, M.; Eerme, K.; Ansko, I.; Veismann, U.; Lätt, S. Modification of spectral ultraviolet doses by different types of overcast cloudiness and atmospheric aerosol. Photochem. Photobiol. 2011, 87, 461–469. [Google Scholar] [CrossRef]
- McKenzie, R.L.; Weinreis, C.; Johnston, P.V.; Liley, B.; Shiona, H.; Kotkamp, M.; Smale, D.; Takegawa, N.; Kondo, Y. Effects of urban pollution on UV spectral irradiances. Atmos. Chem. Phys. 2008, 8, 5683–5697. [Google Scholar] [CrossRef]
- Turner, J.; Parisi, A.V.; Turnbull, D.J. Reflected solar radiation from horizontal, vertical and inclined surfaces: Ultraviolet and visible spectral and broadband behaviour due to solar zenith angle, orientation and surface type. J. Photochem. Photobiol. B 2008, 92, 29–37. [Google Scholar] [CrossRef]
- Utrillas, M.P.; Marín, M.J.; Esteve, A.R.; Salazar, G.; Suarez, H.; Castillo, J.; Martínez-Lozano, J.A. UVER and UV index at high altitude in Northwestern Argentina. J. Photochem. Photobiol. B 2016, 163, 290–295. [Google Scholar] [CrossRef] [PubMed]
- von Thaler, A.K.; Kamenisch, Y.; Berneburg, M. The role of ultraviolet radiation in melanomagenesis. Exp. Dermatol. 2010, 19, 81–88. [Google Scholar] [CrossRef] [PubMed]
- Mitchell, D.; Paniker, L.; Sanchez, G.; Trono, D.; Nairn, R. The etiology of sunlight-induced melanoma in Xiphophorus hybrid fish. Mol. Carcinog. 2007, 46, 679–684. [Google Scholar] [CrossRef] [PubMed]
- Mitchell, D.L.; Fernandez, A.A.; Nairn, R.S.; Garcia, R.; Paniker, L.; Trono, D.; Thames, H.D.; Gimenez-Conti, I. Ultraviolet A does not induce melanomas in a Xiphophorus hybrid fish model. Proc. Natl. Acad. Sci. USA 2010, 107, 9329–9334. [Google Scholar] [CrossRef] [PubMed]
- De Fabo, E.C.; Noonan, F.P.; Fears, T.; Merlino, G. Ultraviolet B but not ultraviolet A radiation initiates melanoma. Cancer Res. 2004, 64, 6372–6376. [Google Scholar] [CrossRef] [PubMed]
- Noonan, F.P.; Zaidi, M.R.; Wolnicka-Glubisz, A.; Anver, M.R.; Bahn, J.; Wielgus, A.; Cadet, J.; Douki, T.; Mouret, S.; Tucker, M.A.; et al. Melanoma induction by ultraviolet A but not ultraviolet B radiation requires melanin pigment. Nat. Commun. 2012, 3, 884. [Google Scholar] [CrossRef] [PubMed]
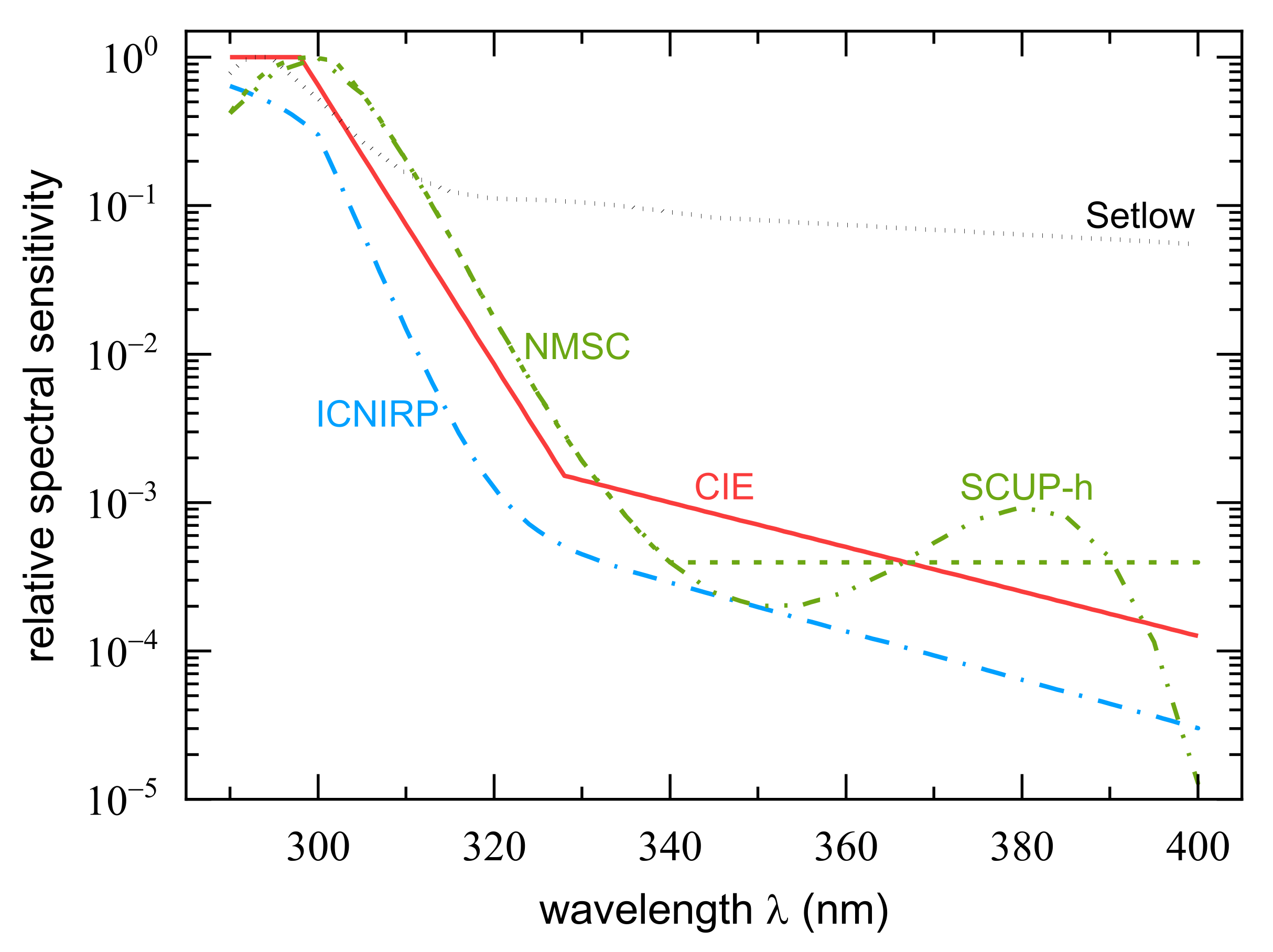
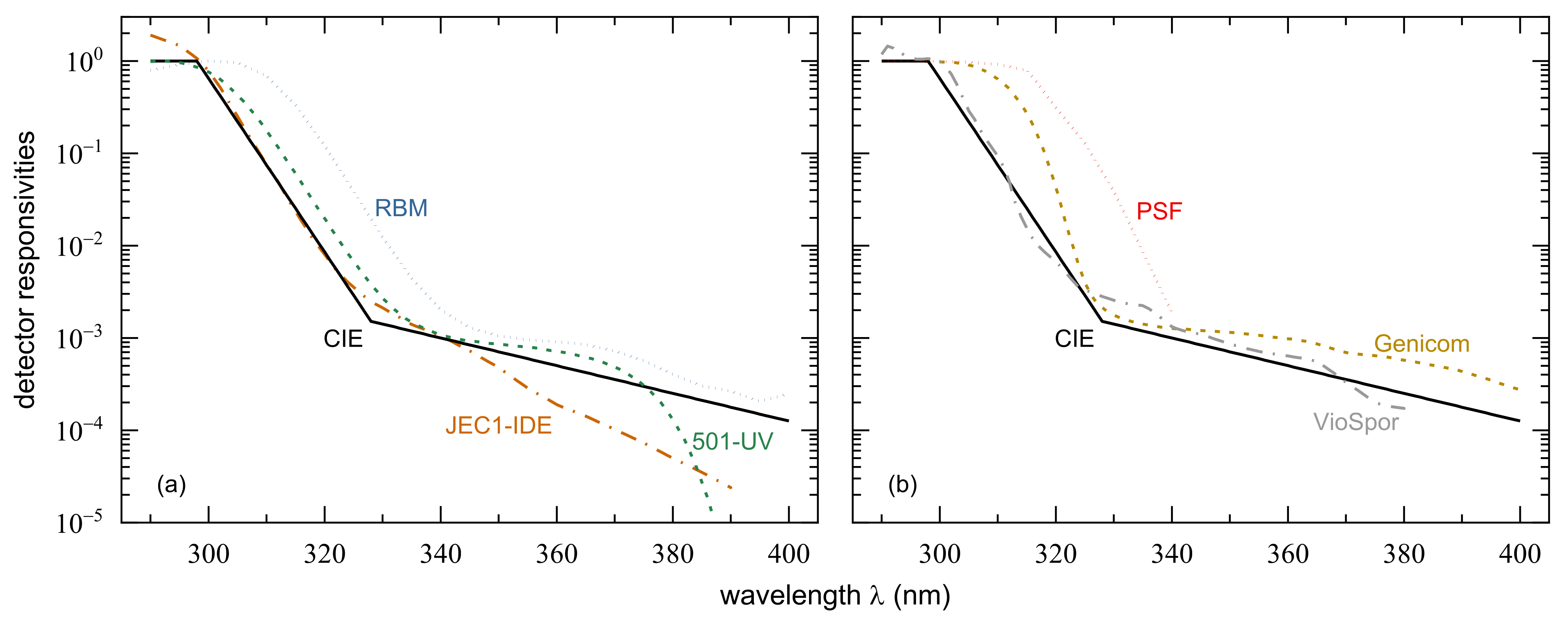

| Description | |
|---|---|
| CIE | standard erythema curve according to Equation (3) established by CIE [24] |
| NMSC | CIE standard curve for non-melanoma skin cancer [25] |
| SCUP-h | experimental data for NMSC induction in mice corrected for differences in mouse and human epidermal transmission, taken from Table 1 in [23] and interpolated semi-logarithmically in steps of 1 nm |
| ICNIRP | “UVR hazards curve” from ICNIRP [31] according to Equation (4) |
| Setlow | combined absorption spectrum of DNA and melanin multiplied with human epidermal transmission as given in Figure 1 of [27], digitized in 1 nm intervals |
| RBM | Robertson–Berger meter response function taken from Table 2 of [41], interpolated semi-logarithmically in steps of 1 nm |
| 501-UV | Solar Light’s UV Biometer 501, representing a modified RBM, taken from the manufacturer’s webpage [42], digitized in 1 nm intervals |
| JEC1-IDE | UVR radiometer based on a silicon carbide photodiode with dielectric filter taken from Figure 2 of [43], digitized and interpolated semi-logarithmically in steps of 1 nm |
| Genicom | UVR radiometer based on an aluminum gallium nitride photodiode from Figure S1 of [44], digitized and interpolated semi-logarithmically in steps of 1 nm |
| PSF | CIE standard polysulfone film dosimeter from Figure 4.4 of [45], digitized and interpolated semi-logarithmically in steps of 1 nm |
| VioSpor | spore film dosimeter, mutant strain modulated with a cut-off filter, taken from Figure 3 of [46], digitized and interpolated semi-logarithmically in steps of 1 nm |
| Peak Sensitivity at λ (nm) | Renormalization Factor | |
|---|---|---|
| CIE | ≤298 | 1.00 |
| NMSC | 299 | 0.96 |
| ICNIRP | 270 | 0.41 |
| Setlow | 293 | 0.75 |
| RBM | 300 | 0.95 |
| 501-UV | 292 | 0.89 |
| JEC1-IDE | 298.5 | 1.19 |
| Genicom | ≤296 | 0.99 |
| PSF | 290 | 0.99 |
| VioSpor | 300 | 1.05 |
| CIE | NMSC | ICNIRP | Setlow | |
|---|---|---|---|---|
| PSF | 16.2 ± 0.8 | 8 ± 1 | 70 ± 5 | 0.37 ± 0.07 |
| RBM | 7.9 ± 0.1 | 4.0 ± 0.3 | 34 ± 1 | 0.18 ± 0.04 |
| Genicom | 5.4 ± 0.4 | 2.69 ± 0.03 | 23 ± 1 | 0.12 ± 0.03 |
| 501-UV | 1.93 ± 0.06 | 0.97 ± 0.05 | 8.4 ± 0.2 | 0.04 ± 0.01 |
| VioSpor | 1.09 ± 0.02 | 0.55 ± 0.03 | 4.73 ± 0.03 | 0.025 ± 0.006 |
| JEC1-IDE | 0.95 ± 0.03 | 0.48 ± 0.02 | 4.12 ± 0.09 | 0.022 ± 0.005 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zölzer, F.; Bauer, S. Solar Ultraviolet Radiation Risk Estimates—A Comparison of Different Action Spectra and Detector Responsivities. Int. J. Environ. Res. Public Health 2021, 18, 4887. https://doi.org/10.3390/ijerph18094887
Zölzer F, Bauer S. Solar Ultraviolet Radiation Risk Estimates—A Comparison of Different Action Spectra and Detector Responsivities. International Journal of Environmental Research and Public Health. 2021; 18(9):4887. https://doi.org/10.3390/ijerph18094887
Chicago/Turabian StyleZölzer, Friedo, and Stefan Bauer. 2021. "Solar Ultraviolet Radiation Risk Estimates—A Comparison of Different Action Spectra and Detector Responsivities" International Journal of Environmental Research and Public Health 18, no. 9: 4887. https://doi.org/10.3390/ijerph18094887
APA StyleZölzer, F., & Bauer, S. (2021). Solar Ultraviolet Radiation Risk Estimates—A Comparison of Different Action Spectra and Detector Responsivities. International Journal of Environmental Research and Public Health, 18(9), 4887. https://doi.org/10.3390/ijerph18094887






