Estimation of Excess Mortality and Years of Life Lost to COVID-19 in Norway and Sweden between March and November 2020
Abstract
1. Introduction
2. Materials and Methods
2.1. Data Sources
2.2. Estimates of Years of Life Lost
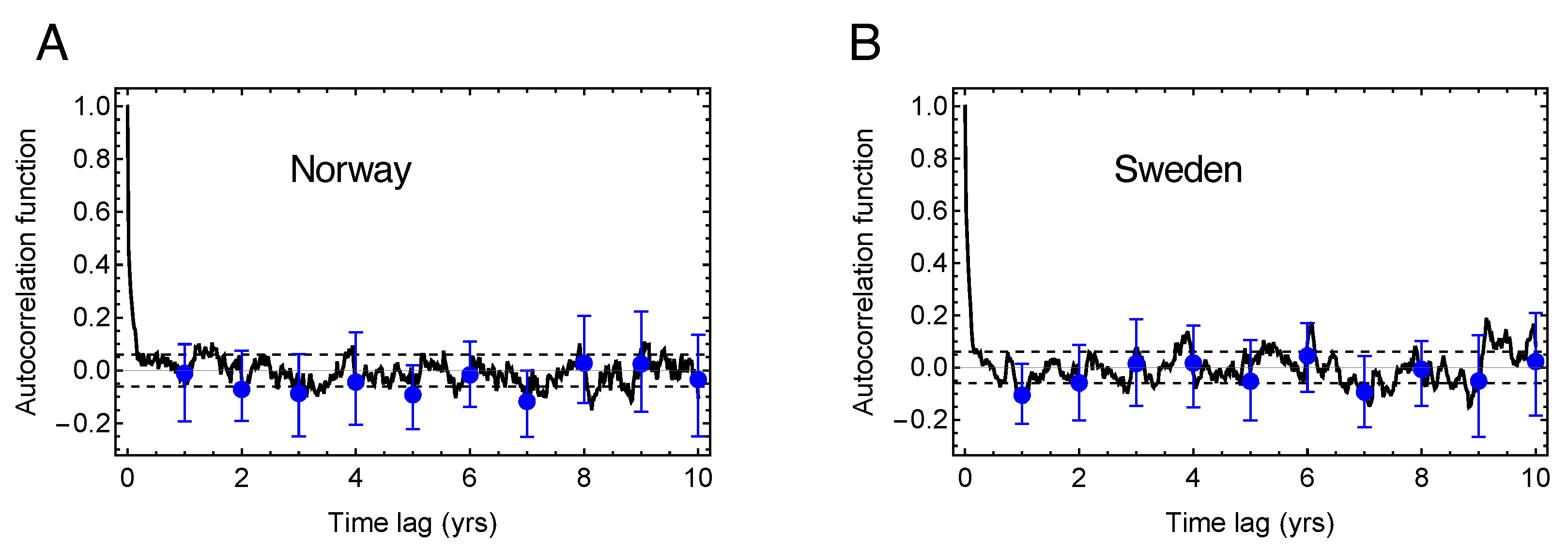
2.3. Estimate of Expected Mortality-Rate Signal
2.4. Estimate of Excess Mortality Rate
2.5. Estimate of Mortality Displacement
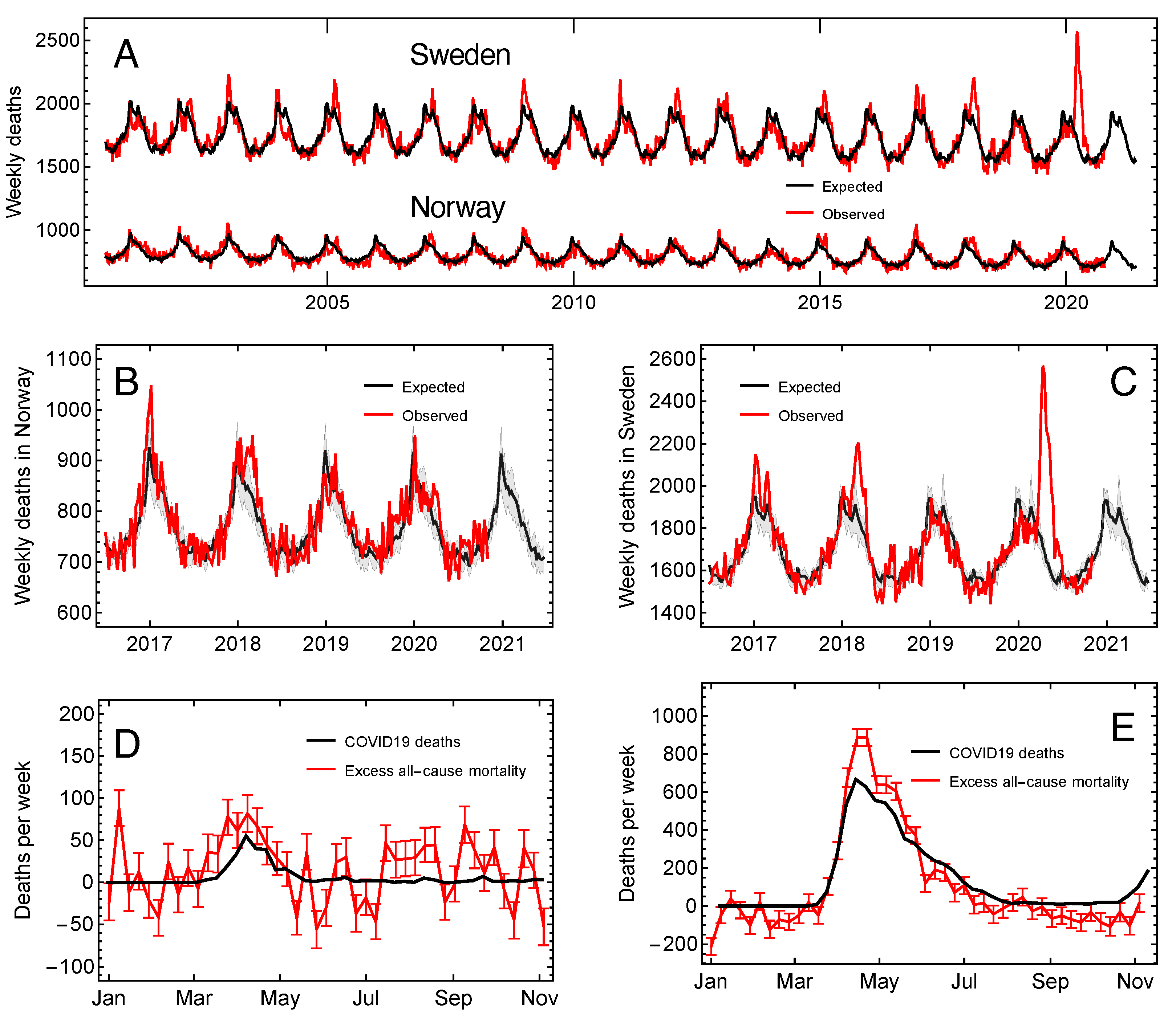
3. Results
3.1. The Expected and Excess Mortality Rate
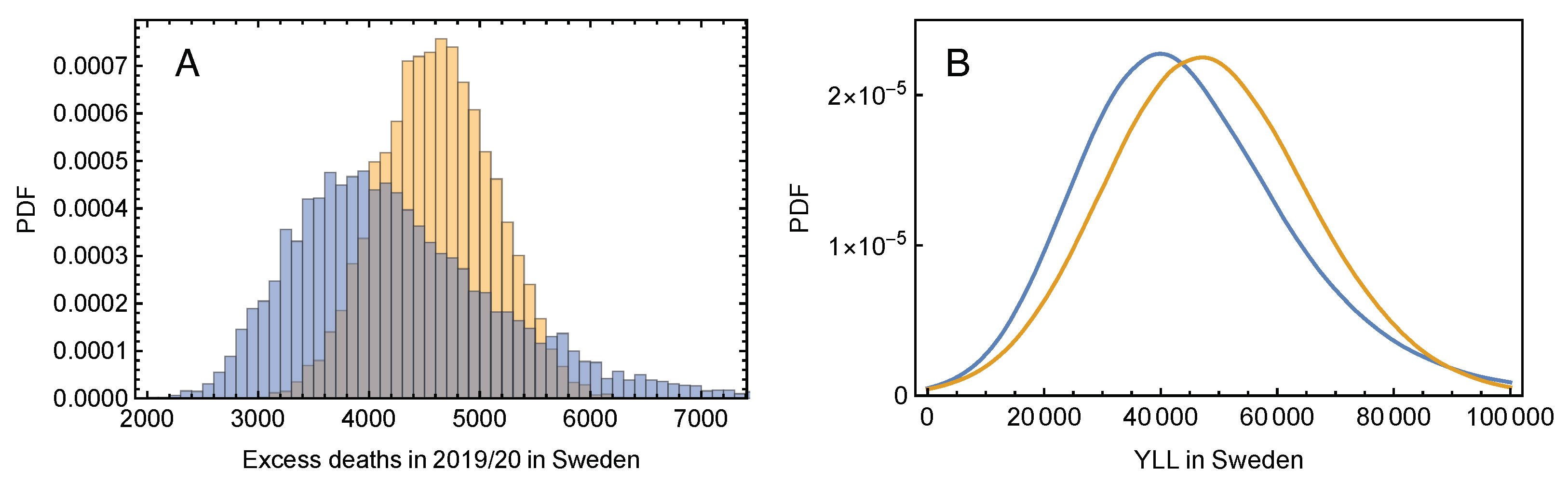
3.2. Excess Mortality and Mortality Displacement
3.3. The Tiny Effect of Mortality Displacement on Excess Deaths and YLL
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Paterlini, M. ‘Closing borders is ridiculous’: The epidemiologist behind Sweden’s controversial coronavirus strategy. Nature 2020, 580, 574. [Google Scholar] [CrossRef] [PubMed]
- Anderson, R.M.; Heesterbeek, H.; Klinkenberg, D.; Hollingsworth, T.D. How will country-based mitigation measures influence the course of the COVID-19 epidemic? Lancet 2020, 395, 931–934. [Google Scholar] [CrossRef]
- Middleton, J.; Lopes, H.; Michelson, K.; Reid, J. Planning for a second wave pandemic of COVID-19 and planning for winter. Int. J. Public Health 2020, 65, 1525–1527. [Google Scholar] [CrossRef] [PubMed]
- Thompson, R.N.; Hollingsworth, T.D.; Isham, V.; Arribas-Bel, D.; Ashby, B.; Britton, T.; Challenor, P.; Chappell, L.H.K.; Clapham, H.; Cunniffe, N.J.; et al. Key questions for modelling COVID-19 exit strategies. Proc. R. Soc. B Biol. Sci. 2020, 287, 20201405. [Google Scholar] [CrossRef] [PubMed]
- Chang, S.L.; Harding, N.; Zachreson, C.; Cliff, O.M.; Prokopenko, M. Modelling transmission and control of the COVID-19 pandemic in Australia. Nat. Commun. 2020, 11, 5710. [Google Scholar] [CrossRef] [PubMed]
- Blayac, T.; Dubois, D.; Duchêne, S.; Nguyen-Van, P.; Ventelou, B.; Willinger, M. Population preferences for inclusive COVID-19 policy responses. Lancet Public Health 2020, 6, e9. [Google Scholar] [CrossRef]
- Kamerlin, S.C.L.; Kasson, P.M. Managing Coronavirus Disease 2019 Spread With Voluntary Public Health Measures: Sweden as a Case Study for Pandemic Control. Clin. Infect. Dis. 2020, 71, 3174. [Google Scholar] [CrossRef] [PubMed]
- Our World in Data. Available online: https://ourworldindata.org (accessed on 15 November 2020).
- Juul, F.E.; Jodal, H.C.; Barua, I.; Refsum, E.; Olsvik, Ø.; Helsingen, L.M.; Løberg, M.; Bretthauer, M.; Kalager, M.; Emilsson, L. Mortality in Norway and Sweden before and after the Covid-19 outbreak: A cohort study. medRxiv 2020. [Google Scholar] [CrossRef]
- Stein, J. The Striking Similarities between Northern Norway and Northern Sweden. What Happened in Northern Norway? – A Comparative and Quantitative Analysis of Political and Demographic Development in Northern Norway from 1950 to 2015. Ph.D. Thesis, UiT—The Arctic University of Norway, Tromsø, Norway, 2019. Available online: https://hdl.handle.net/10037/16364 (accessed on 15 November 2020).
- Grothe-Hammer, M.; Roth, S. Dying is normal, dying with the coronavirus is not: A sociological analysis of the implicit norms behind the criticism of Swedish ‘exceptionalism’. Eur. Soc. 2020. [Google Scholar] [CrossRef]
- Excess Mortality during the Coronavirus Pandemic (COVID-19). Available online: https://ourworldindata.org/excess-mortality-covid (accessed on 12 March 2021).
- Brunner, J.H.; Solheim Sigurdsson, F.; Svennebye, L.; Täube, V. COVID-19: Excess Mortality in Selected European Countries; EFTA Statistical Office Publication, EFTA Statistical Office: Luxembourg, 2020. [Google Scholar]
- EuroMoMo. Available online: https://www.euromomo.eu (accessed on 15 November 2020).
- Smil, V. Don’t be Too Quick to Judge Sweden’s Covid-19 Policy. IEEE Spectr. 2020. Available online: https://spectrum.ieee.org/biomedical/ethics/dont-be-too-quick-to-judge-swedens-covid19-policy (accessed on 15 November 2020).
- Statistics Sweden (SCB). Available online: https://www.scb.se/en/ (accessed on 15 November 2020).
- Statistics Norway (SSB). Available online: https://www.ssb.no/en/ (accessed on 15 November 2020).
- Laake, K.; Sverre, J.M. Winter excess mortality: A comparison between Norway and England plus Wales. Age Ageing 1996, 25, 343–348. [Google Scholar] [CrossRef] [PubMed]
- Schreiber, T.; Schmitz, A. Improved Surrogate Data for Nonlinearity Tests. Phys. Rev. Lett. 1996, 77, 635–638. [Google Scholar] [CrossRef] [PubMed]
- Sørbye, S.H.; Nicolau, P.G.; Rue, H. Model-based bias correction for short AR(1) and AR(2) processes. arXiv 2020, arXiv:2010.05870. [Google Scholar]
- Influenza in Sweden Season 2018–2019, Article Number: 19048-2019, Public Health Agency of Sweden. Available online: https://www.folkhalsomyndigheten.se/publicerat-material/publikationsarkiv/i/influenza-in-sweden/?pub=63511 (accessed on 15 November 2020).
- Tracking COVID-19 Excess Deaths across Countries, The Economist. Available online: https://www.economist.com/graphic-detail/coronavirus-excess-deaths-tracker (accessed on 9 March 2021).
- Oh, I.H.; Ock, M.; Jang, S.Y.; Go, D.S.; Kim, Y.E.; Jung, Y.S.; Kim, K.B.; Park, H.; Jo, M.W.; Yoon, S.J. Years of Life Lost Attributable to COVID-19 in High-incidence Countries. J. Korean Med. Sci. 2020, 35, e300. [Google Scholar] [CrossRef] [PubMed]

| Age Group (yrs) | Proportion of 2020 Deaths | Life Expectancy (yrs) Estimate (SD) |
|---|---|---|
| 50–64 | ||
| 65–79 | ||
| 80–89 | ||
| >90 |
| Year | Excess Mortality in Norway | Excess Mortality in Sweden | ||
|---|---|---|---|---|
| Estimate | (95% CI) | Estimate | (95% CI) | |
| 2000/01 | 334 | |||
| 2001/02 | 866 | 587 | ||
| 2002/03 | 621 | 1227 | ||
| 2003/04 | ||||
| 2004/05 | 331 | |||
| 2005/06 | ||||
| 2006/07 | 59 | 758 | ||
| 2007/08 | ||||
| 2008/09 | 105 | 825 | ||
| 2009/10 | ||||
| 2010/11 | 163 | 87 | ||
| 2011/12 | 633 | 1443 | ||
| 2012/13 | 456 | 1718 | ||
| 2013/14 | ||||
| 2014/15 | 608 | 2131 | ||
| 2015/16 | ||||
| 2016/17 | 682 | 1811 | ||
| 2017/18 | 731 | 1450 | ||
| 2018/19 | ||||
| 2019/20 | 517 | 4329 | ||
| 2020/21 | 646 | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rypdal, M.; Rypdal, K.; Løvsletten, O.; Sørbye, S.H.; Ytterstad, E.; Bianchi, F.M. Estimation of Excess Mortality and Years of Life Lost to COVID-19 in Norway and Sweden between March and November 2020. Int. J. Environ. Res. Public Health 2021, 18, 3913. https://doi.org/10.3390/ijerph18083913
Rypdal M, Rypdal K, Løvsletten O, Sørbye SH, Ytterstad E, Bianchi FM. Estimation of Excess Mortality and Years of Life Lost to COVID-19 in Norway and Sweden between March and November 2020. International Journal of Environmental Research and Public Health. 2021; 18(8):3913. https://doi.org/10.3390/ijerph18083913
Chicago/Turabian StyleRypdal, Martin, Kristoffer Rypdal, Ola Løvsletten, Sigrunn Holbek Sørbye, Elinor Ytterstad, and Filippo Maria Bianchi. 2021. "Estimation of Excess Mortality and Years of Life Lost to COVID-19 in Norway and Sweden between March and November 2020" International Journal of Environmental Research and Public Health 18, no. 8: 3913. https://doi.org/10.3390/ijerph18083913
APA StyleRypdal, M., Rypdal, K., Løvsletten, O., Sørbye, S. H., Ytterstad, E., & Bianchi, F. M. (2021). Estimation of Excess Mortality and Years of Life Lost to COVID-19 in Norway and Sweden between March and November 2020. International Journal of Environmental Research and Public Health, 18(8), 3913. https://doi.org/10.3390/ijerph18083913







