Excess Winter Mortality (EWM) as a Dynamic Forensic Tool: Where, When, Which Conditions, Gender, Ethnicity and Age
Abstract
1. Introduction
2. Materials and Methods
3. Results
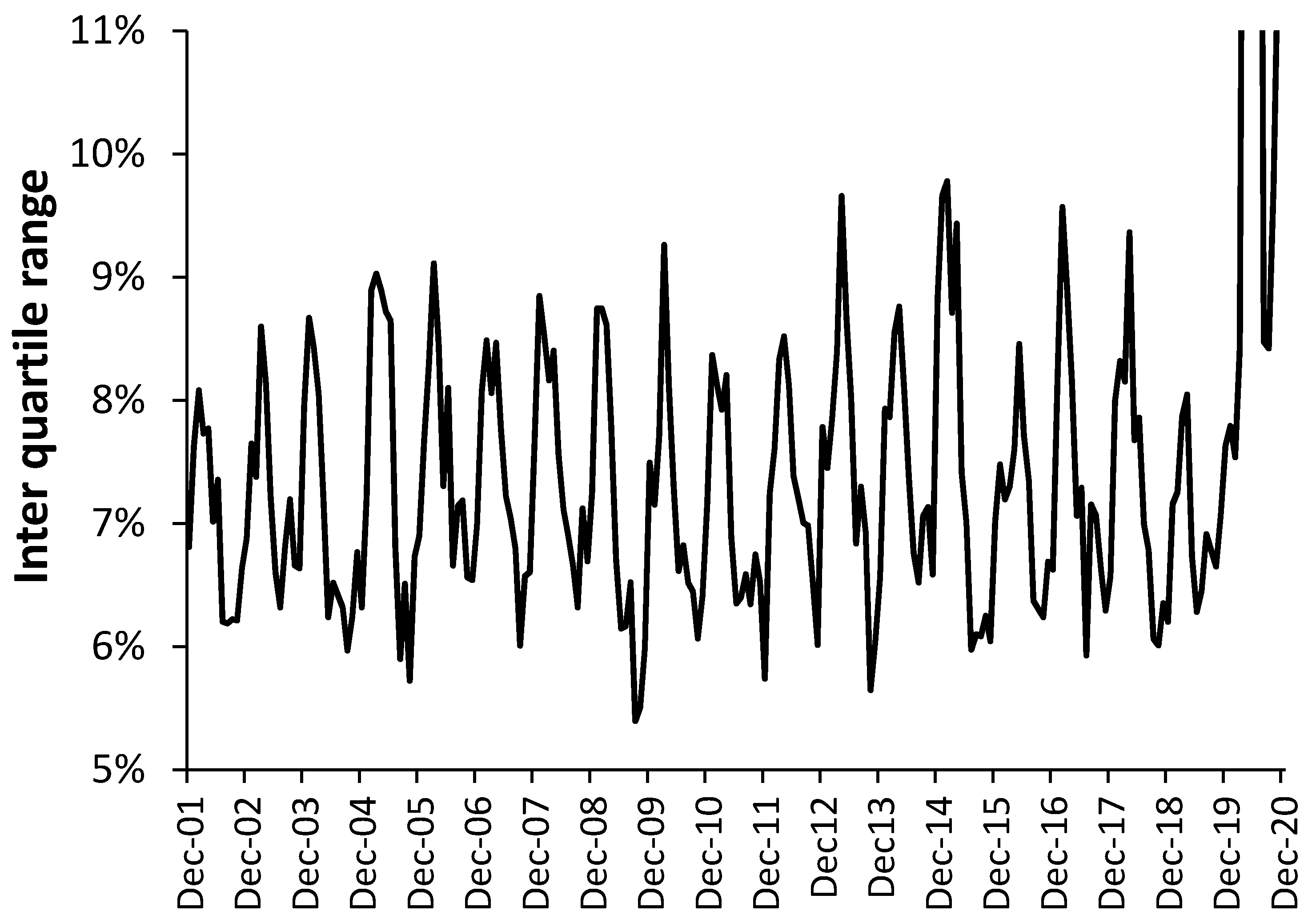
3.1. A Rolling EWM Calculation versus the Original (Static) Method
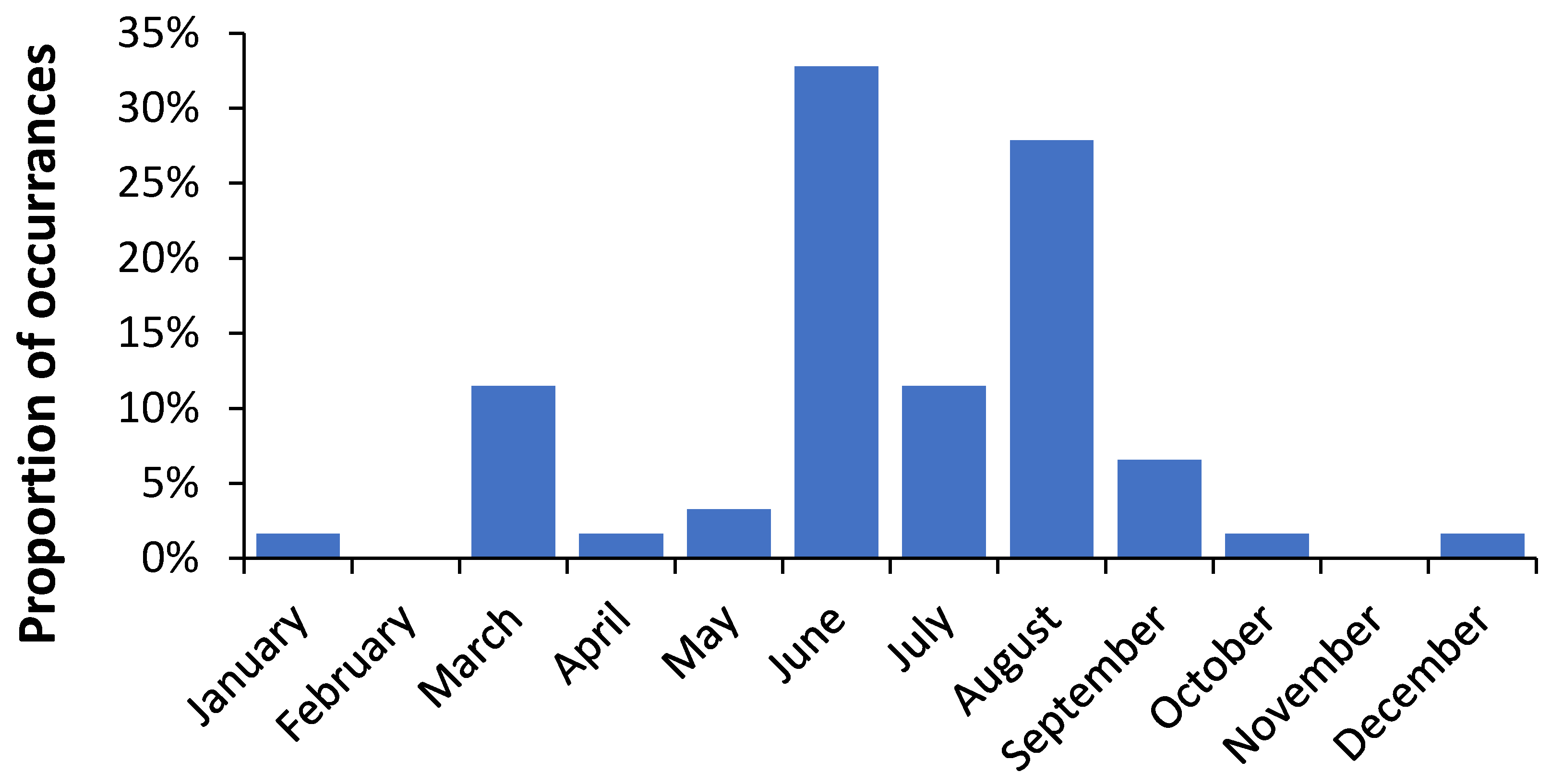
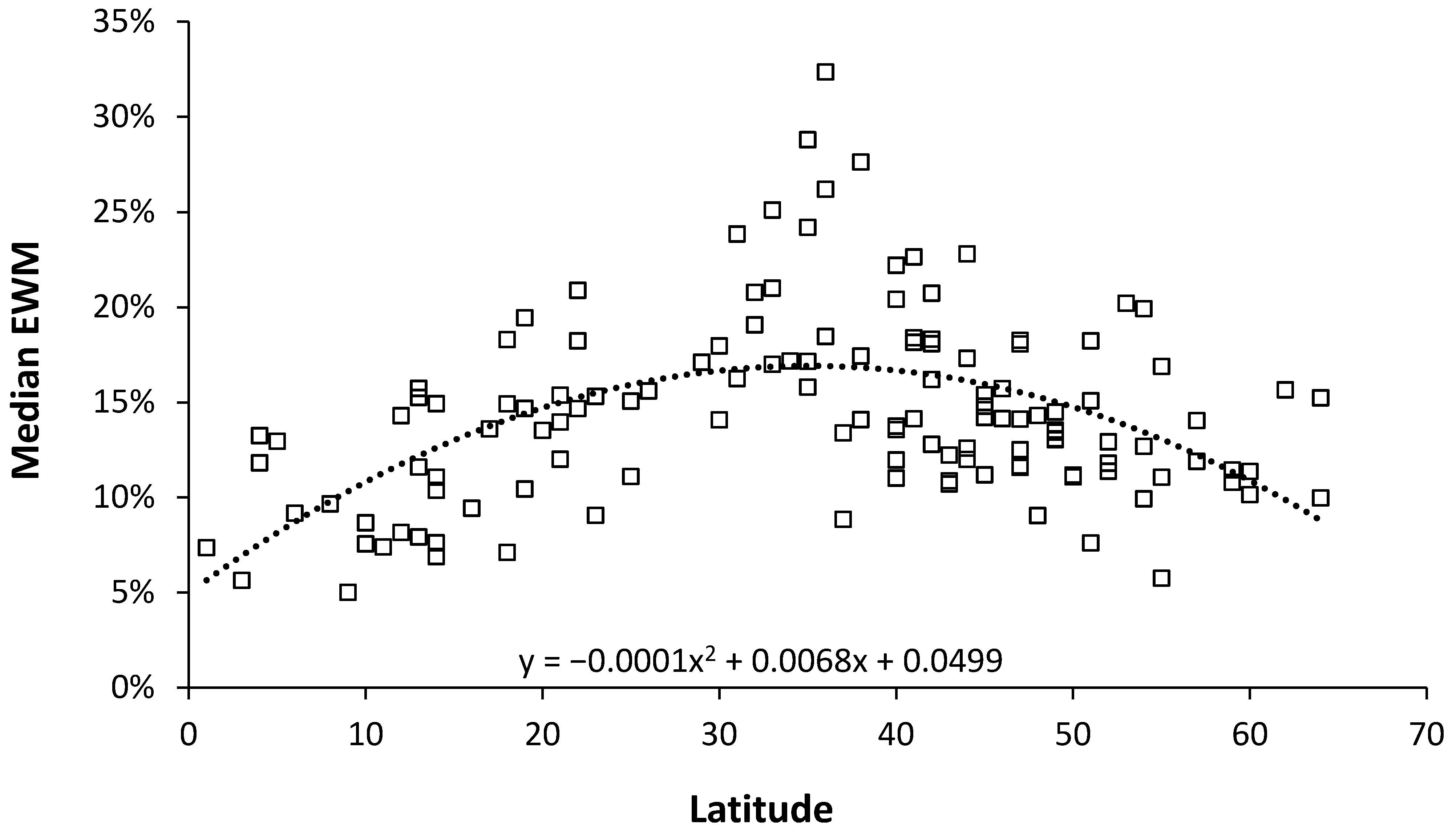
3.2. Role of Latitude
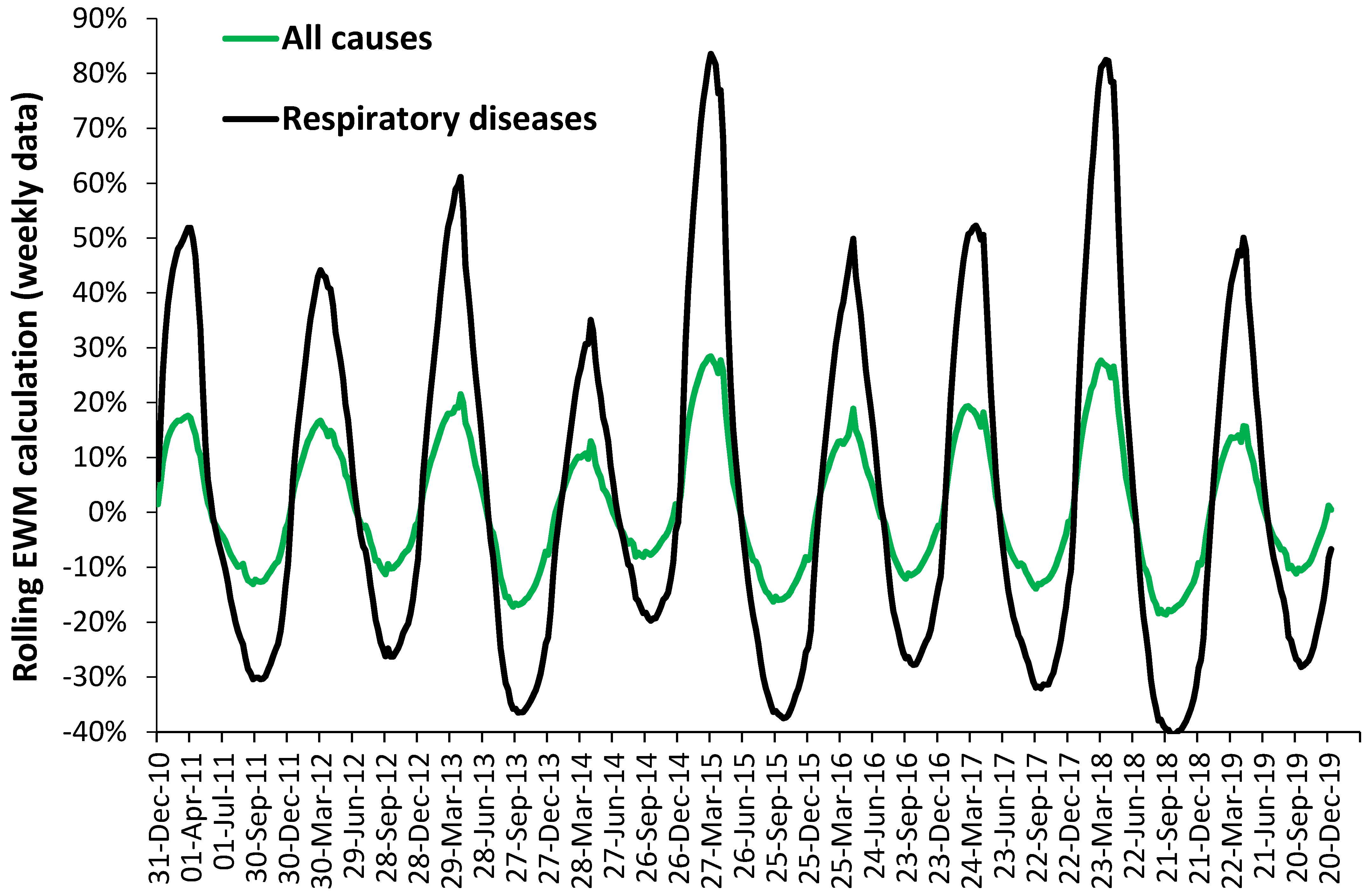
3.3. Role of Respiratory and Other Conditions
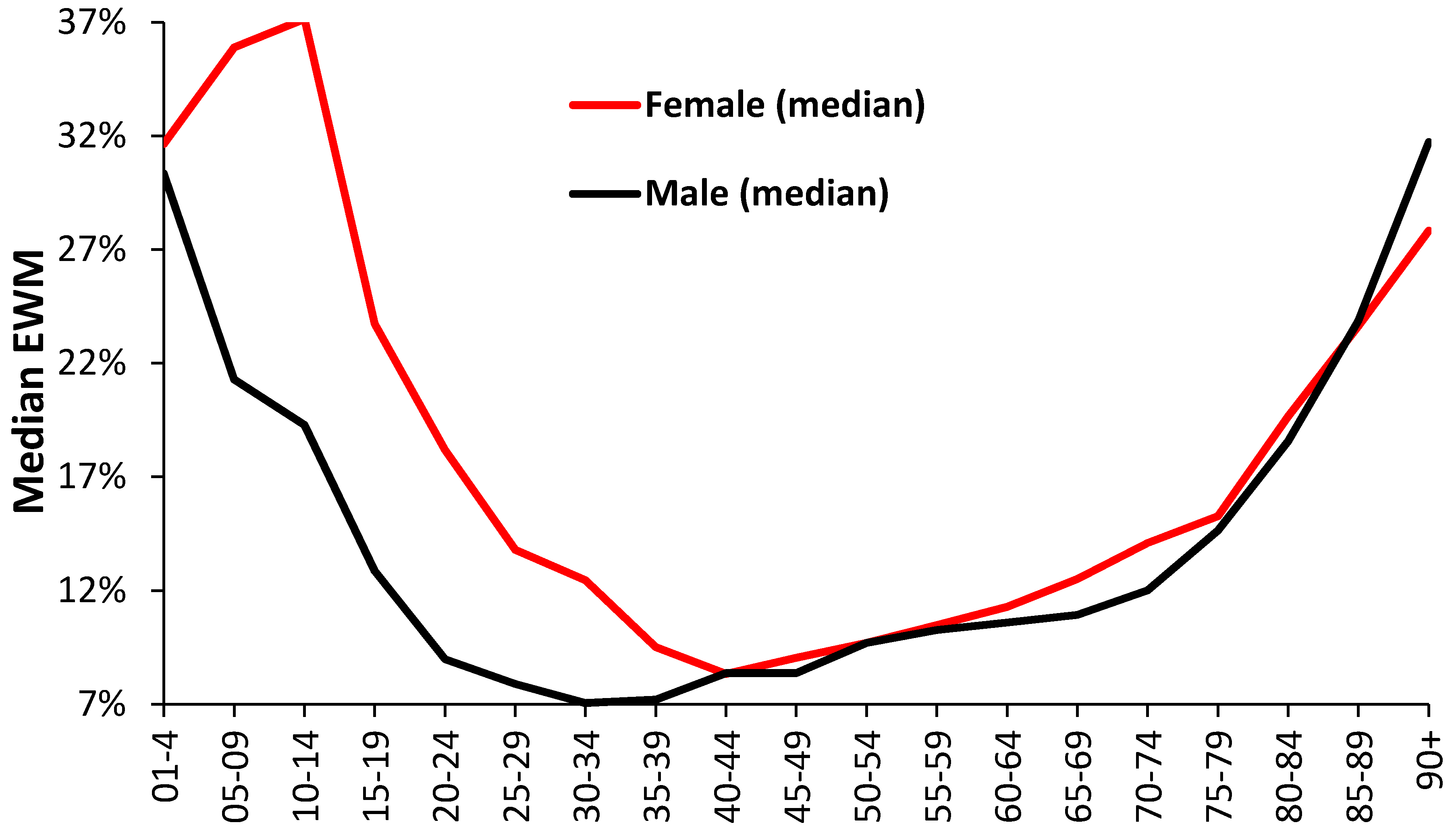
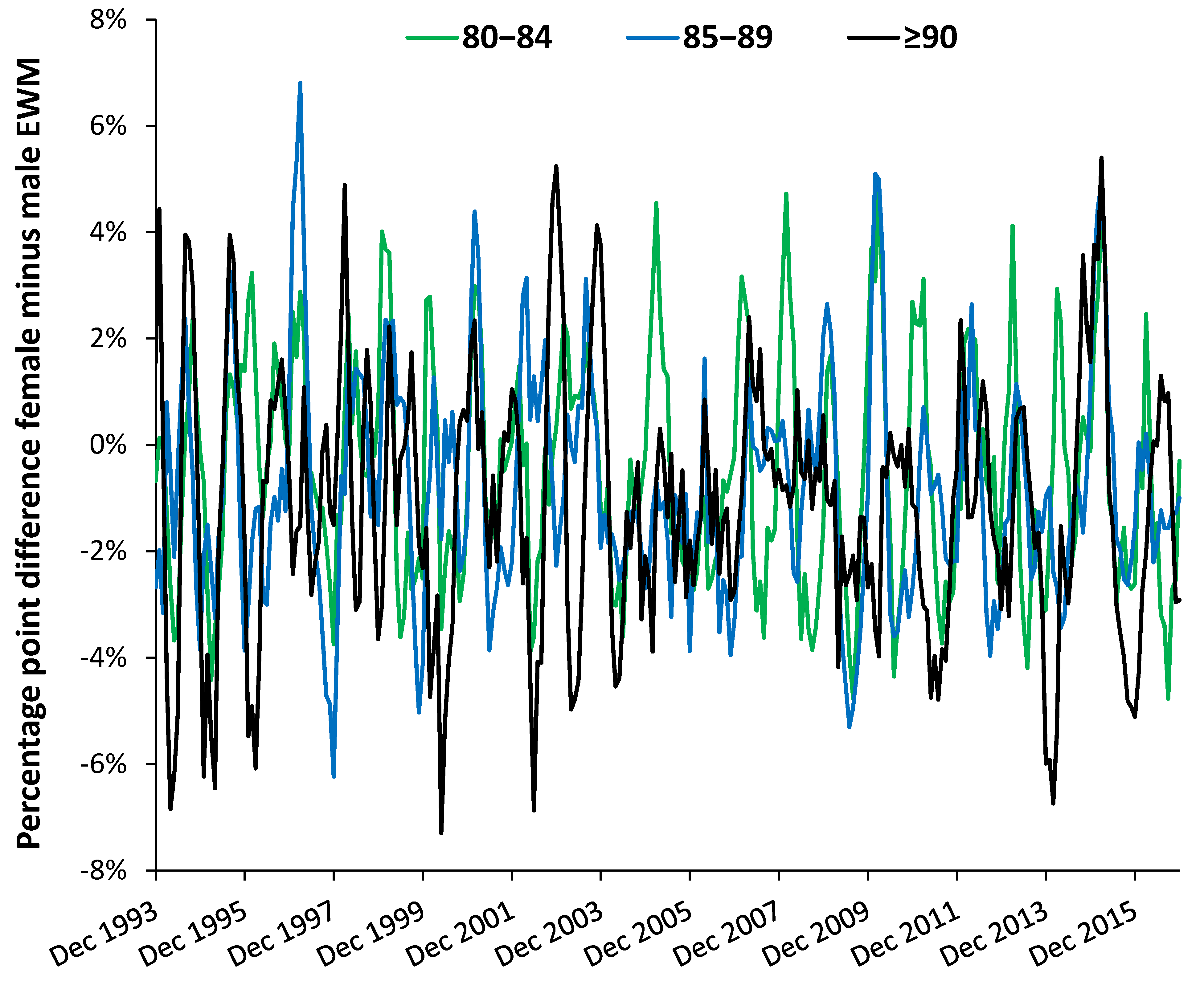
3.4. Role of Age and Gender
3.5. Effect of Location
3.6. Role of Area Deprivation Score
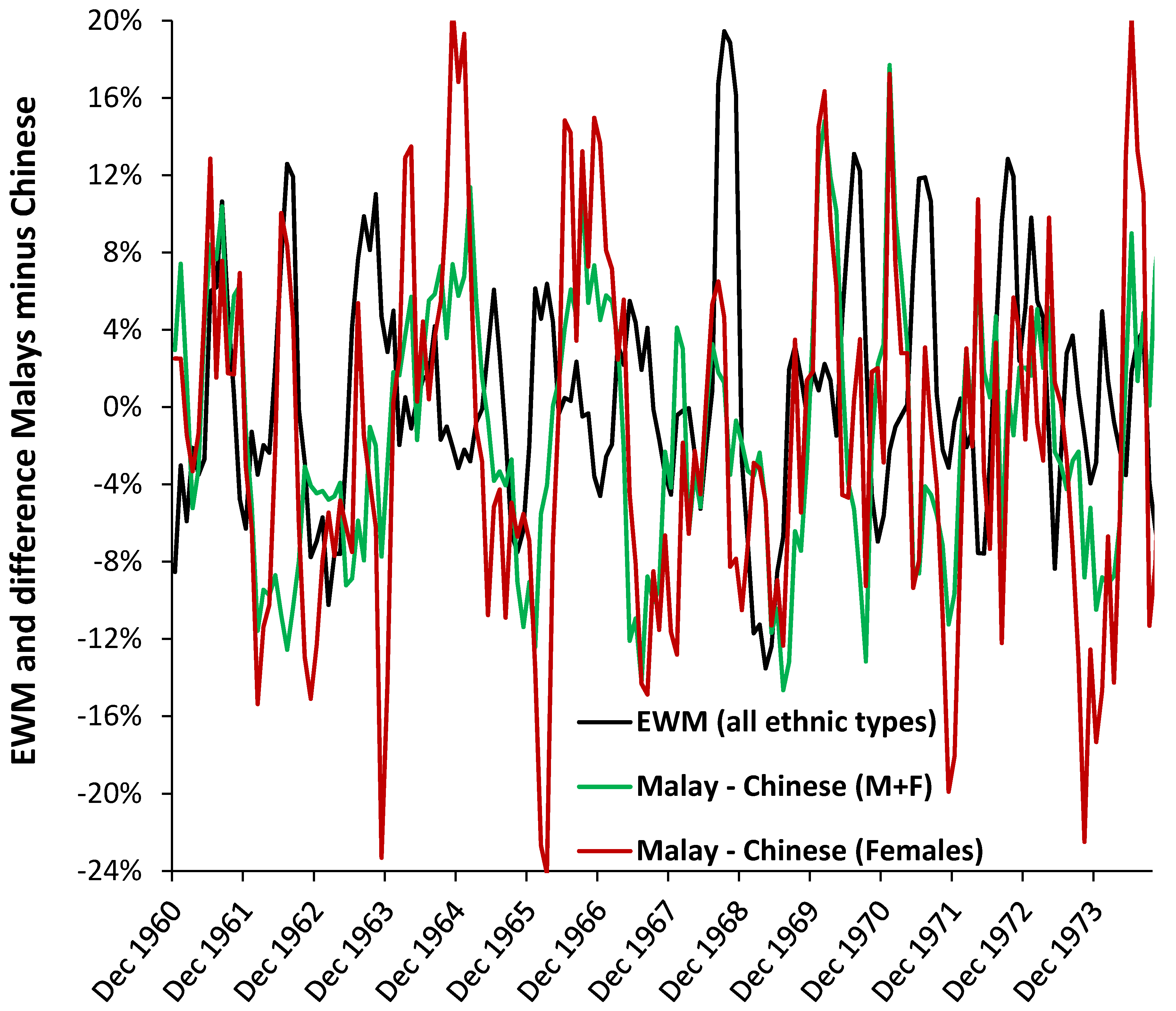
3.7. Roles for Ethnicity
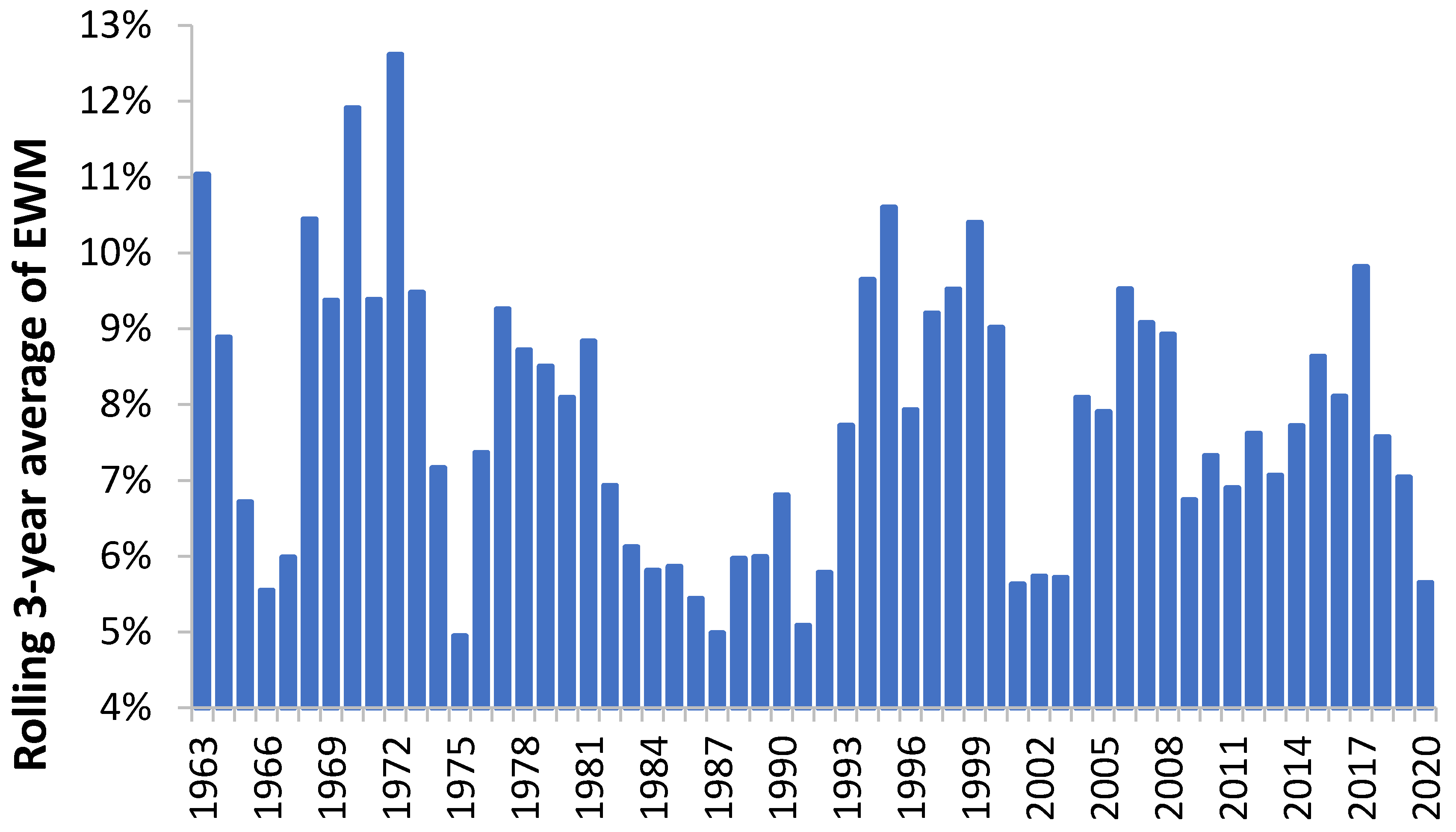
3.8. Factors Affecting the Median Value of EWM
3.9. Pandemic versus Seasonal Influenza
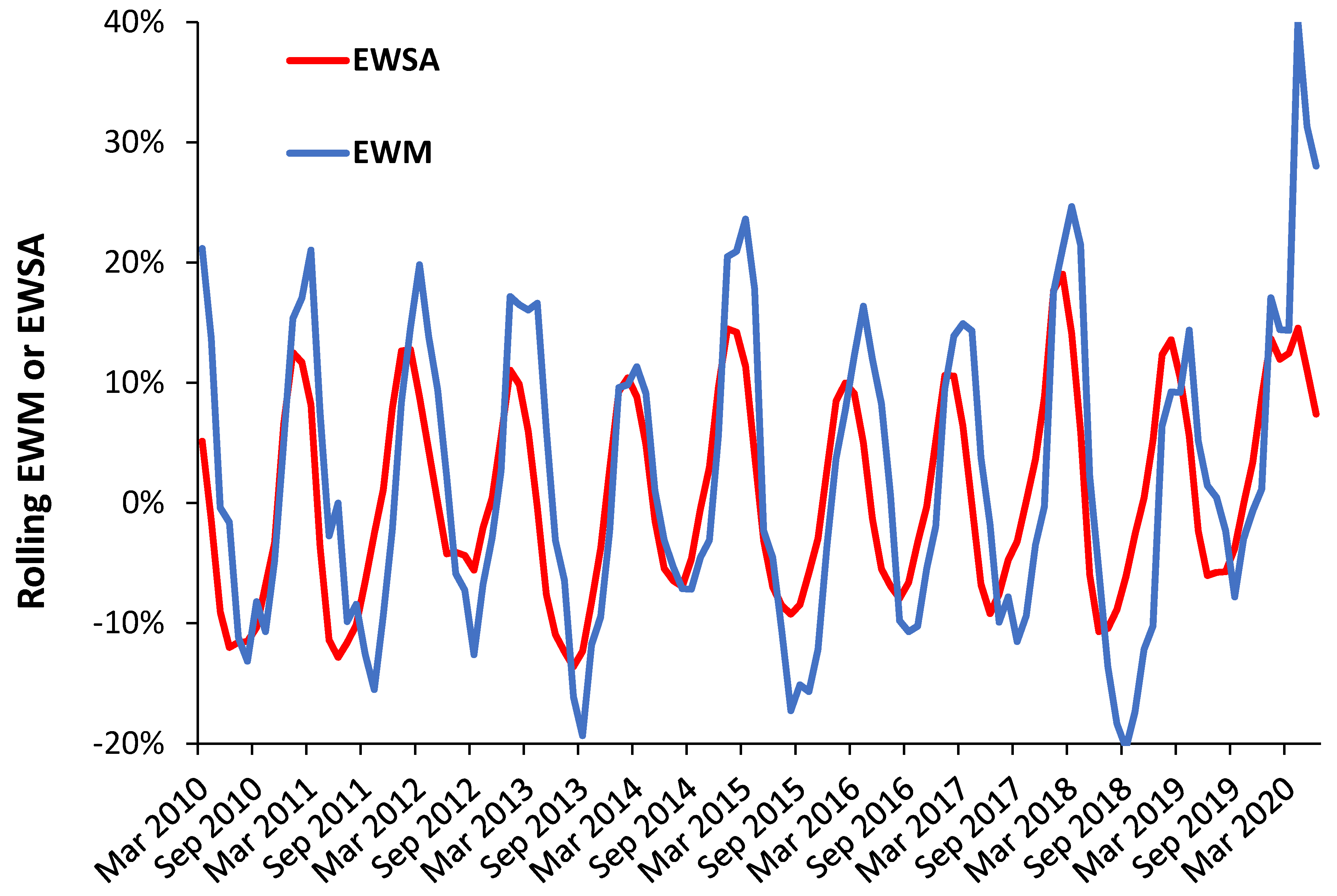
3.10. Deaths and Sickness Absence
3.11. Place of Death
3.12. Sub-National Behavior
4. Discussion
4.1. The Rolling EWM Method
4.2. Role of Latitude
4.3. Respiratory and Other Conditions
4.4. Age and Gender
4.5. Location and Area Deprivation
4.6. Ethnicity
4.7. Age or Nearness to Death
4.8. EWM and Influenza
4.9. Intrpreting Shifts in EWM
4.10. Interpreting the Shape of the Rolling EWM
4.11. Future Research Directions
4.12. Strengths and Limitations
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Johnson, H.; Griffiths, C. Estimating excess winter mortality in England and Wales. Health Stat. Q. 2003, 20, 19–24. Available online: http://www.ons.gov.uk/ons/rel/hsq/health-statistics-quarterly/no--20--winter-2003/estimating-excess-winter-mortality-in-england-and-wales.pdf (accessed on 3 January 2021).
- Teller-Elsberg, J.; Sovacool, B.; Smith, T.; Laine, E. Fuel poverty, excess winter deaths, and energy costs in Vermont: Burdensome for whom? Energy Policy 2016, 90, 81–91. [Google Scholar] [CrossRef]
- Clinch, J.; Healy, J. Housing standards and excess winter mortality. J. Epidemiol. Community Health 2000, 54, 719–720. [Google Scholar] [CrossRef]
- Healy, J. Excess winter mortality in Europe: A cross country analysis identifying key risk factors. J. Epidemiol. Community Health 2003, 57, 784–789. [Google Scholar] [CrossRef] [PubMed]
- NICE. Preventing Excess Winter Deaths and Illness Associated with Cold Homes. Quality Standard [QS117]. 4 March 2016. Available online: https://www.nice.org.uk/guidance/qs117 (accessed on 28 January 2021).
- Jones, R. Excess winter mortality (EWM) and stalling international improvements in life expectancy and mortality rates. Br. J. Healthc. Manag. 2020, 26. [Google Scholar] [CrossRef]
- Jones, R. NHS sickness absence in England—Hidden patterns. Br. J Healthc. Manag. 2020, 26, 1–11. [Google Scholar] [CrossRef]
- Chirakijja, J.; Jayachandran, S.; Ong, P. Inexpensive Heating Reduces Winter Mortality; Working Paper 25681; National Bureau of Economic Research: Cambridge, MA, USA, March 2019. [Google Scholar] [CrossRef]
- Emspak, J. How Fracking Affects Natural Gas Prices. Investopedia, June 2019. Available online: https://www.investopedia.com/articles/markets/080814/how-fracking-affects-natural-gas-prices.asp (accessed on 10 February 2021).
- Fyfe, C.; Barnard, T.; Howden-Chapman, P.; Douwes, J. Association between home insulation and hospital admission rates: Retrospective cohort study using linked data from a national intervention programme. BMJ 2020, 371, m4571. [Google Scholar] [CrossRef]
- Wilkinson, P.; Pattenden, S.; Armstrong, B.; Fletcher, A.; Kovats, R.S.; Mangtani, P.; McMichael, A.J. Vulnerability to winter mortality in elderly people in Britain: Population based study. BMJ 2004, 329, 647. [Google Scholar] [CrossRef] [PubMed]
- UNdata. Deaths by Month of Death. Available online: http://data.un.org/Data.aspx?d=POP&f=tableCode%3A65 (accessed on 3 January 2020).
- EuroStat. Deaths: Total by Month. 2020. Available online: https://ec.europa.eu/eurostat/web/products-datasets/-/demo_mmonth (accessed on 28 January 2021).
- US CDC Wonder Data. Monthly Deaths by State. 2019. Available online: https://wonder.cdc.gov/controller/saved/D76/D57F113 (accessed on 10 January 2021).
- Statistics Canada. Deaths by Month. 2020. Available online: https://www150.statcan.gc.ca/t1/tbl1/en/tv.action?pid=1310070801 (accessed on 18 February 2021).
- Statistisches Bundesamt. 12613: 0006 Deaths: Germany, Month, Sex. Available online: https://ckan.govdata.de/dataset/gestorbene-deutschland-monate-geschlecht (accessed on 28 January 2021).
- Singapore Department of Statistics. Deaths by Ethnic Group, Month and Sex. 2021. Available online: https://www.tablebuilder.singstat.gov.sg/publicfacing/selectVariables.action (accessed on 28 January 2021).
- Michigan Department of Health and Human Services. Monthly Death Counts. Available online: https://www.mdch.state.mi.us/osr/Provisional/MontlyDxCounts.asp (accessed on 2 February 2021).
- Office for National Statistics. Deaths Registered Weekly in England and Wales, Provisional. Available online: https://www.ons.gov.uk/peoplepopulationandcommunity/birthsdeathsandmarriages/deaths/datasets/weeklyprovisionalfiguresondeathsregisteredinenglandandwales (accessed on 28 January 2021).
- Office for National Statistics. Weekly Deaths in England and Wales by Index of Multiple Deprivation (IMD), 2005 to 2018. Available online: https://www.ons.gov.uk/peoplepopulationandcommunity/birthsdeathsandmarriages/deaths/adhocs/10549weeklydeathsinenglandandwalesbyindexofmultipledeprivationimd2005to2018 (accessed on 28 January 2021).
- Office for National Statistics. Deaths Occurring by Single Year of Age, by Sex, Year and Month of Death, for Usual Residents of England and Wales: 1993 to 2014. Available online: https://www.ons.gov.uk/peoplepopulationandcommunity/birthsdeathsandmarriages/deaths/adhocs/006478deathsoccurringbysingleyearofagebysexyearandmonthofdeathforusualresidentsofenglandandwales1993to2014 (accessed on 18 February 2021).
- Office for National Statistics. Deaths Occurring by Single Year of Age, by Sex, Year and Month of Death, for Usual Residents of England and Wales, 2015 to 2016. Available online: https://www.ons.gov.uk/peoplepopulationandcommunity/birthsdeathsandmarriages/deaths/adhocs/009225deathsoccurringbysingleyearofagebysexyearandmonthofdeathforusualresidentsofenglandandwales2015to2016 (accessed on 18 February 2021).
- NHS Digital. NHS Sickness Absence Rates. NHS Sickness Absence Rates April 2020 to June 2020, Provisional Statistics—NHS Digital. Available online: https://digital.nhs.uk/data-and-information/publications/statistical/nhs-sickness-absence-rates/june-2020 (accessed on 26 January 2021).
- Han, J.; Liu, S.; Zhang, J.; Zhou, L.; Fang, Q.; Zhang, J.; Zhang, Y. The impact of temperature extremes on mortality: A time-series study in Jinan, China. BMJ Open 2017, 7, e014741. [Google Scholar] [CrossRef] [PubMed]
- Jones, R. Multidisciplinary insights into health care financial risk and hospital surge capacity, Part 2: High population density is associated with enhanced year-to-year volatility in many aspects of poor health including health care worker sickness absence. J. Health Care Financ. 2021, in press. [Google Scholar]
- Jones, R. Multidisciplinary insights into health care financial risk and hospital surge capacity, Part 3: Outbreaks of a new type or kind of disease create unique risk patterns and confounds traditional trend analysis. J. Health Care Financ. 2021, in press. [Google Scholar]
- Hajat, S.; Kovats, R.; Lachowycz, K. Heat-related and cold-related deaths in England and Wales: Who is at risk? Occup. Environ. Med. 2007, 64, 93–100. [Google Scholar] [CrossRef]
- Shah, S.; Peacock, J. Deprivation and excess winter mortality. J. Epidemiol. Community Health 1999, 53, 499–502. [Google Scholar] [CrossRef]
- English Indices of Multiple Deprivation, File 13: Clinical Commissioning Group Summaries. Available online: https://www.gov.uk/government/statistics/english-indices-of-deprivation-2015 (accessed on 28 January 2021).
- Dickins, S. Deprivation in Wales: How Does Your Area Measure up? BBC News. 27 November 2019. Available online: https://www.bbc.co.uk/news/uk-wales-50564433 (accessed on 18 February 2021).
- Brooks, E. The Poisson Distribution. University of Massachusetts at Amherst, 2005. Available online: https://www.umass.edu/wsp/resources/poisson/ (accessed on 28 January 2021).
- Doshi, P. Trends in recorded influenza mortality: United States, 1900–2004. Am. J. Public Health 2008, 98, 939–945. [Google Scholar] [CrossRef] [PubMed]
- Jones, R. Multidisciplinary insights into health care financial risk and hospital surge capacity, Part 1: Nearness to death, infectious outbreaks, and Covid-19. J. Health Care Financ. 2021, 47. Available online: http://www.healthfinancejournal.com/~junland/index.php/johcf/index (accessed on 28 January 2021).
- Center for Epidemiology and Disease Control. Influenza—United States 1984/85 season. MMWR 1985, 34, 440–444. [Google Scholar]
- Liddell, C.; Morris, C.; Thomson, H.; Guiney, C. Excess winter death in 30 European countries 1980–2013: A critical review of methods. J. Public Health 2016, 38, 806–814. [Google Scholar] [CrossRef]
- Alonso, W.J.; Viboud, C.; Simonsen, L.; Hirano, E.W.; Daufenbach, L.Z.; Miller, M.A. Seasonality of Influenza in Brazil: A Traveling Wave from the Amazon to the Subtropics. Am. J. Epidemiol. 2007, 165, 1434–1442. [Google Scholar] [CrossRef]
- Almeedra, R.; Santana, P.; Vasconcelos, J. Evidence of social deprivation on the spatial patterns of excess winter mortality. Int. J. Public Health 2017, 62, 849–856. [Google Scholar] [CrossRef]
- Laake, K.; Sverre, J. Winter Excess Mortality: A Comparison between Norway and England plus Wales. Age Ageing 1996, 25, 343–348. [Google Scholar] [CrossRef]
- Davie, G.; Baker, M.; Hales, S.; Carlin, J. Trends and determinants of excess winter mortality in New Zealand: 1980 to 2000. BMC Public Health 2007, 7, 263. [Google Scholar] [CrossRef]
- Jones, R. Cycles in gender-related costs for long-term conditions. Brit. J. Healthc. Manag. 2011, 17, 124–125. [Google Scholar] [CrossRef]
- Jones, R. Multidisciplinary insights into health care financial risk and hospital surge capacity, Part 4: What size does a health insurer or health authority need to be to minimise risk? J. Health Care Financ. 2021, 47. Available online: http://www.healthfinancejournal.com/~junland/index.php/johcf/index (accessed on 26 January 2021).
- Wikipedia. Winter Fuel Payment. Available online: https://en.wikipedia.org/wiki/Winter_Fuel_Payment#:~:text=From%20Wikipedia,%20the%20free%20encyclopedia%20The%20Winter%20Fuel,additional%20costs%20of%20heating%20over%20the%20winter%20months (accessed on 29 January 2021).
- Iparraguirre, J. Have winter fuel payments reduced excess winter mortality in England and Wales? J. Public Health 2015, 37, 26–33. [Google Scholar] [CrossRef] [PubMed]
- Henderson, M. An Update to the Decent Homes Standard is Overdue. Here’s How It Should Change. Inside Housing, September 2019. Available online: https://www.insidehousing.co.uk/comment/an-update-to-the-decent-homes-standard-is-overdue-heres-how-it-should-change-63449 (accessed on 29 January 2021).
- Lim, R.B.T.; Zheng, H.; Yang, Q.; Cook, A.R.; Chia, K.S.; Lim, W.Y. Ethnic and gender specific life expectancies of the Singapore population, 1965 to 2009—Converging, or diverging? BMC Public Health 2013, 13, 1012. [Google Scholar] [CrossRef]
- Pin, S.P.; Golmard, J.L.; Cotto, E.; Rothan-Tondeur, M.; Chami, K.; Piette, F. Excess Winter Mortality in France: Influence of temperature, influenza like illness, and residential care status. J. Am. Med Dir. Assoc. 2012, 13, 309.e1–309.e7. [Google Scholar] [CrossRef]
- McLean, H.Q.; Thompson, M.G.; Sundaram, M.E.; Kieke, B.A.; Gaglani, M.; Murthy, K.; Belongia, E.A. Influenza vaccine effectiveness in the United States during 2012–2013: Variable protection by age and virus Type. J. Infect. Dis. 2015, 2011, 1529–1540. [Google Scholar] [CrossRef]
- Davis, R.; Rossier, C.; Enfield, K. The impact of weather on influenza and pneumonia mortality in New York City, 1975–2002: A retrospective study. PLoS ONE 2012, 7, e34091. [Google Scholar] [CrossRef]
- Webster, R.G.; Laver, W.G.; Air, G.M.; Ward, C.; Gerhard, W.; Van Wyke, K.L. The mechanism of antigenic drift in influenza viruses: Analysis of Hong Kong (H3N2) variants with monoclonal antibodies to the hemagglutinin molecule. Ann. N. Y. Acad. Sci. 1980, 354, 142–161. [Google Scholar] [CrossRef]
- Arevalo, C.P.; Le Sage, V.; Bolton, M.J.; Eilola, T.; Jones, J.E.; Kormuth, K.A.; Hensley, S.E. Original antigenic sin priming of influenza virus hemagglutinin stalk antibodies. Proc. Natl. Acad. Sci. USA 2020, 117, 17221–17227. [Google Scholar] [CrossRef] [PubMed]
- Pan, K. Understanding Original Antigenic Sin in Influenza with a Dynamical System. PLoS ONE 2011, 6, e23910. [Google Scholar] [CrossRef]
- Klein, W. The weather and circulation of the winter of 1950–51. Weatherwise 1951, 4, 38–46. [Google Scholar] [CrossRef]
- Marshall, S. Commentary on Infantry Operations and Weapons Usage in Korea. Defense Technical Information Center, October 1952. Available online: https://archive.org/details/DTIC_AD0000342 (accessed on 29 January 2021).
- Viboud, C.; Tam, T.; Fleming, D.; Miller, M.A.; Simonsen, L. 1951 influenza epidemic, England and Wales, Canada, and the United States. Emerg. Infect. Dis. 2006, 12, 661–668. [Google Scholar] [CrossRef]
- Reichert, T.A.; Simonsen, L.; Sharma, A.; Pardo, S.A.; Fedson, D.S.; Miller, M.A. Influenza and the winter increase in mortality in the United States, 1959–1999. Am. J. Epidemiol. 2004, 160, 492–502. [Google Scholar] [CrossRef]
- Nunes, B.; Viboud, C.; Machado, A.; Ringholz, C.; Rebelo-de-Andrade, H.; Nogueira, P.; Miller, M. Excess mortality associated with influenza epidemics in Portugal, 1980 to 2004. PLoS ONE 2011, 6, e20661. [Google Scholar] [CrossRef]
- Donaldson, G.C.; Keating, W.R. Excess winter mortality: Influenza or cold stress? Observational study. BMJ 2002, 324, 89. [Google Scholar] [PubMed]
- WebMD. Traffic Accidents Are Top Cause of Teen Deaths. Available online: https://www.webmd.com/parenting/news/20100505/traffic-accidents-are-top-cause-of-teen-deaths (accessed on 3 February 2021).
- Vestergaard, L.S.; Nielsen, J.; Krause, T.G.; Espenhain, L.; Tersago, K.; Sierra, N.B.; Denissov, G.; Innos, K.; Virtanen, M.J.; Mølbak, K.; et al. Excess all-cause and influenza-attributable mortality in Europe, December 2016 to February 2017. Euro Surveill. 2017, 22, 30506. [Google Scholar] [CrossRef]
- Jones, R. Cancer care and volatility in commissioning. Br. J. Healthc. Manag. 2012, 18, 315–324. [Google Scholar] [CrossRef]
- Jones, R. Diagnoses, deaths and infectious outbreaks. Br. J. Healthc. Manag. 2012, 18, 539–548. [Google Scholar] [CrossRef]


| Variable | Pneum-Onia/Flu | Septic-Emia | COPD | Heart Disease | Stroke | All Other | Cancer | All Deaths |
|---|---|---|---|---|---|---|---|---|
| Maximum | 103% | 41% | 40% | 19% | 19% | 16% | 8% | 15% |
| When | April-18 | March-13 | April-05 | March-05 | March-20 | March-05 | January-04 | March-05 |
| Proportion | 2% | 1% | 6% | 27% | 5% | 36% | 23% | 100% |
| Variable | <1 | 01–14 | 15–44 | 45–64 | 65–74 | 75–84 | >85 |
|---|---|---|---|---|---|---|---|
| Maximum (M + F) | 11.3% | 24.4% | 10.9% | 15.5% | 18.7% | 26.7% | 42.8% |
| Standard Deviation | 5.5% | 9.8% | 4.2% | 6.5% | 8.0% | 11.6% | 16.8% |
| Male (maximum) | 15.7% | 25.6% | 10.9% | 14.0% | 18.0% | 24.5% | 38.3% |
| Female (Maximum) | 20.7% | 42.5% | 15.0% | 17.7% | 21.8% | 30.0% | 45.5% |
| Variable | North West | South East | Yorkshire & Humber | London | Wales | West Midlands | East | North East | East Midlands | South West |
|---|---|---|---|---|---|---|---|---|---|---|
| Annual deaths | 69,548 | 78,470 | 50,580 | 48,387 | 32,249 | 52,659 | 54,535 | 27,032 | 43,140 | 54,681 |
| Maximum EWM | 27.6% | 27.9% | 28.2% | 28.4% | 28.8% | 29.1% | 30.1% | 30.3% | 30.4% | 30.8% |
| STDEV | 11.8% | 12.3% | 12.2% | 11.5% | 12.2% | 12.2% | 12.2% | 11.8% | 12.4% | 11.6% |
| When | 6 April 18 | 13 March 15 | 20 March 15 | 27 March 15 | 6 April 18 | 17 April 15 | 27 March 15 | 23 March 18 | 24 April 15 | 27 March 15 |
| Deprivation Decile | England | Wales | ||
|---|---|---|---|---|
| Maximum | When | Maximum | When | |
| 1 (most deprived) | 26% | 28-March-15 | 35% | 28-April-18 |
| 2 | 28% | 25-April-15 | 32% | 04-April-15 |
| 3 | 29% | 25-April-16 | 39% | 07-April-18 |
| 4 | 29% | 24-March-18 | 31% | 14-April-18 |
| 5 | 31% | 28-March-15 | 34% | 28-April-18 |
| 6 | 30% | 14-March-15 | 30% | 24-March-18 |
| 7 | 29% | 21-March-15 | 31% | 02-May-15 |
| 8 | 29% | 24-March-18 | 37% | 25-April-15 |
| 9 | 30% | 28-March-15 | 32% | 07-April-18 |
| 10 (least deprived) | 29% | 24-March-18 | 28% | 27-April-13 |
| Total | 29% | 28-March-15 | 29% | 28-April-18 |
| Country | Standard Deviation of Rolling EWM |
|---|---|
| Finland, Norway, Iceland, Denmark, Sweden. | 6.6% to 7.6% |
| Netherlands, Germany, Luxembourg, Switzerland, Austria, France, Belgium. | 8.2% to 10.0% |
| Bulgaria, Italy, Greece. | 12.1% to 13.4% |
| UK, Ireland. | 13.9% |
| Spain. | 14.5% |
| Portugal. | 17.5% |
| Parameter | Care Home | Communal Establishment | Hospital | Elsewhere | Home | Hospice |
|---|---|---|---|---|---|---|
| EWM | 40.2% | 31.2% | 30.0% | 20.5% | 18.7% | 7.8% |
| When | 23 March 2018 | 13 April 2018 | 23 March 2018 | 4 May 2018 | 23 March 2018 | 9 February 2018 |
| Proportion | 22% | 0.4% | 47% | 2% | 24% | 6% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jones, R.P. Excess Winter Mortality (EWM) as a Dynamic Forensic Tool: Where, When, Which Conditions, Gender, Ethnicity and Age. Int. J. Environ. Res. Public Health 2021, 18, 2161. https://doi.org/10.3390/ijerph18042161
Jones RP. Excess Winter Mortality (EWM) as a Dynamic Forensic Tool: Where, When, Which Conditions, Gender, Ethnicity and Age. International Journal of Environmental Research and Public Health. 2021; 18(4):2161. https://doi.org/10.3390/ijerph18042161
Chicago/Turabian StyleJones, Rodney P. 2021. "Excess Winter Mortality (EWM) as a Dynamic Forensic Tool: Where, When, Which Conditions, Gender, Ethnicity and Age" International Journal of Environmental Research and Public Health 18, no. 4: 2161. https://doi.org/10.3390/ijerph18042161
APA StyleJones, R. P. (2021). Excess Winter Mortality (EWM) as a Dynamic Forensic Tool: Where, When, Which Conditions, Gender, Ethnicity and Age. International Journal of Environmental Research and Public Health, 18(4), 2161. https://doi.org/10.3390/ijerph18042161






