On the Transmission Dynamics of SARS-CoV-2 in a Temperate Climate
Abstract
:1. Introduction
2. Materials and Methods
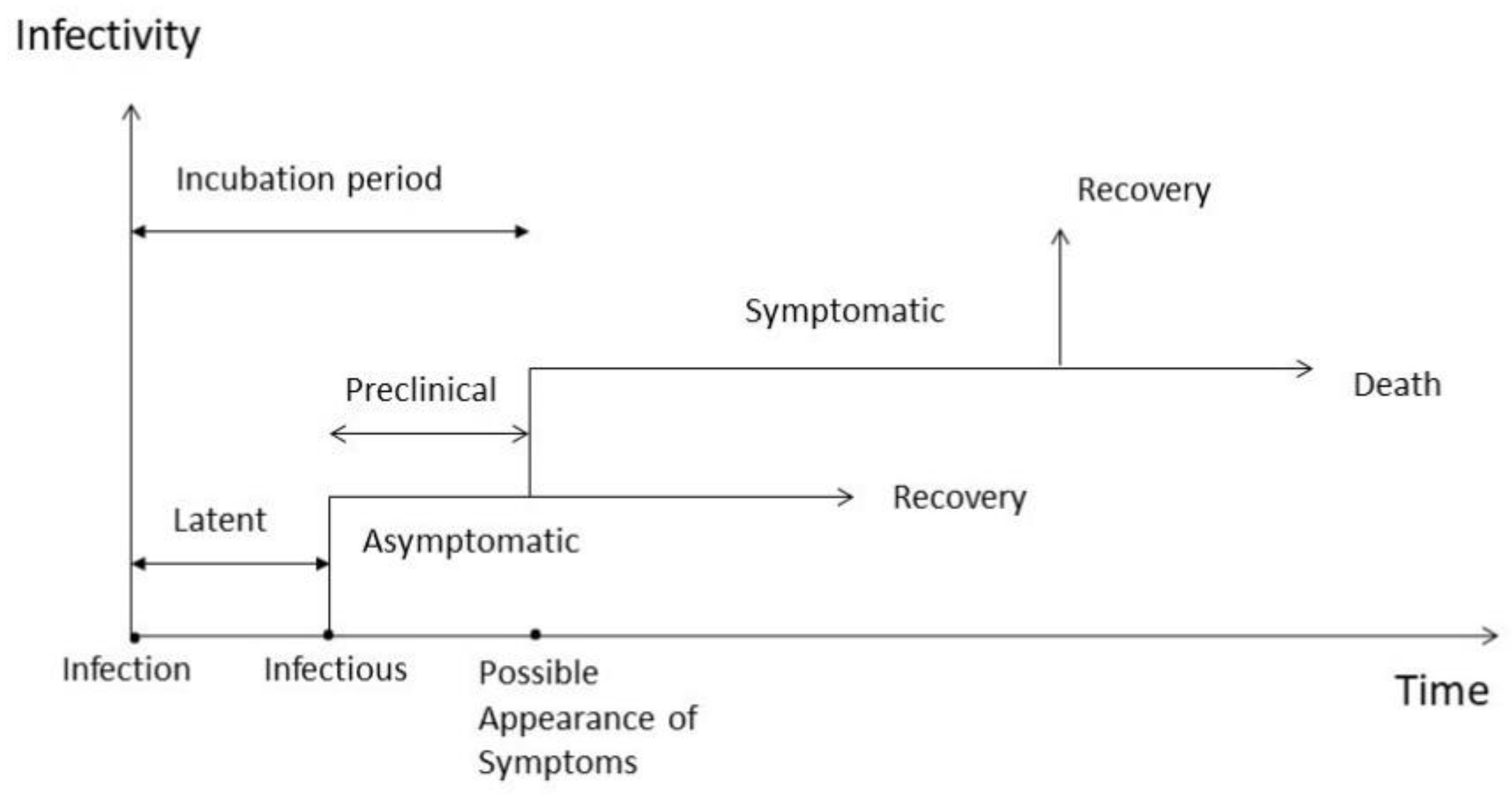
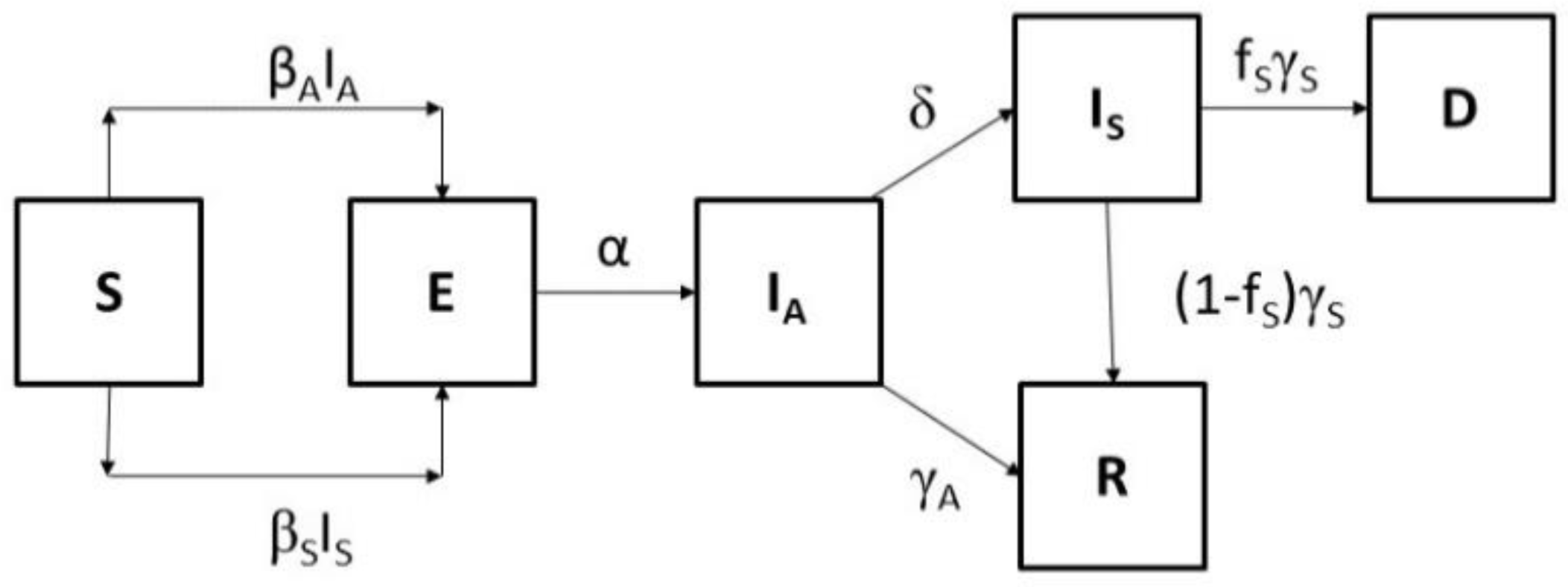
2.1. The Model
2.2. The Basic Reproduction Number
2.3. The Monte Carlo Uncertainty Analysis and the Error Optimization
2.4. The Forecast Horizon
2.5. Clustering of COVID-19 Data
3. Results
3.1. Environmental Clustering of COVID-19 Data
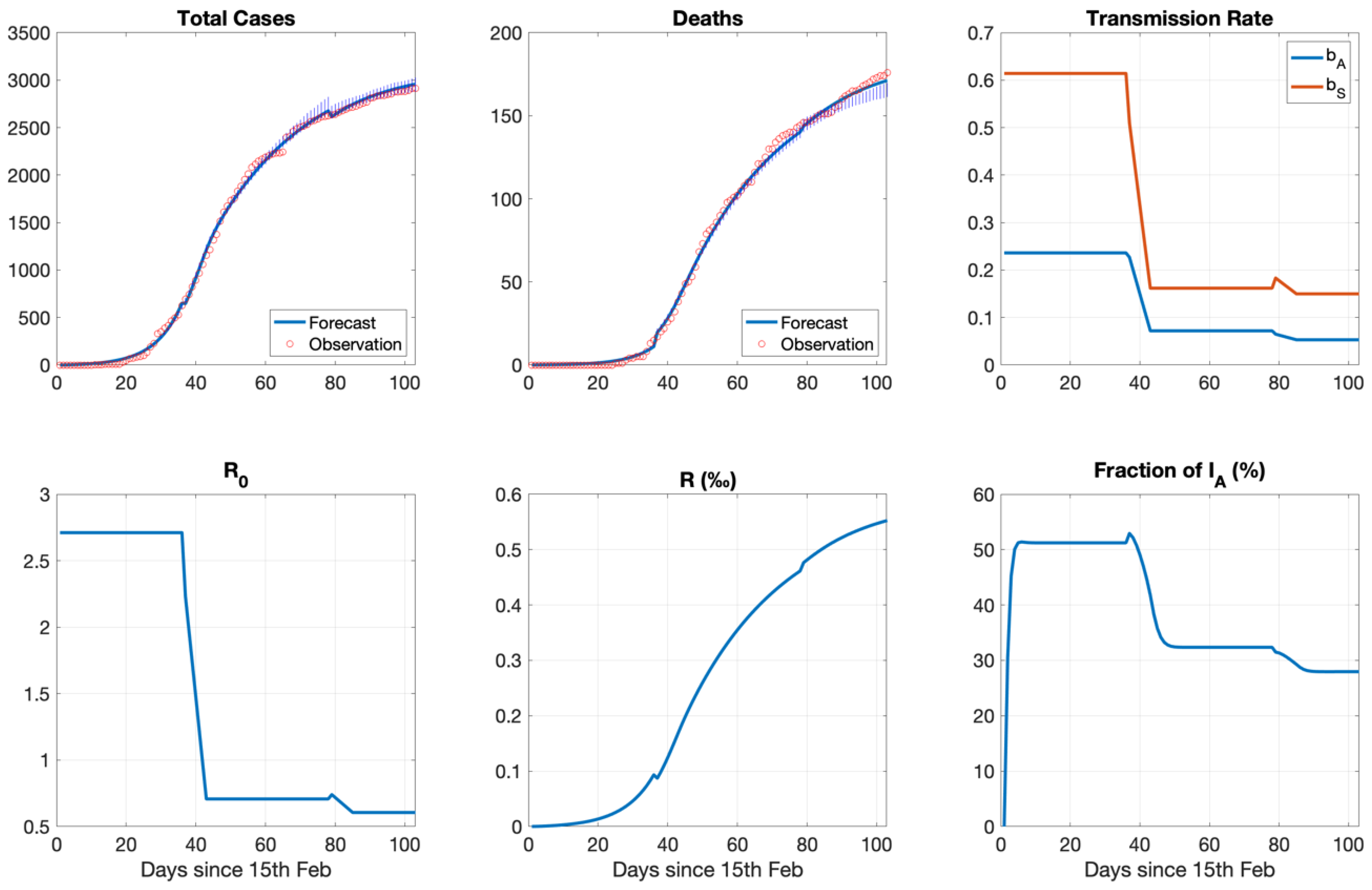
3.2. Model Calibration for Greece: March-April-May 2020
3.3. The Variation of Transmissibility: From March to December 2020
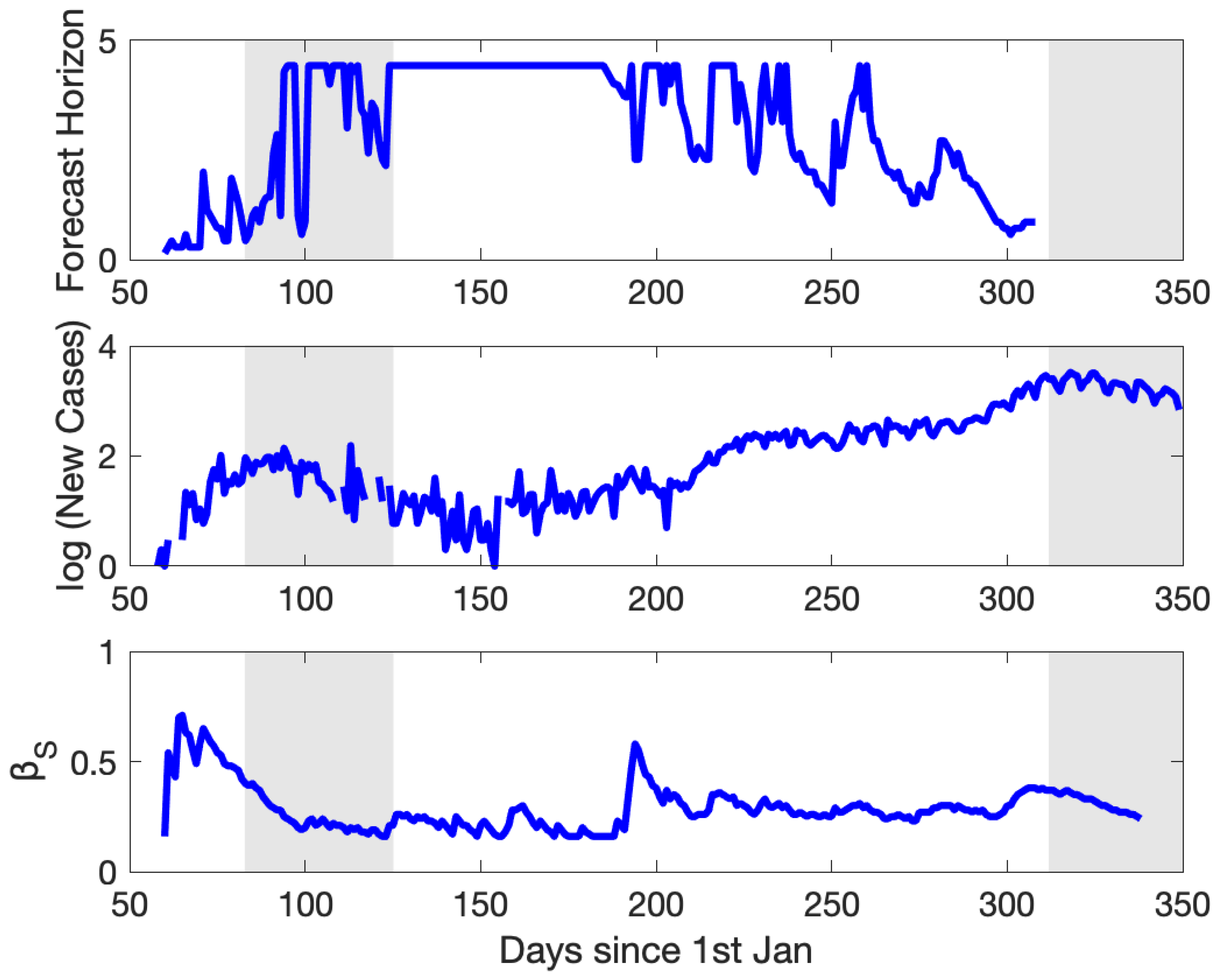
3.4. The Variation of Predictability: From March to December 2020
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Ethics Committee Approval
References
- Furukawa, N.W.; Brooks, J.T.; Sobel, J. Evidence supporting transmission of severe acute respiratory syndrome coronavirus 2 while presymptomatic or asymptomatic. Emerg. Infect. Dis. 2020, 26. [Google Scholar] [CrossRef] [PubMed]
- Bai, Y.; Yao, L.; Wei, T.; Tian, F.; Jin, D.Y.; Chen, L.; Wang, M. Presumed asymptomatic carrier transmission of COVID-19. JAMA 2020, 323, 1406–1407. [Google Scholar] [CrossRef] [Green Version]
- Pan, X.; Chen, D.; Xia, Y.; Wu, X.; Li, T.; Ou, X.; Zhou, L.; Liu, J. Asymptomatic cases in a family cluster with SARS-CoV-2 infection. Lancet Infect. Dis. 2020, 20, 410–411. [Google Scholar] [CrossRef]
- Lytras, T.; Dellis, G.; Flountzi, A.; Hatzianastasiou, S.; Nikolopoulou, G.; Tsekou, K.; Diamantis, Z.; Stathopoulou, G.; Togka, M.; Gerolymatos, G.; et al. High prevalence of SARS-CoV-2 infection in repatriation flights to Greece from three European countries. J. Travel Med. 2020, 27, taaa054. [Google Scholar] [CrossRef] [Green Version]
- Wei, W.E.; Li, Z.; Chiew, C.J.; Yong, S.E.; Toh, M.P.; Lee, V.J. Pre-symptomatic transmission of SARS-CoV-2-Singapore, January 23–March 16, 2020. Morb. Mortal. 2020, 69, 411–415. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hoehl, S.; Rabenau, H.; Berger, A.; Kortenbusch, M.; Cinatl, J.; Bojkova, D.; Behrens, P.; Böddinghaus, B.; Götsch, U.; Naujoks, F.; et al. Evidence of SARS-CoV-2 infection in returning travelers from Wuhan, China. N. Engl. J. Med. 2020, 382, 1278–1280. [Google Scholar] [CrossRef]
- Arons, M.M.; Hatfield, K.M.; Reddy, S.C.; Kimball, A.; James, A.; Jacobs, J.R.; Taylor, J.; Spicer, K.; Bardossy, A.C.; Oakley, L.P.; et al. Presymptomatic SARS-CoV-2 infections and transmission in a skilled nursing facility. N. Engl. J. Med. 2020, 382, 2081–2090. [Google Scholar] [CrossRef] [PubMed]
- Zou, L.; Ruan, F.; Huang, M.; Liang, L.; Huang, H.; Hong, Z.; Yu, J.; Kang, M.; Song, Y.; Xia, J.; et al. SARS-CoV-2 viral load in upper respiratory specimens of infected patients. N. Engl. J. Med. 2020, 382, 1177–1179. [Google Scholar] [CrossRef]
- Du, Z.; Xu, X.; Wu, Y.; Wang, L.; Cowling, B.J.; Meyers, L.A. Serial interval of COVID-19 among publicly reported confirmed cases. Emerg. Infect. Dis. 2020, 26, 1341–1343. [Google Scholar] [CrossRef] [PubMed]
- Li, R.; Pei, S.; Chen, B.; Song, Y.; Zhang, T.; Yang, W.; Shaman, J. Substantial undocumented infection facilitates the rapid dissemination of novel coronavirus (SARS-CoV-2). Science 2020, 368, 489–493. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- He, X.; Lau, E.H.Y.; Wu, P.; Deng, X.; Wang, J.; Hao, X.; Lau, Y.C.; Wong, J.Y.; Guan, Y.; Tan, X.; et al. Temporal dynamics in viral shedding and transmissibility of COVID-19. Nat. Med. 2020, 26, 672–675. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nishiura, H.; Kobayashi, T.; Miyama, T.; Suzuki, A.; Jung, S.-M.; Hayashi, K.; Kinoshita, R.; Yang, Y.; Yuan, B.; Akhmetzhanov, A.R.; et al. Estimation of the asymptomatic ratio of novel coronavirus infections (COVID-19). Int. J. Infect. Dis. 2020, 94, 154–155. [Google Scholar] [CrossRef]
- Mizumoto, K.; Kagaya, K.; Zarebski, A.; Chowell, G. Estimating the asymptomatic proportion of coronavirus disease 2019 (COVID-19) cases on board the Diamond Princess cruise ship, Yokohama, Japan. Eurosurveillance 2020, 25, 2000180. [Google Scholar] [CrossRef] [Green Version]
- Pan, A.; Liu, L.; Wang, C.; Guo, H.; Hao, X.; Wang, Q.; Huang, J.; He, N.; Yu, H.; Lin, X.; et al. Association of public health interventions with the epidemiology of the COVID-19 outbreak in Wuhan, China. JAMA 2020, 323, 1915. [Google Scholar] [CrossRef] [Green Version]
- Wu, J.T.; Leung, K.; Bushman, M.; Kishore, N.; Niehus, R.; De Salazar, P.M.; Cowling, B.J.; Lipsitch, M.; Leung, G.M. Estimating clinical severity of COVID-19 from the transmission dynamics in Wuhan, China. Nat. Med. 2020, 26, 506–510. [Google Scholar] [CrossRef] [Green Version]
- Fraser, C.; Riley, S.; Anderson, R.M.; Ferguson, N.M. Factors that make an infectious disease outbreak controllable. Proc. Natl. Acad. Sci. USA 2004, 101, 6146–6151. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lipsitch, M.; Donnelly, C.A.; Fraser, C.; Blake, I.M.; Cori, A.; Dorigatti, I.; Ferguson, N.M.; Garske, T.; Mills, H.L.; Riley, S.; et al. Potential biases in estimating absolute and relative case-fatality risks during outbreaks. PLoS Negl. Trop. Dis. 2015, 9, e0003846. [Google Scholar] [CrossRef] [Green Version]
- Delamater, P.L.; Street, E.J.; Leslie, T.F.; Yang, Y.T.; Jacobsen, K.H. Complexity of the basic reproduction number (R0). Emerg. Infect. Dis. 2019, 25, 1–4. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Heesterbeek, J.A.P.; Dietz, K. The concept of Roin epidemic theory. Stat. Neerl. 1996, 50, 89–110. [Google Scholar] [CrossRef]
- Koo, J.R.; Cook, A.R.; Park, M.; Sun, Y.; Sun, H.; Lim, J.T.; Tam, C.; Dickens, B.L. Interventions to mitigate early spread of SARS-CoV-2 in Singapore: A modelling study. Lancet Infect. Dis. 2020, 20, 678–688. [Google Scholar] [CrossRef] [Green Version]
- Longini, I.M.; Halloran, M.E.; Nizam, A.; Yang, Y. Containing pandemic influenza with antiviral agents. Am. J. Epidemiol. 2004, 159, 623–633. [Google Scholar] [CrossRef] [Green Version]
- Arino, J.; Brauer, F.; Driessche, P.V.D.; Watmough, J.; Wu, J. A model for influenza with vaccination and antiviral treatment. J. Biol. 2008, 253, 118–130. [Google Scholar] [CrossRef] [PubMed]
- McCaw, J.M.; Wood, J.G.; McCaw, C.T.; McVernon, J. Impact of emerging antiviral drug resistance on influenza containment and spread: Influence of subclinical infection and strategic use of a stockpile containing one or two drugs. PLoS ONE 2008, 3, e2362. [Google Scholar] [CrossRef] [PubMed]
- Stilianakis, N.I.; Perelson, A.S.; Hayden, F.G. Emergence of drug resistance during an influenza epidemic: Insights from a mathematical model. J. Infect. Dis. 1998, 177, 863–873. [Google Scholar] [CrossRef] [PubMed]
- Regoes, R.R.; Bonhoeffer, S. Emergence of Drug-Resistant Influenza Virus: Population Dynamical Considerations. Science 2006, 312, 389–391. [Google Scholar] [CrossRef] [Green Version]
- Débarre, F.; Bonhoeffer, S.; Regoes, R.R. The effect of population structure on the emergence of drug resistance during influenza pandemics. J. R. Soc. Interface 2007, 4, 893–906. [Google Scholar] [CrossRef] [Green Version]
- Alexander, M.E.; Bowman, C.S.; Feng, Z.; Gardam, M.; Moghadas, S.M.; Röst, G.; Wu, J.; Yan, P. Emergence of drug resistance: Implications for antiviral control of pandemic influenza. Proc. R. Soc. B Boil. Sci. 2007, 274, 1675–1684. [Google Scholar] [CrossRef] [Green Version]
- Robinson, M.; Stilianakis, N.I. A model for the emergence of drug resistance in the presence of asymptomatic infections. Math. Biosci. 2013, 243, 163–177. [Google Scholar] [CrossRef]
- Weber, T.P.; Stilianakis, N.I. Inactivation of influenza a viruses in the environment and modes of transmission: A critical review. J. Infect. 2008, 57, 361–373. [Google Scholar] [CrossRef]
- Biryukov, J.; Boydston, J.A.; Dunning, R.A.; Yeager, J.J.; Wood, S.; Reese, A.L.; Ferris, A.; Miller, D.; Weaver, W.; Zeitouni, N.E.; et al. Increasing temperature and relative humidity accelerates inactivation of SARS-CoV-2 on surfaces. MSphere 2020, 5. [Google Scholar] [CrossRef]
- Schuit, M.; Ratnesar-Shumate, S.; Yolitz, J.; Williams, G.; Weaver, W.; Green, B.; Miller, D.; Krause, M.; Beck, K.; Wood, S.; et al. Airborne SARS-CoV-2 is rapidly inactivated by simulated sunlight. J. Infect. Dis. 2020, 222, 564–571. [Google Scholar] [CrossRef]
- Fisman, D. Seasonality of viral infections: Mechanisms and unknowns. Clin. Microbiol. Infect. 2012, 18, 946–954. [Google Scholar] [CrossRef] [Green Version]
- Moriyama, M.; Hugentobler, W.J.; Iwasaki, A. Seasonality of respiratory viral infections. Annu. Rev. Virol. 2020, 7, 83–101. [Google Scholar] [CrossRef]
- Dowell, S.F. Seasonal variation in host susceptibility and cycles of certain infectious diseases. Emerg. Infect. Dis. 2001, 7, 369–374. [Google Scholar] [CrossRef] [PubMed]
- Shaman, J.; Kohn, M. Absolute humidity modulates influenza survival, transmission, and seasonality. Proc. Natl. Acad. Sci. USA 2009, 106, 3243–3248. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cannell, J.J.; Vieth, R.; Umhau, J.C.; Holick, M.F.; Grant, W.B.; Madronich, S.; Garland, C.F.; Giovannucci, E. Epidemic influenza and vitamin D. Epidemiol. Infect. 2006, 134, 1129–1140. [Google Scholar] [CrossRef] [PubMed]
- Azziz-Baumgartner, E.; Dao, C.N.; Nasreen, S.; Bhuiyan, M.U.; Mah-E-Muneer, S.; Al Mamun, A.; Sharker, M.A.Y.; Zaman, R.U.; Cheng, P.; Klimov, A.I.; et al. Seasonality, timing, and climate drivers of influenza activity worldwide. J. Infect. Dis. 2012, 206, 838–846. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shaman, J.; Pitzer, V.E.; Viboud, C.; Grenfell, B.T.; Lipsitch, M. Absolute humidity and the seasonal onset of influenza in the continental United States. PLoS Biol. 2010, 8, e1000316. [Google Scholar] [CrossRef]
- Peci, A.; Winter, A.-L.; Li, L.; Gnaneshan, S.; Liu, J.; Mubareka, S.; Gubbay, J.B. Effects of absolute humidity, relative humidity, temperature, and wind speed on influenza activity in Toronto, Ontario, Canada. Appl. Environ. Microbiol. 2019, 85. [Google Scholar] [CrossRef] [Green Version]
- Tamerius, J.; Nelson, M.I.; Zhou, S.Z.; Viboud, C.; Miller, M.A.; Alonso, W.J. Global influenza seasonality: Reconciling patterns across temperate and tropical regions. Environ. Health Perspect. 2011, 119, 439–445. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bukhari, Q.; Jameel, Y. Will coronavirus pandemic diminish by summer? Electron. J. 2020. [Google Scholar] [CrossRef]
- Neher, R.A.; Dyrdak, R.; Druelle, V.; Hodcroft, E.B.; Albert, J. Potential impact of seasonal forcing on a SARS-CoV-2 pandemic. Swiss Med. Wkly. 2020, 150, w20224. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kissler, S.M.; Tedijanto, C.; Goldstein, E.; Grad, Y.H.; Lipsitch, M. Projecting the transmission dynamics of SARS-CoV-2 through the postpandemic period. Science 2020, 368, 860–868. [Google Scholar] [CrossRef]
- Sajadi, M.M.; Habibzadeh, P.; Vintzileos, A.; Shokouhi, S.; Miralles-Wilhelm, F.; Amoroso, A. Temperature, humidity, and latitude analysis to estimate potential spread and seasonality of coronavirus disease 2019 (COVID-19). JAMA Netw. Open 2020, 3, e2011834. [Google Scholar] [CrossRef]
- Araujo, M.B.; Naimi, B. Spread of SARS-CoV-2 coronavirus likely to be constrained by climate. MedRxiv 2020. [Google Scholar] [CrossRef] [Green Version]
- Wu, J.T.; Leung, K.; Leung, G.M. Nowcasting and forecasting the potential domestic and international spread of the 2019-nCoV outbreak originating in Wuhan, China: A modelling study. Lancet 2020, 395, 689–697. [Google Scholar] [CrossRef] [Green Version]
- Kucharski, A.J.; Russell, T.W.; Diamond, C.; Liu, Y.; Edmunds, J.; Funk, S.; Eggo, R.M.; Sun, F.; Jit, M.; Munday, J.D.; et al. Early dynamics of transmission and control of COVID-19: A mathematical modelling study. Lancet Infect. Dis. 2020, 20, 553–558. [Google Scholar] [CrossRef] [Green Version]
- Kissler, S.; Tedijanto, C.; Lipsitch, M.; Grad, Y. Social distancing strategies for curbing the COVID-19 pandemic. MedRxiv 2020. [Google Scholar] [CrossRef] [Green Version]
- Arino, J.; Portet, S. A simple model for COVID-19. Infect. Dis. Model. 2020, 5, 309–315. [Google Scholar] [CrossRef]
- Gatto, M.; Bertuzzo, E.; Mari, L.; Miccoli, S.; Carraro, L.; Casagrandi, R.; Rinaldo, A. Spread and dynamics of the COVID-19 epidemic in Italy: Effects of emergency containment measures. Proc. Natl. Acad. Sci. USA 2020, 117, 10484–10491. [Google Scholar] [CrossRef] [Green Version]
- Liu, Z.; Magal, P.; Seydi, O.; Webb, G. A COVID-19 epidemic model with latency period. Infect. Dis. Model. 2020, 5, 323–337. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Yan, L.-M.; Wan, L.; Xiang, T.-X.; Le, A.; Liu, J.-M.; Peiris, M.; Poon, L.L.M.; Zhang, W. Viral dynamics in mild and severe cases of COVID-19. Lancet Infect. Dis. 2020, 20, 656–657. [Google Scholar] [CrossRef] [Green Version]
- Driessche, P.V.D.; Watmough, J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 2002, 180, 29–48. [Google Scholar] [CrossRef]
- Bar-On, Y.M.; Flamholz, A.; Phillips, R.; Milo, R. SARS-CoV-2 (COVID-19) by the numbers. eLife 2020, 9. [Google Scholar] [CrossRef] [PubMed]
- COVID19 Greek Government. Available online: https://covid19.gov.gr/covid19-live-analytics/ (accessed on 15 December 2020).
- Dbouk, T.; Drikakis, D. Weather impact on airborne coronavirus survival. Phys. Fluids 2020, 32, 093312. [Google Scholar] [CrossRef]
- University of Wisconsin. Available online: http://weather.uwyo.edu (accessed on 8 May 2020).
- Marr, L.C.; Tang, J.W.; Van Mullekom, J.; Lakdawala, S.S. Mechanistic insights into the effect of humidity on airborne influenza virus survival, transmission and incidence. J. R. Soc. Interface 2019, 16, 20180298. [Google Scholar] [CrossRef]
- Carlson, C.J.; Gomez, A.C.R.; Bansal, S.; Ryan, S.J. Misconceptions about weather and seasonality must not misguide COVID-19 response. Nat. Commun. 2020, 11, 1–4. [Google Scholar] [CrossRef]
- Greek Ministry of Health. Available online: https://www.moh.gov.gr/articles/ministry/grafeio-typoy/press-releases/ (accessed on 15 December 2020).
- McAloon, C.; Collins, A.; Hunt, K.; Barber, A.; Byrne, A.W.; Butler, F.; Casey, M.; Griffin, J.; Lane, E.; McEvoy, D.; et al. Incubation period of COVID-19: A rapid systematic review and meta-analysis of observa-tional research. BMJ Open 2020, 10, e039652. [Google Scholar] [CrossRef]
- Johansson, M.A.; Quandelacy, T.M.; Kada, S.; Prasad, P.V.; Steele, M.; Brooks, J.T.; Slayton, R.B.; Biggerstaff, M.; Butler, J.C. SARS-CoV-2 transmission from people without COVID-19 Symptoms. JAMA Netw. Open 2021, 4, e2035057. [Google Scholar] [CrossRef]
- Castro, M.; Ares, S.; Cuesta, J.A.; Manrubia, S. The turning point and end of an expanding epidemic cannot be precisely forecast. Proc. Natl. Acad. Sci. USA 2020, 117, 26190–26196. [Google Scholar] [CrossRef] [PubMed]
- Palmer, T.N.; Gelaro, R.; Barkmeijer, J.; Buizza, R. Singular vectors, metrics and adaptive observations. J. Atmos. Sci. 1998, 55, 633–653. [Google Scholar] [CrossRef]
- Kioutsioukis, I.; Galmarini, S. De praeceptis ferentis: Good practice in multi-model ensembles. Atmos. Chem. Phys. 2014, 14, 11791–11815. [Google Scholar] [CrossRef] [Green Version]



| Screening Phase | Implementation Phase | ||||
|---|---|---|---|---|---|
| Parameter | Description | Min | Max | μ | σ |
| α | Latency rate (day−1) | 0.3 | 5 | 0.5 | 0.03 |
| βS | Transmission rate between Is and S (day−1) | 0.3 | 1.5 | 0.6 | 0.03 |
| 0.2 | 0.03 | ||||
| 0.2 | 0.03 | ||||
| μ = βA/βS | Transmission rate ratio (day−1) | 0.2 | 1 | 0.35 | 0.037 |
| γA | Recovery rate from subclinical infection (day−1) | 0.07 | 0.5 | 0.25 | 0.03 |
| γS | Recovery rate from clinical symptoms (day−1) | 0.05 | 0.2 | 0.15 | 0.02 |
| δ | Transition rate at which IA becomes IS (day−1) | 0.07 | 0.5 | 0.25 | 0.05 |
| fS | Deaths (%) | 0.01 | 0.09 | 0.05 | 0.005 |
| Probability of Infection (%) | Cases per Million (Median) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| ρv\TAVG | −10–0 | 0–10 | 10–20 | 20–30 | 30–40 | −10–0 | 0–10 | 10–20 | 20–30 | 30–40 |
| 0–5 | 17 | 38 | 72 | 10 | 24 | 3.6 | 11.7 | 10.8 | 0.6 | 0.8 |
| 5–10 | 32 | 50 | 51 | 70 | 3.1 | 5.0 | 1.7 | 2.3 | ||
| 10–15 | 52 | 35 | 77 | 2.3 | 1.2 | 0.9 | ||||
| 15–20 | 29 | 25 | 58 | 1.4 | 0.6 | |||||
| 20–25 | 28 | 37 | 1.1 | 1.8 | ||||||
| Parameter | MC1 | MC2 | ||
|---|---|---|---|---|
| Before Intervention | During Intervention | After Intervention | ||
| α | 0.52 (0.48 0.52) | 0.50 (0.48 0.52) | 0.47 (0.47 0.50) | 0.52 |
| βS | 0.61 (0.59 0.62) | 0.16 (0.16 0.19) | 0.15 (0.14 0.20) | |
| βA | 0.24 (0.22 0.24) | 0.07 (0.07 0.08) | 0.05 (0.05 0.07) | βS/3 |
| γA | 0.23 (0.22 0.26) | 0.22 (0.22 0.26) | 0.26 (0.24 0.27) | 0.24 |
| γS | 0.15 (0.13 0.15) | 0.15 (0.14 0.16) | 0.15 (0.15 0.16) | 0.15 |
| δ | 0.28 (0.24 0.28) | 0.25 (0.23 0.27) | 0.27 (0.23 0.27) | 0.25 |
| fS (%) | 0.041 (0.041 0.046) | 0.057 (0.055 0.058) | 0.059 (0.056 0.060) | 0.03 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kioutsioukis, I.; Stilianakis, N.I. On the Transmission Dynamics of SARS-CoV-2 in a Temperate Climate. Int. J. Environ. Res. Public Health 2021, 18, 1660. https://doi.org/10.3390/ijerph18041660
Kioutsioukis I, Stilianakis NI. On the Transmission Dynamics of SARS-CoV-2 in a Temperate Climate. International Journal of Environmental Research and Public Health. 2021; 18(4):1660. https://doi.org/10.3390/ijerph18041660
Chicago/Turabian StyleKioutsioukis, Ioannis, and Nikolaos I. Stilianakis. 2021. "On the Transmission Dynamics of SARS-CoV-2 in a Temperate Climate" International Journal of Environmental Research and Public Health 18, no. 4: 1660. https://doi.org/10.3390/ijerph18041660
APA StyleKioutsioukis, I., & Stilianakis, N. I. (2021). On the Transmission Dynamics of SARS-CoV-2 in a Temperate Climate. International Journal of Environmental Research and Public Health, 18(4), 1660. https://doi.org/10.3390/ijerph18041660







