Insights into Factors Affecting Traffic Accident Severity of Novice and Experienced Drivers: A Machine Learning Approach
Abstract
1. Introduction
2. Literature Review
2.1. Novice and Experienced Driver in Traffic Accident Analysis
2.2. Traffic Accident Severity Modeling
3. Data Preparation
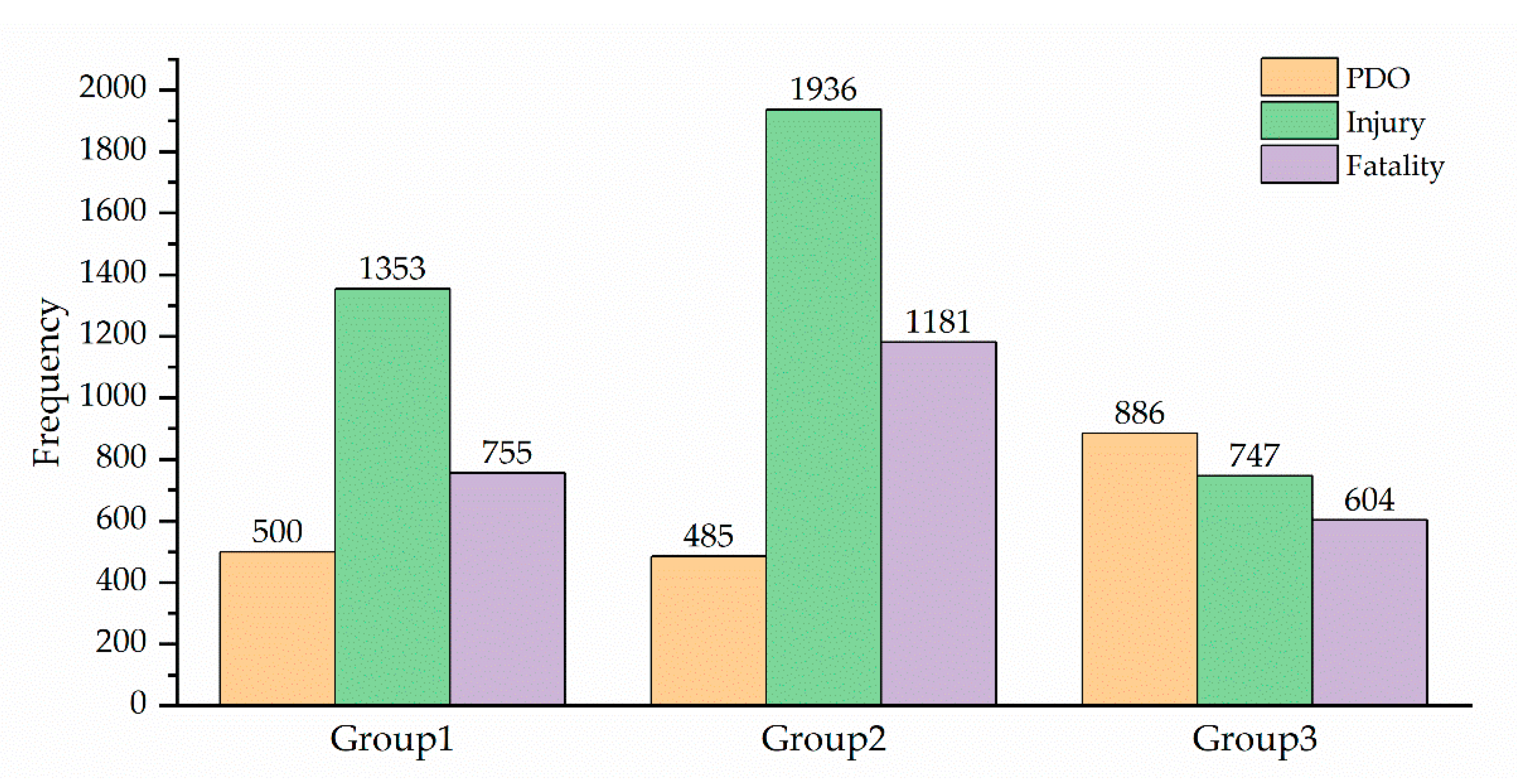
- Group 1: driving experience ≤ 3 years (i.e., novice driver).
- Group 2: 3 years < driving experience ≤ 10 years (i.e., experienced driver).
- Group 3: driving experience > 10 years (i.e., experienced driver).
4. Methodology
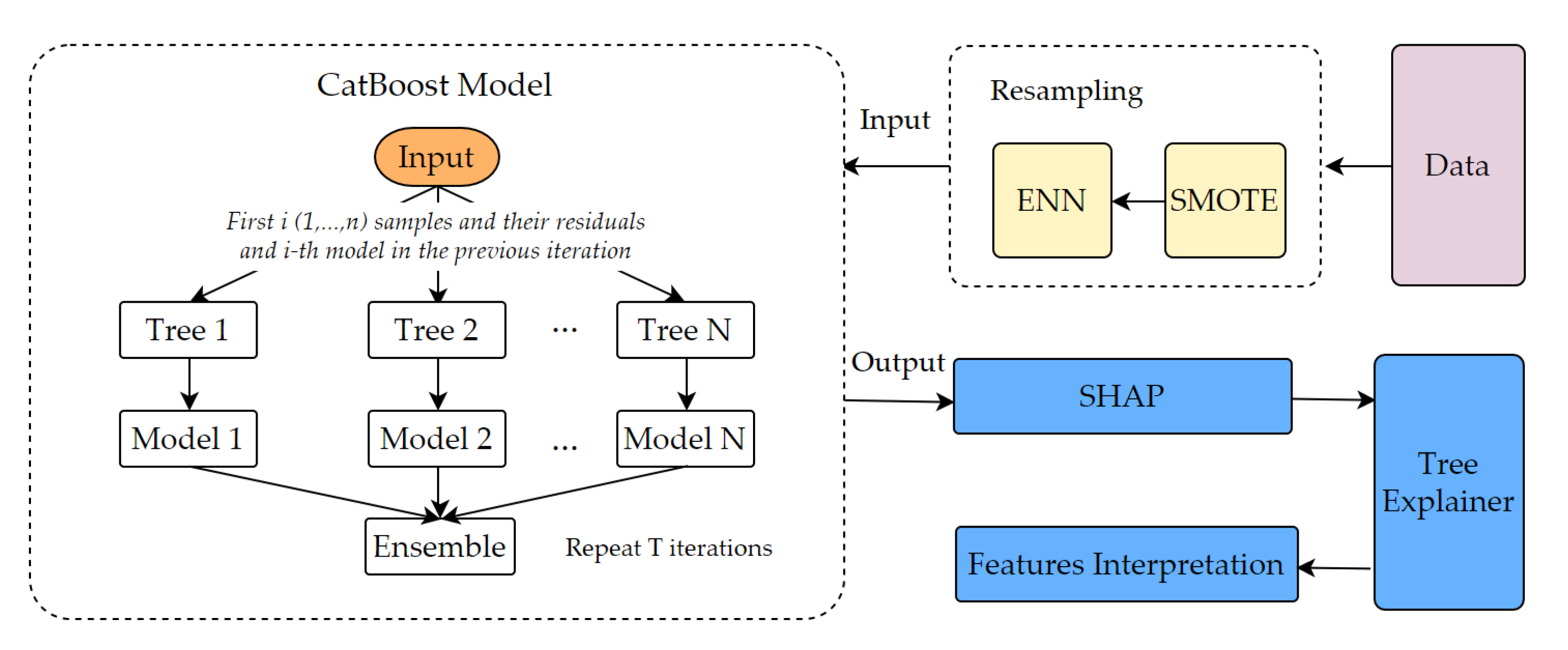
4.1. Data Resampling
4.2. Gradient Boosting
4.3. CatBoost
4.3.1. Ordered TS
4.3.2. Ordered Boosting
4.4. SHAP
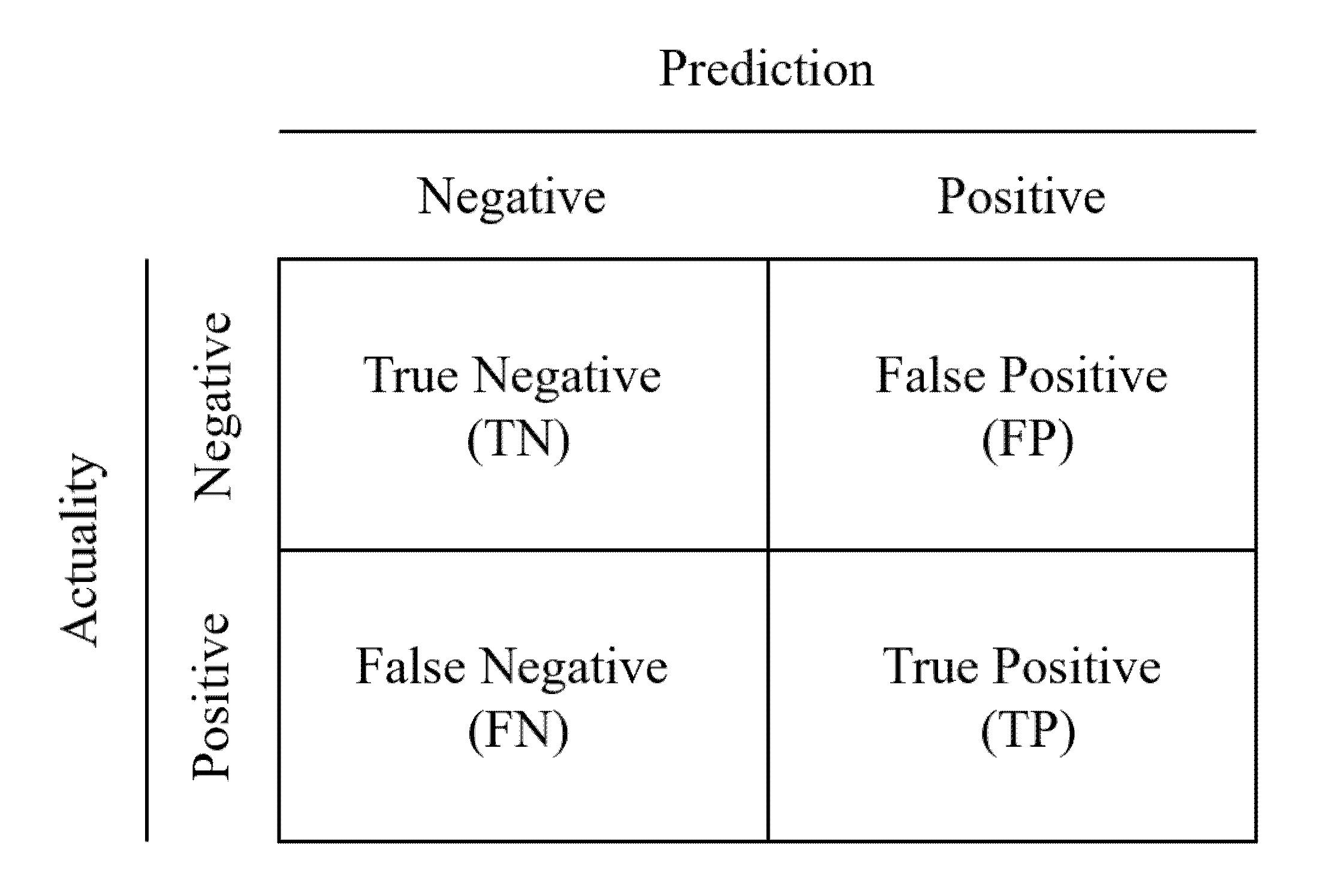
4.5. Performance Measures
5. Results and Discussions
5.1. Model Parameters
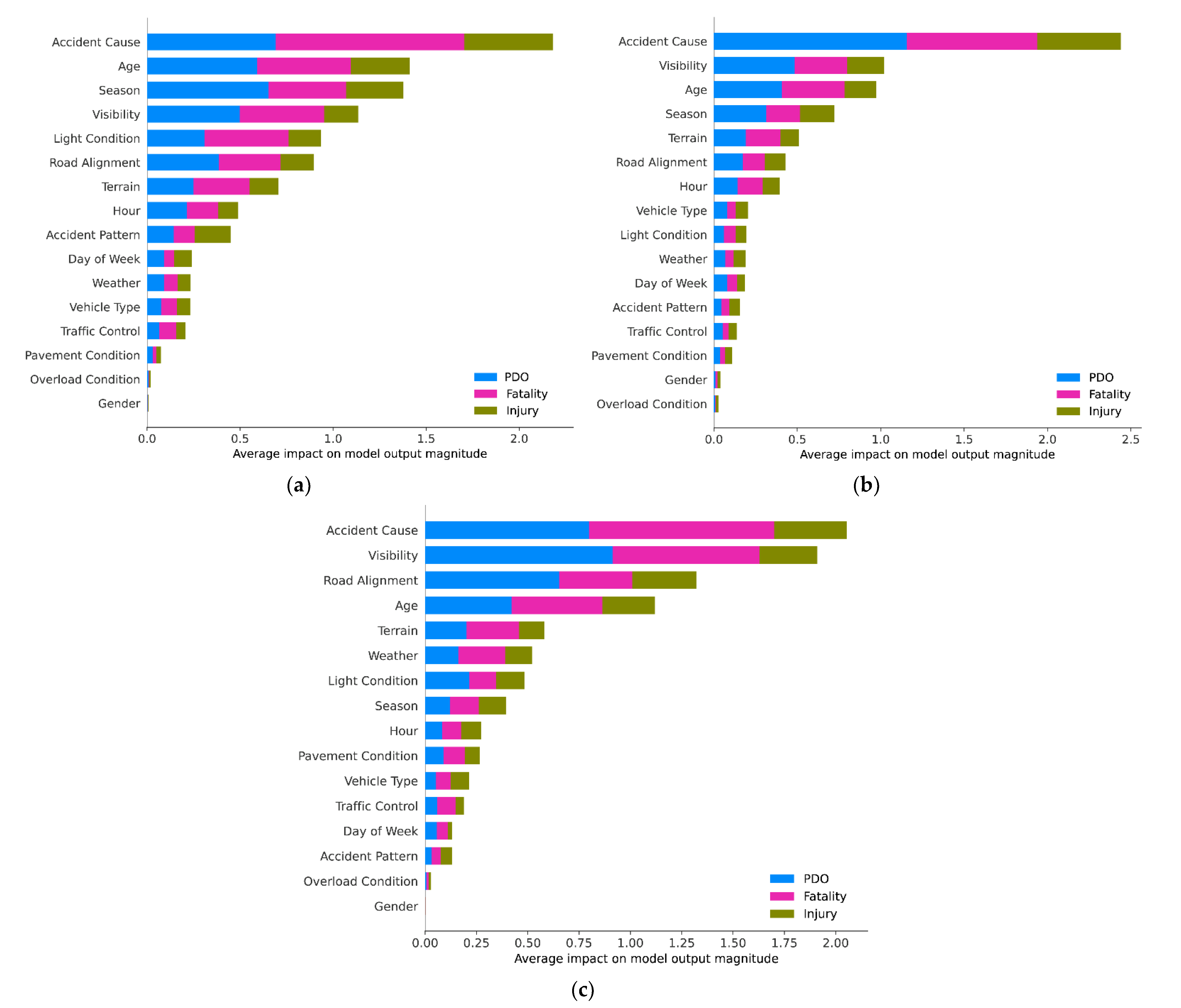
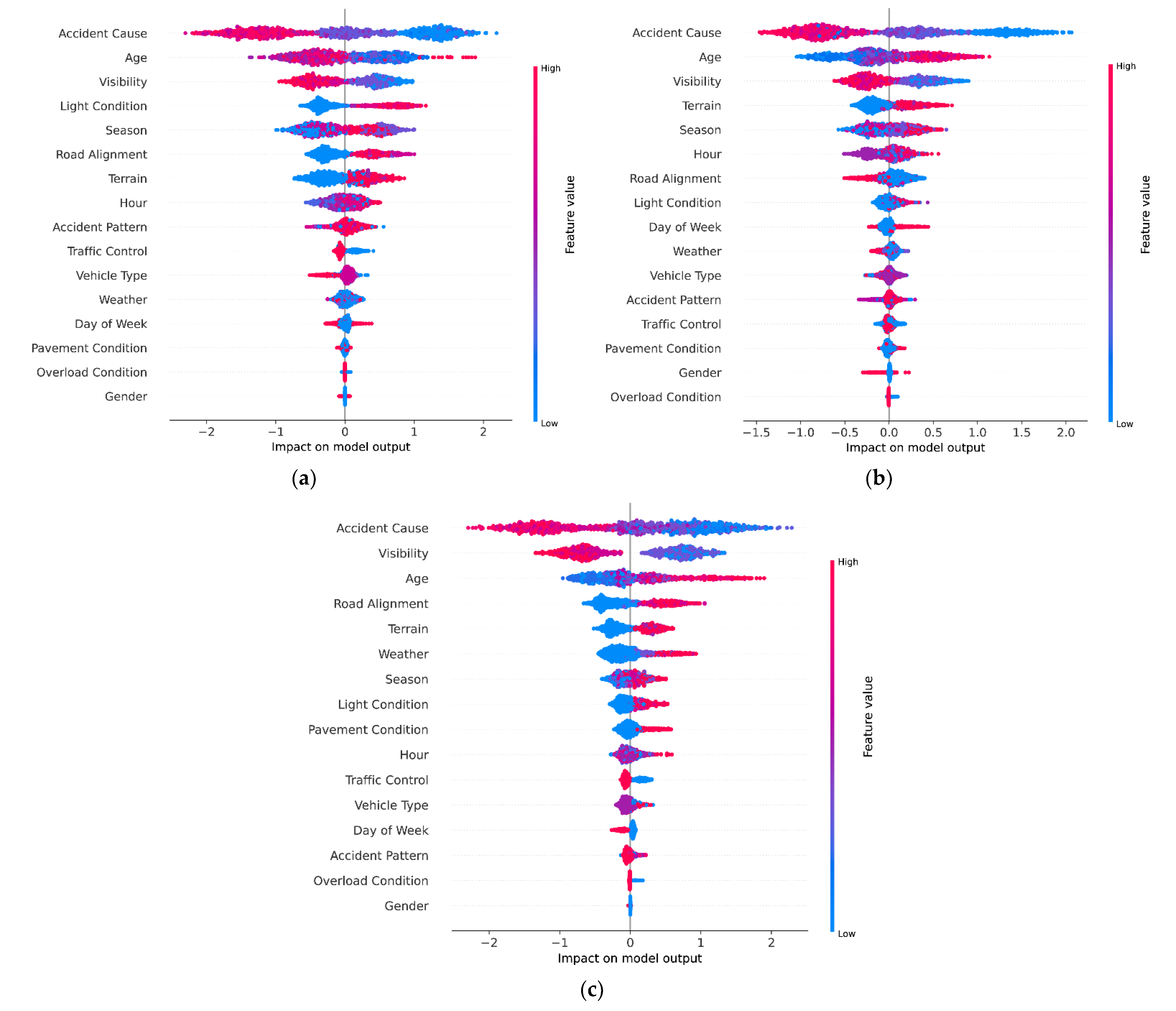
5.2. Feature Analysis
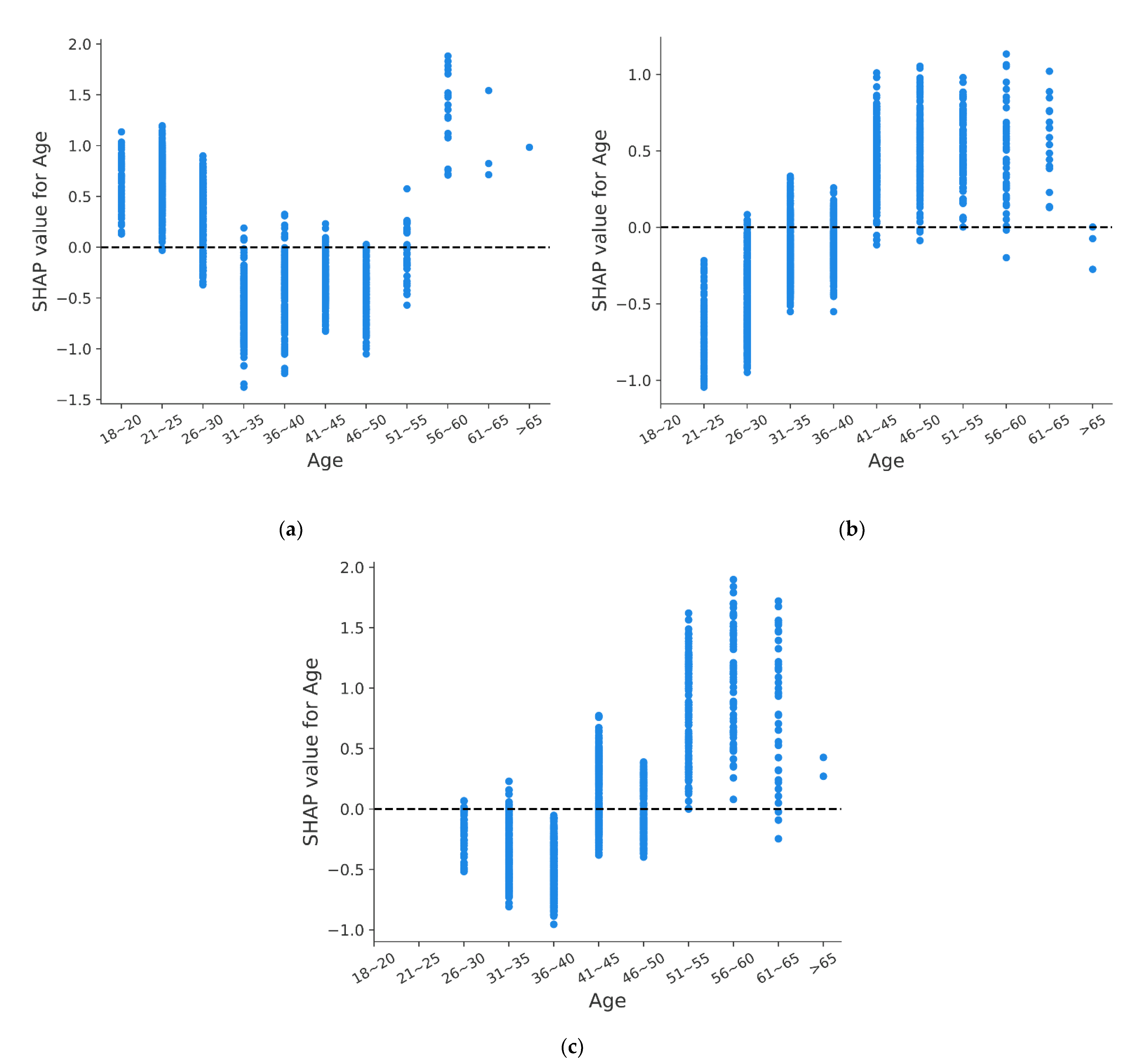
5.3. Feature Dependency Analysis
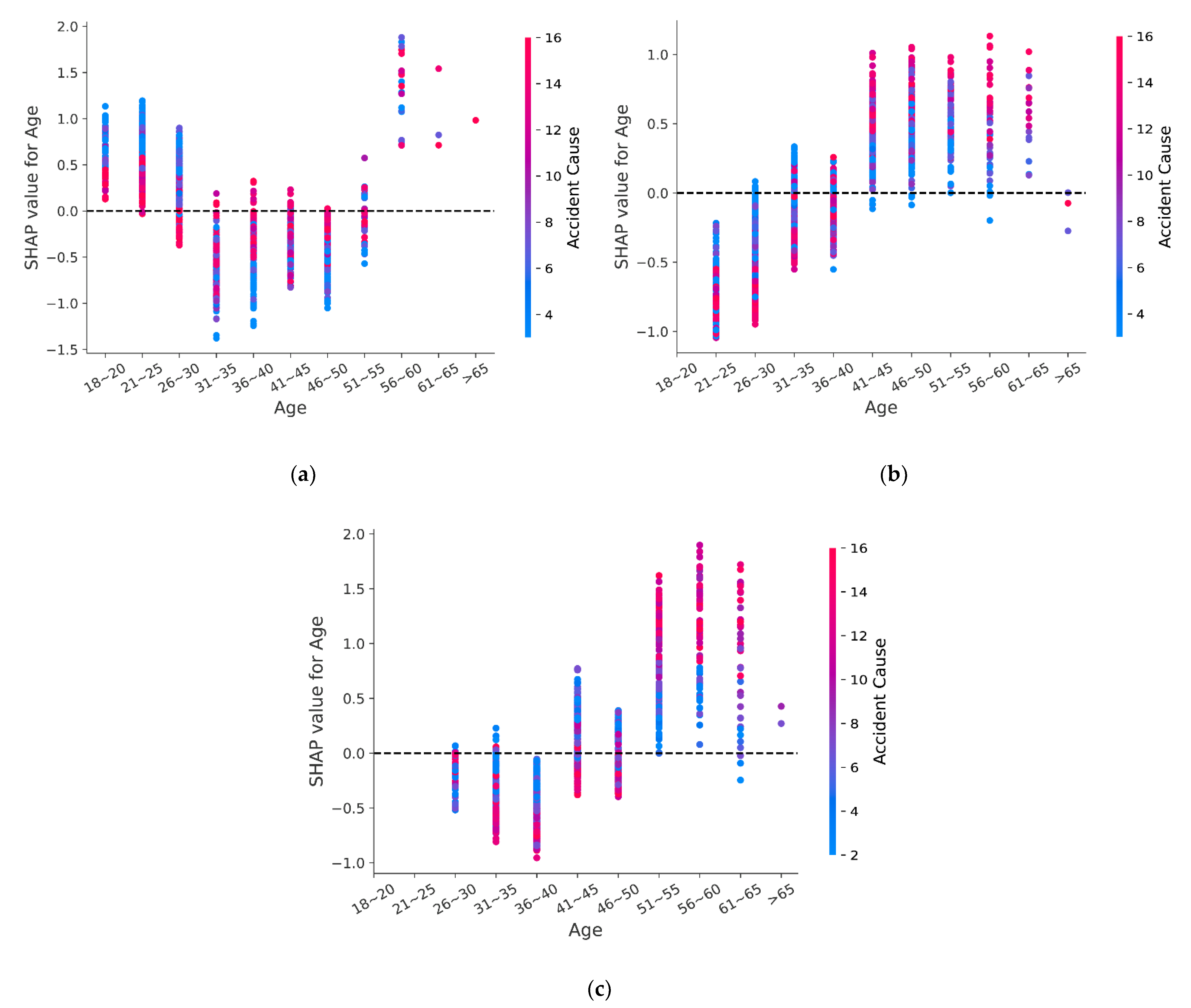
5.4. Feature Interaction Analysis
6. Conclusions
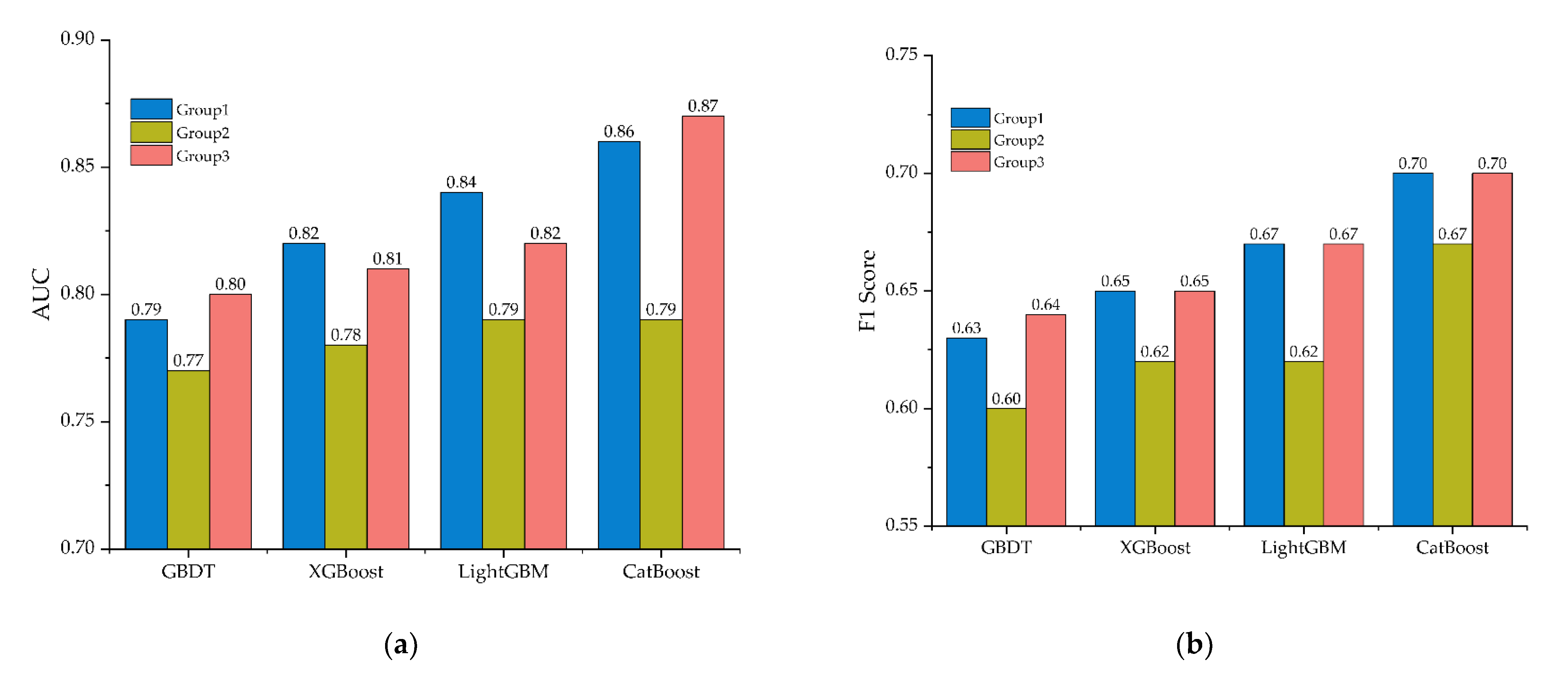
- In the analysis of influencing factors of accident severity, CatBoost generates the best result (AUC: 0.86, 0.79, and 0.87; F1 score: 0.70, 0.67, and 0.70), indicating the application potential of the model in traffic safety.
- Accident cause, age, visibility, light condition, season, road alignment, and terrain are the key factors affecting the severity of traffic accident. Pavement surface condition, overload condition, accident pattern, and gender have the least impact on accident severity. The importance of these features varies for drivers with different driving experience in terms of accident severity.
- The impact of age on fatal accidents is different for drivers with different driving experience. Novice drivers younger than 30 or older than 55 are prone to suffer fatal accidents, but for experienced drivers, the risk of fatal accident decreases when they are young and increases when they are old.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Variable | Description | Group1 | Group2 | Group3 | |||
|---|---|---|---|---|---|---|---|
| N | % | N | % | N | % | ||
| Day of Week | Weekday = 1 | 1928 | 73.93% | 2626 | 72.90% | 1627 | 72.73% |
| Weekend = 2 | 680 | 26.07% | 976 | 27.10% | 610 | 27.27% | |
| Season | Spring: Match to May = 1 | 680 | 26.07% | 922 | 25.60% | 578 | 25.84% |
| Summer: June to August = 2 | 659 | 25.27% | 904 | 25.10% | 553 | 24.72% | |
| Autumn: September to November = 3 | 649 | 24.88% | 867 | 24.07% | 526 | 23.51% | |
| Winter: December to February = 4 | 620 | 23.77% | 909 | 25.24% | 580 | 25.93% | |
| Hour | 0:00~06:59 = 1 | 216 | 8.28% | 314 | 8.72% | 199 | 8.90% |
| 07:00~09:59 = 2 | 414 | 15.87% | 550 | 15.27% | 368 | 16.45% | |
| 10:00~15:59 = 3 | 923 | 35.39% | 1280 | 35.54% | 774 | 34.60% | |
| 16:00~19:59 = 4 | 738 | 28.30% | 982 | 27.26% | 589 | 26.33% | |
| 20:00~23:59 = 5 | 317 | 12.15% | 476 | 13.21% | 307 | 13.72% | |
| Accident Cause | Overloaded or oversized = 1 | 54 | 2.07% | 63 | 1.75% | 57 | 2.55% |
| Driving a vehicle that does not satisfy normal driving requirements = 2 | 70 | 2.68% | 68 | 1.89% | 84 | 3.76% | |
| Speeding = 3 | 620 | 23.77% | 791 | 21.96% | 368 | 16.45% | |
| Drowsy driving = 4 | 30 | 1.15% | 33 | 0.92% | 77 | 3.44% | |
| Traffic signal violation = 5 | 31 | 1.19% | 51 | 1.42% | 59 | 2.64% | |
| Driving without license = 6 | 46 | 1.76% | 94 | 2.61% | 55 | 2.46% | |
| Failing to give way to pedestrians or vehicles as required = 7 | 488 | 18.71% | 670 | 18.60% | 404 | 18.06% | |
| Reversing illegally = 8 | 38 | 1.46% | 75 | 2.08% | 51 | 2.28% | |
| Improper backing = 9 | 158 | 6.06% | 224 | 6.22% | 135 | 6.03% | |
| Illegal parking = 10 | 38 | 1.46% | 49 | 1.36% | 71 | 3.17% | |
| Affecting normal driving when changing lanes = 11 | 117 | 4.49% | 186 | 5.16% | 126 | 5.63% | |
| Improper operation = 12 | 178 | 6.83% | 237 | 6.58% | 95 | 4.25% | |
| Illegal overtaking = 13 | 121 | 4.64% | 149 | 4.14% | 170 | 7.60% | |
| Driving in a place not for traffic = 14 | 257 | 9.85% | 410 | 11.38% | 192 | 8.58% | |
| Illegal vehicle meeting = 15 | 191 | 7.32% | 288 | 8.00% | 148 | 6.62% | |
| Illegally cut in = 16 | 97 | 3.72% | 118 | 3.28% | 57 | 2.55% | |
| Illegal U-turn = 17 | 74 | 2.84% | 96 | 2.67% | 88 | 3.93% | |
| Accident Pattern | The occupants dropped or thrown = 1 | 3 | 0.12% | 6 | 0.17% | 3 | 0.13% |
| Crushing pedestrians = 2 | 53 | 2.03% | 68 | 1.89% | 50 | 2.24% | |
| Vehicle falling = 3 | 23 | 0.88% | 29 | 0.81% | 19 | 0.85% | |
| Vehicle rolled or rolled over = 4 | 71 | 2.72% | 96 | 2.67% | 56 | 2.50% | |
| Vehicle crashes into a non-fixed object = 5 | 3 | 0.12% | 2 | 0.06% | 2 | 0.09% | |
| Vehicle crashes into a fixed object = 6 | 48 | 1.84% | 94 | 2.61% | 55 | 2.46% | |
| Crashing into a stationary vehicle = 7 | 50 | 1.92% | 100 | 2.78% | 84 | 3.76% | |
| Other vehicle-to-vehicle accidents = 8 | 21 | 0.81% | 24 | 0.67% | 25 | 1.12% | |
| Scratch pedestrians = 9 | 317 | 12.15% | 500 | 13.88% | 281 | 12.56% | |
| Other vehicle-pedestrian accidents = 10 | 8 | 0.31% | 7 | 0.19% | 5 | 0.22% | |
| Crashing into a moving vehicle = 11 | 2011 | 77.11% | 2676 | 74.29% | 1657 | 74.07% | |
| Weather | Sunny = 1 | 1882 | 72.16% | 2618 | 72.68% | 1607 | 71.84% |
| Cloudy = 2 | 346 | 13.27% | 476 | 13.21% | 324 | 14.48% | |
| Foggy = 3 | 6 | 0.23% | 8 | 0.22% | 8 | 0.36% | |
| Rainy = 4 | 347 | 13.31% | 469 | 13.02% | 279 | 12.47% | |
| Snowy = 5 | 27 | 1.04% | 31 | 0.86% | 19 | 0.85% | |
| Pavement Surface Condition | Dry = 1 | 2172 | 83.28% | 2994 | 83.12% | 1874 | 83.77% |
| Wet = 2 | 379 | 14.53% | 519 | 14.41% | 309 | 13.81% | |
| Water standing = 3 | 38 | 1.46% | 53 | 1.47% | 33 | 1.48% | |
| Flooding = 4 | 2 | 0.08% | 3 | 0.08% | 3 | 0.13% | |
| Muddy = 5 | 2 | 0.08% | 9 | 0.25% | 1 | 0.04% | |
| Icy or snowy = 6 | 15 | 0.58% | 24 | 0.67% | 17 | 0.76% | |
| Visibility | < 50 m = 1 | 411 | 15.76% | 516 | 14.33% | 349 | 15.60% |
| 50~99 m = 2 | 768 | 29.45% | 1063 | 29.51% | 661 | 29.55% | |
| 100~200 m = 3 | 513 | 19.67% | 698 | 19.38% | 429 | 19.18% | |
| > 200 m = 4 | 916 | 35.12% | 1325 | 36.79% | 798 | 35.67% | |
| Traffic Control | Without signal control = 1 | 729 | 27.95% | 1049 | 29.12% | 602 | 26.91% |
| With signal control = 2 | 1879 | 72.05% | 2553 | 70.88% | 1635 | 73.09% | |
| Light Condition | Day = 1 | 1731 | 66.37% | 2365 | 65.66% | 1453 | 64.95% |
| Dawn = 2 | 21 | 0.81% | 41 | 1.14% | 24 | 1.07% | |
| Dusk = 3 | 40 | 1.53% | 80 | 2.22% | 53 | 2.37% | |
| Dark: streetlight on = 4 | 355 | 13.61% | 493 | 13.69% | 301 | 13.46% | |
| Dark: streetlight off = 5 | 461 | 17.68% | 623 | 17.30% | 406 | 18.15% | |
| Terrain | Plain = 1 | 1561 | 59.85% | 2127 | 59.05% | 1338 | 59.81% |
| Hill = 2 | 208 | 7.98% | 265 | 7.36% | 170 | 7.60% | |
| Mountain = 3 | 839 | 32.17% | 1210 | 33.59% | 729 | 32.59% | |
| Road Alignment | Straight and level = 1 | 1657 | 63.54% | 2322 | 64.46% | 1447 | 64.68% |
| Straight with gradient = 2 | 68 | 2.61% | 103 | 2.86% | 65 | 2.91% | |
| Curved and level = 3 | 339 | 13.00% | 438 | 12.16% | 258 | 11.53% | |
| Curved with gradient = 4 | 544 | 20.86% | 739 | 20.52% | 467 | 20.88% | |
| Gender | Male = 1 | 2476 | 94.94% | 3390 | 94.11% | 2127 | 95.08% |
| Female = 2 | 132 | 5.06% | 212 | 5.89% | 110 | 4.92% | |
| Age | 18~20 = 1 | 110 | 4.22% | 0 | 0.00% | 0 | 0.00% |
| 21~25 = 2 | 541 | 20.74% | 266 | 7.38% | 0 | 0.00% | |
| 26~30 = 3 | 485 | 18.60% | 746 | 20.71% | 49 | 2.19% | |
| 31~35 = 4 | 383 | 14.69% | 711 | 19.74% | 317 | 14.17% | |
| 36~40 = 5 | 411 | 15.76% | 620 | 17.21% | 514 | 22.98% | |
| 41~45 = 6 | 334 | 12.81% | 569 | 15.80% | 511 | 22.84% | |
| 46~50 = 7 | 202 | 7.75% | 345 | 9.58% | 419 | 18.73% | |
| 51~55 = 8 | 99 | 3.80% | 221 | 6.14% | 247 | 11.04% | |
| 56~60 = 9 | 36 | 1.38% | 90 | 2.50% | 119 | 5.32% | |
| 61~65 = 10 | 6 | 0.23% | 31 | 0.86% | 58 | 2.59% | |
| >65 = 11 | 1 | 0.04% | 3 | 0.08% | 3 | 0.13% | |
| Overload Condition | Overloaded = 1 | 205 | 7.86% | 232 | 6.44% | 149 | 6.66% |
| Not overloaded = 2 | 2403 | 92.14% | 3370 | 93.56% | 2088 | 93.34% | |
| Vehicle Type | Trailer = 1 | 196 | 7.52% | 208 | 5.77% | 122 | 5.45% |
| Tractor = 2 | 43 | 1.65% | 49 | 1.36% | 39 | 1.74% | |
| Automobile = 3 | 1955 | 74.96% | 2723 | 75.60% | 1698 | 75.91% | |
| Motorcycle = 4 | 394 | 15.11% | 603 | 16.74% | 363 | 16.23% | |
| Other = 5 | 20 | 0.77% | 19 | 0.53% | 15 | 0.67% | |
References
- Benlagha, N.; Charfeddine, L. Risk factors of road accident severity and the development of a new system for prevention: New insights from China. Accid. Anal. Prev. 2020, 136, 105411. [Google Scholar] [CrossRef]
- Møller, M.; Haustein, S. Factors contributing to young moped rider accidents in Denmark. Accid. Anal. Prev. 2016, 87, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Craen, S.D.; Twisk, D.A.M.; Hagenzieker, M.P.; Elffers, H.; Brookhuis, K.A. Do young novice drivers overestimate their driving skills more than experienced drivers? Different methods lead to different conclusions. Accid. Anal. Prev. 2011, 43, 1660–1665. [Google Scholar] [CrossRef]
- Xiao, D.; Yuan, Q.; Kang, S.; Xu, X. Insights on Crash Injury Severity Control from Novice and Experienced Drivers: A Bivariate Random-Effects Probit Analysis. Discret. Dyn. Nat. Soc. 2021, 2021, 1–13. [Google Scholar] [CrossRef]
- Al-Garawi, N.; Dalhat, M.A.; Aga, O. Assessing the Road Traffic Crashes among Novice Female Drivers in Saudi Arabia. Sustainability 2021, 13, 8613. [Google Scholar] [CrossRef]
- Moral-García, S.; Castellano, J.G.; Mantas, C.J.; Montella, A.; Abellán, J. Decision tree ensemble method for analyzing traffic accidents of novice drivers in urban areas. Entropy 2019, 21, 360. [Google Scholar] [CrossRef] [PubMed]
- Prokhorenkova, L.; Gusev, G.; Vorobev, A.; Dorogush, A.V.; Gulin, A. CatBoost: Unbiased boosting with categorical features. arXiv 2017, arXiv:1706.09516. [Google Scholar]
- Lundberg, S.M.; Lee, S.-I. A unified approach to interpreting model predictions. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 4768–4777. [Google Scholar]
- Wikman, A.-S.; Nieminen, T.; Summala, H. Driving experience and time-sharing during in-car tasks on roads of different width. Ergonomics 1998, 41, 358–372. [Google Scholar] [CrossRef]
- Scott-Parker, B.; Watson, B.; King, M.; Hyde, M.K. Mileage, car ownership, experience of punishment avoidance, and the risky driving of young drivers. Traffic Inj. Prev. 2011, 12, 559–567. [Google Scholar] [CrossRef] [PubMed]
- Ivers, R.; Senserrick, T.; Boufous, S.; Stevenson, M.; Chen, H.-Y.; Woodward, M.; Norton, R. Novice drivers’ risky driving behavior, risk perception, and crash risk: Findings from the DRIVE study. Am. J. Public Health 2009, 99, 1638–1644. [Google Scholar] [CrossRef]
- Ohlhauser, A.D.; Milloy, S.; Caird, J.K. Driver responses to motorcycle and lead vehicle braking events: The effects of motorcycling experience and novice versus experienced drivers. Transp. Res. Part F Psychol. Behav. 2011, 14, 472–483. [Google Scholar] [CrossRef]
- Mitchell, R.; Senserrick, T.; Bambach, M.; Mattos, G. Comparison of novice and full-licenced driver common crash types in New South Wales, Australia, 2001–2011. Accid. Anal. Prev. 2015, 81, 204–210. [Google Scholar] [CrossRef]
- Underwood, G.; Chapman, P.; Brocklehurst, N.; Underwood, J.; Crundall, D. Visual attention while driving: Sequences of eye fixations made by experienced and novice drivers. Ergonomics 2003, 46, 629–646. [Google Scholar] [CrossRef] [PubMed]
- Bedard, M.; Guyatt, G.H.; Stones, M.J.; Hirdes, J.P. The independent contribution of driver, crash, and vehicle characteristics to driver fatalities. Accid. Anal. Prev. 2002, 34, 717–727. [Google Scholar] [CrossRef]
- Ma, C.; Zhou, J.; Yang, D. Causation analysis of hazardous material road transportation accidents based on the ordered logit regression model. Int. J. Environ. Res. Public Health 2020, 17, 1259. [Google Scholar] [CrossRef]
- Chen, C.; Zhang, G.; Huang, H.; Wang, J.; Tarefder, R.A. Examining driver injury severity outcomes in rural non-interstate roadway crashes using a hierarchical ordered logit model. Accid. Anal. Prev. 2016, 96, 79–87. [Google Scholar] [CrossRef]
- Aidoo, E.N.; Ackaah, W. A generalized ordered logit analysis of risk factors associated with driver injury severity. J. Public Health 2021, 29, 471–477. [Google Scholar] [CrossRef]
- Wang, Y.; Luo, Y.; Chen, F. Interpreting risk factors for truck crash severity on mountainous freeways in Jiangxi and Shaanxi, China. Eur. Transp. Res. Rev. 2019, 11, 1–11. [Google Scholar] [CrossRef]
- Zeng, Q.; Hao, W.; Lee, J.; Chen, F. Investigating the Impacts of Real-Time Weather Conditions on Freeway Crash Severity: A Bayesian Spatial Analysis. Int. J. Environ. Res. Public Health 2020, 17, 2768. [Google Scholar] [CrossRef]
- Azimi, G.; Rahimi, A.; Asgari, H.; Jin, X. Severity analysis for large truck rollover crashes using a random parameter ordered logit model. Accid. Anal. Prev. 2020, 135, 105355. [Google Scholar] [CrossRef]
- Xing, Y.; Chen, S.; Zhu, S.; Zhang, Y.; Lu, J. Exploring Risk Factors Contributing to the Severity of Hazardous Material Transportation Accidents in China. Int. J. Environ. Res. Public Health 2020, 17, 1344. [Google Scholar] [CrossRef]
- Shao, X.; Ma, X.; Chen, F.; Song, M.; Pan, X.; You, K. A Random Parameters Ordered Probit Analysis of Injury Severity in Truck Involved Rear-End Collisions. Int. J. Environ. Res. Public Health 2020, 17, 395. [Google Scholar] [CrossRef] [PubMed]
- Chen, F.; Song, M.; Ma, X. Investigation on the Injury Severity of Drivers in Rear-End Collisions Between Cars Using a Random Parameters Bivariate Ordered Probit Model. Int. J. Environ. Res. Public Health 2019, 16, 2632. [Google Scholar] [CrossRef]
- Satoshi, H.; Kenta, H. Factors Affecting Analysis of the Severity of Accidents in Cold and Snowy Areas Using the Ordered Probit Model. Asian Transp. Stud. 2021, 7, 100035. [Google Scholar]
- Xiao, W.; Yuanchang, X.; Lingtao, W.; Liming, J. Quantifying and comparing the effects of key risk factors on various types of roadway segment crashes with LightGBM and SHAP. Accid. Anal. Prev. 2021, 159, 106261. [Google Scholar]
- Zhou, B.; Wang, X.; Zhang, S.; Li, Z.; Sun, S.; Shu, K.; Sun, Q. Comparing factors affecting injury severity of passenger car and truck drivers. IEEE Access 2020, 8, 153849–153861. [Google Scholar] [CrossRef]
- Tang, J.; Liang, J.; Han, C.; Li, Z.; Huang, H. Crash injury severity analysis using a two-layer Stacking framework. Accid. Anal. Prev. 2019, 122, 226–238. [Google Scholar] [CrossRef]
- Li, Z.; Liu, P.; Wang, W.; Xu, C. Using support vector machine models for crash injury severity analysis. Accid. Anal. Prev. 2012, 45, 478–486. [Google Scholar] [CrossRef] [PubMed]
- Yu, R.; Abdel-Aty, M. Utilizing support vector machine in real-time crash risk evaluation. Accid. Anal. Prev. 2013, 51, 252–259. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.; Zhang, G.; Qian, Z.; Tarefder, R.A.; Tian, Z. Investigating driver injury severity patterns in rollover crashes using support vector machine models. Accid. Anal. Prev. 2016, 90, 128–139. [Google Scholar] [CrossRef]
- AlKheder, S.; AlRukaibi, F.; Aiash, A. Risk analysis of traffic accidents’ severities: An application of three data mining models. ISA Trans. 2020, 106, 213–220. [Google Scholar] [CrossRef]
- Mafi, S.; AbdelRazig, Y.; Doczy, R. Machine Learning Methods to Analyze Injury Severity of Drivers from Different Age and Gender Groups. Transp. Res. Rec. 2018, 2672, 171–183. [Google Scholar] [CrossRef]
- Chawla, N.V.; Bowyer, K.W.; Hall, L.O.; Kegelmeyer, W.P. SMOTE: Synthetic minority over-sampling technique. J. Artif. Intell. Res. 2002, 16, 321–357. [Google Scholar] [CrossRef]
- Han, H.; Wang, W.-Y.; Mao, B.-H. Borderline-SMOTE: A new over-sampling method in imbalanced data sets learning. In Proceedings of the Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics); Springer: Berlin/Heidelberg, Germany, 2005; Volume 3644 LNCS, pp. 878–887. [Google Scholar]
- Wilson, D.L. Asymptotic properties of nearest neighbor rules using edited data. IEEE Trans. Syst. Man Cybern. 1972, SMC-2, 408–421. [Google Scholar] [CrossRef]
- Tomek, I. Two Modifications of CNN. IEEE Trans. Syst. Man Cybern. 1976, 6, 769–772. [Google Scholar] [CrossRef]
- Batista, G.E.A.P.A.; Prati, R.C.; Monard, M.C. A study of the behavior of several methods for balancing machine learning training data. ACM SIGKDD Explor. Newsl. 2004, 6, 20–29. [Google Scholar] [CrossRef]
- Wang, C.; Liu, L.; Xu, C.; Lv, W. Predicting Future Driving Risk of Crash-Involved Drivers Based on a Systematic Machine Learning Framework. Int. J. Environ. Res. Public Health 2019, 16, 334. [Google Scholar] [CrossRef] [PubMed]
- Li, G.; Lai, W.; Qu, X. Association between crash attributes and drivers’ crash involvement: A study based on police-reported crash data. Int. J. Environ. Res. Public Health 2020, 17, 9020. [Google Scholar] [CrossRef] [PubMed]
- Mehrannia, P.; Bagi, S.S.G.; Moshiri, B.; Al-Basir, O.A. Deep Representation of Imbalanced Spatio-temporal Traffic Flow Data for Traffic Accident Detection. arXiv 2021, arXiv:2108.09506. [Google Scholar]
- Lee, C.; Li, X. Predicting driver injury severity in single-vehicle and two-vehicle crashes with boosted regression trees. Transp. Res. Rec. 2015, 2514, 138–148. [Google Scholar] [CrossRef]
- Jiang, L.; Xie, Y.; Wen, X.; Ren, T. Modeling highly imbalanced crash severity data by ensemble methods and global sensitivity analysis. J. Transp. Saf. Secur. 2020, 1–23. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. Xgboost: Reliable large-scale tree boosting system. In Proceedings of the 22nd SIGKDD Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 13–17. [Google Scholar]
- Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T.-Y. Lightgbm: A highly efficient gradient boosting decision tree. Adv. Neural Inf. Process. Syst. 2017, 30, 3146–3154. [Google Scholar]
- Lundberg, S.M.; Erion, G.; Chen, H.; DeGrave, A.; Prutkin, J.M.; Nair, B.; Katz, R.; Himmelfarb, J.; Bansal, N.; Lee, S.-I. From local explanations to global understanding with explainable AI for trees. Nat. Mach. Intell. 2020, 2, 56–67. [Google Scholar] [CrossRef] [PubMed]
- Ayoub, J.; Yang, X.J.; Zhou, F. Modeling dispositional and initial learned trust in automated vehicles with predictability and explainability. Transp. Res. Part F Traffic Psychol. Behav. 2021, 77, 102–116. [Google Scholar] [CrossRef]
- Bergstra, J.; Yamins, D.; Cox, D. Making a science of model search: Hyperparameter optimization in hundreds of dimensions for vision architectures. In Proceedings of the International Conference on Machine Learning, Atlanta, GA, USA, 16–21 June 2013; pp. 115–123. [Google Scholar]
- Kumar, S.; Dutta, S.; Chatturvedi, S.; Bhatia, M. Strategies for enhancing training and privacy in blockchain enabled federated learning. In Proceedings of the 2020 IEEE Sixth International Conference on Multimedia Big Data (BigMM), New Delhi, India, 4–26 September 2020; pp. 333–340. [Google Scholar]
- Shyam, R.; Ayachit, S.S.; Patil, V.; Singh, A. Competitive Analysis of the Top Gradient Boosting Machine Learning Algorithms. In 2020 2nd International Conference on Advances in Computing, Communication Control and Networking (ICACCCN); IEEE: Piscataway, NJ, USA, 2020; pp. 191–196. [Google Scholar]
- Liu, H.; Xiao, Q.; Jiao, Z.; Meng, J.; Mu, Y.; Hou, K.; Yu, X.; Guo, S.; Jia, H. LightGBM-Based Prediction of Remaining Useful Life for Electric Vehicle Battery under Driving Conditions. In 2020 IEEE Sustainable Power and Energy Conference (ISPEC); IEEE: Piscataway, NJ, USA, 2020; pp. 2577–2582. [Google Scholar]
- Ahangar, A.N.; Arghand, E.; Ahangar, H.B.; Ganji, S.S. Recognizing the reasons of the accidents based on the rural drivers’ mental patterns using Q analytical method. Saf. Sci. 2020, 125, 104649. [Google Scholar] [CrossRef]
- Shankar, V.; Mannering, F.; Barfield, W. Effect of roadway geometrics and environmental factors on rural freeway accident frequencies. Accid. Anal. Prev. 1995, 27, 371–389. [Google Scholar] [CrossRef]
- Pradhan, A.K.; Pollatsek, A.; Knodler, M.; Fisher, D.L. Can younger drivers be trained to scan for information that will reduce their risk in roadway traffic scenarios that are hard to identify as hazardous? Ergonomics 2009, 52, 657–673. [Google Scholar] [CrossRef]
- Curry, A.E.; Metzger, K.B.; Williams, A.F.; Tefft, B.C. Comparison of older and younger novice driver crash rates: Informing the need for extended Graduated Driver Licensing restrictions. Accid. Anal. Prev. 2017, 108, 66–73. [Google Scholar] [CrossRef]
- Vlakveld, W. Hazard Anticipation of Young Novice Drivers: Assessing and Enhancing the Capabilities of Young Novice Drivers to Anticipate Latent Hazards in Road and Traffic Situations; University of Groningen: Groningen, The Netherlands, 2011. [Google Scholar]
- McKenna, F.P.; Horswill, M.S.; Alexander, J.L. Does anticipation training affect drivers’ risk taking? J. Exp. Psychol. Appl. 2006, 12, 1. [Google Scholar] [CrossRef]
- Hwang, Y.; Hong, G.-R.S. Predictors of driving cessation in community-dwelling older adults: A 3-year longitudinal study. Transp. Res. Part F Traffic Psychol. Behav. 2018, 52, 202–209. [Google Scholar] [CrossRef]
- Mitchell, C.G.B. The licensing and safety of older drivers in Britain. Accid. Anal. Prev. 2013, 50, 732–741. [Google Scholar] [CrossRef] [PubMed]
- Regev, S.; Rolison, J.J.; Moutari, S. Crash risk by driver age, gender, and time of day using a new exposure methodology. J. Saf. Res. 2018, 66, 131–140. [Google Scholar] [CrossRef]
- Mercedes, A.; Rodrigo, S.; Miguel, S. Does longevity impact the severity of traffic crashes? A comparative study of young-older and old-older drivers. J. Saf. Res. 2020, 73, 37–46. [Google Scholar] [CrossRef]
- Boni, R.D.; Bozzetti, M.C.; Hilgert, J.; Sousa, T.; Diemen, L.V.; Benzano, D.; Menegon, G.; Holmer, B.; Duarte, P.d.C.A.V.; Pechansky, F. Factors associated with alcohol and drug use among traffic crash victims in southern Brazil. Accid. Anal. Prev. 2011, 43, 1408–1413. [Google Scholar] [CrossRef]
- McDonald, C.C.; Sommers, M.S. “Good Passengers and Not Good Passengers:” Adolescent Drivers’ Perceptions About Inattention and Peer Passengers. J. Pediatric Nurs. 2016, 31, e375–e382. [Google Scholar] [CrossRef][Green Version]
- Borowsky, A.; Shinar, D.; Oron-Gilad, T. Age and skill differences in driving related hazard perception. Accid. Anal. Prev. 2010, 42, 1240–1249. [Google Scholar] [CrossRef] [PubMed]
- Huestegge, L.; Skottke, E.-M.; Anders, S.; Müsseler, J.; Debus, G. The development of hazard perception: Dissociation of visual orientation and hazard processing. Transp. Res. Part F Psychol. Behav. 2009, 13, 1–8. [Google Scholar] [CrossRef]
- Shinar, D.; Compton, R. Aggressive driving: An observational study of driver, vehicle, and situational variables. Accid. Anal. Prev. 2004, 36, 429–437. [Google Scholar] [CrossRef]
- Yue, X.; Ding, Y.; Hu, H.; Zhao, D. Analysis on the association between driver’s macroscopic characteristics and accident type of urban traffic accidents. In Proceedings of the 2017 36th Chinese Control Conference (CCC), Dalian, China, 26–28 July 2017; pp. 5658–5662. [Google Scholar]
- Noh, Y.; Yoon, Y. Elderly road collision injury outcomes associated with seat positions and seatbelt use in a rapidly aging society—A case study in South Korea. PLoS ONE 2017, 12, e0183043. [Google Scholar] [CrossRef]
| Parameter | Description | Group 1 | Group 2 | Group 3 |
|---|---|---|---|---|
| l2_leaf_reg | Coefficient at the L2 regularization term of the cost function. | 2 | 5 | 5 |
| learning_rate | Used for reducing the gradient step. | 0.15 | 0.3 | 0.25 |
| depth | Depth of the tree. | 8 | 10 | 10 |
| iterations | The maximum number of trees that can be built. | 1000 | 400 | 500 |
| loss_function | The metric to use in training. | MultiClass | MultiClass | MultiClass |
| od_wait | The number of iterations to continue the training after the iteration with the optimal metric value. | 12 | 16 | 14 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, S.; Shao, H.; Ji, X. Insights into Factors Affecting Traffic Accident Severity of Novice and Experienced Drivers: A Machine Learning Approach. Int. J. Environ. Res. Public Health 2021, 18, 12725. https://doi.org/10.3390/ijerph182312725
Chen S, Shao H, Ji X. Insights into Factors Affecting Traffic Accident Severity of Novice and Experienced Drivers: A Machine Learning Approach. International Journal of Environmental Research and Public Health. 2021; 18(23):12725. https://doi.org/10.3390/ijerph182312725
Chicago/Turabian StyleChen, Shuaiming, Haipeng Shao, and Ximing Ji. 2021. "Insights into Factors Affecting Traffic Accident Severity of Novice and Experienced Drivers: A Machine Learning Approach" International Journal of Environmental Research and Public Health 18, no. 23: 12725. https://doi.org/10.3390/ijerph182312725
APA StyleChen, S., Shao, H., & Ji, X. (2021). Insights into Factors Affecting Traffic Accident Severity of Novice and Experienced Drivers: A Machine Learning Approach. International Journal of Environmental Research and Public Health, 18(23), 12725. https://doi.org/10.3390/ijerph182312725






