The Effect of Local and Global Interventions on Epidemic Spreading
Abstract
:1. Introduction
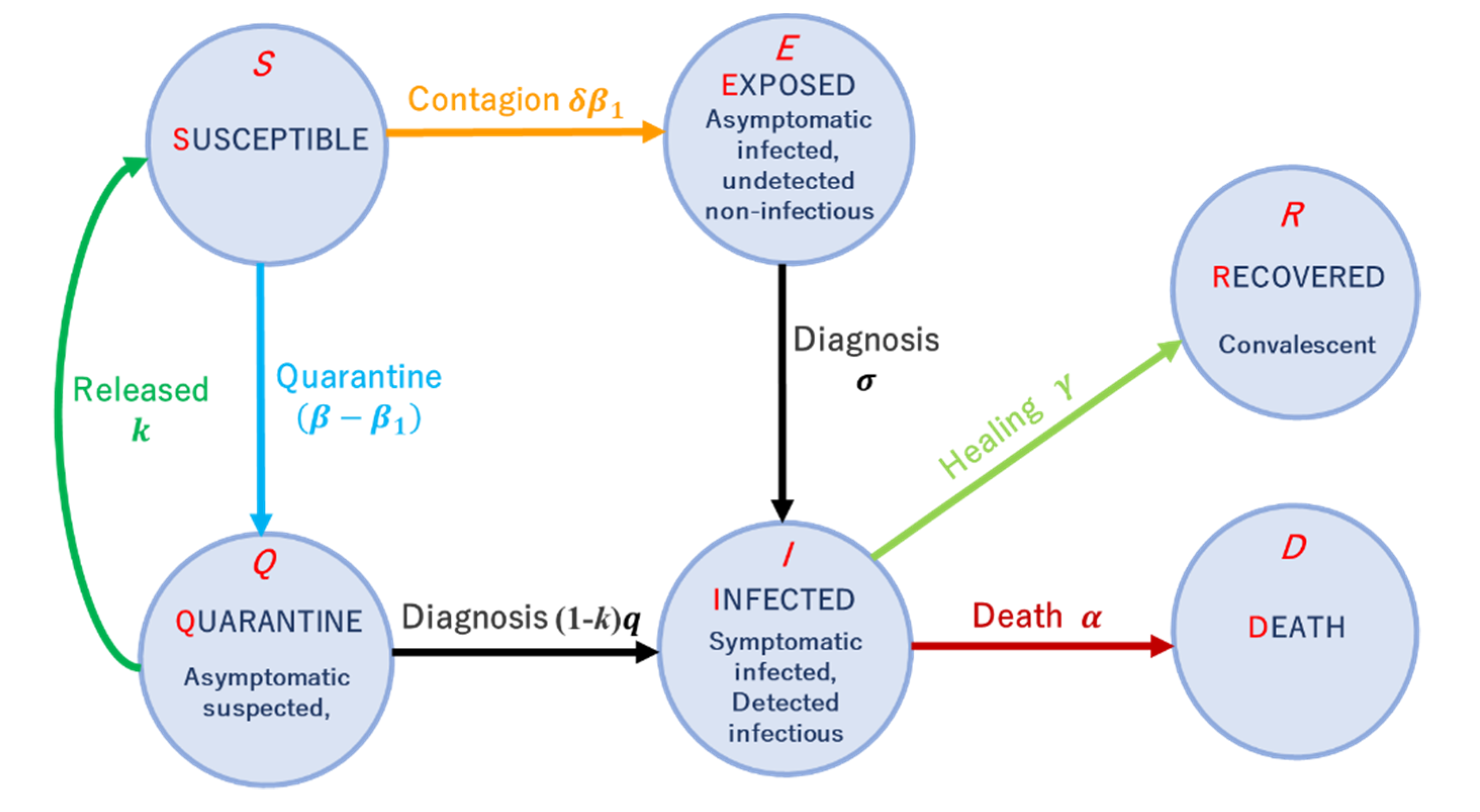
2. Materials and Methods
3. Results
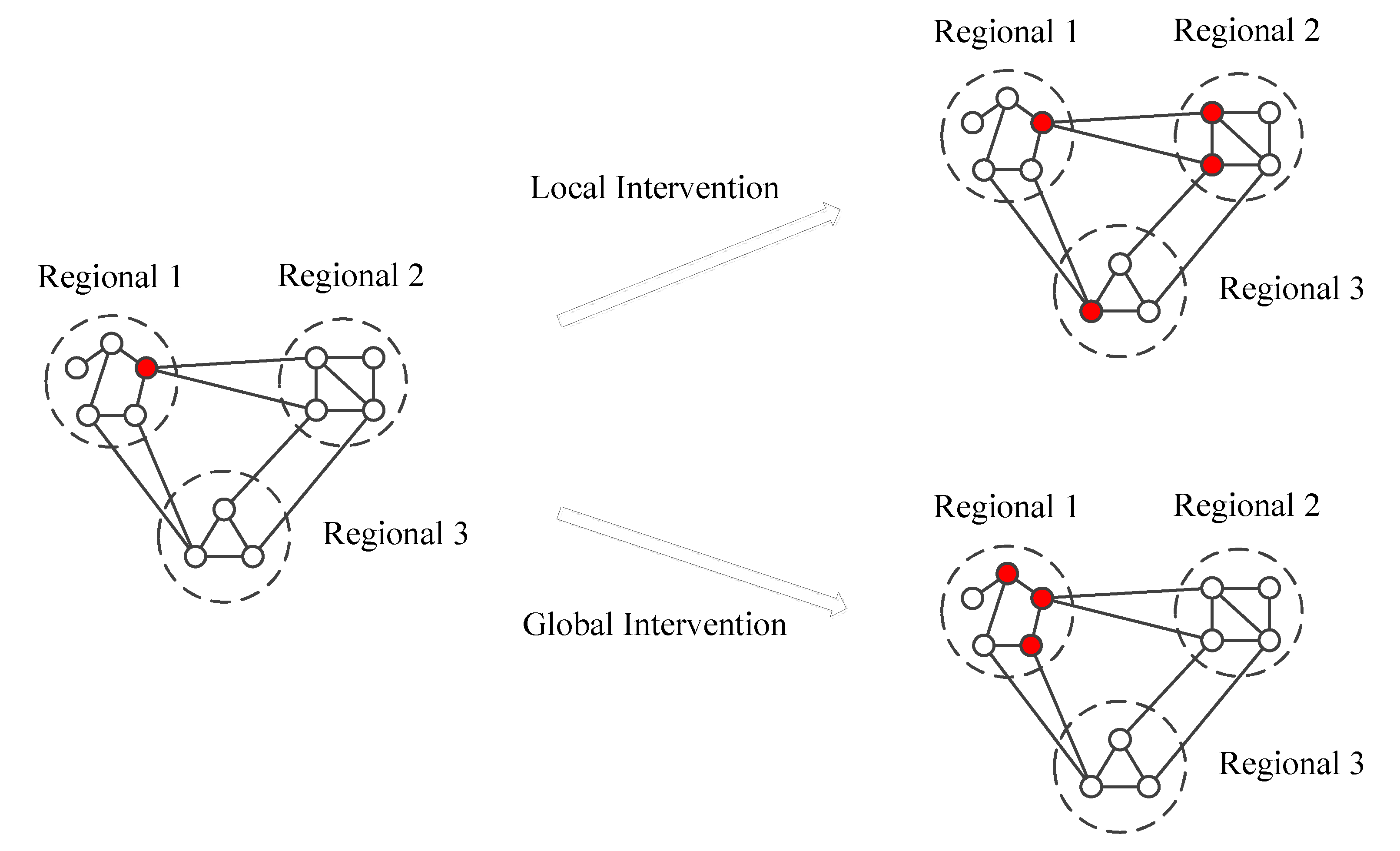
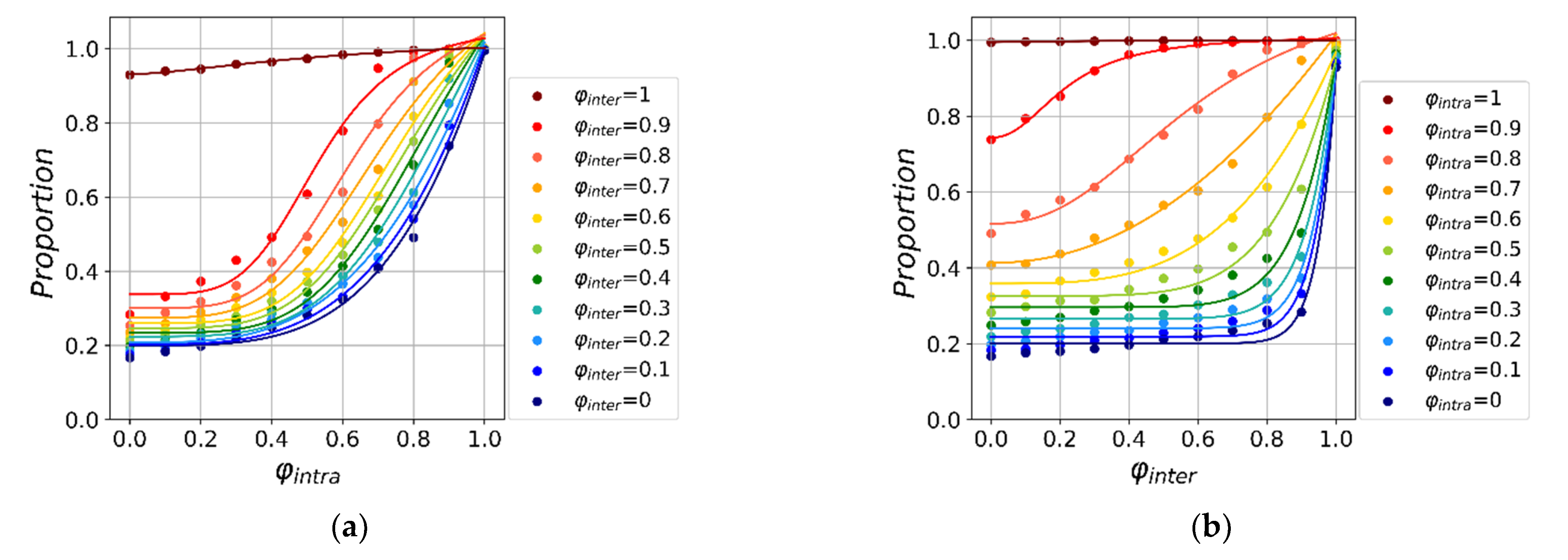
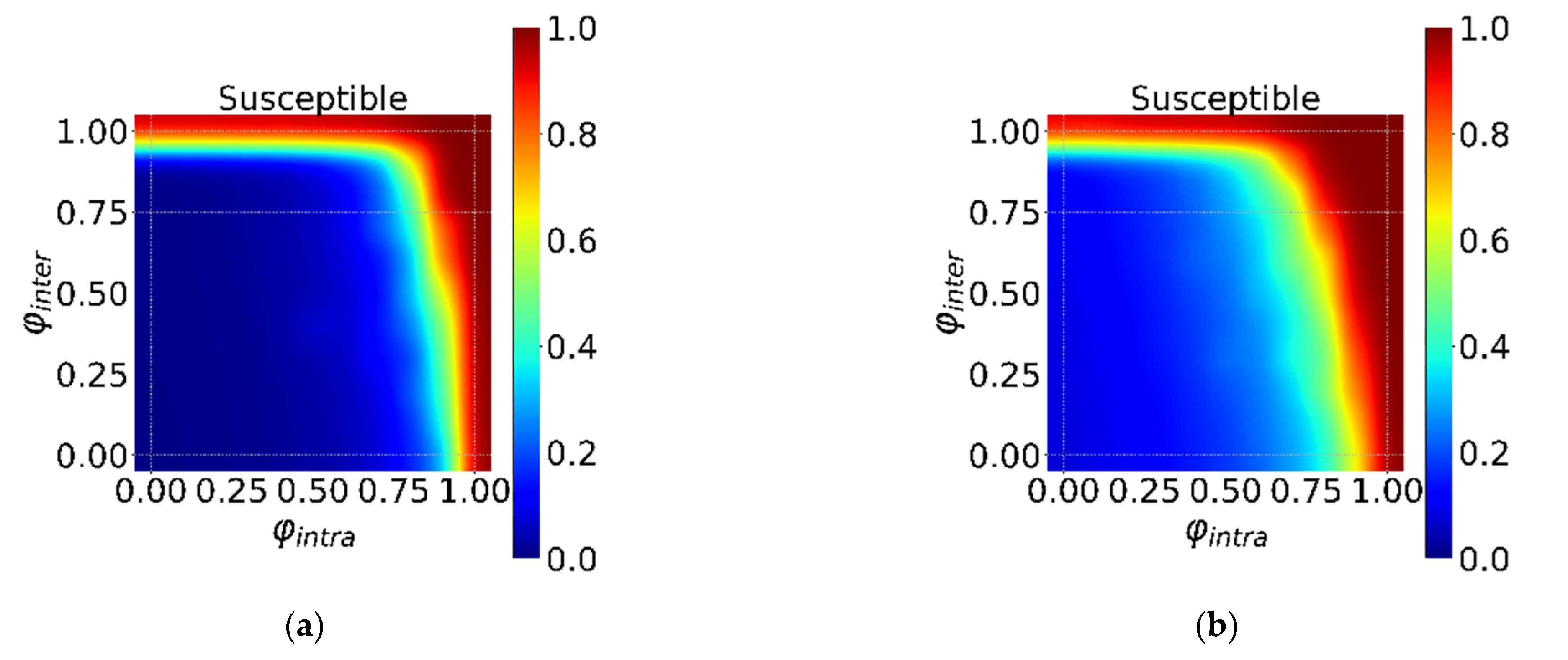
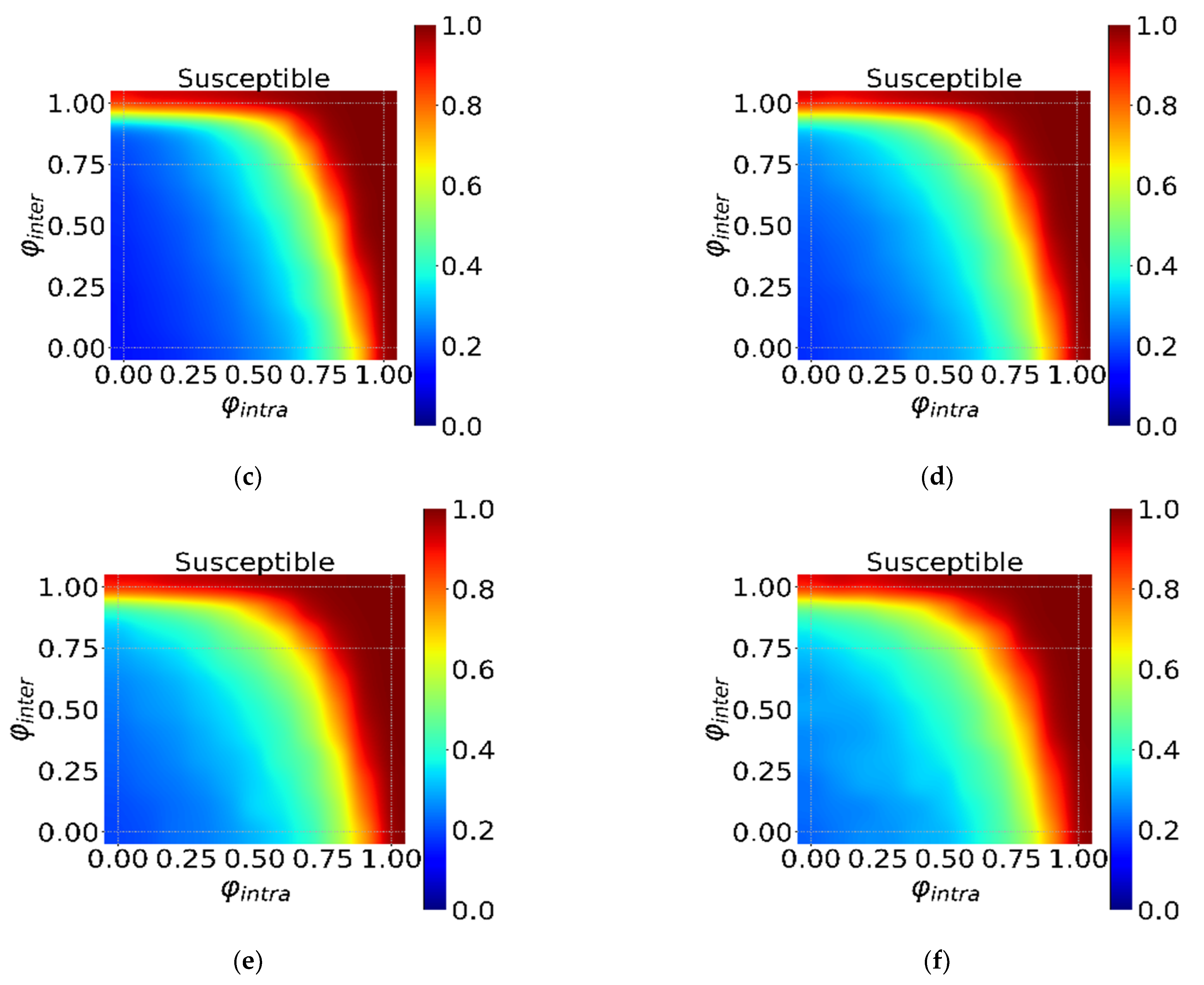
3.1. The Effectiveness of Global and Local Interventions
3.2. The Global and Local Interventions
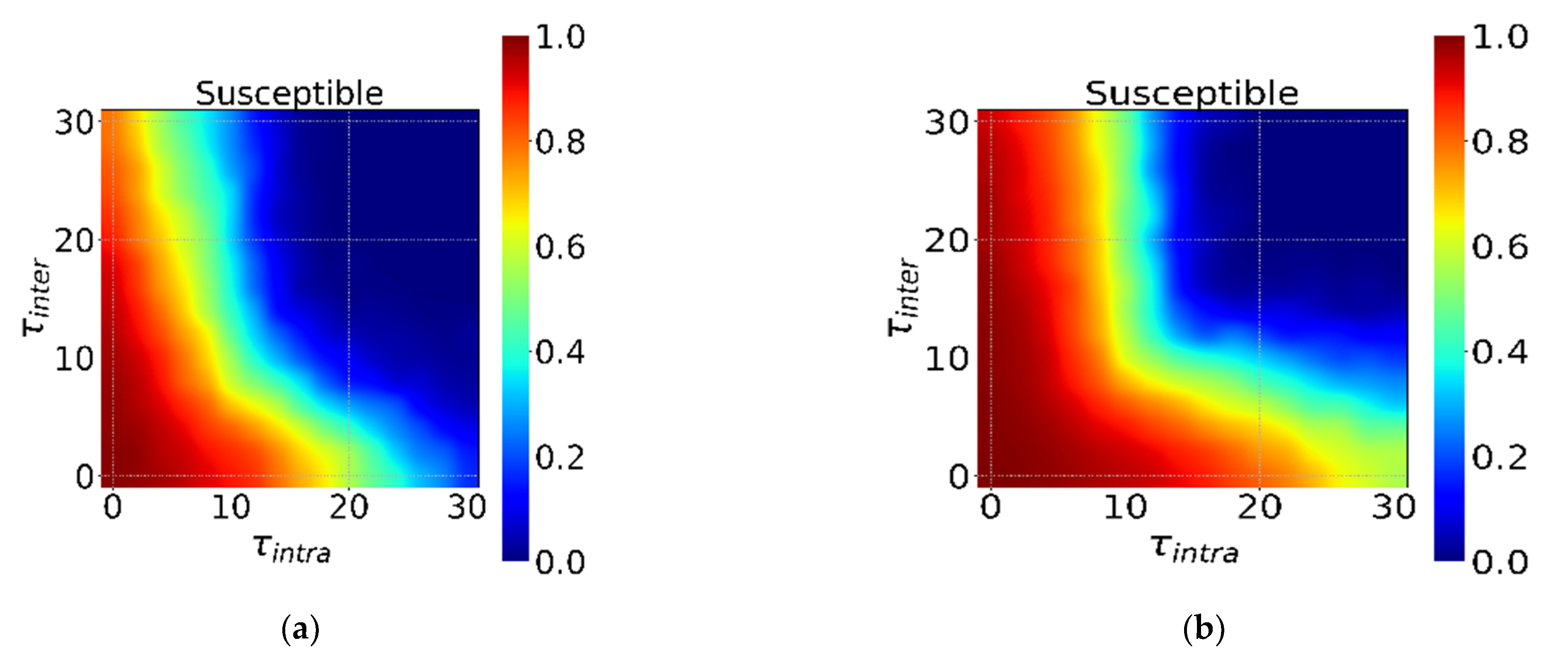
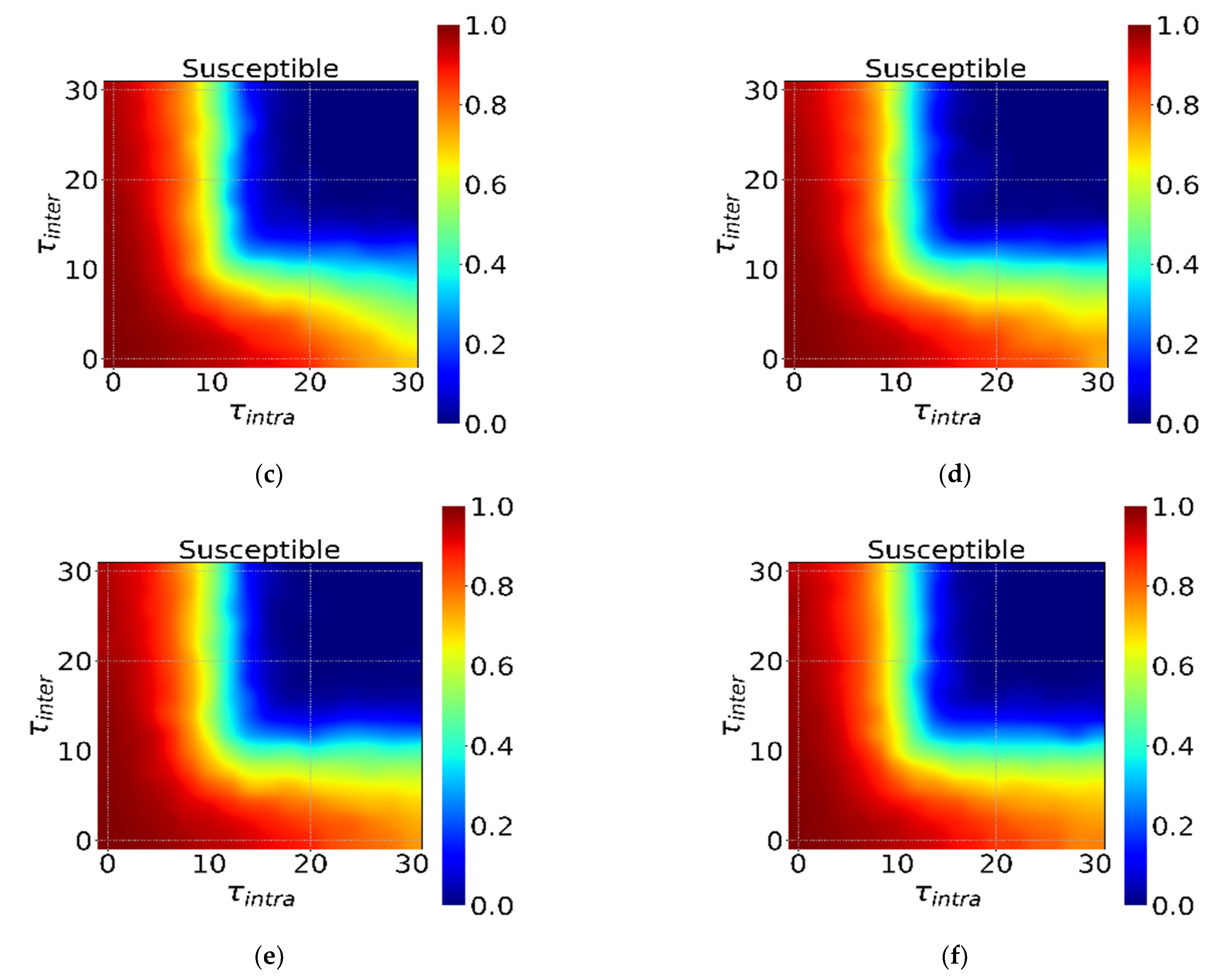
3.3. The Incubation Period and Interventions
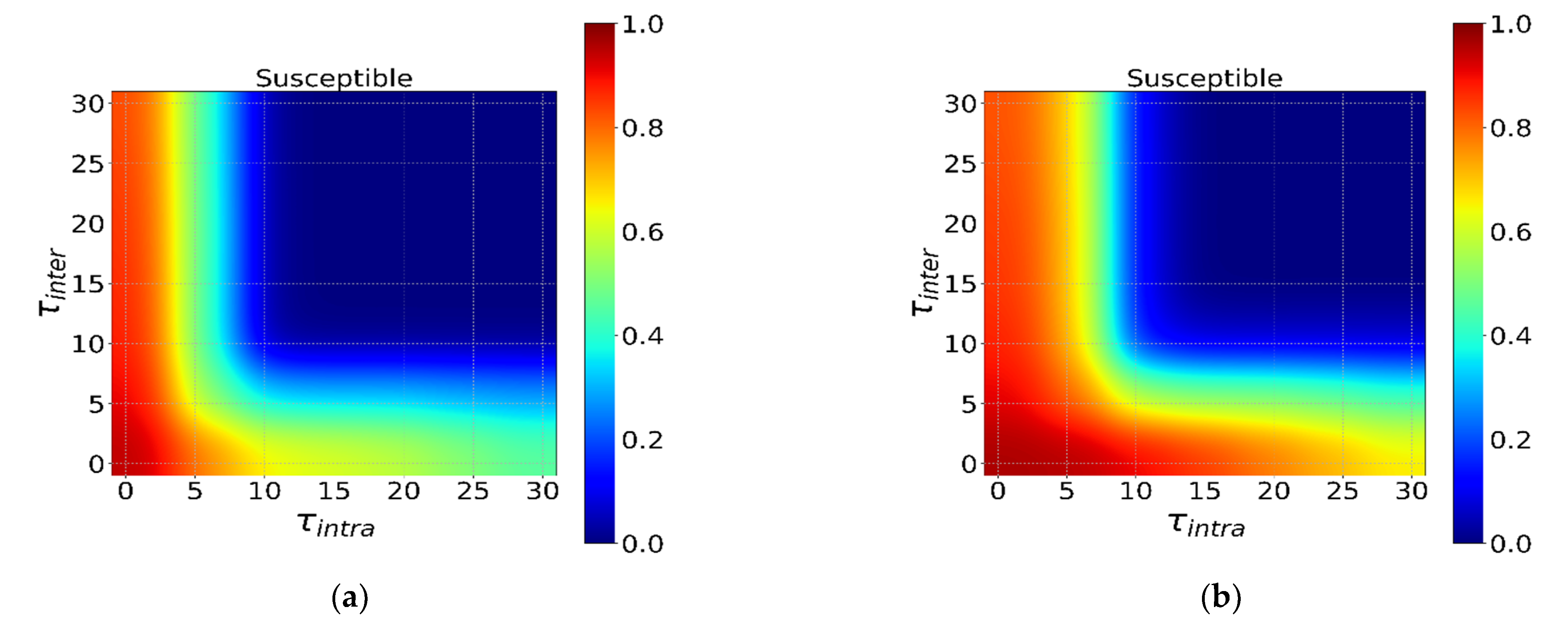
3.4. Initial Distribution of the Infected Individual
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Fong, M.W.; Gao, H.; Wong, J.Y.; Xiao, J.; Shiu, E.Y.C.; Ryu, S.; Cowling, B.J. Nonpharmaceutical measures for pandemic influenza in nonhealthcare settings—Social distancing measures. Emerg. Infect. Dis. 2020, 26, 976–984. [Google Scholar] [CrossRef] [PubMed]
- Ryu, S.; Gao, H.; Wong, J.Y.; Shiu, E.Y.; Xiao, J.; Fong, M.W.; Cowling, B.J. Nonpharmaceutical measures for pandemic influenza in nonhealthcare settings—International travel-related measures. Emerg. Infect. Dis. 2020, 26, 961–966. [Google Scholar] [CrossRef] [PubMed]
- Xiao, J.; Shiu, E.Y.; Gao, H.; Wong, J.Y.; Fong, M.W.; Ryu, S.; Cowling, B.J. Nonpharmaceutical measures for pandemic influenza in nonhealthcare settings—Personal protective and environmental measures. Emerg. Infect. Dis. 2020, 26, 967–975. [Google Scholar] [CrossRef] [PubMed]
- Bonaccorsi, G.; Pierri, F.; Cinelli, M. Economic and social consequences of human mobility restrictions under COVID-19. Proc. Natl. Acad. Sci. USA 2020, 27, 15530–15535. [Google Scholar] [CrossRef]
- Zheng, Q.; Jones, F.K.; Leavitt, S.V.; Ung, L.; Labrique, A.B.; Peters, D.H.; Lee, E.C.; Azman, A.S. HIT-COVID, a global database tracking public health interventions to COVID-19. Sci. Data 2020, 7, 286. [Google Scholar] [CrossRef] [PubMed]
- Tsay, C.; Lejarza, F.; Stadtherr, M.A.; Baldea, M. Modeling, state estimation, and optimal control for the US COVID-19 outbreak. Sci. Rep. 2020, 10, 1071. [Google Scholar] [CrossRef]
- Hsiang, S.; Allen, D.; Annan-Phan, S.; Bell, K.; Bolliger, I.; Chong, T.; Druckenmiller, H.; Huang, L.Y.; Hultgren, A.; Krasovich, E.; et al. The effect of large-scale anti-contagion policies on the COVID-19 pandemic. Nature 2020, 584, 262–267. [Google Scholar] [CrossRef]
- Anderson, S.C.; Mulberry, N.; Edwards, A.M.; Stockdale, J.E.; Iyaniwura, S.A.; Falcao, R.C.; Otterstatter, M.C.; Janjua, N.Z.; Coombs, D.; Colijn, C. How much leeway is there to relax COVID-19 control measures? Epidemics 2021, 35, 100453. [Google Scholar] [CrossRef] [PubMed]
- Samuel, J.; Rahman, M.M.; Ali, G.M.N.; Samuel, Y.; Pelaez, A.; Chong, P.H.J.; Yakubov, M. Feeling Positive About Reopening? New Normal Scenarios from COVID-19 US Reopen Sentiment Analytics. IEEE Access 2020, 8, 142173–142190. [Google Scholar] [CrossRef]
- Silva, C.J.; Cruz, C.; Torres, D.F.; Muñuzuri, A.P.; Carballosa, A.; Area, I.; Nieto, J.J.; Fonseca-Pinto, R.; Passadouro, R.; Dos Santos, E.S.; et al. Optimal control of the COVID-19 pandemic: Controlled sanitary deconfinement in Portugal. Sci. Rep. 2021, 11, 3451. [Google Scholar] [CrossRef]
- Pastorsatorras, R.; Vespignani, A. Epidemic spreading in scale-free networks. Phys. Rev. Lett. 2001, 86, 3200. [Google Scholar] [CrossRef] [Green Version]
- Moreno, Y.; Pastor-Satorras, R.; Vespignani, A. Epidemic outbreaks in complex heterogeneous networks. Eur. Phys. J. B-Condens. Matter Complex Syst. 2002, 26, 521–529. [Google Scholar] [CrossRef]
- Verity, R.; Okell, L.C.; Dorigatti, I.; Winskill, P.; Whittaker, C.; Imai, N.; Cuomo-Dannenburg, G.; Thompson, H.; Walker, P.G.; Fu, H.; et al. Estimates of the severity of coronavirus disease 2019: A model-based analysis. Lancet Infect. Dis. 2020, 20, 669–677. [Google Scholar] [CrossRef]
- Zhou, T.; Liu, Q.; Yang, Z.; Liao, J.; Yang, K.; Bai, W.; Lu, X.; Zhang, W. Preliminary prediction of the basic reproduction number of the Wuhan novel coronavirus 2019-nCoV. J. Evid.-Based Med. 2020, 13, 3–7. [Google Scholar] [CrossRef]
- Wang, L.; Li, J.; Guo, S.; Xie, N.; Yao, L.; Cao, Y.; Day, S.W.; Howard, S.C.; Graff, J.C.; Gu, T.; et al. Real-time estimation and prediction of mortality caused by COVID-19 with patient information based algorithm. Sci. Total Environ. 2020, 1320, 138394. [Google Scholar] [CrossRef] [PubMed]
- Eikenberry, S.E.; Mancuso, M.; Iboi, E.; Phan, T.; Eikenberry, K.; Kuang, Y.; Kostelich, E.; Gumel, A.B. To mask or not to mask: Modeling the potential for face mask use by the general public to curtail the COVID-19 pandemic. Infect. Dis. Model. 2020, 5, 293–308. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.; Lin, C.; Chiu, Y.; Hwang, S.J. Take proactive measures for the pandemic COVID-19 infection in the dialysis facilities. J. Formos. Med. Assoc. 2020, 119, 895–897. [Google Scholar] [CrossRef]
- Yen, M.; Schwartz, J.; Chen, S.; King, C.; Yang, G.; Hsueh, P. Interrupting COVID-19 transmission by implementing enhanced traffic control bundling: Implications for global prevention and control efforts. J. Microbiol. Immunol. Infect. 2020, 52, 377–380. [Google Scholar] [CrossRef] [PubMed]
- Tomar, A.; Gupta, N. Prediction for the spread of COVID-19 in India and effectiveness of preventive measures. Sci. Total Environ. 2020, 728, 138762. [Google Scholar] [CrossRef]
- Zhang, X.; Ma, R.; Wang, L. Predicting turning point, duration and attack rate of COVID-19 outbreaks in major Western countries. Chaos Solitons Fractals 2020, 135, 109829. [Google Scholar] [CrossRef] [PubMed]
- Fanelli, D.; Piazza, F. Analysis and forecast of COVID-19 spreading in China, Italy and France. Chaos Solitons Fractals 2020, 134, 109761. [Google Scholar] [CrossRef]
- Saez, M.; Tobias, A.; Varga, D.; Barceló, M.A. Effectiveness of the measures to flatten the epidemic curve of COVID-19. The case of Spain. Sci. Total Environ. 2020, 727, 138761. [Google Scholar] [CrossRef] [PubMed]
- Jiao, J.; Chen, L.; Cai, S. An SEIRS epidemic model with two delays and pulse vaccination. J. Syst. Sci. Complex. 2008, 21, 217–225. [Google Scholar] [CrossRef]
- Li, X.; Chen, J. Existence and Uniqueness of Endemic States for the Age-Structured Seir Epidemic Model. J. Syst. Sci. Complex. 2006, 19, 114–127. [Google Scholar] [CrossRef]
- Zhang, W.; Meng, X.; Dong, Y. Periodic Solution and Ergodic Stationary Distribution of Stochastic SIRI Epidemic Systems with Nonlinear Perturbations. J. Syst. Sci. Complex. 2019, 32, 1104–1124. [Google Scholar] [CrossRef]
- Yang, H.; Wei, H.; Li, X. Global stability of an epidemic model for vector-borne disease. J. Syst. Sci. Complex. 2010, 23, 279–292. [Google Scholar] [CrossRef]
- Jing, W.; Jin, Z.; Zhang, J. Low-Dimensional SIR Epidemic Models with Demographics on Heterogeneous Networks. J. Syst. Sci. Complex. 2018, 31, 1103–1127. [Google Scholar] [CrossRef]
- Lu, N.; Cheng, K.; Qamar, N.; Huang, K.; Johnson, J.A. Weathering COVID-19 storm: Successful control measures of five Asian countries. Am. J. Infect. Control. 2020, 48, 851–852. [Google Scholar] [CrossRef] [PubMed]
- Tang, B.; Wang, X.; Li, Q.; Bragazzi, N.L.; Tang, S.; Xiao, Y.; Wu, J. Estimation of the Transmission Risk of 2019-nCov and Its Implication for Public Health Interventions. J. Clin. Med. 2020, 9, 462. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, X.; Zhao, X.; Sun, Y. The lockdown of Hubei Province Causing Different Transmission Dynamics of the Novel Coronavirus (2019-nCoV) in Wuhan and Beijing. medRxiv 2020. [Google Scholar] [CrossRef] [Green Version]
- Kraemer, M.U.G.; Yang, C.; Gutierrez, B.; Wu, C.; Klein, B.; Pigott, D.M. The effect of human mobility and control measures on the COVID-19 epidemic in China. Science 2020, 368, 493–497. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chinazzi, M.; Davis, J.T.; Ajelli, M.; Gioannini, C.; Litvinova, M.; Merler, S.; Piontti, A.P.Y.; Mu, K.; Rossi, L.; Sun, K.; et al. The effect of travel restrictions on the spread of the 2019 novel coronavirus (COVID-19) outbreak. Science 2020, 368, 395–400. [Google Scholar] [CrossRef] [Green Version]
- Hellewell, J.; Abbott, S.; Gimma, A.; Bosse, N.I.; Jarvis, C.I.; Russell, T.W.; Munday, J.D.; Kucharski, A.J.; Edmunds, W.J.; Sun, F.; et al. Feasibility of controlling COVID-19 outbreaks by isolation of cases and contacts. Lancet Glob. Health 2020, 8, e488–e496. [Google Scholar] [CrossRef] [Green Version]
- Quilty, B.J.; Clifford, S.; Flasche, S.; Eggo, R.M.; CMMID nCoV Working Group 2. Effectiveness of airport screening at detecting travellers infected with novel coronavirus (2019-nCoV). Eurosurveillance 2020, 25, 2000080. [Google Scholar] [CrossRef] [PubMed]
- Lin, Q.; Zhao, S.; Gao, D.; Lou, Y.; Yang, S.; Musa, S.S.; Wang, M.H.; Cai, Y.; Wang, W.; Yang, L.; et al. China with individual reaction and governmental action. Int. J. Infect. Dis. 2020, 93, 211–216. [Google Scholar] [CrossRef] [PubMed]
- Hinjoy, S.; Tsukayama, R.; Chuxnum, T.; Masunglong, W.; Sidet, C.; Kleeblumjeak, P.; Onsai, N.; Iamsirithaworn, S. Self-assessment of the Thai Department of Disease Control’s communication for international response to COVID-19 in the early phase. Int. J. Infect. Dis. 2020, 96, 205–210. [Google Scholar] [CrossRef] [PubMed]
- López, L.; Rodó, X. A Modified SEIR Model to Predict the COVID-19 Outbreak in Spain and Italy: Simulating Control Scenarios and Multi-Scale Epidemics. Results Phys. 2021, 21, 103746. [Google Scholar] [CrossRef] [PubMed]
- Chowdhury, R.; Heng, K.; Shawon, M.S.R.; Goh, G.; Okonofua, D.; Ochoa-Rosales, C.; Gonzalez-Jaramillo, V.; Bhuiya, A.; Reidpath, D.; Prathapan, S. Dynamic interventions to control COVID-19 pandemic: A multivariate prediction modelling study comparing 16 worldwide countries. Eur. J. Epidemiol. 2020, 35, 389–399. [Google Scholar] [CrossRef]
- Benke, C.; Autenrieth, L.K.; Asselmann, E.; Pané-Farré, C.A. Lockdown, quarantine measures, and social distancing: Associations with depression, anxiety and distress at the beginning of the COVID-19 pandemic among adults from Germany. Psychiatry Res. 2020, 293, 113462. [Google Scholar] [CrossRef]
- Maier, B.F.; Brockmann, D. Effective containment explains subexponential growth in recent confirmed COVID-19 cases in China. Science 2020, 368, 742–746. [Google Scholar] [CrossRef] [Green Version]
- Yan, B.; Zhang, X.; Wu, L.; Zhu, H.; Chen, B. Why Do Countries Respond Differently to COVID-19? A Comparative Study of Sweden, China, France, and Japan. Am. Rev. Public Adm. 2020, 50, 762–769. [Google Scholar] [CrossRef]
- Chiu, W.A.; Fischer, R.; Ndeffo-Mbah, M.L. State-level needs for social distancing and contact tracing to contain COVID-19 in the United States. Nat. Hum. Behav. 2020, 4, 1080–1090. [Google Scholar] [CrossRef] [PubMed]
- López, L.; Rodó, X. The end of social confinement and COVID-19 re-emergence risk. Nat. Hum. Behav. 2020, 4, 746–755. [Google Scholar] [CrossRef] [PubMed]
- Kermack, W.O.; Mckendrick, A.G. A Contribution to the Mathematical Theory of Epidemics. Proc. R. Soc. Lond. Ser. A Contain. Pap. A Math. Phys. Character 1927, 115, 700–721. [Google Scholar] [CrossRef] [Green Version]
- Rǎdulescu, A.; Williams, C.; Cavanagh, K. Management strategies in a SEIR-type model of COVID 19 community spread. Sci. Rep. 2020, 10, 21256. [Google Scholar] [CrossRef] [PubMed]
- Guan, W.J.; Ni, Z.Y.; Hu, Y.; Liang, W.H.; Ou, C.Q.; He, J.X.; Liu, L.; Shan, H.; Lei, C.L.; Hui, D.S. Clinical characteristics of 2019 novel coronavirus infection in China. N. Engl. J. Med. 2020, 382, 1708–1720. [Google Scholar] [CrossRef]
- World Health Organization. Getting Your Workplace Ready for COVID-19: How COVID-19 Spreads. 2020. Available online: https://www.who.int/publications/m/item/getting-your-workplace-ready-for-covid-19-how-covid-19-spreads (accessed on 16 September 2021).
- World Health Organization. COVID-19 Strategy Update-COVID-19: Critical Preparedness, Readiness and Response. 2020. Available online: https://www.who.int/publications/m/item/covid-19-strategy-update (accessed on 22 September 2021).
- Gibbs, H.; Liu, Y.; Pearson, C.A.; Jarvis, C.I.; Grundy, C.; Quilty, B.J.; Diamond, C.; Eggo, R.M. Changing travel patterns in China during the early stages of the COVID-19 pandemic. Nat. Commun. 2020, 11, 5012. [Google Scholar] [CrossRef]
- Firth, J.A.; Hellewell, J.; Klepac, P.; Kissler, S.; Kucharski, A.J.; Spurgin, L.G. Using a real-world network to model localized COVID-19 control strategies. Nat. Med. 2020, 26, 1616–1622. [Google Scholar] [CrossRef]
- Della Rossa, F.; Salzano, D.; Di Meglio, A.; De Lellis, F.; Coraggio, M.; Calabrese, C.; Guarino, A.; Cardona-Rivera, R.; De Lellis, P.; Liuzza, D.; et al. A network model of Italy shows that intermittent regional strategies can alleviate the COVID-19 epidemic. Nat. Commun. 2020, 11, 5106. [Google Scholar] [CrossRef]
- Block, P.; Hoffman, M.; Raabe, I.J.; Dowd, J.B.; Rahal, C.; Kashyap, R.; Mills, M.C. Social network-based distancing strategies to flatten the COVID-19 curve in a post-lockdown world. Nat. Hum. Behav. 2020, 4, 588–596. [Google Scholar] [CrossRef]
- Lancichinetti, A.; Fortunato, S.; Radicchi, F. Benchmark graphs for testing community detection algorithms. Phys. Rev. E 2008, 78, 046110. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cacciapaglia, G.; Cot, C.; Sannino, F. Second wave COVID-19 pandemics in Europe: A temporal playbook. Sci. Rep. 2020, 10, 15514. [Google Scholar] [CrossRef] [PubMed]



| Parameter | Meaning | Value |
|---|---|---|
| N | Number of nodes in the created graph | 2000 |
| k | Desired average degree of nodes in the created graph | 15 |
| maxk | Maximum degree of nodes in the created graph | 50 |
| minc | Minimum size of communities in the graph | 40 |
| maxc | Maximum size of communities in the graph | 70 |
| μ | Fraction of intra-regional edges incident to each node | 0.18 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, J.; Du, H.; Wang, Y.; He, X. The Effect of Local and Global Interventions on Epidemic Spreading. Int. J. Environ. Res. Public Health 2021, 18, 12627. https://doi.org/10.3390/ijerph182312627
Fan J, Du H, Wang Y, He X. The Effect of Local and Global Interventions on Epidemic Spreading. International Journal of Environmental Research and Public Health. 2021; 18(23):12627. https://doi.org/10.3390/ijerph182312627
Chicago/Turabian StyleFan, Jiarui, Haifeng Du, Yang Wang, and Xiaochen He. 2021. "The Effect of Local and Global Interventions on Epidemic Spreading" International Journal of Environmental Research and Public Health 18, no. 23: 12627. https://doi.org/10.3390/ijerph182312627
APA StyleFan, J., Du, H., Wang, Y., & He, X. (2021). The Effect of Local and Global Interventions on Epidemic Spreading. International Journal of Environmental Research and Public Health, 18(23), 12627. https://doi.org/10.3390/ijerph182312627







