Integrating Spatial Modelling and Space–Time Pattern Mining Analytics for Vector Disease-Related Health Perspectives: A Case of Dengue Fever in Pakistan
Abstract
1. Introduction
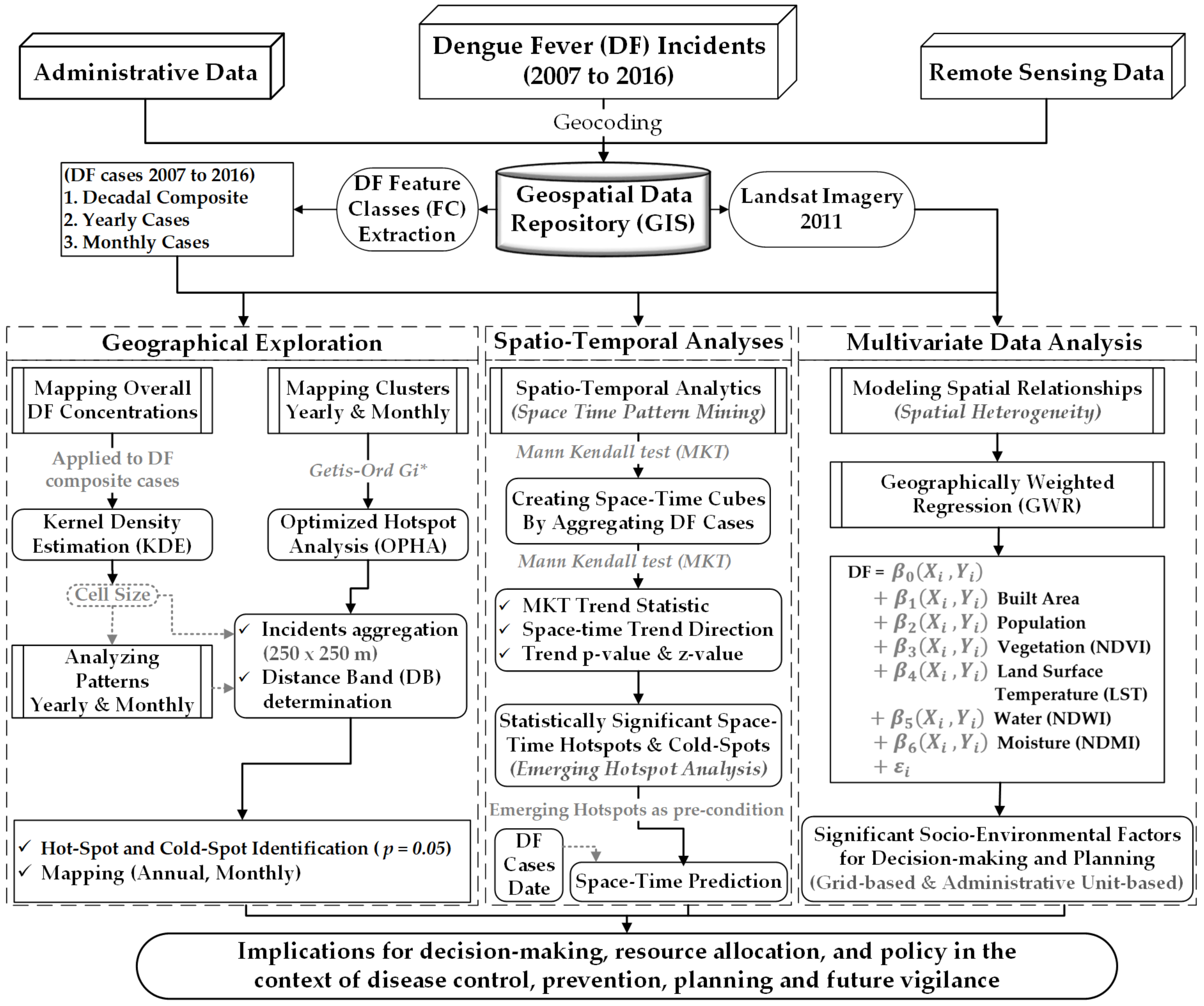
2. Materials and Methods
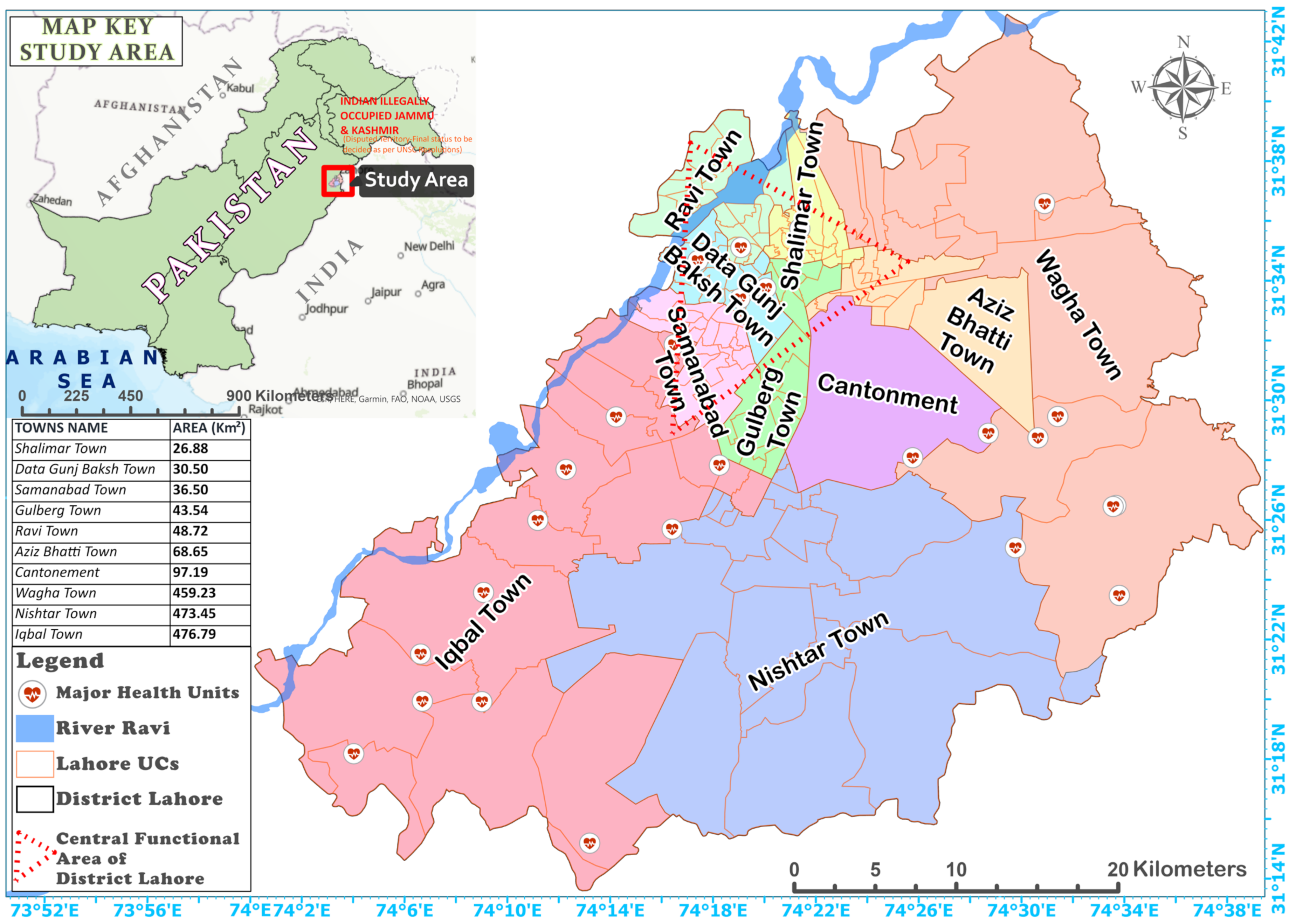
2.1. Study Area
2.2. Data Collection and Geo-Preprocessing
2.3. Spatial Analyses
2.3.1. KDE Analysis
2.3.2. The Optimized Hot Spot Analysis (Yearly and Monthly)
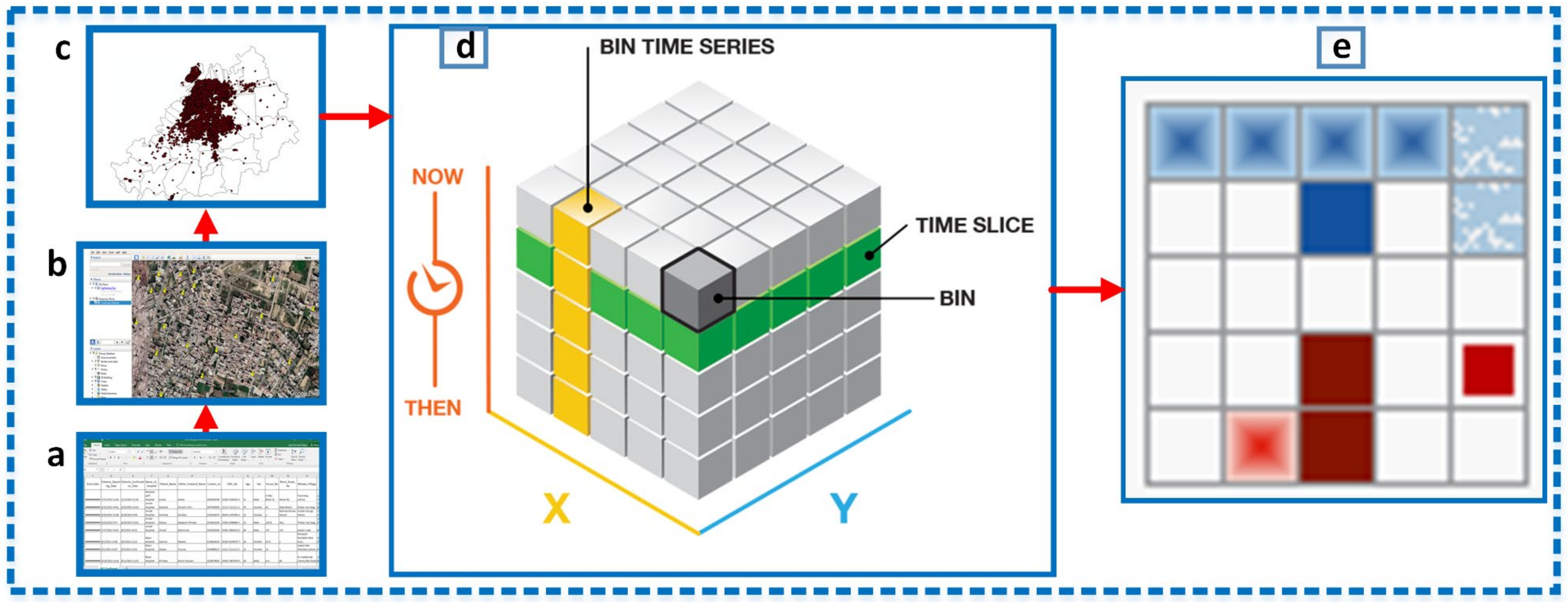
2.4. Space–Time Cube Analysis
- (a)
- First time period bin value < Second time period bin value = +1;
- (b)
- First time period bin value > Second time period bin value = −1;
- (c)
- Both values are same = 0.
Measuring Emerging Hot Spots
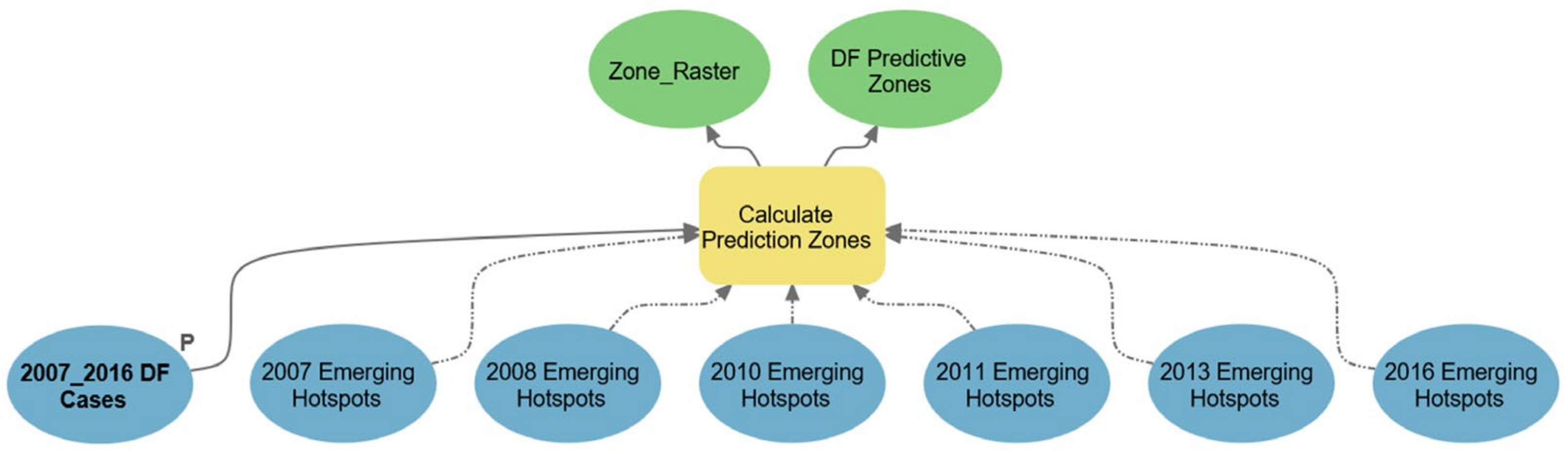
2.5. Modeling the Space–Time Prediction Zones
2.6. Evaluating Different Spatial Socio-Environmental Factors of DF: A Multivariate Analysis
3. Results
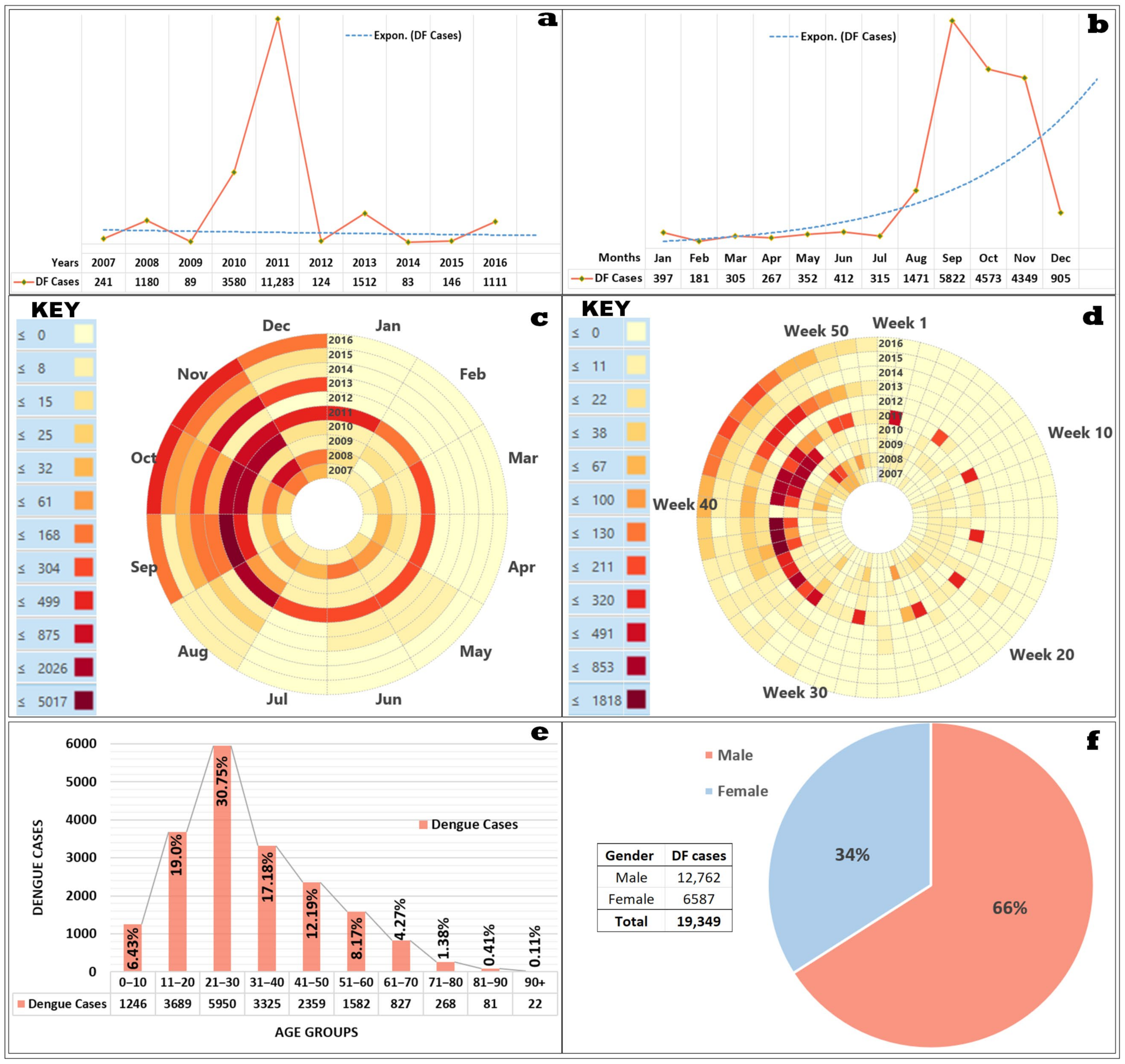
3.1. Exploring DF Frequencies on an Annual and Monthly Basis
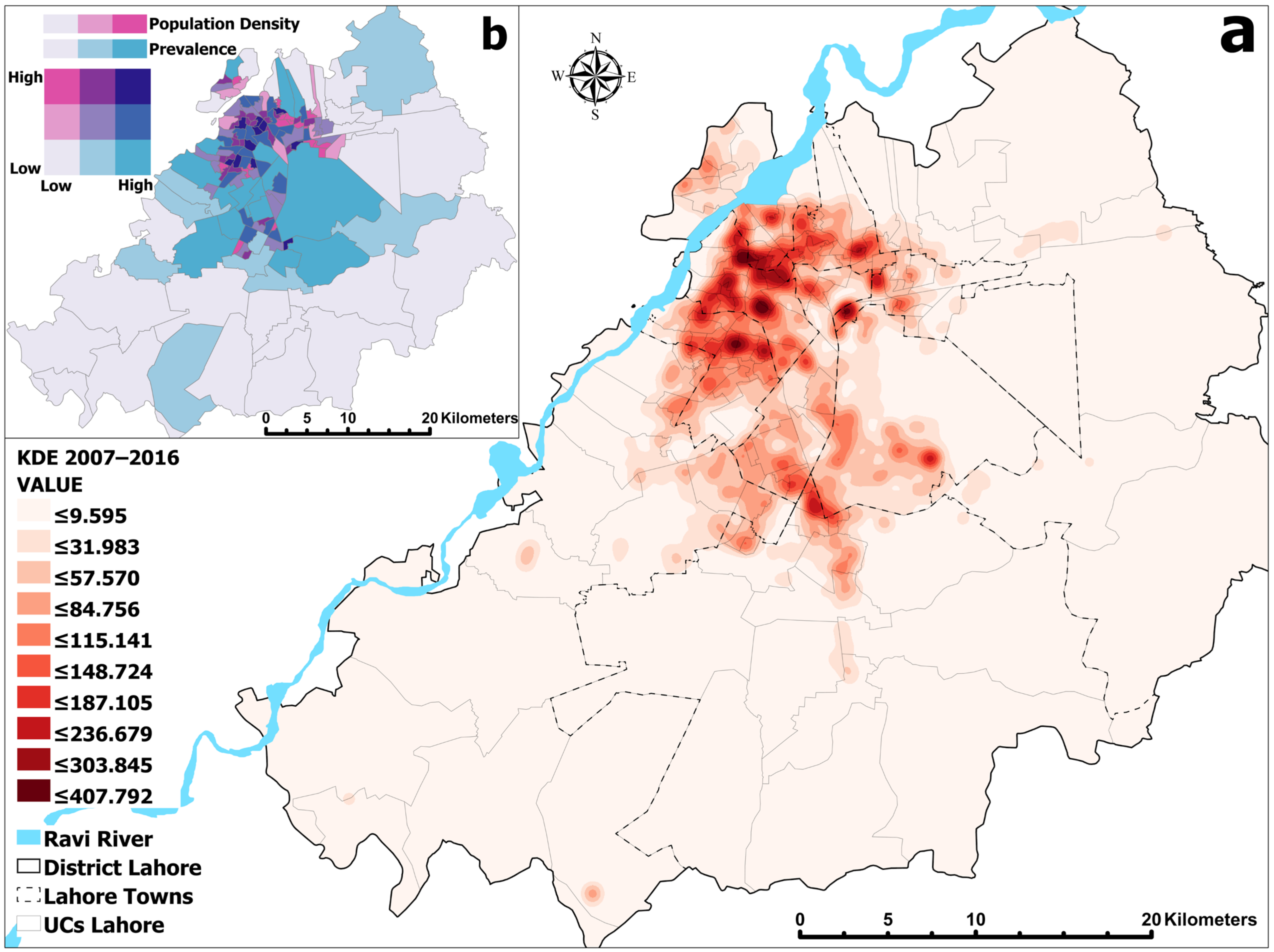
3.2. Spatial Characterization of DF Incidents: Kernel Density Estimation (KDE) Analysis
3.3. Detection of Hot Spots and Cold Spots
3.3.1. Annual Assessment
3.3.2. Monthly Assessment
3.4. Spatial–Temporal Evaluations
3.4.1. Space–Time Cube-Based Mann–Kendall Trend (MKT)
3.4.2. Spatiotemporal Hot Spot Detection: Emerging Hot Spot Analysis
3.4.3. Space–Time Prediction
3.5. Association between Socio-Environmental Factors and DF
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Simmons, C.P.; Farrar, J.; Chau, N.V.V.; Wills, B. Dengue. N. Engl. J. Med. 2012, 366, 1423–1432. [Google Scholar] [CrossRef] [PubMed]
- Moreno-Sanchez, R.; Hayden, M.; Janes, C.; Anderson, G. A web-based multimedia spatial information system to document Aedes aegypti breeding sites and dengue fever risk along the US–Mexico border. Health Place 2006, 12, 715–727. [Google Scholar] [CrossRef]
- DeAntonio, R.; Amaya-Tapia, G.; Ibarra-Nieto, G.; Huerta, G.; Damaso, S.; Guignard, A.; de Boer, M. Incidence of dengue illness in Mexican people aged 6 months to 50 years old: A prospective cohort study conducted in Jalisco. PLoS ONE 2021, 16, e0250253. [Google Scholar] [CrossRef]
- Thiemmeca, S.; Songjang, A.; Punyadee, N.; Kongmanas, K.; Atkinson, J.; Avirutnan, P. Infection of whole blood with dengue virus. Mol. Immunol. 2018, 102, 132–133. [Google Scholar] [CrossRef]
- Mulligan, K.; Elliott, S.; Schuster-Wallace, C. The place of health and the health of place: Dengue fever and urban governance in Putrajaya, Malaysia. Health Place 2012, 18, 613–620. [Google Scholar] [CrossRef] [PubMed]
- Zhu, G.; Xiao, J.; Liu, T.; Zhang, B.; Hao, Y.; Ma, W. Spatiotemporal analysis of the dengue outbreak in Guangdong Province, China. BMC Infect. Dis. 2019, 19, 493. [Google Scholar] [CrossRef] [PubMed]
- Martínez-Bello, D.; López-Quílez, A.; Prieto, A.T. Spatiotemporal modeling of relative risk of dengue disease in Colombia. Stoch. Environ. Res. Risk Assess. 2017, 32, 1587–1601. [Google Scholar] [CrossRef]
- Mustafa, M.; Rasotgi, V.; Jain, S.; Gupta, V. Discovery of fifth serotype of dengue virus (DENV-5): A new public health dilemma in dengue control. Med. J. Armed Forces India 2015, 71, 67–70. [Google Scholar] [CrossRef]
- Desjardins, M.; Casas, I.; Victoria, A.M.; Carbonell, D.; Dávalos, D.; Delmelle, E. Knowledge, attitudes, and practices regarding dengue, chikungunya, and Zika in Cali, Colombia. Health Place 2020, 63, 102339. [Google Scholar] [CrossRef]
- Khormi, H.M.; Kumar, L. Modeling dengue fever risk based on socioeconomic parameters, nationality and age groups: GIS and remote sensing based case study. Sci. Total Environ. 2011, 409, 4713–4719. [Google Scholar] [CrossRef]
- Ahmed, A.; Elduma, A.; Magboul, B.; Higazi, T.; Ali, Y. The First Outbreak of Dengue Fever in Greater Darfur, Western Sudan. Trop. Med. Infect. Dis. 2019, 4, 43. [Google Scholar] [CrossRef]
- Sun, W.; Xue, L.; Xie, X. Spatial-Temporal distribution of dengue and climate characteristics for two clusters in Sri Lanka from 2012 to 2016. Sci. Rep. 2017, 7, 12884. [Google Scholar] [CrossRef]
- WHO. Global Strategy for Dengue Prevention and Control 2012–2020; World Health Organization: Geneva, Switzerland, 2012; pp. 1–49. [Google Scholar]
- Charette, M.; Berrang-Ford, L.; Llanos-Cuentas, E.A.; Cárcamo, C.; Kulkarni, M. What caused the 2012 dengue outbreak in Pucallpa, Peru? A socio-ecological autopsy. Soc. Sci. Med. 2017, 174, 122–132. [Google Scholar] [CrossRef]
- WHO. Dengue Vaccine: WHO Position Paper–September 2018. Wkly. Epidemiol. Rec. 2018, 93, 457–476. [Google Scholar]
- WHO. Dengue and Severe Dengue, 2021. 2021. Available online: https://www.who.int/en/news-room/fact-sheets/detail/dengue-and-severe-dengue (accessed on 14 July 2021).
- Tong, M.X.; Hansen, A.; Hanson-Easey, S.; Xiang, J.; Cameron, S.; Liu, Q.; Liu, X.; Sun, Y.; Weinstein, P.; Han, G.-S.; et al. Dengue control in the context of climate change: Views from health professionals in different geographic regions of China. J. Infect. Public Health 2018, 12, 388–394. [Google Scholar] [CrossRef]
- Ahmed, T.; Hyder, M.Z.; Liaqat, I.; Scholz, M. Climatic Conditions: Conventional and Nanotechnology-Based Methods for the Control of Mosquito Vectors Causing Human Health Issues. Int. J. Environ. Res. Public Health 2019, 16, 3165. [Google Scholar] [CrossRef]
- Herbuela, V.R.D.M.; de Guzman, F.S.; Sobrepeña, G.D.; Claudio, A.B.F.; Tomas, A.C.V.; Reyes, A.-D.; Carmina, M.; Regalado, R.A.; Teodoro, M.M.; Watanabe, K. Depressive and Anxiety Symptoms among Pediatric In-Patients with Dengue Fever: A Case-Control Study. Int. J. Environ. Res. Public Health 2020, 17, 99. [Google Scholar] [CrossRef] [PubMed]
- Naeem, Z.; Sohail, N.; Iftikhar, S. Chapter 7—Bioterrorism, an Emerging Threat. In Trends of Environmental Forensics in Pakistan; Iftikhar, S., Ed.; Academic Press: Cambridge, MA, USA, 2019; pp. 111–124. [Google Scholar]
- Imran, M.; Hamid, Y.; Mazher, A.; Ahmad, S.R. Geo-Spatially modelling dengue epidemics in urban cities: A case study of Lahore, Pakistan. Geocarto Int. 2019, 36, 197–211. [Google Scholar] [CrossRef]
- Mukhtar, M.U.; Mukhtar, M.; Iqbal, N. Dengue fever is an emerging public health concern in the city of Multan, Pakistan: Its seroprevalence and associated risk factors. Microbiol. Immunol. 2018, 62, 729–731. [Google Scholar] [CrossRef] [PubMed]
- Malik, S.M.; Bhutta, Z.A. Reform of primary health care in Pakistan. Lancet 2018, 392, 1375–1377. [Google Scholar] [CrossRef]
- WHO. Outbreak Update—Dengue in Pakistan, 1 December 2019. Available online: http://www.emro.who.int/pandemic-epidemic-diseases/dengue/outbreak-update-dengue-in-pakistan-1-december-2019.html (accessed on 7 July 2020).
- Jahan, F. Dengue Fever (DF) in Pakistan. Asia Pac. Fam. Med. 2011, 10, 1. [Google Scholar] [CrossRef] [PubMed]
- Ali, J. Dengue fever in Pakistan: Challenges, priorities and measures. J. Coast. Life Med. 2015, 3, 834–837. [Google Scholar] [CrossRef]
- Li, H.; Alvi, A.; Fatima, S.; Zafar, F.; Naveed, S.; Khan, K.; Ali, U.; Tariq, A.; Naqvi, G.; Mallick, N. Dengue Fever in Pakistan, Episodes of Epidemic to Endemic: Treatment Challenges, Prevention and Current Facts. J. Bioequiv. Bioavailab. 2017, 09, 473–476. [Google Scholar] [CrossRef]
- Naqvi, S.A.A.; Jan, B.; Shaikh, S.; Kazmi, S.J.H.; Waseem, L.A.; Nasar-U-Minallah, M.; Abbas, N. Changing Climatic Factors Favor Dengue Transmission in Lahore, Pakistan. Environments 2019, 6, 71. [Google Scholar] [CrossRef]
- Naqvi, S.A.A. Measuring the Risk of Dengue Prevalence in Lahore Through Geo-Spatial Techniques; University of Karachi: Karachi, Pakistan, 2015. [Google Scholar]
- Rana, M.S.; Ikram, A.; Alam, M.M.; Salman, M. Novel coronavirus outbreak in Pakistan: Beware of dengue. J. Formos. Med. Assoc. 2020, 120, 765–766. [Google Scholar] [CrossRef]
- Miah, A.; Husna, A. Coinfection, coepidemics of COVID-19, and dengue in dengue-endemic countries: A serious health concern. J. Med. Virol. 2020, 93, 161–162. [Google Scholar] [CrossRef] [PubMed]
- Moore, D.A.; Carpenter, T.E. Spatial Analytical Methods and Geographic Information Systems: Use in Health Research and Epidemiology. Epidemiol. Rev. 1999, 21, 143–161. [Google Scholar] [CrossRef]
- Fuentes-Vallejo, M. Space and space-time distributions of dengue in a hyper-endemic urban space: The case of Girardot, Colombia. BMC Infect. Dis. 2017, 17, 512. [Google Scholar] [CrossRef] [PubMed]
- Nara, A. 1.20—Space-Time GIS and Its Evolution. In Comprehensive Geographic Information Systems; Huang, B., Ed.; Elsevier: Oxford, UK, 2018; pp. 287–302. [Google Scholar]
- Lippi, C.A.; Stewart-Ibarra, A.M.; Romero, M.; Lowe, R.; Mahon, R.; Van Meerbeeck, C.J.; Rollock, L.; Hilaire, M.G.-S.; Trotman, A.R.; Holligan, D.; et al. Spatiotemporal Tools for Emerging and Endemic Disease Hotspots in Small Areas: An Analysis of Dengue and Chikungunya in Barbados, 2013–2016. Am. J. Trop. Med. Hyg. 2020, 103, 149–156. [Google Scholar] [CrossRef] [PubMed]
- Tsheten, T.; Clements, A.C.; Gray, D.J.; Wangchuk, S.; Wangdi, K. Spatial and temporal patterns of dengue incidence in Bhutan: A Bayesian analysis. Emerg. Microbes Infect. 2020, 9, 1360–1371. [Google Scholar] [CrossRef]
- Huang, X.; Yakob, L.; Devine, G.; Frentiu, F.D.; Fu, S.-Y.; Hu, W. Dynamic spatiotemporal trends of imported dengue fever in Australia. Sci. Rep. 2016, 6, 30360. [Google Scholar] [CrossRef]
- Alkhamis, M.A.; Al Youha, S.; Khajah, M.M.; Ben Haider, N.; Alhardan, S.; Nabeel, A.; Al Mazeedi, S.; Al-Sabah, S.K. Spatiotemporal dynamics of the COVID-19 pandemic in the State of Kuwait. Int. J. Infect. Dis. 2020, 98, 153–160. [Google Scholar] [CrossRef]
- Little, E.A.; Anderson, J.F.; Stafford, K.C.; Eisen, L.; Eisen, R.J.; Molaei, G. Predicting spatiotemporal patterns of Lyme disease incidence from passively collected surveillance data for Borrelia burgdorferi sensu lato-infected Ixodes scapularis ticks. Ticks Tick Borne Dis. 2019, 10, 970–980. [Google Scholar] [CrossRef] [PubMed]
- Pilot, E.; Murthy, G.; Nittas, V. Understanding India’s urban dengue surveillance: A qualitative policy analysis of Hyderabad district. Glob. Public Health 2020, 15, 1702–1717. [Google Scholar] [CrossRef]
- Kummitha, R.K.R. Smart technologies for fighting pandemics: The techno- and human- driven approaches in controlling the virus transmission. Gov. Inf. Q. 2020, 37, 101481. [Google Scholar] [CrossRef] [PubMed]
- Bhagavan, S.M. Chapter 4—Global health-care perspective of Dengue viral disease. In Dengue Virus Disease; Qureshi, A.I., Saeed, O., Eds.; Academic Press: Cambridge, MA, USA, 2020; pp. 37–56. [Google Scholar]
- Rosenkrantz, L.; Schuurman, N.; Bell, N.; Amram, O. The need for GIScience in mapping COVID-19. Health Place 2020, 67, 102389. [Google Scholar] [CrossRef] [PubMed]
- Rezaei, M.; Nouri, A.A.; Park, G.S.; Kim, D.H. Application of Geographic Information System in Monitoring and Detecting the COVID-19 Outbreak. Iran. J. Public Health 2020, 49, 114–116. [Google Scholar] [CrossRef] [PubMed]
- Franch-Pardo, I.; Napoletano, B.M.; Rosete-Verges, F.; Billa, L. Spatial analysis and GIS in the study of COVID-19. A review. Sci. Total. Environ. 2020, 739, 140033. [Google Scholar] [CrossRef] [PubMed]
- Shekhar, S.; Li, Y.; Ali, R.Y.; Eftelioglu, E.; Tang, X.; Jiang, Z. 1.19—Spatial and Spatiotemporal Data Mining. In Comprehensive Geographic Information Systems; Huang, B., Ed.; Elsevier: Oxford, UK, 2018; pp. 264–286. [Google Scholar]
- Zambrano, L.I.; Sierra, M.; Lara, B.; Rodríguez-Núñez, I.; Medina, M.T.; Lozada-Riascos, C.O.; Rodríguez-Morales, A.J. Estimating and mapping the incidence of dengue and chikungunya in Honduras during 2015 using Geographic Information Systems (GIS). J. Infect. Public Health 2017, 10, 446–456. [Google Scholar] [CrossRef]
- Wilson, B.; Wilson, N.; Martin, S. Using GIS to Advance Social Economics Research: Geocoding, Aggregation, and Spatial Thinking. Forum Soc. Econ. 2019, 50, 480–504. [Google Scholar] [CrossRef]
- Gilad, O. Spatial Distribution Models. In Encyclopedia of Ecology; Jørgensen, S.E., Fath, B.D., Eds.; Academic Press: Oxford, UK, 2008; pp. 3311–3314. [Google Scholar]
- Pettit, C.J.; Tanton, R.; Hunter, J. An online platform for conducting spatial-statistical analyses of national census data across Australia. Comput. Environ. Urban Syst. 2017, 63, 68–79. [Google Scholar] [CrossRef]
- Keenan, P.B.; Jankowski, P. Spatial Decision Support Systems: Three decades on. Decis. Support Syst. 2018, 116, 64–76. [Google Scholar] [CrossRef]
- Zambrano, L.I.; Rodriguez, E.; Espinoza-Salvado, I.A.; Barahona, I.C.F.; de Oliveira, T.L.; da Veiga, G.L.; da Silva, J.C.; Valle-Reconco, J.A.; Rodríguez-Morales, A.J. Spatial distribution of dengue in Honduras during 2016–2019 using a geographic information systems (GIS)–Dengue epidemic implications for public health and travel medicine. Travel Med. Infect. Dis. 2019, 32, 101517. [Google Scholar] [CrossRef] [PubMed]
- Liu, K.; Sun, J.; Liu, X.; Li, R.; Wang, Y.; Lu, L.; Wu, H.; Gao, Y.; Xu, L.; Liu, Q. Spatiotemporal patterns and determinants of dengue at county level in China from 2005–2017. Int. J. Infect. Dis. 2018, 77, 96–104. [Google Scholar] [CrossRef] [PubMed]
- Delmelle, E.; Hagenlocher, M.; Kienberger, S.; Casas, I. A spatial model of socioeconomic and environmental determinants of dengue fever in Cali, Colombia. Acta Trop. 2016, 164, 169–176. [Google Scholar] [CrossRef]
- Cui, Z.; Lin, D.; Chongsuvivatwong, V.; Zhao, J.; Lin, M.; Ou, J.; Zhao, J. Spatiotemporal patterns and ecological factors of tuberculosis notification: A spatial panel data analysis in Guangxi, China. PLoS ONE 2019, 14, e0212051. [Google Scholar] [CrossRef] [PubMed]
- Akter, R.; Naish, S.; Gatton, M.; Bambrick, H.; Hu, W.; Tong, S. Spatial and temporal analysis of dengue infections in Queensland, Australia: Recent trend and perspectives. PLoS ONE 2019, 14, e0220134. [Google Scholar] [CrossRef] [PubMed]
- Astuti, E.P.; Dhewantara, P.W.; Prasetyowati, H.; Ipa, M.; Herawati, C.; Hendrayana, K. Paediatric dengue infection in Cirebon, Indonesia: A temporal and spatial analysis of notified dengue incidence to inform surveillance. Parasites Vectors 2019, 12, 186. [Google Scholar] [CrossRef] [PubMed]
- Churakov, M.; Villabona-Arenas, C.J.; Kraemer, M.U.G.; Salje, H.; Cauchemez, S. Spatio-Temporal dynamics of dengue in Brazil: Seasonal travelling waves and determinants of regional synchrony. PLoS Negl. Trop. Dis. 2019, 13, e0007012. [Google Scholar] [CrossRef] [PubMed]
- Husnina, Z.; Clements, A.C.A.; Wangdi, K. Forest cover and climate as potential drivers for dengue fever in Sumatra and Kalimantan 2006-2016: A spatiotemporal analysis. Trop. Med. Int. Health 2019, 24, 888–898. [Google Scholar] [CrossRef] [PubMed]
- López-Quílez, A. Spatio-Temporal Analysis of Infectious Diseases. Int. J. Environ. Res. Public Health 2019, 16, 669. [Google Scholar] [CrossRef]
- Ogashawara, I.; Li, L.; Moreno-Madriñán, M.J. Spatial-Temporal Assessment of Environmental Factors Related to Dengue Outbreaks in São Paulo, Brazil. GeoHealth 2019, 3, 202–217. [Google Scholar] [CrossRef] [PubMed]
- Sanna, M.; Wu, J.; Zhu, Y.; Yang, Z.; Lu, J.; Hsieh, Y.-H. Spatial and Temporal Characteristics of 2014 Dengue Outbreak in Guangdong, China. Sci. Rep. 2018, 8, 2344. [Google Scholar] [CrossRef] [PubMed]
- Yajid, M.Z.M.; Dom, N.C.; Camalxaman, S.N.; Nasir, R.A. Spatial-Temporal analysis for identification of dengue risk area in Melaka Tengah district. Geocarto Int. 2019, 35, 1–10. [Google Scholar] [CrossRef]
- Wei, K.; Li, Y. Global evolutionary history and spatio-temporal dynamics of dengue virus type 2. Sci. Rep. 2017, 7, 45505. [Google Scholar] [CrossRef]
- Telle, O.; Vaguet, A.; Yadav, N.K.; Lefebvre, B.; Daudé, E.; Paul, R.; Cebeillac, A.; Nagpal, B.N. The Spread of Dengue in an Endemic Urban Milieu–The Case of Delhi, India. PLoS ONE 2016, 11, e0146539. [Google Scholar] [CrossRef]
- Acharya, B.K.; Cao, C.; Lakes, T.; Chen, W.; Naeem, S. Spatiotemporal analysis of dengue fever in Nepal from 2010 to 2014. BMC Public Health 2016, 16, 849. [Google Scholar] [CrossRef]
- Sharmin, S.; Glass, K.; Viennet, E.; Harley, D. Geostatistical mapping of the seasonal spread of under-reported dengue cases in Bangladesh. PLoS Negl. Trop. Dis. 2018, 12, e0006947. [Google Scholar] [CrossRef]
- Atique, S.; Chan, T.-C.; Chen, C.-C.; Hsu, C.-Y.; Iqtidar, S.; Louis, V.R.; Shabbir, S.A.; Chuang, T.-W. Investigating spatio-temporal distribution and diffusion patterns of the dengue outbreak in Swat, Pakistan. J. Infect. Public Health 2018, 11, 550–557. [Google Scholar] [CrossRef]
- Bhunia, G.S.; Kesari, S.; Chatterjee, N.; Kumar, V.; Das, P. Spatial and temporal variation and hotspot detection of kala-azar disease in Vaishali district (Bihar), India. BMC Infect. Dis. 2013, 13, 64. [Google Scholar] [CrossRef]
- Khalid, B.; Ghaffar, A. Environmental risk factors and hotspot analysis of dengue distribution in Pakistan. Int. J. Biometeorol. 2015, 59, 1721–1746. [Google Scholar] [CrossRef] [PubMed]
- Khan, J.; Khan, I.; Ghaffar, A.; Khalid, B. Epidemiological trends and risk factors associated with dengue disease in Pakistan (1980–2014): A systematic literature search and analysis. BMC Public Health 2018, 18, 745. [Google Scholar] [CrossRef] [PubMed]
- Khalique, F.; Shaheen, R.; Khan, S.A. Spatio-Temporal Investigations of Dengue Fever in Pakistan Through an HL7 Based Public Health Framework for Hotspot Analysis. IEEE Access 2020, 8, 199980–199994. [Google Scholar] [CrossRef]
- Hafeez, S.; Amin, M.; Munir, B.A. Spatial mapping of temporal risk to improve prevention measures: A case study of dengue epidemic in Lahore. Spat. Spatio Temporal Epidemiol. 2017, 21, 77–85. [Google Scholar] [CrossRef]
- Jossart, J.; Theuerkauf, S.J.; Wickliffe, L.C.; Morris, J.A., Jr. Applications of Spatial Autocorrelation Analyses for Marine Aquaculture Siting. Front. Mar. Sci. 2020, 6, 806. [Google Scholar] [CrossRef]
- Ali, Y.; Aslam, Z.; Dar, H.S.; Mumtaz, U. A multi-criteria decision analysis of solid waste treatment options in Pakistan: Lahore City—A case in point. Environ. Syst. Decis. 2018, 38, 528–543. [Google Scholar] [CrossRef]
- Mahwish, S.; Zaheer-ud-Din, K.; Muhammad, A. Some phytosociological studies of chasmophytes and ediphytes of Lahore city. Pak. J. Bot. 2012, 44, 165–169. [Google Scholar]
- GOP. Table-3 Area, Population by Sex, Sex Ratio, Population Density, Urban Proportion Household Size and Annual Growth Rate of Punjab; Pakistan Bureau of Statistics: Islamabad, Pakistan, 2017. Available online: https://www.pbs.gov.pk/sites/default/files//population_census/punjab_tehsil.pdf (accessed on 12 November 2021).
- Qureshi, J.; Mahmood, S.A.; Almas, A.S.; Rafique, H.M.; Irshad, R. Monitoring Spatiotemporal and Micro-Level Climatic Variations in Lahore and Subrubs Using Satellite Imagery and Multi-Source Data. J. Fac. Eng. Technol. 2012, 19, 51–65. [Google Scholar]
- Sarfraz, M.S.; Tripathi, N.K.; Faruque, F.S.; Bajwa, U.I.; Kitamoto, A.; Souris, M. Mapping urban and peri-urban breeding habitats of Aedes mosquitoes using a fuzzy analytical hierarchical process based on climatic and physical parameters. Geospat. Health 2014, 8, 685. [Google Scholar] [CrossRef] [PubMed]
- Ali, M.; Tariq, S.; Mahmood, K.; Daud, A.; Batool, A.; Haq, Z.U. A study of aerosol properties over Lahore (Pakistan) by using AERONET data. Asia Pac. J. Atmos. Sci. 2013, 50, 153–162. [Google Scholar] [CrossRef]
- Jadoon, A.; Batool, S.A.; Chaudhry, M.N. Assessment of factors affecting household solid waste generation and its composition in Gulberg Town, Lahore, Pakistan. J. Mater. Cycles Waste Manag. 2013, 16, 73–81. [Google Scholar] [CrossRef]
- Ahmad, S.; Khan, M.; Khan, M. Epidemilogy and seasonal abundance of canine babesiosis in Lahore, Pakistan. J. Anim. Plant Sci. 2011, 21, 351–353. [Google Scholar]
- Haider, Z.; Ahmad, F.Z.; Mahmood, A.; Waseem, T.; Shafiq, I.; Raza, T.; Qazi, J.; Siddique, N.; Humayun, M.A. Dengue fever in Pakistan: A paradigm shift; changing epidemiology and clinical patterns. Perspect Public Health 2015, 135, 294–298. [Google Scholar] [CrossRef]
- Fatima, Z.; Idrees, M.; Bajwa, M.A.; Tahir, Z.; Ullah, O.; Zia, M.Q.; Hussain, A.; Akram, M.; Khubaib, B.; Afzal, S.; et al. Serotype and genotype analysis of dengue virus by sequencing followed by phylogenetic analysis using samples from three mini outbreaks-2007-2009 in Pakistan. BMC Microbiol. 2011, 11, 200. [Google Scholar] [CrossRef] [PubMed]
- ESRI. Kernel Density (Spatial Analyst); Environmental Systems Research Institute: Redlands, CA, USA, 2019; Available online: https://pro.arcgis.com/en/pro-app/tool-reference/spatial-analyst/kernel-density.htm (accessed on 8 July 2019).
- Anderson, T.K. Kernel density estimation and K-means clustering to profile road accident hotspots. Accid. Anal. Prev. 2009, 41, 359–364. [Google Scholar] [CrossRef] [PubMed]
- Xie, Z.; Yan, J. Kernel Density Estimation of traffic accidents in a network space. Comput. Environ. Urban Syst. 2008, 32, 396–406. [Google Scholar] [CrossRef]
- Kang, Y.; Cho, N.; Son, S. Spatiotemporal characteristics of elderly population’s traffic accidents in Seoul using space-time cube and space-time kernel density estimation. PLoS ONE 2018, 13, e0196845. [Google Scholar] [CrossRef]
- ESRI. Bivariate Colors; Environmental Systems Research Institute: Redlands, CA, USA, 2020; Available online: https://pro.arcgis.com/en/pro-app/2.8/help/mapping/layer-properties/bivariate-colors.htm (accessed on 8 June 2020).
- Bonita, R.; Beaglehole, R.; Kjellström, T. Basic Epidemiology, 2nd ed.; World Health Organization (WHO): Geneva, Switzerland, 2006. [Google Scholar]
- Whiteman, A.; Desjardins, M.R.; Eskildsen, G.A.; Loaiza, J.R. Detecting space-time clusters of dengue fever in Panama after adjusting for vector surveillance data. PLoS Negl. Trop. Dis. 2019, 13, e0007266. [Google Scholar] [CrossRef] [PubMed]
- Su, M.; Lin, M.-C.; Wen, T. Spatial Mapping and Environmental Risk Identification. In Encyclopedia of Environmental Health; Nriagu, J.O., Ed.; Elsevier: Burlington, NJ, USA, 2011; pp. 228–235. [Google Scholar]
- Johnston, D.I.; Viray, M.A.; Ushiroda, J.M.; He, H.; Whelen, A.C.; Sciulli, R.H.; Kunimoto, G.Y.; Park, S.Y. Investigation and Response to an Outbreak of Dengue: Island of Hawaii, 2015–2016. Public Health Rep. 2020, 135, 230–237. [Google Scholar] [CrossRef] [PubMed]
- Seidahmed, O.M.E.; Lu, D.; Chong, C.-S.; Deng, L.; Eltahir, E.A.B. Patterns of Urban Housing Shape Dengue Distribution in Singapore at Neighborhood and Country Scales. GeoHealth 2018, 2, 54–67. [Google Scholar] [CrossRef] [PubMed]
- Bisanzio, D.; Dzul-Manzanilla, F.; Gomez-Dantes, H.; Pavia-Ruz, N.; Hladish, T.J.; Lenhart, A.; Palacio-Vargas, J.; Roldan, J.F.G.; Morales, F.C.; Sanchez-Tejeda, G.; et al. Spatio-Temporal coherence of dengue, chikungunya and Zika outbreaks in Merida, Mexico. PLoS Negl. Trop. Dis. 2018, 12, e0006298. [Google Scholar] [CrossRef]
- MacCormack-Gelles, B.; Neto, A.S.L.; Sousa, G.S.; Nascimento, O.J.D.; Castro, M.C. Evaluation of the usefulness of Aedes aegypti rapid larval surveys to anticipate seasonal dengue transmission between 2012–2015 in Fortaleza, Brazil. Acta Trop. 2020, 205, 105391. [Google Scholar] [CrossRef]
- ESRI. How Hot Spot Analysis (Getis-Ord Gi*) Works; Environmental Systems Research Institute: Redlands, CA, USA, 2020; Available online: https://desktop.arcgis.com/en/arcmap/latest/tools/spatial-statistics-toolbox/h-how-hot-spot-analysis-getis-ord-gi-spatial-stati.htm (accessed on 12 June 2020).
- Sadler, R.C.; Pizarro, J.; Turchan, B.; Gasteyer, S.P.; McGarrell, E.F. Exploring the spatial-temporal relationships between a community greening program and neighborhood rates of crime. Appl. Geogr. 2017, 83, 13–26. [Google Scholar] [CrossRef]
- Li, Y.; Abdel-Aty, M.; Yuan, J.; Cheng, Z.; Lu, J. Analyzing traffic violation behavior at urban intersections: A spatio-temporal kernel density estimation approach using automated enforcement system data. Accid. Anal. Prev. 2020, 141, 105509. [Google Scholar] [CrossRef]
- ESRI. How Creating a Space Time Cube Works; Environmental Systems Research Institute: Redlands, CA, USA, 2020; Available online: https://pro.arcgis.com/en/pro-app/2.8/tool-reference/space-time-pattern-mining/learnmorecreatecube.htm (accessed on 14 June 2020).
- Kendall, M.G. Rank Correlation Methods; Griffin: Oxford, UK, 1948. [Google Scholar]
- Mann, H.B. Nonparametric Tests Against Trend. Econometrica 1945, 13, 245. [Google Scholar] [CrossRef]
- Mendez-Lazaro, P.; Muller-Karger, F.E.; Otis, D.; McCarthy, M.J.; Peña-Orellana, M. Assessing Climate Variability Effects on Dengue Incidence in San Juan, Puerto Rico. Int. J. Environ. Res. Public Health 2014, 11, 9409–9428. [Google Scholar] [CrossRef] [PubMed]
- De Oliveira-Júnior, J.F.; Gois, G.; da Silva, E.B.; Teodoro, P.E.; Johann, J.A.; Junior, C.A.S. Non-Parametric tests and multivariate analysis applied to reported dengue cases in Brazil. Environ. Monit. Assess. 2019, 191, 473. [Google Scholar] [CrossRef]
- De Azevedo, T.S.; Lorenz, C.; Chiaravalloti-Neto, F. Spatiotemporal evolution of dengue outbreaks in Brazil. Trans. R. Soc. Trop. Med. Hyg. 2020, 114, 593–602. [Google Scholar] [CrossRef]
- Shimazaki, H.; Shinomoto, S. A Method for Selecting the Bin Size of a Time Histogram. Neural Comput. 2007, 19, 1503–1527. [Google Scholar] [CrossRef] [PubMed]
- Terrell, G.R.; Scott, D.W. Oversmoothed Nonparametric Density Estimates. J. Am. Stat. Assoc. 1985, 80, 209–214. [Google Scholar] [CrossRef]
- ESRI. Create Space Time Cube By Aggregating Points; Environmental Systems Research Institute: Redlands, CA, USA, 2020; Available online: https://pro.arcgis.com/en/pro-app/2.8/tool-reference/space-time-pattern-mining/create-space-time-cube.htm (accessed on 15 June 2020).
- Piovezan, R.; Visockas, A.; De Azevedo, T.S.; Von Zuben, C.J.; Sallum, M.A.M. Spatial-Temporal distribution of Aedes (Stegomyia) aegypti and locations of recycling units in southeastern Brazil. Parasites Vectors 2019, 12, 541. [Google Scholar] [CrossRef]
- Pohlert, T. Non-Parametric Trend Tests and Change-Point Detection; CRAN: Boston, MA, USA, 2018; Volume 4. [Google Scholar]
- Ullah, S.; You, Q.; Ullah, W.; Ali, A. Observed changes in precipitation in China-Pakistan economic corridor during 1980–2016. Atmos. Res. 2018, 210, 1–14. [Google Scholar] [CrossRef]
- ESRI. How Emerging Hot Spot Analysis Works; Environmental Systems Research Institute: Redlands, CA, USA, 2020; Available online: https://pro.arcgis.com/en/pro-app/2.8/tool-reference/space-time-pattern-mining/learnmoreemerging.htm (accessed on 16 June 2020).
- Kwan, M.-P.; Neutens, T. Space-Time Research in GIScience. Int. J. Geogr. Inf. Sci. 2014, 28, 851–854. [Google Scholar] [CrossRef]
- Mo, C.; Tan, D.; Mai, T.; Bei, C.; Qin, J.; Pang, W.; Zhang, Z. An analysis of spatiotemporal pattern for COIVD-19 in China based on space-time cube. J. Med. Virol. 2020, 92, 1587–1595. [Google Scholar] [CrossRef] [PubMed]
- Rahman, M.; Crawford, T.; Schmidlin, T.W. Spatio-Temporal analysis of road traffic accident fatality in Bangladesh integrating newspaper accounts and gridded population data. GeoJournal 2017, 83, 645–661. [Google Scholar] [CrossRef]
- ESRI. Calculate Prediction Zones. In ArcGIS Solutions for Local Government: Crime Analysis; Environmental Systems Research Institute: Redlands, CA, USA, 2020; Available online: https://solutions.arcgis.com/local-government/help/crime-analysis/tools/calculate-prediction-zones/ (accessed on 17 June 2020).
- Yang, K.; Lejeune, J.; Alsdorf, D.; Lü, B.; Shum, C.K.; Liang, S. Global Distribution of Outbreaks of Water-Associated Infectious Diseases. PLoS Negl. Trop. Dis. 2012, 6, e1483. [Google Scholar] [CrossRef]
- Barreto, M.L.; Teixeira, M.G.; Bastos, F.; Ximenes, R.A.; Barata, R.B.; Rodrigues, L.C. Successes and failures in the control of infectious diseases in Brazil: Social and environmental context, policies, interventions, and research needs. Lancet 2011, 377, 1877–1889. [Google Scholar] [CrossRef]
- Li, C.; Wu, X.; Wang, X.; Yin, J.; Zheng, A.; Yang, X. Ecological environment and socioeconomic factors drive long-term transmission and extreme outbreak of dengue fever in epidemic region of China. J. Clean. Prod. 2020, 279, 123870. [Google Scholar] [CrossRef]
- Chen, T.-H.K.; Chen, V.Y.-J.; Wen, T.-H. Revisiting the role of rainfall variability and its interactive effects with the built environment in urban dengue outbreaks. Appl. Geogr. 2018, 101, 14–22. [Google Scholar] [CrossRef]
- Nishijima, M.; Rocha, F.F. An economic investigation of the dengue incidence as a result of a tailings dam accident in Brazil. J. Environ. Manag. 2019, 253, 109748. [Google Scholar] [CrossRef]
- Fotheringham, A.S.; Charlton, M.E.; Brunsdon, C. Geographically Weighted Regression: A Natural Evolution of the Expansion Method for Spatial Data Analysis. Environ. Plan. A Econ. Space 1998, 30, 1905–1927. [Google Scholar] [CrossRef]
- Ren, H.; Wu, W.; Li, T.; Yang, Z. Urban villages as transfer stations for dengue fever epidemic: A case study in the Guangzhou, China. PLoS Negl. Trop. Dis. 2019, 13, e0007350. [Google Scholar] [CrossRef] [PubMed]
- Lee, K.H.; Heo, J.; Jayaraman, R.; Dawson, S. Proximity to parks and natural areas as an environmental determinant to spatial disparities in obesity prevalence. Appl. Geogr. 2019, 112, 102074. [Google Scholar] [CrossRef]
- Wu, P.-C.; Lay, J.-G.; Guo, H.-R.; Lin, C.-Y.; Lung, S.-C.; Su, H.-J. Higher temperature and urbanization affect the spatial patterns of dengue fever transmission in subtropical Taiwan. Sci. Total. Environ. 2009, 407, 2224–2233. [Google Scholar] [CrossRef] [PubMed]
- Acharya, B.K.; Cao, C.; Lakes, T.; Chen, W.; Naeem, S.; Pandit, S. Modeling the spatially varying risk factors of dengue fever in Jhapa district, Nepal, using the semi-parametric geographically weighted regression model. Int. J. Biometeorol. 2018, 62, 1973–1986. [Google Scholar] [CrossRef]
- Estallo, E.L.; Sangermano, F.; Grech, M.; Ludueña-Almeida, F.; Frías-Cespedes, M.; Ainete, M.; Almirón, W.; Livdahl, T. Modelling the distribution of the vectorAedes aegyptiin a central Argentine city. Med. Vet. Entomol. 2018, 32, 451–461. [Google Scholar] [CrossRef]
- Kalbus, A.; Sampaio, V.D.S.; Boenecke, J.; Reintjes, R. Exploring the influence of deforestation on dengue fever incidence in the Brazilian Amazonas state. PLoS ONE 2021, 16, e0242685. [Google Scholar] [CrossRef]
- Nakhapakorn, K.; Tripathi, N.K.; Nakhapakorn, K. An information value based analysis of physical and climatic factors affecting dengue fever and dengue haemorrhagic fever incidence. Int. J. Health Geogr. 2005, 4, 13. [Google Scholar] [CrossRef]
- Schoof, H. Mating, resting habits and dispersal of Aedes aegypti. Bull. World Health Organ. 1967, 36, 600. [Google Scholar]
- Dzul-Manzanilla, F.; Ibarra-López, J.; Marín, W.B.; Martini-Jaimes, A.; Leyva, J.T.; Correa-Morales, F.; Huerta, H.; Manrique-Saide, P.; Prokopec, G.V.M. Indoor Resting Behavior ofAedes aegypti(Diptera: Culicidae) in Acapulco, Mexico. J. Med. Entomol. 2016, 54, 501–504. [Google Scholar] [CrossRef] [PubMed]
- Schiavina, M.; Freire, S.; MacManus, K. GHS-POP R2019A—GHS population grid multitemporal (1975—1990—2000—2015). Eur. Comm. Jt. Res. Cent. 2019, 10. [Google Scholar] [CrossRef]
- Marti, R.; Li, Z.; Catry, T.; Roux, E.; Mangeas, M.; Handschumacher, P.; Gaudart, J.; Tran, A.; Demagistri, L.; Faure, J.-F.; et al. A Mapping Review on Urban Landscape Factors of Dengue Retrieved from Earth Observation Data, GIS Techniques, and Survey Questionnaires. Remote Sens. 2020, 12, 932. [Google Scholar] [CrossRef]
- Lin, C.-H.; Wen, T.-H. Using Geographically Weighted Regression (GWR) to Explore Spatial Varying Relationships of Immature Mosquitoes and Human Densities with the Incidence of Dengue. Int. J. Environ. Res. Public Health 2011, 8, 2798–2815. [Google Scholar] [CrossRef] [PubMed]
- Tariq, B.; Zaidi, A.Z. Geostatistical modeling of dengue disease in Lahore, Pakistan. SN Appl. Sci. 2019, 1, 459. [Google Scholar] [CrossRef]
- Nakhapakorn, K.; Sancharoen, W.; Mutchimwong, A.; Jirakajohnkool, S.; Onchang, R.; Rotejanaprasert, C.; Tantrakarnapa, K.; Paul, R. Assessment of Urban Land Surface Temperature and Vertical City Associated with Dengue Incidences. Remote Sens. 2020, 12, 3802. [Google Scholar] [CrossRef]
- Tsai, P.-J.; Lin, T.-H.; Teng, H.-J.; Yeh, H.-C. Critical low temperature for the survival of Aedes aegypti in Taiwan. Parasites Vectors 2018, 11, 22. [Google Scholar] [CrossRef]
- Dickin, S.K.; Wallace, C.S.; Elliott, S.J. Developing a Vulnerability Mapping Methodology: Applying the Water-Associated Disease Index to Dengue in Malaysia. PLoS ONE 2013, 8, e63584. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Gurgel, H.; Dessay, N.; Hu, L.; Xu, L.; Gong, P. Semi-Supervised Text Classification Framework: An Overview of Dengue Landscape Factors and Satellite Earth Observation. Int. J. Environ. Res. Public Health 2020, 17, 4509. [Google Scholar] [CrossRef] [PubMed]
- Kumar, S.; Agrawal, S. Prevention of vector-borne disease by the identification and risk assessment of mosquito vector habitats using GIS and remote sensing: A case study of Gorakhpur, India. Nanotechnol. Environ. Eng. 2020, 5, 19. [Google Scholar] [CrossRef]
- Sintayehu, D.W.; Tassie, N.; De Boer, W.F. Present and future climatic suitability for dengue fever in Africa. Infect. Ecol. Epidemiol. 2020, 10, 1782042. [Google Scholar] [CrossRef]
- Zhou, S.; Zhou, S.; Liu, L.; Zhang, M.; Kang, M.; Xiao, J.; Song, T. Examining the Effect of the Environment and Commuting Flow from/to Epidemic Areas on the Spread of Dengue Fever. Int. J. Environ. Res. Public Health 2019, 16, 5013. [Google Scholar] [CrossRef]
- Estallo, E.L.; Ludueña-Almeida, F.F.; Visintin, A.M.; Scavuzzo, C.M.; Lamfri, M.A.; Introini, M.V.; Zaidenberg, M.; Almirón, W.R. Effectiveness of normalized difference water index in modellingAedes aegyptihouse index. Int. J. Remote Sens. 2011, 33, 4254–4265. [Google Scholar] [CrossRef]
- Hsueh, Y.H.; Lee, J.; Beltz, L. Spatio-Temporal patterns of dengue fever cases in Kaoshiung City, Taiwan, 2003–2008. Appl. Geogr. 2012, 34, 587–594. [Google Scholar] [CrossRef]
- Li, C.; Li, F.; Wu, Z.; Cheng, J. Exploring spatially varying and scale-dependent relationships between soil contamination and landscape patterns using geographically weighted regression. Appl. Geogr. 2017, 82, 101–114. [Google Scholar] [CrossRef]
- Hajiloo, F.; Hamzeh, S.; Gheysari, M. Impact assessment of meteorological and environmental parameters on PM2.5 concentrations using remote sensing data and GWR analysis (case study of Tehran). Environ. Sci. Pollut. Res. 2018, 26, 24331–24345. [Google Scholar] [CrossRef] [PubMed]
- Liu, C.; Wu, X.; Wang, L. Analysis on land ecological security change and affect factors using RS and GWR in the Danjiangkou Reservoir area, China. Appl. Geogr. 2019, 105, 1–14. [Google Scholar] [CrossRef]
- ESRI. How Geographically Weighted Regression (GWR) Works; Environmental Systems Research Institute: Redlands, CA, USA, 2020; Available online: https://pro.arcgis.com/en/pro-app/2.8/tool-reference/spatial-statistics/how-geographicallyweightedregression-works.htm (accessed on 19 June 2020).
- Ansong, D.; Ansong, E.K.; Ampomah, A.O.; Adjabeng, B.K. Factors contributing to spatial inequality in academic achievement in Ghana: Analysis of district-level factors using geographically weighted regression. Appl. Geogr. 2015, 62, 136–146. [Google Scholar] [CrossRef]
- Abdullah, A.S.; Salman, M.; Din, M.; Khan, K.; Ahmad, M.; Khan, F.H.; Arif, M. Dengue Outbreaks in Khyber Pakhtunkhwa (KPK), Pakistan in 2017: An Integrated Disease Surveillance and Response System (IDSRS)-Based Report. Pol. J. Microbiol. 2019, 68, 115–119. [Google Scholar] [CrossRef]
- Anwar, F.; Tayyab, M.; Salman, M.; Abdullah, D.M.; Khan, J.; Haq, I. Dengue outbreak 2018 in district Shangla KPK; clinical features and laboratory markers of dengue virus infection. Future Virol. 2020, 15, 693–699. [Google Scholar] [CrossRef]
- Bostan, N.; Javed, S.; Amen, N.E.; Eqani, S.A.M.A.S.; Tahir, F.; Bokhari, H. Dengue fever virus in Pakistan: Effects of seasonal pattern and temperature change on distribution of vector and virus. Rev. Med. Virol. 2016, 27, e1899. [Google Scholar] [CrossRef]
- Telle, O.; Nikolay, B.; Kumar, V.; Benkimoun, S.; Pal, R.; Nagpal, B.; Paul, R.E. Social and environmental risk factors for dengue in Delhi city: A retrospective study. PLoS Negl. Trop. Dis. 2021, 15, e0009024. [Google Scholar] [CrossRef]
- Sumera, A. Dual Burden of COVID-19 and Dengue on Weak Health System of Pakistan. Pak. J. Med. Res. 2020, 59, 88. [Google Scholar]
- Mukhtar, M.; Tahir, Z.; Baloch, T.M.; Mansoor, F.; Kamran, J. Entomological investigations of dengue vectors in epidemic-prone districts of Pakistan during 2006–2010. WHO Dengue Bull. 2011, 35, 99–115. [Google Scholar]
- Chen, Y.; Yang, Z.; Jing, Q.; Huang, J.; Guo, C.; Yang, K.; Chen, A.; Lu, J. Effects of natural and socioeconomic factors on dengue transmission in two cities of China from 2006 to 2017. Sci. Total. Environ. 2020, 724, 138200. [Google Scholar] [CrossRef] [PubMed]
- Akter, R.; Naish, S.; Hu, W.; Tong, S. Socio-Demographic, ecological factors and dengue infection trends in Australia. PLoS ONE 2017, 12, e0185551. [Google Scholar] [CrossRef] [PubMed]
- Bowman, L.R.; Tejeda, G.S.; Coelho, G.E.; Sulaiman, L.H.; Gill, B.S.; McCall, P.J.; Olliaro, P.L.; Ranzinger, S.R.; Quang, L.C.; Ramm, R.S.; et al. Alarm Variables for Dengue Outbreaks: A Multi-Centre Study in Asia and Latin America. PLoS ONE 2016, 11, e0157971. [Google Scholar] [CrossRef]
- Mollalo, A.; Vahedi, B.; Rivera, K.M. GIS-based spatial modeling of COVID-19 incidence rate in the continental United States. Sci. Total. Environ. 2020, 728, 138884. [Google Scholar] [CrossRef] [PubMed]
- Masrur, A.; Yu, M.; Luo, W.; Dewan, A. Space-Time Patterns, Change, and Propagation of COVID-19 Risk Relative to the Intervention Scenarios in Bangladesh. Int. J. Environ. Res. Public Health 2020, 17, 5911. [Google Scholar] [CrossRef]
- Desjardins, M.; Hohl, A.; Delmelle, E. Rapid surveillance of COVID-19 in the United States using a prospective space-time scan statistic: Detecting and evaluating emerging clusters. Appl. Geogr. 2020, 118, 102202. [Google Scholar] [CrossRef]
- Butt, M.H.; Ahmad, A.; Misbah, S.; Mallhi, T.H.; Khan, Y.H. Dengue fever and COVID-19 coinfection; a threat to public health for coepidemic in Pakistan. J. Med. Virol. 2020, 93, 671–672. [Google Scholar] [CrossRef]
- Mahmood, S.; Irshad, A. Employing Geographic Information System and Spatiotemporal Analysis of Dengue Outbreaks in a Metropolitan Area in Pakistan. In Human Viruses: Diseases, Treatments and Vaccines: The New Insights; Ahmad, S.I., Ed.; Springer International Publishing: Cham, Switzerland, 2021; pp. 81–91. [Google Scholar]
- Chakravarti, A.; Arora, R.; Luxemburger, C. Fifty years of dengue in India. Trans. R. Soc. Trop. Med. Hyg. 2012, 106, 273–282. [Google Scholar] [CrossRef]
- Saddique, A.; Rana, M.S.; Alam, M.M.; Ikram, A.; Usman, M.; Salman, M.; Faryal, R.; Massab, U.; Bokhari, H.; Mian, M.S.; et al. Emergence of co-infection of COVID-19 and dengue: A serious public health threat. J. Infect. 2020, 81, e16–e18. [Google Scholar] [CrossRef] [PubMed]
- Mohan, A.; Fakhor, H.; Nimavat, N.; Wara, U.U.; Lal, P.M.; Costa, A.C.D.S.; Ahmad, S.; Essar, M.Y. Dengue and COVID-19: A risk of coepidemic in Ethiopia. J. Med. Virol. 2021, 93, 5680–5681. [Google Scholar] [CrossRef] [PubMed]
- Liu, K.; Zhu, Y.; Xia, Y.; Zhang, Y.; Huang, X.; Huang, J.; Nie, E.; Jing, Q.; Wang, G.; Yang, Z.; et al. Dynamic spatiotemporal analysis of indigenous dengue fever at street-level in Guangzhou city, China. PLoS Negl. Trop. Dis. 2018, 12, e0006318. [Google Scholar] [CrossRef]
- Eisen, L.; Lozano-Fuentes, S. Use of Mapping and Spatial and Space-Time Modeling Approaches in Operational Control of Aedes aegypti and Dengue. PLoS Negl. Trop. Dis. 2009, 3, e411. [Google Scholar] [CrossRef] [PubMed]
- Kache, P.A.; Eastwood, G.; Collins-Palmer, K.; Katz, M.; Falco, R.C.; Bajwa, W.I.; Armstrong, P.M.; Andreadis, T.G.; Diuk-Wasser, M.A. Environmental Determinants of Aedes albopictus Abundance at a Northern Limit of Its Range in the United States. Am. J. Trop. Med. Hyg. 2020, 102, 436–447. [Google Scholar] [CrossRef]
- Wang, S.; Liu, H.; Pu, H.; Yang, H. Spatial disparity and hierarchical cluster analysis of final energy consumption in China. Energy 2020, 197, 117195. [Google Scholar] [CrossRef]
- Tobler, W.R. A Computer Movie Simulating Urban Growth in the Detroit Region. Econ. Geogr. 1970, 46, 234. [Google Scholar] [CrossRef]
- Leitner, M.; Glasner, P.; Kounadi, O. Laws of Geography. Oxf. Res. Encycl. Criminol. Crim. Justice 2018, 1–24. [Google Scholar] [CrossRef][Green Version]
- Ge, Y.; Song, Y.; Wang, J.; Liu, W.; Ren, Z.; Peng, J.; Lu, B. Geographically weighted regression-based determinants of malaria incidences in northern China. Trans. GIS 2016, 21, 934–953. [Google Scholar] [CrossRef]
- Weber, A.V. Exploring Local Influences on Zika Virus Rates in Puerto Rico Utilizing Geographically Weighted Regression. Pap. Appl. Geogr. 2017, 4, 100–112. [Google Scholar] [CrossRef]
- Ehlkes, L.; Krefis, A.C.; Kreuels, B.; Krumkamp, R.; Adjei, O.; Ayim-Akonor, M.; Kobbe, R.; Hahn, A.; Vinnemeier, C.; Loag, W.; et al. Geographically weighted regression of land cover determinants of Plasmodium falciparum transmission in the Ashanti Region of Ghana. Int. J. Health Geogr. 2014, 13, 35. [Google Scholar] [CrossRef] [PubMed]
- Deng, S.-Q.; Yang, X.; Wei, Y.; Chen, J.-T.; Wang, X.-J.; Peng, H.-J. A Review on Dengue Vaccine Development. Vaccines 2020, 8, 63. [Google Scholar] [CrossRef]
- Wilder-Smith, A.; Ooi, E.E.; Horstick, O.; Wills, B. Dengue. Lancet 2019, 393, 350–363. [Google Scholar] [CrossRef]
- Mordecai, E.A.; Cohen, J.M.; Evans, M.V.; Gudapati, P.; Johnson, L.R.; Lippi, C.A.; Miazgowicz, K.; Murdock, C.C.; Rohr, J.R.; Ryan, S.J.; et al. Detecting the impact of temperature on transmission of Zika, dengue, and chikungunya using mechanistic models. PLoS Negl. Trop. Dis. 2017, 11, e0005568. [Google Scholar] [CrossRef] [PubMed]
- Huber, J.H.; Childs, M.L.; Caldwell, J.M.; Mordecai, E.A. Seasonal temperature variation influences climate suitability for dengue, chikungunya, and Zika transmission. PLoS Negl. Trop. Dis. 2018, 12, e0006451. [Google Scholar] [CrossRef] [PubMed]
| Dengue Supportive Factor | Factor Computation | Explanation of Significance | Justification/Reference |
|---|---|---|---|
| Built-up area | The Normalized Difference Built-up index (NDBI) | It is widely indicated that more urban areal development or built-up land positively supports the Aedes aegypti (Urban mosquito) presence. This mosquito thrives in urban settings where there is infrastructural proximity. The indoor places are among the other resting places of Aedes aegypti; the host is at constant risk of frequent bites and infection inside such indoor spaces. | Wu et al. [125]; Acharya et al. [126]; Estallo et al. [127]; Kalbus et al. [128]; Nakhapakorn and Tripathi [129]; Schoof [130]; Dzul-Manzanilla et al. [131] |
| Population | The data downloaded from European Commission’s Global Human Settlement data portal; Schiavina et al. [132] | Dengue is an urban disease; due to the high density of human populations and increased adaptation of Aedes aegypti to densely populated environments. Population density is an important indicator in dengue assessments because the moving of the population from place to place plays a crucial role in dengue epidemics. | Marti et al. [133]; Kalbus et al. [128]; Acharya et al. [126]; Estallo et al. [127]; Lin and Wen [134]; Wu et al. [125] |
| Vegetation | The Normalized Difference Vegetation Index (NDVI) | The Aedes aegypti mosquitoes remain active during diurnal times and their resting habitats are typically associated with vegetation (during daytimes)—that provides ideal shade and, therefore, a microclimate— which is cooler than those in open lands, e.g., bare soil and built-up areas. | Imran et al. [21]; Estallo et al. [127]; Acharya et al. [126]; Tariq and Zaidi [135] |
| Land Surface Temperature (LST) | Calculated from Landsat 5 (Thematic Mapper (TM)); Thermal Band (10.40–12.50 µm) Nakhapakorn et al. [136] | Temperature is considered the paramount meteorological factor influencing ecological distributions of Aedes aegypti mosquitoes. Land surface temperature is used by numerous researchers to assess dengue-related associations. | Tsai et al. [137]; Tariq and Zaidi [135]; Acharya et al. [126]; Imran et al. [21] |
| Water | Computed through the Normalized Difference Water Index (NDWI) | Dengue is one of the water-associated diseases and water proximity could be an important factor in such heterogeneity-based assessments. Water plays a vital role in dengue mosquitoes’ breeding, especially when combined with other factors such as suitable temperature and vegetation. | Dickin et al. [138]; Estallo et al. [127]; Tariq and Zaidi [135]; Li et al. [139]; Acharya et al. [126] |
| Moisture | Computed through the Normalized Difference Moisture Index (NDMI) | The mosquitoes’ vector breeding at any location highly depends on moisture, water, temperature, and vegetation. High moisture levels with high-temperature conditions are climatically optimal for the distribution of Aedes aegypti, which is connected to Dengue Fever. | Kumar and Agrawal [140]; Sintayehu et al. [141] |
| Year | Incidents | Trend | Trend Statistic | p-Value | Interpretation |
|---|---|---|---|---|---|
| 2007 | 241 | Increasing | 2.7563 | 0.0058 | Reject H0 |
| 2008 | 1180 | Increasing | 3.5523 | 0.0004 | Reject H0 |
| 2009 | 89 | Not Significant | 0.2772 | 0.7816 | Accept H0 |
| 2010 | 3580 | Increasing | 5.1586 | 0.0000 | Reject H0 |
| 2011 | 11,283 | Increasing | 3.3984 | 0.0007 | Reject H0 |
| 2012 | 124 | Increasing | 2.1497 | 0.0316 | Reject H0 |
| 2013 | 1512 | Increasing | 5.5800 | 0.0000 | Reject H0 |
| 2014 | 83 | Increasing | 4.2038 | 0.0000 | Reject H0 |
| 2015 | 146 | Increasing | 2.8246 | 0.0047 | Reject H0 |
| 2016 | 1111 | Increasing | 2.5990 | 0.0093 | Reject H0 |
| Variable | Grid-Based | Administrative Unit-Based (UCs) | ||||||
|---|---|---|---|---|---|---|---|---|
| Intercept | NDBI | NDVI | LST | Intercept | NDBI | NDVI | LST | |
| Mean of βs | 6.473 | 0.181 | 0.272 | 27.790 | 15.248 | 0.167 | 0.213 | 20.529 |
| SD of βs | 8.059 | 0.038 | 0.118 | 0.922 | 22.333 | 0.179 | 0.169 | 23.268 |
| Minimum | 0.001 | −0.116 | −0.067 | 23.683 | 0.000 | 0.002 | 0.004 | 0.208 |
| Maximum | 70.009 | 0.402 | 0.574 | 31.646 | 145.439 | 1.454 | 0.839 | 195.225 |
| Median | 3.137 | 0.187 | 0.282 | 27.935 | 8.630 | 0.133 | 0.194 | 17.042 |
| SE | 0.093 | 0.000 | 0.001 | 0.011 | 1.817 | 0.015 | 0.014 | 1.894 |
| Adjusted R2 | 0.84 | 0.73 | ||||||
| Akaike information criterion (AIC) | 39,445.90 | 1175.44 | ||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Naqvi, S.A.A.; Sajjad, M.; Waseem, L.A.; Khalid, S.; Shaikh, S.; Kazmi, S.J.H. Integrating Spatial Modelling and Space–Time Pattern Mining Analytics for Vector Disease-Related Health Perspectives: A Case of Dengue Fever in Pakistan. Int. J. Environ. Res. Public Health 2021, 18, 12018. https://doi.org/10.3390/ijerph182212018
Naqvi SAA, Sajjad M, Waseem LA, Khalid S, Shaikh S, Kazmi SJH. Integrating Spatial Modelling and Space–Time Pattern Mining Analytics for Vector Disease-Related Health Perspectives: A Case of Dengue Fever in Pakistan. International Journal of Environmental Research and Public Health. 2021; 18(22):12018. https://doi.org/10.3390/ijerph182212018
Chicago/Turabian StyleNaqvi, Syed Ali Asad, Muhammad Sajjad, Liaqat Ali Waseem, Shoaib Khalid, Saima Shaikh, and Syed Jamil Hasan Kazmi. 2021. "Integrating Spatial Modelling and Space–Time Pattern Mining Analytics for Vector Disease-Related Health Perspectives: A Case of Dengue Fever in Pakistan" International Journal of Environmental Research and Public Health 18, no. 22: 12018. https://doi.org/10.3390/ijerph182212018
APA StyleNaqvi, S. A. A., Sajjad, M., Waseem, L. A., Khalid, S., Shaikh, S., & Kazmi, S. J. H. (2021). Integrating Spatial Modelling and Space–Time Pattern Mining Analytics for Vector Disease-Related Health Perspectives: A Case of Dengue Fever in Pakistan. International Journal of Environmental Research and Public Health, 18(22), 12018. https://doi.org/10.3390/ijerph182212018









