Associating Land Cover Changes with Patterns of Incidences of Climate-Sensitive Infections: An Example on Tick-Borne Diseases in the Nordic Area
Abstract
:1. Introduction
2. Materials and Methods
2.1. Data Analysis Aspects
2.2. Ecological Aspects of Tick-Borne Diseases
2.3. Borreliosis and Tick-Borne Encephalitis as Two CSIs
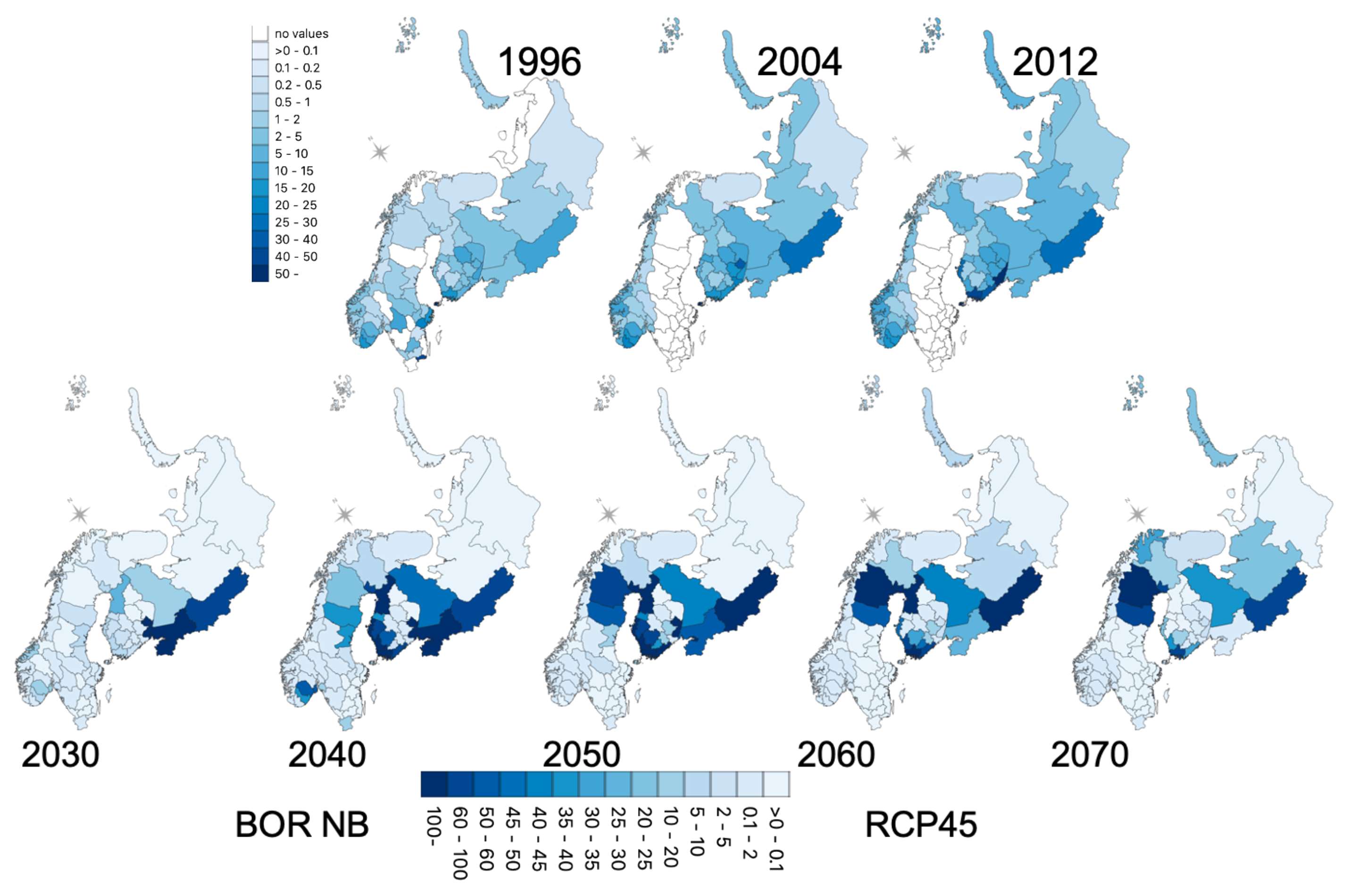
3. Results
3.1. Patterns of Incidence
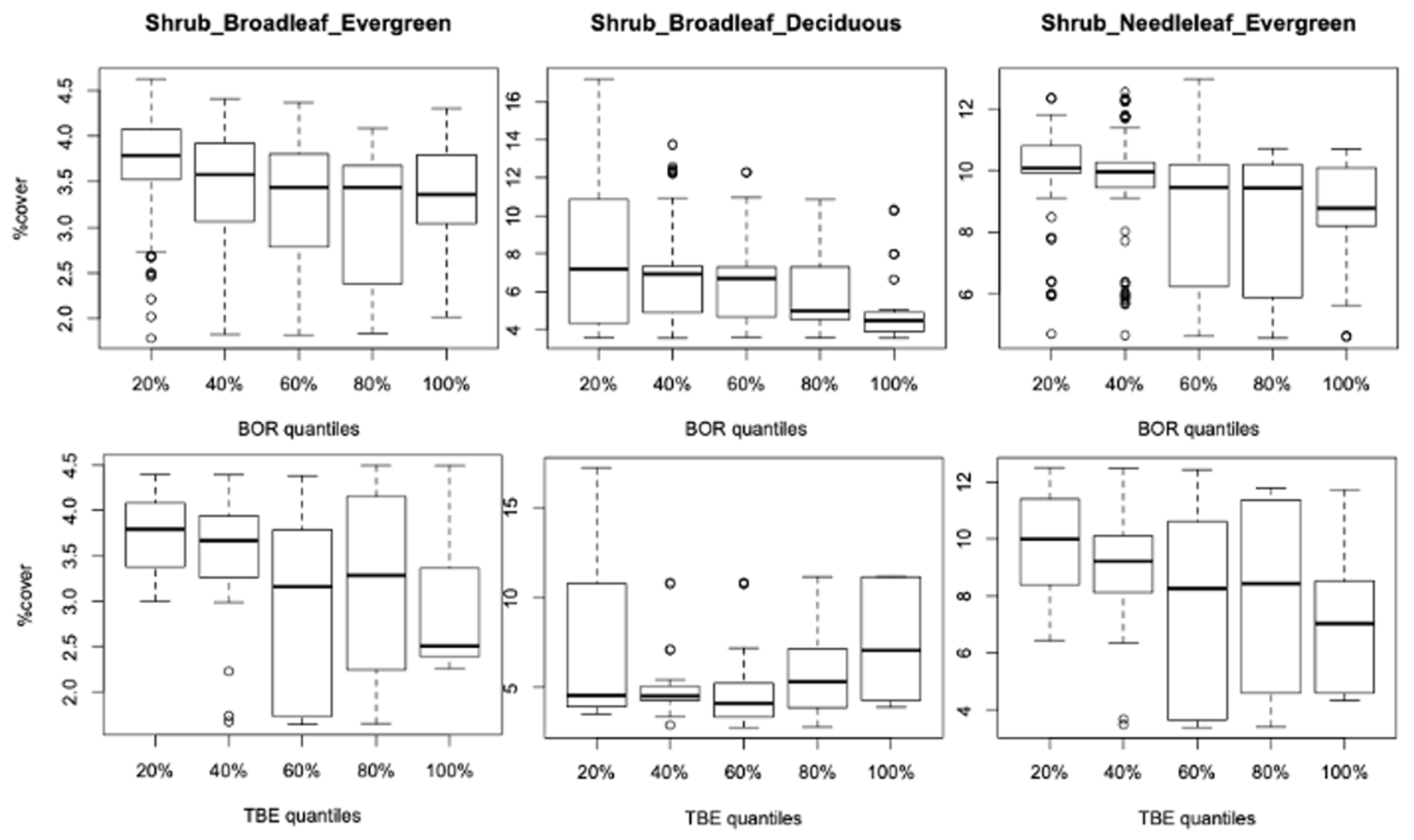
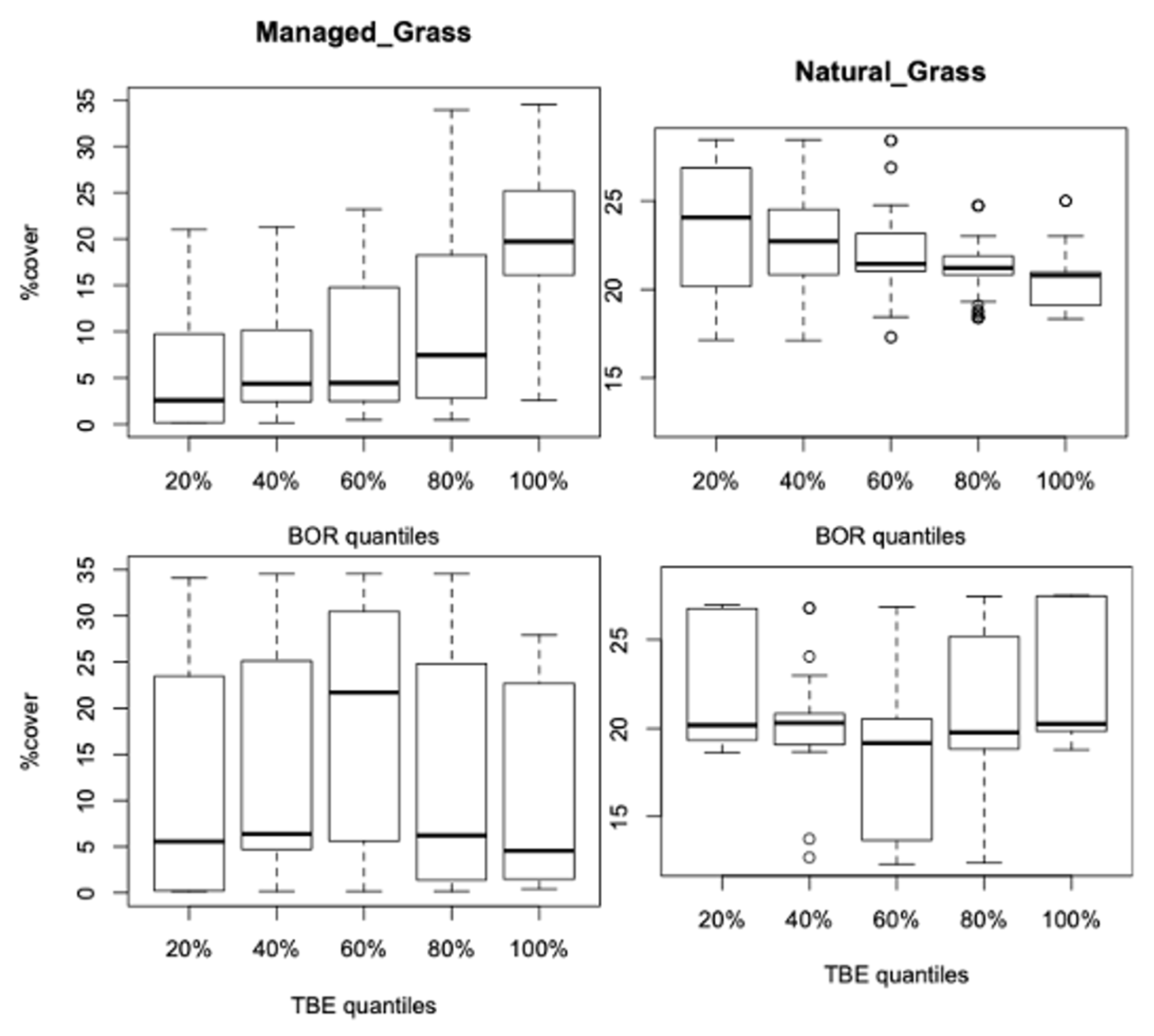
3.2. Vegetation Cover Associations
3.2.1. Vegetation Changes
3.2.2. Associations with Incidence Patterns
3.3. Incidence Levels and Vegetation Changes
3.4. Regression Models
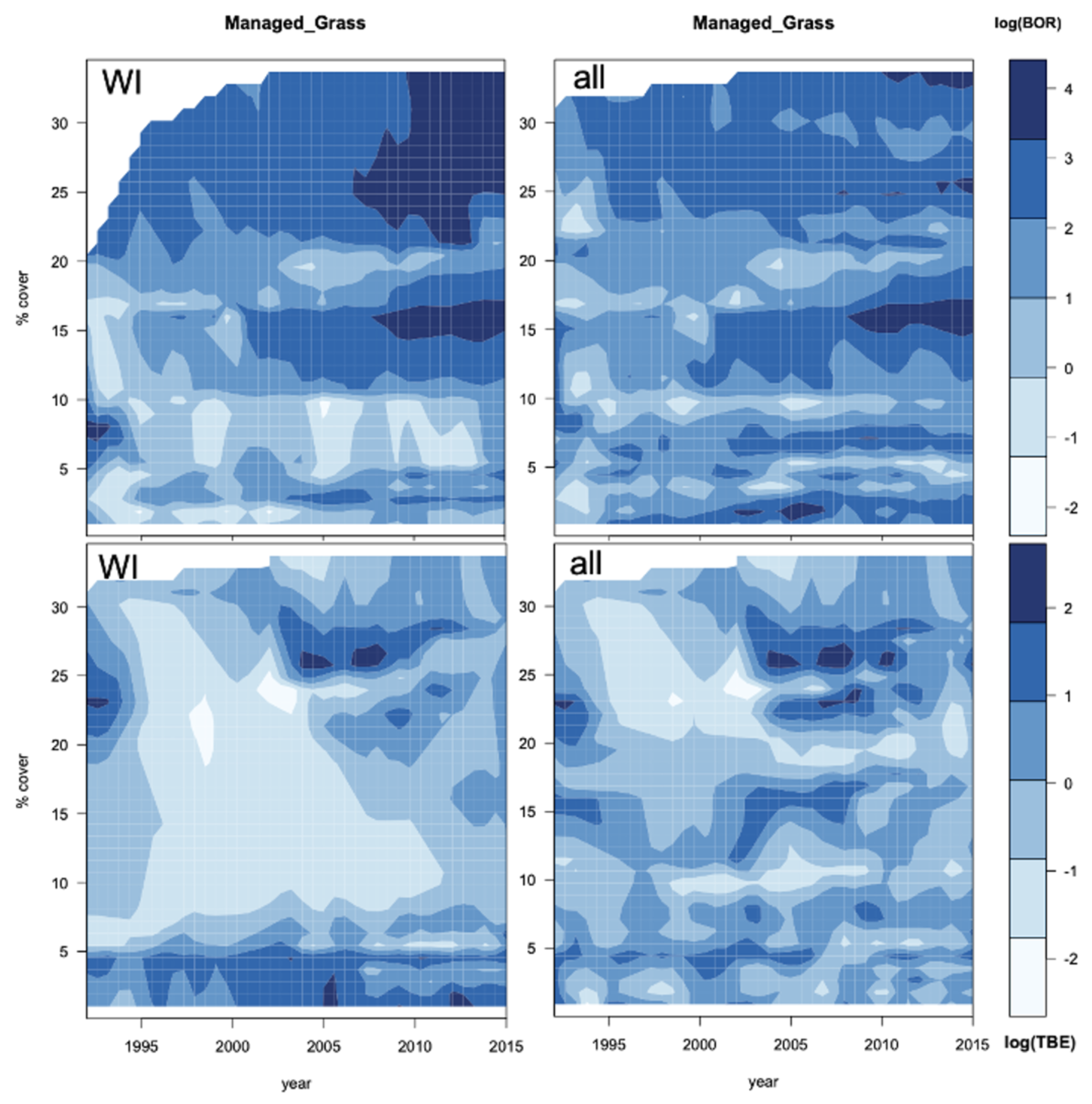
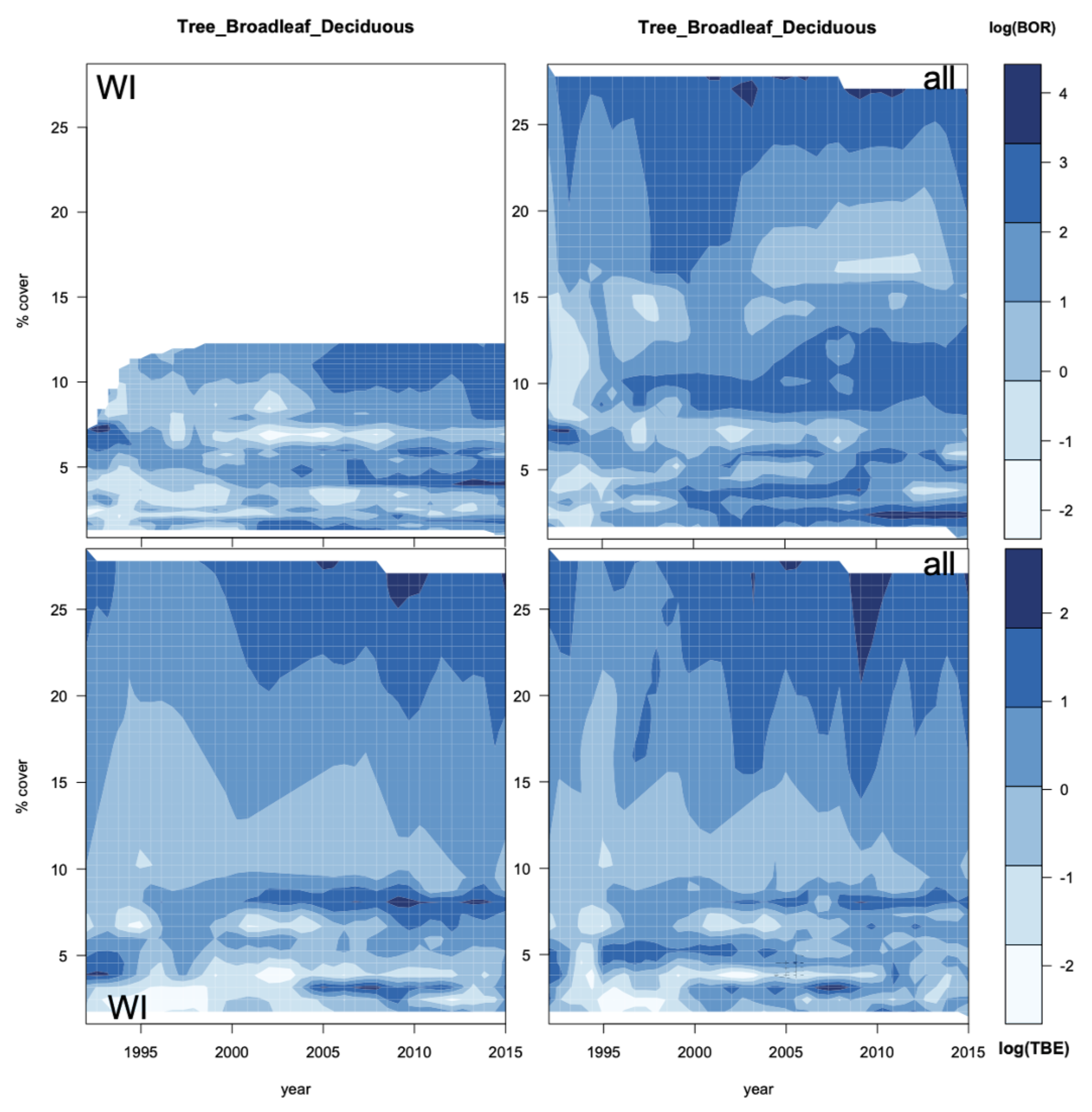
3.5. Geographic Forecasts
4. Discussion
4.1. Is the Vegetation Effect Due to Specific Types, Their Changes over the Period, or Both?
4.2. Are the Differences in Vegetation Association between BOR and TBE Quantitative or Qualitative?
4.3. Are the Temporal Patterns of Associations Different for BOR and TBE?
4.4. Is Regression for WI Districts a Way to Obtain Better Fit or More Meaningful Associations?
4.5. Do the Projections Reflect Real Trends or Increasing Uncertainty?
4.6. Limitations of This Study
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| BOR | Lyme borreliosis |
| BT | either BOR or TBE (inclusive) |
| BTUL | either BOR or TUL (inclusive) |
| BTT | BOR or TBE or TUL (inclusive) |
| CLINF | Climate-change effects on the epidemiology of infectious diseases and the impacts |
| on Northern Societies | |
| CSI | Climate-Sensitive Infectious diseases |
| FCAk | Factorial Correspondence Analysis on k modes |
| GLM | Generalised Linear Model |
| IPCC | International Panel on Climate Change |
| NCoE | Nordforsk Centre of Excellence |
| PCA | Principal Component Analysis |
| PFT | Plant Functional Type (Table A2 ) |
| PTAk | Principal Tensor Analysis on k modes |
| RCP4.5 | Representative Concentration Pathway with 4.5 W/m2 of radiative forcing in 2100 |
| RCP8.5 | Representative Concentration Pathway with 8.5 W/m2 of radiative forcing in 2100 |
| TBE | tick-borne encephalitis |
| TUL | tularemia |
Appendix A. Data Description
Appendix A.1. Health Data
| 20% | 40% | 60% | 80% | 100% | |
|---|---|---|---|---|---|
| BOR | 1.15 | 3.43 | 7.02 | 13.44 | 81.56 |
| TBE | 0.43 | 0.86 | 1.52 | 3.40 | 15.25 |
| TUL | 0.40 | 0.80 | 1.73 | 5.11 | 111.27 |
| BT | 1.01 | 2.95 | 6.80 | 13.30 | 82.31 |
| BTU | 1.88 | 4.53 | 9.03 | 16.95 | 113.98 |
| BTT | 1.7 | 4.57 | 9.60 | 17.04 | 114.25 |
Appendix A.2. Land Cover Data
| PFT Full Name | PFT | Average % Cover |
|---|---|---|
| Tree Needleleaf Evergreen | TNE | 24 |
| Natural Grass | NG | 21 |
| Shrub Needleleaf Evergreen | SNE | 9 |
| Managed Grass | MG | 9 |
| Water | Wa | 8 |
| Shrub Broadleaf Deciduous | SBD | 7 |
| Tree Broadleaf Deciduous | TBD | 5 |
| Shrub Broadleaf Evergreen | SBE | 4 |
| Bare soil | B | 3 |
| Sparse Vegetation | Spv | 3 |
| Mosses and lichens | Mo | 2 |
| Urban | Ur | <2 |
| Tree Broadleaf Evergreen | TBEg | <1 |
| Tree Needleaf Deciduous | TND | <1 |
| Shrub Needleaf Deciduous | SND | <1 |
| Snow Ice | SI | <1 |
| bare_ground (bare_soil) | tropical_broadleaf_evergreen (TBEg, SBE) |
| tropical_broadleaf_raingreen (TBD, TND, SBD) | temperate_needleleaf_evergreen (TNE, SNE) |
| temperate_broadleaf_evergreen (TBEg, SBE) | temperate_broadleaf_summergreen (TBD, TND, SBD) |
| boreal_needleleaf_evergreen (TNE) | boreal_broadleaf_summergreen (TBD) |
| boreal_needleleaf_decideous (TND) | C3_grass (NG) |
| C4_grass (NG) | C3_agriculture (MG) |
| C4_agriculture (MG) | moss_lichen (Mo) |
| boreal_broadleaf_shrubs (SBD, SNE, SND) | C3_grass_arctic (Spv, NG) |
Appendix A.3. Climate Data
Appendix B. Climate Data Simulations
Appendix C. Analysis and Data Science Addendum
Appendix C.1. CTR
Appendix C.2. FCAk Associations
References
- Meredith, M.; Sommerkorn, M.; Cassotta, S.; Derksen, C.; Ekaykin, A.; Hollowed, A.; Kofinas, G.; Mackintosh, A.; Melbourne-Thomas, J.; Muelbert, M.; et al. Polar Regions. In IPCC Special Report on the Ocean and Cryosphere in a Changing Climate; The United Nations’ Intergovernmental Panel: Marrakech, Monaco, 2019. [Google Scholar]
- Song, X.P.; Hansen, M.C.; Stehman, S.V.; Potapov, P.V.; Tyukavina, A.; Vermote, E.F.; Townshend, J.R. Global land change from 1982 to 2016. Nature 2018, 560, 639–643. [Google Scholar] [CrossRef] [PubMed]
- Pecl, G.T.; Araújo, M.B.; Bell, J.D.; Blanchard, J.; Bonebrake, T.C.; Chen, I.C.; Clark, T.D.; Colwell, R.K.; Danielsen, F.; Evengård, B.; et al. Biodiversity redistribution under climate change: Impacts on ecosystems and human well-being. Science 2017, 355. [Google Scholar] [CrossRef] [PubMed]
- Olofsson, J.; Oksanen, L.; Callaghan, T.; Hulme, P.E.; Oksanen, T.; Suominen, O. Herbivores inhibit climate-driven shrub expansion on the tundra. Glob. Chang. Biol. 2009, 15, 2681–2693. [Google Scholar] [CrossRef]
- Olofsson, J.; te Beest, M.; Ericson, L. Complex biotic interactions drive long-term vegetation dynamics in a subarctic ecosystem. Philos. Trans. R. Soc. B Biol. Sci. 2013, 368, 20120486. [Google Scholar] [CrossRef] [Green Version]
- Walther, G.R. Community and ecosystem responses to recent climate change. Philos. Trans. R. Soc. B Biol. Sci. 2010, 365, 2019–2024. [Google Scholar] [CrossRef]
- Van der Putten, W.H.; Macel, M.; Visser, M.E. Predicting species distribution and abundance responses to climate change: Why it is essential to include biotic interactions across trophic levels. Philos. Trans. R. Soc. B Biol. Sci. 2010, 365, 2025–2034. [Google Scholar] [CrossRef]
- Pearson, R.G.; Phillips, S.J.; Loranty, M.M.; Beck, P.S.A.; Damoulas, T.; Knight, S.J.; Goetz, S.J. Shifts in Arctic vegetation and associated feedbacks under climate change. Nat. Clim. Chang. 2013, 3, 673–677. [Google Scholar] [CrossRef]
- Gibb, R.; Redding, D.W.; Chin, K.Q.; Donnelly, C.A.; Blackburn, T.M.; Newbold, T.; Jones, K.E. Zoonotic host diversity increases in human-dominated ecosystems. Nature 2020, 584, 398–402. [Google Scholar] [CrossRef]
- Cable, J.; Barber, I.; Boag, B.; Ellison, A.R.; Morgan, E.R.; Murray, K.; Pascoe, E.L.; Sait, S.M.; Wilson, A.J.; Booth, M. Global change, parasite transmission and disease control: Lessons from ecology. Philos. Trans. R. Soc. B Biol. Sci. 2017, 372, 20160088. [Google Scholar] [CrossRef]
- Gage, K.L.; Burkot, T.R.; Eisen, R.J.; Hayes, E.B. Climate and Vectorborne Diseases. Am. J. Prev. Med. 2008, 35, 436–450. [Google Scholar] [CrossRef]
- Tokarevich, N.; Tronin, A.; Gnativ, B.; Revich, B.; Blinova, O.; Evengard, B. Impact of air temperature variation on the ixodid ticks habitat and tick-borne encephalitis incidence in the Russian Arctic: The case of the Komi Republic. Int. J. Circumpolar Health 2017, 76, 1298882. [Google Scholar] [CrossRef]
- Hvidsten, D.; Frafjord, K.; Gray, J.S.; Henningsson, A.J.; Jenkins, A.; Kristiansen, B.E.; Lager, M.; Rognerud, B.; Slåtsve, A.M.; Stordal, F.; et al. The distribution limit of the common tick, Ixodes ricinus, and some associated pathogens in north-western Europe. Ticks Tick-Borne Dis. 2020, 11, 101388. [Google Scholar] [CrossRef]
- Jaenson, T.G.T.; Värv, K.; Fröjdman, I.; Jääskeläinen, A.; Rundgren, K.; Versteirt, V.; Estrada-Peña, A.; Medlock, J.M.; Golovljova, I. First evidence of established populations of the taiga tick Ixodes persulcatus (Acari: Ixodidae) in Sweden. Parasites Vectors 2016, 9, 377. [Google Scholar] [CrossRef]
- Jore, S.; Vanwambeke, S.O.; Viljugrein, H.; Isaksen, K.; Kristoffersen, A.B.; Woldehiwet, Z.; Johansen, B.; Brun, E.; Brun-Hansen, H.; Westermann, S.; et al. Climate and environmental change drives Ixodes ricinus geographical expansion at the northern range margin. Parasites Vectors 2014, 7, 11. [Google Scholar] [CrossRef] [Green Version]
- Hofmeester, T.R.; Sprong, H.; Jansen, P.A.; Prins, H.H.T.; van Wieren, S.E. Deer presence rather than abundance determines the population density of the sheep tick, Ixodes ricinus, in Dutch forests. Parasites Vectors 2017, 10, 433. [Google Scholar] [CrossRef]
- Tronin, A.; Tokarevich, N.; Blinova, O.; Gnativ, B.; Buzinov, R.; Sokolova, O.; Evengard, B.; Pahomova, T.; Bubnova, L.; Safonova, O. Study of the relationship between the average annual Temperature of atmospheric air and the number of tick-bitten humans in the north of European Russia. Int. J. Environ. Res. Public Health 2020, 17, 8006. [Google Scholar] [CrossRef]
- Jaenson, T.G.; Jaenson, D.G.; Eisen, L.; Petersson, E.; Lindgren, E. Changes in the geographical distribution and abundance of the tick Ixodes ricinus during the past 30 years in Sweden. Parasites Vectors 2012, 5, 8. [Google Scholar] [CrossRef] [Green Version]
- Malkhazova, S.; Pestina, P.; Prasolova, A.; Orlov, D. Emerging natural focal infectious diseases in Russia: A medical–geographical study. Int. J. Environ. Res. Public Health 2020, 17, 8005. [Google Scholar] [CrossRef]
- Rubel, F.; Brugger, K.; Belova, O.A.; Kholodilov, I.S.; Didyk, Y.M.; Kurzrock, L.; García-Pérez, A.L.; Kahl, O. Vectors of disease at the northern distribution limit of the genus Dermacentor in Eurasia: D. reticulatus and D. silvarum. Exp. Appl. Acarol. 2020, 82, 95–123. [Google Scholar] [CrossRef]
- Grandi, G.; Chitimia-Dobler, L.; Choklikitumnuey, P.; Strube, C.; Springer, A.; Albihn, A.; Jaenson, T.G.T.; Omazic, A. First records of adult Hyalomma marginatum and H. rufipes ticks (Acari: Ixodidae) in Sweden. Ticks Tick-Borne Dis. 2020, 11, 101403. [Google Scholar] [CrossRef]
- Hofmeester, T.R.; Coipan, E.C.; Wieren, S.E.v.; Prins, H.H.T.; Takken, W.; Sprong, H. Few vertebrate species dominate the Borrelia burgdorferi s.l. life cycle. Environ. Res. Lett. 2016, 11, 043001. [Google Scholar] [CrossRef] [Green Version]
- Jia, G.; Shevliakova, E.; Artaxo, P.; De Noblet-Ducoudré, N.; Houghton, R.; House, J.; Kitajima, K.; Lennard, C.; Popp, A.; Sirin, A.; et al. Land–Climate Interactions. In Climate Change and Land: An IPCC Special Report on Climate Change, Desertification, Land Degradation, Sustainable Land Management, Food Security, and Greenhouse Gas Fluxes in Terrestrial Ecosystems; The United Nations’ Intergovernmental Panel: Marrakech, Monaco, 2019. [Google Scholar]
- Mod, H.K.; Luoto, M. Arctic shrubification mediates the impacts of warming climate on changes to tundra vegetation. Environ. Res. Lett. 2016, 11, 124028. [Google Scholar] [CrossRef] [Green Version]
- Rydsaa, J.H.; Stordal, F.; Bryn, A.; Tallaksen, L.M. Effects of shrub and tree cover increase on the near-surface atmosphere in northern Fennoscandia. Biogeosciences 2017, 14, 4209–4227. [Google Scholar] [CrossRef] [Green Version]
- Reichle, L.M.; Epstein, H.E.; Bhatt, U.S.; Raynolds, M.K.; Walker, D.A. Spatial heterogeneity of the temporal dynamics of Arctic tundra vegetation. Geophys. Res. Lett. 2018, 45, 9206–9215. [Google Scholar] [CrossRef] [Green Version]
- Vowles, T.; Björk, R.G. Implications of evergreen shrub expansion in the Arctic. J. Ecol. 2019, 107, 650–655. [Google Scholar] [CrossRef] [Green Version]
- Verma, M.; Schulte to Bühne, H.; Lopes, M.; Ehrich, D.; Sokovnina, S.; Hofhuis, S.P.; Pettorelli, N. Can reindeer husbandry management slow down the shrubification of the Arctic? J. Environ. Manag. 2020, 267, 110636. [Google Scholar] [CrossRef]
- Myers-Smith, I.H.; Kerby, J.T.; Phoenix, G.K.; Bjerke, J.W.; Epstein, H.E.; Assmann, J.J.; John, C.; Andreu-Hayles, L.; Angers-Blondin, S.; Beck, P.S.A.; et al. Complexity revealed in the greening of the Arctic. Nat. Clim. Chang. 2020, 10, 106–117. [Google Scholar] [CrossRef] [Green Version]
- Shevtsova, I.; Heim, B.; Kruse, S.; Schröder, J.; Troeva, E.I.; Pestryakova, L.A.; Zakharov, E.S.; Herzschuh, U. Strong shrub expansion in tundra-taiga, tree infilling in taiga and stable tundra in central Chukotka (north-eastern Siberia) between 2000 and 2017. Environ. Res. Lett. 2020, 15, 085006. [Google Scholar] [CrossRef]
- Skarin, A.; Verdonen, M.; Kumpula, T.; Macias-Fauria, M.; Alam, M.; Kerby, J.; Forbes, B.C. Reindeer use of low Arctic tundra correlates with landscape structure. Environ. Res. Lett. 2020, 15, 115012. [Google Scholar] [CrossRef]
- Tømmervik, H.; Forbes, B.C. Focus on recent, present and future Arctic and boreal productivity and biomass changes. Environ. Res. Lett. 2020, 15, 080201. [Google Scholar] [CrossRef]
- Chen, I.C.; Hill, J.K.; Ohlemüller, R.; Roy, D.B.; Thomas, C.D. Rapid range shifts of species associated with high levels of climate warming. Science 2011, 333, 1024–1026. [Google Scholar] [CrossRef] [PubMed]
- Callaghan, T.V.; Jonasson, C.; Thierfelder, T.; Yang, Z.; Hedenås, H.; Johansson, M.; Molau, U.; Van Bogaert, R.; Michelsen, A.; Olofsson, J.; et al. Ecosystem change and stability over multiple decades in the Swedish subarctic: Complex processes and multiple drivers. Philos. Trans. R. Soc. Biol. Sci. 2013, 368, 20120488. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Myers-Smith, I.H.; Hik, D.S. Climate warming as a driver of tundra shrubline advance. J. Ecol. 2018, 106, 547–560. [Google Scholar] [CrossRef]
- Nord, D.C. (Ed.) Nordic Perspectives on the Responsible Development of the Arctic: Pathways to Action; Springer Polar Sciences; Springer Nature: Cham, Switzerland, 2021. [Google Scholar] [CrossRef]
- Cleveland, W.S. Robust locally weighted regression and smoothing scatterplots. J. Am. Stat. Assoc. 1979, 74, 829–836. [Google Scholar] [CrossRef]
- Leibovici, D.G.; Quegan, S.; Comyn-Platt, E.; Hayman, G.; Val Martin, M.; Guimberteau, M.; Druel, A.; Zhu, D.; Ciais, P. Spatio-temporal variations and uncertainty in land surface modelling for high latitudes: Univariate response analysis. Biogeosciences 2020, 17, 1821–1844. [Google Scholar] [CrossRef]
- Leibovici, D.G.; Birkin, M. Simple, multiple and multiway correspondence analysis applied to spatial census-based population microsimulation studies using R. NCRM 2013, 3178, 42. [Google Scholar]
- Druel, A.; Ciais, P.; Krinner, G.; Peylin, P. Modeling the vegetation dynamics of northern shrubs and mosses in the ORCHIDEE land surface model. J. Adv. Model. Earth Syst. 2019, 11, 2020–2035. [Google Scholar] [CrossRef]
- Van Oort, B.E.H.; Hovelsrud, G.K.; Risvoll, C.; Mohr, C.W.; Jore, S. A mini-review of Ixodes ticks climate sensitive infection dispersion risk in the nordic region. Int. J. Environ. Res. Public Health 2020, 17, 5387. [Google Scholar] [CrossRef]
- Jore, S.; Vanwambeke, S.O.; Slunge, D.; Boman, A.; Krogfelt, K.A.; Jepsen, M.T.; Vold, L. Spatial tick bite exposure and associated risk factors in Scandinavia. Infect. Ecol. Epidemiol. 2020, 10, 1764693. [Google Scholar] [CrossRef]
- Fernández-Ruiz, N.; Estrada-Peña, A. Could climate trends disrupt the contact rates between Ixodes ricinus (Acari, Ixodidae) and the reservoirs of Borrelia burgdorferi s.l.? PLoS ONE 2020, 15, e0233771. [Google Scholar] [CrossRef]
- Lindström, A.; Jaenson, T.G. Distribution of the common tick, Ixodes ricinus (Acari: Ixodidae), in different vegetation types in southern Sweden. J. Med Entomol. 2003, 40, 375–378. [Google Scholar] [CrossRef]
- Kilpatrick, A.M.; Dobson, A.D.M.; Levi, T.; Salkeld, D.J.; Swei, A.; Ginsberg, H.S.; Kjemtrup, A.; Padgett, K.A.; Jensen, P.M.; Fish, D.; et al. Lyme disease ecology in a changing world: Consensus, uncertainty and critical gaps for improving control. Philos. Trans. R. Soc. B Biol. Sci. 2017, 372, 20160117. [Google Scholar] [CrossRef]
- Wang, Y.X.G.; Matson, K.D.; Xu, Y.; Prins, H.H.T.; Huang, Z.Y.X.; de Boer, W.F. Forest connectivity, host assemblage characteristics of local and neighboring counties, and temperature jointly shape the spatial expansion of Lyme disease in United States. Remote Sens. 2019, 11, 2354. [Google Scholar] [CrossRef] [Green Version]
- Bingsohn, L.; Beckert, A.; Zehner, R.; Kuch, U.; Oehme, R.; Kraiczy, P.; Amendt, J. Prevalences of tick-borne encephalitis virus and Borrelia burgdorferi sensu lato in Ixodes ricinus populations of the Rhine-Main region, Germany. Ticks Tick-Borne Dis. 2013, 4, 207–213. [Google Scholar] [CrossRef]
- Michelitsch, A.; Wernike, K.; Klaus, C.; Dobler, G.; Beer, M. Exploring the reservoir hosts of tick-borne encephalitis virus. Viruses 2019, 11, 669. [Google Scholar] [CrossRef] [Green Version]
- Lindquist, L.; Vapalahti, O. Tick-borne encephalitis. Lancet 2008, 371, 1861–1871. [Google Scholar] [CrossRef]
- Perez, G.; Bastian, S.; Agoulon, A.; Bouju, A.; Durand, A.; Faille, F.; Lebert, I.; Rantier, Y.; Plantard, O.; Butet, A. Effect of landscape features on the relationship between Ixodes ricinus ticks and their small mammal hosts. Parasites Vectors 2016, 9, 20. [Google Scholar] [CrossRef]
- Medlock, J.M.; Hansford, K.M.; Bormane, A.; Derdakova, M.; Estrada-Peña, A.; George, J.C.; Golovljova, I.; Jaenson, T.G.T.; Jensen, J.K.; Jensen, P.M.; et al. Driving forces for changes in geographical distribution of Ixodes ricinus ticks in Europe. Parasites Vectors 2013, 6, 1. [Google Scholar] [CrossRef] [Green Version]
- Winter, J.M.; Partridge, T.F.; Wallace, D.; Chipman, J.W.; Ayres, M.P.; Osterberg, E.C.; Dekker, E.R. Modeling the sensitivity of blacklegged ticks (Ixodes scapularis) to temperature and land cover in the northeastern United States. J. Med. Entomol. 2021, 58, 416–427. [Google Scholar] [CrossRef]
- Uusitalo, R.; Siljander, M.; Dub, T.; Sane, J.; Sormunen, J.J.; Pellikka, P.; Vapalahti, O. Modelling habitat suitability for occurrence of human tick-borne encephalitis (TBE) cases in Finland. Ticks Tick-Borne Dis. 2020, 11, 101457. [Google Scholar] [CrossRef]
- Omazic, A.; Bylund, H.; Boqvist, S.; Högberg, A.; Björkman, C.; Tryland, M.; Evengård, B.; Koch, A.; Berggren, C.; Malogolovkin, A.; et al. Identifying climate-sensitive infectious diseases in animals and humans in Northern regions. Acta Vet. Scand. 2019, 61, 53. [Google Scholar] [CrossRef] [Green Version]
- Krawczyk, A.I.; van Duijvendijk, G.L.A.; Swart, A.; Heylen, D.; Jaarsma, R.I.; Jacobs, F.H.H.; Fonville, M.; Sprong, H.; Takken, W. Effect of rodent density on tick and tick-borne pathogen populations: Consequences for infectious disease risk. Parasites Vectors 2020, 13, 34. [Google Scholar] [CrossRef] [Green Version]
- Lin, Y.P.; Diuk-Wasser, M.A.; Stevenson, B.; Kraiczy, P. Complement Evasion Contributes to Lyme Borreliae–Host Associations. Trends Parasitol. 2020, 36, 634–645. [Google Scholar] [CrossRef]
- Margos, G.; Fingerle, V.; Reynolds, S. Borrelia bavariensis: Vector switch, niche invasion, and geographical spread of a tick-borne bacterial parasite. Front. Ecol. Evol. 2019, 7, 401. [Google Scholar] [CrossRef] [Green Version]
- Wallenhammar, A.; Lindqvist, R.; Asghar, N.; Gunaltay, S.; Fredlund, H.; Davidsson, A.; Andersson, S.; Överby, A.K.; Johansson, M. Revealing new tick-borne encephalitis virus foci by screening antibodies in sheep milk. Parasites Vectors 2020, 13, 185. [Google Scholar] [CrossRef] [Green Version]
- Springer, A.; Glass, A.; Topp, A.K.; Strube, C. Zoonotic tick-borne pathogens in temperate and cold regions of Europe—A review on the prevalence in domestic animals. Front. Vet. Sci. 2020, 7, 604910. [Google Scholar] [CrossRef]
- Vázquez, D.P.; Gianoli, E.; Morris, W.F.; Bozinovic, F. Ecological and evolutionary impacts of changing climatic variability. Biol. Rev. 2017, 92, 22–42. [Google Scholar] [CrossRef] [Green Version]
- Roslin, T.; Antão, L.; Hällfors, M.; Meyke, E.; Lo, C.; Tikhonov, G.; Delgado, M.d.M.; Gurarie, E.; Abadonova, M.; Abduraimov, O.; et al. Phenological shifts of abiotic events, producers and consumers across a continent. Nat. Clim. Chang. 2021, 11, 241–248. [Google Scholar] [CrossRef]
- Laaksonen, M.; Klemola, T.; Feuth, E.; Sormunen, J.J.; Puisto, A.; Mäkelä, S.; Penttinen, R.; Ruohomäki, K.; Hänninen, J.; Sääksjärvi, I.E.; et al. Tick-borne pathogens in Finland: Comparison of Ixodes ricinus and I. persulcatus in sympatric and parapatric areas. Parasites Vectors 2018, 11, 556. [Google Scholar] [CrossRef] [Green Version]
- Gray, J.; Kahl, O.; Zintl, A. What do we still need to know about Ixodes ricinus? Ticks Tick-Borne Dis. 2021, 12, 101682. [Google Scholar] [CrossRef]
- Jaenson, T.G.T.; Petersson, E.H.; Jaenson, D.G.E.; Kindberg, J.; Pettersson, J.H.O.; Hjertqvist, M.; Medlock, J.M.; Bengtsson, H. The importance of wildlife in the ecology and epidemiology of the TBE virus in Sweden: Incidence of human TBE correlates with abundance of deer and hares. Parasites Vectors 2018, 11, 477. [Google Scholar] [CrossRef] [PubMed]
- Thierfelder, T.; Larsolle, A.; Leibovici, D.G.; Ikonen, J.; Juval, C. Metadata Concerning the CLINF Climate and Landscape Data, Disseminated via CLINF GIS. Available online: https://clinf.org/home/clinf-geographic-information-system/ (accessed on 7 July 2021).
- Thierfelder, T.; Berggren, C.; Omazic, A.; Evengård, B. Metadata Concerning the Diseases Data Stored under the Directory “Human CSI”, Where CSI Means “Climate Sensitive Infections”. Available online: https://clinf.org/home/clinf-geographic-information-system/ (accessed on 7 July 2021).
- Dufresne, J.L.; Foujols, M.A.; Denvil, S.; Caubel, A.; Marti, O.; Aumont, O.; Balkanski, Y.; Bekki, S.; Bellenger, H.; Benshila, R.; et al. Climate change projections using the IPSL-CM5 Earth System Model: From CMIP3 to CMIP5. Clim. Dyn. 2013, 40, 2123–2165. [Google Scholar] [CrossRef]
- Leibovici, D.G. Spatio-temporal multiway decompositions using principal tensor analysis on k-modes: The R package PTAk. J. Stat. Softw. 2010, 34, 1–34. [Google Scholar] [CrossRef] [Green Version]
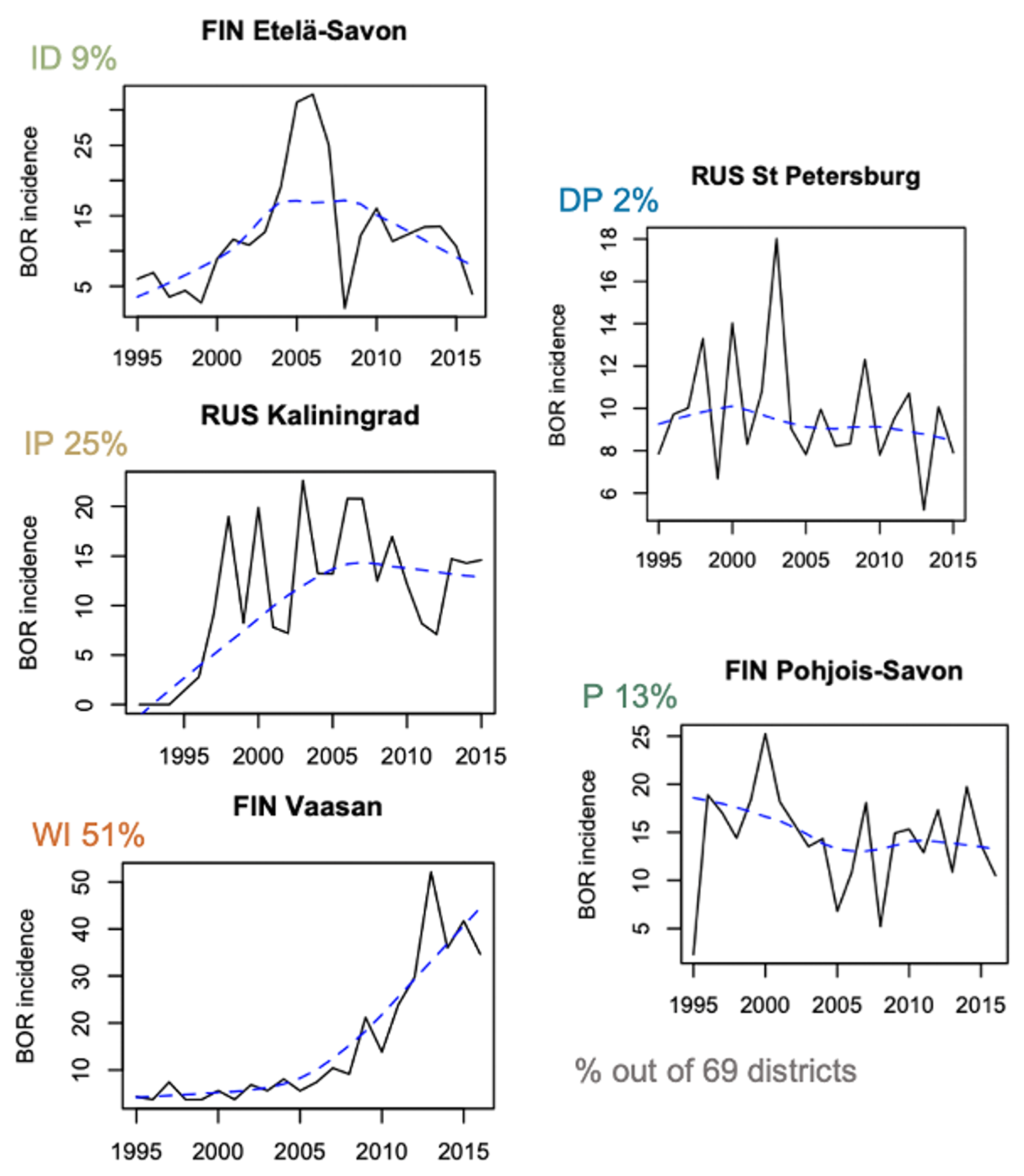

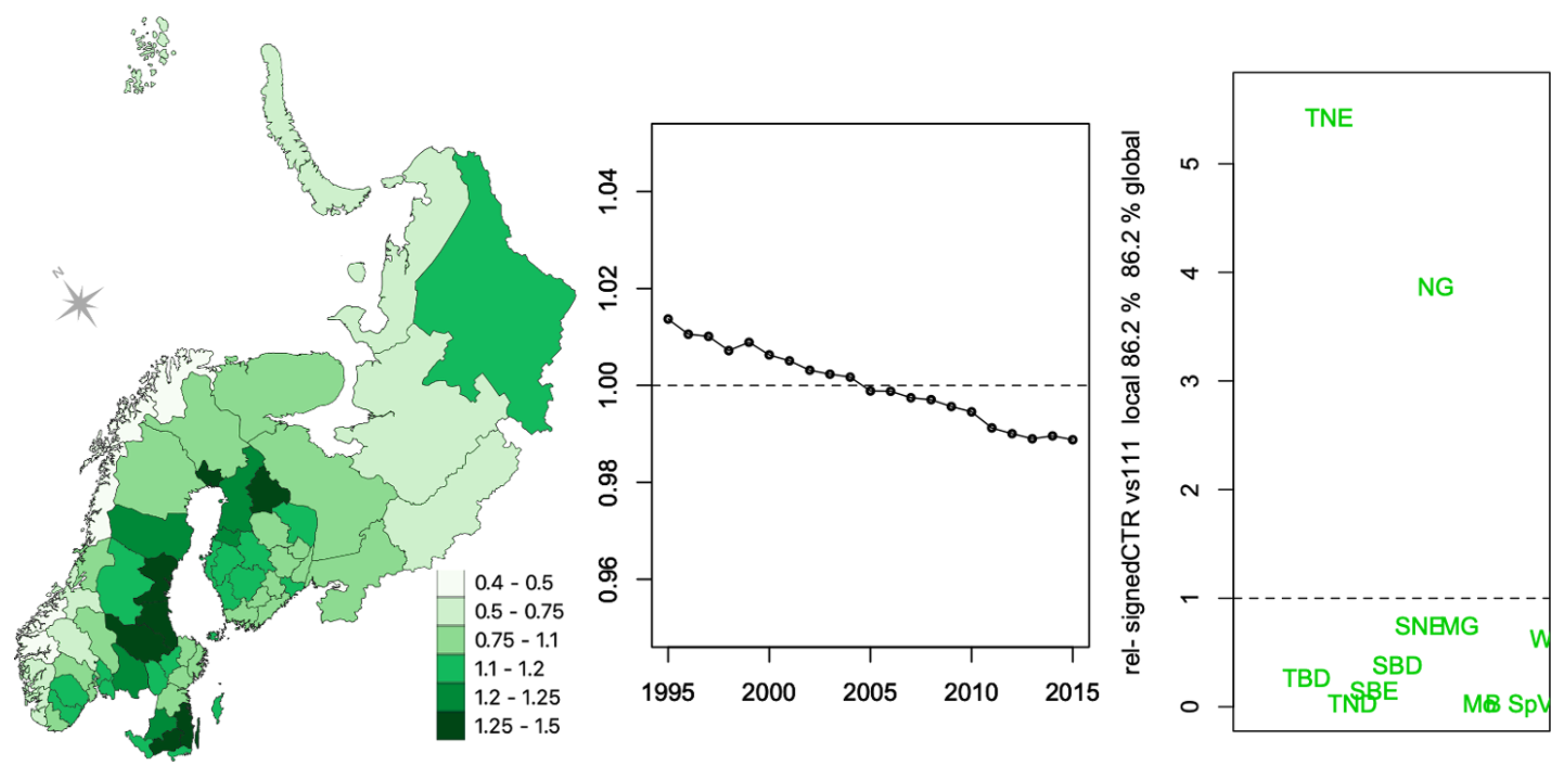
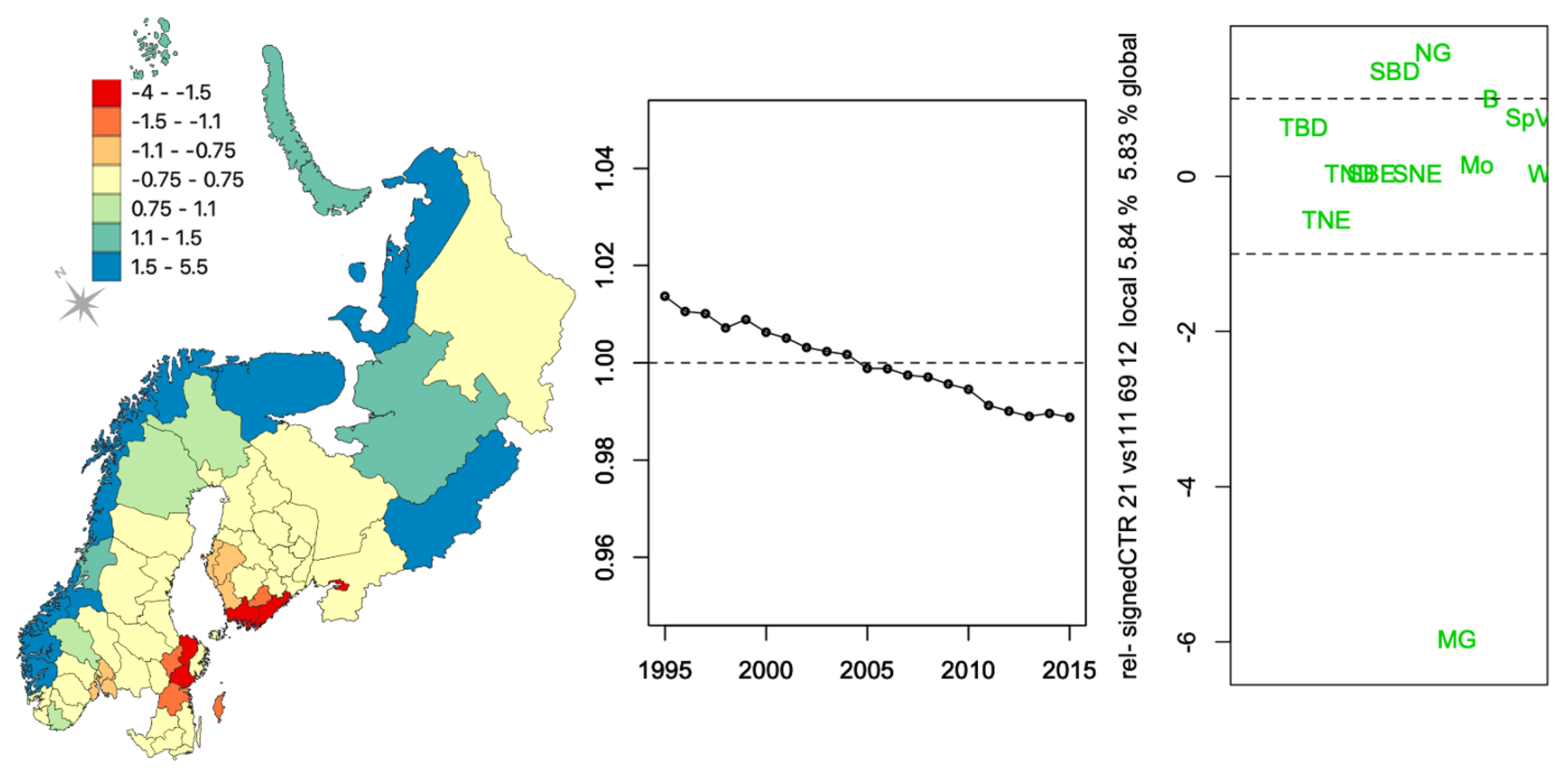
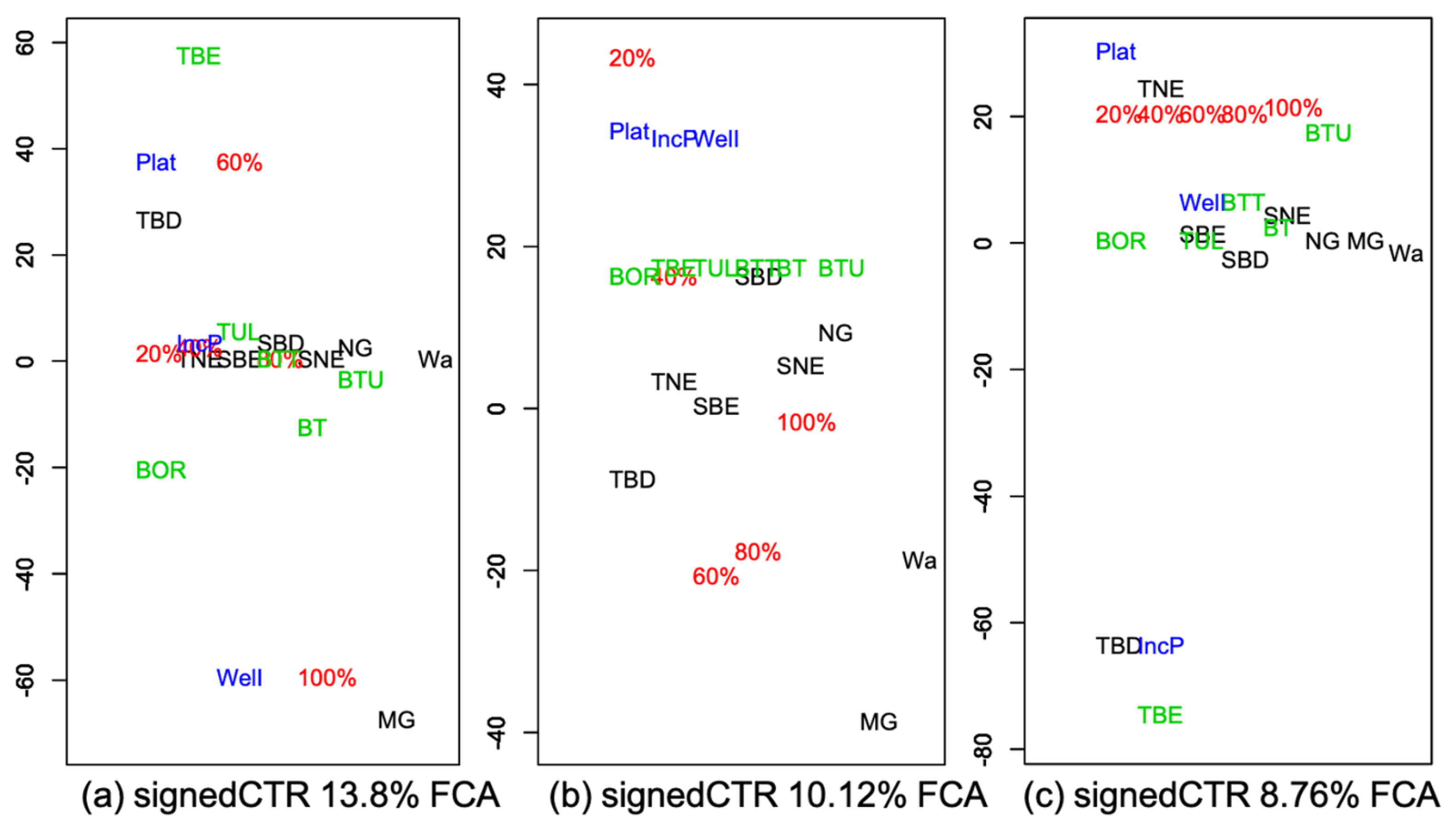

| TBE | ||||||||
|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | na | BOR (N = 69) | ||
| BOR | Decrease–Plateau 1 | 0 | 1 | 0 | 0 | 1 | 0 | 2 |
| Plateau 2 | 0 | 3 | 2 | 1 | 2 | 1 | 9 | |
| Increase–Decrease 3 | 0 | 2 | 0 | 2 | 2 | 0 | 6 | |
| Increase–Plateau 4 | 0 | 2 | 3 | 3 | 5 | 4 | 17 | |
| Well-Increasing 5 | 0 | 4 | 7 | 6 | 13 | 5 | 35 | |
| TBE (N = 59) | 0 | 12 | 12 | 12 | 23 | 10 | ||
| BT (N = 69) | 7 | 6 | 12 | 19 | 25 | |||
| All Districts | WI Districts | |||||||
|---|---|---|---|---|---|---|---|---|
| BOR | TBE | BOR | TBE | |||||
| Rank | Gaussian | Neg Bin | Gaussian | Neg Bin | Gaussian | Neg Bin | Gaussian | Neg Bin |
| 1 | +TBD | +MG | +NG | +MG | +TBD | +TBD | SBD | SBD |
| 2 | TND | +NG | SBE | +++TND | SBD | −SBD | TNE | ++Spv |
| 3 | +++SBE | SBD | +Mo | ++SNE | Spv | +MG | +++NG | +++NG |
| 4 | SNE | +TND | −Spv | +NG | TNE | TNE | −MG | −TNE |
| 5 | −SBD | +++SBE | −SBD | +Mo | ++++SNE | +++SNE | TBD | −MG |
| 6 | +MG | ++Spv | +MG | SBE | Mo | Mo | Mo | −TBD |
| 7 | −Spv | SNE | SBE | −Spv | SBE | −Mo | ||
| 8 | ++Mo | +Mo | +++TND | SBE | ++TND | |||
| AIC | 6909 | 18909 | 2326 | 8895 | 3524 | 9405 | 1066 | 4327 |
| 49% | 21% | 50% | 26% | 58% | 51% | 68% | 58% | |
| 10.28 | 28332 | 2.35 | 3664 | 8.85 | 9953 | 1.9 | 2215 | |
| Neg Bin Regressions on WI Districts and | ||||
|---|---|---|---|---|
| 1000 × BOR | 1000 × TBE | |||
| Rank | Coefficients (s.e.) | Coefficients (s.e.) | ||
| 1 | t°_avSum | 4.89 (0.45) | C3_grass | 175.7 (18.7) |
| 2 | soilhum_avSum | −3.78 (0.38) | temp_broad_summergreen | −313.1 (30.6) |
| 3 | t°_avSum_1 | 3.89 (0.42) | temp_needle_evergreen | −115.2 (13.9) |
| 4 | boreal_broad_summergreen | 25.6 (3.58) | boreal_broad_summergreen | −47.3 (7.65) |
| 5 | C3_grass | 19.6 (2.82) | C3_agriculture | −17.1 (2.72) |
| 6 | t°_avWin_1 | 2.05 (0.34) | soilhum_maxSum | 7.13 (1.44) |
| 7 | temp_needle_evergreen | −16.7 (2.93) | soilhum_avSum | 2.34 (0.45) |
| 8 | moss_lichen | −19.5 (3.99) | precip_max | −1.83 (0.43) |
| 9 | precip_avSum | 2.54 (0.47) | moss_lichen | −37.0 (10.8) |
| 10 | soilhum_maxSum_1 | −1.79 (0.40) | C3_grass_arctic | −56.0 (18.4) |
| 11 | t°_maxWin | −1.13 (0.31) | t°_maxSum_1 | 1.02 (0.51) |
| 12 | boreal_needle_deciduous | −59.2 (17.3) | ||
| 13 | precip_av_1 | 1.77 (0.62) | ||
| 14 | soilhum_maxSum | 2.25 (0.98) | ||
| 15 | boreal_needle_evergreen | −2.58 (1.25) | ||
| AIC | 8760.6 | 3916.2 | ||
| 56% | 66% | |||
| 9504.4 | 1991.8 | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Leibovici, D.G.; Bylund, H.; Björkman, C.; Tokarevich, N.; Thierfelder, T.; Evengård, B.; Quegan, S. Associating Land Cover Changes with Patterns of Incidences of Climate-Sensitive Infections: An Example on Tick-Borne Diseases in the Nordic Area. Int. J. Environ. Res. Public Health 2021, 18, 10963. https://doi.org/10.3390/ijerph182010963
Leibovici DG, Bylund H, Björkman C, Tokarevich N, Thierfelder T, Evengård B, Quegan S. Associating Land Cover Changes with Patterns of Incidences of Climate-Sensitive Infections: An Example on Tick-Borne Diseases in the Nordic Area. International Journal of Environmental Research and Public Health. 2021; 18(20):10963. https://doi.org/10.3390/ijerph182010963
Chicago/Turabian StyleLeibovici, Didier G., Helena Bylund, Christer Björkman, Nikolay Tokarevich, Tomas Thierfelder, Birgitta Evengård, and Shaun Quegan. 2021. "Associating Land Cover Changes with Patterns of Incidences of Climate-Sensitive Infections: An Example on Tick-Borne Diseases in the Nordic Area" International Journal of Environmental Research and Public Health 18, no. 20: 10963. https://doi.org/10.3390/ijerph182010963
APA StyleLeibovici, D. G., Bylund, H., Björkman, C., Tokarevich, N., Thierfelder, T., Evengård, B., & Quegan, S. (2021). Associating Land Cover Changes with Patterns of Incidences of Climate-Sensitive Infections: An Example on Tick-Borne Diseases in the Nordic Area. International Journal of Environmental Research and Public Health, 18(20), 10963. https://doi.org/10.3390/ijerph182010963










