Quest for Optimal Regression Models in SARS-CoV-2 Wastewater Based Epidemiology
Abstract
:1. Introduction
2. Methodology
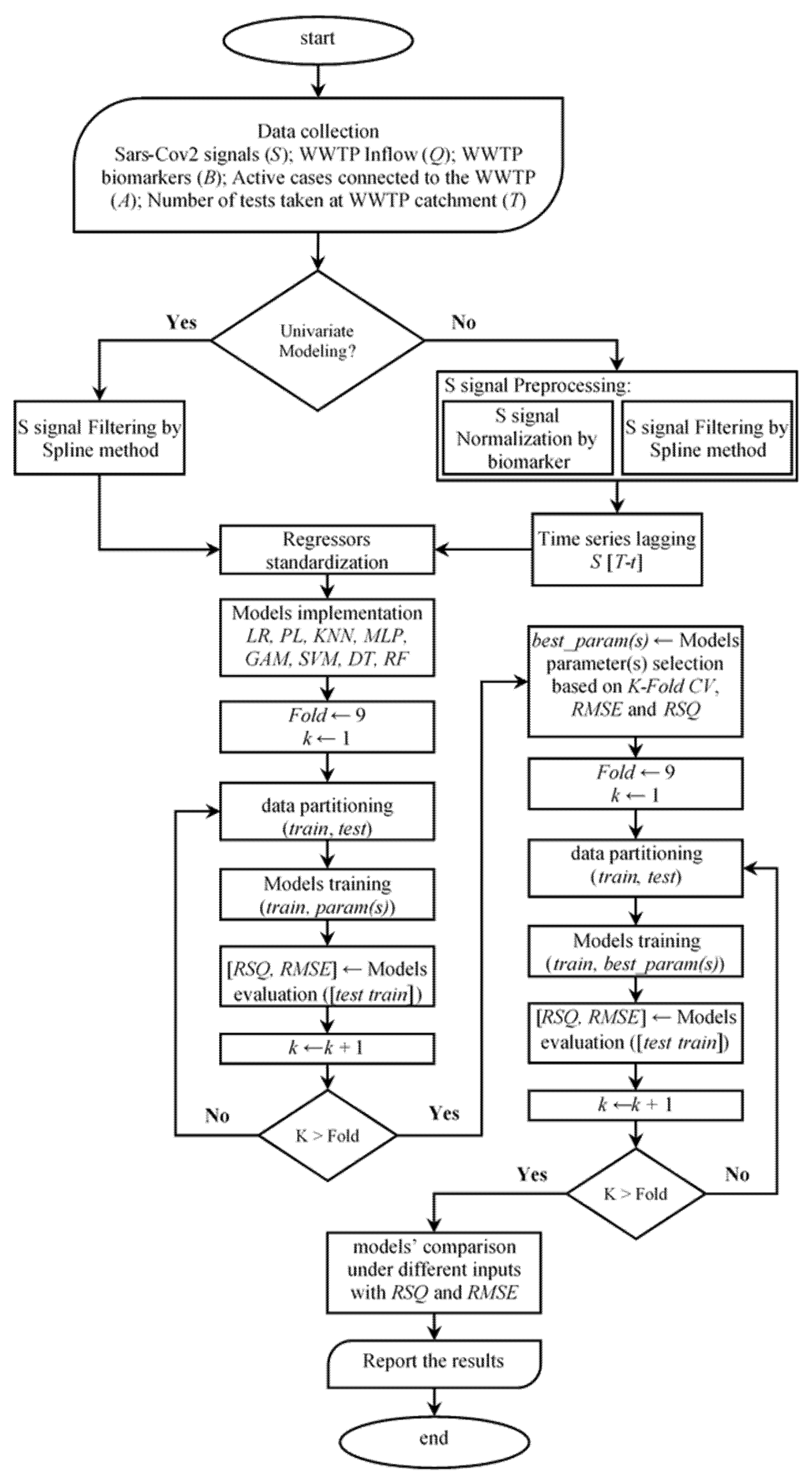
2.1. Modelling Procedure
- In the first category of the proposed modelling algorithm, the only source of information is the timeline of the wastewater signal, that is, the SARS-CoV-2 N1-gene copy numbers. Typically, this signal comes with significant noise and outliers, which influence the model training performance [45] Thus, a time series filtering method (the Spline method is used herein; [46]) is applied to filter out the noisy information adhered to the gene copy numbers.
- In the second category, in addition to the gene copy number, the information on the number of tests taken in the communities is used where available (in only two of the case studies). In addition, we apply further data pre-processing steps such as population-normalisation of the viral load, time lag, and time series filtering (as in the first category), the details of which are discussed in Section 2.3, Section 2.4 and Section 2.5.
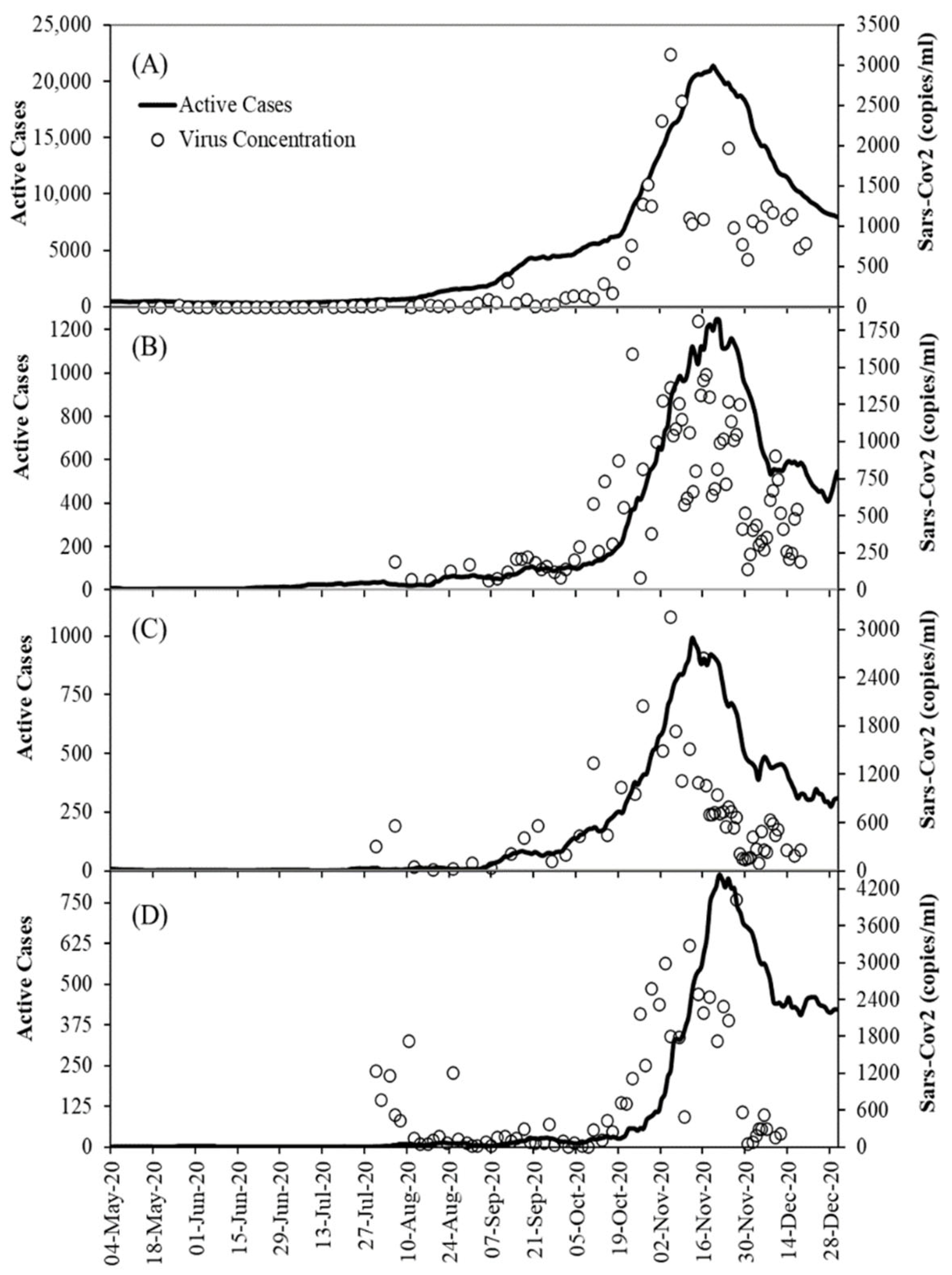
2.2. Dataset
2.3. Normalisation
2.4. Filtering
2.5. Lagging
2.6. Regression Models
2.7. Evaluation
3. Results and discussion
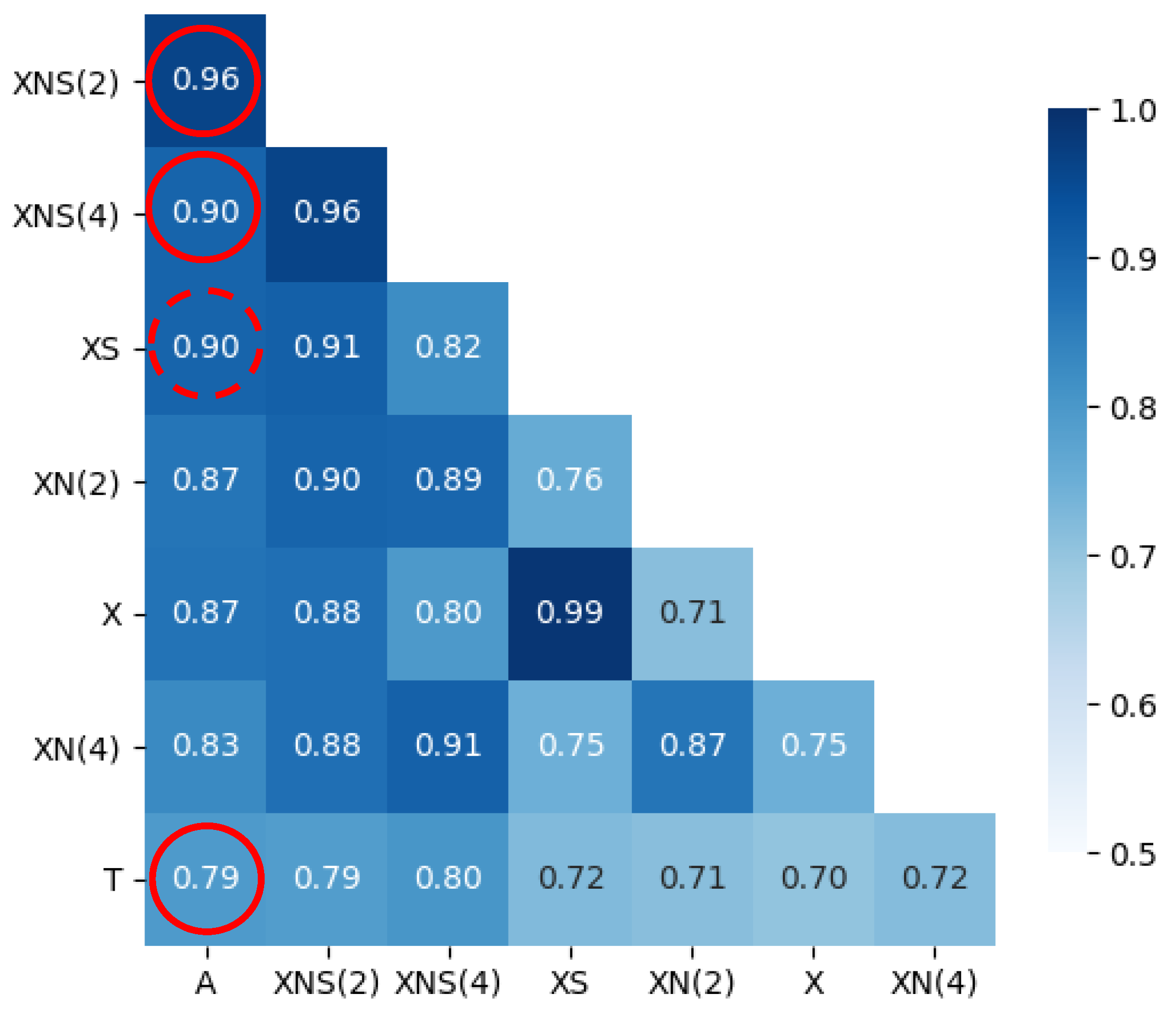
3.1. Time Series Lag
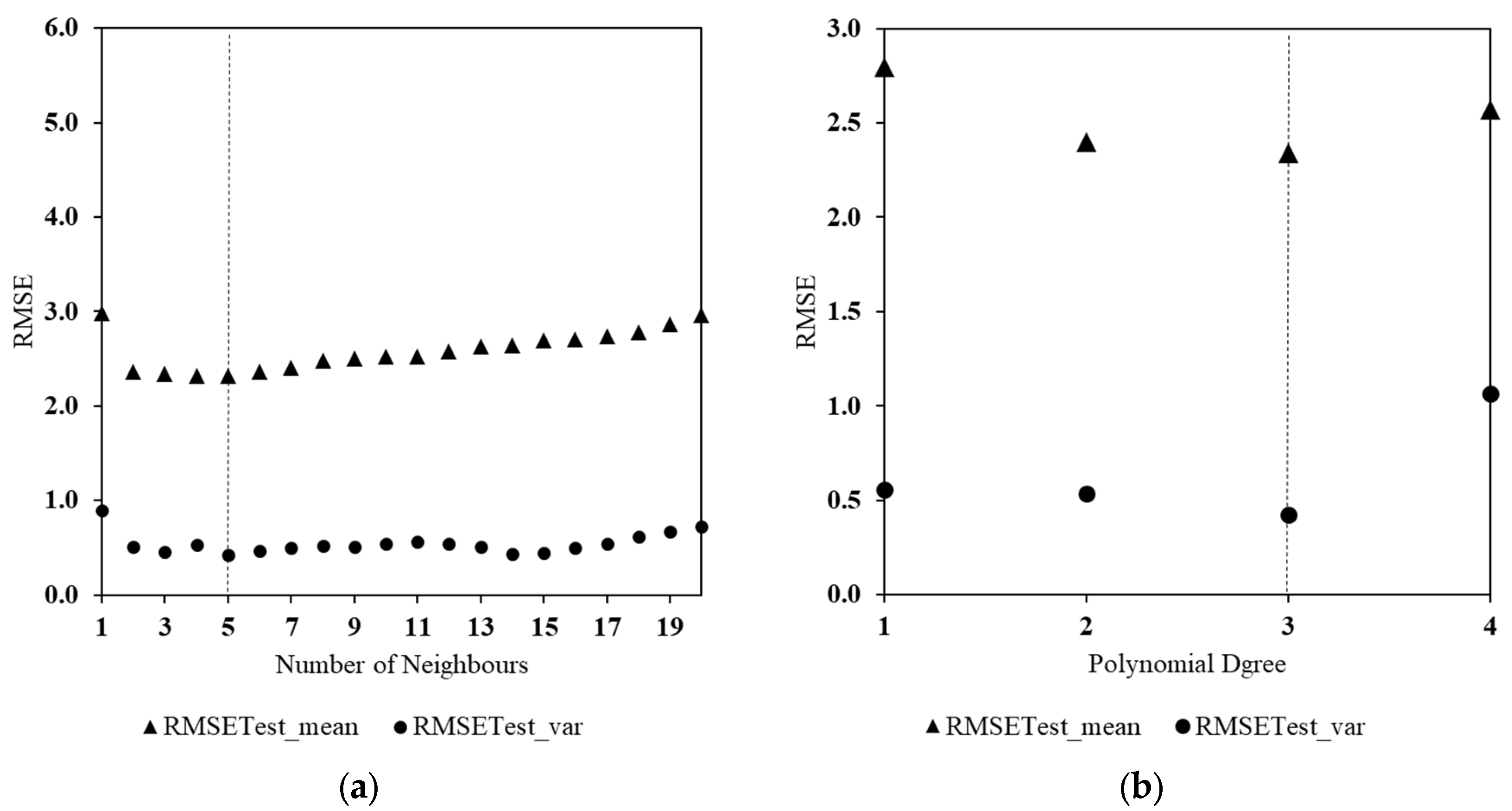
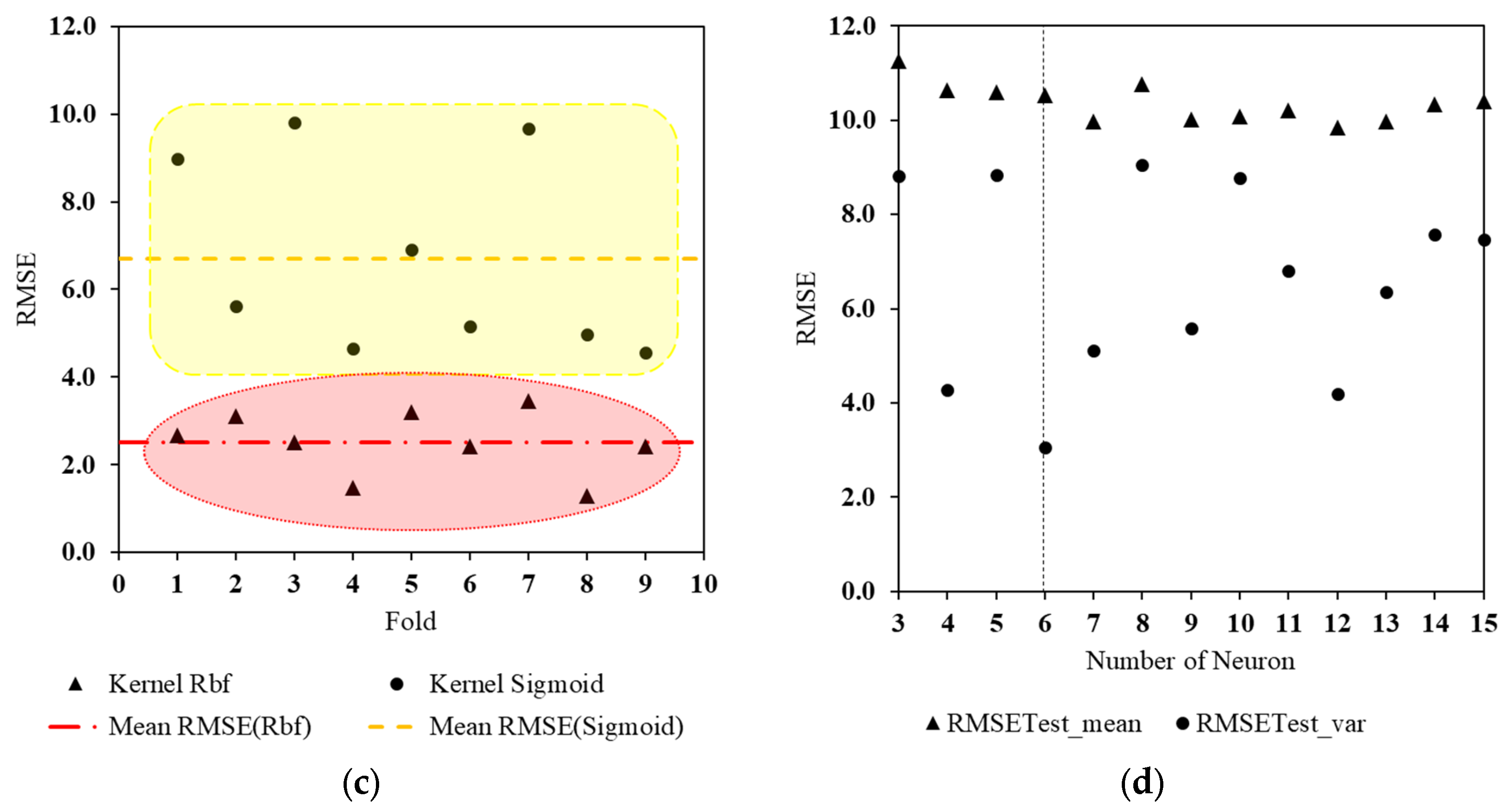
3.2. Global Parameter Tuning
3.3. Model Metrics
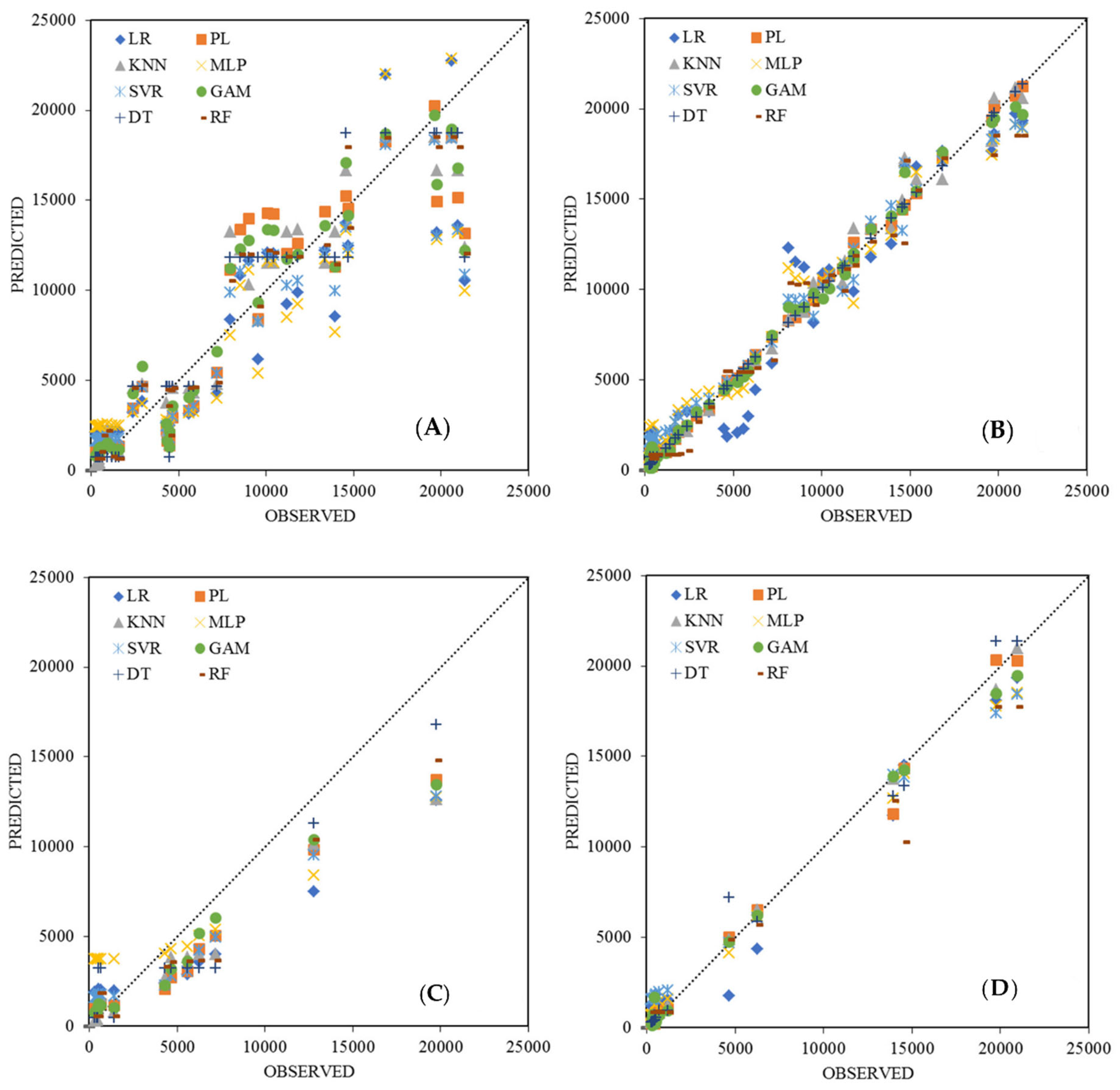
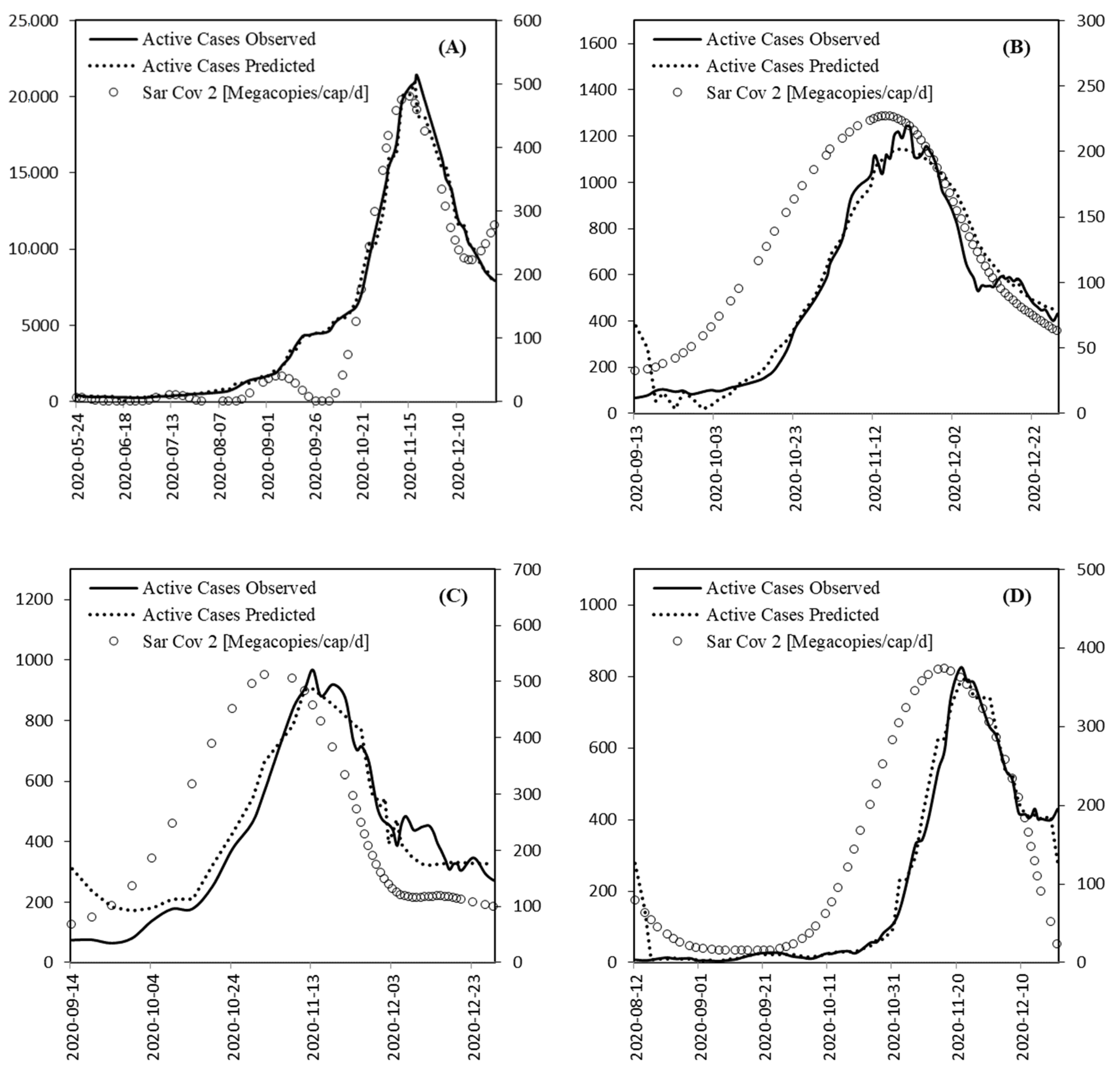
3.4. Model Comparison
4. Conclusions
- There is a consistent time shift between the (earlier) wastewater signal and the clinical test records, varying from 2 to 7 days in our dataset—depending both on time period and site;
- A thorough pre-processing of the data, such as population-based normalisation and smoothing, leads to more robust models and is important for practical application;
- The inclusion of additional information (most importantly the time lag and number of tests taken) by applying multivariate models significantly increases the performance of all investigated models;
- All multivariate models are generally applicable for the regression, and even a simple linear regression can be used, despite showing the poorest performance.
- While the differences are small, PL and KNN outperform more complex models such as GAM, SVR, and MLP;
- As seen from above, regression between the wastewater signal and incidence values is derived easily—also, in a practical context. The information supplements—but could even replace—individual testing for incidence.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B

References
- Metcalf, T.G.; Melnick, J.L.; Estes, M.K. Environmental Virology: From Detection of Virus in Sewage and Water by Isolation to Identification by Molecular Biology—A Trip of over 50 Years. Annu. Rev. Microbiol. 1995, 49, 461–487. [Google Scholar] [CrossRef] [PubMed]
- Kittigul, L.; Raengsakulrach, B.; Siritantikorn, S.; Kanyok, R.; Utrarachkij, F.; Diraphat, P.; Thirawuth, V.; Siripanichgon, K.; Pungchitton, S.; Chitpirom, K.; et al. Detection of Poliovirus, Hepatitis A Virus and Rotavirus from Sewage and Water Samples. Southeast Asian J. Trop. Med. Public Health 2000, 31, 41–46. [Google Scholar] [PubMed]
- Medema, G.; Heijnen, L.; Elsinga, G.; Italiaander, R.; Brouwer, A. Presence of SARS-Coronavirus-2 RNA in Sewage and Correlation with Reported COVID-19 Prevalence in the Early Stage of the Epidemic in the Netherlands. Environ. Sci. Technol. Lett. 2020, 7, 511–516. [Google Scholar] [CrossRef]
- Heijnen, L.; Medema, G. Surveillance of Influenza A and the Pandemic Influenza A (H1N1) 2009 in Sewage and Surface Water in the Netherlands. J. Water Health 2011, 9, 434–442. [Google Scholar] [CrossRef] [Green Version]
- Prado, T.; Fumian, T.M.; Mannarino, C.F.; Resende, P.C.; Motta, F.C.; Eppinghaus, A.L.F.; Chagas do Vale, V.H.; Braz, R.M.S.; de Andrade, J.D.S.R.; Maranhão, A.G.; et al. Wastewater-Based Epidemiology as a Useful Tool to Track SARS-CoV-2 and Support Public Health Policies at Municipal Level in Brazil. Water Res. 2021, 191, 116810. [Google Scholar] [CrossRef]
- Sims, N.; Kasprzyk-Hordern, B. Future Perspectives of Wastewater-Based Epidemiology: Monitoring Infectious Disease Spread and Resistance to the Community Level. Environ. Int. 2020, 139, 105689. [Google Scholar] [CrossRef]
- Ahmed, W.; Angel, N.; Edson, J.; Bibby, K.; Bivins, A.; O’Brien, J.W.; Mueller, J.F. First confirmed detection of SARS-CoV-2 in untreated wastewater in Australia: A proof of concept for the wastewater surveillance of COVID-19 in the community. Sci. Total Environ. 2020, 728, 138764. [Google Scholar] [CrossRef]
- Mallapaty, S. How Sewage Could Reveal True Scale of Coronavirus Outbreak. Nature 2020, 580, 176–177. [Google Scholar] [CrossRef] [Green Version]
- Mlejnkova, H.; Sovova, K.; Vasickova, P.; Ocenaskova, V.; Jasikova, L.; Juranova, E. Preliminary Study of SARS-CoV-2 Occurrence in Wastewater in the Czech Republic. Int. J. Environ. Res. Public Health 2020, 17, 5508. [Google Scholar] [CrossRef]
- Zhang, D.; Wang, X.; Gao, L.; Gong, Y. Predict and Analyze Exchange Rate Fluctuations Accordingly Based on Quantile Regression Model and K-Nearest Neighbor. J. Phys. Conf. Ser. 2021, 1813, 012016. [Google Scholar] [CrossRef]
- Arora, S.; Nag, A.; Sethi, J.; Rajvanshi, J.; Saxena, S.; Shrivastava, S.K.; Gupta, A.B. Sewage surveillance for the presence of SARS-CoV-2 genome as a useful wastewater based epidemiology (WBE) tracking tool in India. Water Sci. Technol. 2020, 82, 2823–2836. [Google Scholar] [CrossRef]
- Murakami, M.; Hata, A.; Honda, R.; Watanabe, T. Letter to the Editor: Wastewater-Based Epidemiology Can Overcome Representativeness and Stigma Issues Related to COVID-19. Environ. Sci. Technol. 2020, 54, 5311. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xagoraraki, I.; O’Brien, E. Wastewater-Based Epidemiology for Early Detection of Viral Outbreaks. In Women in Engineering and Science; Springer: Cham, Switzerland, 2020; pp. 75–97. [Google Scholar] [CrossRef] [Green Version]
- Gonzalez, R.; Curtis, K.; Bivins, A.; Bibby, K.; Weir, M.H.; Yetka, K.; Thompson, H.; Keeling, D.; Mitchell, J.; Gonzalez, D. COVID-19 Surveillance in Southeastern Virginia Using Wastewater-Based Epidemiology. Water Res. 2020, 186, 116296. [Google Scholar] [CrossRef] [PubMed]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Wurtzer, S.; Marechal, V.; Mouchel, J.M.; Maday, Y.; Teyssou, R.; Richard, E.; Almayrac, J.L.; Moulin, L. Evaluation of Lockdown Impact on SARS-CoV-2 Dynamics Through Viral Genome Quantification in Paris Wastewaters. medRxiv 2020. [Google Scholar] [CrossRef]
- Kumar, M.; Patel, A.K.; Shah, A.V.; Raval, J.; Rajpara, N.; Joshi, M.; Joshi, C.G. First Proof of the Capability of Wastewater Surveillance for COVID-19 in India through Detection of Genetic Material of SARS-CoV-2. Sci. Total Environ. 2020, 746, 141326. [Google Scholar] [CrossRef]
- Wu, F.; Zhang, J.; Xiao, A.; Gu, X.; Lee, W.L.; Armas, F.; Kauffman, K.; Hanage, W.; Matus, M.; Ghaeli, N.; et al. SARS-CoV-2 Titers in Wastewater Are Higher than Expected from Clinically Confirmed Cases. mSystems 2020, 5, e00614-20. [Google Scholar] [CrossRef] [PubMed]
- D’Aoust, P.M.; Graber, T.E.; Mercier, E.; Montpetit, D.; Alexandrov, I.; Neault, N.; Baig, A.T.; Mayne, J.; Zhang, X.; Alain, T.; et al. Catching a Resurgence: Increase in SARS-CoV-2 Viral RNA Identified in Wastewater 48 h before COVID-19 Clinical Tests and 96 h before Hospitalizations. Sci. Total Environ. 2021, 770, 145319. [Google Scholar] [CrossRef] [PubMed]
- Randazzo, W.; Truchado, P.; Cuevas-Ferrando, E.; Simón, P.; Allende, A.; Sánchez, G. SARS-CoV-2 RNA in Wastewater Anticipated COVID-19 Occurrence in a Low Prevalence Area. Water Res. 2020, 181, 115942. [Google Scholar] [CrossRef]
- Markt, R.; Bergthaler, A.; Bock, C.; Büchel-Marxer, M.; Grünbacher, D.; Mayr, M.; Peer, E.; Pedrazzini, M.; Penz, T.; Rauch, W.; et al. First detection and abundance of SARS-CoV-2 in wastewater in Liechtenstein: A surveillance in estimation of prevalence and impact of the SARS-CoV-2 B. 1.1.7 variant. 2021, submitted. [Google Scholar]
- Breslow, N.E. Generalized Linear Models: Checking Assumptions and Strengthening Conclusions. Stat. Appl. 1996, 8, 23–41. [Google Scholar]
- Osborne, J.W.; Waters, E. Four Assumptions of Multiple Regression That Researchers Should Always Test. Pract. Assess. Res. Eval. 2002, 8, 2. [Google Scholar]
- Centers for Disease Control and Prevention. Evaluating and Testing Persons for Coronavirus Disease 2019 (COVID-19); Centers for Disease Control and Prevention: Atlanta, GA, USA, 2020. [Google Scholar]
- Pettit, S.D.; Jerome, K.R.; Rouquié, D.; Mari, B.; Barbry, P.; Kanda, Y.; Matsumoto, M.; Hester, S.; Wehmas, L.; Botten, J.W.; et al. “All In”: A Pragmatic Framework for COVID-19 Testing and Action on a Global Scale. EMBO Mol. Med. 2020, 12, e12634. [Google Scholar] [CrossRef]
- Rashid, Z.Z.; Othman, S.N.; Abdul Samat, M.N.; Ali, U.K.; Wong, K.K. Diagnostic Performance of COVID-19 Serology Assays. Malays. J. Pathol. 2020, 42, 13–21. [Google Scholar]
- Gudbjartsson, D.F.; Helgason, A.; Jonsson, H.; Magnusson, O.T.; Melsted, P.; Norddahl, G.L.; Saemundsdottir, J.; Sigurdsson, A.; Sulem, P.; Agustsdottir, A.B.; et al. Spread of SARS-CoV-2 in the Icelandic Population. N. Engl. J. Med. 2020, 382, 2302–2315. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Chen, L.; Deng, Q.; Zhang, G.; Wu, K.; Ni, L.; Yang, Y.; Liu, B.; Wang, W.; Wei, C.; et al. The Presence of SARS-CoV-2 RNA in the Feces of COVID-19 Patients. J. Med. Virol. 2020, 92, 833–840. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yang, R.; Gui, X.; Xiong, Y. Comparison of Clinical Characteristics of Patients with Asymptomatic vs. Symptomatic Coronavirus Disease 2019 in Wuhan, China. JAMA Netw. Open 2020, 3, e2010182. [Google Scholar] [CrossRef]
- Bi, Q.; Wu, Y.; Mei, S.; Ye, C.; Zou, X.; Zhang, Z.; Liu, X.; Wei, L.; Truelove, S.A.; Zhang, T.; et al. Epidemiology and transmission of COVID-19 in 391 cases and 1286 of their close contacts in Shenzhen, China: A retrospective cohort study. Lancet Infect Dis. 2020, 20, 911–919. [Google Scholar] [CrossRef]
- Tang, A.N.; Tong, Z.D.; Wang, H.L.; Dai, Y.X.; Li, K.F.; Liu, J.N.; Wu, W.J.; Yuan, C.; Yu, M.L.; Li, P.; et al. Detection of Novel Coronavirus by RT-PCR in Stool Specimen from Asymptomatic Child, China. Emerg. Infect. Dis. 2020, 26, 1337–1339. [Google Scholar] [CrossRef]
- Banks, A.P.; Lai, F.Y.; Mueller, J.F.; Jiang, G.; Carter, S.; Thai, P.K. Potential impact of the sewer system on the applicability of alcohol and tobacco biomarkers in wastewater-based epidemiology. Drug Test. Anal. 2020, 10, 530–538. [Google Scholar] [CrossRef] [PubMed]
- Eramo, A.; Morales Medina, W.R.M.; Fahrenfeld, N.L. Factors Associated with Elevated Levels of Antibiotic Resistance Genes in Sewer Sediments and Wastewater. Environ. Sci. Water Res. Technol. 2020, 6, 1697–1710. [Google Scholar] [CrossRef] [PubMed]
- Rath, S.; Tripathy, A.; Tripathy, A.R. Prediction of New Active Cases of Coronavirus Disease (COVID-19) Pandemic Using Multiple Linear Regression Model. Diabetes Metab. Syndr. 2020, 14, 1467–1474. [Google Scholar] [CrossRef] [PubMed]
- Muhammad, L.J.; Islam, M.M.; Usman, S.S.; Ayon, S.I. Predictive Data Mining Models for Novel Coronavirus (COVID-19) Infected Patients’ Recovery. SN Comput. Sci. 2020, 1, 206. [Google Scholar] [CrossRef] [PubMed]
- Sujath, R.; Chatterjee, J.M.; Hassanien, A.E. A Machine Learning Forecasting Model for COVID-19 Pandemic in India. Stoch. Environ. Res. Risk Assess. 2020, 34, 959–972. [Google Scholar] [CrossRef] [PubMed]
- Saqib, M. Forecasting COVID-19 Outbreak Progression Using Hybrid Polynomial-Bayesian Ridge Regression Model. Appl. Intell. 2021, 51, 2703–2713. [Google Scholar] [CrossRef]
- Parbat, D.; Chakraborty, M. A Python Based Support Vector Regression Model for Prediction of COVID19 Cases in India. Chaos Solitons Fract. 2020, 138, 109942. [Google Scholar] [CrossRef] [PubMed]
- Fayyoumi, E.; Idwan, S.; AboShindi, H. Machine Learning and Statistical Modelling for Prediction of Novel COVID-19 Patients Case Study: Jordan. IJACSA Int. J. Adv. Comput. Sci. Appl. 2020, 11, 122–126. [Google Scholar] [CrossRef]
- Vallejo, J.A.; Rumbo-Feal, S.; Conde-Pérez, K.; López-Oriona, Á.; Tarrío, J.; Reif, R.; Ladra, S.; Rodiño-Janeiro, B.K.; Nasser, M.; Cid, Á.; et al. Highly Predictive Regression Model of Active Cases of COVID-19 in a Population by Screening Wastewater Viral Load. medRxiv 2020. [Google Scholar] [CrossRef]
- Hemalatha, M.; Kiran, U.; Kuncha, S.K.; Kopperi, H.; Gokulan, C.G.; Mohan, S.V.; Mishra, R.K. Surveillance of SARS-CoV-2 Spread Using Wastewater-Based Epidemiology: Comprehensive Study. Sci. Total Environ. 2021, 768, 144704. [Google Scholar] [CrossRef]
- Huang, Y.; Zhang, Y.; Li, N.; Chambers, J. Robust Student’st Based Nonlinear Filter and Smoother. IEEE Trans. Aerosp. Electron. Syst. 2016, 52, 2586–2596. [Google Scholar] [CrossRef] [Green Version]
- Been, F.; Rossi, L.; Ort, C.; Rudaz, S.; Delémont, O.; Esseiva, P. Population normalization with ammonium in wastewater-based epidemiology: Application to illicit drug monitoring. Environ. Sci. Technol. 2014, 48, 8162–8169. [Google Scholar] [CrossRef] [PubMed]
- Tscharke, B.J.; O’Brien, J.W.; Ort, C.; Grant, S.; Gerber, C.; Bade, R.; Thai, P.K.; Thomas, K.V.; Mueller, J.F. Harnessing the Power of the Census: Characterizing Wastewater Treatment Plant Catchment Populations for Wastewater-Based Epidemiology. Environ. Sci. Technol. 2019, 53, 10303–10311. [Google Scholar] [CrossRef] [PubMed]
- Arabzadeh, R.; Gruenbacher, D.M.; Insam, H.; Kreuzinger, N.; Markt, R.; Rauch, W. Data filtering methods for SARS-CoV-2 wastewater surveillance. Water Sci. Technol. 2021, 84, 1324–1339. [Google Scholar] [CrossRef] [PubMed]
- Reinsch, C.H. Smoothing by Spline Functions. Numer. Math. 1967, 10, 177–183. [Google Scholar] [CrossRef]
- Sharma, P.; Singh, J. Machine Learning Based Effort Estimation Using Standardization. In Proceedings of the 2018 International Conference on Computing, Power and Communication Technologies (GUCON), Greater Noida, India, 28–29 September 2018; IEEE Publications: Piscataway, NJ, USA, 2019; pp. 716–720. [Google Scholar]
- Stone, M. An Asymptotic Equivalence of Choice of Model by Cross-Validation and Akaike’s Criterion. J. R. Stat. Soc. B 1977, 39, 44–47. [Google Scholar] [CrossRef]
- Choi, P.M.; Tscharke, B.J.; Donner, E.; O’Brien, J.W.; Grant, S.C.; Kaserzon, S.L.; Mackie, R.; O’Malley, E.; Crosbie, N.D.; Thomas, K.V.; et al. Wastewater-Based Epidemiology Biomarkers: Past, Present and Future. TrAC Trends Anal. Chem. 2018, 105, 453–469. [Google Scholar] [CrossRef]
- Eubank, R.L. Spline Smoothing and Nonparametric Regression; Marcel Dekker Inc.: New York, NY, USA, 1988. [Google Scholar]
- Silverman, B.W. Some Aspects of the Spline Smoothing Approach to Non-Parametric Regression Curve Fitting. J. R. Stat. Soc. B 1985, 47, 1–21. [Google Scholar] [CrossRef]
- Dean, R.T.; Dunsmuir, W.T. Dangers and Uses of Cross-Correlation in Analyzing Time Series in Perception, Performance, Movement, and Neuroscience: The Importance of Constructing Transfer Function Autoregressive Models. Behav. Res. Methods 2016, 48, 783–802. [Google Scholar] [CrossRef] [Green Version]
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Automat. Contr. 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Yan, X.; Su, X. Linear Regression Analysis: Theory and Computing; World Scientific Publishing: Singapore, 2009. [Google Scholar]
- Stigler, S.M. Gergonne’s 1815 Paper on the Design and Analysis of Polynomial Regression Experiments. Hist. Math. 1974, 1, 431–439. [Google Scholar] [CrossRef] [Green Version]
- Amar, L.A.; Taha, A.A.; Mohamed, M.Y. Prediction of the final size for COVID-19 epidemic using machine learning: A case study of Egypt. Infect. Dis. Model. 2020, 5, 622–634. [Google Scholar] [CrossRef]
- Zhang, S.; Li, X.; Zong, M.; Zhu, X.; Cheng, D. Learning k for kNN Classification. ACM Trans. Intell. Syst. Technol. 2017, 8, 1–19. [Google Scholar] [CrossRef] [Green Version]
- Pourhomayoun, M.; Shakibi, M. Predicting Mortality Risk in Patients with COVID-19 Using Artificial Intelligence to Help Medical Decision-Making. medRxiv 2020. [Google Scholar] [CrossRef] [Green Version]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning: Data Mining, Inference, and Prediction; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Awad, M.; Khanna, R. Support vector regression. In Efficient Learning Machines; Apress: Berkeley, CA, USA, 2015; pp. 67–80. [Google Scholar]
- Ribeiro, M.H.D.M.; da Silva, R.G.; Mariani, V.C.; Coelho, L.D.S. Short-Term Forecasting COVID-19 Cumulative Confirmed Cases: Perspectives for Brazil. Chaos Solitons Fract. 2020, 135, 109853. [Google Scholar] [CrossRef]
- Hastie, T.J.; Tibshirani, R.J. Generalized Additive Models. Stat. Sci. 1986, 1, 297–310. [Google Scholar] [CrossRef]
- Prata, D.N.; Rodrigues, W.; Bermejo, P.H. Temperature Significantly Changes COVID-19 Transmission in (Sub) Tropical Cities of Brazil. Sci. Total Environ. 2020, 729, 138862. [Google Scholar] [CrossRef] [PubMed]
- Loh, W.Y. Classification and Regression Trees. WIREs Data Min. Knowl. Discov. 2011, 1, 14–23. [Google Scholar] [CrossRef]
- Karnon, J. A Simple Decision Analysis of a Mandatory Lockdown Response to the COVID-19 Pandemic. Appl. Health Econ. Health Policy 2020, 18, 329–331. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Prakash, K.B.; Imambi, S.S.; Ismail, M.; Kumar, T.P.; Pawan, Y.N. Analysis, Prediction and Evaluation of COVID-19 Datasets Using Machine Learning Algorithms. Int. J. Emerg. Trends Eng. Res. 2020, 5, 2199–2204. [Google Scholar] [CrossRef]
- Picard, R.R.; Cook, R.D. Cross-Validation of Regression Models. J. Am. Stat. Assoc. 1984, 79, 575–583. [Google Scholar] [CrossRef]
- Benesty, J.; Chen, J.; Huang, Y.; Cohen, I. Pearson correlation coefficient. In Noise Reduction in Speech Processing; Springer: Berlin/Heidelberg, Germany, 2009; pp. 1–4. [Google Scholar] [CrossRef]
- Taylor, K.E. Summarizing Multiple Aspects of Model Performance in a Single Diagram. J. Geophys. Res. 2001, 106, 7183–7192. [Google Scholar] [CrossRef]


| WWTP | Start Date | End Date | Avg. Daily SARS-CoV-2 Gene Copies/mL | Avg. Daily Active Cases | Avg. Daily Number of Tests | Avg. Daily Inflow (m3/d) | Population (1 January 2020) | Avg. Daily NH4-N (mg/L) |
|---|---|---|---|---|---|---|---|---|
| A | 4 May 2020 | 30 Dec 2020 | 464 | 5325 | 4218 | 539,450 | 1,900,000 | 38.09 |
| B | 3 Aug 2020 | 28 Dec 2020 | 609 | 249 | 1126 | 83,187 | 320,681 | 29.49 |
| C | 27 Jul 2020 | 28 Dec 2020 | 658 | 186 | 16,344 | 41,696 | 28.90 | |
| D | 27 Jul 2020 | 21 Dec 2020 | 781 | 136 | 4899 | 23,600 | 34.18 |
| Model | Reference | Application in Covid 19 Modeling |
|---|---|---|
| Linear (LR) | [54] | [34] |
| Polynomial (PL) | [55] | [56] |
| K Nearest Neighbor (KNN) | [57] | [58] |
| Multilayer Perceptron (MLP) | [59] | [36] |
| Support Vector Regression (SVR) | [60] | [61] |
| Generalized Additive Models (GAM) | [62] | [63] |
| Decision Tree (DT) | [64] | [65] |
| Random Forest (RF) | [15] | [66] |
| WWTP | Models Metrics | ||||||
|---|---|---|---|---|---|---|---|
| R-Squared | Adj. R-Squared | F_Statistic | Prob (F-Statistic) | Log-Likelihood | AIC | BIC | |
| A | 0.939 | 0.936 | 303.600 | 0.000 | −554.100 | 1116.000 | 1125.000 |
| B | 0.942 | 0.939 | 365.600 | 0.000 | −425.690 | 859.400 | 868.500 |
| C | 0.868 | 0.862 | 148.300 | 0.000 | −280.880 | 567.800 | 573.400 |
| D | 0.873 | 0.869 | 196.800 | 0.000 | −356.860 | 719.700 | 726.000 |
| Models parameters | |||||||
| Const. | S2 * | S3 | S4 | S5 | S7 | T ** | |
| A | 573.150 | 49.890 | - | −16.710 | - | - | 0.003 |
| B | −278.660 | 3.230 | - | - | - | 2.040 | 0.001 |
| C | 167.425 | - | - | - | 2.482 | −1.060 | - |
| D | −69.215 | - | 1.035 | - | - | 0.916 | - |
| Parameters significance: P > │t│ | |||||||
| A | 0.193 | 0.000 | - | 0.001 | - | - | 0.010 |
| B | 0.000 | 0.000 | - | - | - | 0.000 | 0.000 |
| C | 0.000 | - | - | - | 0.000 | 0.000 | - |
| D | 0.001 | - | 0.000 | - | - | 0.000 | - |
| Model/WWTP | A | B | C | D |
|---|---|---|---|---|
| DT | ||||
| GAM | ○ | ○ | ||
| KNN | ● | ● | ○ | |
| LR | ||||
| MLP | ● | |||
| PL | ○ | ○ | ○ | ○ |
| RF | ||||
| SVR | ○ | ● |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aberi, P.; Arabzadeh, R.; Insam, H.; Markt, R.; Mayr, M.; Kreuzinger, N.; Rauch, W. Quest for Optimal Regression Models in SARS-CoV-2 Wastewater Based Epidemiology. Int. J. Environ. Res. Public Health 2021, 18, 10778. https://doi.org/10.3390/ijerph182010778
Aberi P, Arabzadeh R, Insam H, Markt R, Mayr M, Kreuzinger N, Rauch W. Quest for Optimal Regression Models in SARS-CoV-2 Wastewater Based Epidemiology. International Journal of Environmental Research and Public Health. 2021; 18(20):10778. https://doi.org/10.3390/ijerph182010778
Chicago/Turabian StyleAberi, Parisa, Rezgar Arabzadeh, Heribert Insam, Rudolf Markt, Markus Mayr, Norbert Kreuzinger, and Wolfgang Rauch. 2021. "Quest for Optimal Regression Models in SARS-CoV-2 Wastewater Based Epidemiology" International Journal of Environmental Research and Public Health 18, no. 20: 10778. https://doi.org/10.3390/ijerph182010778
APA StyleAberi, P., Arabzadeh, R., Insam, H., Markt, R., Mayr, M., Kreuzinger, N., & Rauch, W. (2021). Quest for Optimal Regression Models in SARS-CoV-2 Wastewater Based Epidemiology. International Journal of Environmental Research and Public Health, 18(20), 10778. https://doi.org/10.3390/ijerph182010778







