Can Innovation Agglomeration Reduce Carbon Emissions? Evidence from China
Abstract
1. Introduction
2. Theoretical Model and Research Hypothesis
2.1. Effect of Innovation Agglomeration on Carbon Emission Intensity
2.2. Influence of Energy Intensity on Carbon Emission Intensity
2.3. The Mediating Effect of Energy Intensity between Innovation Agglomeration and Carbon Emission Intensity
3. Data Description and Empirical Model
3.1. Data Description
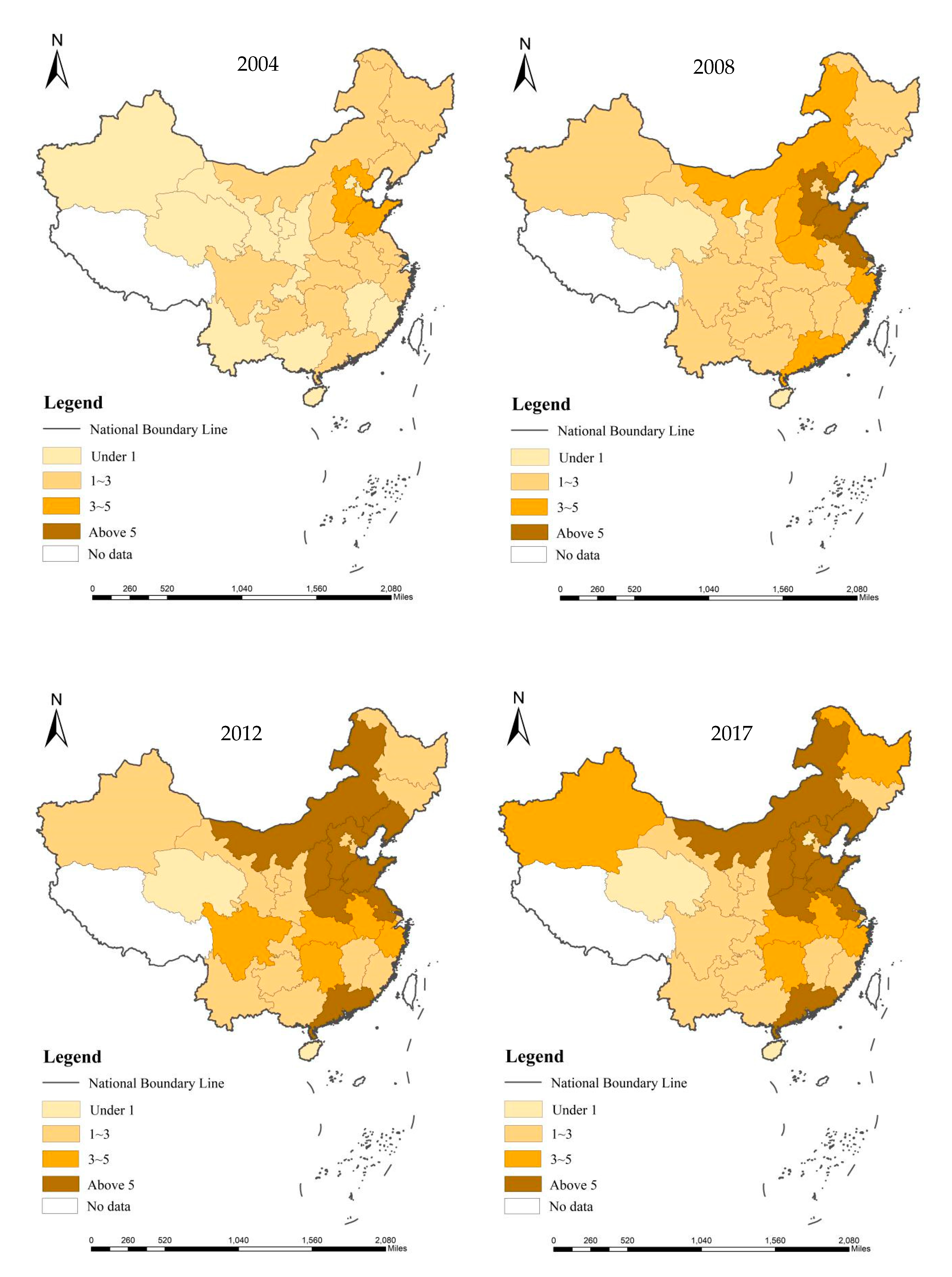
3.1.1. Explained Variable: Carbon Emission Intensity (CO2)
3.1.2. Core Explanatory Variables
3.1.3. Control Variables
3.2. Data Source
3.3. Empirical Model
Test Model for the Effect of Innovation Agglomeration and Energy Intensity on Carbon Emission Intensity
3.4. Parameter Estimation Method
4. Empirical Results and Discussion
4.1. Spatial Correlation Test Results
4.2. Impact of Innovation Agglomeration and Energy Intensity on Carbon Emission—An Empirical Test of Hypothesis 1 and Hypothesis 2
4.2.1. Regression Results
4.2.2. Further Testing by Subregion
4.3. Energy Intermediation Effect Test Based on Carbon Emission
5. Conclusions and Suggestion
- (1)
- The time lag terms of carbon emission intensity and energy intensity are significant at 1%, and the spatial correlation coefficient is also significant, which indicate that energy intensity and carbon emission intensity have strong spatio-temporal dependence effect. To be more specific, these two variables not only show path-dependence in the dimension of time, but also produce significant spatial spillover effect. For instance, if these two variables in the last period are at a high level, then in the next period they may also continue to rise. It indicates that once the industrial path and technological path are formed, great efforts may be required to change the evolutionary path of carbon emission. Therefore, there is still a long and tough way for the implementation of carbon emission reduction. In the spatial dimension, the carbon emission intensity and energy intensity among regions show a significantly positive spatial correlation, suggesting that China’s current work in terms of carbon emission reduction must be implemented through constructing cooperative linkage effect among regions. It is necessary to strengthen regional cooperation by establishing a joint prevention and control mechanism across administrative regions, forming a coordinated pollution control system in various regions, and clarifying environmental pollution control responsibilities.
- (2)
- Innovation agglomeration may have dual effect of saving energy and reducing emission and the critical value of innovation agglomeration’s emission reduction effect (5.0100) is larger than that of energy conservation effect (3.0309). There is a significant inverted U-shaped curve relationship between innovation agglomeration and carbon emission intensity. When the logarithm of innovation agglomeration exceeds 5.0100, it will have a significant effect on carbon emission reduction. Similarly, there is also a significant inverted U-shaped curve relationship between innovation agglomeration and energy intensity. Therefore, when the level of innovation agglomeration is low, agglomeration will promote the increase of energy intensity. When the logarithm of innovation agglomeration exceeds 3.0309, it can show significant inhibition effect on energy intensity, that is, innovation agglomeration has energy conservation effect. At present, the degree of innovation agglomeration in some developed provinces in China has already passed the critical point, above which innovation agglomeration produces the effect of saving energy and reducing emission. Hence, it could be expected that with the continuous improvement of regional innovation agglomeration level in China, the effect of technological innovation in saving energy and reducing emission will be realized in a larger scope. In China’s inshore areas, there is a significant inverted U-shaped curve relationship between innovation agglomeration and energy intensity or carbon emission intensity. However, in inland areas, innovation agglomeration does not appear to have a significant non-linear effect on carbon emissions, limited to the left part of the inverted U-shaped curve. That is, innovation agglomeration acted as a role in promoting the carbon emission intensity of inland areas. In the meantime, energy intensity has a non-linear positive promotion effect on carbon emissions. Accordingly, more attention should be paid to inshore areas, because they may contribute more to reducing the level of carbon emission in China. We need to adjust the regional innovation system, strengthen cooperation between inshore and inland areas, and facilitate the interconnection and sharing of innovative information resources.
- (3)
- There are direct and indirect paths on the mechanism for innovation agglomeration to affect carbon emission. When the logarithm of energy intensity exceeds 0.8536, carbon emission will be inhibited, which will have a significantly negative correlation between them. Therefore, on the one hand, innovation agglomeration can directly reduce carbon emission intensity through its various positive externalities. On the other hand, innovation agglomeration influences carbon emission through energy intensity, that is, energy intensity acts as its intermediary variable. The specific action mechanism is as follows: When the level of innovation agglomeration is low, it will promote the increase of energy intensity and reduce energy intensity, thus contributing to the decline of carbon emission intensity. As for industrial enterprises, they should be guided to improve production technology and promote energy intensive utilization. We should encourage enterprise to develop green manufacturing industries such as energy conservation and environmental protection industries, new energy equipment, and new energy vehicles, to drive the green upgrading and transformation of industry.
- (4)
- Compared with other studies, the conclusion in this paper is consistent with the researches of Lin et al. (2013) [82] and Zhang et al. (2017) [83], which show that China’s carbon emission intensity has a strong spatio-temporal dependence effect. However, differently from the studies of Li et al. (2020) [28] and Xue et al. (2020) [29], our empirical results show that in China’s inland areas, innovation increases the carbon emissions, while for the whole of China, the relationship between innovation and carbon emissions is nonlinear. Meanwhile, similar to Feng et al. (2019) [84], there is a threshold effect between technological innovation and carbon emissions. The difference is that our paper not only tests the threshold effect between innovation agglomeration and carbon emission intensity, but also empirically studies the nonlinear relationship with energy intensity, showing an energy saving effect of innovation agglomeration. Although this research has made some valuable achievements, it also has some limitations. Firstly, carbon emission intensity is calculated following the provincial data of China. It could be more accurate to use urban data to describe carbon emission intensity in China and the corresponding spatial correlation. Secondly, this paper uses regional patent data to calculate innovation agglomeration by output density model. However, innovation agglomeration includes not only innovation output, but also the aggregation of talents and R&D funds in specific regions, which is the direction that can be expanded in future research.
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Shi, A. The impact of population pressure on global carbon dioxide emissions, 1975–1996: Evidence from pooled cross-country data. Ecol. Econ. 2003, 44, 29–42. [Google Scholar] [CrossRef]
- Fernando, Y.; Hor, W.L. Impacts of energy management practices on energy efficiency and carbon emissions reduction: A survey of Malaysian manufacturing firms. Resour. Conserv. Recycl. 2017, 126, 62–73. [Google Scholar] [CrossRef]
- Li, W.; Sun, W.; Li, G.; Cui, P.; Wu, W.; Jin, B. Temporal and spatial heterogeneity of carbon intensity in China’s construction industry. Resour. Conserv. Recycl. 2017, 126, 162–173. [Google Scholar] [CrossRef]
- Watanabe, C. Identification of the role of renewable energy—A view from Japan challenge—The new sunshine program. Renew. Energy 1995, 6, 237–274. [Google Scholar] [CrossRef]
- Efthimeros, G.A.; Tsahalis, D.T. Intensified energy-saving technologies developed in EU-funded research: A review. Appl. Therm. Eng. 2000, 20, 1607–1613. [Google Scholar] [CrossRef]
- Zhang, P.D.; Yang, Y.L.; Shi, J.; Zheng, Y.H.; Wang, L.S.; Li, X.R. Opportunities and challenges for renewable energy policy in China. Renew. Sustain. Energy Rev. 2009, 13, 439–449. [Google Scholar]
- Tanatvanit, S.; Limmeechokchai, B.; Chungpaibulpatana, S. Sustainable energy development strategies: Implications of energy demand management and renewable energy in Thailand. Renew. Sustain. Energy Rev. 2003, 7, 367–395. [Google Scholar] [CrossRef]
- Connor, P.M. UK renewable energy policy: A review. Renew. Sustain. Energy Rev. 2003, 7, 65–82. [Google Scholar]
- Lorenzoni, I.; Nicholson-cole, S.; Whitmarsh, L. Barriers perceived to engaging with climate change among the UK public and their policy implications. Glob. Environ. Chang. 2007, 17, 445–459. [Google Scholar] [CrossRef]
- Nameroff, T.J.; Garant, R.J.; Albert, M.B. Adoption of green chemistry: An analysis based on US patents. Res. Policy. 2004, 33, 959–974. [Google Scholar] [CrossRef]
- Kang, Y.Q.; Zhao, T.; Yang, Y.Y. Environmental Kuznets curve for CO2 emissions in China: A spatial panel data approach. Ecol. Indic. 2016, 63, 231–239. [Google Scholar] [CrossRef]
- Nutakor, F.; Bizumuremyi, S.; Li, J.; Liu, W. Does the Environmental Kuznets Curve for CO2 Emissions Exist for Rwanda? Evidence from Bootstrapped Rolling-Window Granger Causality Test. Sustainability 2020, 12, 8636. [Google Scholar] [CrossRef]
- Bi, K.; Yang, M.; Zahid, L.; Zhou, X. A New Solution for City Distribution to Achieve Environmental Benefits within the Trend of Green Logistics: A Case Study in China. Sustainability 2020, 12, 8312. [Google Scholar] [CrossRef]
- Ke, H.Q.; Yang, W.Y.; Liu, X.Y.; Fan, F. Does Innovation Efficiency Suppress the Ecological Footprint? Empirical Evidence from 280 Chinese Cities. Int. J. Environ. Res. Public Health 2020, 17, 6826. [Google Scholar] [CrossRef]
- Loevinsohn, M.E.; Mugarura, J.; Nkusi, A. Cooperation and innovation by farmer groups-scale in the development of Rwandan valley farming systems. Agric. Syst. 1994, 46, 141–155. [Google Scholar] [CrossRef]
- Fan, F.; Zhang, X.R.; Yang, W.Y.; Liu, C.L. Spatiotemporal Evolution of China’s ports in the International Container Transport Network under Upgraded Industrial Structure. Transp. J. 2021, 60, 43–69. [Google Scholar]
- Megahed, S.; Scrosati, B. Lithium-ion rechargeable batteries. J. Power Sources 1994, 51, 79–104. [Google Scholar] [CrossRef]
- Lovell, H. Discourse and innovation journeys: The case of low energy housing in the UK. Technol. Anal. Strateg. Manag. 2008, 20, 613–632. [Google Scholar] [CrossRef]
- Coad, A.; Haan, P.D.; Woersdorfer, J.S. Consumer support for environmental policies: An application to purchases of green cars. Ecol. Econ. 2009, 68, 2078–2086. [Google Scholar] [CrossRef]
- Acemoglu, D.; Aghion, P.; Bursztyn, L.; Hemous, D. The environment and directed technical change. Am. Econ. Rev. 2012, 102, 131–166. [Google Scholar] [CrossRef]
- Bosetti, V.; Carraro, C.; Galeotti, M.; Massetti, E.; Tavoni, M. Witch—A world induced technical change hybrid model. Hybrid Model 2006, 27, 13–38. [Google Scholar] [CrossRef]
- Gerlagh, R. Measuring the value of induced technological change. Energy Policy 2007, 35, 5287–5297. [Google Scholar] [CrossRef]
- Jin, P.Z.; Zhang, Y.B.; Peng, X. The double-edged effect of technological progress in carbon dioxide emissions reduction: Empirical evidence from 35 sub-industrial sectors in China. Stud. Sci. Sci. 2014, 32, 706–716. [Google Scholar]
- Fisher-Vanden, K.; Jefferson, G.H.; Liu, H.M.; Tao, Q. What is Driving China’s Decline in Energy Intensity? Resour. Energy Econ. 2004, 26, 2287–2295. [Google Scholar] [CrossRef]
- Yan, F.Z.; Su, L.; Qiao, J. The relationship between industrial agglomeration development and environmental pollution: Evidence from China’s manufacturing industry. Stud. Sci. Sci. 2011, 29, 79–83. [Google Scholar]
- Hou, J.; Teo, T.S.H.; Zhou, F. Does industrial green transformation successfully facilitate a decrease in carbon intensity in China? An environmental regulation perspective. J. Clean. Prod. 2018, 184, 1060–1071. [Google Scholar] [CrossRef]
- Ma, Z.Y.; Liu, Y. Spatio-temporal patterns of key climate technology innovation differences: A case of countries along ‘the belt and road’. China Popul. Resour. Environ. 2017, 27, 102–111. [Google Scholar]
- Li, J.; Ma, J.; Wei, W. Analysis and Evaluation of the Regional Characteristics of Carbon Emission Efficiency for China. Sustainability 2020, 12, 3138. [Google Scholar] [CrossRef]
- Xue, L.M.; Meng, S.; Wang, J.-X.; Liu, L.; Zheng, Z.-X. Influential Factors Regarding Carbon Emission Intensity in China: A Spatial Econometric Analysis from a Provincial Perspective. Sustainability 2020, 12, 8097. [Google Scholar] [CrossRef]
- Shen, N. Spatial agglomeration, scale threshold and technological innovation: An Empirical Analysis Based on census data of Chinese manufacturing enterprises. J. Manag. Eng. 2014, 4, 21–27. [Google Scholar]
- Shao, S.; Zhang, K.; Dou, J.M. Effects of Economic Agglomeration on Energy Saving and Emission Reduction: Theory and Empirical Evidence from China. Manag. World 2019, 35, 36–60. [Google Scholar]
- Yu, H.C.; Liu, Y.; Liu, C.L.; Fan, F. Spatiotemporal Variation and Inequality in China’s Economic Resilience across Cities and Urban Agglomerations. Sustainability 2018, 10, 4754. [Google Scholar] [CrossRef]
- Rupasingha, A.; Goetz, S.J.; Debertin, D.L.; Pagoulatos, A. The environmental Kuznets curve for US counties: A spatial econometric analysis with extensions. Pap. Reg. Sci. 2004, 83, 407–424. [Google Scholar] [CrossRef]
- Burnett, J.W.; Bergstrom, J.C.; Dorfman, J.H. A Spatial Panel Data Approach to Estimating U.S. State-Level Energy Emissions. Energy Econ. 2013, 40, 396–404. [Google Scholar] [CrossRef]
- Zhang, K.; Zhang, Z.Y.; Liang, Q.M. An empirical analysis of the green paradox in China: From the perspective of fiscal decentralization. Energy Policy 2017, 103, 203–211. [Google Scholar] [CrossRef]
- Vallés-Giménez, J.; Zárate-Marco, A. A Dynamic Spatial Panel of Subnational GHG Emissions: Environmental Effectiveness of Emissions Taxes in Spanish Regions. Sustainability 2020, 12, 2872. [Google Scholar] [CrossRef]
- Zheng, X.; Yu, Y.; Wang, J.; Deng, H. Identifying the determinants and spatial nexus of provincial carbon intensity in China: A dynamic spatial panel approach. Reg. Environ. Chang. 2014, 14, 1651–1661. [Google Scholar] [CrossRef]
- Xiong, L.; De Jong, M.; Wang, F.; Cheng, B.; Yu, C. Spatial Spillover Effects of Environmental Pollution in China’s Central Plains Urban Agglomeration. Sustainability 2018, 10, 994. [Google Scholar] [CrossRef]
- Ushifusa, U.; Tomohara, A. Productivity and Labor Density: Agglomeration Effects over Time. Atl. Econ. J. 2013, 14, 123–132. [Google Scholar] [CrossRef]
- Han, C.; Phillips, P.C.B. GMM Estimation for Dynamic Panels with Fixed Effects and Strong at Unity. Economet. Theory 2010, 26, 119–151. [Google Scholar] [CrossRef]
- Jacbos, J. The Economy of Cities; Random House: New York, NY, USA, 1969. [Google Scholar]
- Porter, M. The Competitive Advantage of Nations; Free Press: New York, NY, USA, 1990. [Google Scholar]
- Ciccone, A.; Hall, R.E. Productivity the Density of Economic Activity. Am. Econ. Rev. 1996, 86, 54–70. [Google Scholar]
- Eva, J.; Drahomira, P.; Magdalena, B.D.; Lubor, H. The Age of Clusters and Its Influence on Their Activity Preferences. Technol. Econ. Dev. Econ. 2013, 19, 621–637. [Google Scholar]
- Ramanathan, R. An Analysis of Energy Consumption and Carbon Dioxide Emissions in Countries of the Middle East and North in Africa. Energy 2005, 30, 2831–2842. [Google Scholar] [CrossRef]
- Chung, Y.H.; Fare, R.; Grosskopf, S. Productivity and Undersirable Outputs: A Directional Distance Function Approach. J. Environ. Manag. 1997, 51, 229–240. [Google Scholar] [CrossRef]
- Xiao, Z.L.; Fan, F. Convergence in China’s high-tech industry development performance: A spatial panel model. Appl. Econ. 2017, 49, 5296–5308. [Google Scholar]
- Yang, R.F. Industrial Agglomeration, Foreign Direct Investment and Environmental Pollution. Econ. Manag. J. 2015, 2, 11–19. [Google Scholar]
- Ding, W.; Gilli, M.; Mazzanti, M.; Nicolli, F. Green inventions and greenhouse gas emission dynamics: A close examination of provincial Italian data. Environ. Econ. Policy Stud. 2016, 18, 1–17. [Google Scholar]
- Tu, Z.G. Strategic Measures to Reduce China’s Carbon Emissions: Based on an Index Decomposition Analysis of Carbon Emission in Eight Industries. Soc. Sci. China 2014, 35, 78–94. [Google Scholar]
- Pezfjd, L.; Montalvo, C.A. comprehensive review of the evolving and cumulative nature of eco-innovation in the chemical industry. J. Clean Prod. 2015, 102, 30–43. [Google Scholar]
- Zhou, P.; Ang, B.W.; Han, J.Y. Total factor carbon emission performance: A Malmquist index analysis. Energy Econ. 2010, 32, 194–201. [Google Scholar] [CrossRef]
- Lin, X.; Polenske, K.R. Input–Output Anatomy of China’s Energy Use Changes in the 1980s. Econ. Syst. Res. 2006, 1, 67–84. [Google Scholar] [CrossRef]
- Liu, N.; Fan, F. Threshold effect of international technology spillovers on China’s regional economic growth. Technol. Anal. Strateg. Manag. 2020, 32, 923–935. [Google Scholar] [CrossRef]
- Xie, J.; Sun, Q.; Wang, S.; Li, X.; Fan, F. Does environmental regulation affect export quality? theory and evidence from China. Int. J. Environ. Res. Public Health 2020, 17, 8237. [Google Scholar] [CrossRef] [PubMed]
- Fan, F.; Cao, D.L.; Ma, N. Is Improvement of Innovation Efficiency Conducive to Haze Governance? Empirical Evidence from 283 Chinese Cities. Int. J. Environ. Res. Public Health 2020, 17, 6095. [Google Scholar] [CrossRef] [PubMed]
- Grazif, V.; Waisman, H.A. Simple Model of Agglomeration Economies with Environmental Externalities. AFD Res. Pap. 2016. No.2016-18. [Google Scholar]
- Zhang, J.Q.; Chen, T.T.; Fan, F. Empirical Research on Time-Varying Characteristics and Efficiency of the Chinese Economy and Monetary Policy: Evidence from the MI-TVP-VAR Model. Appl. Econ. 2018, 50, 3596–3613. [Google Scholar] [CrossRef]
- Rodriguez, M.C.; Dupont-Courtade, L.; Oueslat, W. Air Pollution and Urban Structure Linkage Evidence from European Cities. Renew. Sustain. Energy Rev. 2016, 53, 1–9. [Google Scholar] [CrossRef]
- Shen, N.; Wang, Q.W.; Zhao, Z.Y. Trade relation, Spatial Agglomeration and Carbon Emission—An Analysis of New Economic Geography. Manag. World 2014, 1, 176–177. [Google Scholar]
- Glaser, E.L.; Kahn, M.E. The Greenness of Cites: Carbon Dioxide Emissions and Urban Development. J. Urban Econ. 2010, 67, 404–418. [Google Scholar] [CrossRef]
- Otsuka, A.; Goto, M.; Sueyoshi, T. Efficiency and Agglomeration Economics: The Case of Japanese Manufacturing Industries. Reg. Sci. Policy Pract. 2014, 6, 195–212. [Google Scholar] [CrossRef]
- The Intergovernmental Panel on Climate Change (IPCC). 2006 IPCC Guidelines for National Greenhouse Gas Inventories; Institute for Global Environmental Strategies (IGES): Hayama, Kanagawa, Japan, 2006. [Google Scholar]
- Zhang, H.; Wei, X.P. Green Paradox or Forced Emission-reduction: Dual Effect of Environmental Regulation on Carbon Emissions. China Popul. Resour. Environ. 2014, 24, 21–29. [Google Scholar]
- Verspagen, B.; Schoenmakers, W. The Spatial Dimension of Knowledge Spillovers in Europe. J. Econ. Geogr. 2004, 4, 23–42. [Google Scholar] [CrossRef]
- Feldman, M.P. The Geography of Innovation; Kluwer Academic Publishers: Boston, MA, USA, 1994. [Google Scholar]
- Fingleton, B.; Igliori, D.C.; Moore, B. Employment Growth of Small High-technology Firms and the Role of Horizontal Clustering: Evidence from Computing Services and R&D in Great Britain, 1991–2000. Urban Stud. 2014, 41, 773–799. [Google Scholar]
- Fan, F.; Lian, H.; Wang, S. Can regional collaborative innovation improve innovation efficiency? An empirical study of Chinese cities. Growth Chang. 2020, 51, 440–463. [Google Scholar] [CrossRef]
- Zhang, K.; Wang, D.F. The interaction and Spatial Spillover between Agglomeration and Pollution. China Ind. Econ. 2014, 6, 70–82. [Google Scholar]
- Grossman, G.; Krueger, A. Economic growth and the environment. Q. J. Econ. 1995, 110, 353–377. [Google Scholar] [CrossRef]
- Lan, J.; Kakinaka, M.; Huang, X. Foreign Direct Investment, Human Capital and Environmental Pollution in China. Environ. Resour. Econ. 2012, 51, 255–275. [Google Scholar] [CrossRef]
- Perry, S. Do Urbanization and Industrialization Affect Energy Intensity in Developing Countries. Energy Econ. 2013, 37, 52–59. [Google Scholar]
- Zhang, J.Q.; Wang, S.; Yang, P.L.; Fan, F.; Wang, X.L. Analysis of Scale Factors on China’s Sustainable Development Efficiency Based on Three-Stage DEA and a Double Threshold Test. Sustainability 2020, 12, 2225. [Google Scholar] [CrossRef]
- He, J. Pollution Haven Hypothesis and Environmental Impacts of Foreign Direct Investment: The Case of Industrial Emission of Sulfur Dioxide(SO2) in Chinese Provinces. Ecol. Econ. 2006, 14, 228–245. [Google Scholar] [CrossRef]
- Liu, S.; Fan, F.; Zhang, J.Q. Are Small Cities More Environmentally Friendly? An Empirical Study from China. Int. J. Environ. Res. Public Health 2019, 16, 727. [Google Scholar] [CrossRef]
- Wang, X.L.; Wang, S.; Fan, F.; Ye, X.H. Marketization as a channel of international technology diffusion and green total factor productivity: Research on the spillover effect from China’s first-tier cities. Technol. Anal. Strateg. Manag. 2020. [Google Scholar] [CrossRef]
- Shao, S.; Yang, L.L.; Yu, M.B.; Yu, M.L. Estimation, Characteristics and Determinants of Energy-related Industrial CO2 Emissions in Shanghai (China), 1994~2009. Energy Policy 2011, 39, 6476–6494. [Google Scholar] [CrossRef]
- Elhorst, J.P. Software for spatial panels. Int. Reg. Sci. Rev. 2014, 37, 389–405. [Google Scholar] [CrossRef]
- Wooldridge, J.M. Introductory Econometrics: A Modern Approach, 2nd ed.; South—Western College Pub.: Cincinnati, OH, USA, 2002. [Google Scholar]
- Pan, W.Q.; Zhang, R.J.; Pan, Y.G. CO2 emissions from inland and coastal China: Different perspectives based on end-product production. J. Tsinghua Univ. (Sci. Technol.) 2016, 56, 4. [Google Scholar]
- Baron, R.M.; Kenny, D.A. The Moderator-mediator Variable Distinction in Social Psychological Research: Conceptual, Strategic, and Statistical Considerations. J. Personal. Soc. Psychol. 1986, 51, 1173–1182. [Google Scholar] [CrossRef]
- Lin, S.L.; Zhang, Z.X.; Liu, G.P. Technological innovation, spatial agglomeration and regional carbon productivity. China Pop. Res. Environ. 2013, 23, 36–45. [Google Scholar]
- Zhang, Y.J.; Peng, Y.L.; Ma, C.Q.; Shen, B. Can environmental innovation facilitate carbon emissions reduction? Evidence from China. Energy Policy 2017, 100, 18–28. [Google Scholar] [CrossRef]
- Feng, M.; Li, X. Technological Innovation Threshold Characteristic of the Impact of Environmental Regulation on Carbon Emission Based on Chinese Provincial Panel Data. J. Sci. Ind. Res. 2019, 78, 274–277. [Google Scholar]
| Variable Name | External | Stage of Development | Environmental Effect | Main Mechanisms |
|---|---|---|---|---|
| Innovation agglomeration | 1 < λ < 1/αl | Initial stage; Acceleration stage | Promotion | Pursuing economic interests; Lax environmental regulation |
| 1 < α < 1/αl | Mature stage | Inhibition | Green technology spillover; Economies of scale; Resetting technological trajectory; Greening industrial structure | |
| Energy intensity | 1 < λ < 1/αl | Initial stage; Acceleration stage | Promotion | Increasing demand for energy; Outdated energy conservation Technologies; Lax environmental regulation |
| 1 < α < 1/αl | Mature stage | Inhibition | Reasonable energy allocation structure; Clean energy structure; |
| Variable Types | Index Selection | Symbol | Indicator Description | Variable Source |
|---|---|---|---|---|
| Explained variable | Carbon emission | CO2 | Carbon emission from non-farm | China Energy Statistics Yearbook (2005–2018) |
| Core explanatory variable | Innovation agglomeration | Agin | Number of patents granted /administrative area | China Science and Technology Statistical Yearbook (2005–2018) |
| Energy intensity | Sen | Energy consumption/industrial value-added | China Energy Statistics Yearbook (2005–2018) | |
| Control variables | Labor productivity | Ip | Industrial output/employment | China Statistical Yearbook (2005–2018) China Science and Technology Statistical Yearbook (2005–2018) China Environmental Yearbook (2005–2018) |
| Per capita income level | Pcin | GDP/population | ||
| urbanization | Ur | Urban population/total population | ||
| Energy consumption structure | Es | Coal consumption/energy consumption | ||
| Industrial structure | Ind | Industrial value-added/GDP | ||
| Opening up | Open | Total imports and exports/GDP | ||
| Environmental regulation | Er | Environmental expenditure/GDP | ||
| Marketing | Mar | Marketization index | Marketization Index Report |
| Model Type | Static Durbin | Dynamic Durbin | ||||
|---|---|---|---|---|---|---|
| Model | 3 | 13 | 14 | 4 | 15 | 16 |
| Global Moran’s I [P] | 0.2308 *** (0.000) | 0.7664 *** (0.000) | 0.2480 *** (0.000) | 0.6665 *** (0.000) | 0.7843 *** (0.000) | 0.7412 *** (0.000) |
| LM-lag [P] | 29.8825 *** (0.000) | 4.1013 ** (0.042) | 35.0508 *** (0.000) | 19.6130 *** (0.000) | 21.5171 *** (0.000) | 36.154 *** (0.000) |
| LM-error [P] | 29.8802 *** (0.000) | 5.1024 ** (0.023) | 35.0545 *** (0.000) | 244.2844 *** (0.000) | 349.7951 *** (0.000) | 318.7048 *** (0.000) |
| Variable | OLS-FE | SYS-GMM | Static Durbin | Dynamic Durbin |
|---|---|---|---|---|
| Model | 1 | 2 | 3 | 4 |
| L.CO2 | 0.4630 *** (5.08) | 0.3618 *** (2.90) | ||
| Agin | 0.2648 *** (4.80) | 0.0835 (0.27) | 0.2119 *** (4.11) | 0.3498 *** (4.01) |
| sAgin | −0.0388 *** (−4.32) | −0.0135 (−0.27) | −0.0169 * (−1.96) | −0.0462 *** (−3.03) |
| Sen | 0.1332 ** (2.43) | 0.1405 *** (2.92) | 0.1837 *** (3.59) | 0.1549 ** (1.99) |
| sSen | −0.0113 (−0.22) | −0.0117 (−0.23) | −0.0111 ** (−2.53) | −0.0126 ** (−2.17) |
| Lp | 0.2170 * (1.69) | 0.4042 (1.36) | 0.3286 *** (2.66) | 0.4020 ** (2.43) |
| Eco | 0.8076 (1.24) | 0.6237 (0.98) | 0.6714 (1.06) | 0.8919 ** (2.53) |
| sEco | −0.0033 (−0.11) | −0.0292 −(0.44) | −0.0606 ** (−2.04) | −0.1013 * (−1.88) |
| Ur | 0.5703 (1.07) | 0.5314 (0.96) | 0.1632 * (1.77) | 0.4041 * (1.76) |
| sUr | 0.3674 (1.34) | 0.5088 (0.54) | 0.2009 (0.08) | 0.2016 ** (2.00) |
| Es | 0.2102 *** (4.44) | 0.0971 ** (2.22) | 0.2401 *** (5.13) | 0.2191 *** (5.33) |
| Ind | 0.0984 (1.56) | 0.2384 ** (2.07) | 0.2276 *** (3.78) | 0.0802 * (1.88) |
| Open | −0.0319 *** (−2.21) | −0.0637 *** (−2.19) | −0.0349 (−1.41) | −0.0786 ** (−2.37) |
| Er | −0.0429 ** (−1.97) | −0.0603 ** (−2.58) | −0.0408 ** (−2.31) | −0.0577 ** (−2.21) |
| Mar | 0.4414 *** (5.29) | 0.7056 *** (7.14) | 0.0813 *** (4.37) | 0.4139 *** (3.65) |
| Cons | 2.4114 (0.72) | −7.2394 (−0.77) | 5.9700 * (1.86) | 3.1693 (0.44) |
| F(Wald) [P] | 164.52 (0.00) | 174.64 (0.00) | 3065.36 (0.00) | 933.27 (0.00) |
| AR(2) | 1.1386 | 0.6563 | ||
| Sargan[P] | 27.2539 (0.9997) | 26.8437 (0.9998) | ||
| Log | 362.0113 | 218.7573 | ||
| Rho | 0.3184 *** (4.14) | 2.5591 *** (5.75) | ||
| Obs | 420 | 390 | 420 | 390 |
| Variable | Static Durbin | Dynamic Durbin | ||
|---|---|---|---|---|
| Inshore | Inland | Inshore | Inland | |
| Model | 5 | 6 | 7 | 8 |
| L.CO2 | 0.9904 *** (7.81) | 0.5082 *** (5.64) | ||
| Agin | 3.36388 *** (2.66) | 0.2914 *** (4.09) | 2.4505 *** (3.11) | 0.2231 *** (3.50) |
| sAgin | −0.4753 *** (−2.92) | −0.0096 (−0.64) | −0.2696 *** (−2.73) | −0.0076 (−0.59) |
| Sen | 0.1703 (0.50) | 0.1440 ** (2.13) | 0.9114 *** (5.20) | 0.2248 *** (3.66) |
| sSen | −1.1120 *** (−3.16) | 0.0748 (1.53) | −0.2696 *** (−2.73) | 0.2200 *** (3.98) |
| Lp | 1.4830 ** (2.57) | 0.4170 *** (2.85) | 1.1699 *** (3.60) | 0.4493 *** (2.96) |
| Eco | 0.9276 *** (4.34) | 0.0103 (0.01) | 0.9447 *** (3.90) | 0.2053 (1.48) |
| sEco | −0.0595 *** (−4.63) | −0.0464 (−0.99) | −0.4814 *** (−4.62) | −0.2952 (−0.81) |
| Ur | 0.3033 *** (4.34) | 0.3959 (0.53) | 1.2274 (1.32) | 0.4504 (0.69) |
| sUr | 0.0595 (4.63) | 0.2262 (0.60) | 0.7340 * (1.88) | 0.0324 (0.31) |
| Es | 0.5864 *** (3.20) | 0.0742 (0.92) | 0.2773 ** (2.09) | 0.0192 (0.15) |
| Ind | 0.0550 *** (3.61) | 0.0704 ** (0.68) | 1.1550 *** (4.97) | 0.0802 * (1.88) |
| Open | −0.4801 ** (−2.01) | −0.0683 ** (−2.15) | −0.7651 *** (−6.72) | −0.0123 (−0.28) |
| Er | −0.0095 (−0.15) | −0.0410 (−1.40) | −0.0257 ** (−2.31) | −0.0509 (−1.42) |
| Mar | 0.4753 *** (4.08) | 0.5238 *** (4.44) | 1.6531 *** (4.36) | 0.5308 *** (3.36) |
| Cons | 2.4114 (0.72) | 3.1624 (0.33) | −37.0666 *** (−3.28) | −10.1274 (−0.94) |
| F(Wald) [P] | 164.52 (0.00) | 174.64 (0.00) | 865.36 (0.00) | 706.66 (0.00) |
| AR(2) | 0.7115 | 0.7654 | ||
| Sargan [P] | 28.4182 (0.9995) | 27.2240 (0.9876) | ||
| Rho | 0.3225 *** (4.58) | 0.1028 ** (2.36) | 2.8445 *** (6.78) | 2.0112 *** (3.38) |
| Log | 124.4714 | 169.7098 | 132.5438 | 159.5702 |
| Obs | 154 | 266 | 143 | 247 |
| Variable | OLS-FE | SYS-GMM | Static Durbin | Dynamic Durbin | ||||
|---|---|---|---|---|---|---|---|---|
| L.Sen | L.CO2 | L.Sen | L.CO2 | L.Sen | L.CO2 | L.Sen | L.CO2 | |
| Model | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| L.CO2 | 0.3728 *** (5.13) | 0.4857 *** (3.47) | ||||||
| L.Sen | 0.9253 *** (29.78) | 0.7690 *** (3.88) | ||||||
| Agin | 0.1001 * (1.74) | 0.2743 *** (4.57) | 0.1292 ** (2.25) | 0.1997 ** (2.53) | 0.0440 * (1.87) | 0.2287 *** (3.81) | 0.1334 * (1.92) | 0.4609 *** (4.77) |
| sAgin | −0.0334 *** (−3.68) | −0.0362 *** (−4.45) | −0.0259 *** (−2.93) | −0.0315 ** (−2.29) | −0.0233 ** (−2.47) | −0.0151 *** (−2.41) | −0.0357 *** (−4.08) | −0.0228 *** (−2.63) |
| Lp | 0.3005 ** (2.21) | 0.2817 ** (2.13) | 0.1603 (1.55) | 0.4919 (1.16) | 0.1737 (1.25) | 0.3941 *** (3.08) | 0.1176 * (1.95) | 0.2821 ** (2.31) |
| Eco | 2.7502 *** (4.07) | 1.2542 * (1.91) | 0.8761 (1.20) | 0.1129 (0.712) | 2.2406 (3.32) | 0.0264 (0.04) | 1.6020 ** (2.26) | 0.347 (0.62) |
| sEco | −0.1359 *** (−4.24) | −0.0260 (−0.84) | 0.1802 (0.46) | 0.0306 (0.79) | −0.1088 ** (−2.57) | −0.0265 (0.87) | −0.0756 ** (−2.25) | −0.0266 (−1.40) |
| Ur | 1.1311 *** (2.00) | 0.8794 (1.61) | 0.1300 (0.20) | 2.240* (1.91) | 1.2511 ** (2.57) | 0.5657 (1.14) | 1.0111 ** (2.01) | 0.5967* (1.89) |
| sUr | 0.7325 ** (2.54) | 0.5826 ** (2.09) | 0.1802 (0.46) | 0.9450 (1.16) | 0.6778 ** (2.57) | 0.2419 (0.94) | 0.6920 ** (2.58) | 0.2529 (0.54) |
| Es | 0.0286 (0.43) | 0.2458 *** (5.30) | 0.0575 (0.23) | 0.1425 *** (3.14) | 0.2024 *** (4.19) | 0.2764 *** (6.21) | 0.9584 ** (2.20) | 0.2184 *** (5.08) |
| Ind | −0.0200 (−0.44) | 0.1327 ** (2.06) | 0.0703 (1.50) | 0.4197 *** (3.69) | 0.0516 (0.74) | 0.2392 *** (3.85) | 0.2148 *** (3.04) | 0.0663 ** (2.53) |
| Open | −0.0232 (−0.85) | 0.2182 *** (4.90) | −0.0349 ** (−2.50) | −0.071 6*** (−6.69) | −0.0631 ** (−2.32) | −0.0334 (−1.33) | −0.0376 * (−1.71) | −0.0337 *** (−2.37) |
| Er | −0.0003 (−0.01) | −0.0424 * (−1.89) | −0.0181 ** (−2.56) | −0.5331 ** (−2.46) | −0.0423 * (−1.75) | −0.0302 (−1.40) | −0.0051 (−0.24) | −0.0386 * (−1.89) |
| Mar | 0.1993 ** (2.27) | 0.5090 *** (5.98) | 0.1050 *** (4.09) | 0.7751 *** (8.82) | 0.0247 (0.28) | 0.4119 (4.92) | 0.2739 *** (2.92) | 0.2829 *** (4.59) |
| Cons | −13.032 *** (−3.72) | 0.4936 (0.15) | 4.8002 (1.27) | 1.6620 (0.30) | −10.3551 ** (−2.29) | 2.9768 (0.91) | −9.1185 (−1.21) | 2.2134 (0.29) |
| F(Wald) [P] | 69.78 (0.00) | 185.58 (0.00) | 218.76 (0.00) | 282.88 (0.000) | 907.63 (0.00) | 923.12 (0.00) | 882.12 (0.00) | 858.53 (0.00) |
| AR(2) | 0.9698 | 1.0845 | 0.8760 | 0.7665 | ||||
| Sargon [P] | 15.6689 (0.8690) | 25.3948 (0.9864) | 27.2341 (0.9997) | 26.3129 (0.9998) | ||||
| Rho | 0.1640 ** (2.03) | 0.3763 *** (4.93) | 2.5743 * (1.85) | 2.1680 *** (5.38) | ||||
| Log | 299.3801 | 312.3365 | 256.8333 | 253.4485 | ||||
| Obs | 420 | 420 | 390 | 390 | 420 | 420 | 390 | 390 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Yu, H.; Zhang, K.; Zhao, L.; Fan, F. Can Innovation Agglomeration Reduce Carbon Emissions? Evidence from China. Int. J. Environ. Res. Public Health 2021, 18, 382. https://doi.org/10.3390/ijerph18020382
Zhang J, Yu H, Zhang K, Zhao L, Fan F. Can Innovation Agglomeration Reduce Carbon Emissions? Evidence from China. International Journal of Environmental Research and Public Health. 2021; 18(2):382. https://doi.org/10.3390/ijerph18020382
Chicago/Turabian StyleZhang, Jianqing, Haichao Yu, Keke Zhang, Liang Zhao, and Fei Fan. 2021. "Can Innovation Agglomeration Reduce Carbon Emissions? Evidence from China" International Journal of Environmental Research and Public Health 18, no. 2: 382. https://doi.org/10.3390/ijerph18020382
APA StyleZhang, J., Yu, H., Zhang, K., Zhao, L., & Fan, F. (2021). Can Innovation Agglomeration Reduce Carbon Emissions? Evidence from China. International Journal of Environmental Research and Public Health, 18(2), 382. https://doi.org/10.3390/ijerph18020382






