A Statistical Model to Assess Risk for Supporting COVID-19 Quarantine Decisions
Abstract
:1. Introduction
1.1. COVID-19 Pandemic and Situation in Germany
1.2. Quarantine Decisions in Germany
- had face-to-face contact for at least 15 min or
- had direct contact to bodily fluids or
- were exposed to a relevant aerosol concentration.
1.3. Structure of the Paper
2. Materials and Methods
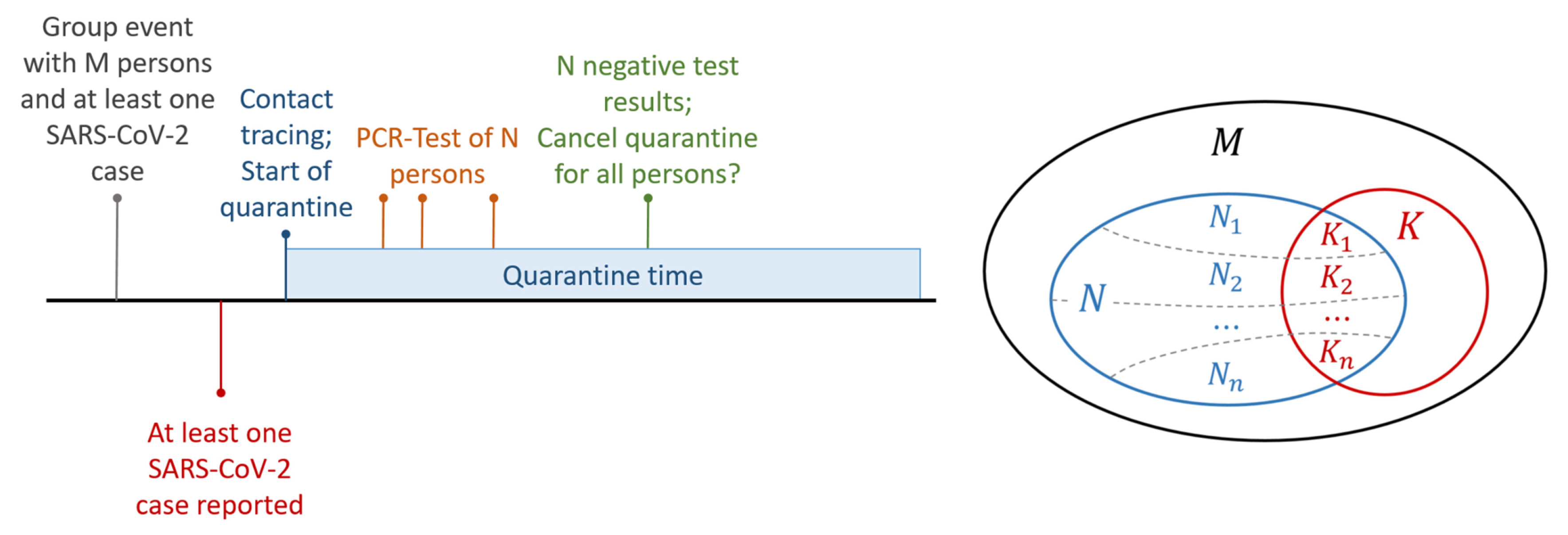
2.1. Use Case
“Under which conditions can a group quarantine be released (earlier) such that the probability of overlooking a (secondary) infection is low?”
“How likely is it that there is no secondary infection, given all N out of M people are tested negative?”
2.2. Statistical Model
2.3. Prior Distribution
2.4. Likelihood
3. Result
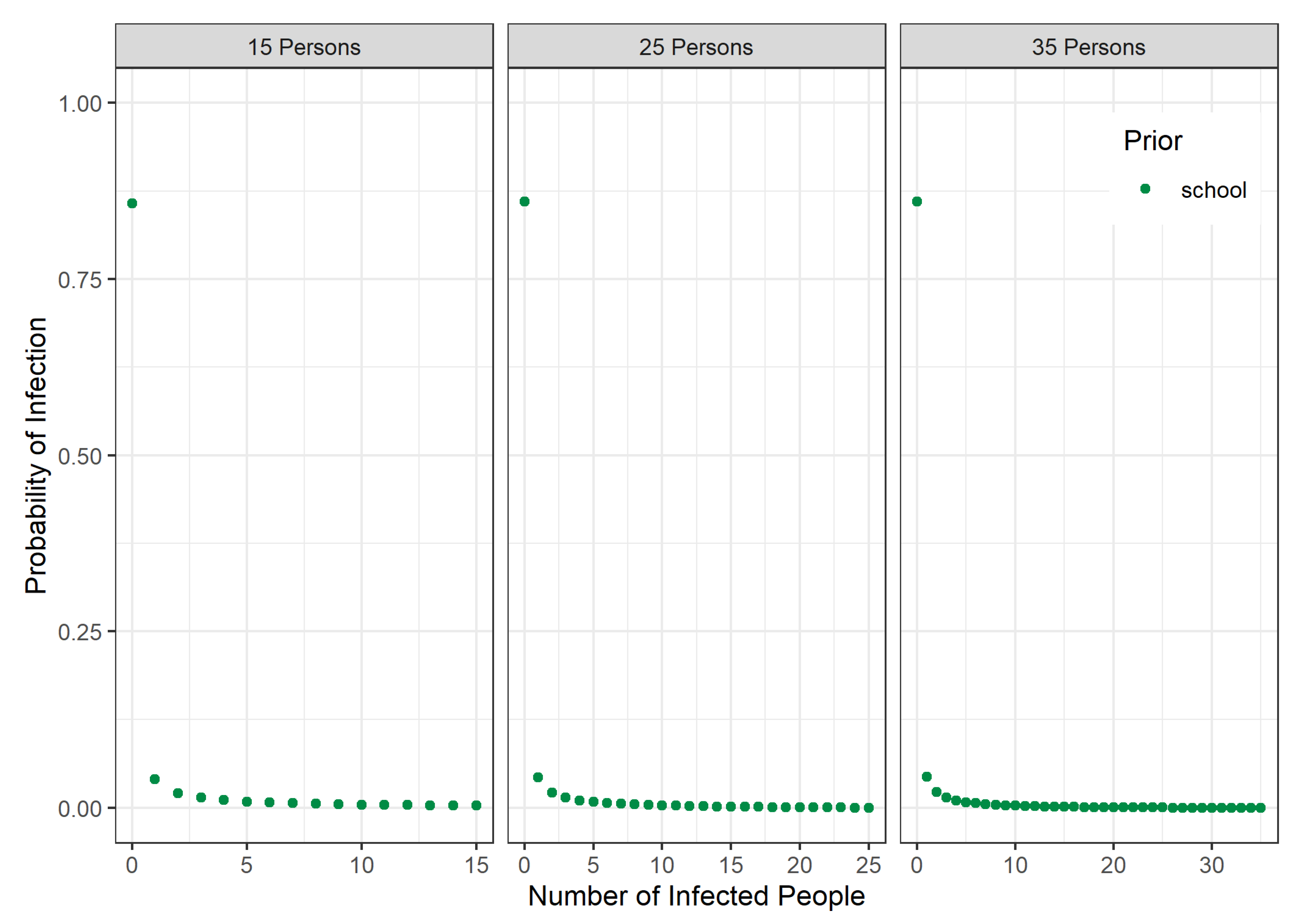
3.1. Prior Distribution for School Classes
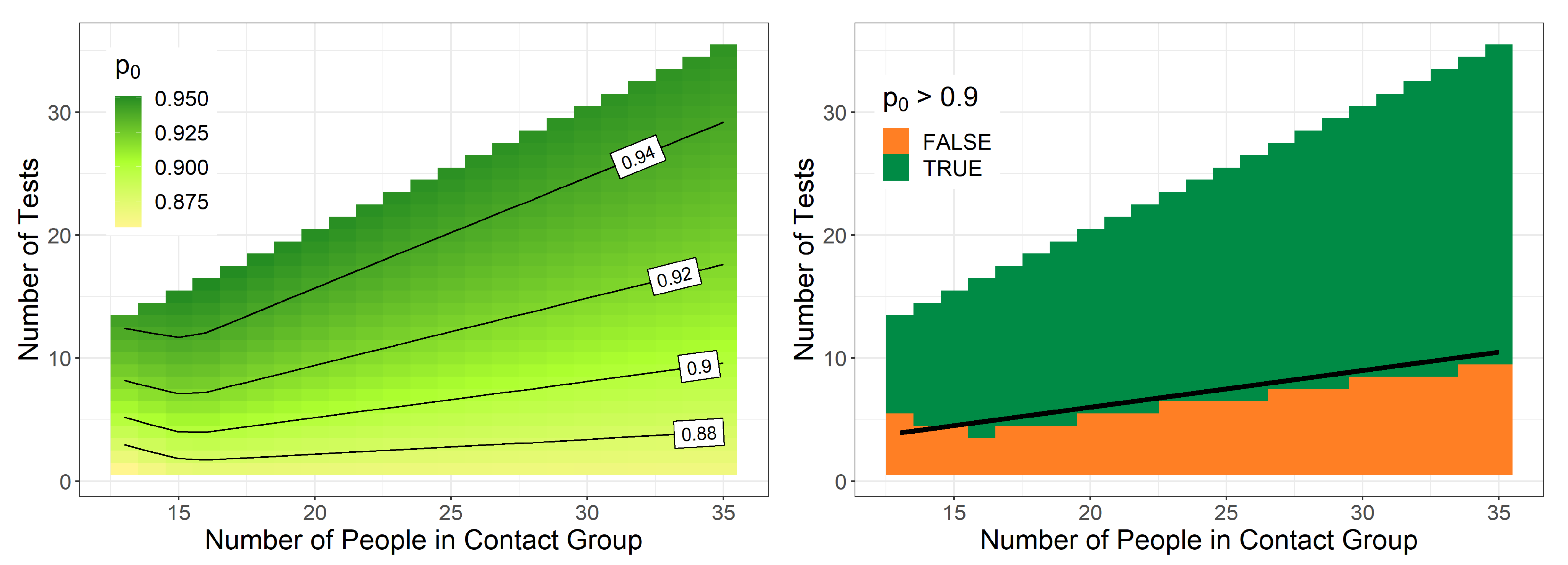
3.2. Posterior Probabilities and Decision Support for School Classes
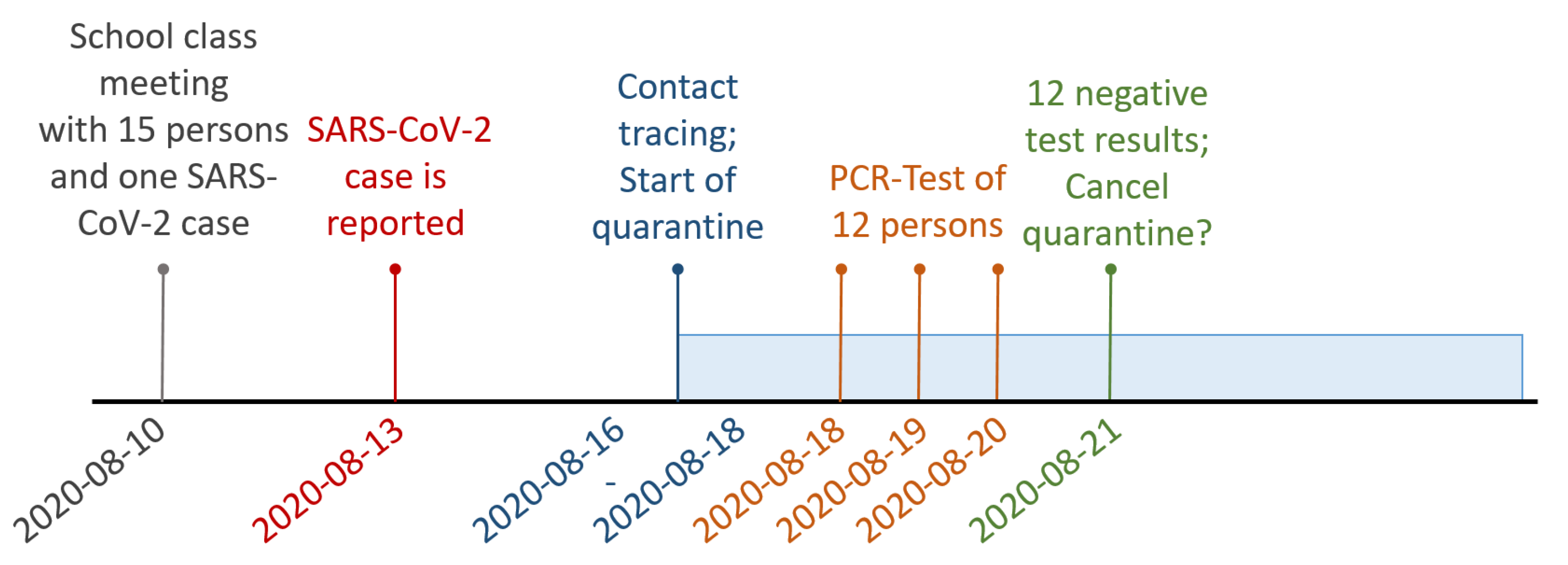
3.3. Decision about Quarantine Cancellation for School Classes
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- World Health Organization. COVID-19 Weekly Epidemiological Update Edition 45, Published 22 June 2021. Available online: https://apps.who.int/iris/bitstream/handle/10665/342009/CoV-weekly-sitrep22Jun21-eng.pdf?sequence=1&isAllowed=y (accessed on 30 June 2021).
- Robert Koch Institut. COVID-19: Fallzahlen in Deutschland und Weltweit. Available online: https://www.rki.de/DE/Content/InfAZ/N/Neuartiges_Coronavirus/Situationsberichte/Jun_2021/2021-06-24-en.pdf?__blob=publicationFile (accessed on 30 June 2021).
- Robert Koch Institut. Täglicher Lagebericht des RKI zur Coronavirus-Krankheit-2019 (COVID-19) 27.08.2020. Available online: https://www.rki.de/DE/Content/InfAZ/N/Neuartiges_Coronavirus/Situationsberichte/2020-08-27-de.pdf?__blob=publicationFile (accessed on 22 September 2020).
- Bundesamt für Justiz. Gesetz zur Verhütung und Bekämpfung von Infektionskrankheiten beim Menschen (Infektionsschutzgesetz—IfSG). Available online: https://www.gesetze-im-internet.de/ifsg/IfSG.pdf (accessed on 15 September 2020).
- Glasmacher, S.; Kurth, R. Globaler Alarm. Spektrum der Wissenschaft. 2006, pp. 12–17. Available online: https://www.rki.de/DE/Content/InfAZ/N/Neue_Infektionskrankheiten/Globaler-Alarm.pdf?__blob=publicationFile (accessed on 30 August 2021).
- Robert Koch Institut. Kontaktpersonennachverfolgung bei Respiratorischen Erkrankungen durch das Coronavirus SARS-CoV-2. Available online: https://www.rki.de/DE/Content/InfAZ/N/Neuartiges_Coronavirus/Kontaktperson/Management.html (accessed on 31 August 2020).
- Robert Koch Institut. Infektionsumfeld von erfassten COVID-19-Ausbrüchen in Deutschland. Available online: https://www.rki.de/DE/Content/Infekt/EpidBull/Archiv/2020/Ausgaben/38_20.pdf?__blob=publicationFile (accessed on 31 August 2020).
- Chen, J.; Guo, X.; Pan, H.; Zhong, S. What determines city’s resilience against epidemic outbreak: Evidence from China’s COVID-19 experience. Sustain. Cities Soc. 2021, 70, 102892. [Google Scholar] [CrossRef] [PubMed]
- Samui, P.; Mondal, J.; Khajanchi, S. A mathematical model for COVID-19 transmission dynamics with a case study of India. Chaos Solitons Fractals 2020, 140, 110173. [Google Scholar] [CrossRef] [PubMed]
- Forecasting Team. Modeling COVID-19 scenarios for the United States. Nat. Med. 2021, 27, 94–105. [Google Scholar] [CrossRef] [PubMed]
- Mandal, M.; Jana, S.; Nandi, S.K.; Khatua, A.; Adak, S.; Kar, T. A model based study on the dynamics of COVID-19: Prediction and control. Chaos Solitons Fractals 2020, 136, 109889. [Google Scholar] [CrossRef]
- Althouse, B.M.; Wenger, E.A.; Miller, J.C.; Scarpino, S.V.; Allard, A.; Hébert-Dufresne, L.; Hu, H. Stochasticity and heterogeneity in the transmission dynamics of SARS-CoV-2. arXiv 2020, arXiv:2005.13689. [Google Scholar]
- Lelieveld, J.; Helleis, F.; Borrmann, S.; Cheng, Y.; Drewnick, F.; Haug, G.; Klimach, T.; Sciare, J.; Su, H.; Pöschl, U. Model Calculations of Aerosol Transmission and Infection Risk of COVID-19 in Indoor Environments. Int. J. Environ. Res. Public Health 2020, 17, 8114. [Google Scholar] [CrossRef]
- Robert Koch Institut. Abwägung der Dauer von Quarantäne und Isolierung bei COVID-19; Toleranzen Gegenüber Bioziden Wirkstoffen. Available online: https://www.rki.de/DE/Content/Infekt/EpidBull/Archiv/2020/Ausgaben/39_20.pdf?__blob=publicationFile (accessed on 14 October 2020).
- Byrd, R.H.; Lu, P.; Nocedal, J.; Zhu, C. A limited memory algorithm for bound constrained optimization. SIAM J. Sci. Comput. 1995, 16, 1190–1208. [Google Scholar] [CrossRef]
- Quest Diagnostics. SARS-CoV-2 RNA, Qualitative Real-Time RT-PCR (Test Code 39433): Package Insert. Available online: https://www.fda.gov/media/136231/download (accessed on 12 November 2020).
- Kucirka, L.M.; Lauer, S.A.; Laeyendecker, O.; Boon, D.; Lessler, J. Variation in false-negative rate of reverse transcriptase polymerase chain reaction–based SARS-CoV-2 tests by time since exposure. Ann. Intern. Med. 2020, 173, 262–267. [Google Scholar] [CrossRef] [PubMed]
- Fontanet, A.; Tondeur, L.; Madec, Y.; Grant, R.; Besombes, C.; Jolly, N.; Pellerin, S.F.; Ungeheuer, M.N.; Cailleau, I.; Kuhmel, L.; et al. Cluster of COVID-19 in northern France: A retrospective closed cohort study. medRxiv 2020, 20071134. [Google Scholar] [CrossRef]
- Heavey, L.; Casey, G.; Kelly, C.; Kelly, D.; McDarby, G. No evidence of secondary transmission of COVID-19 from children attending school in Ireland, 2020. Eurosurveill 2020, 25, 2000903. [Google Scholar] [CrossRef] [PubMed]
- Macartney, K.; Quinn, H.E.; Pillsbury, A.J.; Koirala, A.; Deng, L.; Winkler, N.; Katelaris, A.L.; O’Sullivan, M.V.; Dalton, C.; Wood, N.; et al. Transmission of SARS-CoV-2 in Australian educational settings: A prospective cohort study. Lancet Child Adolesc. Health 2020, 4, 807–816. [Google Scholar] [CrossRef]
- Mossong, J.; Mombaerts, L.; Veiber, L.; Pastore, J.; Le Coroller, G.; Schnell, M.; Masi, S.; Huiart, L.; Wilmes, P. SARS-CoV-2 transmission in educational settings during an early summer epidemic wave in Luxembourg, 2020. BMC Infect. Dis. 2021, 21, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Sekretariat der Ständigen Konferenz der Kultusminister der Länderin der Bundesrepublik Deutschland. Vorgaben für die Klassenbildung, Schuljahr 2019/2020. Available online: https://www.kmk.org/fileadmin/Dateien/pdf/Statistik/Dokumentationen/2019-09-16_Klassenbildung_2019.pdf (accessed on 25 June 2021).
- Berger, J.O. Statistical Decision Theory and Bayesian Analysis; Springer: New York, NY, USA, 1985. [Google Scholar]
| Category | Infection Risk |
|---|---|
| 1. | high, close contact to infectious person |
| 2. | low, sparse contact to infectious person |
| 3. | medical staff with adequate protection |
| Case Number | Date of Last Contact | PCR Test Date | PCR Test Result |
|---|---|---|---|
| 1 | 10 August 2020 | — | — |
| 2 | 10 August 2020 | — | — |
| 3 | 10 August 2020 | — | — |
| 4 | 10 August 2020 | 18 August 2020 | negative |
| 5 | 10 August 2020 | 19 August 2020 | negative |
| 6 | 10 August 2020 | 19 August 2020 | negative |
| 7 | 10 August 2020 | 19 August 2020 | negative |
| 8 | 10 August 2020 | 20 August 2020 | negative |
| 9 | 10 August 2020 | 19 August 2020 | negative |
| 10 | 10 August 2020 | 19 August 2020 | negative |
| 11 | 10 August 2020 | 19 August 2020 | negative |
| 12 | 10 August 2020 | 19 August 2020 | negative |
| 13 | 10 August 2020 | 19 August 2020 | negative |
| 14 | 10 August 2020 | 19 August 2020 | negative |
| 15 | 10 August 2020 | 19 August 2020 | negative |
| 16 | 16 August 2020 | 19 August 2020 | negative |
| 17 | 18 August 2020 | 24 August 2020 | negative |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jäckle, S.; Röger, E.; Dicken, V.; Geisler, B.; Schumacher, J.; Westphal, M. A Statistical Model to Assess Risk for Supporting COVID-19 Quarantine Decisions. Int. J. Environ. Res. Public Health 2021, 18, 9166. https://doi.org/10.3390/ijerph18179166
Jäckle S, Röger E, Dicken V, Geisler B, Schumacher J, Westphal M. A Statistical Model to Assess Risk for Supporting COVID-19 Quarantine Decisions. International Journal of Environmental Research and Public Health. 2021; 18(17):9166. https://doi.org/10.3390/ijerph18179166
Chicago/Turabian StyleJäckle, Sonja, Elias Röger, Volker Dicken, Benjamin Geisler, Jakob Schumacher, and Max Westphal. 2021. "A Statistical Model to Assess Risk for Supporting COVID-19 Quarantine Decisions" International Journal of Environmental Research and Public Health 18, no. 17: 9166. https://doi.org/10.3390/ijerph18179166
APA StyleJäckle, S., Röger, E., Dicken, V., Geisler, B., Schumacher, J., & Westphal, M. (2021). A Statistical Model to Assess Risk for Supporting COVID-19 Quarantine Decisions. International Journal of Environmental Research and Public Health, 18(17), 9166. https://doi.org/10.3390/ijerph18179166






