Infectivity Upsurge by COVID-19 Viral Variants in Japan: Evidence from Deep Learning Modeling
Abstract
:1. Introduction
2. Materials and Methods
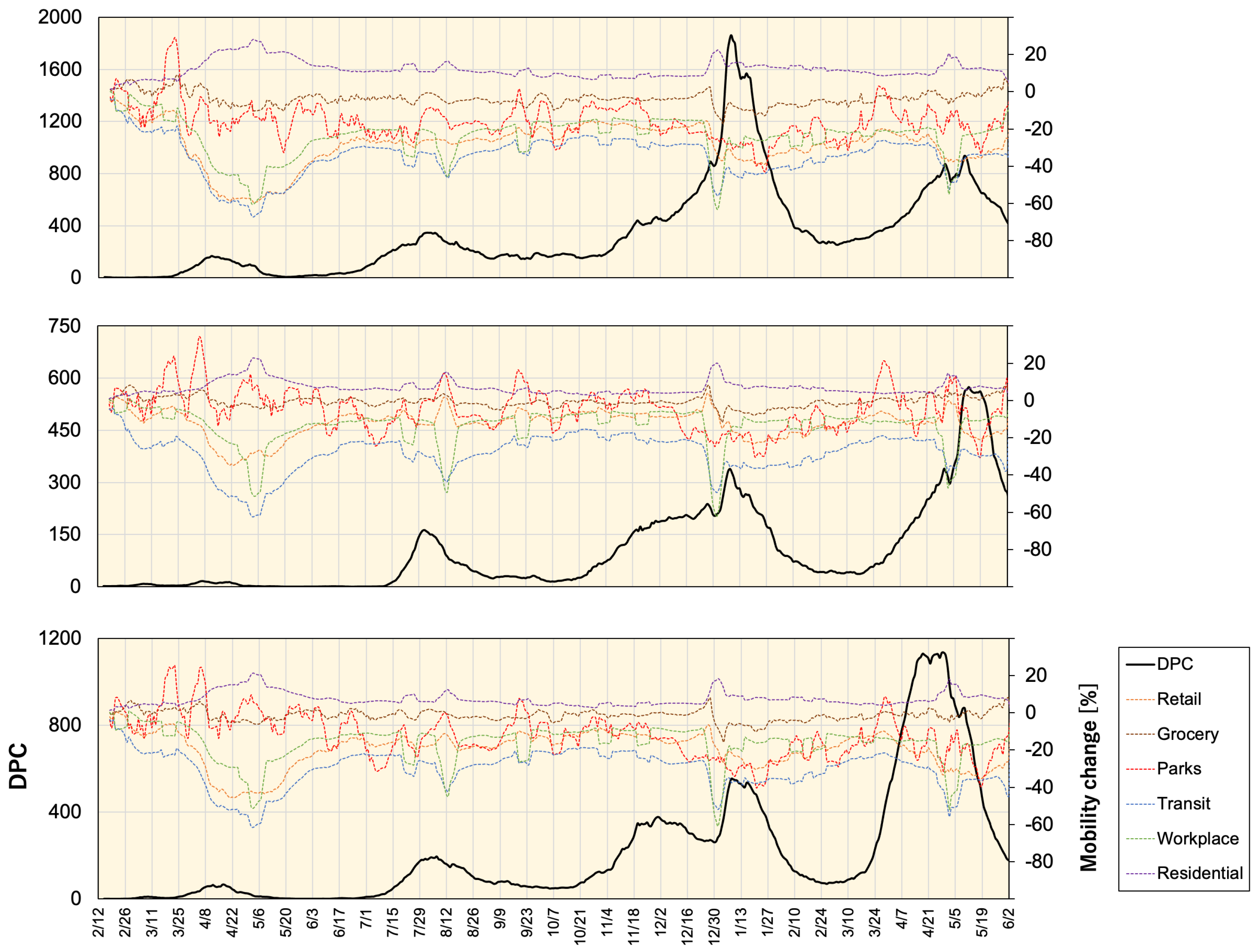
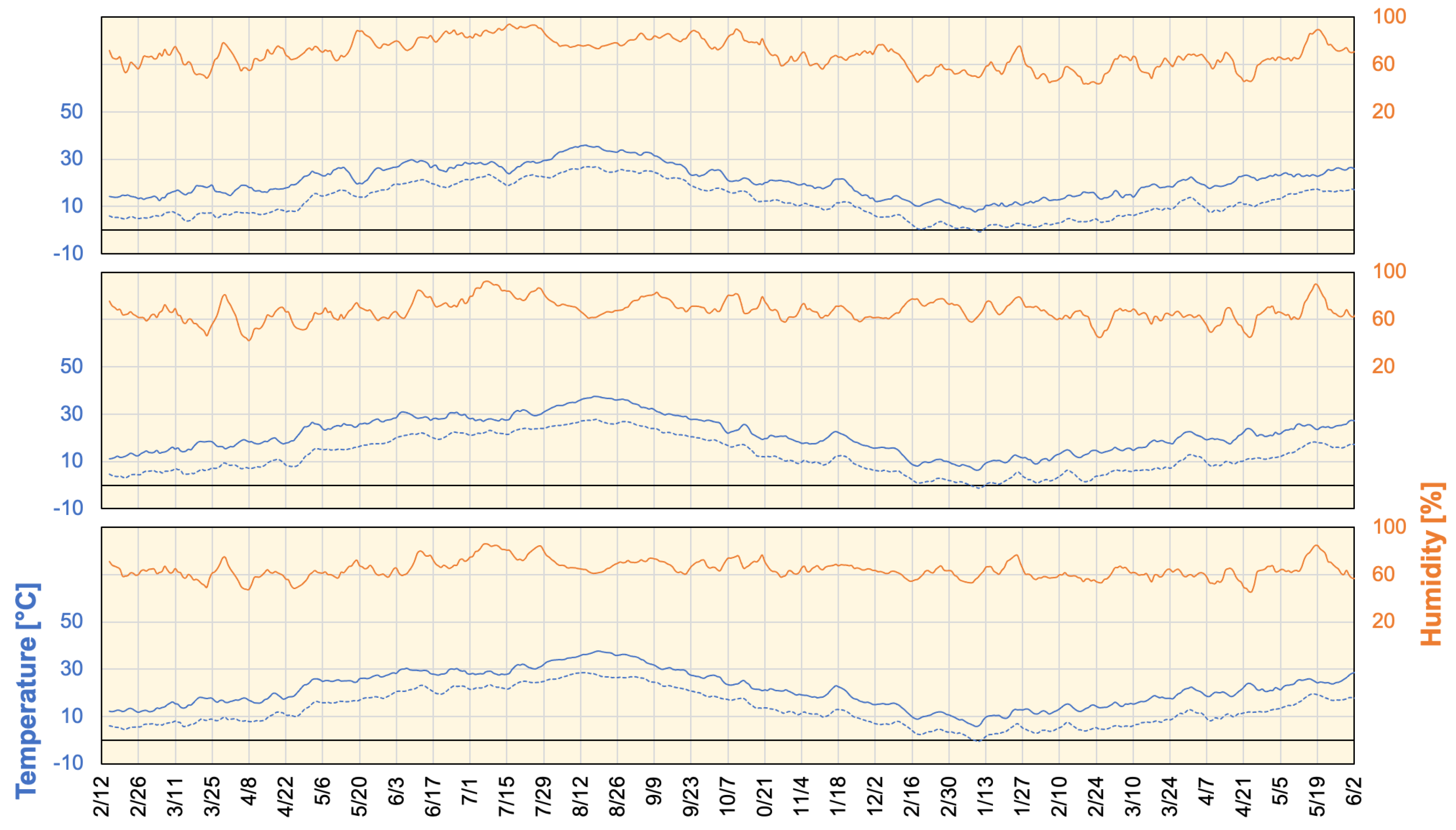
2.1. Data Collection and Processing
2.2. Forecasting Deep Learning Model
2.3. Validation Metrics
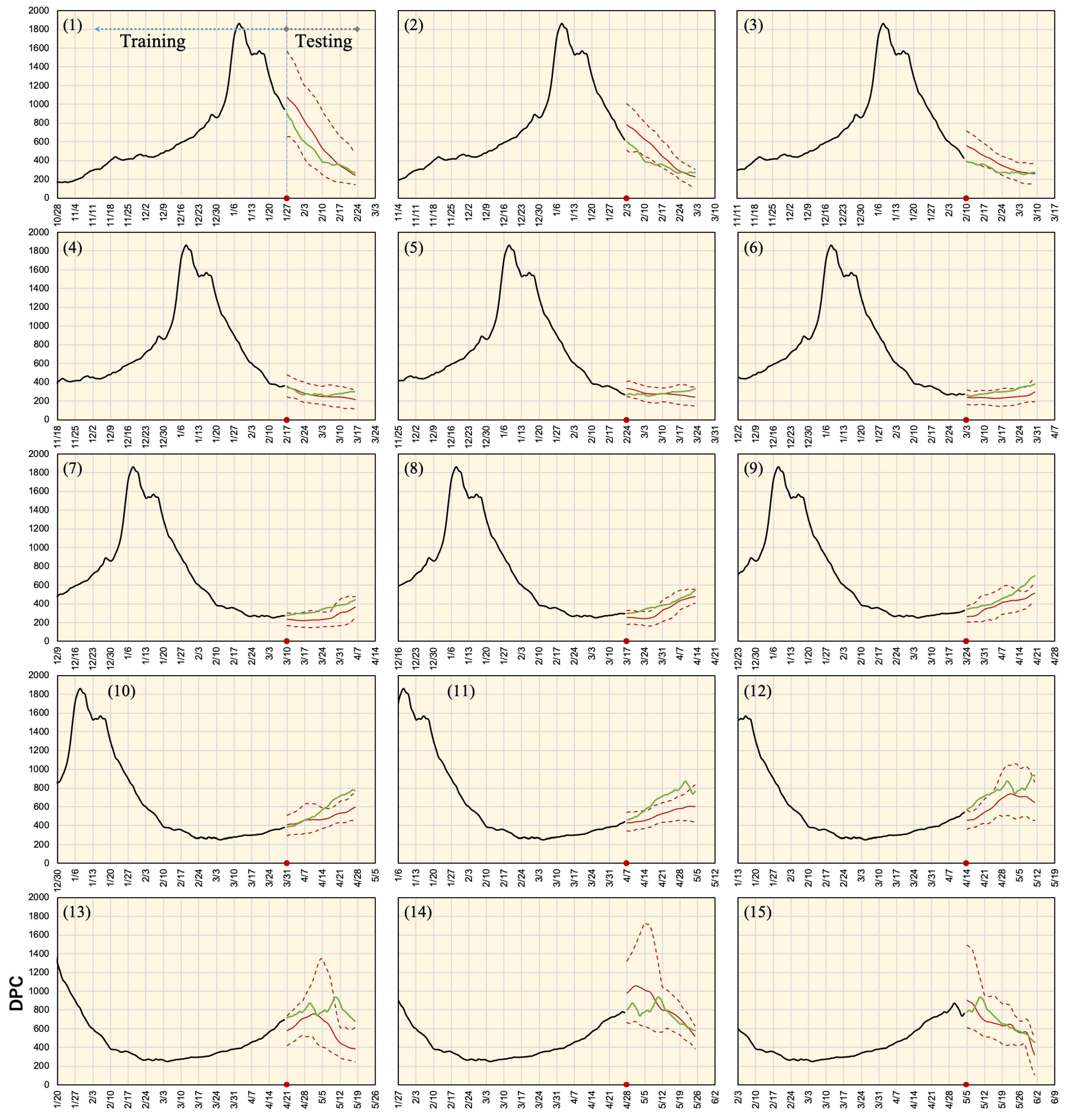
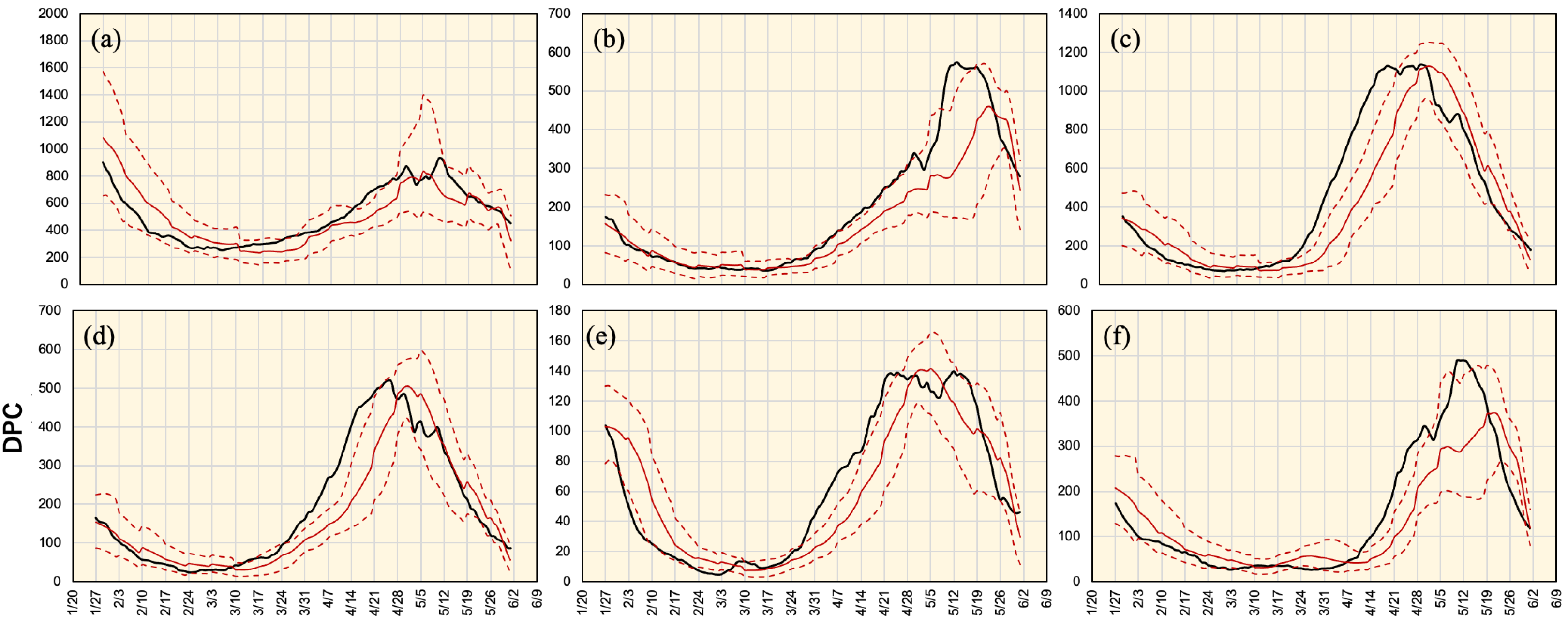
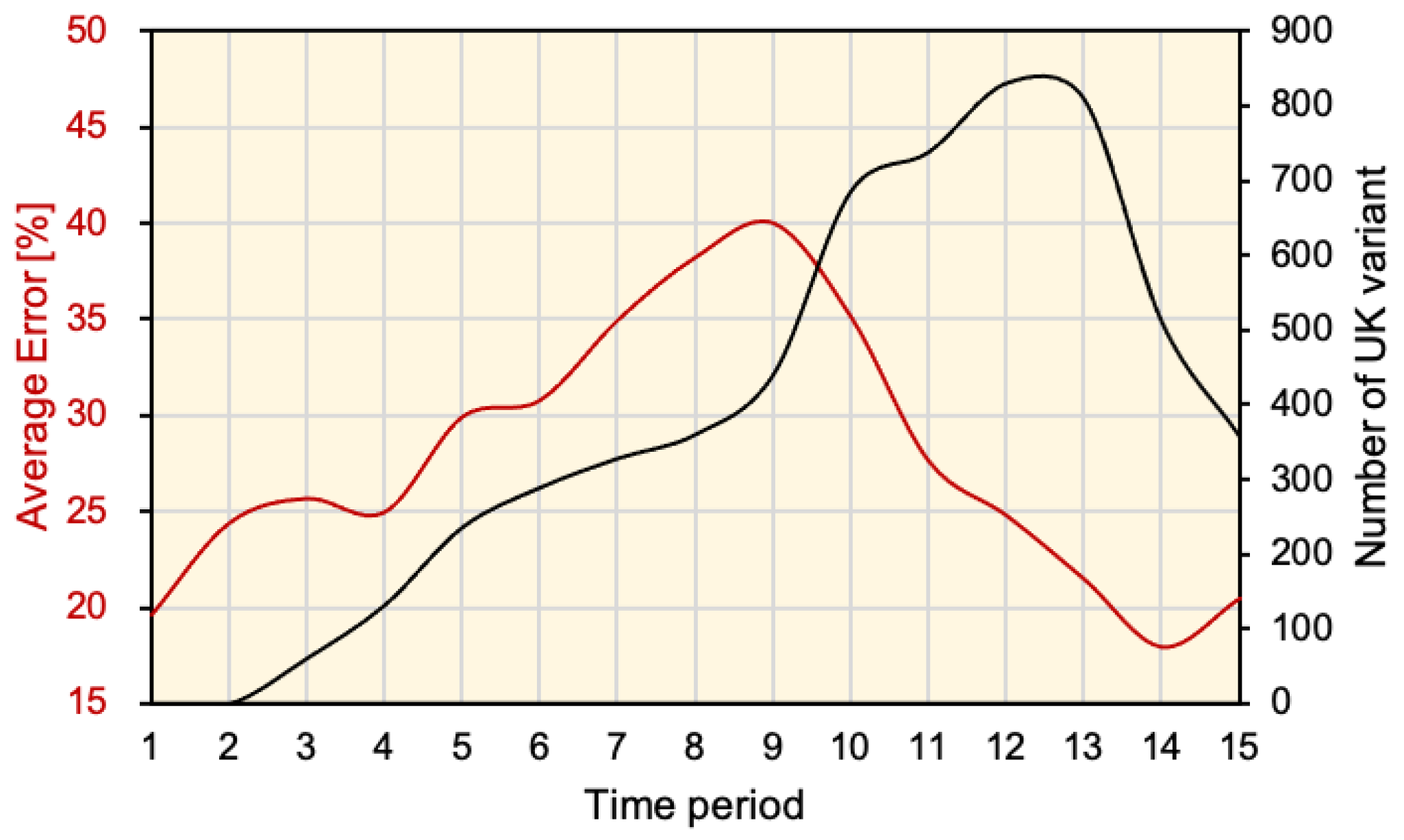
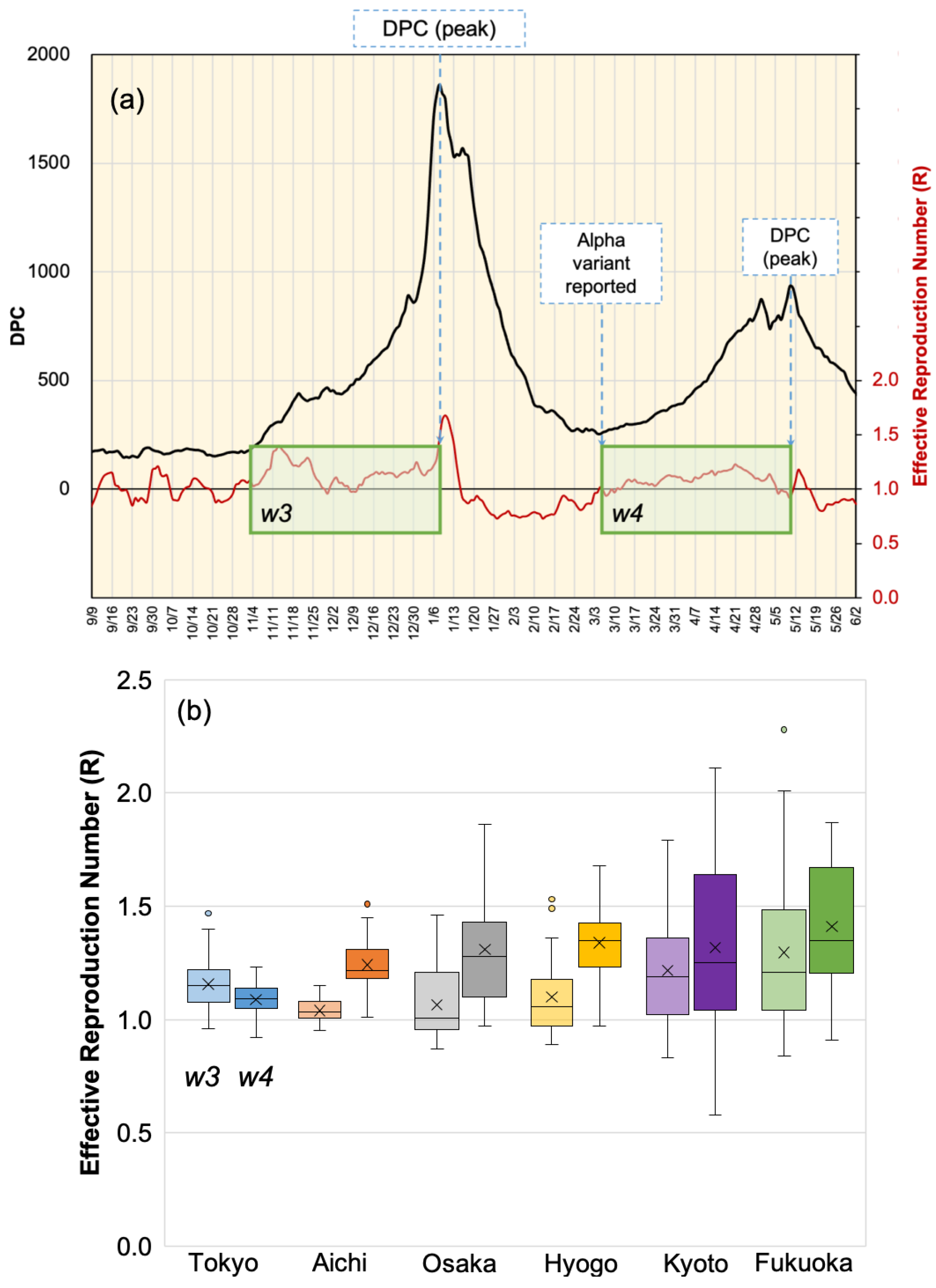
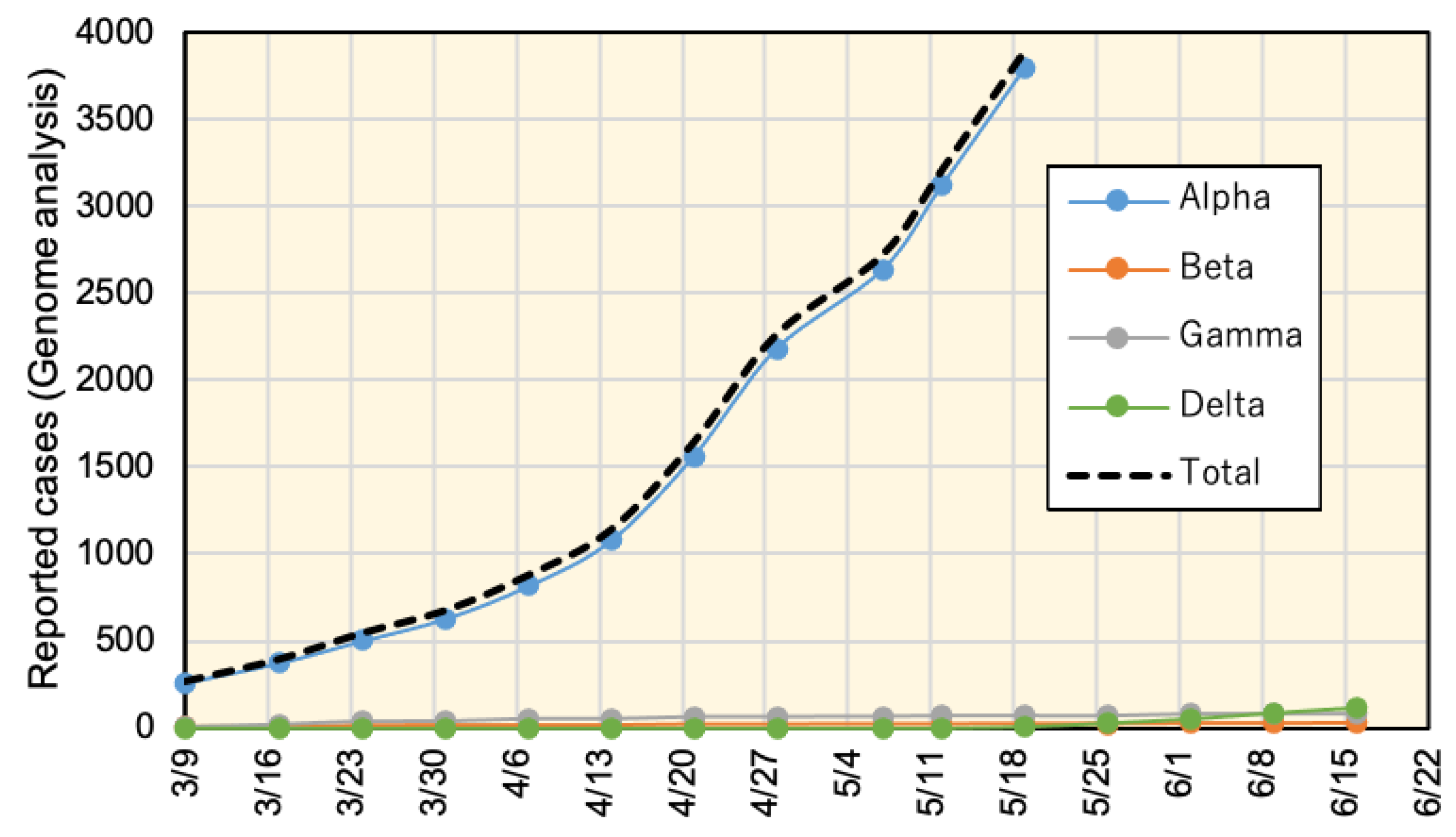
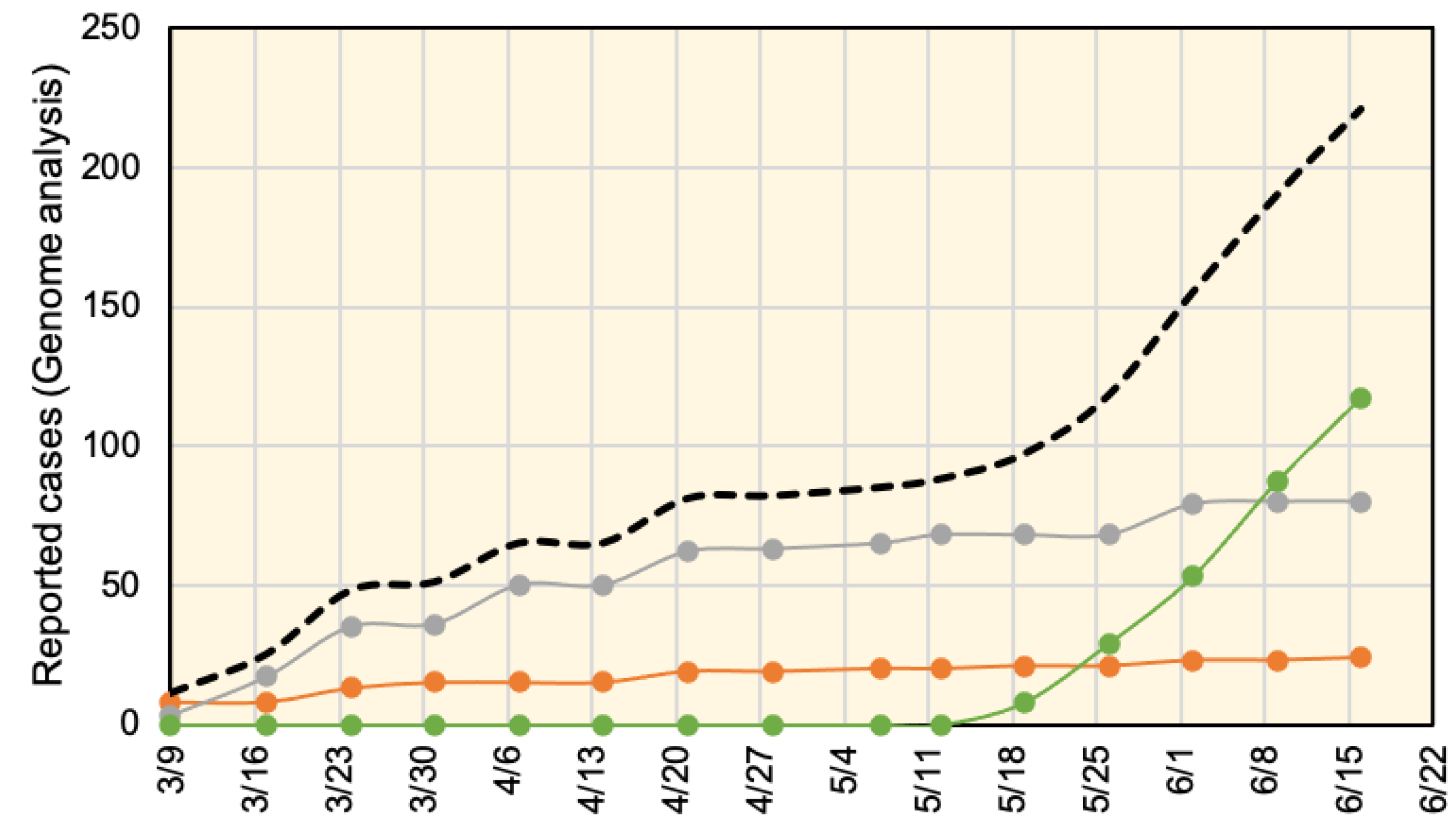
3. Results
3.1. Selection of Data Blend
3.2. Prediction of DPC
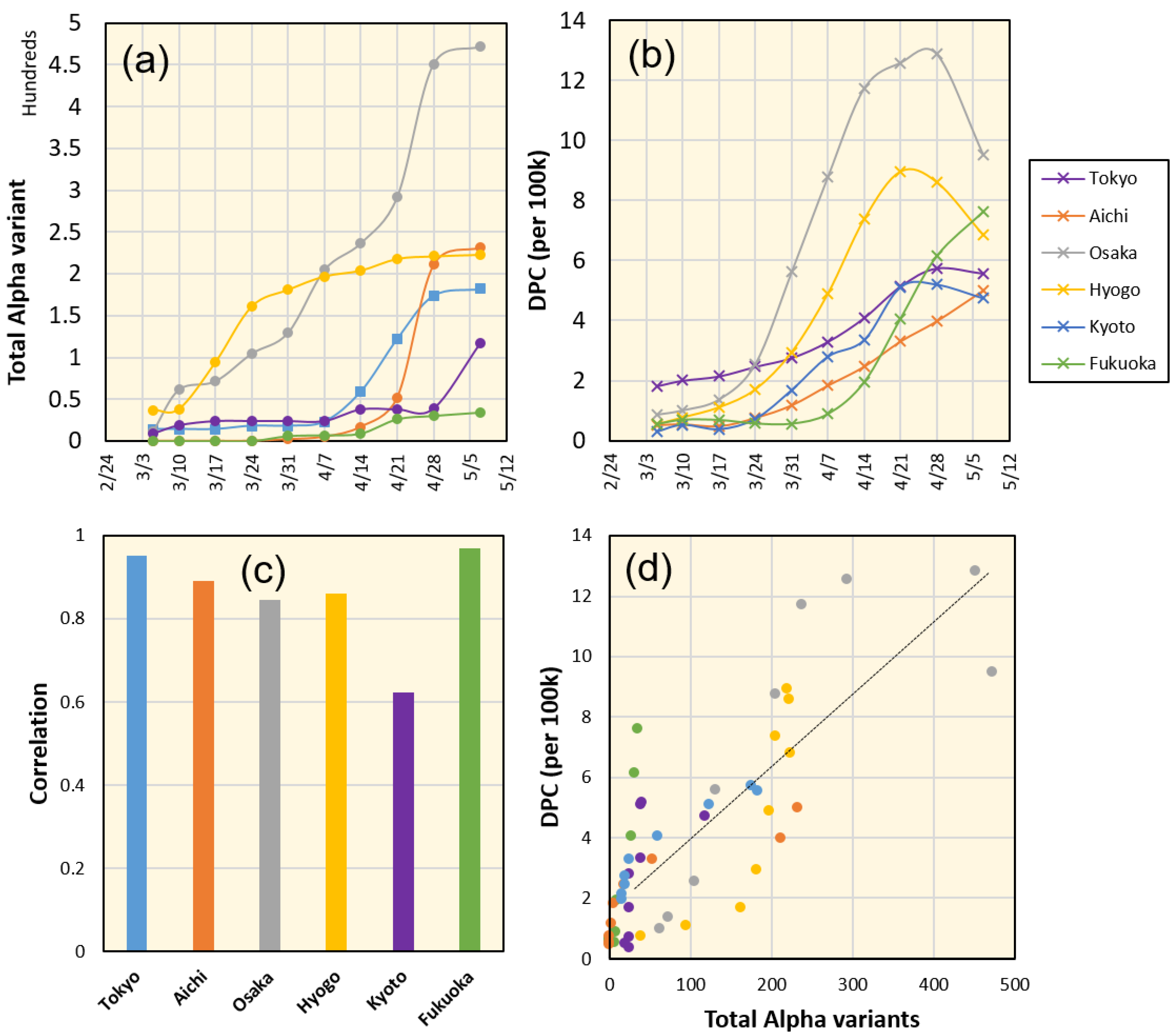
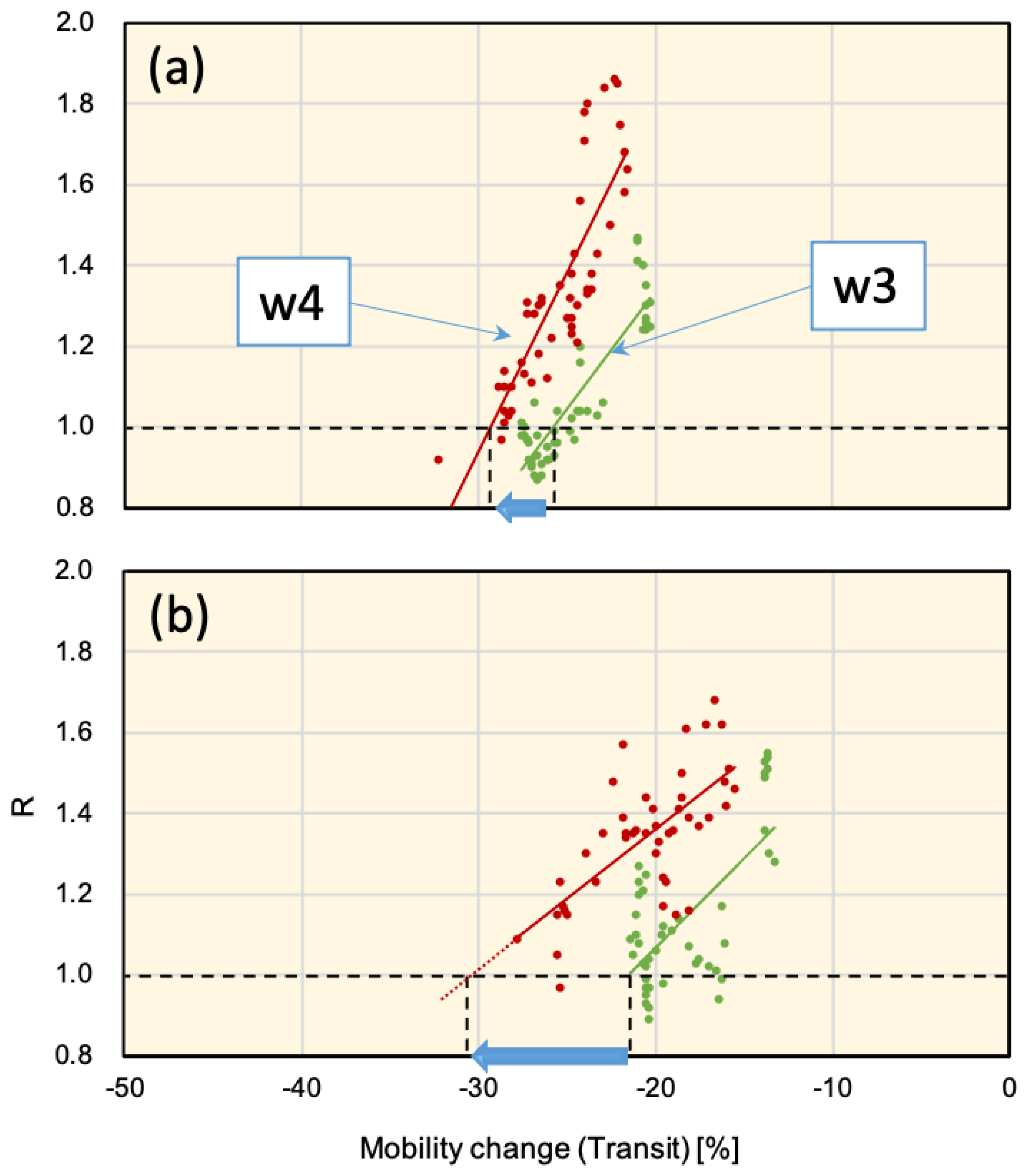
3.3. Effective Reproduction Number
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ozili, P.K.; Arun, T. Spillover of COVID-19: Impact on the Global Economy. SSRN Electron. J. 2020. [Google Scholar] [CrossRef] [Green Version]
- De-Leon, H.; Calderon-Margalit, R.; Pederiva, F.; Ashkenazy, Y.; Gazit, D. First indication of the effect of COVID-19 vaccinations on the course of the outbreak in Israel. medRxiv 2021. [Google Scholar] [CrossRef]
- Mofijur, M.; Fattah, I.R.; Alam, M.A.; Islam, A.S.; Ong, H.C.; Rahman, S.A.; Najafi, G.; Ahmed, S.; Uddin, M.A.; Mahlia, T. Impact of COVID-19 on the social, economic, environmental and energy domains: Lessons learnt from a global pandemic. Sustain. Prod. Consum. 2021, 26, 343–359. [Google Scholar] [CrossRef]
- Musa, S.S.; Qureshi, S.; Zhao, S.; Yusuf, A.; Mustapha, U.T.; He, D. Mathematical modeling of COVID-19 epidemic with effect of awareness programs. Infect. Dis. Model. 2021, 6, 448–460. [Google Scholar] [CrossRef]
- Banik, R.; Rahman, M.; Sikder, T.; Gozal, D. COVID-19 in Bangladesh: Public awareness and insufficient health facilities remain key challenges. Public Health 2020, 183, 50–51. [Google Scholar] [CrossRef] [PubMed]
- Sun, C.X.; He, B.; Mu, D.; Li, P.L.; Zhao, H.T.; Li, Z.L.; Zhang, M.L.; Feng, L.Z.; Zheng, J.D.; Cheng, Y.; et al. Public Awareness and Mask Usage during the COVID-19 Epidemic: A Survey by China CDC New Media. Biomed. Environ. Sci. 2020, 33, 639–645. [Google Scholar] [CrossRef] [PubMed]
- Weiss, H.H. The SIR model and the foundations of public health. Mater. Mat. 2013, 2013, 0001–17. [Google Scholar]
- Klepac, P.; Pomeroy, L.W.; Bjørnstad, O.N.; Kuiken, T.; Osterhaus, A.D.; Rijks, J.M. Stage-structured transmission of phocine distemper virus in the Dutch 2002 outbreak. Proc. R. Soc. B Biol. Sci. 2009, 276, 2469–2476. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Arik, S.O.; Li, C.L.; Yoon, J.; Sinha, R.; Epshteyn, A.; Le, L.T.; Menon, V.; Singh, S.; Zhang, L.; Yoder, N.; et al. Interpretable Sequence Learning for COVID-19 Forecasting. arXiv 2020, arXiv:2008.00646. [Google Scholar]
- Carli, R.; Cavone, G.; Epicoco, N.; Scarabaggio, P.; Dotoli, M. Model predictive control to mitigate the COVID-19 outbreak in a multi-region scenario. Annu. Rev. Control. 2020, 50, 373–393. [Google Scholar] [CrossRef]
- Rahimi, I.; Chen, F.; Gandomi, A.H. A review on COVID-19 forecasting models. Neural Comput. Appl. 2021. [Google Scholar] [CrossRef]
- Tomar, A.; Gupta, N. Prediction for the spread of COVID-19 in India and effectiveness of preventive measures. Sci. Total Environ. 2020, 728, 138762. [Google Scholar] [CrossRef] [PubMed]
- Zhang, G.; Liu, X. Prediction and control of COVID-19 spreading based on a hybrid intelligent model. PLoS ONE 2021, 16, e0246360. [Google Scholar] [CrossRef]
- Noh, J.; Danuser, G. Estimation of the fraction of COVID-19 infected people in U.S. states and countries worldwide. PLoS ONE 2021, 16, e0246772. [Google Scholar] [CrossRef]
- Devaraj, J.; Madurai Elavarasan, R.; Pugazhendhi, R.; Shafiullah, G.; Ganesan, S.; Jeysree, A.K.; Khan, I.A.; Hossain, E. Forecasting of COVID-19 cases using deep learning models: Is it reliable and practically significant? Results Phys. 2021, 21, 103817. [Google Scholar] [CrossRef] [PubMed]
- Mousavi, M.; Salgotra, R.; Holloway, D.; Gandomi, A.H. COVID-19 Time Series Forecast Using Transmission Rate and Meteorological Parameters as Features. IEEE Comput. Intell. Mag. 2020, 15, 34–50. [Google Scholar] [CrossRef]
- Balli, S. Data analysis of Covid-19 pandemic and short-term cumulative case forecasting using machine learning time series methods. Chaos Solitons Fractals 2021, 142, 110512. [Google Scholar] [CrossRef]
- Melin, P.; Sánchez, D.; Monica, J.C.; Castillo, O. Optimization using the firefly algorithm of ensemble neural networks with type-2 fuzzy integration for COVID-19 time series prediction. Soft Comput. 2021. [Google Scholar] [CrossRef] [PubMed]
- Krutikov, M.; Hayward, A.; Shallcross, L. Spread of a Variant SARS-CoV-2 in Long-Term Care Facilities in England. N. Engl. J. Med. 2021, 384, 1671–1673. [Google Scholar] [CrossRef]
- Davies, N.G.; Abbott, S.; Barnard, R.C.; Jarvis, C.I.; Kucharski, A.J.; Munday, J.D.; Pearson, C.A.; Russell, T.W.; Tully, D.C.; Washburne, A.D.; et al. Estimated transmissibility and impact of SARS-CoV-2 lineage B.1.1.7 in England. Science 2021, 372. [Google Scholar] [CrossRef]
- Volz, E.; Mishra, S.; Chand, M.; Barrett, J.C.; Johnson, R.; Geidelberg, L.; Hinsley, W.R.; Laydon, D.J.; Dabrera, G.; O’Toole, Á.; et al. Transmission of SARS-CoV-2 Lineage B.1.1.7 in England: Insights from linking epidemiological and genetic data. medRxiv 2021. [Google Scholar] [CrossRef]
- Nouvellet, P.; Bhatia, S.; Cori, A.; Ainslie, K.E.; Baguelin, M.; Bhatt, S.; Boonyasiri, A.; Brazeau, N.F.; Cattarino, L.; Cooper, L.V.; et al. Reduction in mobility and COVID-19 transmission. Nat. Commun. 2021, 12, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Badr, H.S.; Du, H.; Marshall, M.; Dong, E.; Squire, M.M.; Gardner, L.M. Association between mobility patterns and COVID-19 transmission in the USA: A mathematical modelling study. Lancet Infect. Dis. 2020, 20, 1247–1254. [Google Scholar] [CrossRef]
- Kraemer, M.U.; Yang, C.H.; Gutierrez, B.; Wu, C.H.; Klein, B.; Pigott, D.M.; Du Plessis, L.; Faria, N.R.; Li, R.; Hanage, W.P.; et al. The effect of human mobility and control measures on the COVID-19 epidemic in China. Science 2020, 368, 493–497. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cartenì, A.; Di Francesco, L.; Martino, M. How mobility habits influenced the spread of the COVID-19 pandemic: Results from the Italian case study. Sci. Total Environ. 2020, 741, 140489. [Google Scholar] [CrossRef]
- Ma, Y.; Zhao, Y.; Liu, J.; He, X.; Wang, B.; Fu, S.; Yan, J.; Niu, J.; Zhou, J.; Luo, B. Effects of temperature variation and humidity on the death of COVID-19 in Wuhan, China. Sci. Total Environ. 2020, 724, 138226. [Google Scholar] [CrossRef]
- Xie, J.; Zhu, Y. Association between ambient temperature and COVID-19 infection in 122 cities from China. Sci. Total Environ. 2020, 724, 138201. [Google Scholar] [CrossRef]
- Wu, Y.; Jing, W.; Liu, J.; Ma, Q.; Yuan, J.; Wang, Y.; Du, M.; Liu, M. Effects of temperature and humidity on the daily new cases and new deaths of COVID-19 in 166 countries. Sci. Total Environ. 2020, 729, 139051. [Google Scholar] [CrossRef]
- Rashed, E.A.; Kodera, S.; Gomez-Tames, J.; Hirata, A. Influence of Absolute Humidity, Temperature and Population Density on COVID-19 Spread and Decay Durations: Multi-Prefecture Study in Japan. Int. J. Environ. Res. Public Health 2020, 17, 5354. [Google Scholar] [CrossRef]
- Kodera, S.; Rashed, E.A.; Hirata, A. Correlation between COVID-19 Morbidity and Mortality Rates in Japan and Local Population Density, Temperature, and Absolute Humidity. Int. J. Environ. Res. Public Health 2020, 17, 5477. [Google Scholar] [CrossRef]
- Diao, Y.; Kodera, S.; Anzai, D.; Gomez-Tames, J.; Rashed, E.A.; Hirata, A. Influence of population density, temperature, and absolute humidity on spread and decay durations of COVID-19: A comparative study of scenarios in China, England, Germany, and Japan. One Health 2021, 12, 100203. [Google Scholar] [CrossRef] [PubMed]
- Majumder, P.; Ray, P.P. A systematic review and meta-analysis on correlation of weather with COVID-19. Sci. Rep. 2021, 11, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Briz-Redón, Á.; Serrano-Aroca, Á. The effect of climate on the spread of the COVID-19 pandemic: A review of findings, and statistical and modelling techniques. Prog. Phys. Geogr. Earth Environ. 2020, 44, 591–604. [Google Scholar] [CrossRef]
- Espejo, W.; Celis, J.E.; Chiang, G.; Bahamonde, P. Environment and COVID-19: Pollutants, impacts, dissemination, management and recommendations for facing future epidemic threats. Sci. Total Environ. 2020, 747, 141314. [Google Scholar] [CrossRef]
- Rashed, E.A.; Hirata, A. One-year lesson: Machine learning prediction of COVID-19 positive cases with meteorological data and mobility estimate in Japan. Int. J. Environ. Res. Public Health 2021, 18, 5736. [Google Scholar] [CrossRef] [PubMed]
- Lauer, S.A.; Grantz, K.H.; Bi, Q.; Jones, F.K.; Zheng, Q. The Incubation Period of Coronavirus Disease 2019 (COVID-19) From Publicly Reported Confirmed Cases: Estimation and Application. Ann. Intern. Med. 2020, 172, 577–582. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Thiagarajan, K. Why is India having a COVID-19 surge? BMJ 2021, 373. [Google Scholar] [CrossRef]
- Zaki, N.; Mohamed, E.A. The estimations of the COVID-19 incubation period: A scoping reviews of the literature. J. Infect. Public Health 2021, 14, 638–646. [Google Scholar] [CrossRef]
- Omori, R.; Mizumoto, K.; Chowell, G. Changes in testing rates could mask the novel coronavirus disease (COVID-19) growth rate. Int. J. Infect. Dis. 2020, 94, 116–118. [Google Scholar] [CrossRef]
- Sheikh, A.; McMenamin, J.; Taylor, B.; Robertson, C. SARS-CoV-2 Delta VOC in Scotland: Demographics, risk of hospital admission, and vaccine effectiveness. Lancet 2021. [Google Scholar] [CrossRef]
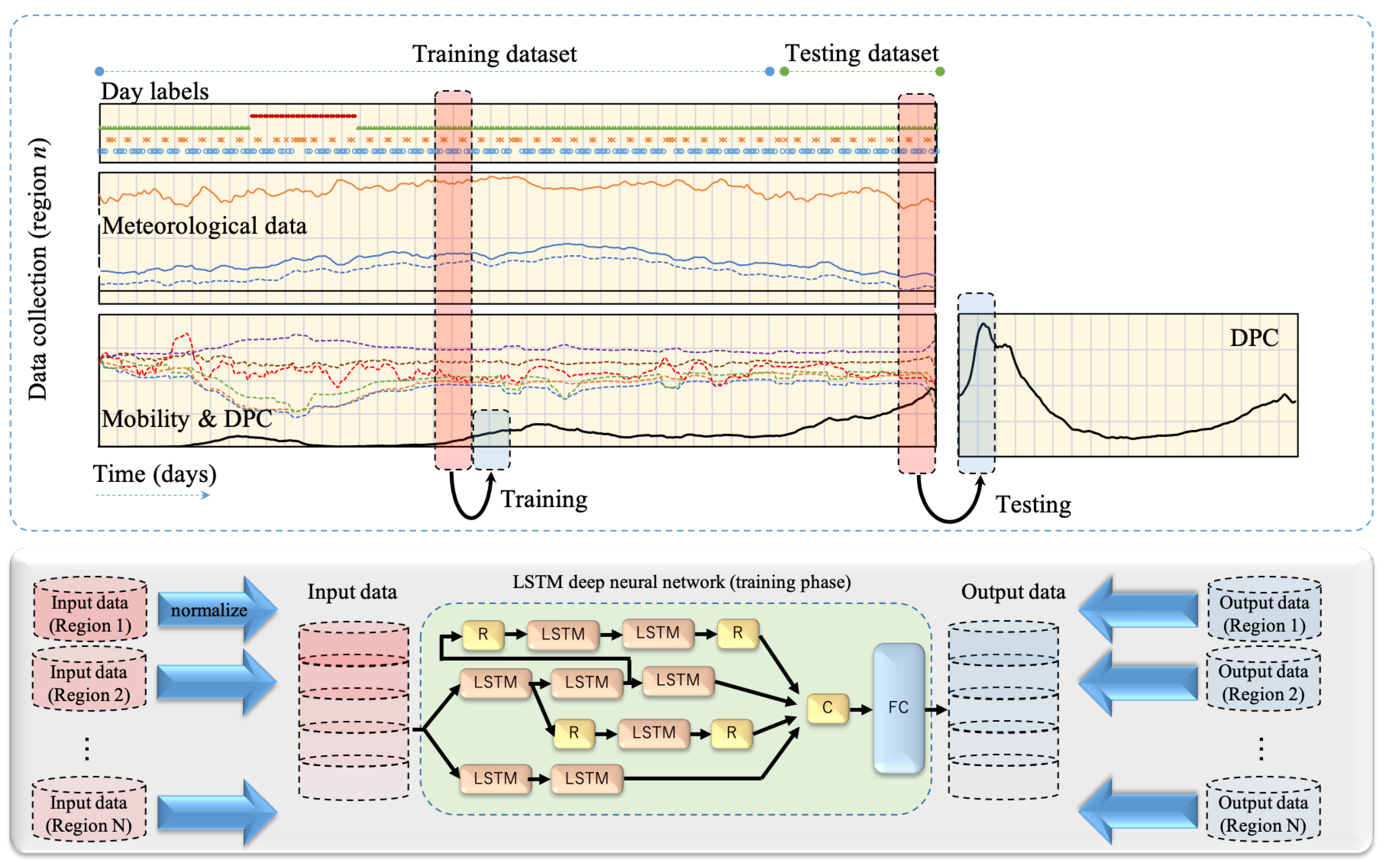
| Period# | Training | Testing | ||
|---|---|---|---|---|
| from | to | from | to | |
| 1 | 15 February 2020 | 26 January 2021 | 27 January 2021 | 23 February 2021 |
| 2 | ⋯ | 2 February 2021 | 3 February 2021 | 2 March 2021 |
| 3 | ⋯ | 9 February 2021 | 10 February 2021 | 9 March 2021 |
| 4 | ⋯ | 16 February 2021 | 17 February 2021 | 16 March 2021 |
| 5 | ⋯ | 23 February 2021 | 24 February 2021 | 23 March 2021 |
| 6 | ⋯ | 2 March 2021 | 3 March 2021 | 30 March 2021 |
| 7 | ⋯ | 9 March 2021 | 10 March 2021 | 6 April 2021 |
| 8 | ⋯ | 16 March 2021 | 17 March 2021 | 13 April 2021 |
| 9 | ⋯ | 23 March 2021 | 24 March 2021 | 20 April 2021 |
| 10 | ⋯ | 30 March 2021 | 31 March 2021 | 27 April 2021 |
| 11 | ⋯ | 6 April 2021 | 7 April 2021 | 4 May 2021 |
| 12 | ⋯ | 13 April 2021 | 14 April 2021 | 11 May 2021 |
| 13 | ⋯ | 20 April 2021 | 21 April 2021 | 18 May 2021 |
| 14 | ⋯ | 27 April 2021 | 28 April 2021 | 25 May 2021 |
| 15 | ... | 4 May 2021 | 5 May 2021 | 1 June 2021 |
| Scenarios | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| Day labels | ✓ | ✓ | ✓ | ✓ |
| Meteorological data | ✓ | ✗ | ✗ | ✓ |
| Mobility | ✗ | Transit only | ✓ | ✓ |
| DPC | ✓ | ✓ | ✓ | ✓ |
| Tokyo | 46.0 | 37.3 | 19.0 | 16.3 |
| Aichi | 26.5 | 22.6 | 23.2 | 23.9 |
| Osaka | 26.0 | 20.9 | 24.9 | 18.4 |
| Hyogo | 25.1 | 17.4 | 12.6 | 19.5 |
| Kyoto | 23.4 | 24.6 | 22.0 | 15.0 |
| Fukuoka | 25.6 | 24.5 | 27.7 | 30.7 |
| Average | 28.8 | 24.6 | 21.6 | 20.6 |
| Period# | Tokyo | Aichi | Osaka | Hyogo | Kyoto | Fukuoka | Avg. |
|---|---|---|---|---|---|---|---|
| 1 | 22.66 | 15.80 | 21.72 | 12.87 | 18.45 | 26.09 | 19.60 |
| 2 | 29.40 | 25.14 | 19.33 | 26.64 | 25.16 | 20.61 | 24.38 |
| 3 | 22.75 | 21.74 | 23.15 | 24.34 | 40.61 | 21.34 | 25.66 |
| 4 | 9.35 | 20.47 | 25.33 | 22.99 | 56.25 | 15.35 | 24.96 |
| 5 | 11.31 | 11.88 | 24.76 | 39.81 | 59.08 | 32.62 | 29.91 |
| 6 | 19.75 | 15.91 | 32.37 | 32.53 | 40.59 | 43.53 | 30.78 |
| 7 | 24.20 | 21.75 | 42.51 | 38.40 | 38.26 | 44.61 | 34.95 |
| 8 | 15.73 | 23.80 | 49.90 | 33.02 | 30.02 | 76.87 | 38.22 |
| 9 | 17.15 | 27.16 | 52.69 | 43.10 | 44.51 | 55.30 | 39.99 |
| 10 | 14.68 | 26.37 | 38.93 | 39.97 | 40.20 | 50.39 | 35.09 |
| 11 | 21.72 | 23.43 | 24.68 | 28.21 | 24.81 | 42.67 | 27.59 |
| 12 | 18.16 | 30.17 | 18.87 | 21.54 | 16.56 | 43.28 | 24.77 |
| 13 | 23.99 | 33.94 | 7.56 | 13.82 | 13.24 | 36.13 | 21.45 |
| 14 | 13.80 | 21.37 | 23.09 | 20.29 | 11.81 | 17.19 | 17.93 |
| 15 | 9.37 | 21.42 | 24.42 | 22.50 | 18.48 | 26.59 | 20.46 |
| Avg. | 18.27 | 22.69 | 28.62 | 28.00 | 31.87 | 36.84 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rashed, E.A.; Hirata, A. Infectivity Upsurge by COVID-19 Viral Variants in Japan: Evidence from Deep Learning Modeling. Int. J. Environ. Res. Public Health 2021, 18, 7799. https://doi.org/10.3390/ijerph18157799
Rashed EA, Hirata A. Infectivity Upsurge by COVID-19 Viral Variants in Japan: Evidence from Deep Learning Modeling. International Journal of Environmental Research and Public Health. 2021; 18(15):7799. https://doi.org/10.3390/ijerph18157799
Chicago/Turabian StyleRashed, Essam A., and Akimasa Hirata. 2021. "Infectivity Upsurge by COVID-19 Viral Variants in Japan: Evidence from Deep Learning Modeling" International Journal of Environmental Research and Public Health 18, no. 15: 7799. https://doi.org/10.3390/ijerph18157799
APA StyleRashed, E. A., & Hirata, A. (2021). Infectivity Upsurge by COVID-19 Viral Variants in Japan: Evidence from Deep Learning Modeling. International Journal of Environmental Research and Public Health, 18(15), 7799. https://doi.org/10.3390/ijerph18157799







