Targeting Malaria Hotspots to Reduce Transmission Incidence in Senegal
Abstract
1. Introduction
- Focused Mass Drug Administration (MDA), consisting of systematically treating individuals in a selected geographic area with antimalarial drugs, without screening for infection.
- Focused Mass Screen and Treat (MSAT), consisting of malaria screening, using a rapid diagnostic test and providing treatment to those with a positive test result, in a selected area.
- Seasonal Malaria Chemoprevention (SMC), consisting of intermittently administrating preventive antimalarial treatment to children during the main transmission period.
- Long-Lasting Insecticide-treated Nets (LLIN), intended to avoid mosquito bites, relying on physical and chemical barriers of manufactured nets.
2. Materials and Methods
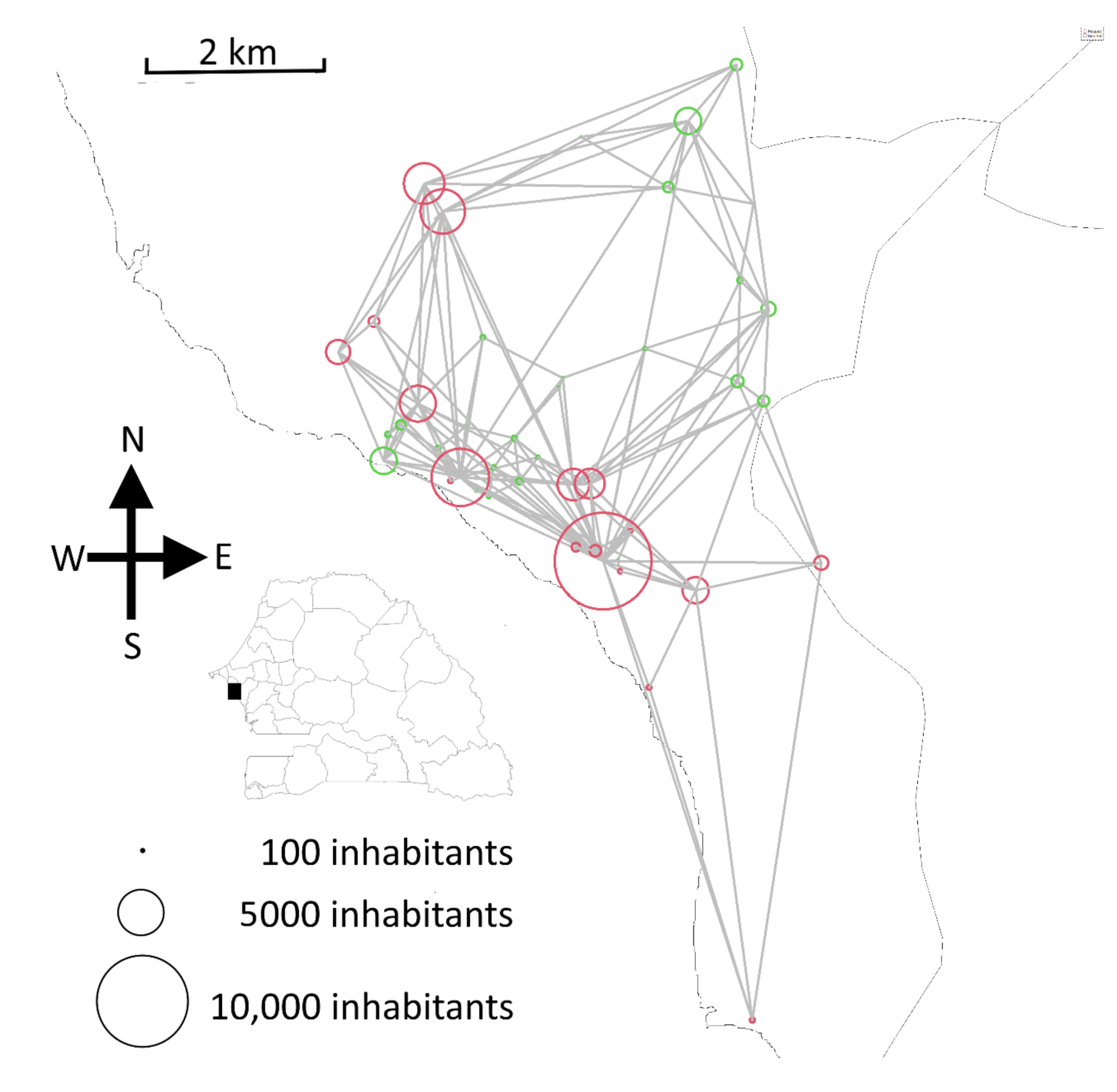
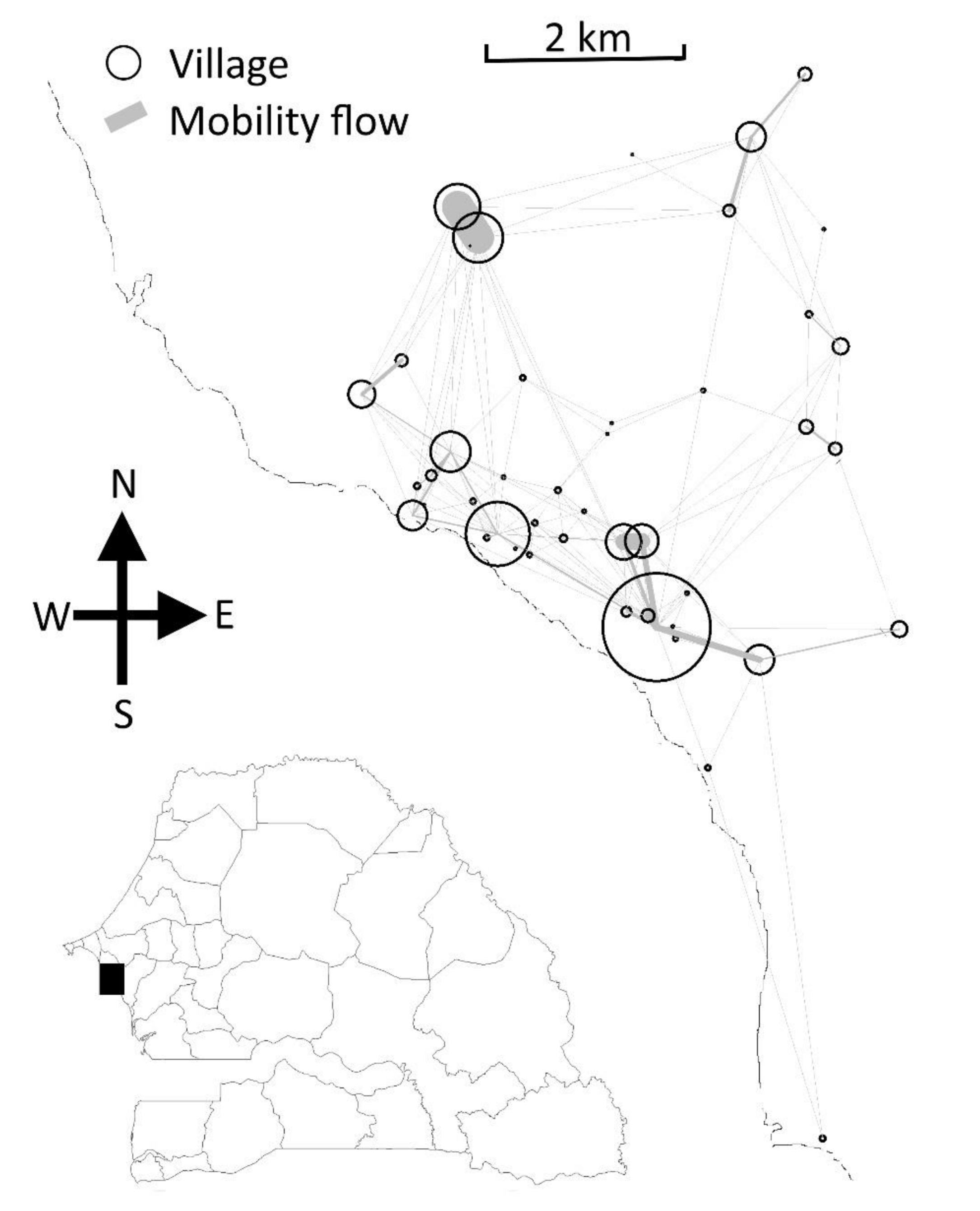
2.1. Study Area and Dataset
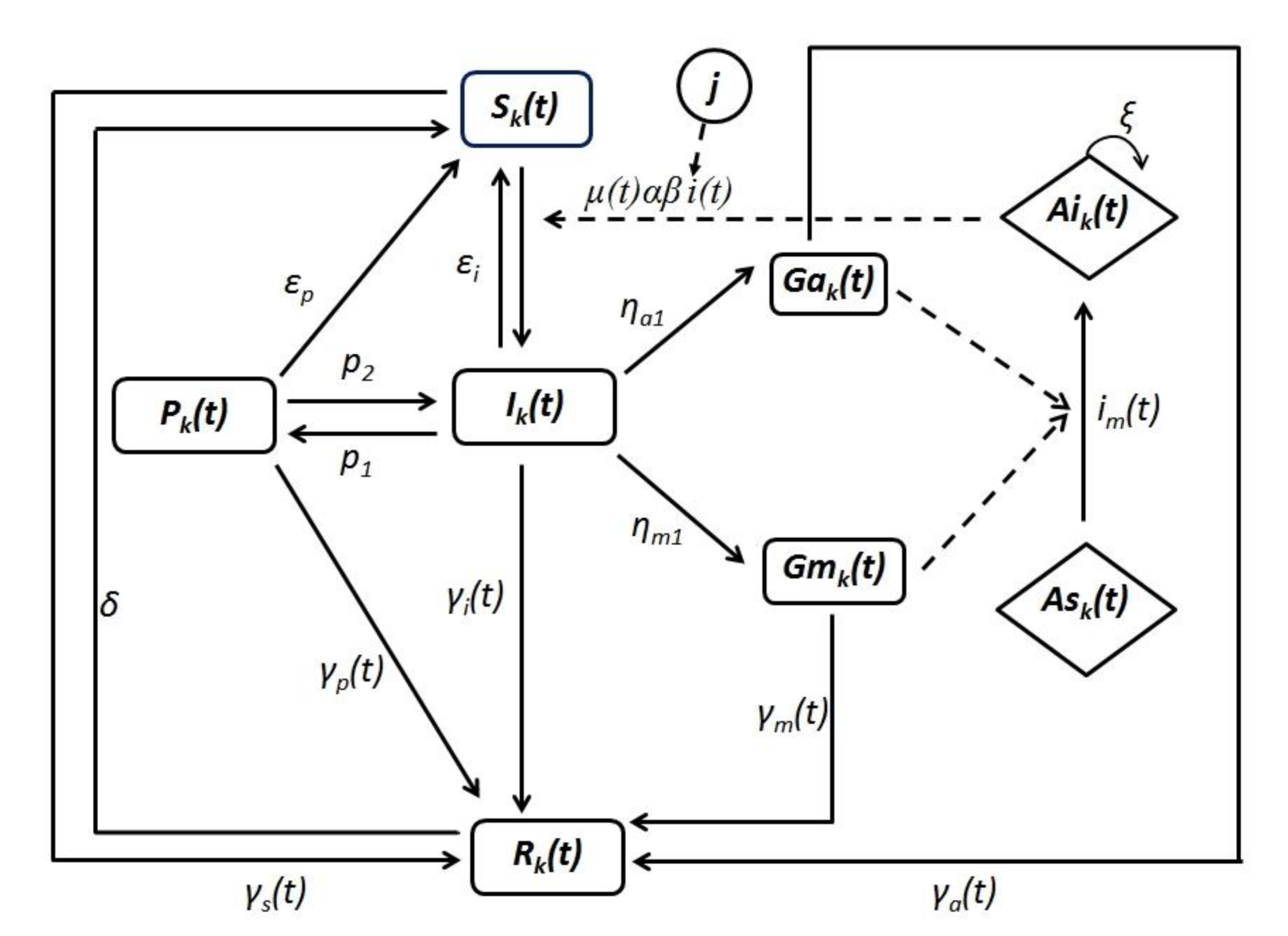
2.2. Model Structure
2.3. Model Calibration
2.4. Hotspots Definitions and Interventions
- Low transmission period hotspots (LT hotspots) were defined as villages reporting at least one malaria case in the previous low transmission period (December to May).
- High transmission period hotspots (HT hotspots) were villages with the highest malaria incidences during the previous transmission season (June to November).
- High connectivity hotspots (HC hotspots) were villages highly connected to neighboring villages based on human mobility potential.
3. Results
3.1. Parameters Estimates and Sensitivity Analysis
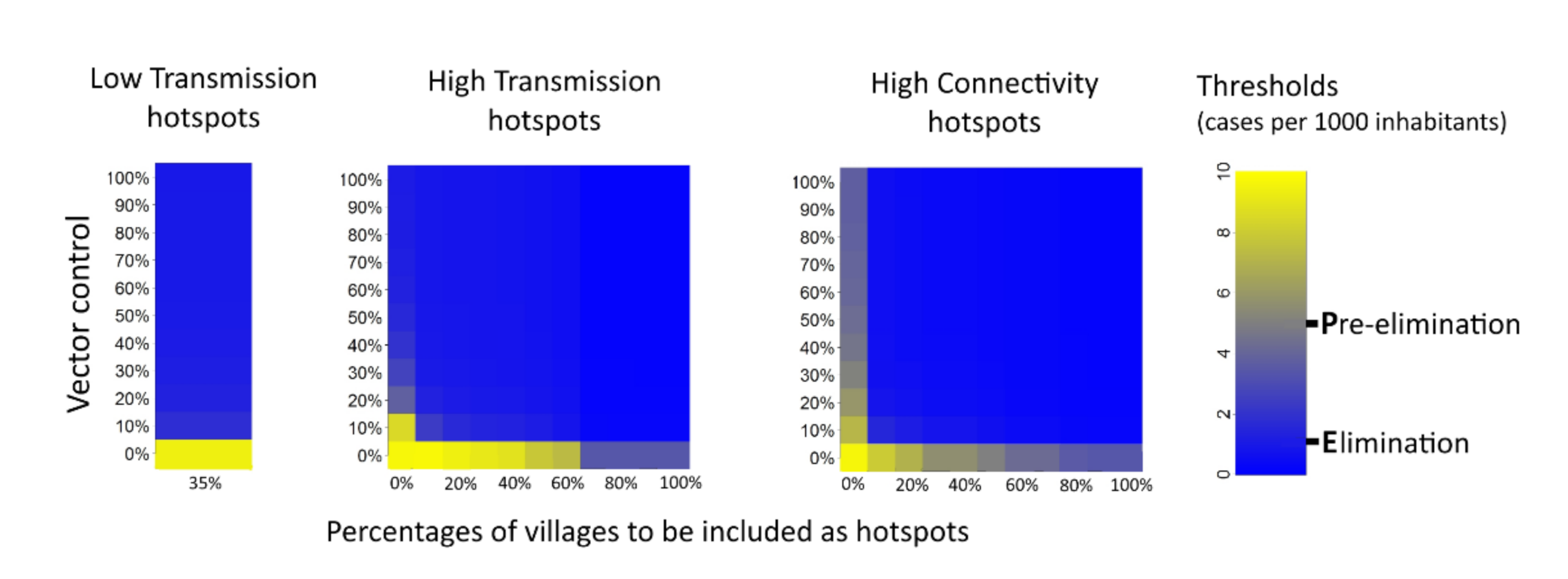
3.2. Sensitivity of Hotspot Definitions
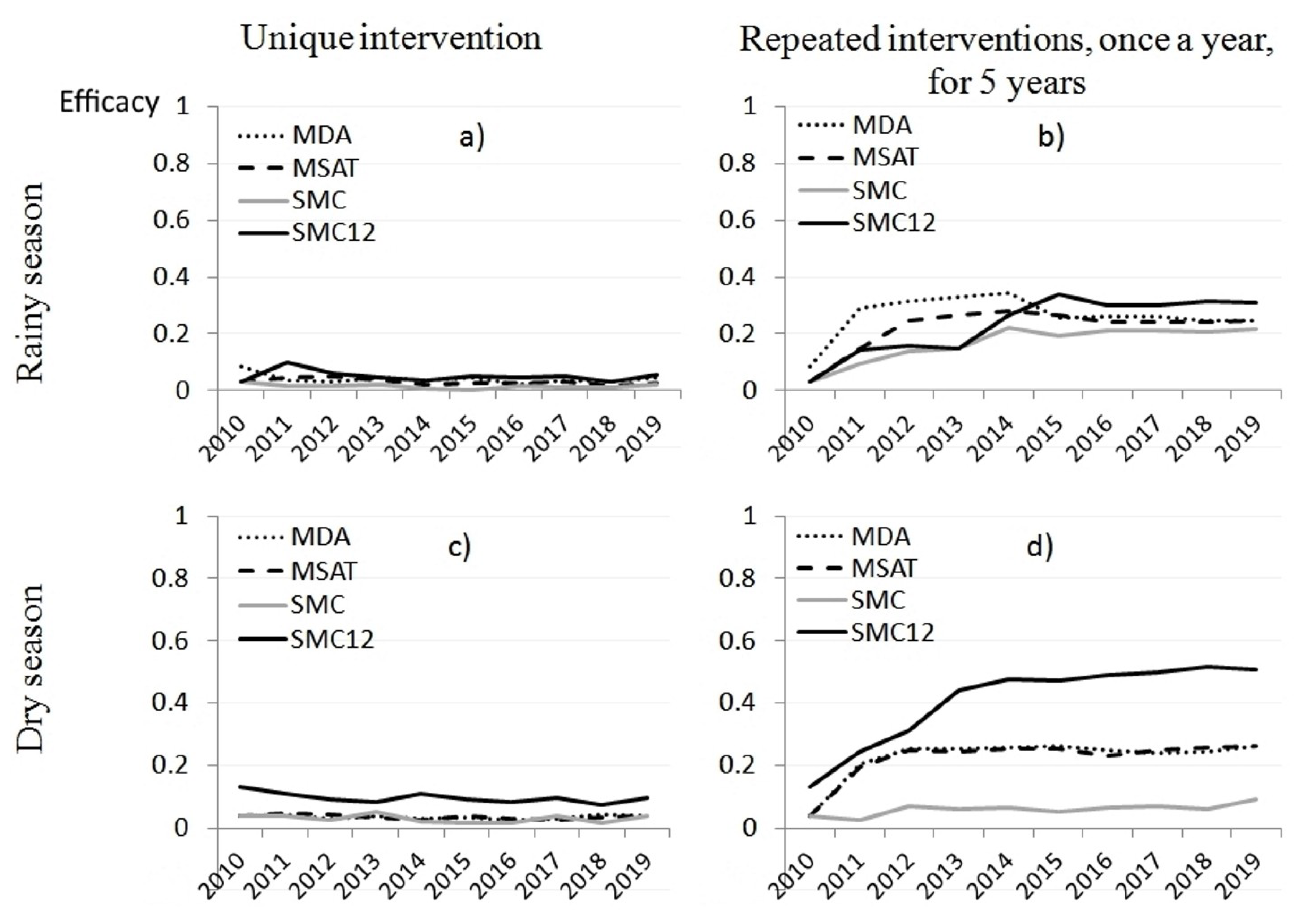
3.3. Intervention Simulations
3.4. Pre-Elimination/Elimination Stage
3.5. Rebound Effects Due to Human Mobility
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
List of Abbreviations
| LLIN | long-lasting insecticide-treated bed nets |
| RDT | rapid diagnostic tests |
| ACT | artemisinin-based combination therapy |
| WHO | World Health Organization |
| MDA | mass drug administration |
| MSAT | mass screen and treat |
| SMC | seasonal malaria chemoprevention |
| SEIR | susceptible-exposed-infected-recovered |
| GPS | global positioning system |
| MCMC | Markov Chain Monte Carlo |
| LT hotspots | low transmission period hotspots |
| HT hotspots | high transmission period hotspots |
| HC hotspots | high connectivity hotspots |
| HTP | high transmission period |
| LTP | low transmission period |
| EIR | entomological inoculation rate |
| IRS | indoor residual spraying |
Appendix A
Appendix A.1. Model Description
- : proportion of humans susceptible to malaria infection.
- : proportion of blood-stage infected humans, with few gametocytes, not immune and positive to rapid diagnostic test (RDT).
- : proportion of humans with partial immunity (premunition). Individuals could remain in this state for many years, but could lose their immunity if pregnant or on cessation of exposure. They were assumed to be RDT positive and with few gametocytes.
- : proportion of infected humans, gametocyte-positive, asymptomatic.
- : proportion of infected humans, gametocyte-positive, symptomatic.
- : proportion of humans who were temporarily not susceptible to new infection, as a result of the prophylactic effect of treatment.
- : proportion of female mosquitoes that carry sporozoites in their salivary glands.
- : proportion of female mosquitoes that have survived the cycle and were free from malaria sporozoites.
- : proportion of people in the overall population, who are away at a given time (visiting other villages than their own village).
- : anopheles’ density (ratio of the number of female anopheles to the number of humans, at time t).
- : number of bites per female anopheles per night.
- : probability that a person bitten by an infectious mosquito becomes infected.
- , , and are rectangular pulse functions. where c represents coverage and Δ the duration of intervention in weeks.
- : rate at which susceptible individuals are treated.
- : rate at which blood-stage infected individuals are treated.
- : rate at which naturally immune individuals are treated. Naturally immune individuals are assumed RDT positive. Susceptible individuals are RDT negative.
- : rate at which asymptomatic gametocyte carriers are treated. Asymptomatic gametocyte carriers are assumed RDT positive.
- : rate at which symptomatic gametocyte carriers are treated. This corresponds to access to care, in periods of no intervention.
- : transition rate from blood-stage infection, to asymptomatic gametocyte carriage.
- : transition rate from blood-stage infection, to symptomatic gametocyte carriage.
- : transition rate from blood-stage infection to premunition.
- : transition rate from premunition to blood-stage infection (loss of premunition).
- δ: transition rate from resistant to susceptible (loss of the protection due to treatment).
- : probability that a mosquito, biting a symptomatic gametocyte carrier, got infected.
- : probability that a mosquito, biting an asymptomatic gametocyte carrier, got infected.
- : mortality rate of mosquitoes.
- : relative probabilities of travel from remote locations j, to local village k.
- : rainfall at week t.
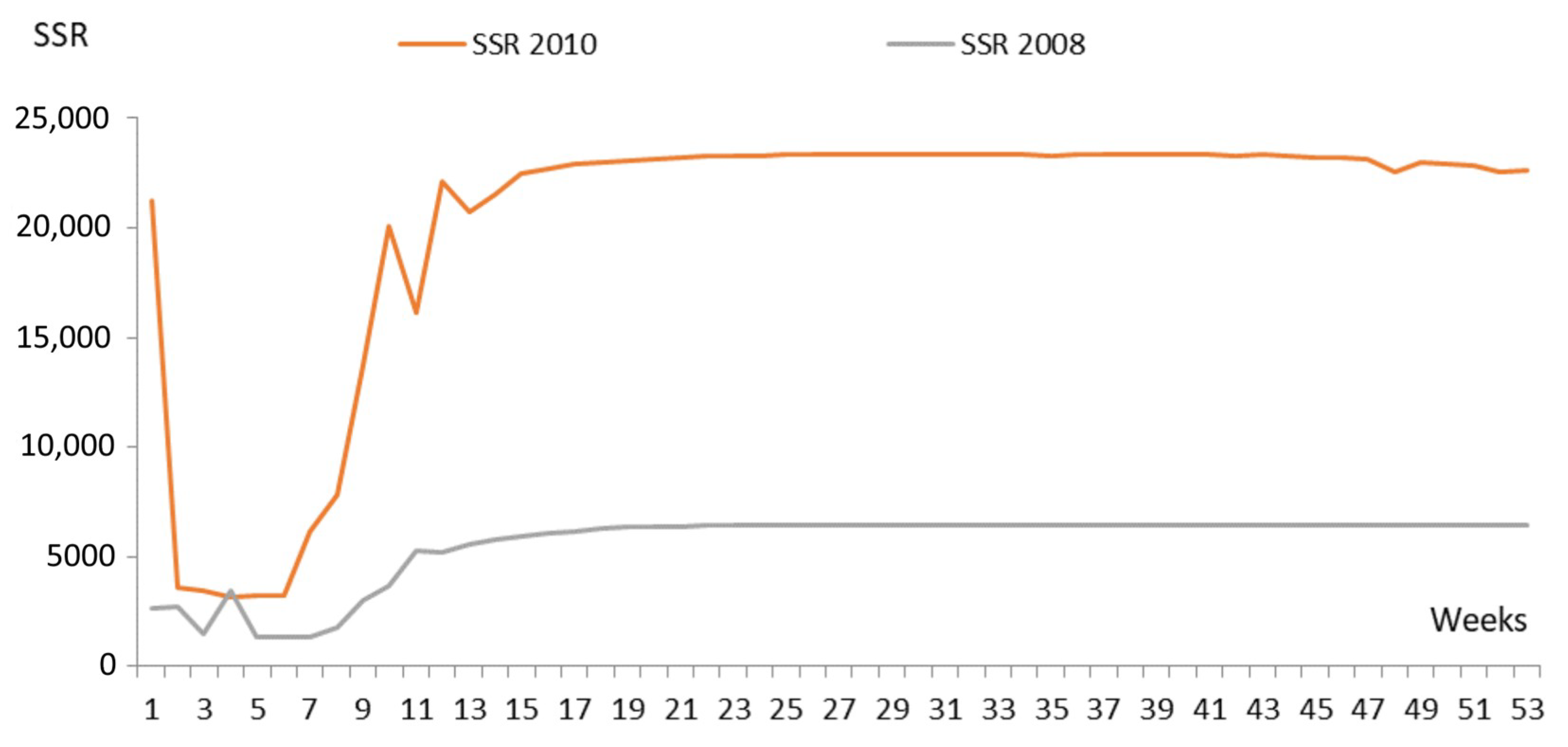
Appendix A.2. Model Parameters
| Parameter Symbol | Parameter Description | References | Parameter Values | 95% C.I. |
|---|---|---|---|---|
| Anopheles density in relation to hosts | [27,31] | 0–12 (min–max) | ||
| Mosquito biting rate | [45] | 0.46 bite/anopheles/night | ||
| Human susceptibility to infection | [45] | 0.3 | ||
| EIR | Entomological Inoculation Rate | [46] | 0 to 2.16/per person/year | |
| Mosquito susceptibility to infection from symptomatic humans | [45] | 0.80 | ||
| Mosquito susceptibility to infection from asymptomatic humans | Expert opinion | 0.08 ) | ||
| Transition rate from blood-stage parasitemia to symptomatic infection with gametocytemia | [47] | 0.1 days−1 | ||
| Transition rate from blood-stage parasitemia to asymptomatic infection with gametocytemia | [47] | 0.1 days−1 | ||
| Transition rate from post-treatment protection, to susceptible | [48,49] | 0.032 days−1 | ||
| Daily mosquito mortality rate | [45] | 0.18 | ||
| Rate of the acquisition of premunition | fitted | 0.0002 days−1 | 0.0001–0.00035 days−1 | |
| Rate of the loss of premunition | fitted | 0.0002 days−1 | 0.0001–0.00035 days−1 | |
| Usual recovery rate by access to care, not related to specific interventions | fitted | 0.37 days−1 | 0.20–0.51 days−1 | |
| Proportion of people who are away from their home village at a given time | fitted | 0.01 | 0.09–0.2 |
| Compartment | Assigned Value | Reference |
|---|---|---|
| . Proportion of plasmodium falciparum infection in humans, in dry season | [27,45] | |
| = 0.2, Proportion of pre-immune individuals | 0.16 [46] B0.27 [47] 0.23-0.32 [31] | |
| Proportion of symptomatic malaria in dry season. Average dry season incidence estimated from all the dataset (5years data) | [48] | |
| Proportion of asymptomatic gametocyte carriers were assumed 10 times lower than symptomatic (expert advice) | ||
| . Continuous access to treatment for symptomatic malaria. | ||
| Proportion of female anopheles that carry sporozoites, in dry season | [27,45] | |
| Calculated |
Appendix B
Appendix B.1. Simulation of Interventions Targeting HT Hotspots
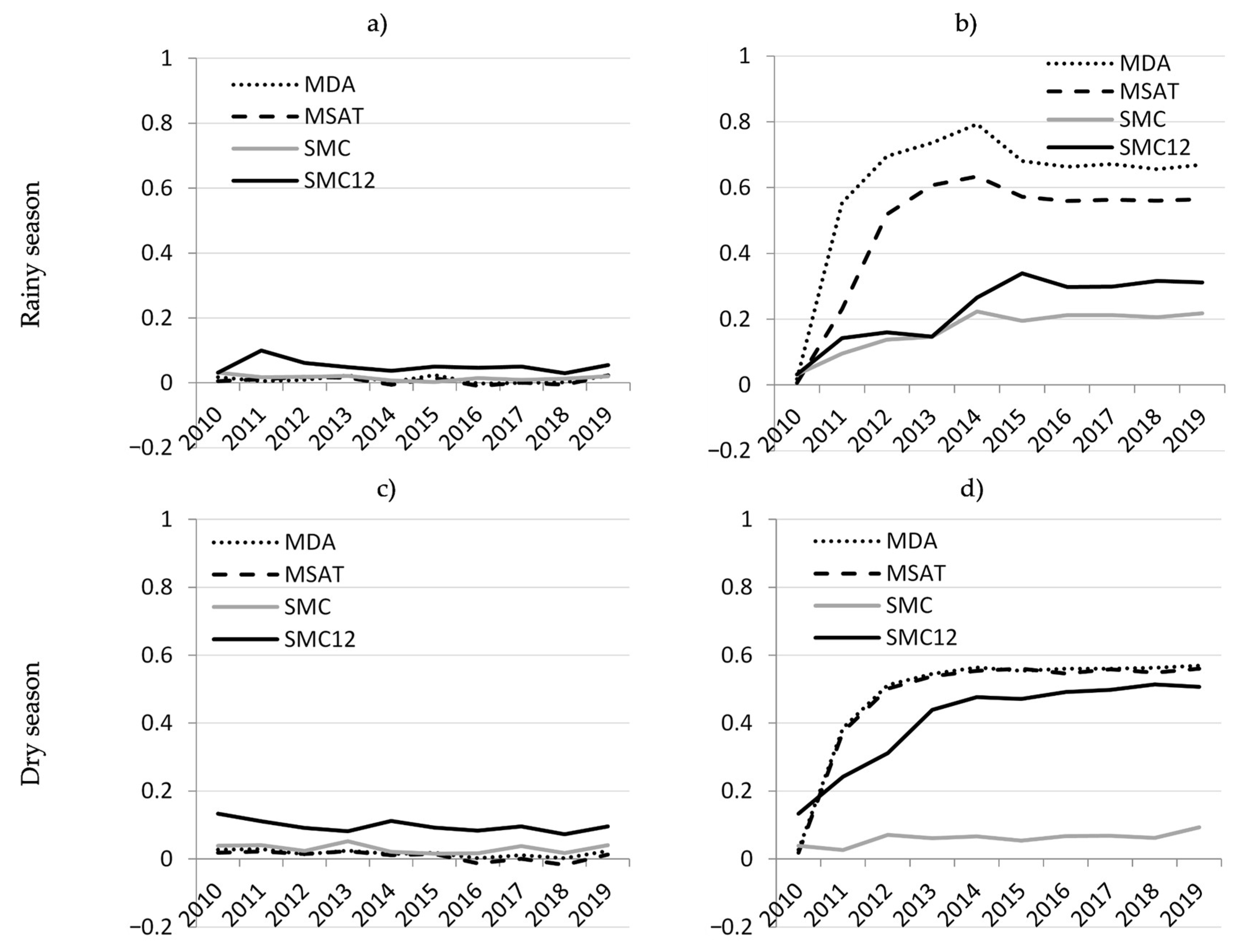
Appendix B.2. Simulation of Interventions Targeting HT Hotspots
References
- World Health Organization (WHO). World Malaria Report 2018. Available online: https://www.who.int/malaria/publications/world-malaria-report-2018/en/ (accessed on 30 October 2020).
- Wotodjo, A.N.; Richard, V.; Boyer, S.; Doucoure, S.; Diagne, N.; Touré-Baldé, A.; Tall, A.; Faye, N.; Gaudart, J.; Trape, J.-F.; et al. The implication of long-lasting insecticide-treated net use in the resurgence of malaria morbidity in a Senegal malaria endemic village in 2010–2011. Parasites Vectors 2015, 8, 267. [Google Scholar] [CrossRef] [PubMed]
- Sarrassat, S.; Senghor, P.; le Hesran, J.Y. Trends in malaria morbidity following the introduction of artesunate plus amodiaquine combination in M’lomp village dispensary, south-western Senegal. Malar. J. 2008, 7, 215. [Google Scholar] [CrossRef] [PubMed]
- Trape, J.F.; Tall, A.; Sokhna, C.; Ly, A.B.; Diagne, N.; Ndiath, O.; Mazenot, C.; Richard, V.; Badiane, A.; Dieye-Ba, F.; et al. The rise and fall of malaria in a West African rural community, Dielmo, Senegal, from 1990 to 2012: A 22 year longitudinal study. Lancet Infect. Dis. 2014, 14, 476–488. [Google Scholar] [CrossRef]
- Programme National de Lutte contre le Paludisme (PNLP). Plan Stratégique National de Lutte Contre le Paludisme au Sénégal 2016–2020. Available online: http://www.pnlp.sn/wp-content/uploads/2016/08/PNLP_PSN_VFF_03-02-2016.pdf (accessed on 30 October 2020).
- Coulibaly, D.; Rebaudet, S.; Travassos, M.A.; Tolo, Y.; Laurens, M.B.; Kone, A.K.; Traore, K.; Guindo, A.B.; Diarra, I.; Niangaly, A.; et al. Spatio-temporal analysis of malaria within a transmission season in Bandiagara, Mali. Malar. J. 2013, 12, 82. [Google Scholar] [CrossRef]
- Xu, X.; Zhou, G.; Wang, Y.; Hu, Y.; Ruan, Y.; Fan, Q.; Yang, Z.; Yan, G.; Cui, L. Microgeographic heterogeneity of border malaria during elimination phase, Yunnan Province, China, 2011–2013. Emerg. Infect. Dis. 2016, 22, 1363–1370. [Google Scholar] [CrossRef]
- Bousema, T.; Griffin, J.T.; Sauerwein, R.W.; Smith, D.L.; Churcher, T.S.; Takken, W.; Ghani, A.; Drakeley, C.; Gosling, R. Hitting hotspots: Spatial targeting of malaria for control and elimination. PLoS Med. 2012, 9, e1001165. [Google Scholar] [CrossRef]
- Bejon, P.; Williams, T.N.; Liljander, A.; Noor, A.M.; Wambua, J.; Ogada, E.; Olotu, A.; Osier, F.H.A.; Hay, S.I.; Farnert, A.; et al. Stable and unstable malaria hotspots in longitudinal cohort studies in Kenya. PLoS Med. 2010, 7, e1000304. [Google Scholar] [CrossRef]
- Bousema, T.; Stevenson, J.; Baidjoe, A.Y.; Stresman, G.; Griffin, J.T.; Kleinschmidt, I.; Remarque, E.J.; Vulule, J.; Bayoh, M.N.; Laserson, K.; et al. The impact of hotspot-targeted interventions on malaria transmission: Study protocol for a cluster-randomized controlled trial. Trials 2013, 14, 36. [Google Scholar] [CrossRef]
- Moonasar, D.; Morris, N.; Kleinschmidt, I.; Maharaj, R.; Raman, J.; Mayet, N.; Benson, F.; Durrheim, D.; Blumberg, L. What will move malaria control to elimination in South Africa? Afr. Med. J. 2013, 103, 801–806. [Google Scholar] [CrossRef][Green Version]
- Mandal, S.; Sarkar, R.; Sinha, S. Mathematical models of malaria—A review. Malar. J. 2011, 10, 202. [Google Scholar] [CrossRef]
- Gaudart, J.; Touré, O.; Dessay, N.; Dicko, A.; Ranque, S.; Forest, L.; Demongeot, J.; Doumbo, O.K. Modelling malaria incidence with environmental dependency in a locality of Sudanese savannah area, Mali. Malar. J. 2009, 8, 61. [Google Scholar] [CrossRef] [PubMed]
- Silal, S.P.; Little, F.; Barnes, K.I.; White, L.J. Hitting a moving target: A model for malaria elimination in the presence of population movement. PLoS ONE 2015, 10, e0144990. [Google Scholar] [CrossRef] [PubMed]
- Smith, T.; Maire, N.; Trape, J.-F.; Ross, A.; Rogier, C.; Molineaux, L. An epidemiologic model of the incidence of acute illness in Plasmodium falciparum malaria. Am. J. Trop. Med. Hyg. 2006, 75, 56–62. [Google Scholar] [CrossRef] [PubMed]
- Laneri, K.; Paul, R.; Tall, A.; Faye, J.; Diene-Sarr, F.; Sokhna, C.; Trape, J.-F.; Rodó, X. Dynamical malaria models reveal how immunity buffers effect of climate variability. Proc. Natl. Acad. Sci. USA 2015, 112, 8786–8791. [Google Scholar] [CrossRef]
- Slater, H.C.; Foy, B.D.; Kobylinski, K.; Chaccour, C.; Watson, O.J.; Hellewell, J.; Aljayyoussi, G.; Bousema, T.; Burrows, J.; D’Alessandro, U.; et al. Ivermectin as a novel complementary malaria control tool to reduce incidence and prevalence: A modelling study. Lancet Infect. Dis. 2020, 20, 498–508. [Google Scholar] [CrossRef]
- Prothero, R.M. Disease and mobility: A neglected factor in epidemiology. Int. J. Epidemiol. 1977, 6, 259–267. [Google Scholar] [CrossRef]
- Cissé, B.; Ba, E.H.; Sokhna, C.; Ndiaye, J.L.; Gomis, J.F.; Dial, Y.; Pitt, C.; Ndiaye, M.; Cairns, M.; Faye, E.; et al. Effectiveness of seasonal malaria chemoprevention in children under ten years of age in Senegal: A stepped-wedge cluster-randomised trial. PLoS Med. 2016, 13, e1002175. [Google Scholar] [CrossRef]
- R Development Core Team. R: A Language and Environment for Statistical Computing 2015. Available online: http://www.R-project.org (accessed on 30 October 2020).
- Soetaert, K.; Petzoldt, T.; Setzer, R.W. R Package deSolve: Solving Differential Equations. Available online: http://cran.r-project.org/web/packages/deSolve/vignettes/deSolve.pdf (accessed on 19 December 2020).
- Soetaert, K.; Petzoldt, T. Inverse modelling, sensitivity and Monte Carlo Analysis in R Using Package FME. J. Stat. Softw. 2010, 33, 28. [Google Scholar] [CrossRef]
- Karney, C.F.F. Algorithms for geodesics. J. Geod. 2013, 87, 43–55. [Google Scholar] [CrossRef]
- Simini, F.; González, M.C.; Maritan, A.; Barabási, A.L. A universal model for mobility and migration patterns. Nature 2012, 484, 96–100. [Google Scholar] [CrossRef]
- Greenberg, J.A.; DiMenna, M.A.; Hanelt, B.; Hofkin, B.V. Analysis of post-blood meal flight distances in mosquitoes utilizing zoo animal blood meals. J. Vector Ecol. 2012, 37, 83–89. [Google Scholar] [CrossRef] [PubMed]
- Doolan, D.L.; Dobaño, C.; Baird, J.K. Acquired immunity to malaria. Clin. Microbiol. Rev. 2009, 22, 13–36. [Google Scholar] [CrossRef] [PubMed]
- Ndiath, M.O.; Sarr, J.B.; Gaayeb, L.; Mazenot, C.; Sougoufara, S.; Konaté, L.; Remoue, F.; Hermann, E.; Trape, J.-F.; Riveau, G.; et al. Low and seasonal malaria transmission in the middle Senegal River basin: Identification and characteristics of Anopheles vectors. Parasites Vectors 2012, 5, 21. [Google Scholar] [CrossRef] [PubMed]
- Krefis, A.C.; Nkrumah, B.; Fobil, J.; Loag, W.; Ranft, U.; Acquah, S.; Adu-Sarkodie, Y.; Krüger, A.; Sarpong, N.; Schwarz, N.G.; et al. Modeling the relationship between precipitation and malaria incidence in children from a holoendemic area in Ghana. Am. J. Trop. Med. Hyg. 2011, 84, 285–291. [Google Scholar] [CrossRef]
- Parham, P.E.; Michael, E. Modeling the effects of weather and climate change on malaria transmission. Env. Health Perspect. 2010, 118, 620–626. [Google Scholar] [CrossRef]
- Doucet, A.; de Freitas, N.; Gordon, N. Sequential Monte Carlo Methods in Practice; Springer: New York, NY, USA, 2001. [Google Scholar]
- Males, S.; Gaye, O.; Garcia, A. Long-term asymptomatic carriage of Plasmodium falciparum protects from malaria attacks: A prospective study among Senegalese children. Clin. Infect. Dis. 2008, 46, 516–522. [Google Scholar] [CrossRef]
- Jiang, B. Street hierarchies: A minority of streets account for a majority of traffic flow. Int. J. Geogr. Inf. Sci. 2009, 23, 1033–1048. [Google Scholar] [CrossRef]
- Bousema, T.; Drakeley, C.; Gesase, S.; Hashim, R.; Magesa, S.; Mosha, F.; Otieno, S.; Carneiro, I.; Cox, J.; Msuya, E.; et al. Identification of hot spots of malaria transmission for targeted malaria control. J. Infect. Dis. 2010, 201, 1764–1774. [Google Scholar] [CrossRef]
- Agence Nationale de Statistique et de la Démographie (ANSD). Situation Économique et Sociale du Sénégal en 2011 n.d. Available online: http://www.ansd.sn/ressources/ses/chapitres/1-Demographie_2011.pdf (accessed on 30 October 2020).
- Imwong, M.; Thuy-Nhien, N.T.; Tripura, R.; Peto, T.J.; Lee, S.J.; Lwin, K.M.; Suangkanarat, P.; Jeeyapant, A.; Vihokhern, B.; Wongsaen, K.; et al. The epidemiology of subclinical malaria infections in South-East Asia: Findings from cross-sectional surveys in Thailand-Myanmar border areas, Cambodia, and Vietnam. Malar. J. 2015, 14, 381. [Google Scholar] [CrossRef]
- Gerardin, J.; Bever, C.A.; Hamainza, B.; Miller, J.M.; Eckhoff, P.A.; Wenger, E.A. Optimal population-level infection detection strategies for malaria control and elimination in a spatial model of malaria transmission. PLoS Comput. Biol. 2016, 12, e1004707. [Google Scholar] [CrossRef]
- Kangoye, D.T.; Noor, A.M.; Midega, J.T.; Ngoi, J.; Mkabili, D.; Mogeni, P.; Kerubo, C.; Akoo, P.; Mwangangi, J.; Drakeley, C.; et al. Malaria hotspots defined by clinical malaria, asymptomatic carriage, PCR and vector numbers in a low transmission area on the Kenyan Coast. Malar. J. 2016, 15, 213. [Google Scholar] [CrossRef] [PubMed]
- Sturrock, H.J.; Hsiang, M.S.; Cohen, J.M.; Smith, D.L.; Greenhouse, B.; Bousema, T.; Gosling, R.D. Targeting asymptomatic malaria infections: Active surveillance in control and elimination. PLoS Med. 2013, 10, e1001467. [Google Scholar] [CrossRef] [PubMed]
- Silal, S.P.; Little, F.; Barnes, K.I.; White, L.J. Towards malaria elimination in Mpumalanga, South Africa: A population-level mathematical modelling approach. Malar. J. 2014, 13, 297. [Google Scholar] [CrossRef] [PubMed]
- Bousema, T.; Stresman, G.; Baidjoe, A.Y.; Bradley, J.; Knight, P.; Stone, W.; Osoti, V.; Makori, E.; Owaga, C.; Odongo, W.; et al. The impact of hotspot-targeted interventions on malaria transmission in Rachuonyo South District in the Western Kenyan Highlands: A cluster-randomized controlled trial. PLoS Med. 2016, 13, e1001993. [Google Scholar] [CrossRef] [PubMed]
- Bengtsson, L.; Gaudart, J.; Lu, X.; Moore, S.; Wetter, E.; Sallah, K.; Rebaudet, S.; Piarroux, R. Using mobile phone data to predict the spatial spread of cholera. Sci. Rep. 2015, 5, 8923. [Google Scholar] [CrossRef]
- Kaneko, A.; Taleo, G.; Kalkoa, M.; Yamar, S.; Kobayakawa, T.; Björkman, A. Malaria eradication on islands. Lancet 2000, 356, 1560–1564. [Google Scholar] [CrossRef]
- Song, J.-P.; Socheat, D.; Tan, B.; Dara, P.; Deng, C.; Sreng, S.; Seila, S.; Ou, F.; Jian, H.; Qiao, L.G. Rapid and effective malaria control in Cambodia through mass administration of artemisinin-piperaquine. Malar. J. 2010, 9, 57. [Google Scholar] [CrossRef]
- Kondrashin, A.V.; Baranova, A.M.; Ashley, E.A.; Recht, J.; White, N.J.; Sergiev, V.P. Mass primaquine treatment to eliminate vivax malaria: Lessons from the past. Malar. J. 2014, 13, 51. [Google Scholar] [CrossRef]
- Sagna, A.B.; Gaayeb, L.; Sarr, J.B.; Senghor, S.; Poinsignon, A.; Boutouaba-Combe, S.; Schacht, A.-M.; Hermann, E.; Faye, N.; Remoue, F.; et al. Plasmodium falciparum infection during dry season: IgG responses to Anopheles gambiae salivary gSG6-P1 peptide as sensitive biomarker for malaria risk in Northern Senegal. Malar. J. 2013, 12, 301. [Google Scholar] [CrossRef]
- Diallo, A.; Ndam, N.T.; Moussiliou, A.; Dos Santos, S.; Ndonky, A.; Borderon, M.; Oliveau, S.; Lalou, R.; le Hesran, J.-Y. Asymptomatic carriage of plasmodium in urban Dakar: The risk of malaria should not be underestimated. PLoS ONE 2012, 7, e31100. [Google Scholar] [CrossRef]
- Le Port, A.; Cot, M.; Etard, J.F.; Gaye, O.; Migot-Nabias, F.; Garcia, A. Relation between Plasmodium falciparum asymptomatic infection and malaria attacks in a cohort of Senegalese children. Malar. J. 2008, 7, 193. [Google Scholar] [CrossRef] [PubMed]
- Townes, L.R.; Mwandama, D.; Mathanga, D.P.; Wilson, M.L. Elevated dry-season malaria prevalence associated with fine-scale spatial patterns of environmental risk: A case-control study of children in rural Malawi. Malar. J. 2013, 12, 407. [Google Scholar] [CrossRef] [PubMed]
- Thiam, S.; Thwing, J.; Diallo, I.; Fall, F.B.; Diouf, M.B.; Perry, R.; Ndiop, M.; Diouf, M.L.; Cisse, M.; Diaw, M.M.; et al. Scale-up of home-based management of malaria based on rapid diagnostic tests and artemisinin-based combination therapy in a resource-poor country: Results in Senegal. Malar. J. 2012, 11, 334. [Google Scholar] [CrossRef] [PubMed]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sallah, K.; Giorgi, R.; Ba, E.-H.; Piarroux, M.; Piarroux, R.; Cisse, B.; Gaudart, J. Targeting Malaria Hotspots to Reduce Transmission Incidence in Senegal. Int. J. Environ. Res. Public Health 2021, 18, 76. https://doi.org/10.3390/ijerph18010076
Sallah K, Giorgi R, Ba E-H, Piarroux M, Piarroux R, Cisse B, Gaudart J. Targeting Malaria Hotspots to Reduce Transmission Incidence in Senegal. International Journal of Environmental Research and Public Health. 2021; 18(1):76. https://doi.org/10.3390/ijerph18010076
Chicago/Turabian StyleSallah, Kankoé, Roch Giorgi, El-Hadj Ba, Martine Piarroux, Renaud Piarroux, Badara Cisse, and Jean Gaudart. 2021. "Targeting Malaria Hotspots to Reduce Transmission Incidence in Senegal" International Journal of Environmental Research and Public Health 18, no. 1: 76. https://doi.org/10.3390/ijerph18010076
APA StyleSallah, K., Giorgi, R., Ba, E.-H., Piarroux, M., Piarroux, R., Cisse, B., & Gaudart, J. (2021). Targeting Malaria Hotspots to Reduce Transmission Incidence in Senegal. International Journal of Environmental Research and Public Health, 18(1), 76. https://doi.org/10.3390/ijerph18010076






