Integration of Fuzzy Matter-Element Method and 3D-QSAR Model for Generation of Environmentally Friendly Quinolone Derivatives
Abstract
1. Introduction
2. Materials and Methods
2.1. Data Sources
2.2. Calculation of the CI Based on Fuzzy Matter-Element Method
2.2.1. Construction of Composite Fuzzy Matter-Element Matrix about QAs’ CI
2.2.2. Determination of Subordination Membership Degree of QAs’ CI
2.2.3. Determination of Standard Fuzzy Matter-Element and Variance Compound Fuzzy Matter-Element Matrix for the CI of QAs’ IRI and UVI
2.2.4. Determination of Weighting for Evaluation Index of the CI of QAs’ IRI and UVI
2.2.5. Euclidean Closeness Calculation for the CI of QAs’ IRI and UVI
2.3. Construction of 3D-QSAR Model to Generate Environmentally Friendly QAs
3. Results and Discussion
3.1. Calculation of QAs’ IRI and UVI based on DFT
3.2. Determination of CI of QAs’ IRI and UVI Based on Fuzzy Matter-Element Method
3.2.1. Subordination Membership Degree, Standard Fuzzy Matter-Element and Variance Compound Fuzzy Matter-Element Matrix
3.2.2. Comprehensive Weightings for CI of QAs’ IRI and UVI
3.2.3. CI of QAs’ IRI and UVI
3.3. Construction and Evaluation of 3D-QSAR Model Based on CI of QAs’ IRI and UVI
3.3.1. Construction of the 3D-QSAR Model
3.3.2. Performance Evaluation of the 3D-QSAR Model
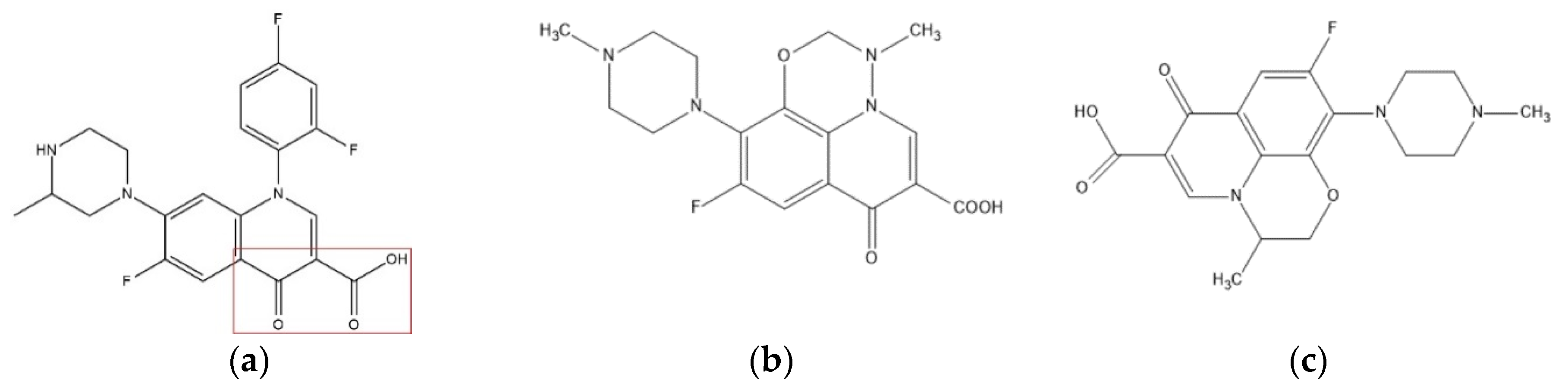
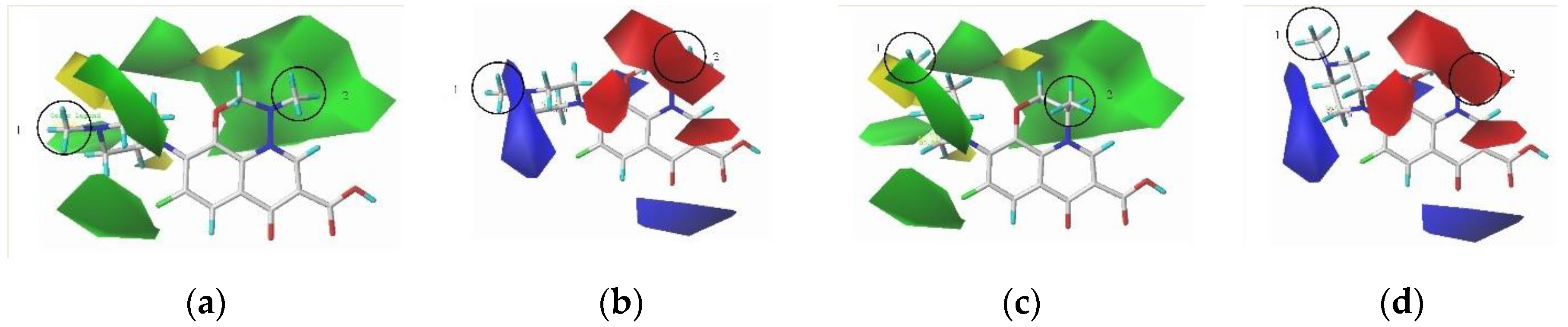
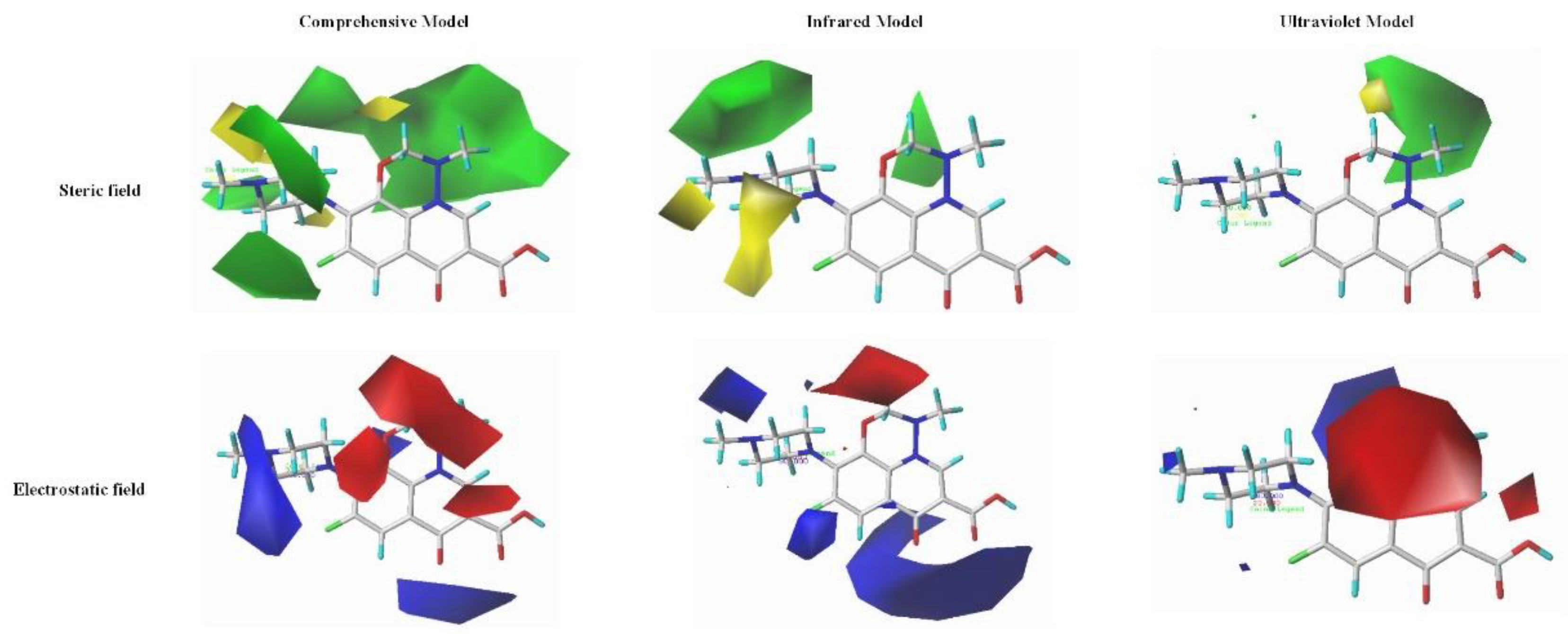
3.4. Determination of Substitution Characteristics Based on the Contour Maps
3.5. Evaluation of Molecular Spectral Characteristics, Functional Characteristics, Environmental Friendliness, and Stability of the QA Derivatives
3.5.1. Molecular Spectral Characteristics
3.5.2. The Enhancement of CI, IRI, and UVI of QA Derivatives’
The Quantitative Mechanism Analysis of the Spectral Enhancement of QA Derivatives Based on the Contour Map
The Quantitative Mechanism Analysis of the Spectral Enhancement of QA Derivatives Based on the Modified Positions and the Properties of Substituted Groups
3.5.3. Molecular Stability Evaluation of QA Derivatives
3.5.4. Functional and Environmental Friendliness Evaluation of QA derivatives
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Ma, X. Analysis on Typical Drug Record of Irrational Use of Anti-infective Drugs. China Pharm. 2005, 16, 453–454. (In Chinese) [Google Scholar]
- Chen, X. The track of clinical medication changes in the past 40 years. New Ed. Pharmacol. 1994, 29, 631–634. (In Chinese) [Google Scholar]
- Van Doorslaer, X.; Dewulf, J.; Van Langenhove, H.; Demeestere, K. Fluoroquinolone antibiotics: An emerging class of environmental micropollutants. Sci. Total. Environ. 2014, 500, 250–269. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Q.Q. Emission Estimation, Multimedia Fate Modeling and Risk Assessment of Typical Emerging Pollutants at River Basin Scale in China. Ph.D. Thesis, Guangzhou Institute of Geochemistry, Chinese Academy of Sciences, Guangzhou, China, 2015. (In Chinese). [Google Scholar]
- Chen, W.P.; Peng, C.W.; Yang, Y.; Wu, Y.M. Distribution Characteristics and Risk Analysis of Antibiotic in the Groundwater in Beijing. Environ. Sci. 2017, 38, 5074–5080. (In Chinese) [Google Scholar]
- Serna, R.L.; Jurado, A.; Vázquez-Suñé, E.; Carrera, J.; Petrovic, M.; Barceló, J. Occurrence of 95 pharmaceuticals and transformation products in urban groundwaters underlying the metropolis of Barcelona, Spain. Environ. Pollut. 2013, 174, 305–315. [Google Scholar] [CrossRef]
- Fick, J.; Söderström, H.; Lindberg, R.H.; Phan, C.; Tysklind, M.; Larsson, D.G.J. Contamination of surface, ground, and drinking water from pharmaceutical production. Environ. Toxicol. Chem. 2009, 28, 2522. [Google Scholar] [CrossRef]
- Bai, Y.; Meng, W.; Xu, J.; Zhang, Y.; Guo, C. Occurrence, distribution and bioaccumulation of antibiotics in the Liao River Basin in China. Environ. Sci. Process. Impacts 2014, 16, 586. [Google Scholar] [CrossRef]
- Li, W.; Shi, Y.; Gao, L.; Liu, J.; Cai, Y. Occurrence of antibiotics in water, sediments, aquatic plants, and animals from Baiyangdian Lake in North China. Chemosphere 2012, 89, 1307–1315. [Google Scholar] [CrossRef]
- Li, W.; Shi, Y.; Gao, L.; Liu, J.; Cai, Y. Investigation of antibiotics in mollusks from coastal waters in the Bohai Sea of China. Environ. Pollut. 2012, 162, 56–62. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, H. 3D-QSAR studies on 1,2,4-triazolyl 5-azaspiro [2.4]-heptanes as D 3 R antagonists. Chem. Phys. Lett. 2018, 704, 11–20. [Google Scholar] [CrossRef]
- Verma, J.; Khedkar, V.; Coutinho, E. 3D-QSAR in Drug Design - A Review. Curr. Top. Med. Chem. 2010, 10, 95–115. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Chu, Z.; Yang, J.; Li, Y. Pentachlorophenol molecule design with lower bioconcentration through 3D-QSAR associated with molecule docking. Environ. Sci. Pollut. Res. 2017, 24, 25114–25125. [Google Scholar] [CrossRef] [PubMed]
- Tong, J.; Wu, Y.; Bai, M.; Zhan, P. 3D-QSAR and molecular docking studies on HIV protease inhibitors. J. Mol. Struct. 2017, 1129, 17–22. [Google Scholar] [CrossRef]
- Gu, W.; Chen, Y.; Zhang, L.; Li, Y. Prediction of octanol-water partition coefficient for polychlorinated naphthalenes through three-dimensional QSAR models. Hum. Ecol. Risk Assess. Int. J. 2016, 23, 1–16. [Google Scholar] [CrossRef]
- Zhao, X.; Zhao, Y.; Ren, Z.; Li, Y. Combined QSAR/QSPR and molecular docking study on fluoroquinolones to reduce biological enrichment. Comput. Boil. Chem. 2019, 79, 177–184. [Google Scholar] [CrossRef]
- Zhao, X.; Wang, X.; Li, Y. Combined HQSAR method and molecular docking study on genotoxicity mechanism of quinolones with higher genotoxicity. Environ. Sci. Pollut. Res. 2019, 26, 34830–34853. [Google Scholar] [CrossRef]
- Petersen, J.C. Thermodynamic study by infrared spectroscopy of the association of 2-quinolone, some carboxylic acids, and the corresponding 2-quinolone-acid mixed dimers. J. Phys. Chem. 1971, 75, 1129–1135. [Google Scholar] [CrossRef]
- Efthimiadou, E.K.; Sanakis, Y.; Katsaros, N.; Karaliota, A.; Psomas, G. Transition metal complexes with the quinolone antibacterial agent pipemidic acid: Synthesis, characterization and biological activity. Polyhedron 2007, 26, 1148–1158. [Google Scholar] [CrossRef]
- Skyrianou, K.C.; Perdih, F.; Turel, I.; Kessissoglou, D.P.; Psomas, G. Nickel–quinolones interaction. Part 2—Interaction of nickel(II) with the antibacterial drug oxolinic acid. J. Inorg. Biochem. 2010, 104, 161–170. [Google Scholar] [CrossRef]
- Zampakou, M.; Akrivou, M.; Andreadou, E.G.; Raptopoulou, C.P.; Psycharis, V.; Pantazaki, A.A.; Psomas, G. Structure, antimicrobial activity, DNA- and albumin-binding of manganese(II) complexes with the quinolone antimicrobial agents oxolinic acid and enrofloxacin. J. Inorg. Biochem. 2013, 121, 88–99. [Google Scholar] [CrossRef]
- Bailac, S.; Ballesteros, O.; Jiménez-Lozano, E.; Barron, D.; Nebota, V.S.; Navalón, A.; Vílchez, J.; Barbosa, J. Determination of quinolones in chicken tissues by liquid chromatography with ultraviolet absorbance detection. J. Chromatogr. A 2004, 1029, 145–151. [Google Scholar] [CrossRef] [PubMed]
- Hayashi, M.; Lin, S.H.; Raschke, M.B.; Shen, Y.R. A Molecular Theory for Doubly Resonant IR−UV-vis Sum-Frequency Generation†. J. Phys. Chem. A 2002, 106, 2271–2282. [Google Scholar] [CrossRef]
- Zeng, X.; Qu, R.; Feng, M.; Chen, J.; Wang, L.; Wang, Z. Photodegradation of Polyfluorinated Dibenzo-p-Dioxins in Organic Solvents: Experimental and Theoretical Studies. Environ. Sci. Technol. 2016, 50, 8128–8134. [Google Scholar] [CrossRef] [PubMed]
- Qiu, Y.; Li, Y. A theoretical method for the high-sensitivity fluorescence detection of PAEs through double-substitution modification. Environ. Sci. Pollut. Res. 2018, 25, 34684–34692. [Google Scholar] [CrossRef] [PubMed]
- Luze, Y.; Miao, L. 3D-QSAR Model of Polybrominated Biphenyls Tri-effect Modified by Standard Deviation Standardization Method and Its Application in Environmental Friendly Molecular Modification. Chem. J. Chin. Univ. 2019, 40, 2471–2479. (In Chinese) [Google Scholar]
- Wang, C.; Wu, A.; Lu, H.; Bao, T.; Liu, X. Predicting rockburst tendency based on fuzzy matter-element model. Int. J. Rock Mech. Min. Sci. 2015, 75, 224–232. [Google Scholar] [CrossRef]
- Yang, Q.L.; Guo, Y.B. An entropy fuzzy matter element model for assessment of water resource carrying capacity. Geogr. Geo-Inform. Sci. 2010, 26, 89–92. [Google Scholar]
- Liu, N.; Zou, Z. Water quality evaluation based on improved fuzzy matter-element method. J. Environ. Sci. 2012, 24, 1210–1216. [Google Scholar] [CrossRef]
- Rai, A.K.; Devlani, N.; Kher, V.H. Spectra and decay rates of bb? meson using Gaussian wave function. In Proceedings of the EPJ Web of Conferences, Dresden, Germany, 25–29 August 2014. [Google Scholar]
- Qu, R.; Liu, H.; Feng, M.; Yang, X.; Wang, Z. Investigation on Intramolecular Hydrogen Bond and Some Thermodynamic Properties of Polyhydroxylated Anthraquinones. J. Chem. Eng. Data 2012, 57, 2442–2455. [Google Scholar] [CrossRef]
- Meyer, M.; Steinke, T.; Brandl, M.; Sühnel, J. Density functional study of guanine and uracil quartets and of guanine quartet/metal ion complexes. J. Comput. Chem. 2000, 22, 109–124. [Google Scholar] [CrossRef]
- Li, M.; Liu, H.; Zhang, E. Comprehensive Benefit Evaluation of Land Renovation Based on Multiple Indicators. J. Anhui Agric. Sci. 2018, 46, 214–217. (In Chinese) [Google Scholar]
- Pan, X.; Liu, H.; Huan, J.; Sui, Y.; Hong, H. Allocation Model of Carbon Emission Permits for the Electric Power Industry with a Combination Subjective and Objective Weighting Approach. Energies 2020, 13, 706. [Google Scholar] [CrossRef]
- Chen, Y.; Cai, X.; Jiang, L.; Li, Y. Prediction of octanol-air partition coefficients for polychlorinated biphenyls (PCBs) using 3D-QSAR models. Ecotoxicol. Environ. Saf. 2016, 124, 202–212. [Google Scholar] [CrossRef] [PubMed]
- Li, M.; Wei, D.; Zhao, H.; Du, Y. Genotoxicity of quinolones: Substituents contribution and transformation products QSAR evaluation using 2D and 3D models. Chemosphere 2014, 95, 220–226. [Google Scholar] [CrossRef]
- Chu, Z.; Li, Y. Designing modified polybrominated diphenyl ether BDE-47, BDE-99, BDE-100, BDE-183, and BDE-209 molecules with decreased estrogenic activities using 3D-QSAR, pharmacophore models coupled with resolution V of the 210-3 fractional factorial design and molecular docking. J. Hazard. Mater. 2019, 364, 151–162. [Google Scholar] [CrossRef]
- Zhao, Y.; Li, Y. Design of environmentally friendly neonicotinoid insecticides with bioconcentration tuning and Bi-directional selective toxic effects. J. Clean. Prod. 2019, 221, 113–121. [Google Scholar] [CrossRef]
- Qian, S.; Qiao, L.; Xu, W.; Jiang, K.; Wang, Y.; Lin, H. An inner filter effect-based near-infrared probe for the ultrasensitive detection of tetracyclines and quinolones. Talanta 2018, 194, 598–603. [Google Scholar] [CrossRef]
- Turiel, E.; Bordin, G.; Rodríguez, A.R. Trace enrichment of (fluoro)quinolone antibiotics in surface waters by solid-phase extraction and their determination by liquid chromatography–ultraviolet detection. J. Chromatogr. A 2003, 1008, 145–155. [Google Scholar] [CrossRef]
- Zhao, Y.; Gu, W.; Li, Y. Molecular design of 1,3,5,7-TetraCN derivatives with reduced bioconcentration using 3D-QSAR modeling, full factorial design, and molecular docking. J. Mol. Graph. Model. 2018, 84, 197–214. [Google Scholar] [CrossRef]
- Zhao, Y.; Li, Y. Modified neonicotinoid insecticide with bi-directional selective toxicity and drug resistance. Ecotoxicol. Environ. Saf. 2018, 164, 467–473. [Google Scholar] [CrossRef]
- Gu, W.; Zhao, Y.; Li, Q.; Li, Y. Environmentally friendly polychlorinated naphthalenes (PCNs) derivatives designed using 3D-QSAR and screened using molecular docking, density functional theory and health-based risk assessment. J. Hazard. Mater. 2019, 363, 316–327. [Google Scholar] [CrossRef] [PubMed]
- Gu, W.; Li, Q.; Li, Y. Environment-friendly PCN derivatives design and environmental behavior simulation based on a multi-activity 3D-QSAR model and molecular dynamics. J. Hazard. Mater. 2020, 393, 122339. [Google Scholar] [CrossRef] [PubMed]
- Hou, Y.; Zhao, Y.; Li, Q.; Li, Y. Highly biodegradable fluoroquinolone derivatives designed using the 3D-QSAR model and biodegradation pathways analysis. Ecotoxicol. Environ. Saf. 2020, 191, 110186. [Google Scholar] [CrossRef] [PubMed]
- Clark, M.; Cramer, R.D.; Van Opdenbosch, N. Validation of the general purpose tripos 5.2 force field. J. Comput. Chem. 1989, 10, 982–1012. [Google Scholar] [CrossRef]
- Gasteiger, J.; Marsili, M. Iterative partial equalization of orbital electronegativity—A rapid access to atomic charges. Tetrahedron 1980, 36, 3219–3228. [Google Scholar] [CrossRef]
- Leach, A.R. Molecular Modelling: Principles and Applications, 2nd ed.; Pearson Education Ltd.: Essex, UK, 2001; Volume 410, pp. 457–460. [Google Scholar]
- Golbraikh, A.; Tropsha, A. Beware of q2! J. Mol. Graph. Model. 2002, 20, 269–276. [Google Scholar] [CrossRef]
- Li, X.; Ye, L.; Shi, W.; Liu, H.; Liu, C.; Qian, X.; Zhu, Y.; Yu, H. In silico study on hydroxylated polychlorinated biphenyls as androgen receptor antagonists. Ecotoxicol. Environ. Saf. 2013, 92, 258–264. [Google Scholar] [CrossRef]
- Roy, K. On some aspects of validation of predictive quantitative structure–activity relationship models. Expert Opin. Drug Discov. 2007, 2, 1567–1577. [Google Scholar] [CrossRef]
- Tropsha, A. Best Practices for QSAR Model Development, Validation, and Exploitation. Mol. Informatics 2010, 29, 476–488. [Google Scholar] [CrossRef]
- Jiang, L.; Li, Y. Modification of PBDEs (BDE-15, BDE-47, BDE-85 and BDE-126) biological toxicity, bio-concentration, persistence and atmospheric long-range transport potential based on the pharmacophore modeling assistant with the full factor experimental design. J. Hazard. Mater. 2016, 307, 202–212. [Google Scholar] [CrossRef]
- Aldred, K.J.; Kerns, R.J.; Osheroff, N. Mechanism of Quinolone Action and Resistance. Biochemistry 2014, 53, 1565–1574. [Google Scholar] [CrossRef] [PubMed]
- Jackson, S.H.; Cowan-Ellsberry, C.E.; Thomas, G. Use of Quantitative Structural Analysis to Predict Fish Bioconcentration Factors for Pesticides. J. Agric. Food Chem. 2009, 57, 958–967. [Google Scholar] [CrossRef] [PubMed]
| No. | Name | IRI | UVI |
|---|---|---|---|
| Compound 1 | Difloxacin | 1924.76 | 2829.18 |
| Compound 2 | Enrofloxacin | 1289.58 | 4394.34 |
| Compound 3 | Norfloxacin | 1180.48 | 4627.19 |
| Compound 4 | Lomefloxacin | 1788.98 | 1950.61 |
| Compound 5 | Ofloxacin | 1428.91 | 3692.38 |
| Compound 6 | Pefloxacin | 1587.11 | 3542.25 |
| Compound 7 | Fleroxacin | 1882.42 | 1842.68 |
| Compound 8 | Ciprofloxacin | 1247.65 | 4045.59 |
| Compound 9 | Balofloxacin | 1368.19 | 3220.34 |
| Compound 10 | Marbofloxacin | 1265.41 | 264.82 |
| Compound 11 | Pipemidic acid | 2430.36 | 2563.72 |
| Compound 12 | Cinoxacin | 1631.51 | 9680.14 |
| Compound 13 | Enoxacin | 3427.59 | 8254.09 |
| Compound 14 | Gatifloxacin | 1363.79 | 2835.67 |
| Compound 15 | Levofloxacin | 1943.37 | 575.6 |
| Compound 16 | Rufloxacin | 1015.14 | 437.85 |
| Compound 17 | Pazufloxacin | 800.37 | 4259.61 |
| Compound 18 | Nadifloxacin | 1623.96 | 2878.37 |
| Compound 19 | Sparfloxacin | 1185.52 | 2542.11 |
| Compound 20 | Sarafloxacin | 1539.67 | 2605.82 |
| Compound 21 | Besifloxacin | 1682.72 | 3943.26 |
| Compound 22 | Clinafloxacin | 1571.06 | 4875.36 |
| Compound 23 | Grepafloxacin | 1489.4 | 2390.87 |
| Compound 24 | Temafloxacin | 2155.95 | 8643.35 |
| Mi | R’mn | RΔ | Normalization | |||
|---|---|---|---|---|---|---|
| C1 | C2 | C1 | C2 | C1 | C2 | |
| M1 | 0.5615 | 0.2923 | 0.1922 | 0.5009 | 0.4280 | 0.2724 |
| M2 | 0.3762 | 0.4540 | 0.3891 | 0.2982 | 0.1862 | 0.4386 |
| M3 | 0.3444 | 0.4780 | 0.4298 | 0.2725 | 0.1447 | 0.4633 |
| M4 | 0.5219 | 0.2015 | 0.2285 | 0.6376 | 0.3763 | 0.1790 |
| M5 | 0.4169 | 0.3814 | 0.3400 | 0.3826 | 0.2392 | 0.3640 |
| M6 | 0.4630 | 0.3659 | 0.2883 | 0.4020 | 0.2995 | 0.3481 |
| M7 | 0.5492 | 0.1904 | 0.2032 | 0.6555 | 0.4119 | 0.1676 |
| M8 | 0.3640 | 0.4179 | 0.4045 | 0.3388 | 0.1702 | 0.4016 |
| M9 | 0.3992 | 0.3327 | 0.3610 | 0.4453 | 0.2161 | 0.3139 |
| M10 | 0.3692 | 0.0274 | 0.3979 | 0.9460 | 0.1770 | 0.0000 |
| M11 | 0.7091 | 0.2648 | 0.0846 | 0.5405 | 0.6204 | 0.2442 |
| M12 | 0.4760 | 1.0000 | 0.2746 | 0.0000 | 0.3164 | 1.0000 |
| M13 | 1.0000 | 0.8527 | 0.0000 | 0.0217 | 1.0000 | 0.8485 |
| M14 | 0.3979 | 0.2929 | 0.3625 | 0.4999 | 0.2145 | 0.2730 |
| M15 | 0.5670 | 0.0595 | 0.1875 | 0.8846 | 0.4351 | 0.0330 |
| M16 | 0.2962 | 0.0452 | 0.4954 | 0.9116 | 0.0817 | 0.0184 |
| M17 | 0.2335 | 0.4400 | 0.5875 | 0.3136 | 0.0000 | 0.4243 |
| M18 | 0.4738 | 0.2973 | 0.2769 | 0.4937 | 0.3135 | 0.2776 |
| M19 | 0.3459 | 0.2626 | 0.4279 | 0.5437 | 0.1466 | 0.2419 |
| M20 | 0.4492 | 0.2692 | 0.3034 | 0.5341 | 0.2814 | 0.2486 |
| M21 | 0.4909 | 0.4074 | 0.2591 | 0.3512 | 0.3358 | 0.3907 |
| M22 | 0.4584 | 0.5036 | 0.2934 | 0.2464 | 0.2933 | 0.4897 |
| M23 | 0.4345 | 0.2470 | 0.3198 | 0.5670 | 0.2623 | 0.2258 |
| M24 | 0.6290 | 0.8929 | 0.1376 | 0.0115 | 0.5160 | 0.8899 |
| Entropy | Entropy Weights | Comprehensive Weights | |||
|---|---|---|---|---|---|
| S1 | S2 | W1 | W2 | W’1 | W’2 |
| −0.9966 | −0.9950 | 0.5002 | 0.4998 | 0.5001 | 0.4999 |
| ei | Comprehensive Effects | ei | Comprehensive Effects | ei | Comprehensive Effects |
|---|---|---|---|---|---|
| e1 | 0.4113 | e9 | 0.3651 | e17 | 0.3288 |
| e2 | 0.4138 | e10 | 0.1803 | e18 | 0.3793 |
| e3 | 0.4074 | e11 | 0.4409 | e19 | 0.3030 |
| e4 | 0.3419 | e12 | 0.6295 | e20 | 0.3529 |
| e5 | 0.3989 | e13 | 0.8958 | e21 | 0.4476 |
| e6 | 0.4125 | e14 | 0.3433 | e22 | 0.4805 |
| e7 | 0.3447 | e15 | 0.2678 | e23 | 0.3341 |
| e8 | 0.3904 | e16 | 0.1613 | e24 | 0.7269 |
| No. | Calculated Value | Predicted Value | Relative Deviation |
|---|---|---|---|
| a Compound 3 | 0.4074 | 0.3990 | 2.06% |
| a Compound 4 | 0.3419 | 0.3540 | −3.54% |
| b Compound 7 | 0.3447 | 0.3970 | −15.17% |
| a Compound 8 | 0.3904 | 0.4170 | −6.81% |
| a Compound 9 | 0.3651 | 0.3620 | 0.85% |
| a Compound 10 | 0.1803 | 0.1630 | 9.60% |
| a Compound 11 | 0.4409 | 0.4430 | −0.48% |
| a Compound 12 | 0.6295 | 0.6520 | −3.57% |
| a Compound 15 | 0.2678 | 0.2680 | −0.07% |
| a Compound 16 | 0.1613 | 0.1950 | −20.89% |
| b Compound 18 | 0.3793 | 0.3800 | −0.18% |
| b Compound 20 | 0.3529 | 0.3770 | −6.83% |
| a Compound 21 | 0.4476 | 0.4300 | 3.93% |
| a Compound 22 | 0.4805 | 0.4390 | 8.64% |
| a Compound 23 | 0.3341 | 0.3290 | 1.53% |
| a,b Compound 24 | 0.7269 | 0.7240 | 0.40% |
| QA Derivatives | Position of Substitution | CI | Relative Deviation | IRI | Relative Deviation | UVI | Relative Deviation | |
|---|---|---|---|---|---|---|---|---|
| 1-Position | 2-Position | |||||||
| Marbofloxacin | CH3 | CH3 | 0.1803 | 1265.4100 | 264.8200 | |||
| Derivative 1 | SiH3 | - | 0.2820 | 56.41% | 2046.4446 | 61.72% | 920.4496 | 247.58% |
| Derivative 2 | C2H5 | - | 0.2690 | 49.20% | 2128.1390 | 68.18% | 749.8942 | 183.17% |
| Derivative 3 | PH2 | - | 0.2850 | 58.07% | 2051.1622 | 62.09% | 916.2205 | 245.98% |
| Derivative 4 | C3H7 | - | 0.2690 | 49.20% | 2113.4890 | 67.02% | 711.2135 | 168.56% |
| Derivative 5 | C4H9 | - | 0.2690 | 49.20% | 2133.0449 | 68.57% | 714.4963 | 169.80% |
| Derivative 6 | C5H11 | - | 0.2690 | 49.20% | 2133.0449 | 68.57% | 712.8530 | 169.18% |
| Derivative 7 | - | CH2F | 0.3510 | 94.68% | 2051.1622 | 62.09% | 1492.7944 | 463.70% |
| Derivative 8 | - | C2H3 | 0.3210 | 78.04% | 2023.0192 | 59.87% | 1205.0359 | 355.04% |
| Derivative 9 | - | C2H | 0.3100 | 71.94% | 1976.9696 | 56.23% | 805.3784 | 204.12% |
| Derivative 10 | - | CH2OH | 0.2930 | 62.51% | 2013.7242 | 59.14% | 972.7472 | 267.32% |
| Derivative 11 | - | NH2 | 0.3030 | 68.05% | 2051.1622 | 62.09% | 629.5062 | 137.71% |
| Derivative 12 | - | NO | 0.3530 | 95.78% | 2009.0928 | 58.77% | 1061.6956 | 300.91% |
| Derivative 13 | - | NO2 | 0.3590 | 99.11% | 1995.2623 | 57.68% | 1142.8783 | 331.57% |
| Derivative 14 | SiH3 | CH2F | 0.3550 | 96.89% | 2060.6299 | 62.84% | 1442.1154 | 444.56% |
| Derivative 15 | PH2 | CH2F | 0.3510 | 94.68% | 2046.4446 | 61.72% | 1492.7944 | 463.70% |
| Derivative 16 | C3H7 | CH2F | 0.8050 | 346.48% | 2511.8864 | 98.50% | 8729.7137 | 3196.47% |
| Derivative 17 | C4H9 | CH2F | 0.8060 | 347.03% | 2511.8864 | 98.50% | 8729.7137 | 3196.47% |
| Derivative 18 | C5H11 | CH2F | 0.8060 | 347.03% | 2511.8864 | 98.50% | 8729.7137 | 3196.47% |
| Derivative 19 | H | C2H3 | 0.8150 | 352.02% | 2624.2185 | 107.38% | 9571.9407 | 3514.51% |
| Derivative 20 | SiH3 | C2H3 | 0.8210 | 355.35% | 2630.2680 | 107.86% | 9354.0567 | 3432.23% |
| Derivative 21 | C2H5 | C2H3 | 0.8190 | 354.24% | 2630.2680 | 107.86% | 9332.5430 | 3424.11% |
| Derivative 22 | PH2 | C2H3 | 0.8180 | 353.69% | 2630.2680 | 107.86% | 9506.0479 | 3489.63% |
| Derivative 23 | C3H7 | C2H3 | 0.8210 | 355.35% | 2636.3314 | 108.34% | 8356.0302 | 3055.36% |
| Derivative 24 | C4H9 | C2H3 | 0.8210 | 355.35% | 2636.3314 | 108.34% | 8298.5077 | 3033.64% |
| Derivative 25 | C5H11 | C2H3 | 0.8210 | 355.35% | 2654.6056 | 109.78% | 7870.4579 | 2872.00% |
| Derivative 26 | H | C2H | 0.8160 | 352.58% | 2570.3958 | 103.13% | 9549.9259 | 3506.20% |
| Derivative 27 | SiH3 | C2H | 0.8210 | 355.35% | 2594.1794 | 105.01% | 9141.1324 | 3351.83% |
| Derivative 28 | C2H5 | C2H | 0.8210 | 355.35% | 2612.1614 | 106.43% | 8974.2879 | 3288.83% |
| Derivative 29 | PH2 | C2H | 0.8170 | 353.13% | 2588.2129 | 104.54% | 9484.1846 | 3481.37% |
| Derivative 30 | C3H7 | C2H | 0.7960 | 341.49% | 2588.2129 | 104.54% | 6180.1640 | 2233.72% |
| Derivative 31 | C4H9 | C2H | 0.7960 | 341.49% | 2588.2129 | 104.54% | 5807.6442 | 2093.05% |
| Derivative 32 | C5H11 | C2H | 0.7950 | 340.93% | 2588.2129 | 104.54% | 5754.3994 | 2072.95% |
| Derivative 33 | H | CH2OH | 0.8200 | 354.80% | 2523.4808 | 99.42% | 9660.5088 | 3547.95% |
| Derivative 34 | SiH3 | CH2OH | 0.8260 | 358.13% | 2535.1286 | 100.34% | 9397.2331 | 3448.54% |
| Derivative 35 | C2H5 | CH2OH | 0.8250 | 357.57% | 2535.1286 | 100.34% | 8749.8378 | 3204.07% |
| Derivative 36 | PH2 | CH2OH | 0.8220 | 355.91% | 2529.2980 | 99.88% | 9616.1228 | 3531.19% |
| Derivative 37 | C3H7 | CH2OH | 0.8230 | 356.46% | 2523.4808 | 99.42% | 8933.0548 | 3273.26% |
| Derivative 38 | C4H9 | CH2OH | 0.8230 | 356.46% | 2529.2980 | 99.88% | 8974.2879 | 3288.83% |
| Derivative 39 | C5H11 | CH2OH | 0.8230 | 356.46% | 2529.2980 | 99.88% | 8974.2879 | 3288.83% |
| Derivative 40 | H | NH2 | 0.7920 | 339.27% | 2546.8303 | 101.27% | 8609.9375 | 3151.24% |
| Derivative 41 | SiH3 | NH2 | 0.8000 | 343.70% | 2558.5859 | 102.19% | 8317.6377 | 3040.86% |
| Derivative 42 | C2H5 | NH2 | 0.8020 | 344.81% | 2582.2602 | 104.07% | 8336.8118 | 3048.11% |
| Derivative 43 | PH2 | NH2 | 0.8010 | 344.26% | 2582.2602 | 104.07% | 8336.8118 | 3048.11% |
| Derivative 44 | C3H7 | NH2 | 0.7720 | 328.18% | 2594.1794 | 105.01% | 6123.5039 | 2212.33% |
| Derivative 45 | C4H9 | NH2 | 0.3450 | 91.35% | 2162.7185 | 70.91% | 2805.4336 | 959.37% |
| Derivative 46 | C5H11 | NH2 | 0.3730 | 106.88% | 2187.7616 | 72.89% | 2792.5438 | 954.51% |
| Derivative 47 | H | NO | 0.3200 | 77.48% | 2137.9621 | 68.95% | 1606.9413 | 506.81% |
| Derivative 48 | SiH3 | NO | 0.2730 | 51.41% | 2192.8049 | 73.29% | 1166.8096 | 340.60% |
| Derivative 49 | C2H5 | NO | 0.2420 | 34.22% | 2157.7444 | 70.52% | 984.0111 | 271.58% |
| Derivative 50 | PH2 | NO | 0.4150 | 130.17% | 1972.4227 | 55.87% | 2074.9135 | 683.52% |
| Derivative 51 | C3H7 | NO | 0.2440 | 35.33% | 2128.1390 | 68.18% | 990.8319 | 274.15% |
| Derivative 52 | C4H9 | NO | 0.2460 | 36.44% | 2137.9621 | 68.95% | 933.2543 | 252.41% |
| Derivative 53 | C5H11 | NO | 0.2460 | 36.44% | 2128.1390 | 68.18% | 937.5620 | 254.04% |
| Derivative 54 | H | NO2 | 0.3170 | 75.82% | 2079.6967 | 64.35% | 1534.6170 | 479.49% |
| Derivative 55 | SiH3 | NO2 | 0.2530 | 40.32% | 2113.4890 | 67.02% | 1156.1122 | 336.57% |
| Derivative 56 | C2H5 | NO2 | 0.2340 | 29.78% | 2094.1125 | 65.49% | 1324.3415 | 400.09% |
| Derivative 57 | C3H7 | NO2 | 0.2350 | 30.34% | 2074.9135 | 63.97% | 918.3326 | 246.78% |
| Derivative 58 | C4H9 | NO2 | 0.2360 | 30.89% | 2089.2961 | 65.11% | 889.2011 | 235.78% |
| Derivative 59 | C5H11 | NO2 | 0.2360 | 30.89% | 2089.2961 | 65.11% | 870.9636 | 228.89% |
| Derivative 60 | H | CHO | 0.4500 | 149.58% | 1981.5270 | 56.59% | 3019.9517 | 1040.38% |
| Derivative 61 | SiH3 | CHO | 0.4110 | 127.95% | 1896.7059 | 49.89% | 2488.8573 | 839.83% |
| Derivative 62 | C2H5 | CHO | 0.3270 | 81.36% | 1909.8533 | 50.93% | 1753.8805 | 562.29% |
| Derivative 63 | C3H7 | CHO | 0.3130 | 73.60% | 1918.6687 | 51.62% | 1774.1895 | 569.96% |
| Derivative 64 | C4H9 | CHO | 0.3260 | 80.81% | 1927.5249 | 52.32% | 2032.3570 | 667.45% |
| Derivative 65 | C5H11 | CHO | 0.3270 | 81.36% | 1923.0917 | 51.97% | 2018.3664 | 662.17% |
| Derivative 66 | H | COOH | 0.4550 | 152.36% | 2065.3802 | 63.22% | 2951.2092 | 1014.42% |
| Derivative 67 | SiH3 | COOH | 0.3960 | 119.63% | 2074.9135 | 63.97% | 2301.4418 | 769.06% |
| Derivative 68 | C2H5 | COOH | 0.3170 | 75.82% | 1995.2623 | 57.68% | 1923.0917 | 626.19% |
| Derivative 69 | C3H7 | COOH | 0.3030 | 68.05% | 1986.0949 | 56.95% | 1905.4607 | 619.53% |
| Derivative 70 | C4H9 | COOH | 0.3130 | 73.60% | 1986.0949 | 56.95% | 2108.6281 | 696.25% |
| Levofloxacin | CH3 | CH3 | 0.2678 | 1943.3700 | 575.6000 | |||
| Derivative 71 | C4H9 | 0.7850 | 193.13% | 2409.9054 | 24.01% | 7430.1914 | 1190.86% | |
| Derivative 72 | C4H9 | C2H3 | 0.7500 | 180.06% | 2636.3314 | 35.66% | 5834.4510 | 913.63% |
| Derivative 73 | C3H7 | OH | 0.7430 | 177.45% | 2552.7013 | 31.35% | 2108.6281 | 266.34% |
| Derivative 74 | C3H7 | OH | 0.6690 | 149.81% | 2328.0913 | 19.80% | 1741.8069 | 202.61% |
| Derivative 75 | H | OH | 0.7210 | 169.23% | 2404.3628 | 23.72% | 3881.5037 | 574.34% |
| Derivative 76 | OCH3 | 0.7670 | 186.41% | 2488.8573 | 28.07% | 7328.2453 | 1173.15% | |
| Derivative 77 | C2H5 | OCH3 | 0.7420 | 177.07% | 2624.2185 | 35.03% | 5296.6344 | 820.19% |
| Derivative 78 | SiH3 | OCH3 | 0.7560 | 182.30% | 2529.2980 | 30.15% | 7533.5556 | 1208.82% |
| Derivative 79 | C5H11 | OCH3 | 0.7560 | 182.30% | 2477.4221 | 27.48% | 1496.2357 | 159.94% |
| Derivative 80 | C3H7 | CN | 0.7550 | 181.93% | 2618.1830 | 34.72% | 6095.3690 | 958.96% |
| Derivative 81 | SiH3 | NO | 0.7560 | 182.30% | 2275.0974 | 17.07% | 3169.5675 | 450.65% |
| Derivative 82 | NO2 | 0.7530 | 181.18% | 2642.4088 | 35.97% | 5035.0061 | 774.74% | |
| Derivative 83 | C2H5 | NO2 | 0.7590 | 183.42% | 2466.0393 | 26.89% | 5223.9619 | 807.57% |
| Derivative 84 | SiH3 | NO2 | 0.7680 | 186.78% | 2387.8113 | 22.87% | 7177.9429 | 1147.04% |
| Derivative 85 | C3H7 | NO2 | 0.7530 | 181.18% | 2506.1093 | 28.96% | 5105.0500 | 786.91% |
| Derivative 86 | C4H9 | NO2 | 0.7540 | 181.55% | 2588.2129 | 33.18% | 5495.4087 | 854.73% |
| Derivative 87 | CHO | 0.7850 | 193.13% | 2488.8573 | 28.07% | 1741.8069 | 202.61% | |
| Molecular Substitution Type | QA Derivatives | Modified Positions and Properties of Substituted Groups | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 1-Position Positive | Relative Deviation | 2-Position Negative | Relative Deviation | 2-Position Bigger Group | Relative Deviation | 2-Position Coupling | 1, 2-Position Coupling | ||
| Marbofloxacin/Levofloxacin | 2.331 | - | 2.331 | - | 15 | - | - | - | |
| Monosubstitution | Derivative 1 | 2.120 | 9.05% | - | - | - | - | - | - |
| Derivative 2 | 2.315 | 0.69% | - | - | - | - | - | - | |
| Derivative 3 | 2.154 | 7.59% | - | - | - | - | - | - | |
| Derivative 4 | 2.314 | 0.73% | - | - | - | - | - | - | |
| Derivative 5 | 2.313 | 0.77% | - | - | - | - | - | - | |
| Derivative 6 | 2.312 | 0.82% | - | - | - | - | - | - | |
| Derivative 71 | 2.313 | 0.77% | - | - | - | - | - | - | |
| Derivative 7 | - | - | 2.644 | 13.43% | 33 | 120.00% | 66.71% | - | |
| Derivative 8 | - | - | 2.358 | 1.16% | 27 | 80.00% | 40.58% | - | |
| Derivative 9 | - | - | 2.530 | 8.54% | 25 | 66.67% | 37.60% | - | |
| Derivative 10 | - | - | 2.491 | 6.86% | 31 | 106.67% | 56.77% | - | |
| Derivative 11 | - | - | 2.437 | 4.55% | 16 | 6.67% | 5.61% | - | |
| Derivative 12 | - | - | 2.920 | 25.27% | 30 | 100.00% | 62.63% | - | |
| Derivative 13 | - | - | 3.104 | 33.16% | 46 | 206.67% | 119.91% | - | |
| Derivative 76 | - | - | 2.460 | 5.53% | 31 | 106.67% | 56.10% | - | |
| Derivative 82 | - | - | 3.104 | 33.16% | 46 | 206.67% | 119.91% | - | |
| Derivative 87 | - | - | 2.647 | 13.56% | 29 | 93.33% | 53.44% | - | |
| Disubstituted | Derivative 14 | 2.120 | 9.05% | 2.644 | 13.43% | 33 | 120.00% | 85.90% | 94.95% |
| Derivative 15 | 2.154 | 7.59% | 2.644 | 13.43% | 33 | 120.00% | 85.90% | 93.49% | |
| Derivative 16 | 2.314 | 0.73% | 2.644 | 13.43% | 33 | 120.00% | 85.90% | 86.63% | |
| Derivative 17 | 2.313 | 0.77% | 2.644 | 13.43% | 33 | 120.00% | 85.90% | 86.67% | |
| Derivative 18 | 2.312 | 0.82% | 2.644 | 13.43% | 33 | 120.00% | 85.90% | 86.71% | |
| Derivative 19 | 2.200 | 5.62% | 2.358 | 1.16% | 27 | 80.00% | 54.77% | 60.39% | |
| Derivative 20 | 2.120 | 9.05% | 2.358 | 1.16% | 27 | 80.00% | 54.77% | 63.82% | |
| Derivative 21 | 2.315 | 0.69% | 2.358 | 1.16% | 27 | 80.00% | 54.77% | 55.46% | |
| Derivative 22 | 2.154 | 7.59% | 2.358 | 1.16% | 27 | 80.00% | 54.77% | 62.36% | |
| Derivative 23 | 2.314 | 0.73% | 2.358 | 1.16% | 27 | 80.00% | 54.77% | 55.50% | |
| Derivative 24 | 2.313 | 0.77% | 2.358 | 1.16% | 27 | 80.00% | 54.77% | 55.54% | |
| Derivative 25 | 2.312 | 0.82% | 2.358 | 1.16% | 27 | 80.00% | 54.77% | 55.59% | |
| Derivative 26 | 2.200 | 5.62% | 2.530 | 8.54% | 25 | 66.67% | 48.07% | 53.69% | |
| Derivative 27 | 2.120 | 9.05% | 2.530 | 8.54% | 25 | 66.67% | 48.07% | 57.12% | |
| Derivative 28 | 2.315 | 0.69% | 2.530 | 8.54% | 25 | 66.67% | 48.07% | 48.75% | |
| Derivative 29 | 2.154 | 7.59% | 2.530 | 8.54% | 25 | 66.67% | 48.07% | 55.66% | |
| Derivative 30 | 2.314 | 0.73% | 2.530 | 8.54% | 25 | 66.67% | 48.07% | 48.79% | |
| Derivative 31 | 2.313 | 0.77% | 2.530 | 8.54% | 25 | 66.67% | 48.07% | 48.84% | |
| Derivative 32 | 2.312 | 0.82% | 2.530 | 8.54% | 25 | 66.67% | 48.07% | 48.88% | |
| Derivative 33 | 2.200 | 5.62% | 2.491 | 6.86% | 31 | 106.67% | 74.73% | 80.35% | |
| Derivative 34 | 2.120 | 9.05% | 2.491 | 6.86% | 31 | 106.67% | 74.73% | 83.78% | |
| Derivative 35 | 2.315 | 0.69% | 2.491 | 6.86% | 31 | 106.67% | 74.73% | 75.42% | |
| Derivative 36 | 2.154 | 7.59% | 2.491 | 6.86% | 31 | 106.67% | 74.73% | 82.32% | |
| Derivative 37 | 2.314 | 0.73% | 2.491 | 6.86% | 31 | 106.67% | 74.73% | 75.46% | |
| Derivative 38 | 2.313 | 0.77% | 2.491 | 6.86% | 31 | 106.67% | 74.73% | 75.50% | |
| Derivative 39 | 2.312 | 0.82% | 2.491 | 6.86% | 31 | 106.67% | 74.73% | 75.54% | |
| Derivative 40 | 2.200 | 5.62% | 2.437 | 4.55% | 16 | 6.67% | 5.99% | 11.61% | |
| Derivative 41 | 2.120 | 9.05% | 2.437 | 4.55% | 16 | 6.67% | 5.99% | 15.04% | |
| Derivative 42 | 2.315 | 0.69% | 2.437 | 4.55% | 16 | 6.67% | 5.99% | 6.67% | |
| Derivative 43 | 2.154 | 7.59% | 2.437 | 4.55% | 16 | 6.67% | 5.99% | 13.58% | |
| Derivative 44 | 2.314 | 0.73% | 2.437 | 4.55% | 16 | 6.67% | 5.99% | 6.72% | |
| Derivative 45 | 2.313 | 0.77% | 2.437 | 4.55% | 16 | 6.67% | 5.99% | 6.76% | |
| Derivative 46 | 2.312 | 0.82% | 2.437 | 4.55% | 16 | 6.67% | 5.99% | 6.80% | |
| Derivative 47 | 2.200 | 5.62% | 2.920 | 25.27% | 30 | 100.00% | 76.09% | 81.71% | |
| Derivative 48 | 2.120 | 9.05% | 2.920 | 25.27% | 30 | 100.00% | 76.09% | 85.14% | |
| Derivative 49 | 2.315 | 0.69% | 2.920 | 25.27% | 30 | 100.00% | 76.09% | 76.77% | |
| Derivative 50 | 2.154 | 7.59% | 2.920 | 25.27% | 30 | 100.00% | 76.09% | 83.68% | |
| Derivative 51 | 2.314 | 0.73% | 2.920 | 25.27% | 30 | 100.00% | 76.09% | 76.82% | |
| Derivative 52 | 2.313 | 0.77% | 2.920 | 25.27% | 30 | 100.00% | 76.09% | 76.86% | |
| Derivative 53 | 2.312 | 0.82% | 2.920 | 25.27% | 30 | 100.00% | 76.09% | 76.90% | |
| Derivative 54 | 2.200 | 5.62% | 3.104 | 33.16% | 46 | 206.67% | 151.15% | 156.76% | |
| Derivative 55 | 2.120 | 9.05% | 3.104 | 33.16% | 46 | 206.67% | 151.15% | 160.20% | |
| Derivative 56 | 2.315 | 0.69% | 3.104 | 33.16% | 46 | 206.67% | 151.15% | 151.83% | |
| Derivative 57 | 2.314 | 0.73% | 3.104 | 33.16% | 46 | 206.67% | 151.15% | 151.87% | |
| Derivative 58 | 2.313 | 0.77% | 3.104 | 33.16% | 46 | 206.67% | 151.15% | 151.92% | |
| Derivative 59 | 2.312 | 0.82% | 3.104 | 33.16% | 46 | 206.67% | 151.15% | 151.96% | |
| Derivative 60 | 2.200 | 5.62% | 2.647 | 13.56% | 29 | 93.33% | 67.80% | 73.42% | |
| Derivative 61 | 2.120 | 9.05% | 2.647 | 13.56% | 29 | 93.33% | 67.80% | 76.86% | |
| Derivative 62 | 2.315 | 0.69% | 2.647 | 13.56% | 29 | 93.33% | 67.80% | 68.49% | |
| Derivative 63 | 2.314 | 0.73% | 2.647 | 13.56% | 29 | 93.33% | 67.80% | 68.53% | |
| Derivative 64 | 2.313 | 0.77% | 2.647 | 13.56% | 29 | 93.33% | 67.80% | 68.58% | |
| Derivative 65 | 2.312 | 0.82% | 2.647 | 13.56% | 29 | 93.33% | 67.80% | 68.62% | |
| Derivative 66 | 2.200 | 5.62% | 2.769 | 18.79% | 45 | 200.00% | 142.01% | 147.63% | |
| Derivative 67 | 2.120 | 9.05% | 2.769 | 18.79% | 45 | 200.00% | 142.01% | 151.06% | |
| Derivative 68 | 2.315 | 0.69% | 2.769 | 18.79% | 45 | 200.00% | 142.01% | 142.70% | |
| Derivative 69 | 2.314 | 0.73% | 2.769 | 18.79% | 45 | 200.00% | 142.01% | 142.74% | |
| Derivative 70 | 2.313 | 0.77% | 2.769 | 18.79% | 45 | 200.00% | 142.01% | 142.79% | |
| Derivative 72 | 2.313 | 0.77% | 2.358 | 1.16% | 27 | 80.00% | 54.77% | 55.54% | |
| Derivative 73 | 2.314 | 0.73% | 2.585 | 10.90% | 17 | 13.33% | 12.55% | 13.28% | |
| Derivative 74 | 2.314 | 0.73% | 2.585 | 10.90% | 17 | 13.33% | 12.55% | 13.28% | |
| Derivative 75 | 2.200 | 5.62% | 2.585 | 10.90% | 17 | 13.33% | 12.55% | 18.17% | |
| Derivative 77 | 2.315 | 0.69% | 2.460 | 5.53% | 31 | 106.67% | 74.30% | 74.99% | |
| Derivative 78 | 2.120 | 9.05% | 2.460 | 5.53% | 31 | 106.67% | 74.30% | 83.36% | |
| Derivative 79 | 2.312 | 0.82% | 2.460 | 5.53% | 31 | 106.67% | 74.30% | 75.12% | |
| Derivative 80 | 2.314 | 0.73% | 2.792 | 19.78% | 26 | 73.33% | 56.20% | 56.92% | |
| Derivative 81 | 2.120 | 9.05% | 2.920 | 25.27% | 30 | 100.00% | 76.09% | 85.14% | |
| Derivative 83 | 2.315 | 0.69% | 3.104 | 33.16% | 46 | 206.67% | 151.15% | 151.83% | |
| Derivative 84 | 2.120 | 9.05% | 3.104 | 33.16% | 46 | 206.67% | 151.15% | 160.20% | |
| Derivative 85 | 2.314 | 0.73% | 3.104 | 33.16% | 46 | 206.67% | 151.15% | 151.87% | |
| Derivative 86 | 2.313 | 0.77% | 3.104 | 33.16% | 46 | 206.67% | 151.15% | 151.92% | |
| QA Derivatives | Positive Frequency Value | QA Derivatives | Positive Frequency Value | QA Derivatives | Positive Frequency Value |
|---|---|---|---|---|---|
| Derivative 1 | 20.78 | Derivative 30 | 14.97 | Derivative 59 | 10.15 |
| Derivative 2 | 17.07 | Derivative 31 | 14.85 | Derivative 60 | 28.78 |
| Derivative 3 | 19.93 | Derivative 32 | 12.63 | Derivative 61 | 18.22 |
| Derivative 4 | 15.47 | Derivative 33 | 24.17 | Derivative 62 | 25.68 |
| Derivative 5 | 14.17 | Derivative 34 | 17.19 | Derivative 63 | 23.33 |
| Derivative 6 | 13.15 | Derivative 35 | 18.39 | Derivative 64 | 21.80 |
| Derivative 7 | 25.16 | Derivative 36 | 19.52 | Derivative 65 | 18.79 |
| Derivative 8 | 21.84 | Derivative 37 | 19.74 | Derivative 66 | 28.44 |
| Derivative 9 | 22.60 | Derivative 38 | 14.32 | Derivative 67 | 23.12 |
| Derivative 10 | 20.75 | Derivative 39 | 13.44 | Derivative 68 | 24.75 |
| Derivative 11 | 21.58 | Derivative 40 | 31.02 | Derivative 69 | 22.49 |
| Derivative 12 | 24.54 | Derivative 41 | 20.39 | Derivative 70 | 20.99 |
| Derivative 13 | 22.29 | Derivative 42 | 17.77 | Derivative 71 | 15.37 |
| Derivative 14 | 20.67 | Derivative 43 | 20.83 | Derivative 72 | 11.09 |
| Derivative 15 | 20.88 | Derivative 44 | 20.82 | Derivative 73 | 15.30 |
| Derivative 16 | 18.33 | Derivative 45 | 15.87 | Derivative 74 | 16.74 |
| Derivative 17 | 17.08 | Derivative 46 | 12.92 | Derivative 75 | 28.59 |
| Derivative 18 | 14.97 | Derivative 47 | 24.63 | Derivative 76 | 21.50 |
| Derivative 19 | 21.27 | Derivative 48 | 19.56 | Derivative 77 | 16.28 |
| Derivative 20 | 16.15 | Derivative 49 | 21.39 | Derivative 78 | 19.62 |
| Derivative 21 | 19.96 | Derivative 50 | 14.89 | Derivative 79 | 9.36 |
| Derivative 22 | 18.43 | Derivative 51 | 13.37 | Derivative 80 | 18.66 |
| Derivative 23 | 16.27 | Derivative 52 | 12.78 | Derivative 81 | 16.26 |
| Derivative 24 | 15.53 | Derivative 53 | 7.10 | Derivative 82 | 21.73 |
| Derivative 25 | 14.51 | Derivative 54 | 23.28 | Derivative 83 | 20.00 |
| Derivative 26 | 24.80 | Derivative 55 | 20.02 | Derivative 84 | 21.43 |
| Derivative 27 | 18.49 | Derivative 56 | 17.86 | Derivative 85 | 18.49 |
| Derivative 28 | 21.60 | Derivative 57 | 13.65 | Derivative 86 | 11.53 |
| Derivative 29 | 20.14 | Derivative 58 | 12.72 | Derivative 87 | 23.13 |
| QA Derivatives | Genotoxicity | Relative Deviation | Bioaccumulation | Relative Deviation | Biodegradability | Relative Deviation |
|---|---|---|---|---|---|---|
| Marbofloxacin | 8.4600 | 1.1840 | 1.7050 | |||
| Derivative 1 | 9.5390 | 12.75% | 0.9650 | −18.50% | 1.7070 | 0.12% |
| Derivative 2 | 9.8690 | 16.65% | 1.1630 | −1.77% | 1.7250 | 1.17% |
| Derivative 3 | 9.3760 | 10.83% | 0.8900 | −24.83% | 1.7130 | 0.47% |
| Derivative 4 | 9.6020 | 13.50% | 1.1730 | −0.93% | 1.7240 | 1.11% |
| Derivative 5 | 9.5320 | 12.67% | 1.1740 | −0.84% | 1.7250 | 1.17% |
| Derivative 6 | 9.6380 | 13.92% | 1.1750 | −0.76% | 1.7240 | 1.11% |
| Derivative 7 | 9.0310 | 6.75% | 1.3610 | 14.95% | 1.7190 | 0.82% |
| Derivative 8 | 8.9180 | 5.41% | 1.3730 | 15.96% | 1.7290 | 1.41% |
| Derivative 9 | 8.5310 | 0.84% | 1.2810 | 8.19% | 1.7170 | 0.70% |
| Derivative 10 | 9.2950 | 9.87% | 1.5920 | 34.46% | 1.7030 | −0.12% |
| Derivative 11 | 9.8810 | 16.80% | 1.1110 | −6.17% | 1.7130 | 0.47% |
| Derivative 12 | 8.4810 | 0.25% | 1.5260 | 28.89% | 1.6900 | −0.88% |
| Derivative 13 | 9.0470 | 6.94% | 1.2460 | 5.24% | 1.7350 | 1.76% |
| Derivative 14 | 9.6010 | 13.49% | 1.1590 | −2.11% | 1.7160 | 0.65% |
| Derivative 15 | 9.4670 | 11.90% | 1.0520 | −11.15% | 1.7190 | 0.82% |
| Derivative 16 | 9.8060 | 15.91% | 0.6090 | −48.56% | 1.4940 | −12.38% |
| Derivative 17 | 9.7360 | 15.08% | 0.6080 | −48.65% | 1.4940 | −12.38% |
| Derivative 18 | 9.8420 | 16.34% | 0.6060 | −48.82% | 1.4940 | −12.38% |
| Derivative 19 | 9.2230 | 9.02% | 0.5660 | −52.20% | 1.5050 | −11.73% |
| Derivative 20 | 9.4870 | 12.14% | 0.5650 | −52.28% | 1.4990 | −12.08% |
| Derivative 21 | 9.9670 | 17.81% | 0.5720 | −51.69% | 1.5000 | −12.02% |
| Derivative 22 | 9.4730 | 11.97% | 0.5430 | −54.14% | 1.5040 | −11.79% |
| Derivative 23 | 9.7000 | 14.66% | 0.5760 | −51.35% | 1.5070 | −11.61% |
| Derivative 24 | 9.6300 | 13.83% | 0.5760 | −51.35% | 1.5060 | −11.67% |
| Derivative 25 | 9.7350 | 15.07% | 0.5760 | −51.35% | 1.5100 | −11.44% |
| Derivative 26 | 8.8350 | 4.43% | 0.5470 | −53.80% | 1.5260 | −10.50% |
| Derivative 27 | 8.9990 | 6.37% | 0.5450 | −53.97% | 1.5230 | −10.67% |
| Derivative 28 | 9.5790 | 13.23% | 0.5550 | −53.13% | 1.5290 | −10.32% |
| Derivative 29 | 9.0860 | 7.40% | 0.5230 | −55.83% | 1.5220 | −10.73% |
| Derivative 30 | 9.3130 | 10.08% | 0.5910 | −50.08% | 1.5270 | −10.44% |
| Derivative 31 | 9.2430 | 9.26% | 0.5950 | −49.75% | 1.5290 | −10.32% |
| Derivative 32 | 9.3480 | 10.50% | 0.5970 | −49.58% | 1.5300 | −10.26% |
| Derivative 33 | 9.6000 | 13.48% | 0.5350 | −54.81% | 1.5060 | −11.67% |
| Derivative 34 | 9.7820 | 15.63% | 0.5330 | −54.98% | 1.5010 | −11.96% |
| Derivative 35 | 10.3440 | 22.27% | 0.5450 | −53.97% | 1.5030 | −11.85% |
| Derivative 36 | 9.8510 | 16.44% | 0.5120 | −56.76% | 1.5020 | −11.91% |
| Derivative 37 | 10.0780 | 19.13% | 0.5440 | −54.05% | 1.4980 | −12.14% |
| Derivative 38 | 10.0070 | 18.29% | 0.5440 | −54.05% | 1.4990 | −12.08% |
| Derivative 39 | 10.1130 | 19.54% | 0.5440 | −54.05% | 1.5010 | −11.96% |
| Derivative 40 | 10.1700 | 20.21% | 0.5020 | −57.60% | 1.5130 | −11.26% |
| Derivative 41 | 10.1300 | 19.74% | 0.4950 | −58.19% | 1.5120 | −11.32% |
| Derivative 42 | 10.9140 | 29.01% | 0.5150 | −56.50% | 1.5090 | −11.50% |
| Derivative 43 | 10.4210 | 23.18% | 0.4680 | −60.47% | 1.5150 | −11.14% |
| Derivative 44 | 10.6480 | 25.86% | 0.5600 | −52.70% | 1.5180 | −10.97% |
| Derivative 45 | 10.5810 | 25.07% | 1.1810 | −0.25% | 1.7350 | 1.76% |
| Derivative 46 | 10.6870 | 26.32% | 1.1840 | 0.00% | 1.7340 | 1.70% |
| Derivative 47 | 8.7900 | 3.90% | 1.4680 | 23.99% | 1.7140 | 0.53% |
| Derivative 48 | 8.8820 | 4.99% | 1.5270 | 28.97% | 1.7120 | 0.41% |
| Derivative 49 | 9.5340 | 12.70% | 1.6600 | 40.20% | 1.7140 | 0.53% |
| Derivative 50 | 10.2130 | 20.72% | 1.2030 | 1.60% | 1.7480 | 2.52% |
| Derivative 51 | 9.2680 | 9.55% | 1.6710 | 41.13% | 1.7140 | 0.53% |
| Derivative 52 | 9.1970 | 8.71% | 1.6780 | 41.72% | 1.7150 | 0.59% |
| Derivative 53 | 9.3030 | 9.96% | 1.6730 | 41.30% | 1.7150 | 0.59% |
| Derivative 54 | 9.3480 | 10.50% | 1.2920 | 9.12% | 1.7150 | 0.59% |
| Derivative 55 | 9.5060 | 12.36% | 1.2600 | 6.42% | 1.7170 | 0.70% |
| Derivative 56 | 10.0920 | 19.29% | 1.5080 | 27.36% | 1.7190 | 0.82% |
| Derivative 57 | 9.8260 | 16.15% | 1.5030 | 26.94% | 1.7150 | 0.59% |
| Derivative 58 | 9.7550 | 15.31% | 1.5080 | 27.36% | 1.7150 | 0.59% |
| Derivative 59 | 9.8610 | 16.56% | 1.5100 | 27.53% | 1.7160 | 0.65% |
| Derivative 60 | 8.7220 | 3.10% | 0.8730 | −26.27% | 1.6940 | −0.65% |
| Derivative 61 | 9.2850 | 9.75% | 0.9190 | −22.38% | 1.6930 | −0.70% |
| Derivative 62 | 9.4710 | 11.95% | 1.1430 | −3.46% | 1.7000 | −0.29% |
| Derivative 63 | 9.1970 | 8.71% | 1.1680 | −1.35% | 1.7000 | −0.29% |
| Derivative 64 | 9.1270 | 7.88% | 1.1810 | −0.25% | 1.7020 | −0.18% |
| Derivative 65 | 9.2330 | 9.14% | 1.1870 | 0.25% | 1.7000 | −0.29% |
| Derivative 66 | 8.8390 | 4.48% | 1.2240 | 3.38% | 1.7380 | 1.94% |
| Derivative 67 | 9.4460 | 11.65% | 1.2440 | 5.07% | 1.7430 | 2.23% |
| Derivative 68 | 9.5880 | 13.33% | 1.5060 | 27.20% | 1.7430 | 2.23% |
| Derivative 69 | 9.3150 | 10.11% | 1.5320 | 29.39% | 1.7400 | 2.05% |
| Derivative 70 | 9.2440 | 9.27% | 1.5460 | 30.57% | 1.7350 | 1.76% |
| Levofloxacin | 7.9750 | 1.4590 | 1.7070 | |||
| Derivative 71 | 8.9340 | 12.03% | 1.5280 | 4.73% | 1.4730 | −13.71% |
| Derivative 72 | 8.7350 | 9.53% | 1.4300 | −1.99% | 1.4750 | −13.59% |
| Derivative 73 | 9.0150 | 13.04% | 1.5230 | 4.39% | 1.5320 | −10.25% |
| Derivative 74 | 9.3700 | 17.49% | 1.3630 | −6.58% | 1.7120 | 0.29% |
| Derivative 75 | 9.0220 | 13.13% | 1.4800 | 1.44% | 1.6800 | −1.58% |
| Derivative 76 | 8.4140 | 5.50% | 1.5220 | 4.32% | 1.4980 | −12.24% |
| Derivative 77 | 9.4620 | 18.65% | 1.3840 | −5.14% | 1.4730 | −13.71% |
| Derivative 78 | 8.9870 | 12.69% | 1.6650 | 14.12% | 1.4560 | −14.70% |
| Derivative 79 | 9.0140 | 13.03% | 1.2830 | −12.06% | 1.5410 | −9.72% |
| Derivative 80 | 8.7330 | 9.50% | 1.5340 | 5.14% | 1.5350 | −10.08% |
| Derivative 81 | 8.5510 | 7.22% | 1.6340 | 11.99% | 1.7030 | −0.23% |
| Derivative 82 | 8.1340 | 1.99% | 1.5160 | 3.91% | 1.4660 | −14.12% |
| Derivative 83 | 9.1820 | 15.13% | 1.6460 | 12.82% | 1.4190 | −16.87% |
| Derivative 84 | 8.4940 | 6.51% | 1.5230 | 4.39% | 1.4390 | −15.70% |
| Derivative 85 | 8.9160 | 11.80% | 1.5790 | 8.22% | 1.4700 | −13.88% |
| Derivative 86 | 8.8460 | 10.92% | 1.5280 | 4.73% | 1.4610 | −14.41% |
| Derivative 87 | 7.9940 | 0.24% | 1.5970 | 9.46% | 1.5430 | −9.61% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Zhang, B.; Huang, W.; Cantwell, C.; Chen, B. Integration of Fuzzy Matter-Element Method and 3D-QSAR Model for Generation of Environmentally Friendly Quinolone Derivatives. Int. J. Environ. Res. Public Health 2020, 17, 3239. https://doi.org/10.3390/ijerph17093239
Li X, Zhang B, Huang W, Cantwell C, Chen B. Integration of Fuzzy Matter-Element Method and 3D-QSAR Model for Generation of Environmentally Friendly Quinolone Derivatives. International Journal of Environmental Research and Public Health. 2020; 17(9):3239. https://doi.org/10.3390/ijerph17093239
Chicago/Turabian StyleLi, Xixi, Baiyu Zhang, Wendy Huang, Cuirin Cantwell, and Bing Chen. 2020. "Integration of Fuzzy Matter-Element Method and 3D-QSAR Model for Generation of Environmentally Friendly Quinolone Derivatives" International Journal of Environmental Research and Public Health 17, no. 9: 3239. https://doi.org/10.3390/ijerph17093239
APA StyleLi, X., Zhang, B., Huang, W., Cantwell, C., & Chen, B. (2020). Integration of Fuzzy Matter-Element Method and 3D-QSAR Model for Generation of Environmentally Friendly Quinolone Derivatives. International Journal of Environmental Research and Public Health, 17(9), 3239. https://doi.org/10.3390/ijerph17093239







