Intrinsic Cross-Correlation Analysis of Hydro-Meteorological Data in the Loess Plateau, China
Abstract
1. Introduction
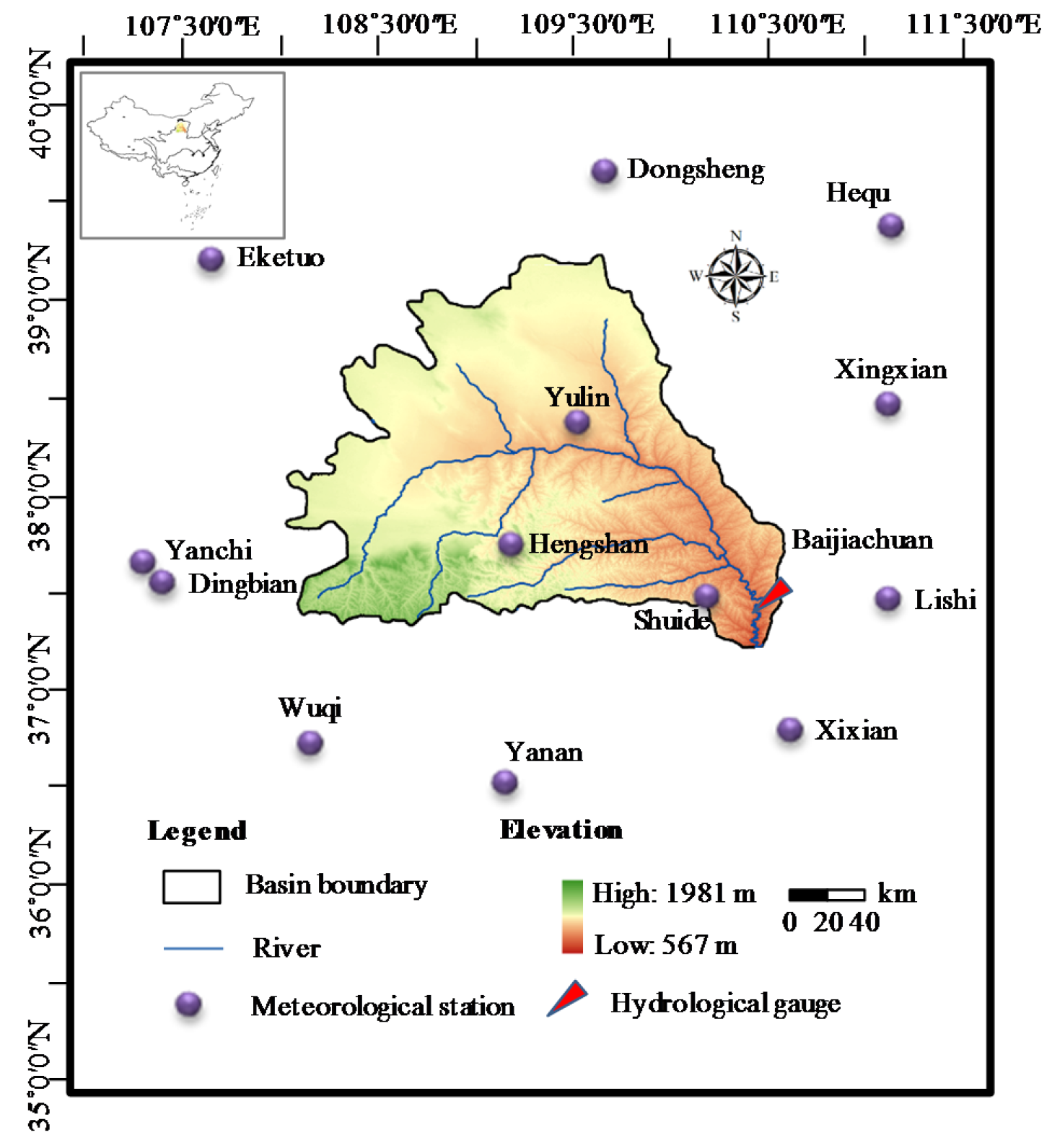
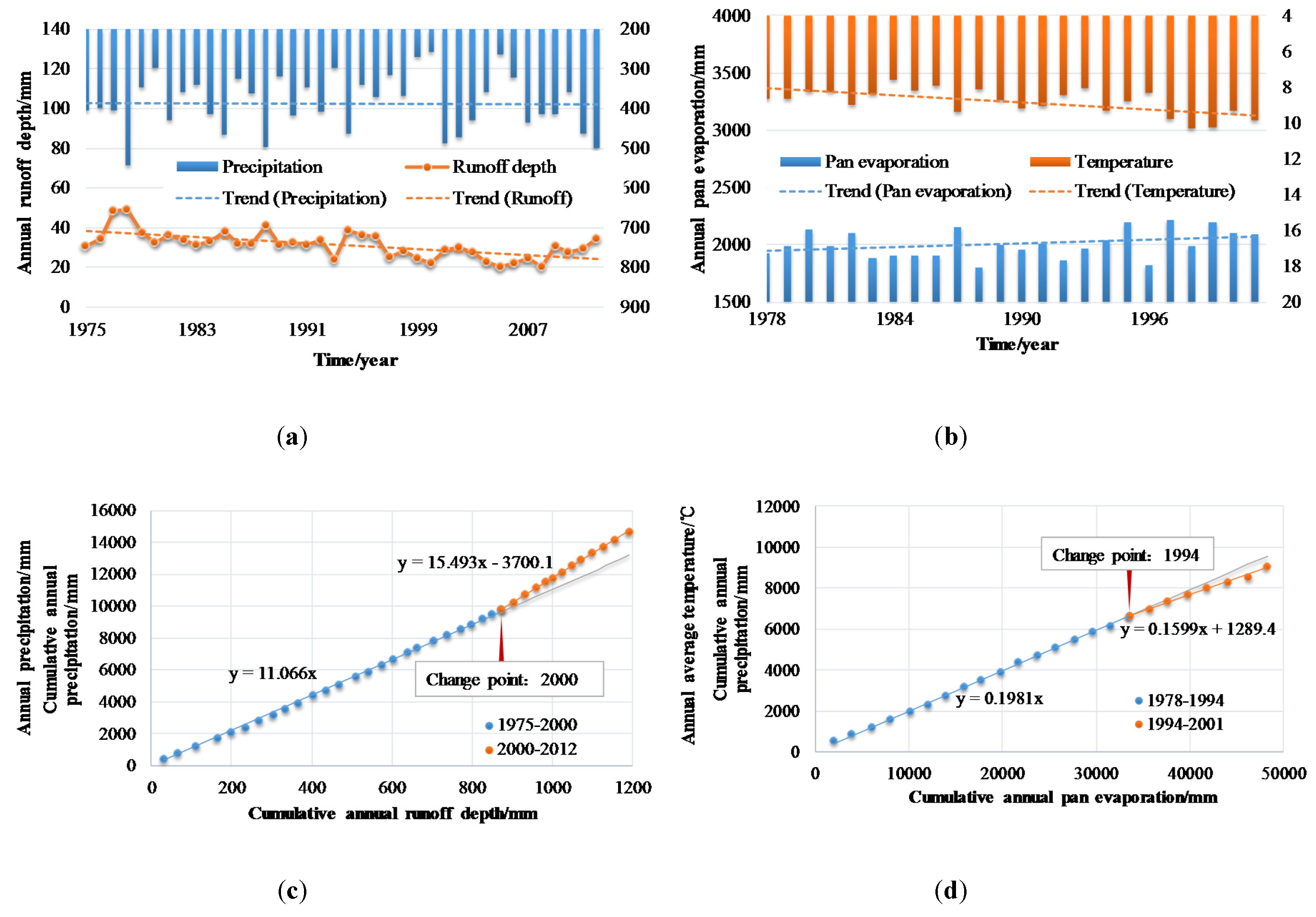
2. Study Area and Data
3. Methodology
3.1. DPCCA
- Suppose three time series , where . We can define cumulative series aswhere , .
- Divide the entire cumulative series into overlapping boxes, where represents the difference between sequence numbers corresponding to the first and last values in a box. Each box () contains , values, starting at and ending at where represents the time scale. In each box , we can determine the ‘‘local trend’’ by using a polynomial fit, and the linear fit was adopted in this study (). Accordingly, the time scale will vary between and . For climatic records, the second-order polynomial fit is normally enough. Then the detrended residual as the difference between the original cumulative series and the local trend , namely “detrended walk”, can be further defined aswhere , , n + 1 < s < N−1.
- Based on each detrended residual series corresponding to , the covariance between any two residuals can be calculated aswhere . Then, a covariance matrix can be constructed as
- The cross-correlation levels between any two series, i.e., and , can be estimated asand the coefficients matrix can further be obtained aswhere , represents the level of cross-correlation on time scales of . It is the so-called DCCA cross-correlation coefficients.
- 5.
- Before using the partial-correlation technique, the inverse matrix of can be calculated as
- 6.
- For any two series and , the partial-cross-correlation level can be determined aswhere the coefficients can be used to characterize the “intrinsic” correlation between the two series on time scales of . Then, the partial cross-correlation levels on different time scales can be further estimated by changing s. Similar to Pearson correlation coefficient, the larger the absolute value of the coefficients is, the stronger the correlation is. In other words, the closer the coefficients are to 1 or −1, the stronger the correlation is, while the closer is to 0, the weaker the correlation is. In addition, the degree of correlation can be determined through the range of correlation coefficient, including extremely strong, strong, medium, weak, and extremely weak/no, as shown in Table 1.
3.2. TDPCCA
- For a given time scale , based on the results in step 1 and 2 in Section 3.1, the detrended residual sequences can built the point-to-points structure as follows
- Then a new matrix can be obtained for the time series as
- According to Equations (3) and (5), the cross-correlation coefficients between two series and can be calculated, as follows
- For time point , the correlation matrix by using Equations (3) and (5) can be obtained.
- According to Equation (7), the inverse matrix of can be calculated.
- The partial-cross-correlation coefficients can be estimated by the following equation for any two series and .
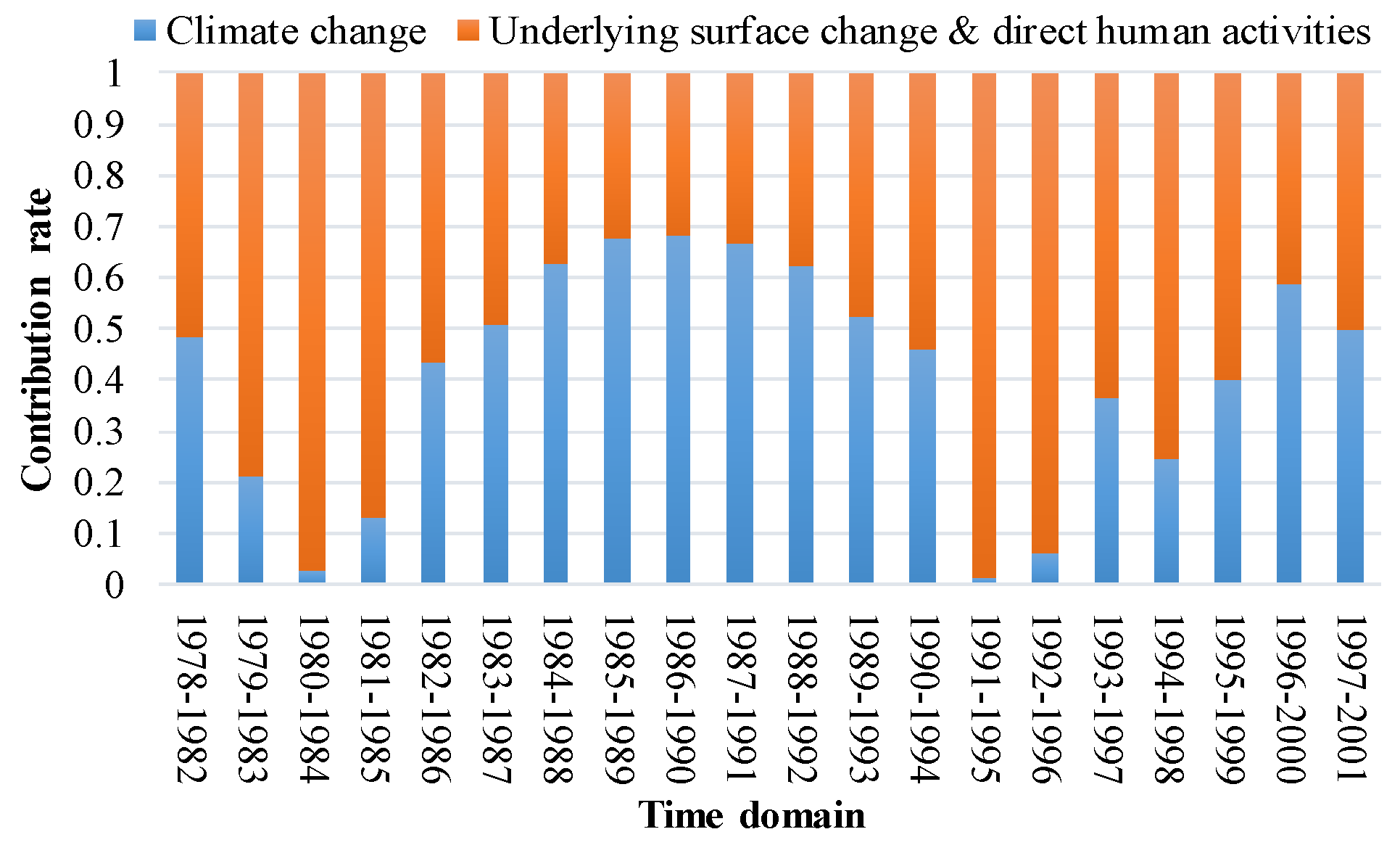
3.3. Impact Assessment of Correlation Change
4. Results
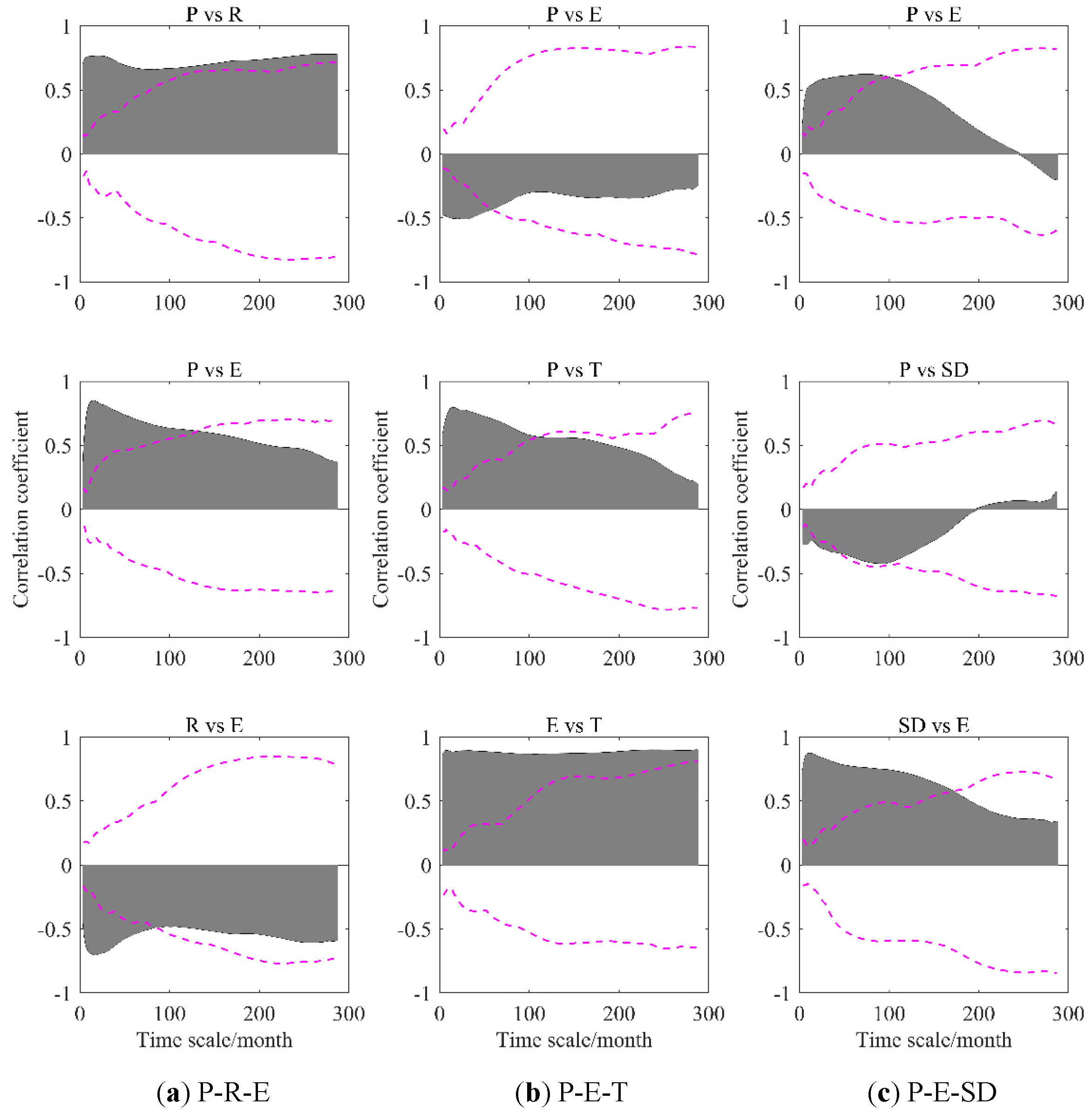
4.1. Correlations of Hydro-Meteorological Variables
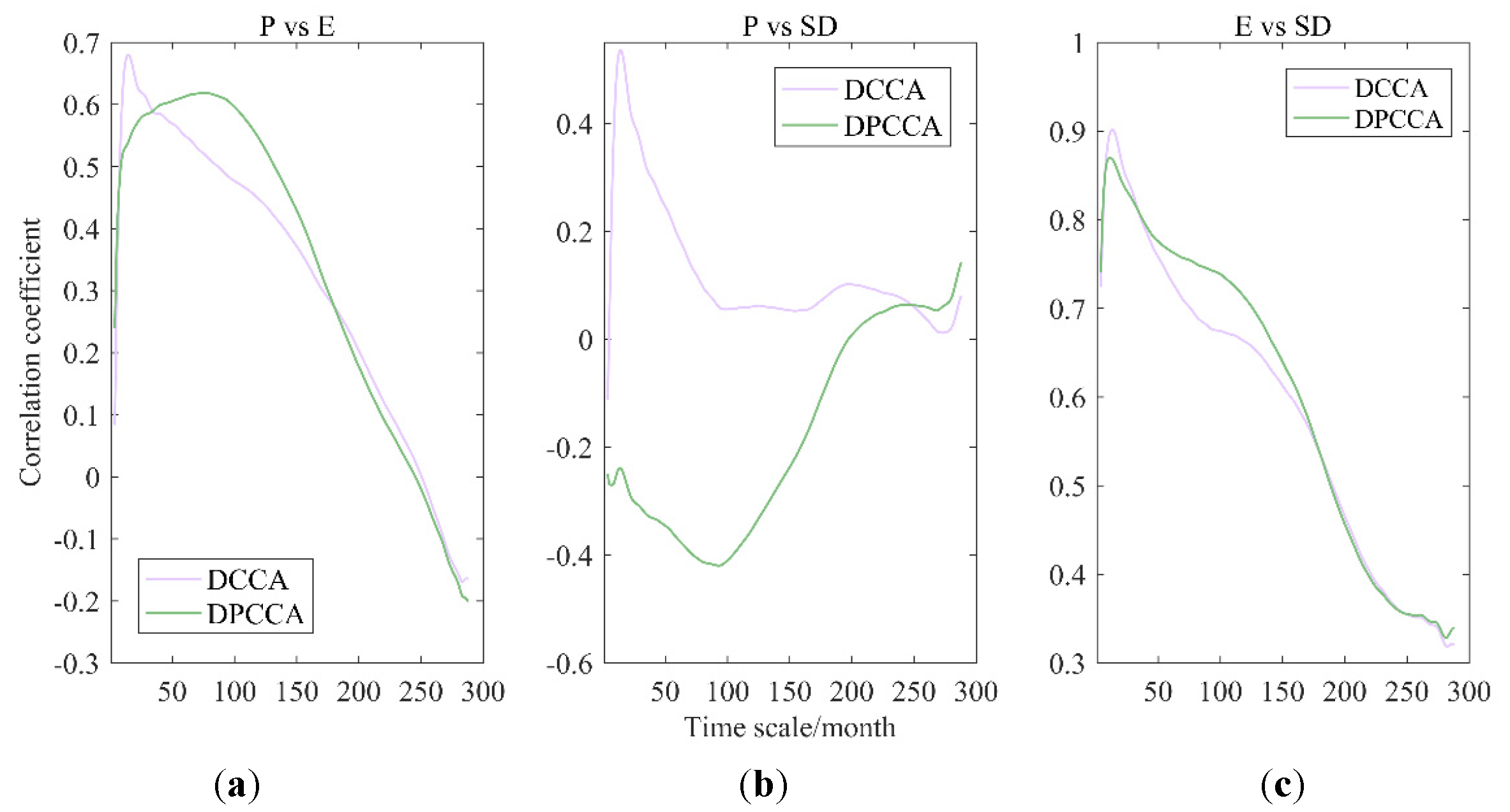
4.1.1. P-R-E
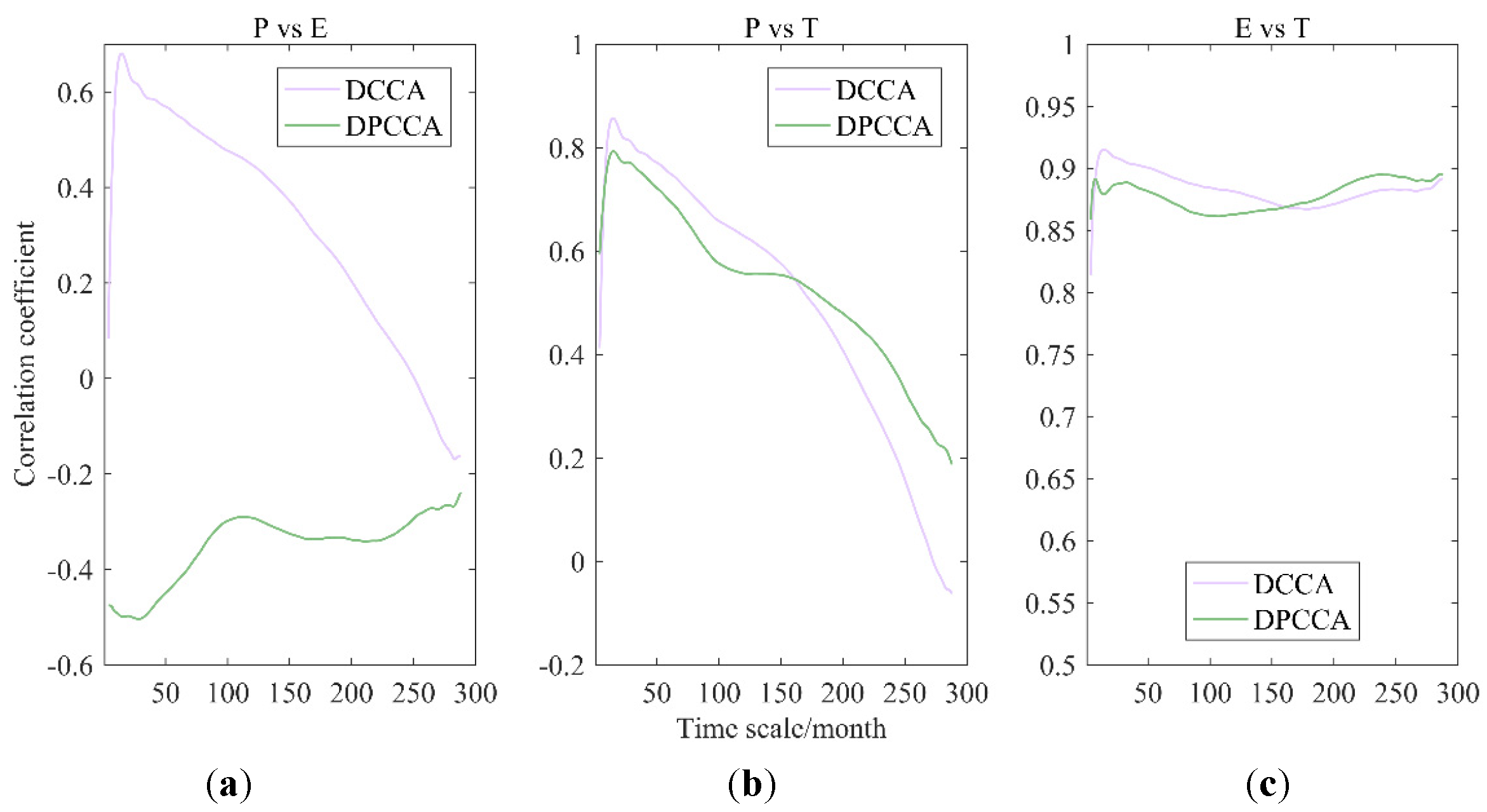
4.1.2. P-E-T
4.1.3. P-E-SD
4.2. Testing for Significance of Intrinsic Correlation
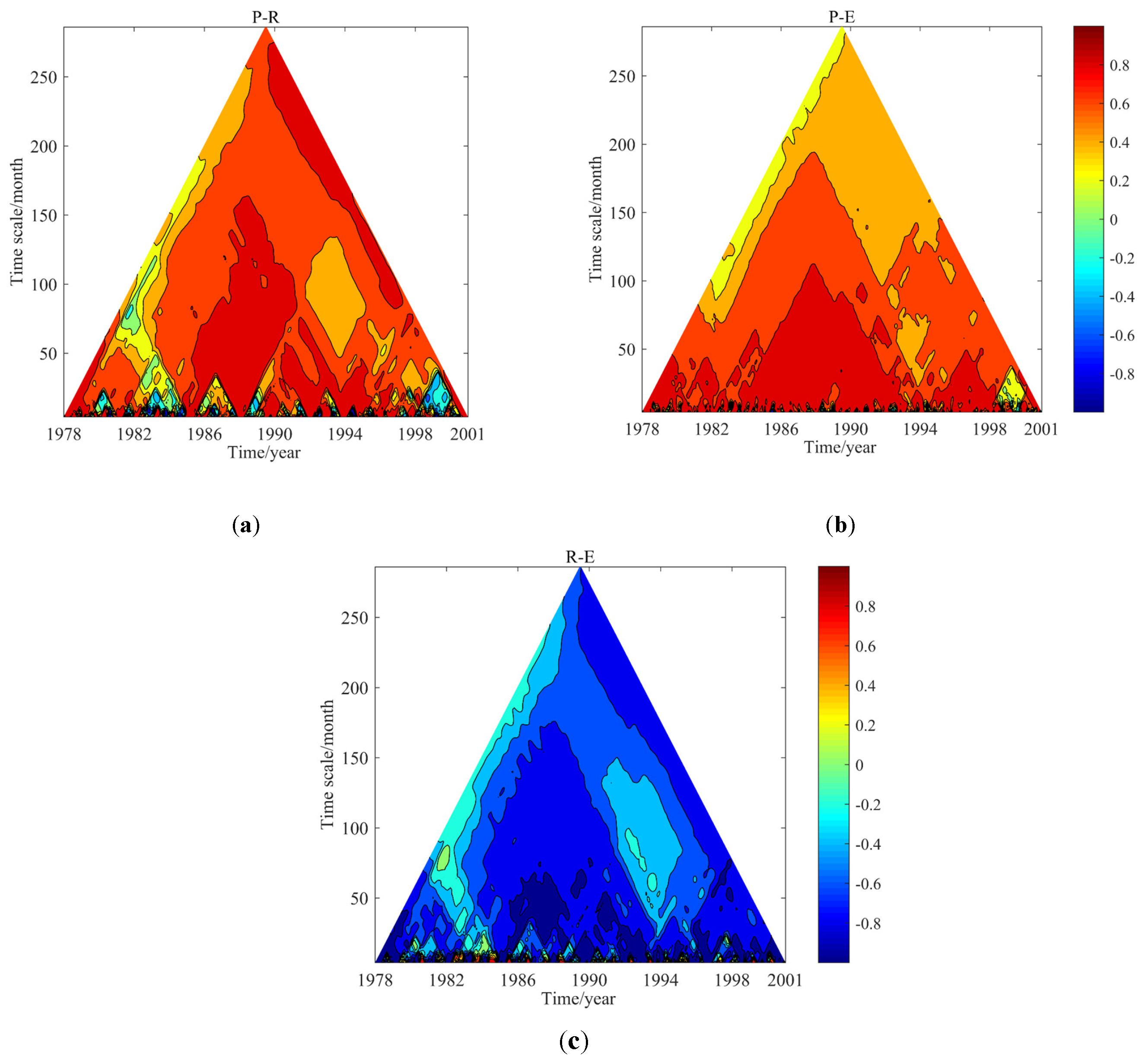
4.3. Temporal Evolution of DPCCA
5. Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Zhao, Y.; Deng, X.; Zhang, S.; Liu, Z.; Liu, C.; Han, G.; Wu, X. Impact of observational time window on coupled data assimilation: Simulation with a simple climate model. Nonlin. Processes Geophys. 2017, 24, 681–694. [Google Scholar] [CrossRef]
- Zhang, Q.; Liu, J.; Yu, X.; Chen, L. Scale effects on runoff and a decomposition analysis of the main driving factors in Haihe Basin mountainous area. Sci. Total Environ. 2019, 690, 1089–1099. [Google Scholar] [CrossRef]
- Ruigar, H.; Golian, S. Assessing the correlation between climate signals and monthly mean and extreme precipitation and discharge of Golestan Dam Watershed. Earth Sci. Res. J. 2015, 19, 65–72. [Google Scholar]
- Yettella, V.; Weiss, J.B.; Kay, J.E.; Pendergrass, A. An ensemble covariance framework for quantifying forced climate variability and its time of emergence. J. Clim. 2018, 31, 4117–4133. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, H.; Li, J.; Li, J. AGCT: A hybrid model for identifying abrupt and gradual change in hydrological time series. Environ. Earth Sci. 2019, 78, 433. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, B.; Lan, T.; Shi, J.; Lu, S. Change-point detection and variation assessment of the hydrologic regime of the Wenyu River. Toxicol. Environ. Chem. 2015, 98, 1–20. [Google Scholar] [CrossRef]
- Zhang, Z.; Chen, X.; Xu, C.; Yuan, L.; Yong, B.; Yan, S. Evaluating the non-stationary relationship between precipitation and streamflow in nine major basins of China during the past 50 years. J. Hydrol. 2011, 409, 81–93. [Google Scholar] [CrossRef]
- Barnett, T.P. The interaction of multiple time scales in the tropical climate system. J. Clim. 1991, 4, 269–285. [Google Scholar] [CrossRef]
- Sang, Y. A review on the applications of wavelet transform in hydrology time series analysis. Atmos. Res. 2013, 122, 8–15. [Google Scholar] [CrossRef]
- Mandejin, M.R.R.; Siahpoosh, S. Relationship between strategic thinking and knowledge management (case study: Iran’s Ministry of economic affairs and finance). J. Appl. Sci. 2015, 15, 367–373. [Google Scholar] [CrossRef][Green Version]
- Chang, F.J.; Wu, T.C.; Tsai, W.P.; Herricks, E.E. Defining the ecological hydrology of Taiwan Rivers using multivariate statistical methods. J. Hydrol. 2009, 376, 235–242. [Google Scholar] [CrossRef]
- Schreyer, M.; Paulin, R.; Trutschnig, W. On the exact region determined by Kendall’s tau and Spearman’s rho. J. R. Statist. Soc. B 2015, 79, 613–633. [Google Scholar] [CrossRef]
- Mahmud, M.R.; Hashim, M.; Reba, M.N.M. How Effective is the New Generation of GPM Satellite Precipitation in Characterizing the Rainfall Variability over Malaysia? Asia Pacific J. Atmos. Sci. 2017, 53, 375–384. [Google Scholar] [CrossRef]
- Furman, E.; Zitikis, R. Beyond the Pearson correlation: Heavy-tailed risks, weighted Gini correlations, and a Gini-type weighted insurance pricing model. Astin Bull. 2017, 47, 919–942. [Google Scholar] [CrossRef]
- Koskinen, L. Copula Theory and Its Applications edited by Piotr Jaworski, Fabrizio Durante, Wolfgang Hardle and Tomasz Rychlik. Int. Stat. Rev. 2012, 80, 328. [Google Scholar] [CrossRef]
- Zebende, G.F. DCCA cross-correlation coefficient: Quantifying level of cross-correlation. Phys. A Stat. Mech. Applic. 2011, 390, 614–618. [Google Scholar] [CrossRef]
- Vassoler, R.T.; Zebende, G.F. DCCA cross-correlation coefficient apply in time series of air temperature and air relative humidity. Phys. A Stat. Mech. Applic. 2012, 391, 2438–2443. [Google Scholar] [CrossRef]
- Yuan, N.; Fu, Z.; Zhang, H.; Piao, L.; Xoplaki, E.; Luterbacher, J. Detrended partial-cross-correlation analysis: A new method for analyzing correlations in complex system. Sci. Rep. 2015, 5, 8143. [Google Scholar] [CrossRef]
- Yuan, N.; Xoplaki, E.; Zhu, C.; Luterbacher, J. A novel way to detect correlations on multi-time scales, with temporal evolution and for multi-variables. Sci. Rep. 2016, 6, 27707. [Google Scholar] [CrossRef]
- Shen, C.; Li, C. An analysis of the intrinsic cross-correlations between API and meteorological elements using DPCCA. Phys. A Stat. Mech. Applic. 2016, 446, 100–109. [Google Scholar] [CrossRef]
- Yan, C.; Zhai, L.; Zhang, H.; Wang, H.; Jin, N. Cross-correlation analysis of interfacial wave and droplet entrainment in horizontal liquid-liquid two-phase flows. Chem. Eng. J. 2017, 320, 416–426. [Google Scholar] [CrossRef]
- Liu, C.; Jhone, Y.; Hsu, C.; Teng, P.; Lu, M.; Yang, C. Detrended Partial Cross-Correlation Analysis of Age-Related Changes. In Proceedings of the 2016 International Conference on Advanced Materials for Science and Engineering (ICAMSE), Tainan, China, 12–13 November 2016. [Google Scholar]
- Sivakumar, B. Correlation dimension estimation of hydrological series and data size requirement: Myth and reality. Hydrol. Sci. J. 2005, 50, 591–603. [Google Scholar] [CrossRef]
- Cheng, L.; Ma, L.; Yang, M.; Wan, G.; Wang, X. Changes of temperature and precipitation and their impacts on runoff in the upper Taohe River in northwest China from 1956 to 2014. Environ. Earth Sci. 2019, 78, 423. [Google Scholar] [CrossRef]
- Yang, D.; Sun, F.; Liu, Z.; Cong, Z.; Lei, Z. Interpreting the complementary relationship in non-humid environments based on the Budyko and Penman hypotheses. Geophys. Res. Lett. 2006, 33, L18402. [Google Scholar] [CrossRef]
- Zhang, H.; Singh, V.P.; Wang, B.; Yu, Y. CEREF: A hybrid data-driven model for forecasting annual streamflow from a socio-hydrological system. J. Hydrol. 2016, 540, 246–256. [Google Scholar] [CrossRef]
- Tian, X.; Zhao, G.; Mu, X.; Zhang, P.; Tian, P.; Gao, P.; Sun, W. Hydrologic alteration and possible underlying causes in the Wuding river, China. Sci. Total Environ. 2019, 693, 133556. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Huang, Q.; Zhang, Q.; Gu, L.; Chen, K.; Yu, Q. Changes in the long-term hydrological regimes and the impacts of human activities in the main Wei River, China. Hydrol. Sci. J. 2015, 61, 1054–1068. [Google Scholar] [CrossRef]
- Chen, X. Contributions of climate change and human activities to ET and GPP trends over North China Plain from 2000 to 2014. J. Geogr. Sci. 2017, 27, 661–680. [Google Scholar] [CrossRef]
- Maher, N.; Milinski, S.; Suarez-Gutierrez, L.; Botzet, M.; Kornblueh, L.; Takano, Y.; Dobrynin, M. The max planck institute grand ensemble: Enabling the Eexploration of climate system variability. JAMES 2019, 11, 2050–2069. [Google Scholar] [CrossRef]
- Seyoum, W.M.; Milewski, A.M.; Durham, M.C. Understanding the relative impacts of natural processes and human activities on the hydrology of the Central Rift Valley lakes, East Africa. Hydrol. Process. 2015, 29, 4312–4324. [Google Scholar] [CrossRef]
- Dai, A. Drought under global warming: A review. Wiley Interdiscip. Rev. Clim. Change 2012, 6, 617. [Google Scholar] [CrossRef]
- Guo, Q.; Yang, Y.; Xiong, X. Using hydrologic simulation to identify contributions of climate change and human activity to runoff changes in the Kuye river basin, China. Environ. Earth Sci. 2016, 75, 417. [Google Scholar] [CrossRef]
- Cong, J.; Xiong, L.; Wang, D.; Liu, P.; Guo, S.; Xu, C. Separating the impacts of climate change and human activities on runoff using the Budyko-type equations with time-varying parameters. J. Hydrol. 2015, 522, 326–338. [Google Scholar]
- Liu, J.; Zhang, Q.; Singh, V.P.; Shi, P. Contribution of multiple climatic variables and human activities to streamflow changes across China. J. Hydrol. 2017, 545, 145–162. [Google Scholar] [CrossRef]
- Yang, H.; Luo, P.; Wang, J.; Mou, C.; Mo, L.; Wang, Z.; Fu, Y.; Lin, H.; Yang, Y.; Bhatta, L.D. Ecosystem evapotranspiration as a response to climate and vegetation coverage changes in northwest Yunnan, China. PLoS ONE 2015, 10, e0134795. [Google Scholar] [CrossRef]
- Zhang, M.; Wei, X.; Sun, P.; Liu, S. The effect of forest harvesting and climatic variability on runoff in a large watershed: The case study in the upper minjiang river of Yangtze river basin. J. Hydrol. 2012, 464, 1–11. [Google Scholar] [CrossRef]
- Xu, M.; Wang, G. Accelerate the construction of warping dams in the loess plateau area. Yellow River 2000, 22, 26–28 (In Chinese). (In Chinese) [Google Scholar]

| Correlation Degree | Extremely Strong | Strong | Medium | Weak | Extremely Weak/No |
|---|---|---|---|---|---|
| Range of correlation coefficient | 0.8–1.0 | 0.6–0.8 | 0.4–0.6 | 0.2–0.4 | 0–0.2 |
| Three-Element-Composed System | P-R-E | P-E-T | P-E-SD | ||||||
|---|---|---|---|---|---|---|---|---|---|
| P-R | P-E | R-E | P-E | P-T | E-T | P-E | P-SD | E-SD | |
| Significant time-scales (month) | Ind * | ≤129 | ≤83 | ≤57 | ≤109 | Ind | ≤98 | ≤43 | ≤170 |
| Peak value | 0.762 | 0.847 | −0.698 | −0.504 | 0.793 | 0.891 | 0.618 | −0.334 | 0.87 |
| Time scale corresponding to peak value (month) | 22 | 15 | 17 | 29 | 15 | 8 | 76 | 43 | 11 |
| Mean coefficient | 0.718 | 0.698 | −0.595 | −0.481 | 0.688 | 0.878 | 0.584 | −0.29 | 0.739 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, X.; Zhang, H.; Gong, X.; Wei, X.; Dang, C.; Zhi, T. Intrinsic Cross-Correlation Analysis of Hydro-Meteorological Data in the Loess Plateau, China. Int. J. Environ. Res. Public Health 2020, 17, 2410. https://doi.org/10.3390/ijerph17072410
Wei X, Zhang H, Gong X, Wei X, Dang C, Zhi T. Intrinsic Cross-Correlation Analysis of Hydro-Meteorological Data in the Loess Plateau, China. International Journal of Environmental Research and Public Health. 2020; 17(7):2410. https://doi.org/10.3390/ijerph17072410
Chicago/Turabian StyleWei, Xiaowei, Hongbo Zhang, Xinghui Gong, Xingchen Wei, Chiheng Dang, and Tong Zhi. 2020. "Intrinsic Cross-Correlation Analysis of Hydro-Meteorological Data in the Loess Plateau, China" International Journal of Environmental Research and Public Health 17, no. 7: 2410. https://doi.org/10.3390/ijerph17072410
APA StyleWei, X., Zhang, H., Gong, X., Wei, X., Dang, C., & Zhi, T. (2020). Intrinsic Cross-Correlation Analysis of Hydro-Meteorological Data in the Loess Plateau, China. International Journal of Environmental Research and Public Health, 17(7), 2410. https://doi.org/10.3390/ijerph17072410






