Integer Versus Fractional Order SEIR Deterministic and Stochastic Models of Measles
Abstract
1. Introduction
2. Methods
2.1. Preliminaries
Fractional Calculus
2.2. Fractional Stochastic Process
2.3. Measles Model via Fractional Differential Equations (FDE)
2.4. Measles Model via Ordinary Differential Equations (ODE)
2.5. Measles Model via -Dependent Ordinary Differential Equations
2.6. Model Analysis
- the disease free equilibrium and
- the endemic equilibrium
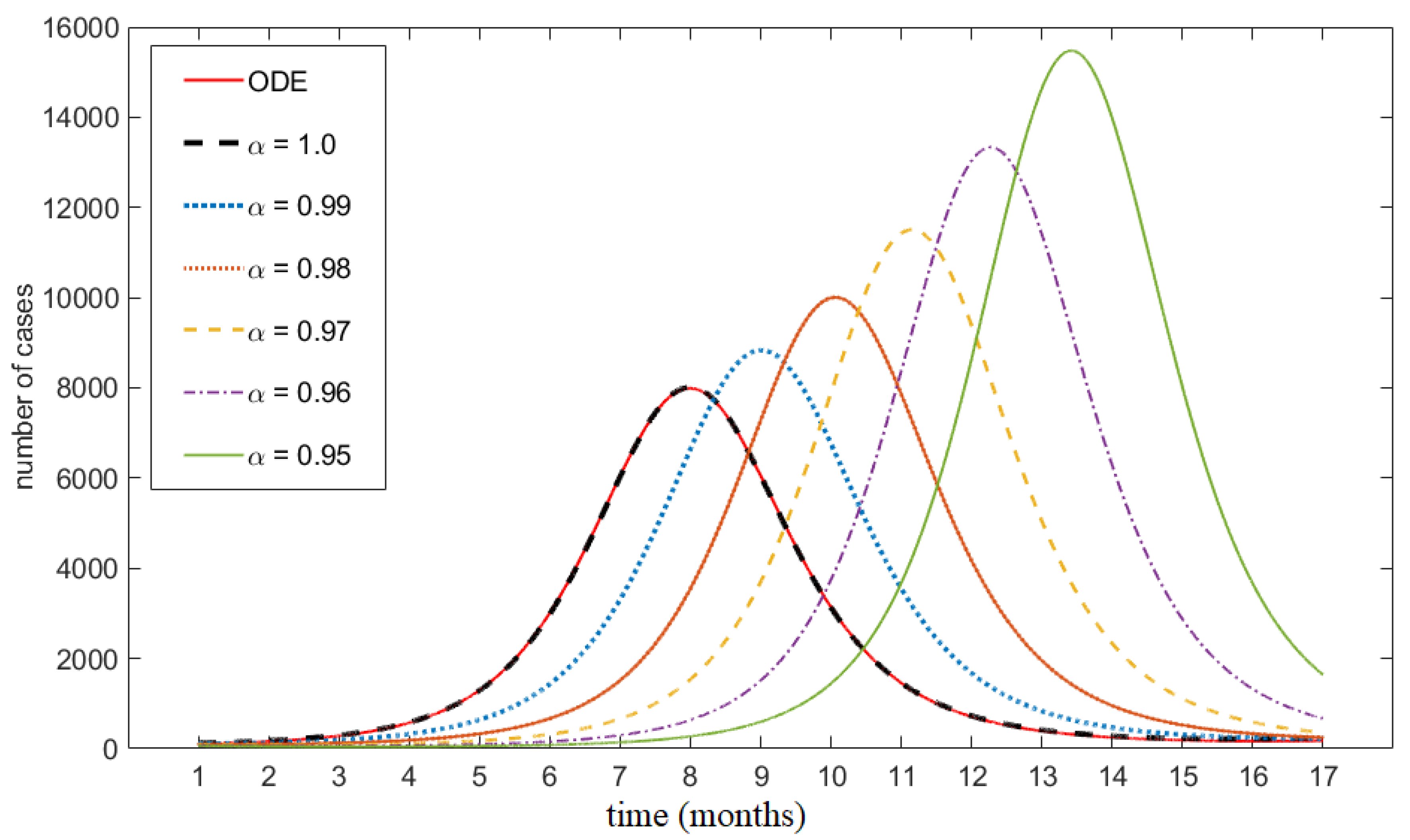
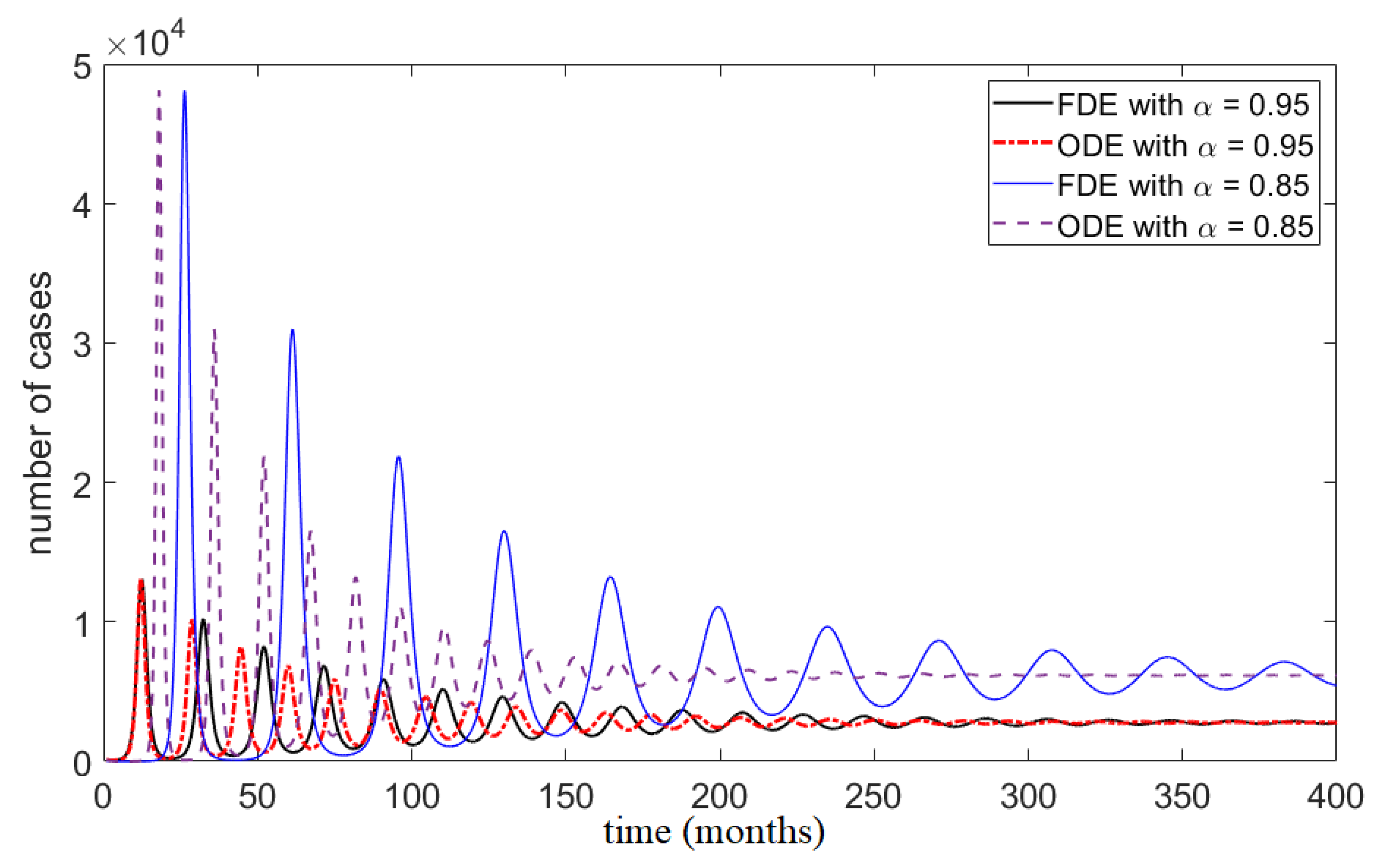
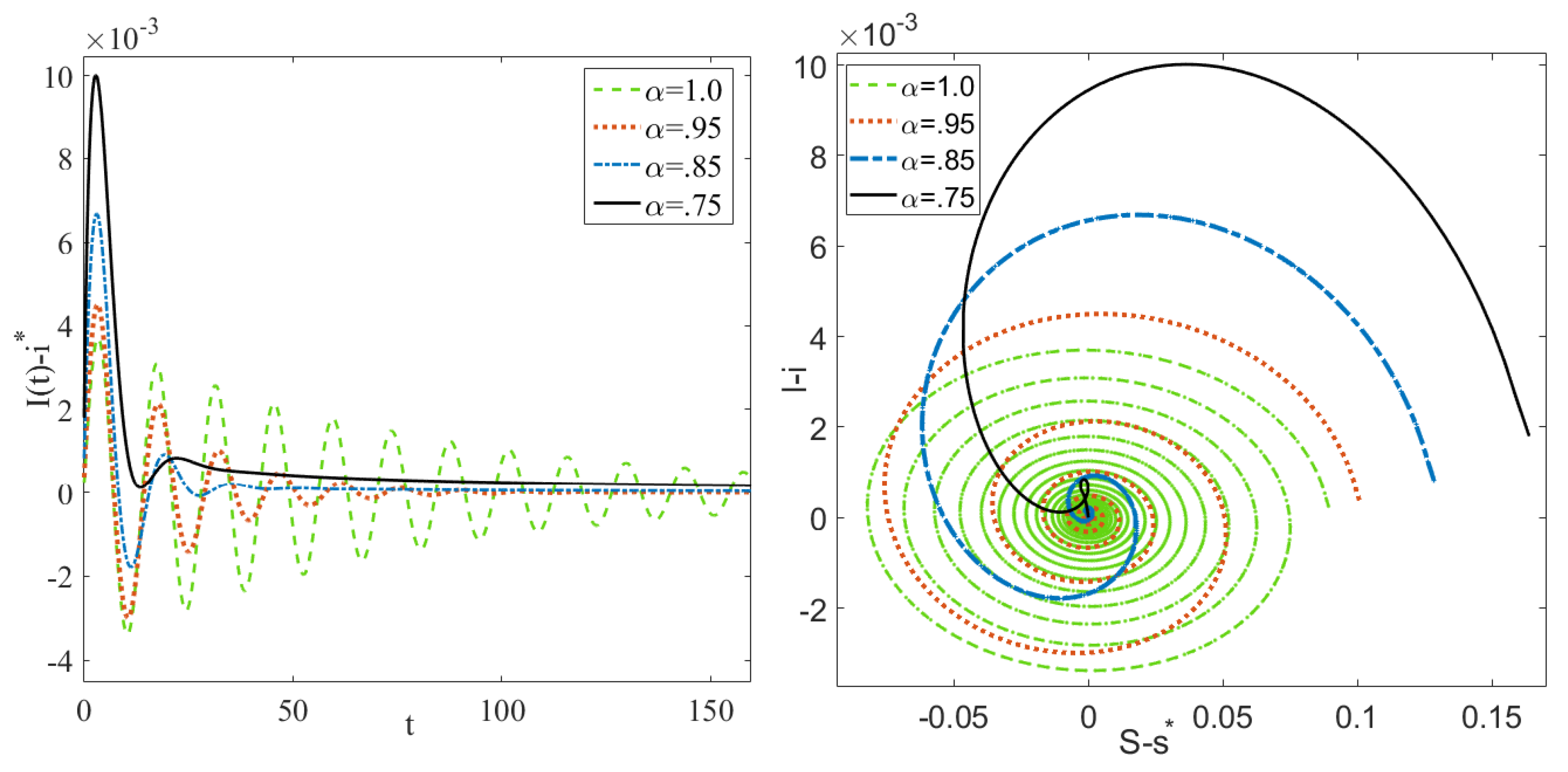
2.7. Numerical Simulations
| Algorithm 1 Numerical solution of for with . |
| Input: Output: |
| begin |
| Divide the interval into n sub-intervals using
|
| for |
| Divide the interval into further m sub-intervals using
|
| Solve the system with using Euler or Runge-Kutta methods on . |
| Retain . |
| end |
| Return . |
| end |
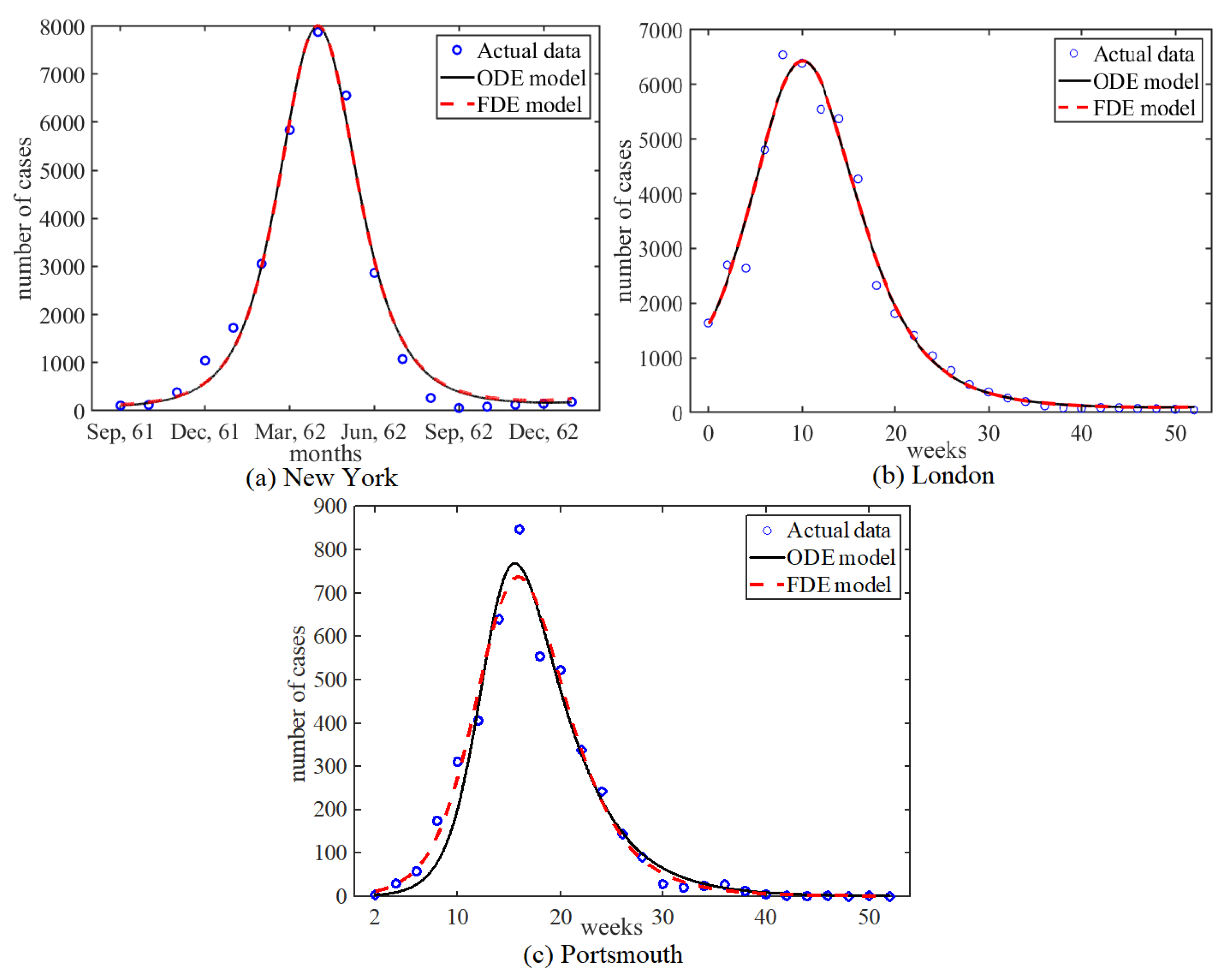
2.8. Fitting FDE and ODE Models to Measles Data
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Some Definitions and Proofs
Fractional Birth and Death Process
Appendix B. Data Sets and Parameter Estimation
Appendix B.1. New York
| Year | Months | Cases | Year | Months | Cases | Year | Months | Cases |
|---|---|---|---|---|---|---|---|---|
| 1961 | September | 109 | 1962 | March | 5839 | 1962 | September | 58 |
| 1961 | October | 123 | 1962 | April | 7875 | 1962 | October | 86 |
| 1961 | November | 383 | 1962 | May | 6555 | 1962 | November | 125 |
| 1961 | December | 1043 | 1962 | June | 2866 | 1962 | December | 145 |
| 1962 | January | 1725 | 1962 | July | 1075 | 1963 | January | 184 |
| 1962 | February | 3056 | 1962 | August | 266 |
Appendix B.2. London
| weeks | 0 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | 22 | 24 | 26 |
| cases | 1636 | 2700 | 2639 | 4805 | 6543 | 6389 | 5545 | 5374 | 4272 | 2322 | 1810 | 1409 | 1037 | 767 |
| weeks | 28 | 30 | 32 | 34 | 36 | 38 | 40 | 42 | 44 | 46 | 48 | 50 | 52 | |
| cases | 514 | 375 | 265 | 199 | 121 | 86 | 76 | 89 | 87 | 73 | 70 | 59 | 45 |
Appendix B.3. Portsmouth
| weeks | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | 22 | 24 | 26 | 28 | 30 |
| cases | 4 | 30 | 58 | 174 | 310 | 407 | 640 | 847 | 555 | 523 | 337 | 242 | 144 | 91 | 29 |
| weeks | 32 | 34 | 36 | 38 | 40 | 42 | 44 | 46 | 48 | 50 | 52 | ||||
| cases | 21 | 25 | 28 | 13 | 5 | 2 | 1 | 2 | 0 | 2 | 0 |
Appendix B.4. Parameter Estimations
| Data | Model | Estimated Parameters, | SSE | AIC | BIC |
|---|---|---|---|---|---|
| New York | ODE | 250.54 | 253.87 | ||
| FDE | 255.36 | 259.53 | |||
| London | ODE | 389.36 | 394.54 | ||
| FDE | 393.34 | 398.85 | |||
| Portsmouth | ODE | 277.94 | 282.98 | ||
| FDE | 271.92 | 278.21 |
References
- Bernoulli, D. Essai d’une nouvelle analyse de la mortalité causée par la petite vérole. Mém. Math. Phys. Acad. R. Sci. Paris 1766, 1, 1–45. [Google Scholar]
- Ross, R. An Application of the Theory of Probabilities to the Study of a priori Pathometry. Part I. Proc. R. Soc. A Math. Phys. Eng. Sci 1916, 92, 204–230. [Google Scholar] [CrossRef]
- Brownlee, J. Certain Aspects of the Theory of Epidemiology in Special Relation to Plague. Proc. R. Soc. Med. 1918, 11, 85–132. [Google Scholar] [CrossRef] [PubMed]
- Greenwood, M.; Yule, G.U. An Inquiry into the Nature of Frequency Distributions Representative of Multiple Happenings with Particular Reference to the Occurrence of Multiple Attacks of Disease or of Repeated Accidents. J. R. Stat. Soc. 1920, 83, 255. [Google Scholar] [CrossRef]
- Kermack, W.O.; McKendrick, A.G. A Contribution to the Mathematical Theory of Epidemics. In Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences; Royal Society: London, UK, 1927. [Google Scholar]
- Soper, H.E. The Interpretation of Periodicity in Disease Prevalence. J. R. Stat. Soc. 1929, 92, 34. [Google Scholar] [CrossRef]
- Greenwood, M. On the Statistical Measure of Infectiousness. J. Hyg. 1931, 31, 336–351. [Google Scholar] [CrossRef]
- Greenwood, M. The statistical study of infectious diseases. J. R. Stat. Society. Ser. A 1946, 109, 85–110. [Google Scholar] [CrossRef]
- Bartlett, M.S. Some Evolutionary Stochastic Processes. J. R. Stat. Soc. Ser. B 1949, 11, 211–229. [Google Scholar] [CrossRef]
- Bailey, N.T.J. The Total Size of a General Stochastic Epidemic. Biometrika 1953, 40, 177. [Google Scholar] [CrossRef]
- Bailey, N.T.J. The Mathematical Theory of Infectious Diseases and Its Applications; Griffin and Company Ltd.: Bucks, UK, 1975; p. 413. [Google Scholar]
- Anderson, R.M. The Population Dynamics of Infectious Diseases: Theory And Applications; Springer: Cham, Switzerland, 1982. [Google Scholar]
- Hethcote, H.W. The Mathematics of Infectious Diseases. SIAM Rev. 2005, 42, 599–653. [Google Scholar] [CrossRef]
- Keeling, M.J.; Danon, L. Mathematical modelling of infectious diseases. Br. Med. Bull. 2009, 92, 33–42. [Google Scholar] [CrossRef] [PubMed]
- Anderson, R.M.; May, R.M. Infectious Diseases of Humans: Dynamics and Control; Oxford University Press: Oxford, UK, 1991. [Google Scholar]
- Castillo-Chavez, C.; Blower, S.; van den Driessche, P.; Kirschner, D.; Abdul-Aziz, Y. Mathematical Approaches for Emerging an Reemerging Infectious Diseases; Springer: Cham, Switzerland, 2002. [Google Scholar] [CrossRef]
- Temime, L.; Hejblum, G.; Setbon, M.; Valleron, A. The rising impact of mathematical modelling in epidemiology: Antibiotic resistance research as a case study. Epidemiol. Infect. 2008, 136, 289. [Google Scholar] [CrossRef] [PubMed]
- Fisman, D.N.; Hauck, T.S.; Tuite, A.R.; Greer, A.L. An IDEA for Short Term Outbreak Projection: Nearcasting Using the Basic Reproduction Number. PLoS ONE 2013, 8, e83622. [Google Scholar] [CrossRef] [PubMed]
- Ahmed, E.; Elgazzar, A.S. On fractional order differential equations model for nonlocal epidemics. Phys. A Stat. Mech. Appl. 2007, 379, 607–614. [Google Scholar] [CrossRef]
- Demirci, E.; Unal, A.; Özalp, N. A fractional order SEIR model with density dependent death rate. Hacettepe J. Math. Stat. 2011, 40, 287–295. [Google Scholar]
- Al-Sheikh, S.A. Modeling and Analysis of an SEIR Epidemic Model with a Limited Resource for Treatment Modeling and Analysis of an SEIR Epidemic Model with a Limited Resource for Treatment Modeling and Analysis of an SEIR Epidemic Model with a Limited Resource for Treatme. Type Double Blind Peer Rev. Int. Res. J. Publ. Glob. J. Inc. 2012, 12, 56–66. [Google Scholar]
- Diethelm, K. A fractional calculus based model for the simulation of an outbreak of dengue fever. Nonlinear Dyn. 2013, 71, 613–619. [Google Scholar] [CrossRef]
- Li, J.; Cui, N. Dynamic analysis of an SEIR model with distinct incidence for exposed and infectives. Sci. World J. 2013, 2013, 1–5. [Google Scholar] [CrossRef]
- El-Shahed, M.; El-Naby, F.A. Fractional calculus model for for childhood diseases and vaccines. Appl. Math. Sci. 2014, 8, 4859–4866. [Google Scholar] [CrossRef][Green Version]
- Dold, E.A.; Eckmann, B.; Accola, R.D.M. Lecture Notes in Mathematics; Springer: Berlin/Heidelberg, Germany, 1975. [Google Scholar]
- Almeida, R.; Brito da Cruz, A.M.; Martins, N.; Monteiro, M.T.T. An epidemiological MSEIR model described by the Caputo fractional derivative. Int. J. Dyn. Control 2018, 7, 776–784. [Google Scholar] [CrossRef]
- Area, I.; Batarfi, H.; Losada, J.; Nieto, J.J.; Shammakh, W.; Torres, Á. On a fractional order Ebola epidemic model. Adv. Differ. Equ. 2015, 2015, 278. [Google Scholar] [CrossRef]
- Haggett, P. The Geographical Structure of Epidemics; Clarendon Press: Oxford, UK, 2000; p. 149. [Google Scholar]
- Bjørnstad, O.N.; Finkenstädt, B.F.; Grenfell, B.T. Dynamics of Measles Epidemics: Estimating Scaling of. Ecol. Monogr. 2002, 72, 169–184. [Google Scholar] [CrossRef]
- Xia, Y.; Bjørnstad, O.N.; Grenfell, B.T. Measles Metapopulation Dynamics: A Gravity Model for Epidemiological Coupling and Dynamics. Am. Nat. 2004, 164, 267–281. [Google Scholar] [CrossRef] [PubMed]
- Greenwood, P.E.; Gordillo, L.F. Stochastic epidemic modeling. In Mathematical and Statistical Estimation Approaches in Epidemiology; Springer: Cham, Switzerland, 2009; pp. 31–52. [Google Scholar] [CrossRef]
- Vasilyeva, O.; Oraby, T.; Lutscher, F. Aggregation and environmental transmission in Chronic Wasting Disease. Math. Biosci. Eng. 2015, 12. [Google Scholar] [CrossRef]
- Aranda, D.F.; Trejos, D.Y.; Valverde, J.C. A fractional-order epidemic model for bovine Babesiosis disease and tick populations. Open Phys. 2017, 15, 360–369. [Google Scholar] [CrossRef]
- Angstmann, C.; Henry, B.; McGann, A. A Fractional-Order Infectivity and Recovery SIR Model. Fractal Fract. 2017, 1, 11. [Google Scholar] [CrossRef]
- Sardar, T.; Rana, S.; Chattopadhyay, J. A mathematical model of dengue transmission with memory. Commun. Nonlinear Sci. Numer. Simul. 2015, 22, 511–525. [Google Scholar] [CrossRef]
- Saeedian, M.; Khalighi, M.; Azimi-Tafreshi, N.; Jafari, G.R.; Ausloos, M. Memory effects on epidemic evolution: The susceptible-infected-recovered epidemic model. Phys. Rev. E 2017, 95, 022409. [Google Scholar] [CrossRef]
- Laskin, N. Fractional Poisson process. Commun. Nonlinear Sci. Numer. Simul. 2003, 8, 201–213. [Google Scholar] [CrossRef]
- Uchaikin, V.V.; Cahoy, D.O.; Sibatov, R.T. Fractional Pprocesses: From poisson to branching one. Int. J. Bifurc. Chaos 2008, 18, 2717–2725. [Google Scholar] [CrossRef]
- Orsingher, E.; Polito, F.; Sakhno, L. Fractional Non-Linear, Linear and Sublinear Death Processes. J. Stat. Phys. 2010, 141, 68–93. [Google Scholar] [CrossRef]
- Orsingher, E.; Polito, F. Fractional pure birth processes. Bernoulli 2010, 16, 858–881. [Google Scholar] [CrossRef]
- Meerschaert, M.M.; Nane, E.; Vellaisamy, P. The fractional poisson process and the inverse stable subordinator. Electron. J. Probab. 2011, 16, 1600–1620. [Google Scholar] [CrossRef]
- Garra, R.; Polito, F. A note on fractional linear pure birth and pure death processes in epidemic models. Phys. A Stat. Mech. Appl. 2011, 390, 3704–3709. [Google Scholar] [CrossRef]
- Orsingher, E.; Polito, F. On a fractional linear birth–death process. Bernoulli 2011, 17, 114–137. [Google Scholar] [CrossRef]
- Orsingher, E.; Ricciuti, C.; Toaldo, B. Population models at stochastic times. Adv. Appl. Probab. 2016, 48, 481–498. [Google Scholar] [CrossRef][Green Version]
- Di Crescenzo, A.; Martinucci, B.; Meoli, A. A fractional counting process and its connection with the poisson process. Alea 2016, 13, 291–307. [Google Scholar] [CrossRef]
- Kumar, A.; Leonenko, N.; Pichler, A. Fractional risk process in insurance. Math. Financ. Econ. 2020, 14, 43–65. [Google Scholar] [CrossRef]
- Podlubny, I. Geometric and Physical Interpretation of Fractional Integration and Fractional Differentiation. arXiv 2008. Available online: https://arxiv.org/pdf/math/0110241.pdf (accessed on 18 March 2020).
- Özalp, N.; Demirci, E. A fractional order SEIR model with vertical transmission. Math. Comp. Modell. 2011, 54, 1–6. [Google Scholar] [CrossRef]
- Earn, D.J.; Rohani, P.; Bolker, B.M.; Grenfell, B.T. A simple model for complex dynamical transitions in epidemics. Science 2000, 287, 667–670. [Google Scholar] [CrossRef]
- Allen, L.J.S. Stochastic Population and Epidemic Models; Springer: Cham, Switzerland, 2015. [Google Scholar] [CrossRef]
- Allen, L. An Introduction to Stochastic Processes with Applications to Biology, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar] [CrossRef]
- Di Crescenzo, A.; Meoli, A. On a fractional alternating Poisson process. AIMS Math. 2016, 1, 212. [Google Scholar] [CrossRef]
- Konno, H.; Pázsit, I. Fractional Linear Birth-Death Stochastic Process—An Application of Heun’s Differential Equation. Rep. Math. Phys. 2018, 82, 1–20. [Google Scholar] [CrossRef]
- Mandelbrot, B.; Taylor, H.M. On the Distribution of Stock Price Differences. Oper. Res. 1967, 15, 1057–1062. [Google Scholar] [CrossRef]
- Demirici, E.; Özalp, N. A method for solving differential equations of fractional order. J. Comput. Appl. Math. 2012, 236, 2754–2762. [Google Scholar] [CrossRef]
- Piryatinska, A.; Saichev, A.; Woyczynski, W. Models of anomalous diffusion: The subdiffusive case. Phys. A Stat. Mech. Appl. 2005, 349, 375–420. [Google Scholar] [CrossRef]
- Apostolou, M. Numerical Algorithms and Mathematics for Ode Models of Measles. Ph.D. Thesis, University of Porshmouth, Porshmouth, UK, 2011. [Google Scholar]

| Transition | Rate |
|---|---|
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Islam, M.R.; Peace, A.; Medina, D.; Oraby, T. Integer Versus Fractional Order SEIR Deterministic and Stochastic Models of Measles. Int. J. Environ. Res. Public Health 2020, 17, 2014. https://doi.org/10.3390/ijerph17062014
Islam MR, Peace A, Medina D, Oraby T. Integer Versus Fractional Order SEIR Deterministic and Stochastic Models of Measles. International Journal of Environmental Research and Public Health. 2020; 17(6):2014. https://doi.org/10.3390/ijerph17062014
Chicago/Turabian StyleIslam, Md Rafiul, Angela Peace, Daniel Medina, and Tamer Oraby. 2020. "Integer Versus Fractional Order SEIR Deterministic and Stochastic Models of Measles" International Journal of Environmental Research and Public Health 17, no. 6: 2014. https://doi.org/10.3390/ijerph17062014
APA StyleIslam, M. R., Peace, A., Medina, D., & Oraby, T. (2020). Integer Versus Fractional Order SEIR Deterministic and Stochastic Models of Measles. International Journal of Environmental Research and Public Health, 17(6), 2014. https://doi.org/10.3390/ijerph17062014





