1. Introduction
Work organization is defined as the way in which work is structured, managed, and processed [
1]. Job rotation belongs to a group of work organizational strategies that seek to reduce workers’ exposure to ergonomic hazards by introducing variation in the tasks performed by the workers. It consists of an exchange of workers among the different workstations from time to time. A job rotation system generates benefits not only for workers but also for the company. From the workers point of view, job rotation has a positive influence as it reduces monotony [
2] and boredom [
3], reduces the level of stress, increases employee satisfaction [
4,
5] and extends the range of skills [
6,
7,
8], retains skills for a cross-trained workforce [
9], and enables workers to observe and correct deviations at an earlier production stage, which improves product quality. It also facilitates the integration of disabled workers [
10], reduces fatigue and physical stress and, as a result, the incidence of work-related musculoskeletal disorders (WRMDs) [
7,
11,
12].
The ergonomic exposure risk of a worker depends on three factors: the magnitude of the risk, exposure time, and frequency. Job rotation can act on the exposure time and frequency factors. Therefore, job rotation can be considered a preventive strategy against risk factors associated with WRMDs, such as repetitive movements, load handling, inadequate postures, or vibrations [
13]. However, there is no consensus on the real effectiveness of job rotation to prevent these ergonomics risk factors [
14]. While some studies reported positive effects of rotation on the prevalence of WRMDs or musculoskeletal pain [
15,
16], some others found undesirable effects in the long run [
17,
18]. The criteria used for deployment of job rotation may explain the heterogeneity of results [
14]. Obtaining the expected benefits on WRMDs will only be achieved if important criteria are considered, for example, the number of workers involved, the number and duration of rotations and pauses, the use of different muscle groups in each rotation, or the physical and psychical limitations of workers [
19]. On the other hand, it is important to note that rotation has no effect on the magnitude of the risk. Therefore, critical jobs that demand great effort or that expose workers to hazardous tasks must not be included in rotation programs. Reducing the risk of critical tasks before including them in a rotation program is essential to obtain efficient rotation schedules [
2,
20].
Job rotation reduces the incidence of musculoskeletal injuries and the level of absenteeism. Rotation fosters employee learning because it increases the possibility of assigning them to different tasks [
21], and it also results in ‘firm learning’, i.e., employers learn more about their employees [
22]. In general terms, companies that introduce job rotation systems are more innovative in their working methods because when the workers are rotated to other jobs, their skills and abilities can be used to improve the working tools and methods.
Developing a job rotation plan is a complex problem. The type of job rotation implemented affects the results in terms of satisfaction and productivity [
23,
24], and there are a lot of criteria and restrictions that must be considered simultaneously to obtain an efficient solution. For example, it is necessary to find the sequence of tasks that maximizes the variation in the muscle groups being utilized by the workers [
25,
26] and the optimal length of the rotation interval to reduce monotony and boredom. Simultaneously, organizational demands such as balance between job and salary must be met, and the physical and mental capacity of employees to develop the assigned tasks must be considered. Otherwise, the result may be a poorly designed job rotation plan that can adversely affect the working conditions [
27].
Several approaches to design job rotation schedules can be found in the literature [
28]. Given a set of workers and workstations, obtaining an optimal rotation schedule according to some criteria is a combinatorial optimization problem. Although there are some other techniques applied to the resolution of this kind of problems, such as Integer Programming [
9,
10,
29], one the most common ways to obtain good solutions in short times is using heuristics and metaheuristics like genetic algorithms or tabu search [
25,
30,
31,
32,
33,
34,
35,
36,
37]. This paper presents RGA, an evolutionary algorithm [
38] to generate job rotation schedules aimed to prevent WRMDs, that simultaneously solves important organizational problems found when rotation schedules are implemented in real environments. A rotation plan establishes the workstations that a set of workers occupy in each rotation. If the number of workstations (and workers) implied in the rotation system is large, the procedures to generate job rotation schedules generate solutions that involve complex workstations sequences that workers must follow. For example,
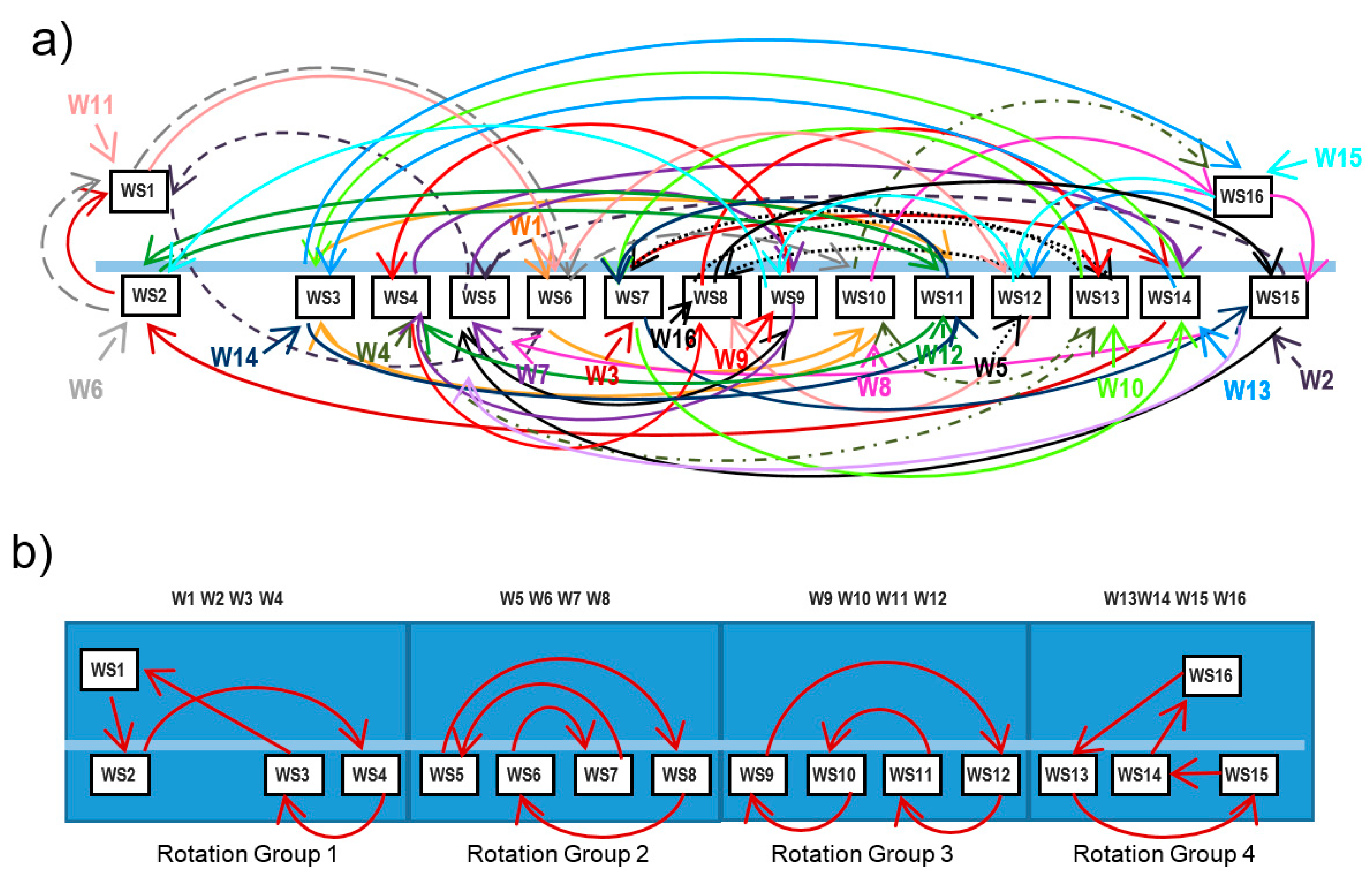
Figure 1a shows a rotation schedule with 4 rotations in which 16 workers rotate occupying 16 workstations. Each worker is assigned to 4 different workstations and follows a different route.
Implementing a complex rotation schedule, like that shown in
Figure 1a, supposes some organizational problems [
39]. Each worker must follow a different and complex path, and the workers must memorize the sequence of workstations. For example, Worker 11 occupies the Workstation WS1 in the first rotation, WS6 in the second, WS12 in the third rotation, and the workstation WS8 in the last rotation. All the workers follow this kind of sequence and the movement of the workers in each rotation is a bit chaotic, leading to confusion and waste of time. On the other hand, in assembly lines it is usual that one worker (hereafter called monitor) who is responsible for a small group of workers. In some cases, the monitor may not be assigned to a particular workstation. Monitors are intended to replace workers that temporary leave his workstation, or during changeovers in job rotations in order to avoid interruptions and delays in the production process. In this work setting, implementing job rotation schedules presents difficulties for both monitors and the rest of workers. The workers assigned to one monitor follow very different sequences of workstations, making the monitoring task difficult. In each rotation, the monitor may be in different positions and workers must look for the monitor in the event of problems or substitutions. In many cases, these problems lead to abandoning rotation plans.
A commonly used strategy to implement more simple rotation schedules is grouping the workstations in several small rotation groups. For example,
Figure 1b shows that the 16 workstations of the previous example have been grouped in four rotation groups. Each rotation group has four workstations and four workers assigned to them. In the example of the Figure, workstations 1 to 4 form the rotation group 1, and workers 1 to 4 are assigned to these workstations. Then, four independent rotation schedules are generated, one for each rotation group.
Although this approach avoids the organizational problems found in generating a global schedule for the complete set of workstations, it has important drawbacks. Usually, the rotations groups are created grouping workstations that are close to each other, without considering ergonomics criteria in the clustering process. In the same way, workers are assigned to rotation groups considering only organizational issues. However, to achieve the benefits expected from job rotation, it would be convenient that the movements required in the tasks developed in the workstations in the same rotation group were different. In the same way, workers should be assigned to rotation groups considering their capacities, preferences, and temporal disabilities.
To face these problems, this work proposes a different approach to create job rotation schedules. The RGA algorithm generates rotation schedules grouping the workstations to be included in the rotation plan so that a set of workers rotate cyclically over a small number of workstations. The algorithm determines how to cluster the workstations, which workers are best suited for each rotation group and the rotation sequence. This aims to: decrease the risk of musculoskeletal injuries, increase the diversification of the tasks to be performed throughout the workday, consider the possible disabilities of employees, and simplify changeovers and the monitoring task.
This paper is structured as follows:
Section 2 describes the RGA algorithm,
Section 3 shows a case study in an auto parts assembly line and the results are exposed in
Section 4.
Section 5 provides a discussion on results and, finally,
Section 6 shows conclusions based on our findings.
3. Case Study
This section describes the procedure used to verify the ability of the RGA algorithm to generate cyclic job rotation schedules that minimize the effects of repetitive movements while simplifying scheduled changeovers at each rotation. To do this, RGA was used to design a cyclic rotation schedule for a set of 16 workplaces and workers in a spare parts assembly line.
Cyclic rotation schedules are preferable from an organizational point of view. However, it is not the same from an ergonomics point of view. All the solutions in the RGA’s initial population are cyclic rotation schedules. On the other hand, crossover and mutation in RGA are closed operators (they always produce valid cyclic schedules) and then, all the solutions in the population of RGA are always cyclic rotation schedules. Therefore, the solution space in which RGA searches for a solution to the problem is formed by all the possible cyclic rotation schedules. This solution space is a subset of all the possible schedules (including all the no-cyclic schedules). As a result, from an ergonomics point of view, the quality of the best schedule in the RGA´s solution space will be equal or worse than that of the best schedule in the global solution space including no-cyclic schedules.
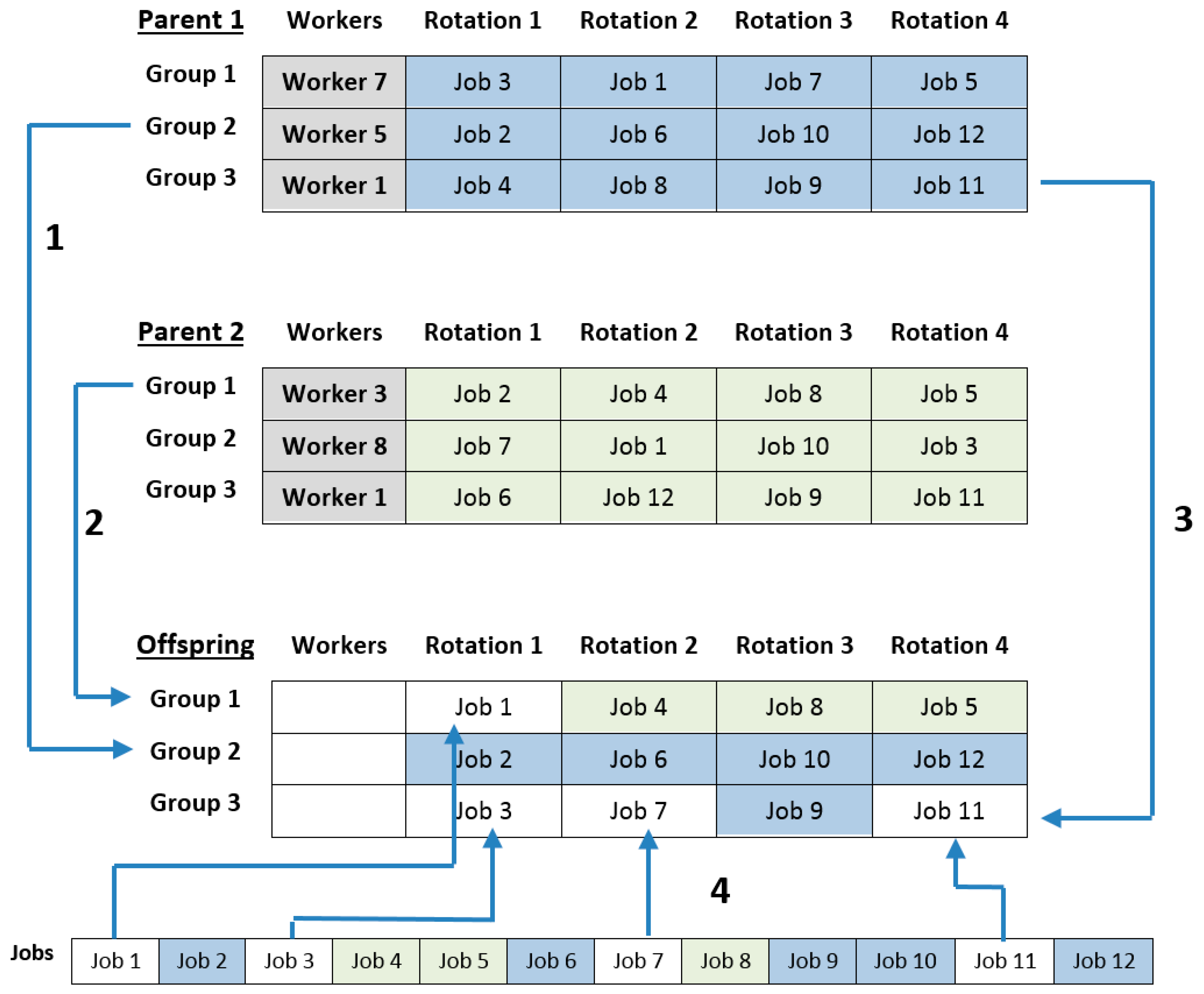
RGA’s approach looks for a compromise between ergonomics and organizational criteria to generate rotation schedules. To check this compromise, the problem under consideration was solved using RGA to obtain the best cyclic rotation schedule. Then, a modified version of the algorithm (RGAm) was used to obtain the best no-cyclic job rotation schedule. Finally, the scores of the fitness function of both solutions were compared. To create a schedule in RGAm, the workers are randomly assigned to the workstations without creating rotation groups. In the same way, the crossover operator does not consider rotation groups and creates offspring from parents in an unrestricted way.
In the analyzed spare parts assembly line, there was an eight-hour workday. RGA was used to design a cyclic rotation schedule with four rotations; the first three rotations with a duration of 2 h, and the last one of 1 h. There was one-hour break for lunch between the second and the third rotations. All the 16 workstations belonged to same line and the distances between them allow for quick changeovers. The 16 workers had skills to perform the task required at any of the workstations.
3.1. Scores of the Workers and the Workstations
The movements and the skills needed to perform the task in each workstation of the assembly line were analyzed. Scores between 0 and 3 were assigned to each item of the movements group (
Table 1) depending on the frequency of each movement (
Table 2). In the same way, the medical staff of the manufacturing plant collaborated to assign scores to the items of the workers depending on their capacity to perform each movement and to decide if some worker had some limitation to perform some activity.
Table 3 shows the scores of the items of the movements group for each workstation and for each worker. The skills and capacities needed in each workstation and the skills and limitations of the workers were matched to determine which workers should not be assigned to some jobs (penalized assignments).
Table 4 shows the penalized assignments.
3.2. Parameters Used in the RGA
The duration of the rotations was set to two hours for the first, second, and third rotation and one hour for the fourth. tmax (the maximum consecutive time that a worker can be assigned to a workstation) was set to 2 h. In this way, the solutions that assigned a worker to the same workstation in two consecutive rotations were penalized. The coefficients I1 to I18 were set to 1 (see Equation (1)). These coefficients represent the relative importance of each item with respect to the rest of the items. In this case, all of them were considered to have the same level of importance.
Equation (2) increases the scores of the items of a worker after each rotation if the items of the workstations of previous rotations are bigger than a threshold value (th). In the same Equation, the parameter rd regulates the size of the effect of tasks performed in preceding rotations on the items of the worker in later rotations. Considering the advice of the medical staff, the value of the parameter th was set to 1.5 and rd was set to 3.
Some tests were performed to establish the best combination of the rest of the parameters of RGA. In general, RGA is a robust algorithm and slight changes in the parameters do not affect the results. After running the algorithm several times, the population size (n) was set to 50, the crossover probability (pc) was set to 0.6, and the mutation probability (pm) to 0.3. The elitism rate (Er) was set to 1.
4. Results
RGA was run 10 times using the scores shown in
Table 3 and the penalizations shown in
Table 4. Each run stopped after 10,000 iterations. Then, the modified version of the algorithm (RGAm) was run 10 times using the same scores and parameters to obtain the best no-cyclic job rotation schedule. The algorithms were executed in a personal computer with a 2.7 GHz CPU of 4 cores and 32 GB RAM. The mean execution time for the 10 runs was 8.36 min for the RGA and 6.24 min for the RGAm algorithm.
The results of each execution of RGA and RGAm are shown in
Table 5;
Table 6, respectively. The first column of the tables shows the run number, the second (Iteration) shows the generation in which the best schedule was found, and the third (Best Fitness), the fitness value of the best schedule. The fourth column (Workers mean value) indicates the mean contribution of the assignments of each worker to the total fitness of the best solution. Finally, the last column shows the standard deviation of the contribution of the assignments of each worker to the fitness of the best solution. The values of the last column indicate if the tasks have been evenly assigned to the workers. A high value in this column means that some workers have been assigned to tougher workstations (with high scores in the movements items) while others performs lighter ones. Therefore, lower values are preferable in this column.
The algorithms were able to obtain feasible solutions in all the runs and the restrictions of the problem were satisfied. The fitness value of the best schedule provided by the RGA 492.80, while the value of best solution obtained by RGAm was 477.33. The workers mean value was 31.84 for RGA and 29.96 for RGAm. On average, RGA obtained the best fitness in iteration 3643 and RGAm in iteration 4861.90.
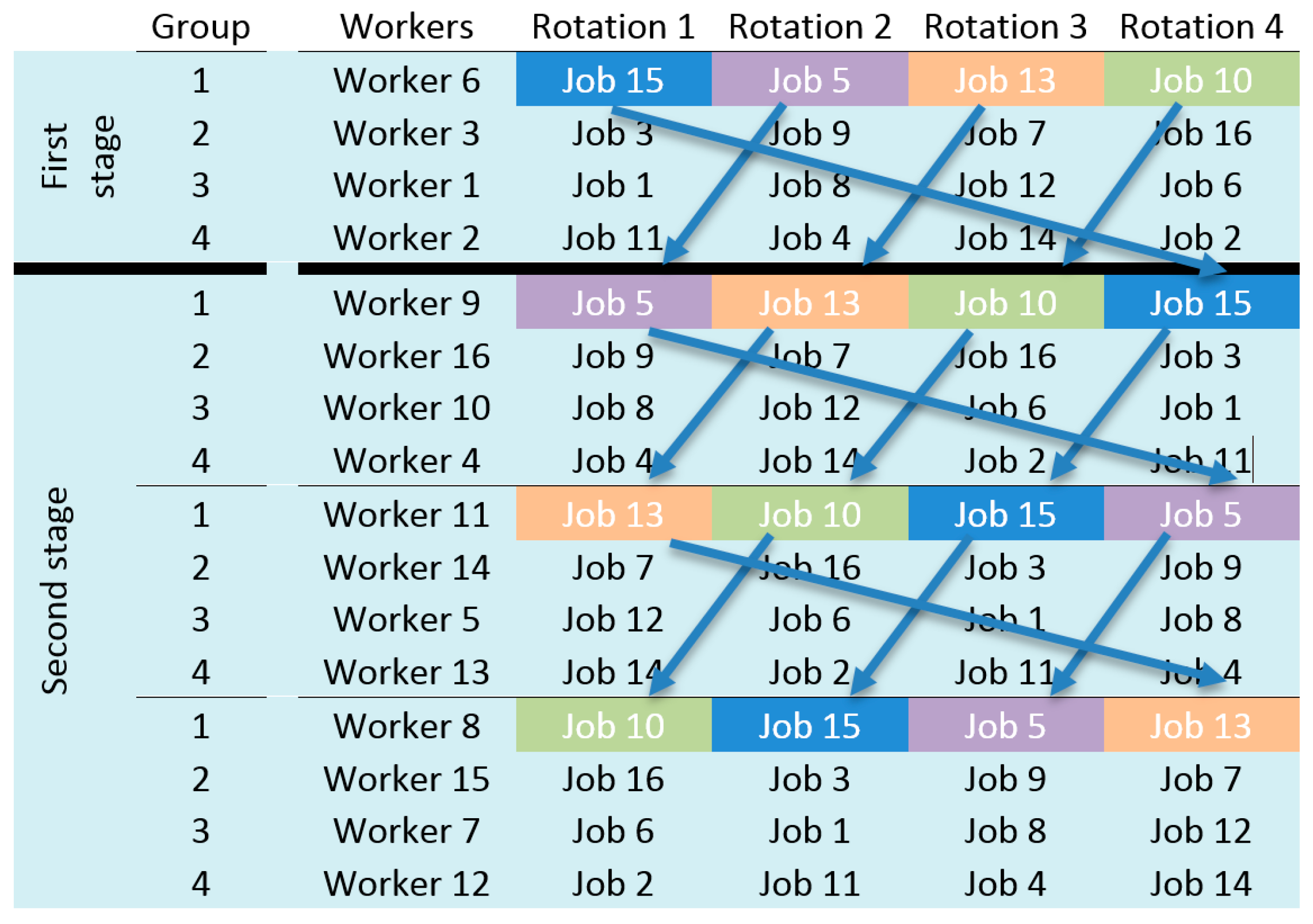
RGA found the best schedule in Run 3 (
Table 7). The first rotation group was formed by the workstations 15, 5, 13, and 10 and the workers 6, 9, 11, and 8. The group 2 consisted of workstations 3, 9, 7, 16 and workers 3, 16, 14, and 15. Group 3 included workstations 1, 8, 12, and 6 and workers 1, 10, 5, and 7. Finally, group 4 consisted of workstations 2, 4, 13, and 12 and workers 2, 4, 13, and 12. This solution met the constraints imposed on the problem and the workers were allocated in different workstations in each rotation. This was true even for disabled workers whose limitations prevented them from performing several movements or activities. On the contrary, in the best solution generated by RGAm (
Table 8), the worker 12 was assigned to the same workstation in two non-consecutive rotations (rotation 1 and 3).
The last column in the
Table 7;
Table 8 indicates the contribution of the assignments of each worker to the total fitness of the solution. The balance in the assignments of the workers was very similar in the best solution found by both RGA and RGAm. The best RGA solution was slightly more balanced than the best RGAm solution. In the best RGA solution, the largest imbalance was between worker 9, with an average cost of 24.23, and worker 14 with an average cost of 47.49. In the best RGAm solution, the largest difference was found between worker 7, with an average cost of 20.04, and worker 14, with an average cost of 45.55. Worker 14 was the worker with more cost in both solutions. Worker 14 had limitations in some movements and skills and could not occupy several workstations, which meant less possibilities for both algorithms when trying to achieve more favorable and less imbalanced assignments compared to those of other workers. The same happened with worker 12, whose cost was 46 in the best RGA solution and 42.04 in the best RGAm solution.
5. Discussion
The RGA algorithm generates rotation schedules grouping the workstations to be included in the rotation plan in such a way that a set of workers rotate cyclically over a small number of workstations. The algorithm determines how to cluster the workstations, which workers are best suited for each rotation group, and the rotation sequence. Solutions obtained using RGA may decrease the risk of musculoskeletal injuries, increase the diversification of the tasks to be performed throughout the workday, and consider the possible disabilities of employees. In addition, RGA simplifies changeovers between rotations, avoiding delays in the production process, while facilitating the monitoring tasks. The computational experiences show the ability of the RGA algorithm for solving the problem of the generation of rotation schedules considering simultaneously multiple criteria and constraints creating rotation groups. Under these conditions, the algorithm provides good results with small computation time. In the case under study, the model was able to obtain solutions in which workers rotate cyclically over four workstations while minimizing movement repetitiveness and may balance the cumulative effect of fatigue and stress.
The space of solutions of the current problem, in which only cyclic schedules are considered valid solutions, is a subgroup of the space of solutions to the problem without workstations clustering. This suggests that, necessarily, the value of the fitness function of the best solution in the RGA solution space will be greater than or equal to the value of the best solution without job clustering. In fact, the RGAm version of the algorithm, was able to generate a solution to our test problem with a slightly lower value of the objective function than RGA. To check if the best solution obtained using RGA is significantly worse from an ergonomic point of view than that obtained using RGAm, it would be convenient to know the optimum solution to the problem, but it is not possible to obtain that value in an analytical way. Therefore, we used another reference to compare both solutions. One thousand random rotations schedules were generated as solutions to our test problem and the values of the fitness function were calculated. The mean value of the fitness function was 649.22 (SD 16.06) and the mean cost by the worker was 40.58 (SD 15.92).
The fitness value of the best rotation schedule obtained using RGA was 492.80 and using RGAm was 477.33. Therefore, the fitness of the best cyclic schedule was 24.09% better than the mean fitness of random schedules, and the fitness of the best no-cyclic schedule was 26.47% better. The difference between both algorithms compared to the random allocation is 2.38%. Therefore, although the best cyclic rotation schedule is slightly worse than the best no-cyclic schedule from the ergonomics point of view, the difference is small, and it is compensated by the benefits of a better work organization.
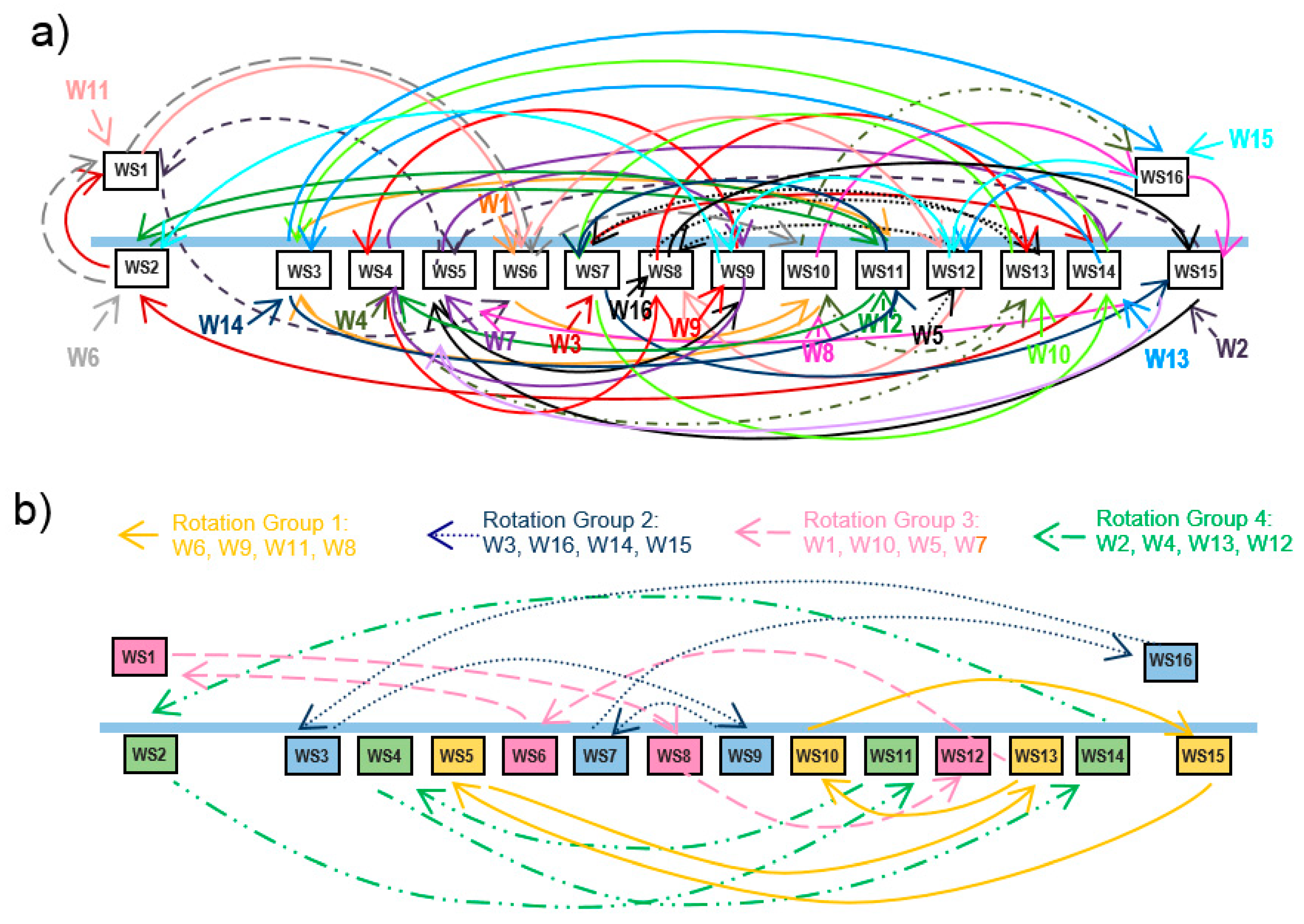
The
Figure 5 shows the workers’ paths during a working day for the best cyclic solution (
Figure 5a) and the best no-cyclic solution (
Figure 5b). The no-cyclic solution shows some organizational problems such as the diversity and complexity of the routes followed by the workers or the chaotic movement of the workers during changeovers. On the other hand, the best cyclic solution simplifies the workers’ paths during the working day. The rotation groups allow knowing the workstations around which the workers would rotate, enabling a better organization and monitorization of the work. The problems derived from the implementation of a solution like that shown in
Figure 5a, entail, in many occasions, an abandonment of the rotation plan. Hence, the organizational benefits obtained with the use of the RGA seem to make up the increase of the value of the fitness function.
The ergonomics criteria considered in this work are mainly intended to reduce the exposure of workers to repetitive movements. However, other criteria can be included in the process to reduce the exposure of the workers to other musculoskeletal disorders risk factors or to prevent musculoskeletal pain or disability. One of the advantages of our proposal is the additive model used in the fitness function of RGA. This additive model gives the possibility of including new factors and criteria to be considered to generate the job rotation schedules. Each new criterion can be included, adding a new term to the fitness function with a weighting coefficient to consider its relative importance with respect to other criteria. In this way, for example, the Nordic Musculoskeletal Questionnaire [
43] could be used to consider the workers musculoskeletal pain, the NIOSH lifting equation [
44] to take into account the effects of handling loads or the Rapid Entire Body Assessment (REBA) [
45] for awkward postures. The results of the application of each of these evaluating tools could be included as items to be considered and added to the evaluating function with their corresponding weighting coefficients.