Agile Six Sigma in Healthcare: Case Study at Santobono Pediatric Hospital
Abstract
1. Introduction
- Van Hoek et al. [8] defined agile as “everything related to customer response and market turbulence that requires specific skills achieved using Lean Thinking”.
- Robarts [9] defined it as “the company ability to grow in a competitive and changeable market, to respond quickly to rapid changes in the markets driven by the improvement of products and services based on customer needs”.
- Furthermore, Lee defined it as “a set of strategies that solves the problem of uncertainty and the variability of demand by increasing the flexibility of the system” [10].
1.1. Patient No-Shows
1.2. Objective of the Study
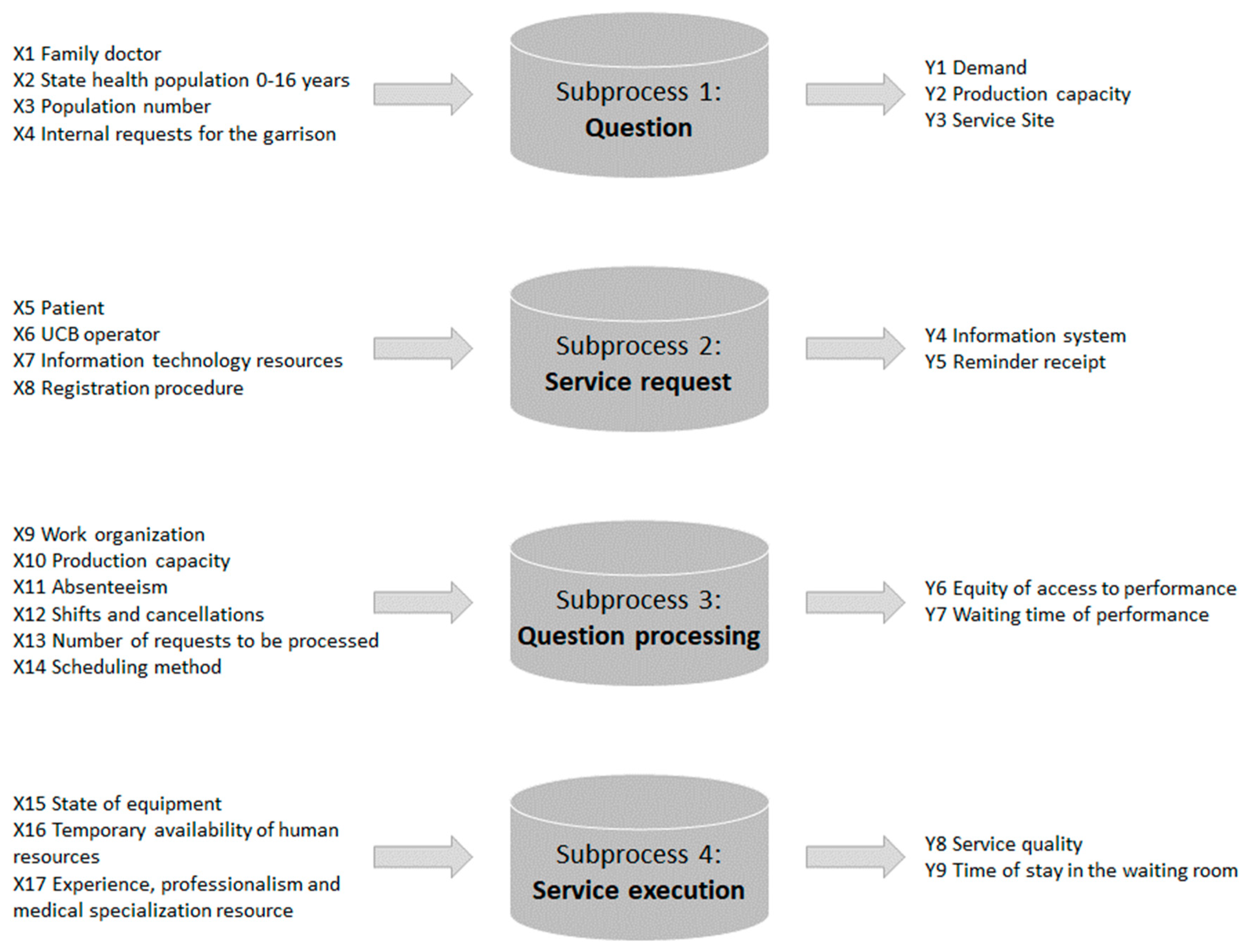
2. Materials and Methods
- Santobono Hospital, divided into four pavilions: “Santobono”, “Torre”, “Volano”, and “Ravaschieri”, located in Naples;
- Pausilipon Hospital: located in Naples.
- Management of absentee patients and changes in and cancellations of services; and
- Waiting lists.
- Description of the visit booked (operative unit, department, type of service);
- Number of visits booked;
- Date and time when the visit is booked;
- How the visit is booked (over the phone/in person/other);
- ID booking;
- ID patient;
- ID visit;
- ID acceptance;
- Date and time when the visit is scheduled;
- Date and time when the patient is admitted;
- Time when the visit is assigned to the patient;
- Time when the patient is assigned for the visit; and
- Type of patient (chronic/first visit/other).
3. Results and Discussion
3.1. Define
- Project title: Agile and Six Sigma to reduce patient absenteeism.
- Question: Excessive absenteeism in the Presidium Hospital.
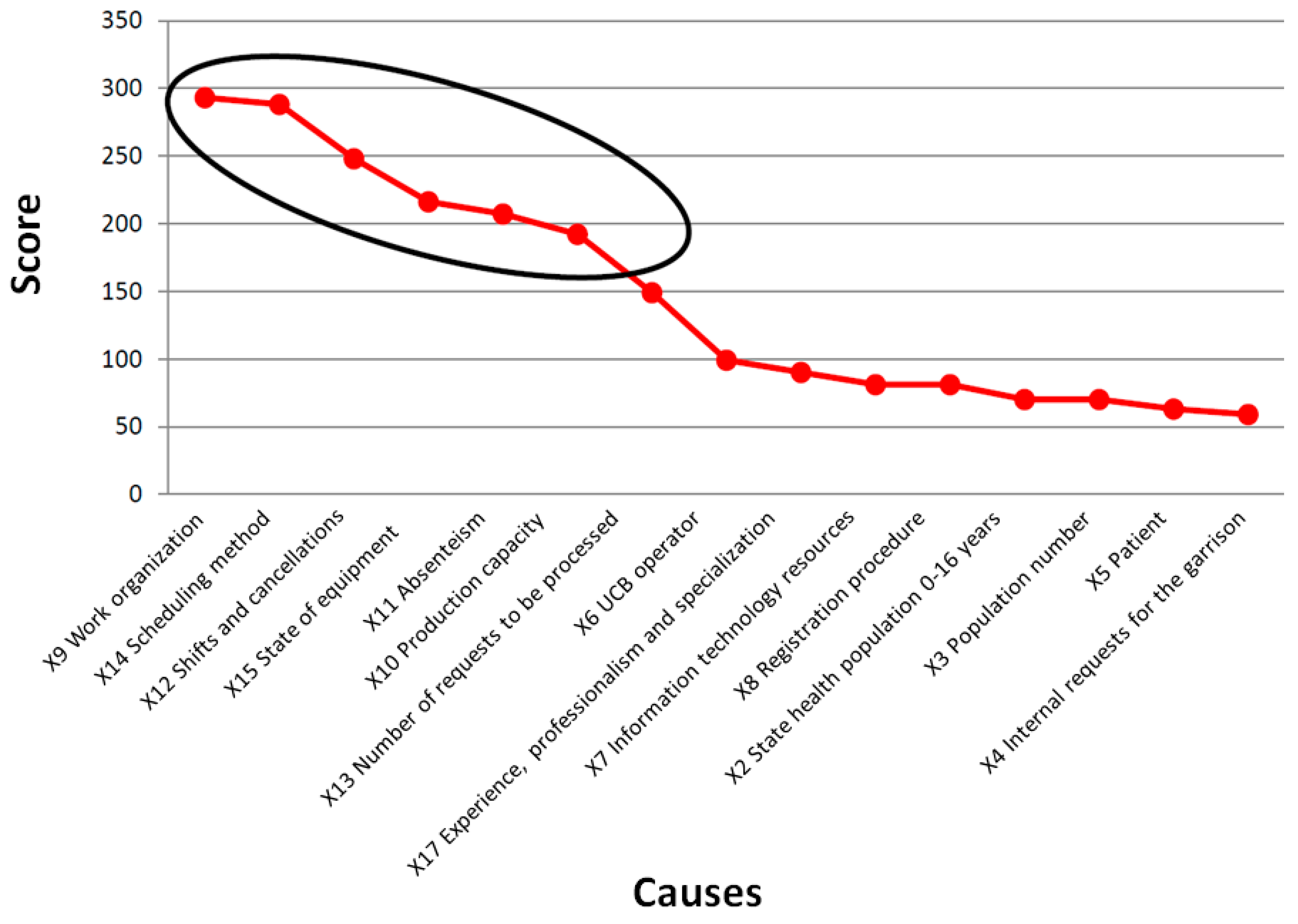
- Critical to quality (CTQ): X9 Work organization, X14 Scheduling method, X12 Shifts and cancellations, X15 State of equipment, X11 Absenteeism, X10 Production capacity.
- Objective: To realize corrective measures to reduce/increase the CTQ elements.
- Team members:
- Timeline:Define: August 2016Measure: September 2016Analyse: October 2016Improve: November 2016Control: November–February 2017
- Within scope: Absenteeism of patients within the hospital context.
- Out of scope: Other management problems regarding medical visits.
3.2. Measure
3.3. Analyse
- Average waiting time: The difference between the agenda date (or date of referral) and the booking date, expressed in days;
- Standard deviation: The dispersion of waiting time with respect to its average value, expressed in days;
- Max: The maximum waiting time recorded for the performance in question, expressed in days;
- Min: The minimum waiting time recorded for the performance in question, expressed in days; and
- Total: The number of services booked.
- Otolaryngology,
- General neurology,
- Emergency surgery,
- General orthopaedics,
- Infant neuropsychiatry,
- Dermatology,
- Medical day hospital,
- Cardiology.
- Otolaryngology: 31% and 20%.
- General neurology: 25% and 30%.
- Emergency surgery: 47% and 3.3%.
- General orthopaedics: 34% and 24%.
- Infant neuropsychiatry: 56% and 85%.
- Dermatology: 53% and 42%.
- Medical day hospital: 49% and 54%.
- Cardiology: 33% and 19%.
3.4. Simulation
- Waiting list of the service;
- Minimum waiting time;
- Maximum waiting time; and
- Waiting steady time: the time needed to work through the entire queue.
- Capacity calendar creation: This is defined as the sequence of days, in Julian format, in which the availability of the service to be simulated is open. Formally, the calendar is an n x 2 matrix, where n are the simulated days and for each day, the date and value of available services are shown—that is, the maximum number of visits expected on that particular day. From the real system, on average, the daily scheduled bookings are equal to 11, i.e., normally 10 plus an additional unit of overbooking.
- Booking calendar creation: This is defined as the sequence of the total bookings made by patients on different days of the week during a time window of amplitude necessary to work through the entire queue. To generate this calendar, first, the total daily bookings, recorded by the real system, were checked in the January–December 2016 time window and on different days of the week. This control was used to evaluate the homogeneity of bookings for the “day” factor and for the “month” factor.
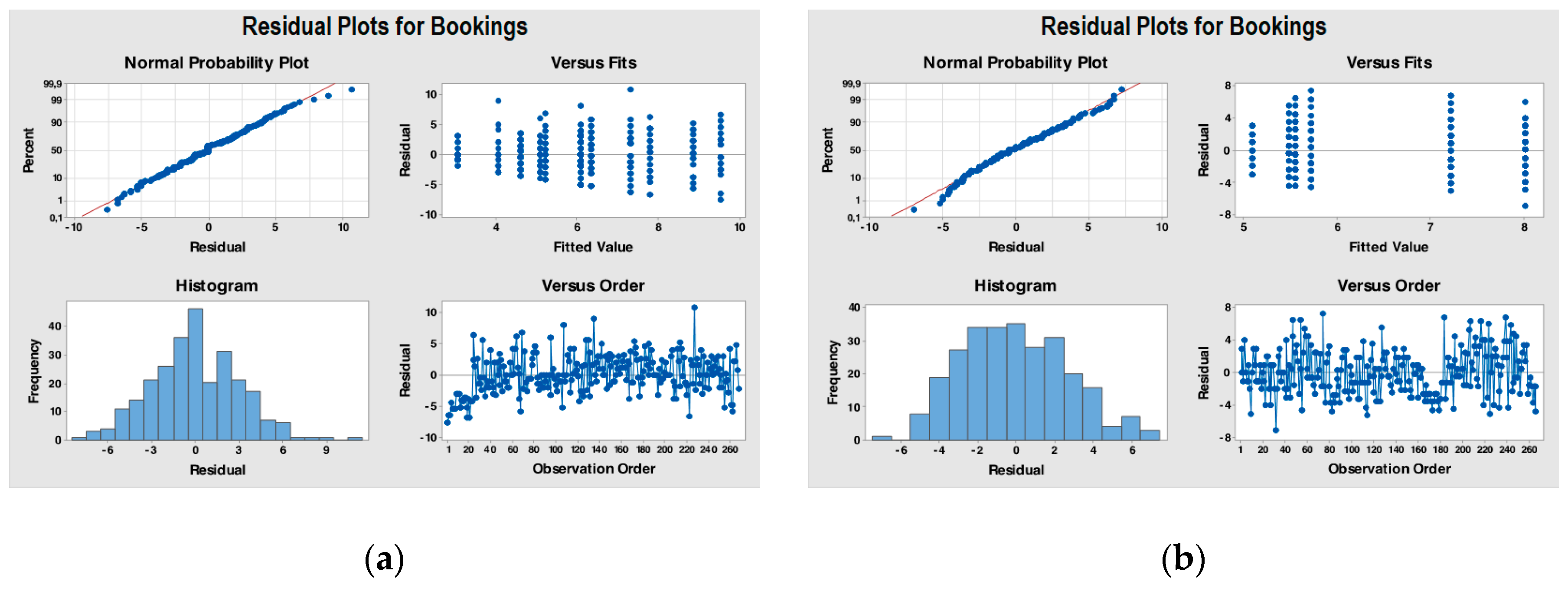
3.5. Model Validation
- K-S test statistic: 0.160.
- K-S critical value (approximately): 0.254.
- Alpha level: 0.05.
3.6. Improve
- #Under: The number of visits below the expected availability;
- #Over: The number of visits exceeding the expected availability;
- Average under: This considers those visits below the expected availability, evaluating the difference between the simulated value and the real value. Average under is the average value among the registered gaps;
- Average over: This considers those visits above the expected availability, evaluating the difference between the simulated value and the real value. Average over is the average value among registered gaps;
- Diff.: The absolute value of the difference between the average under and the average over;
- Equilibrium: The average value among the gaps between the average under and the average over. If one imagines that the overbooking level is a faucet, positive values of the equilibrium indicate an overflow and, therefore, overbooking; in contrast, negative values indicate a clogged or malfunctioning faucet;
- Steady time: The number of days required to work through the entire queue.
3.7. Control
4. Conclusions
Limitation of the Study and Future Developments
Author Contributions
Funding
Conflicts of Interest
References
- Chiocca, D.; Guizzi, G.; Murino, T.; Revetria, R.; Romano, E. A Methodology for Supporting Lean Healthcare. In Modern Advances in Intelligent Systems and Tools; Ding, W., Jiang, H., Ali, M., Li, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 93–99. [Google Scholar]
- Revetria, R.; Catania, A.; Cassettari, L.; Guizzi, G.; Romano, E.; Murino, T.; Improta, G.; Fujita, H. Improving Healthcare Using Cognitive Computing Based Software: An Application in Emergency Situation. In Advanced Research in Applied Artificial Intelligence; Jiang, H., Ding, W., Ali, M., Wu, X., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 477–490. [Google Scholar]
- Nicosia, F. Il Nuovo Ospedale è Snello. Far Funzionare Gli Ospedali con il Lean Healthcare: Consigli Pratici e Sostenibilità; Franco Angeli: Milano, Italy, 2010; ISBN 978-88-568-2919-8. [Google Scholar]
- Goldman, S.L.; Nagel, R.N. Management, technology and agility: The emergence of a new era in manufacturing. Int. J. Technol. Manag. 1993, 8, 18–38. [Google Scholar]
- Improta, G.; Balato, G.; Romano, M.; Carpentieri, F.; Bifulco, P.; Russo, M.A.; Rosa, D.; Triassi, M.; Cesarelli, M. Lean Six Sigma: A new approach to the management of patients undergoing prosthetic hip replacement surgery. J. Eval. Clin. Pract. 2015, 21, 662–672. [Google Scholar] [CrossRef]
- Improta, G.; Balato, G.; Romano, M.; Ponsiglione, A.M.; Raiola, E.; Russo, M.A.; Cuccaro, P.; Santillo, L.C.; Cesarelli, M. Improving performances of the knee replacement surgery process by applying DMAIC principles. J. Eval. Clin. Pract. 2017, 23, 1401–1407. [Google Scholar] [CrossRef]
- Converso, G.; Improta, G.; Mignano, M.; Santillo, L.C. A simulation approach for agile production logic implementation in a hospital emergency unit. In Proceedings of the International Conference on Intelligent Software Methodologies, Tools, and Techniques, Naples, Italy, 15–17 September 2015; Springer: Berlin/Heidelberg, Germany, 2015; pp. 623–634. [Google Scholar]
- Hoek, R.I.; van Harrison, A.; Christopher, M. Measuring agile capabilities in the supply chain. Int. J. Oper. Prod. Manag. 2001, 21, 126–148. [Google Scholar] [CrossRef]
- Robarts, J.M. Practical Considerations for Distributed Agile Projects. In Proceedings of the Agile 2008, Toronto, ON, Canada, 4–8 August 2008; IEEE Computer Society: Washington, DC, USA, 2008; pp. 327–332. [Google Scholar]
- Lee, H.L. The triple-A supply chain. Harv. Bus. Rev. 2004, 82, 102–113. [Google Scholar]
- Carvalho, H.; Duarte, S.; Cruz Machado, V. Lean, agile, resilient and green: Divergences and synergies. Int. J. Lean Six Sigma 2011, 2, 151–179. [Google Scholar] [CrossRef]
- Christopher, M. Creating supply chain resilience through agile six sigma. Crit. Eye 2004, 7, 24–28. [Google Scholar]
- Southard, P.B.; Chandra, C.; Kumar, S. RFID in healthcare: A Six Sigma DMAIC and simulation case study. Int. J. Health Care Qual. Assur. 2012, 25, 291–321. [Google Scholar] [CrossRef]
- Montella, E.; Cicco, M.V.D.; Ferraro, A.; Centobelli, P.; Raiola, E.; Triassi, M.; Improta, G. The application of Lean Six Sigma methodology to reduce the risk of healthcare–associated infections in surgery departments. J. Eval. Clin. Pract. 2017, 23, 530–539. [Google Scholar] [CrossRef]
- Improta, G.; Balato, G.; Ricciardi, C.; Russo, M.A.; Santalucia, I.; Triassi, M.; Cesarelli, M. Lean Six Sigma in healthcare: Fast track surgery for patients undergoing prosthetic hip replacement surgery. TQM J. 2019, 31, 526–540. [Google Scholar] [CrossRef]
- Improta, G.; Cesarelli, M.; Montuori, P.; Santillo, L.C.; Triassi, M. Reducing the risk of healthcare-associated infections through Lean Six Sigma: The case of the medicine areas at the Federico II University Hospital in Naples (Italy). J. Eval. Clin. Pract. 2018, 24, 338–346. [Google Scholar] [CrossRef]
- Improta, G.; Russo, M.A.; Triassi, M.; Converso, G.; Murino, T.; Santillo, L.C. Use of the AHP methodology in system dynamics: Modelling and simulation for health technology assessments to determine the correct prosthesis choice for hernia diseases. Math. Biosci. 2018, 299, 19–27. [Google Scholar] [CrossRef]
- Vijay, S.A. Reducing and Optimizing the Cycle Time of Patients Discharge Process in a Hospital Using Six Sigma Dmaic Approach. Int. J. Qual. Res. 2014, 8, 169–182. [Google Scholar]
- Tayntor, C.B. Six SIGMA Software Development; Auerbach Publications: New York, NY, USA, 2002; ISBN 978-0-8493-1193-2. [Google Scholar]
- Hamid, A.M.E. Application of Six Sigma Methodology in Software Development. In Proceedings of the 2018 International Conference on Computer, Control, Electrical, and Electronics Engineering (ICCCEEE), Khartoum, Sudan, 12–14 August 2018; pp. 1–5. [Google Scholar]
- Asghar, B.; Awan, I.; Bhatti, A.M. Process Improvement through Reduction in Software Defects using Six Sigma Methods. In Proceedings of the 2018 Portland International Conference on Management of Engineering and Technology (PICMET), Honolulu, HI, USA, 19–23 August 2018; pp. 1–11. [Google Scholar]
- Safaie, M. Capability maturity model integration with approach of agile Six Sigma. Int. J. Agile Syst. Manag. 2017, 10, 1–33. [Google Scholar] [CrossRef]
- Alipour, P.; Laux, C.; Hoffa, D.; Bentley, L. Agile Six Sigma–A Descriptive Approach. In Proceedings of the 7th International Conference on Lean Six Sigma, Dubai, United Arab Emirates, 7–8 May 2018; Heriot Watt University: Dubai, United Arab Emirates, 2018. [Google Scholar]
- Fehlmann, T.; Santillo, L. From story points to cosmic function points in agile software development–a six sigma perspective. In Proceedings of the Metrikon-Software Metrik Kongress, Stuttgart, Germany, 10–12 November 2010; p. 28. [Google Scholar]
- Morris, P.D. The Perfect Process Storm: Integration of CMMI, Agile, and Lean Six Sigma; Ogden Air Logistics Center Hill afb ut Software Maintenance Squadron: Virginia, VA, USA, 2012; p. 517. [Google Scholar]
- Deyo, R.A.; Inui, T.S. Dropouts and broken appointments. A literature review and agenda for future research. Med. Care 1980, 18, 1146–1157. [Google Scholar] [CrossRef]
- Rust, R.T.; Oliver, R.L. Should we delight the customer? J. Acad. Mark. Sci. 2000, 28, 86. [Google Scholar] [CrossRef]
- Guzek, L.M.; Gentry, S.D.; Golomb, M.R. The estimated cost of “no-shows” in an academic pediatric neurology clinic. Pediatr. Neurol. 2015, 52, 198–201. [Google Scholar] [CrossRef]
- Wendler, T.; Loef, C. Workflow management—Integration technology for efficient radiology. Medicamundi 2001, 45, 41–49. [Google Scholar]
- Parente, C.A.; Salvatore, D.; Gallo, G.M.; Cipollini, F. Using overbooking to manage no-shows in an Italian healthcare center. BMC Health Serv. Res. 2018, 18, 185. [Google Scholar] [CrossRef]
- LaGanga, L.R.; Lawrence, S.R. Clinic Overbooking to Improve Patient Access and Increase Provider Productivity*. Decis. Sci. 2007, 38, 251–276. [Google Scholar] [CrossRef]
- Gurol-Urganci, I.; de Jongh, T.; Vodopivec-Jamsek, V.; Atun, R.; Car, J. Mobile phone messaging reminders for attendance at healthcare appointments. Cochrane Database Syst. Rev. 2013, 12, CD007458. [Google Scholar] [CrossRef]
- Lee, S.; Min, D.; Ryu, J.; Yih, Y. A simulation study of appointment scheduling in outpatient clinics: Open access and overbooking. Simulation 2013, 89, 1459–1473. [Google Scholar] [CrossRef]
- LaGanga, L.R. Lean service operations: Reflections and new directions for capacity expansion in outpatient clinics. J. Oper. Manag. 2011, 29, 422–433. [Google Scholar] [CrossRef]
- Antony, J. Six Sigma vs Lean. Int. J. Product. Perform. Manag. 2011, 60, 185–190. [Google Scholar] [CrossRef]
- Black, J.R.; Miller, D.; Sensel, J. The Toyota Way to Healthcare Excellence: Increase Efficiency and Improve Quality with Lean; HAP/Health Administration Press: Ann Arbor, MI, USA, 2016; ISBN 978-1-56793-782-4. [Google Scholar]
- Zeng, B.; Turkcan, A.; Lin, J.; Lawley, M. Clinic scheduling models with overbooking for patients with heterogeneous no-show probabilities. Ann. Oper. Res. 2010, 178, 121–144. [Google Scholar] [CrossRef]
- Kaandorp, G.C.; Koole, G. Optimal outpatient appointment scheduling. Health Care Manag. Sci. 2007, 10, 217–229. [Google Scholar] [CrossRef]
- Liu, N.; Ziya, S. Panel Size and Overbooking Decisions for Appointment-Based Services under Patient No-Shows. Prod. Oper. Manag. 2014, 23, 2209–2223. [Google Scholar] [CrossRef]
- Zacharias, C.; Pinedo, M. Appointment Scheduling with No-Shows and Overbooking. Prod. Oper. Manag. 2014, 23, 788–801. [Google Scholar] [CrossRef]
- Samorani, M.; LaGanga, L. Outpatient Appointment Scheduling Given Individual Day-Dependent No-Show Predictions; Social Science Research Network: Rochester, NY, USA, 2013. [Google Scholar]
- Banks, J.; Carson, J., II; Nelson, B.L.; Nicol, D.M. Discrete—Event System Simulation; Pearson: Harlow, UK, 2005; ISBN 978-7-111-17194-2. [Google Scholar]
- Baril, C.; Gascon, V.; Miller, J.; Côté, N. Use of a discrete-event simulation in a Kaizen event: A case study in healthcare. Eur. J. Oper. Res. 2016, 249, 327–339. [Google Scholar] [CrossRef]
- Glover, M.J.; Jones, E.; Masconi, K.L.; Sweeting, M.J.; Thompson, S.G. Discrete Event Simulation for Decision Modeling in Health Care: Lessons from Abdominal Aortic Aneurysm Screening. Med. Decis. Mak. 2018, 38, 439–451. [Google Scholar] [CrossRef]
- Zhang, X. Application of discrete event simulation in health care: A systematic review. BMC Health Serv. Res. 2018, 18, 687. [Google Scholar] [CrossRef]
- Womack, J.P.; Jones, D.T. Lean Thinking. Come Creare Valore e Bandire Gli Sprechi; goWare & Guerini Next: Florence, Italy, 2017; ISBN 978-88-6896-188-6. [Google Scholar]
- Ofei-Dodoo, S.; Kellerman, R.; Hartpence, C.; Mills, K.; Manlove, E. Why Patients Miss Scheduled Outpatient Appointments at Urban Academic Residency Clinics: A Qualitative Evaluation. Kans. J. Med. 2019, 12, 57–61. [Google Scholar]
- Clouse, K.M.; Williams, K.A.; Harmon, J.M. Improving the No-Show Rate of New Patients in Outpatient Psychiatric Practice: An Advance Practice Nurse-Initiated Telephone Engagement Protocol Quality Improvement Project. Perspect. Psychiatr. Care 2017, 53, 127–134. [Google Scholar] [CrossRef]
- Percac-Lima, S.; Singer, D.E.; Cronin, P.R.; Chang, Y.; Zai, A.H. Can Text Messages Improve Attendance to Primary Care Appointments in Underserved Populations? J. Health Care Poor Underserved 2016, 27, 1709–1725. [Google Scholar] [CrossRef]
- Huang, Y.; Hanauer, D.A. Patient no-show predictive model development using multiple data sources for an effective overbooking approach. Appl. Clin. Inform. 2014, 5, 836–860. [Google Scholar]
- Cohen-Yatziv, L.; Cohen, M.J.; Halevy, J.; Kaliner, E. No-shows in ambulatory clinics and non-utilized appointments for elective operations in selected surgical departments at a tertiary hospital in Israel. Isr. J. Health Policy Res. 2019, 8, 64. [Google Scholar] [CrossRef]

| Medium Wait (Days) | Max Wait (Days) | Min Wait (Days) | Chaos (%) | Inefficiency (%) |
|---|---|---|---|---|
| 208 | 421 | 0 | 56 | 85 |
| Bookings Per Month | |||||
| DF | Adj SS | Adj MS | F-Value | p-Value | |
| Month | 11 | 837.2 | 76.106 | 7.86 | 0.000 |
| Error | 256 | 2477.4 | 9.677 | ||
| Total | 267 | 3314.6 | |||
| Bookings Per Day | |||||
| DF | Adj SS | Adj MS | F-Value | p-Value | |
| Day | 6 | 62.64 | 12.527 | 2.00 | 0.079 |
| Error | 261 | 1632.02 | 6.253 | ||
| Total | 267 | 1694.66 | |||
| S | R2 | R2 (adj) | R2 (pred) | |
|---|---|---|---|---|
| Bookings per month | 3.11084 | 25.26% | 22.05% | 18.23% |
| Bookings per day | 2.50059 | 3.70% | 16.5% | 14.6% |
| Scenario | Overbooking Levels | #Under | #Over | Average Under | Average Over | Diff. | Equilibrium | Steady Time |
|---|---|---|---|---|---|---|---|---|
| 1 | 18 | 118 | 35 | −3.52 | 2.63 | 0.89 | −2.12 | 615 |
| 2 | 19 | 107 | 39 | −3.34 | 2.71 | 0.63 | −1.73 | 581 |
| 3 | 20 | 62 | 34 | −3.27 | 3.02 | 0.25 | −1.13 | 551 |
| 4 | 21 | 74 | 47 | −3.16 | 3.06 | 0.10 | −0.74 | 523 |
| 5 | 22 | 60 | 48 | −3.15 | 3.48 | 0.33 | −0.20 | 495 |
| 6 | 23 | 52 | 51 | −2.94 | 3.67 | 0.73 | 0.33 | 474 |
| 7 | 24 | 44 | 53 | −2.77 | 3.74 | 0.97 | 0.78 | 454 |
| 8 | 25 | 32 | 52 | −2.88 | 4.10 | 1.22 | 1.44 | 432 |
| Scenario 4 | Scenario 5 | Scenario 6 | Scenario 7 | |
|---|---|---|---|---|
| Tot. occurrences | 43 | 48 | 51 | 54 |
| Tot. useful days | 133 | 123 | 112 | 104 |
| % occur./useful days | 32% | 39% | 46% | 52% |
| Scenario 4 | Scenario 5 | Scenario 6 | Scenario 7 | |
|---|---|---|---|---|
| Covered visits | 27 | 19 | 20 | 19 |
| Tot. occurrences | 18 | 29 | 31 | 35 |
| Tot. useful days | 139 | 123 | 112 | 104 |
| % occur./useful days | 13% | 24% | 28% | 34% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Improta, G.; Guizzi, G.; Ricciardi, C.; Giordano, V.; Ponsiglione, A.M.; Converso, G.; Triassi, M. Agile Six Sigma in Healthcare: Case Study at Santobono Pediatric Hospital. Int. J. Environ. Res. Public Health 2020, 17, 1052. https://doi.org/10.3390/ijerph17031052
Improta G, Guizzi G, Ricciardi C, Giordano V, Ponsiglione AM, Converso G, Triassi M. Agile Six Sigma in Healthcare: Case Study at Santobono Pediatric Hospital. International Journal of Environmental Research and Public Health. 2020; 17(3):1052. https://doi.org/10.3390/ijerph17031052
Chicago/Turabian StyleImprota, Giovanni, Guido Guizzi, Carlo Ricciardi, Vincenzo Giordano, Alfonso Maria Ponsiglione, Giuseppe Converso, and Maria Triassi. 2020. "Agile Six Sigma in Healthcare: Case Study at Santobono Pediatric Hospital" International Journal of Environmental Research and Public Health 17, no. 3: 1052. https://doi.org/10.3390/ijerph17031052
APA StyleImprota, G., Guizzi, G., Ricciardi, C., Giordano, V., Ponsiglione, A. M., Converso, G., & Triassi, M. (2020). Agile Six Sigma in Healthcare: Case Study at Santobono Pediatric Hospital. International Journal of Environmental Research and Public Health, 17(3), 1052. https://doi.org/10.3390/ijerph17031052









