Neuromuscular Strategies in Stretch–Shortening Exercises with Increasing Drop Heights: The Role of Muscle Coactivation in Leg Stiffness and Power Propulsion
Abstract
1. Introduction
2. Materials and Methods
2.1. Participants
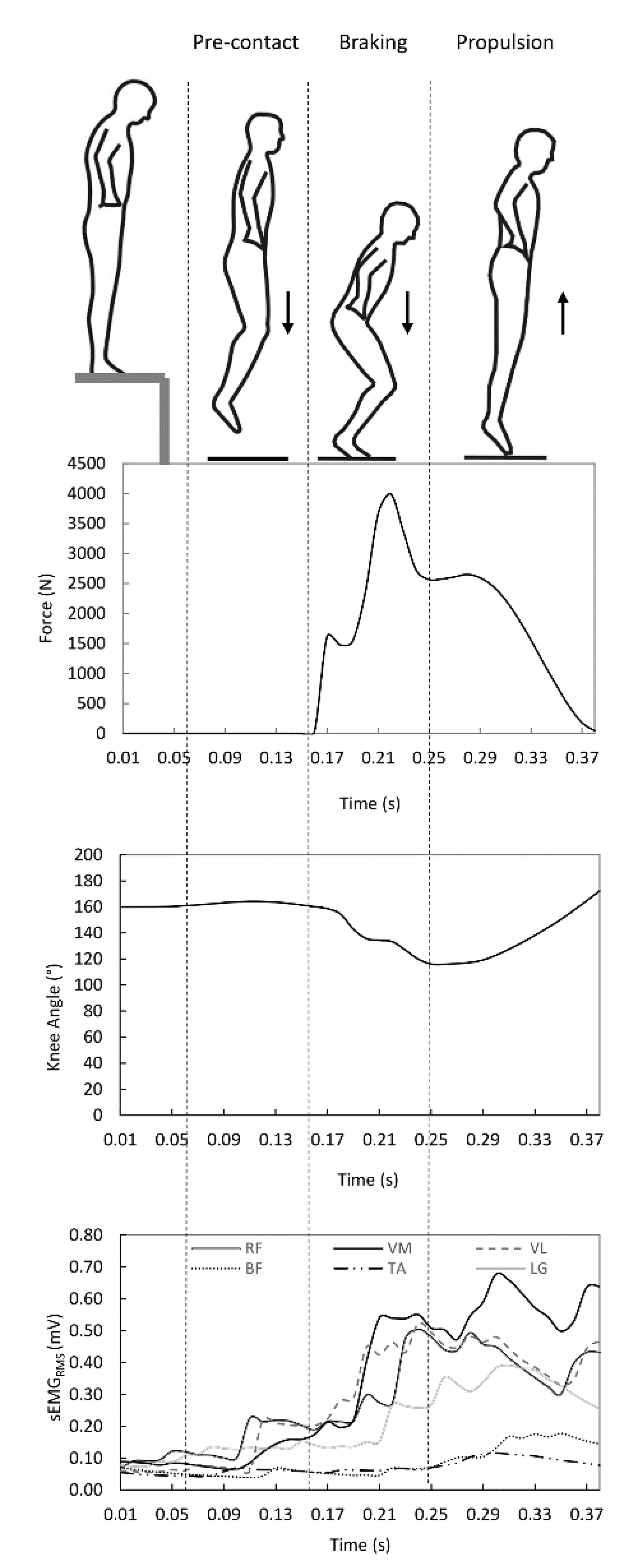
2.2. Study Design and Measurements
2.2.1. Ground Reaction Force
2.2.2. EMG Activity
2.3. Data Analysis
2.3.1. Coactivation Index
2.3.2. Power and Velocity
2.4. Statistical Analysis
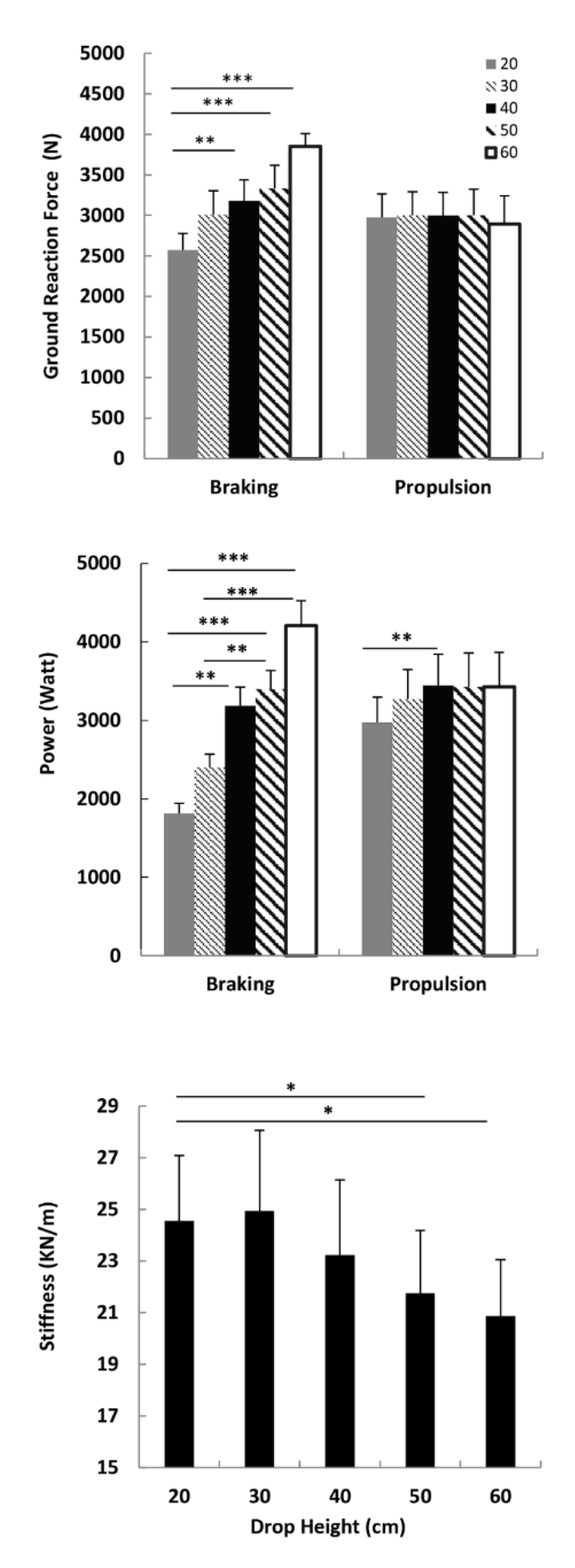
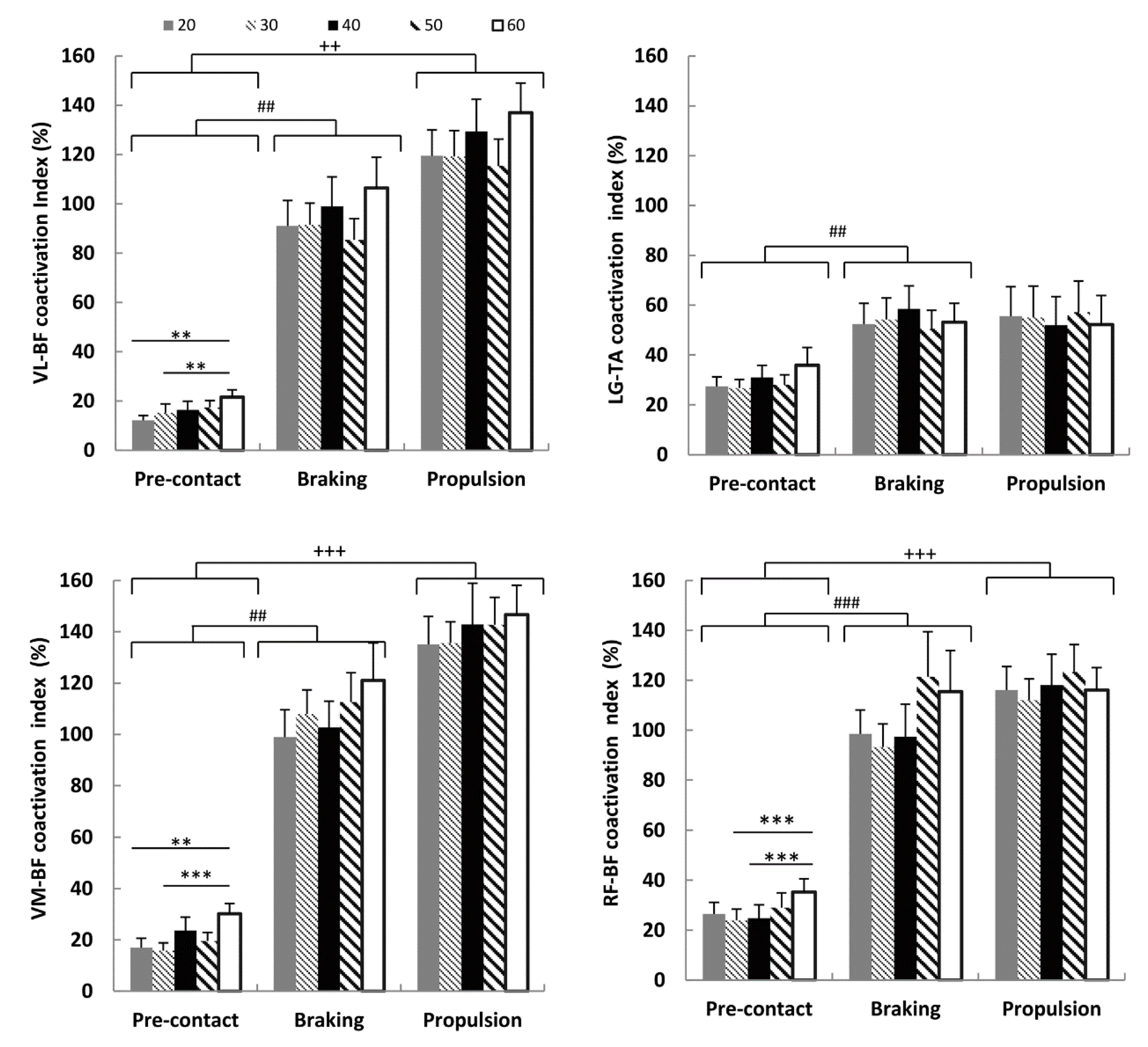
3. Results
3.1. Measurements Reliability
3.2. Ground Reaction Force, Power and Leg Stiffness
3.3. Coactivation Index and Drop Height
3.4. Coactivation Index, Power and Leg Stiffness
4. Discussion
Limitation
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Santello, M. Review of motor control mechanisms underlying impact absorption from falls. Gait Posture 2005, 21, 85–94. [Google Scholar] [CrossRef] [PubMed]
- Komi, P.V. Stretch-shortening cycle: A powerful model to study normal and fatigued muscle. J. Biomech. 2000, 33, 1197–1206. [Google Scholar] [CrossRef]
- Ishikawa, M.; Komi, P.V. Effects of different dropping intensities on fascicle and tendinous tissue behavior during stretch-shortening cycle exercise. J. Appl. Physiol. 2004, 96, 848–852. [Google Scholar] [CrossRef] [PubMed]
- Ishikawa, M.; Niemelä, E.; Komi, P.V. Interaction between fascicle and tendinous tissues in short-contact stretch-shortening cycle exercise with varying eccentric intensities. J. Appl. Physiol. 2005, 99, 217–223. [Google Scholar] [CrossRef] [PubMed]
- Taube, W.; Leukel, C.; Gollhofer, A. How Neurons Make Us Jump: The Neural Control of Stretch-Shortening Cycle Movements. Exerc. Sport Sci. Rev. 2012, 40, 106–115. [Google Scholar] [CrossRef] [PubMed]
- Leukel, C.; Gollhofer, A.; Keller, M.; Taube, W. Phase- and task-specific modulation of soleus H-reflexes during drop-jumps and landings. Exp. Brain Res. 2008, 190, 71–79. [Google Scholar] [CrossRef]
- Komi, P.V.; Bosco, C. Utilization of stored elastic energy in leg extensor muscles by men and women. Med. Sci. Sports Exerc. 1978, 10, 10. [Google Scholar]
- Bosco, C.; Vitasalo, J.T.; Komi, P.V.; Luhtanen, P. Combined effect of elastic energy and myoelectrical potentiation during stretch-shortening cycle exercise. Acta Physiol. Scand. 1982, 114, 557–565. [Google Scholar] [CrossRef]
- Viitasalo, J.T.; Bosco, C. Electromechanical behaviour of human muscles in vertical jumps. Eur. J. Appl. Physiol. 1982, 48, 253–261. [Google Scholar] [CrossRef]
- Gollhofer, A.; Strojnik, V.; Rapp, W.; Schweizer, L. Behaviour of triceps surae muscle-tendon complex in different jump conditions. Eur. J. Appl. Physiol. 1992, 64, 283–291. [Google Scholar] [CrossRef]
- Viitasalo, J.T.; Salo, A.; Lahtinen, J. Neuromuscular functioning of athletes and non-athletes in the drop jump. Eur. J. Appl. Physiol. 1998, 78, 432–440. [Google Scholar] [CrossRef] [PubMed]
- Avela, J.; Komi, P.V.; Santos, P.M. Effects of differently induced stretch loads on neuromuscular control in drop jump exercise. Eur. J. Appl. Physiol. 1996, 72, 553–562. [Google Scholar] [CrossRef] [PubMed]
- Leukel, C.; Taube, W.; Gruber, M.; Hodapp, M.; Gollhofer, A. Influence of falling height on the excitability of the soleus H-reflex during drop-jumps. Acta Physiol. 2008, 192, 569–576. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.-I.; Peng, H.-T. Biomechanical Comparisons of Single- and Double-Legged Drop Jumps with Changes in Drop Height. Int. J. Sports Med. 2013, 35, 522–527. [Google Scholar] [CrossRef] [PubMed]
- Di Giminiani, R.; Petricola, S. The Power Output-Drop Height Relationship to Determine the Optimal Dropping Intensity and to Monitor the Training Intervention. J. Strength Cond. Res. 2016, 30, 117–125. [Google Scholar] [CrossRef]
- Santello, M.; McDonagh, M.J.N.; Challis, J.H. Visual and non-visual control of landing movements in humans. J. Physiol. 2001, 537, 313–327. [Google Scholar] [CrossRef]
- Santello, M.; McDonagh, M. The control of timing and amplitude of EMG activity in landing movements in humans. Exp. Physiol. 1998, 83, 857–874. [Google Scholar] [CrossRef]
- Arampatzis, A.; Bruggermann, G.-P.; Morey Klapsing, G. Leg stiffness and mechanical energetic processes during jumping on a sprung surface. Med. Sci. Sports Exerc. 2001, 33, 923–931. [Google Scholar] [CrossRef]
- Taube, W.; Leukel, C.; Schubert, M.; Gruber, M.; Rantalainen, T.; Gollhofer, A. Differential Modulation of Spinal and Corticospinal Excitability During Drop Jumps. J. Neurophysiol. 2008, 99, 1243–1252. [Google Scholar] [CrossRef]
- Horita, T.; Komi, P.; Nicol, C.; Kyröläinen, H. Interaction between pre-landing activities and stiffness regulation of the knee joint musculoskeletal system in the drop jump: Implications to performance. Eur. J. Appl. Physiol. 2002, 88, 76–84. [Google Scholar] [CrossRef]
- Hobara, H.; Muraoka, T.; Omuro, K.; Gomi, K.; Sakamoto, M.; Inoue, K.; Kanosue, K. Knee stiffness is a major determinant of leg stiffness during maximal hopping. J. Biomech. 2009, 42, 1768–1771. [Google Scholar] [CrossRef] [PubMed]
- Kubo, K.; Tsunoda, N.; Kanehisa, H.; Fukunaga, T. Activation of agonist and antagonist muscles at different joint angles during maximal isometric efforts. Eur. J. Appl. Physiol. 2004, 91, 349–352. [Google Scholar] [CrossRef] [PubMed]
- Baratta, R.; Solomonow, M.; Zhou, B.H.; Letson, D.; Chuinard, R.; D’Ambrosia, R. Muscular coactivation: The role of the antagonist musculature in maintaining knee stability. Am. J. Sports Med. 1988, 16, 113–122. [Google Scholar] [CrossRef] [PubMed]
- DeMers, M.S.; Hicks, J.L.; Delp, S.L. Preparatory co-activation of the ankle muscles may prevent ankle inversion injuries. J. Biomech. 2017, 52, 17–23. [Google Scholar] [CrossRef]
- Arai, A.; Ishikawa, M.; Ito, A. Agonist–antagonist muscle activation during drop jumps. Eur. J. Sport Sci. 2013, 13, 490–498. [Google Scholar] [CrossRef] [PubMed]
- Bobbert, M.F.; Mackay, M.; Schinkelshoek, D.; Huijing, P.A.; van Ingen Schenau, G.J. Biomechanical analysis of drop and countermovement jumps. Eur. J. Appl. Physiol. 1986, 54, 566–573. [Google Scholar] [CrossRef]
- Prieske, O.; Muehlbauer, T.; Mueller, S.; Krueger, T.; Kibele, A.; Behm, D.G.; Granacher, U. Effects of surface instability on neuromuscular performance during drop jumps and landings. Eur. J. Appl. Physiol. 2013, 113, 2943–2951. [Google Scholar] [CrossRef]
- Ritzmann, R.; Freyler, K.; Krause, A.; Gollhofer, A. Bouncing on Mars and the Moon—The role of gravity on neuromuscular control: Correlation of muscle activity and rate of force development. J. Appl. Physiol. 2016, 121, 1187–1195. [Google Scholar] [CrossRef]
- Helm, M.; Ritzmann, R.; Gollhofer, A.; Freyler, K. Anticipation modulates neuromechanics of drop jumps in known or unknown ground stiffness. PLoS ONE 2019, 14, e0211276. [Google Scholar] [CrossRef]
- Helm, M.; Freyler, K.; Waldvogel, J.; Gollhofer, A.; Ritzmann, R. The relationship between leg stiffness, forces and neural control of the leg musculature during the stretch-shortening cycle is dependent on the anticipation of drop height. Eur. J. Appl. Physiol. 2019, 119, 1981–1999. [Google Scholar] [CrossRef]
- Helm, M.; Freyler, K.; Waldvogel, J.; Lauber, B.; Gollhofer, A.; Ritzmann, R. Anticipation of drop height affects neuromuscular control and muscle-tendon mechanics. Scand. J. Med. Sci. Sports 2020, 30, 46–63. [Google Scholar] [CrossRef] [PubMed]
- Meier, C.; Frank, C.; Gröben, B.; Schack, T. Verbal Instructions and Motor Learning: How Analogy and Explicit Instructions Influence the Development of Mental Representations and Tennis Serve Performance. Front. Psychol. 2020, 11, 2. [Google Scholar] [CrossRef] [PubMed]
- Kovacs, I.; Tihanyi, J.; DeVita, P.; Racz, L.; Barrier, J.; Hortobagyi, T. Foot placement modifies kinematics and kinetics during drop jumping. Med. Sci. Sports Exerc. 1999, 31, 708–716. [Google Scholar] [CrossRef] [PubMed]
- Yokoyama, H.; Oda, A.; Makino, M.; Ishikawa, T.; Shikanai, K.; Tsukamoto, T.; Tsuda, E. Effects of different oral instructions on kinematic and kinetic parameters during drop vertical jump. J. Phys. Ther. Sci. 2019, 31, 670–674. [Google Scholar] [CrossRef][Green Version]
- Di Giminiani, R.; Masedu, F.; Padulo, J.; Tihanyi, J.; Valenti, M. The EMG activity–acceleration relationship to quantify the optimal vibration load when applying synchronous whole-body vibration. J. Electromyogr. Kinesiol. 2015, 25, 853–859. [Google Scholar] [CrossRef]
- Herrington, L.; Waterman, R.; Smith, L. Electromyographic analysis of shoulder muscles during press-up variations and progressions. J. Electromyogr. Kinesiol. 2015, 25, 100–106. [Google Scholar] [CrossRef]
- Hermens, H.J.; Freriks, B.; Disselhorst-Klug, C.; Rau, G. Development of recommendations for SEMG sensors and sensor placement procedures. J. Electromyogr. Kinesiol. 2000, 10, 361–374. [Google Scholar] [CrossRef]
- Burden, A. How should we normalize electromyograms obtained from healthy participants? What we have learned from over 25years of research. J. Electromyogr. Kinesiol. 2010, 20, 1023–1035. [Google Scholar] [CrossRef]
- Lyle, M.A.; Valero-Cuevas, F.J.; Gregor, R.J.; Powers, C.M. Control of dynamic foot-ground interactions in male and female soccer athletes: Females exhibit reduced dexterity and higher limb stiffness during landing. J. Biomech. 2014, 47, 512–517. [Google Scholar] [CrossRef]
- Cavagna, G.A. Force platforms as ergometers. J. Appl. Physiol. 1975, 39, 174–179. [Google Scholar] [CrossRef]
- Schmitt, L.C.; Rudolph, K.S. Muscle stabilization strategies in people with medial knee osteoarthritis: The effect of instability. J. Orthop. Res. 2008, 26, 1180–1185. [Google Scholar] [CrossRef] [PubMed]
- Di Giminiani, R.; Tihanyi, J.; Masedu, F. Gender differences on neuromuscular strategy during drop jump: A comment on Helm et al. (2019). Eur. J. Appl. Physiol. 2020, 120, 2555–2556. [Google Scholar] [CrossRef] [PubMed]
- Helm, M.; Freyler, K.; Waldvogel, J.; Gollhofer, A.; Ritzmann, R. Response to: Gender differences on neuromuscular strategy during drop jump: A comment on Helm et al. (2019) by Di Giminiani et al. Eur. J. Appl. Physiol. 2020, 120, 2557–2558. [Google Scholar] [CrossRef] [PubMed]
- Zajac, F.E. Muscle coordination of movement: A perspective. J. Biomech. 1993, 26, 109–124. [Google Scholar] [CrossRef]
- Kellis, E.; Arabatzi, F.; Papadopoulos, C. Muscle co-activation around the knee in drop jumping using the co-contraction index. J. Electromyogr. Kinesiol. 2003, 13, 229–238. [Google Scholar] [CrossRef]
- Fiorentino, N.M.; Lin, J.S.; Ridder, K.B.; Guttman, M.A.; McVeigh, E.R.; Blemker, S.S. Rectus Femoris Knee Muscle Moment Arms Measured in Vivo During Dynamic Motion With Real-Time Magnetic Resonance Imaging. J. Biomech. Eng. 2013, 135, 044501–0445015. [Google Scholar] [CrossRef] [PubMed]
- Gambelli, C.N.; Theisen, D.; Willems, P.A.; Schepens, B. Human motor control of landing from a drop in simulated microgravity. J. Appl. Physiol. 2016, 121, 760–770. [Google Scholar] [CrossRef]
- Gambelli, C.N.; Theisen, D.; Willems, P.A.; Schepens, B. Motor Control of Landing from a Jump in Simulated Hypergravity. PLoS ONE 2015, 10, e0141574. [Google Scholar] [CrossRef]
- Gambelli, C.N.; Theisen, D.; Willems, P.A.; Schepens, B. Motor control of landing from a countermovement jump in simulated microgravity. J. Appl. Physiol. 2016, 120, 1230–1240. [Google Scholar] [CrossRef]
- Dyhre-Poulsen, P.; Simonsen, E.B.; Voigt, M. Dynamic control of muscle stiffness and H reflex modulation during hopping and jumping in man. J. Physiol. 1991, 437, 287–304. [Google Scholar] [CrossRef]
- Lesinski, M.; Prieske, O.; Beurskens, R.; Behm, D.G.; Granacher, U. Effects of drop height and surface instability on neuromuscular activation during drop jumps. Scand. J. Med. Sci. Sports 2017, 27, 1090–1098. [Google Scholar] [CrossRef] [PubMed]
- Lesinski, M.; Prieske, O.; Beurskens, R.; Behm, D.; Granacher, U. Effects of Drop-height and Surface Instability on Jump Performance and Knee Kinematics. Int. J. Sports Med. 2017, 39, 50–57. [Google Scholar] [CrossRef] [PubMed]
- Jamaludin, N.I.; Sahabuddin, F.N.A.; Raja Ahmad Najib, R.K.M.; Shamshul Bahari, M.L.H.; Shaharudin, S. Bottom-Up Kinetic Chain in Drop Landing among University Athletes with Normal Dynamic Knee Valgus. Int. J. Environ. Res. Public Health 2020, 17, 4418. [Google Scholar] [CrossRef] [PubMed]
- Mackala, K.; Rauter, S.; Simenko, J.; Kreft, R.; Stodolka, J.; Krizaj, J.; Coh, M.; Vodicar, J. The Effect of Height on Drop Jumps in Relation to Somatic Parameters and Landing Kinetics. Int. J. Environ. Res. Public. Health 2020, 17, 5886. [Google Scholar] [CrossRef]
- Stearns-Reider, K.M.; Powers, C.M. Rate of Torque Development and Feedforward Control of the Hip and Knee Extensors: Gender Differences. J. Mot. Behav. 2018, 50, 321–329. [Google Scholar] [CrossRef]
- Myer, G.D.; Ford, K.R.; McLean, S.G.; Hewett, T.E. The Effects of Plyometric versus Dynamic Stabilization and Balance Training on Lower Extremity Biomechanics. Am. J. Sports Med. 2006, 34, 445–455. [Google Scholar] [CrossRef]
- Estevan, I.; Monfort-Torres, G.; Farana, R.; Zahradnik, D.; Jandacka, D.; García-Massó, X. Children’s Single-Leg Landing Movement Capability Analysis According to the Type of Sport Practiced. Int. J. Environ. Res. Public. Health 2020, 17, 6414. [Google Scholar] [CrossRef]
| Leg Stiffness | SEM | p Values | |
|---|---|---|---|
| Drop height | −1.487 | 0.486 | 0.002 |
| VM–BF | 0.054 | 0.025 | 0.034 |
| VL–BF | 0.043 | 0.028 | 0.127 |
| RF–BF | 0.045 | 0.022 | 0.046 |
| LG–TA | 0.002 | 0.042 | 0.961 |
| Power Propulsion | SEM | p Values | |
|---|---|---|---|
| Drop height | 124.8 | 42.22 | 0.003 |
| VM–BF | 2.820 | 2.387 | 0.238 |
| VL–BF | 2.573 | 2.690 | 0.339 |
| RF–BF | 3.259 | 1.990 | 0.101 |
| LG–TA | 17.74 | 5.786 | 0.002 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Di Giminiani, R.; Giovannelli, A.; Capuano, L.; Izzicupo, P.; Di Blasio, A.; Masedu, F. Neuromuscular Strategies in Stretch–Shortening Exercises with Increasing Drop Heights: The Role of Muscle Coactivation in Leg Stiffness and Power Propulsion. Int. J. Environ. Res. Public Health 2020, 17, 8647. https://doi.org/10.3390/ijerph17228647
Di Giminiani R, Giovannelli A, Capuano L, Izzicupo P, Di Blasio A, Masedu F. Neuromuscular Strategies in Stretch–Shortening Exercises with Increasing Drop Heights: The Role of Muscle Coactivation in Leg Stiffness and Power Propulsion. International Journal of Environmental Research and Public Health. 2020; 17(22):8647. https://doi.org/10.3390/ijerph17228647
Chicago/Turabian StyleDi Giminiani, Riccardo, Aldo Giovannelli, Lorenzo Capuano, Pascal Izzicupo, Andrea Di Blasio, and Francesco Masedu. 2020. "Neuromuscular Strategies in Stretch–Shortening Exercises with Increasing Drop Heights: The Role of Muscle Coactivation in Leg Stiffness and Power Propulsion" International Journal of Environmental Research and Public Health 17, no. 22: 8647. https://doi.org/10.3390/ijerph17228647
APA StyleDi Giminiani, R., Giovannelli, A., Capuano, L., Izzicupo, P., Di Blasio, A., & Masedu, F. (2020). Neuromuscular Strategies in Stretch–Shortening Exercises with Increasing Drop Heights: The Role of Muscle Coactivation in Leg Stiffness and Power Propulsion. International Journal of Environmental Research and Public Health, 17(22), 8647. https://doi.org/10.3390/ijerph17228647








