Time between Symptom Onset, Hospitalisation and Recovery or Death: Statistical Analysis of Belgian COVID-19 Patients
Abstract
1. Introduction
2. Methods
2.1. Clinical Surveillance of COVID-19 Hospitalized Patients
2.2. Statistical Model
3. Results
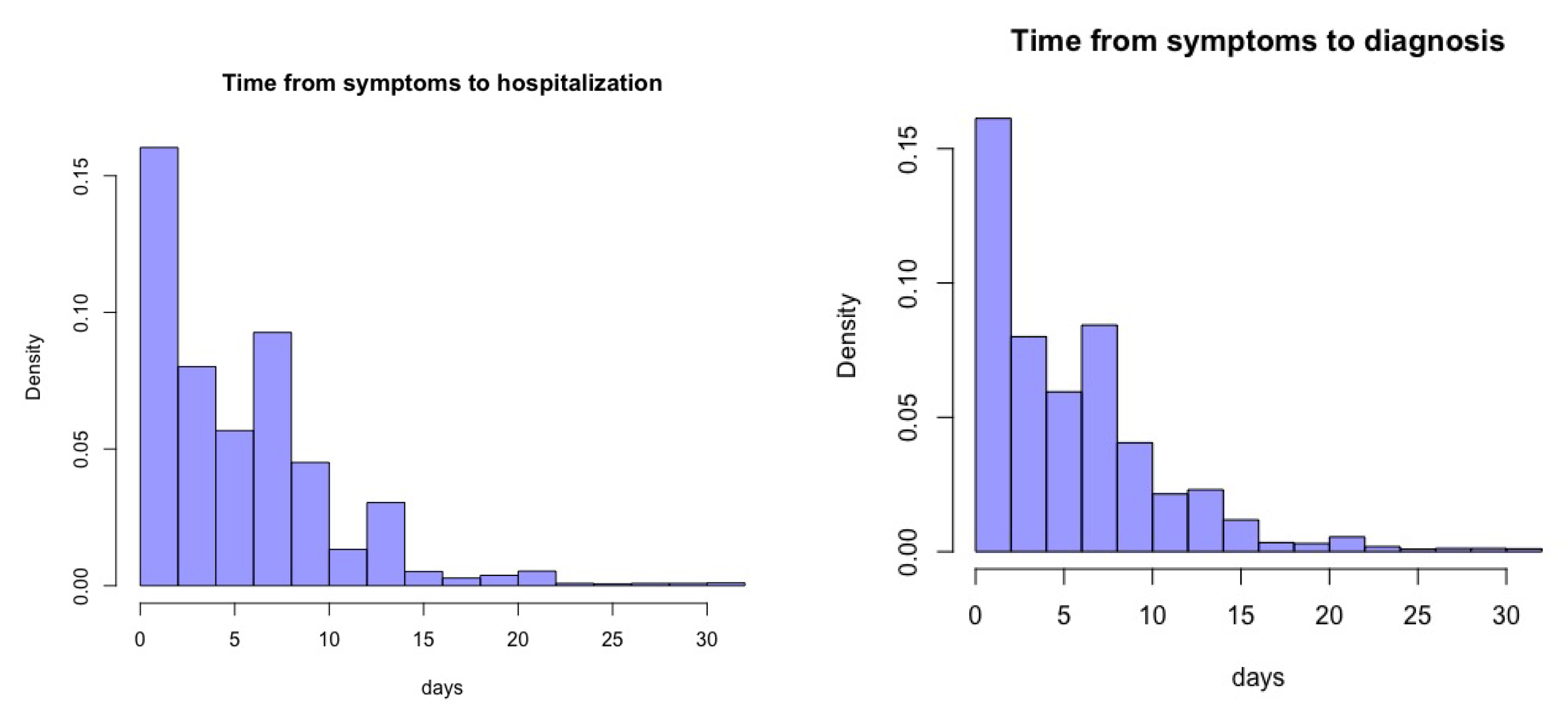
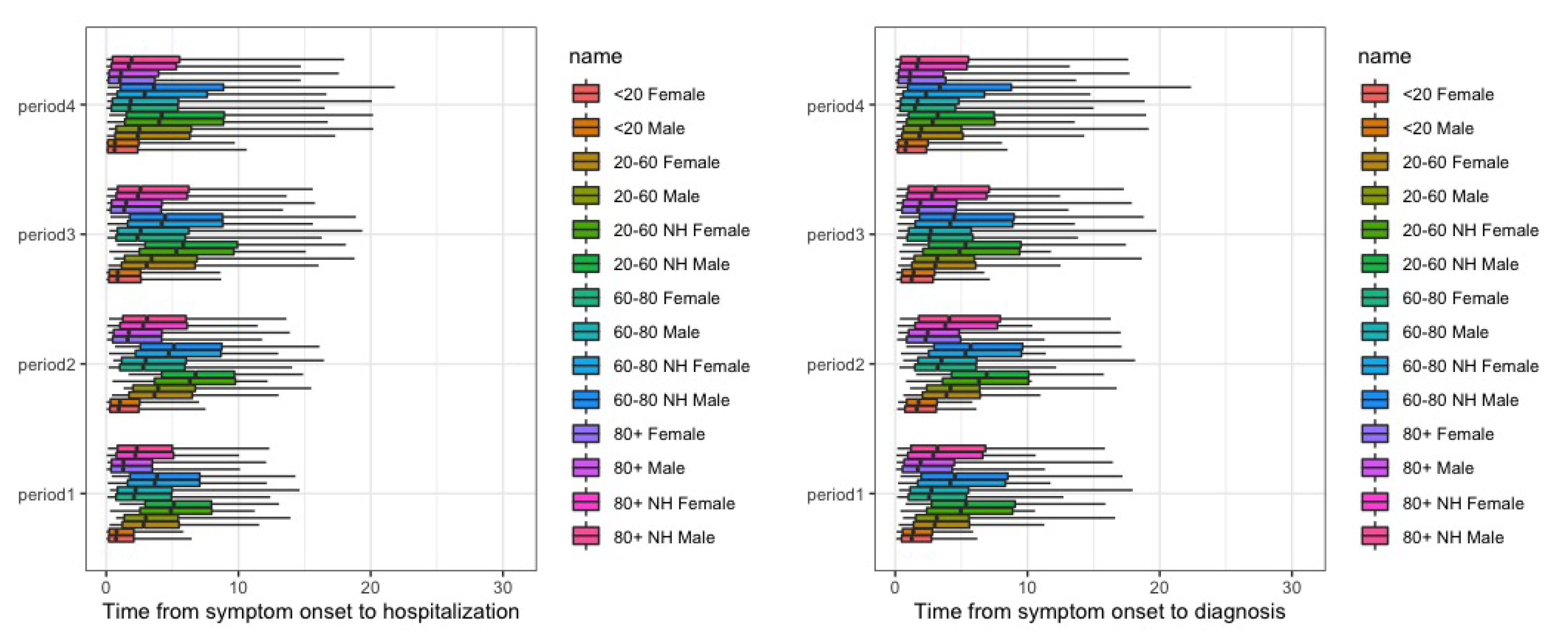
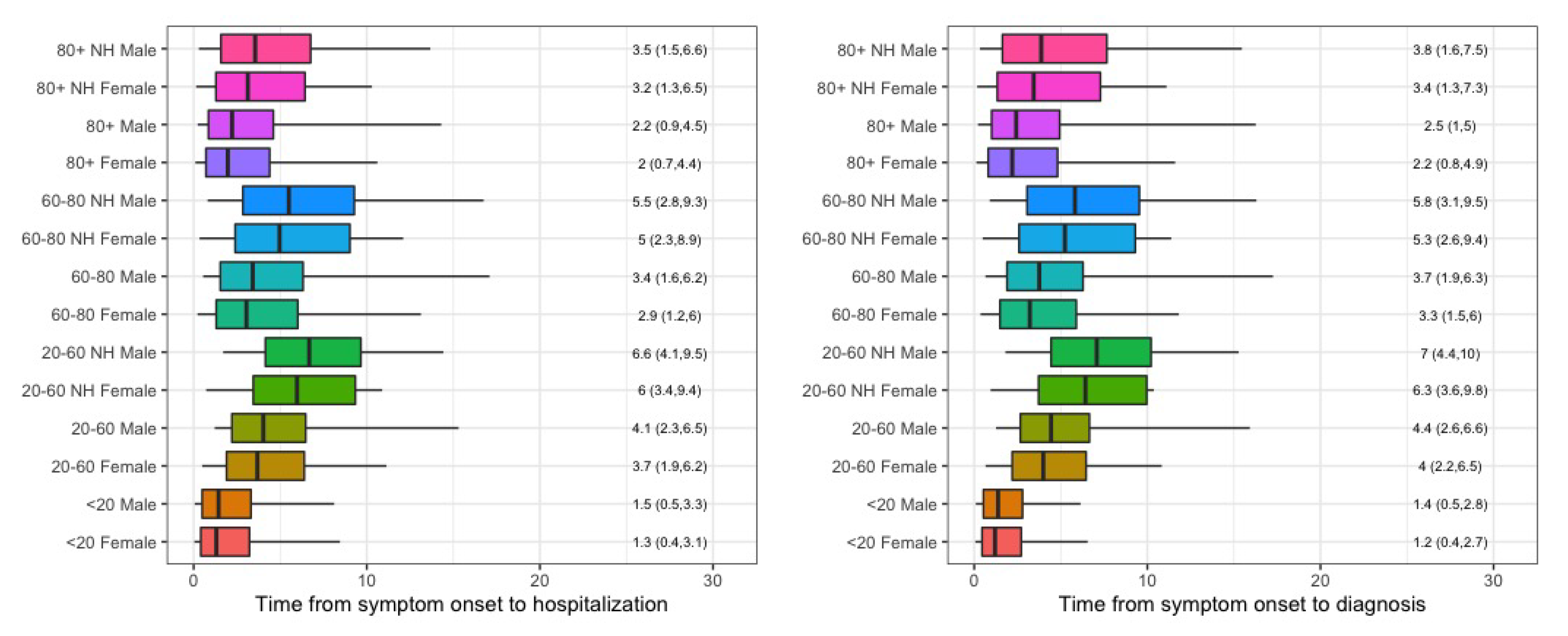
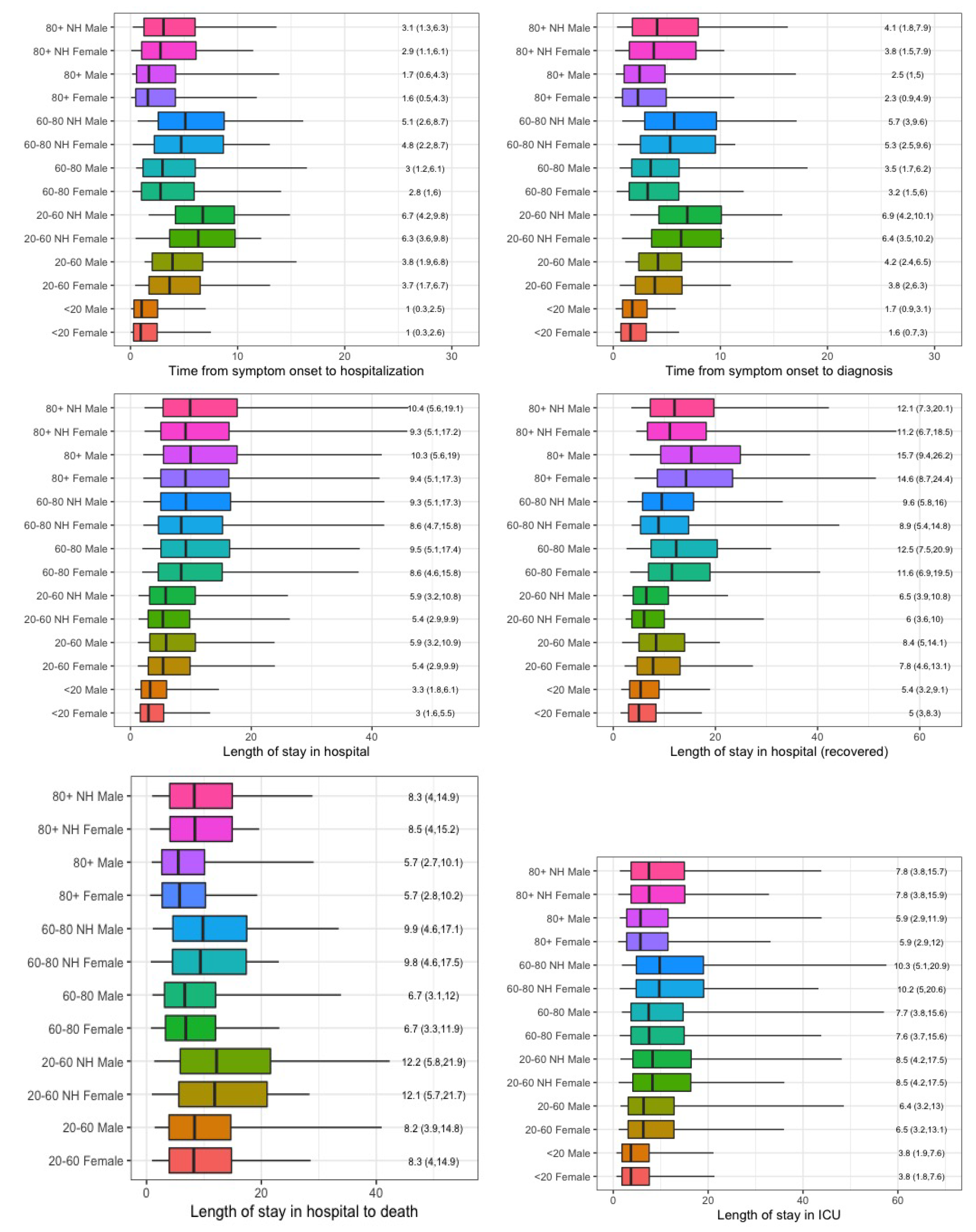
3.1. Symptom Onset to Hospitalization and to Diagnosis
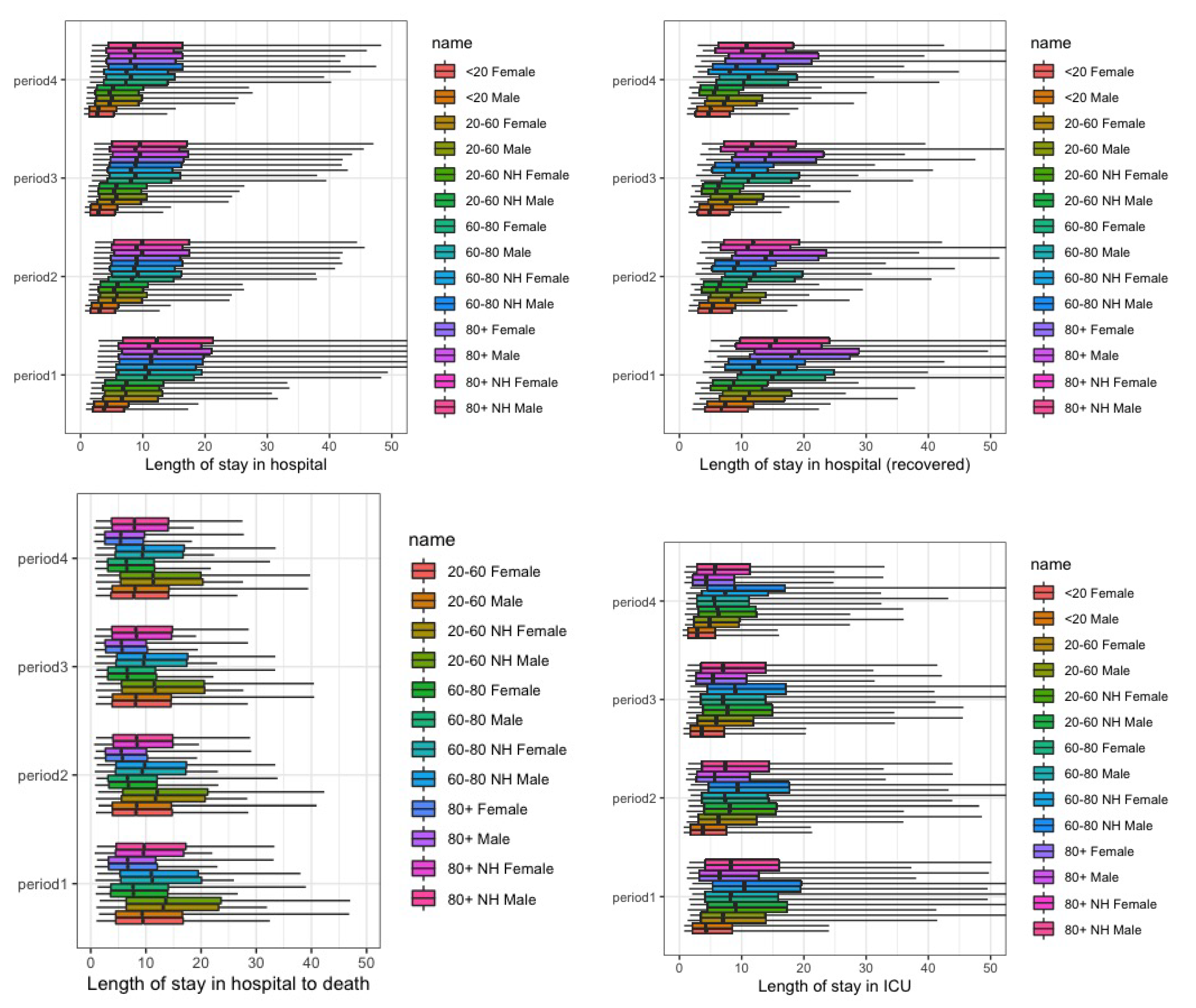
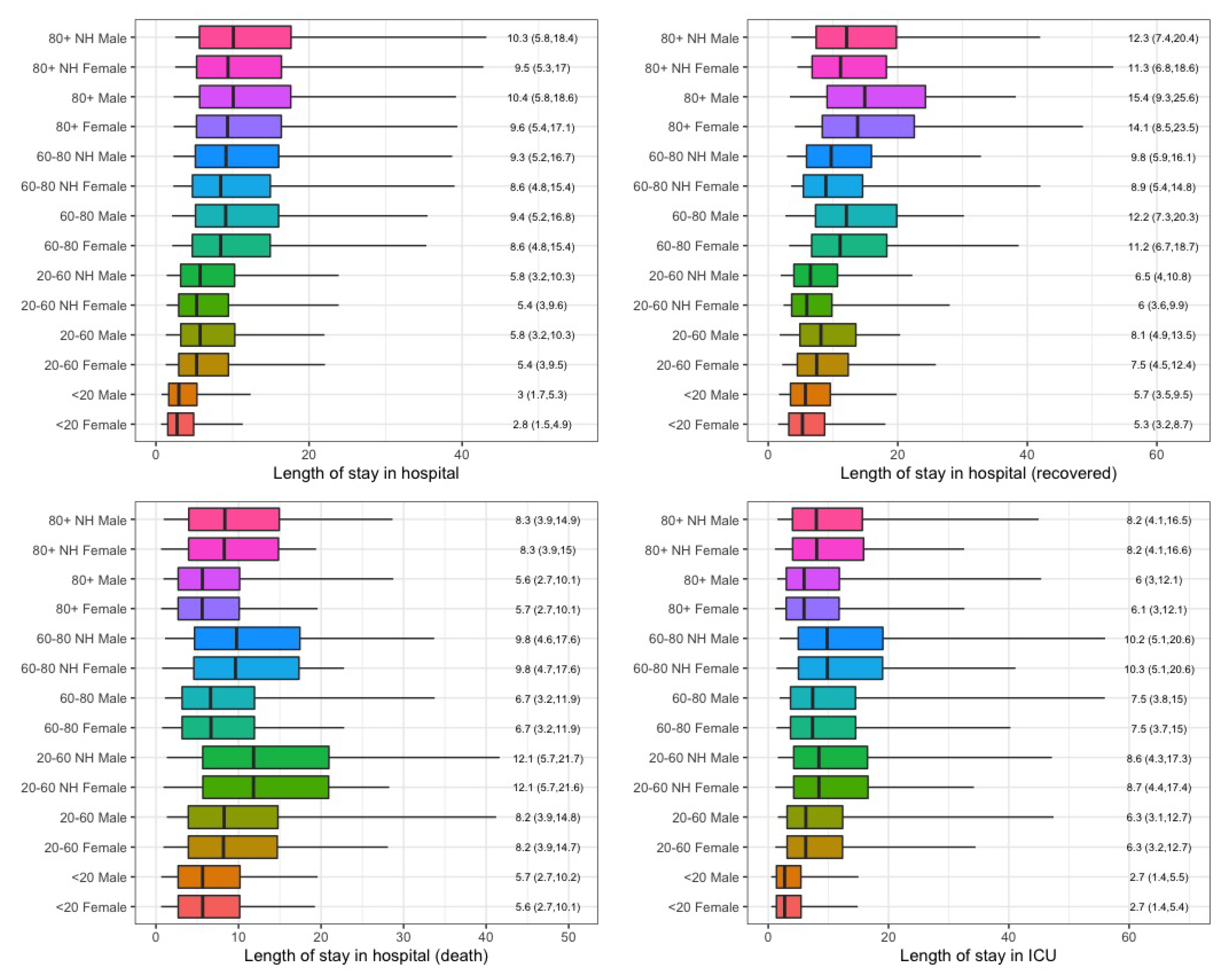
3.2. Length of Stay in Hospital
4. Discussion
Author Contributions
Funding
Conflicts of Interest
Appendix A. (Inclusion/Exclusion Criteria)
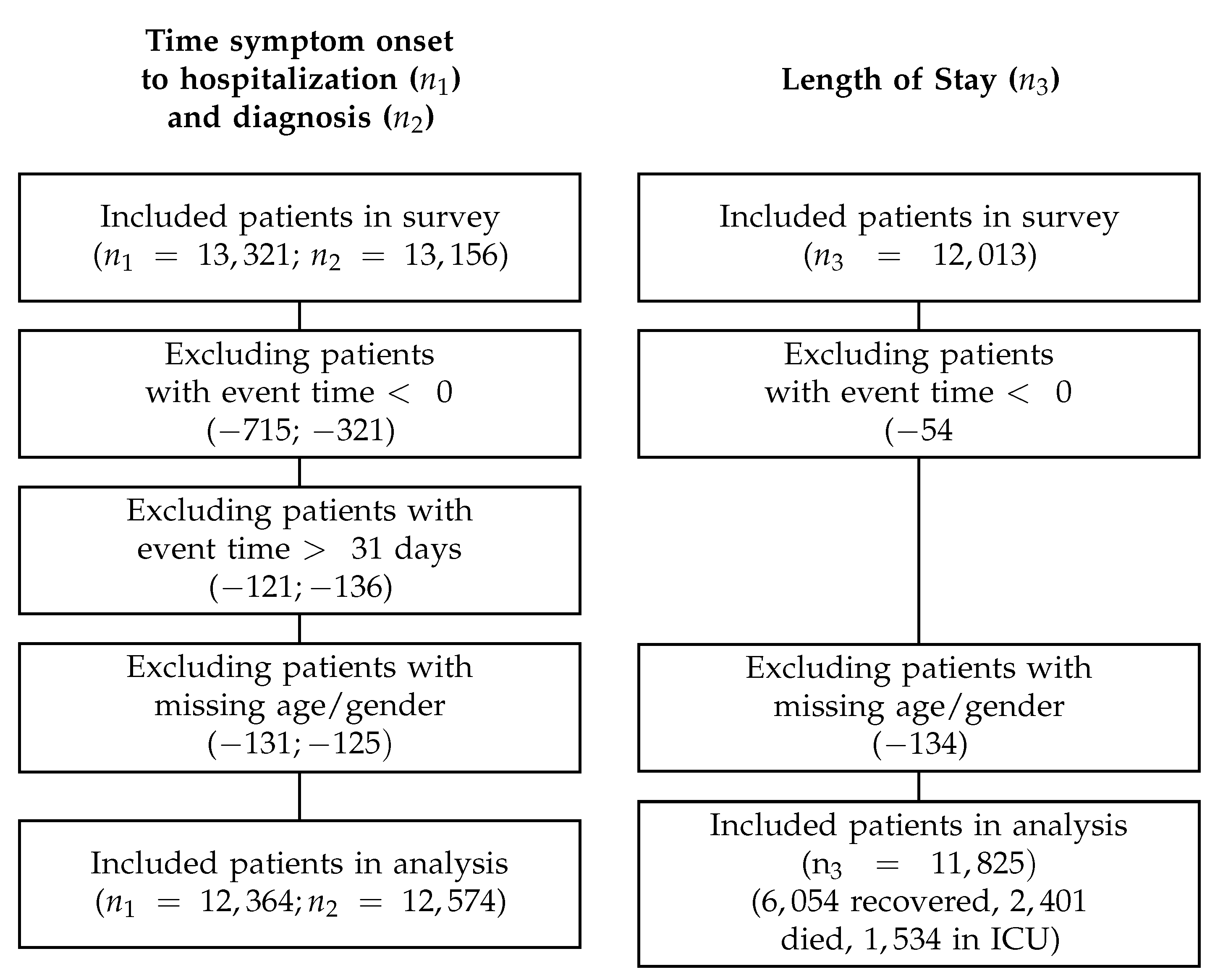
Appendix B. (Patient Characteristics)
| Nursing Home | Total | |||
|---|---|---|---|---|
| Age | Yes | No | Unknown | |
| 0–19 | 0 (0.0%) | 159 (61.4%) | 99 (38.2%) | 258 |
| 20–59 | 80 (1.8%) | 2506 (58.8%) | 1752 (40.4%) | 4338 |
| 60–79 | 652 (11.9%) | 2585 (47.2%) | 2243 (40.9%) | 5480 |
| 80+ | 1605 (35.3%) | 1562 (34.4%) | 1375 (30.3%) | 4542 |
| Total | 2337 (16.0%) | 6812 (46.6%) | 5469 (37.4%) | 14,618 |
Appendix C. (Descriptive Analysis)

| Mean | Median | N | ||||||
|---|---|---|---|---|---|---|---|---|
| Symptom onset—hospitalization | ||||||||
| Overall | 5.6 | 5.0 | 0.0 | 2.0 | 8.0 | 20.0 | 12,364 | |
| Gender | Male | 5.9 | 5.0 | 0.0 | 2.0 | 8.0 | 20.0 | 6700 |
| Female | 5.2 | 4.0 | 0.0 | 1.0 | 7.0 | 20.0 | 5664 | |
| Age | <20 | 3.0 | 1.0 | 0.0 | 0.0 | 4.0 | 14.0 | 227 |
| 20–60 | 6.8 | 7.0 | 0.0 | 3.0 | 9.0 | 20.0 | 4166 | |
| 60–80 | 5.8 | 5.0 | 0.0 | 2.0 | 8.0 | 21.0 | 4717 | |
| >80 | 3.9 | 2.0 | 0.0 | 0.0 | 6.0 | 16.0 | 3254 | |
| Nursing home | Yes | 3.6 | 2.0 | 0.0 | 0.0 | 5.0 | 15.0 | 1863 |
| No | 5.9 | 5.0 | 0.0 | 2.0 | 8.0 | 20.0 | 5885 | |
| Unknown | 5.9 | 5.0 | 0.0 | 2.0 | 8.0 | 21.0 | 4605 | |
| Period | 01 March to 20 March | 4.7 | 4.0 | 0.0 | 1.0 | 7.0 | 14.0 | 1365 |
| 21 March to 30 March | 6.2 | 6.0 | 0.0 | 3.0 | 9.0 | 16.0 | 4593 | |
| 31 March to 18 April | 5.6 | 4.0 | 0.0 | 1.0 | 8.0 | 21.0 | 4432 | |
| 19 April to 12 June | 4.8 | 3.0 | 0.0 | 0.0 | 7.0 | 21.0 | 1974.0 | |
| Symptom onset—diagnosis | ||||||||
| Overall | 5.8 | 5.0 | 0.0 | 2.0 | 8.0 | 20.0 | 12,574 | |
| Gender | Male | 6.1 | 5.0 | 0.0 | 2.0 | 8.0 | 20.0 | 6798 |
| Female | 5.5 | 4.0 | 0.0 | 1.0 | 8.0 | 21.0 | 5776 | |
| Age | <20 | 3.5 | 2.0 | 0.0 | 1.0 | 5.0 | 13.3 | 227 |
| 20–60 | 6.8 | 7.0 | 0.0 | 3.0 | 9.0 | 19.0 | 4131 | |
| 60–80 | 6.1 | 5.0 | 0.0 | 2.0 | 8.0 | 21.0 | 4838 | |
| >80 | 4.3 | 3.0 | 0.0 | 1.0 | 6.0 | 19.6 | 3378 | |
| Nursing home | Yes | 3.6 | 2.0 | 0.0 | 1.0 | 5.0 | 15.0 | 1745 |
| No | 6.0 | 5.0 | 0.0 | 2.0 | 8.0 | 20.0 | 6190 | |
| Unknown | 6.3 | 6.0 | 0.0 | 2.0 | 9.0 | 21.0 | 4628 | |
| Period | 01 March to 20 March | 5.6 | 4.0 | 0.0 | 2.0 | 8.0 | 21.0 | 1629 |
| 21 March to 30 March | 6.6 | 7.0 | 0.0 | 3.0 | 9.0 | 17.0 | 4623 | |
| 31 March to 18 April | 5.6 | 4.0 | 0.0 | 1.0 | 8.0 | 21.0 | 4427 | |
| 19 April to 12 June | 4.4 | 3.0 | 0.0 | 0.0 | 7.0 | 21.0 | 1895 | |
| Mean | Median | N | ||||||
|---|---|---|---|---|---|---|---|---|
| Length of stay in hospital | ||||||||
| Overall | 11.0 | 8.0 | 1.0 | 4.0 | 14.0 | 40.0 | 11,825 | |
| Gender | Male | 11.3 | 8.0 | 1.0 | 5.0 | 14.0 | 42.0 | 6290 |
| Female | 10.7 | 8.0 | 1.0 | 4.0 | 14.0 | 38.0 | 5535 | |
| Age | <20 | 3.9 | 3.0 | 0.0 | 2.0 | 5.0 | 15.0 | 202 |
| 20–60 | 8.2 | 6.0 | 1.0 | 3.0 | 10.0 | 31.0 | 3865 | |
| 60–80 | 12.3 | 9.0 | 1.0 | 5.0 | 15.0 | 44.0 | 4425 | |
| >80 | 12.9 | 10.0 | 1.0 | 5.0 | 17.0 | 41.0 | 3333 | |
| Nursing home | Yes | 11.5 | 9.0 | 1.0 | 5.0 | 16.0 | 34.0 | 1945 |
| No | 11.1 | 8.0 | 1.0 | 4.0 | 14.0 | 43.0 | 5453 | |
| Unknown | 10.6 | 8.0 | 1.0 | 4.0 | 13.0 | 40.0 | 4421 | |
| Period | 01 March to 20 March | 14.7 | 10.0 | 1.0 | 6.0 | 19.0 | 53.0 | 1479 |
| 21 March to 30 March | 10.9 | 8.0 | 1.0 | 4.0 | 13.0 | 42.0 | 4214 | |
| 31 March to 18 April | 10.5 | 8.0 | 1.0 | 4.0 | 14.0 | 36.0 | 4300 | |
| 19 April to 12 June | 9.2 | 7.0 | 1.0 | 4.0 | 13.0 | 29.0 | 1832.0 | |
| Length of stay in ICU | ||||||||
| Overall | 12.2 | 8.0 | 1.0 | 4.0 | 17.0 | 42.7 | 1534 | |
| Gender | Male | 12.7 | 9.0 | 1.0 | 4.0 | 18.0 | 43.0 | 1062 |
| Female | 11.2 | 7.0 | 1.0 | 3.0 | 15.0 | 40.2 | 472 | |
| Age | <20 | 5.2 | 3.0 | 1.2 | 2.0 | 5.5 | 17.5 | 11 |
| 20–60 | 11.5 | 8.0 | 1.0 | 4.0 | 16.0 | 38.5 | 580 | |
| 60–80 | 13.3 | 9.0 | 1.0 | 4.0 | 19.0 | 45.0 | 796 | |
| >80 | 9.9 | 7.0 | 1.0 | 3.0 | 13.0 | 41.0 | 147 | |
| Nursing home | Yes | 8.7 | 6.0 | 1.0 | 3.0 | 11.2 | 35.9 | 96 |
| No | 13.3 | 9.0 | 1.0 | 4.0 | 19.0 | 46.0 | 749 | |
| Unknown | 11.5 | 8.0 | 1.0 | 4.0 | 16.0 | 41.0 | 688 | |
| Period | 01 March to 20 March | 14.1 | 10.0 | 1.0 | 5.0 | 20.0 | 45.9 | 284 |
| 21 March to 30 March | 12.8 | 8.0 | 1.0 | 4.0 | 18.0 | 44.0 | 691 | |
| 31 March to 18 April | 11.2 | 8.0 | 1.0 | 4.0 | 16.0 | 37.2 | 434 | |
| 19 April to 12 June | 8.0 | 6.0 | 1.0 | 3.0 | 11.0 | 25.9 | 125.0 | |
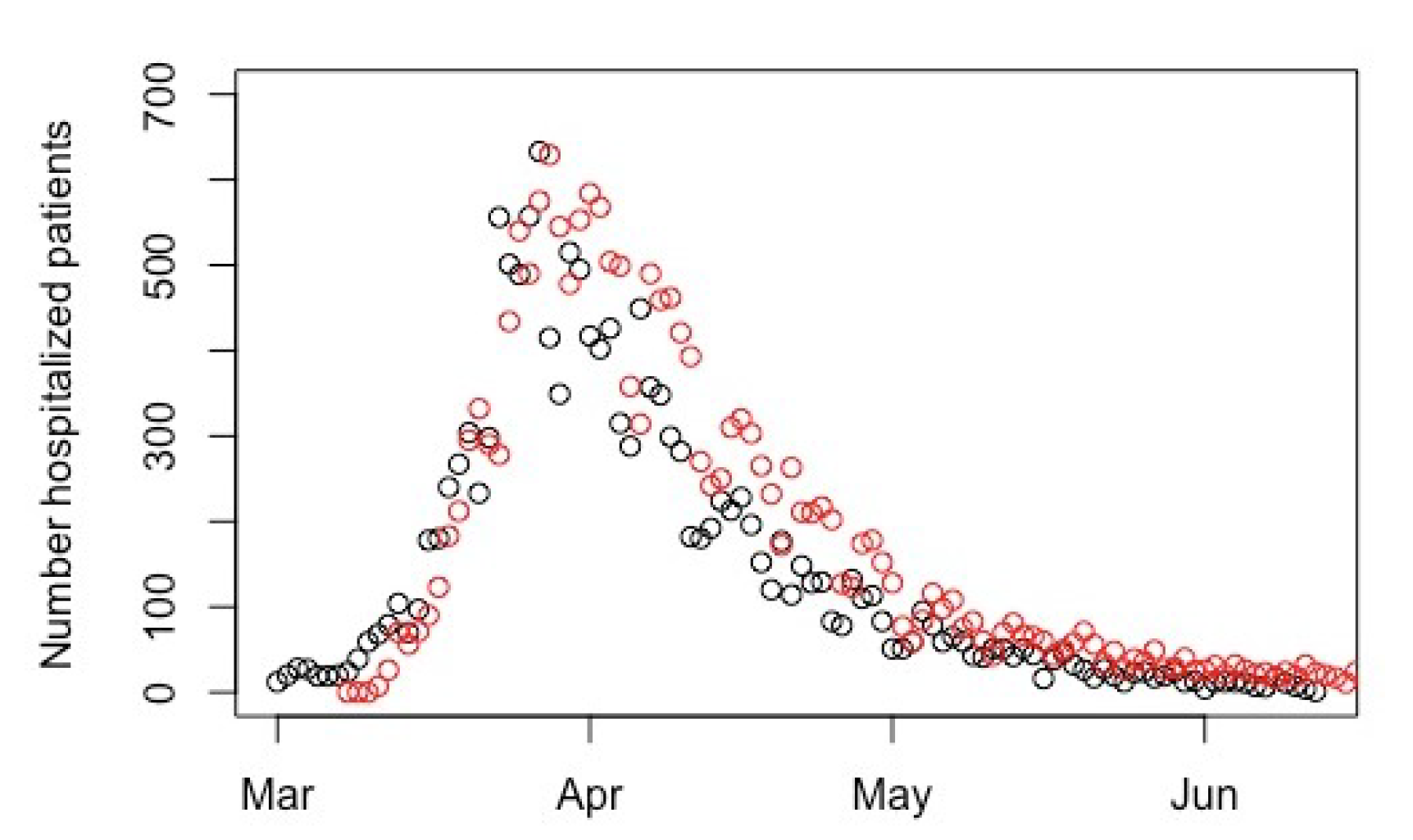
Appendix D. (Figures)

Appendix E. (Collaborators)
| Name | Institution |
|---|---|
| Amir-Samy Aouachria | Centre Hospitalier Chrétien, Liège |
| Kristof Bafort | Mariaziekenhuis, Pelt |
| Leïla Belkhir | Cliniques Universitaires Saint-Luc, Brussels |
| Nathalie Bossuyt | Sciensano |
| Vincent Colombie | Centre Hospitalier Epicura, Baudour |
| Nicolas Dauby | Centre Hospitalier Universitaire Saint-Pierre, Brussels |
| Paul De Munter | Universitair Ziekenhuis Leuven, Leuven |
| Jessika Deblonde | Sciensano |
| Didier Delmarcelle | Clinique St. Jean, Brussels |
| Mélanie Delvallee | Centre Hospitalier de Wallonie Picarde, Tournai |
| Rémy Demeester | Centre Hospitalier Universitaire de Charleroi, Charleroi |
| Thierry Dugernier | Clinique Saint-Pierre, Ottignies |
| Xavier Holemans | Grand Hôpital de Charleroi, Charleroi |
| Frédéric Thys | Grand Hôpital de Charleroi, Charleroi |
| Benjamin Kerzmann | Clinique Notre Dame de Grâce, Gosselies |
| Pierre Yves Machurot | Centre Hospitalier de l’Ardenne |
| Philippe Minette | Centres Hospitaliers Jolimont |
| Jean-Marc Minon | Centre Hospitalier Régional de la Citadelle, Liège |
| Saphia Mokrane | Hôpitaux Iris Sud, Brussels |
| Catherine Nachtergal | Cliniques de l’Europe, Brussels |
| Séverine Noirhomme | Centre Hospitalier Régional de Namur |
| Denis Piérard | Universitair Ziekenhuis Brussel, Brussels |
| Camelia Rossi | Centre Hospitalier Universitaire Ambroise Paré, Mons |
| Carole Schirvel | CHIREC, Brussels |
| Erica Sermijn | A.S.Z. Ziekenhuis, Aalst |
| Frank Staelens | OLV Ziekenhuis, Aalst |
| Filip Triest | Algemeen Ziekenhuis Sint Lucas, Gent |
| Dominique Van Beckhoven | Sciensano |
| Nina Van Goethem | Sciensano |
| Jens Van Praet | Algemeen Ziekenhuis Sint Jan, Brugge-Oostende |
| Anke Vanhoenacker | Ziekenhuisnetwerk Antwerpen |
| Sarah Cooreman | Algemeen Ziekenhuis. Monica |
| Elise Willems | Algemeen Ziekenhuis Nikolaas, Sint-Niklaas |
| Chloé Wyndham-Thomas | Sciensano |
References
- Vekaria, B.; Overton, C.E.; Wisniowski, A.; Ahmad, S.H.; Aparicio-Castro, A.; Curran-Sebastian, J.; Eddleston, J.; Hanley, N.A.; House, T.; Kim, J.; et al. Hospital length of stay for COVID-19 patients: Data-driven methods for forward planning. MedRXiv 2020. [Google Scholar] [CrossRef]
- Donnely, C.A.; Ghani, A.C.; Leung, G.M.; Hedley, A.J.; Fraser, C.; Riley, S.; Abu-Raddad, L.J.; Ho, L.M.; Thach, T.Q.; Chau, P. Epidemiological determinants of spread of causal agent of severe acute respiratory syndrom in Hong Kong. Lancet 2003, 361, 1761–1766. [Google Scholar] [CrossRef]
- Van Goethem, N.; Vilain, A.; Wyndham-Thomas, C.; Deblonde, J.; Bossuyt, N.; Rebolledo, J.; Lernout, T.; Quoilin, S.; Melis, V.; Van Beckhoven, D. Rapid establishment of a national surveillance of COVID-19 hospitalizations in Belgium. Arch. Public Health 2020, submitted. [Google Scholar]
- Held, L.; Hens, N.; O’Neill, P.; Wallinga, J. Handbook of Infectious Diseases Data Analysis; Chapman & Hall/CRC: Boca Raton, FL, USA, 2020. [Google Scholar]
- Hens, N.; Calatayud, L.; Kurkela, S.; Tamme, T.; Wallinga, J. Robust reconstruction and analysis of outbreak data: Influenza A (H1N1)v transmission in a school-based population. Am. J. Epidemiol. 2012, 24, 224–250. [Google Scholar] [CrossRef] [PubMed]
- Cowling, B.J.; Fang, V.J.; Riley, S.; Peiris, J.S.; Leung, G.M. Estimation of the serial interval of influenza. Epidemiology. 2009, 20, 344–347. [Google Scholar] [CrossRef] [PubMed]
- Reich, N.G.; Lessler, J.; Cummings, D.A.T.; Brookmeyer, R. Estimating incubation period distributions with coarse data. Stat. Med. 2009, 28, 2769–2784. [Google Scholar] [CrossRef] [PubMed]
- Linton, N.M.; Kobayashi, T.; Yang, Y.; Hayashi, K.; Akhmetzhanov, A.R.; Jung, S.; Yyan, B.; Kinoshita, R.; Nishiura, H. Incubation period and other epidemiological characteristics of 2019 novel Coronavirus infections with right truncation: A statistical analysis of publicly available case data. J. Clin. Med. 2020, 9, 538. [Google Scholar] [CrossRef] [PubMed]
- Sun, J. Statistical Analysis of Interval-Censored Failure Time Data; Springer: New York, NY, USA, 2006. [Google Scholar]
- Wang, D.; Hu, B.; Hu, C.; Zhu, F.; Liu, X.; Zhang, J.; Wang, B.; Xiang, H.; Cheng, Z.; Xiong, Y.; et al. Clinical Characteristics of 138 Hospitalized Patients With 2019 Novel Coronavirus-Infected Pneumonia in Wuhan, China. JAMA 2020, 323, 1061–1069. [Google Scholar] [CrossRef] [PubMed]
- Huang, C.; Wang, Y.; Li, X.; Ren, L.; Zhao, P.J.; Hu, Y.; Zhang, P.L.; Fan, G.; Xu, J.; Gu, X.; et al. Clinical features of patients infected with 2019 novel coronavirus in Wuhan, China. Lancet 2020, 395, 497–506. [Google Scholar] [CrossRef]
- Zhou, F.; Yu, T.; Du, R.; Fan, G.; Liu, Y.; Liu, Z.; Xiang, J.; Wang, Y.; Song, B.; Gu, X.; et al. Clinical course and risk factors for mortality of adult inpatients with COVID-19 in Wuhan, China: A retrospective cohort study. Lancet 2020. [Google Scholar] [CrossRef]
- CDC. Interim Clinical Guidance for Management of Patients with Confirmed Coronavirus Disease (COVID-19). Available online: https://www.cdc.gov/coronavirus/2019-ncov/hcp/ (accessed on 10 September 2020).
- Skinner, C.J.; Holt, D.; Smith, T.M.F. Analysis of Complex Surveys; John Wiley: New York, NY, USA, 1989. [Google Scholar]
- Abrams, S.; Wambua, J.; Santermans, E.; Willem, L.; Kuylen, E.; Coletti, P.K.; Libin, P.; Faes, C.; Petrof, O.; Herzog, S.A.; et al. Modeling the early phase of the Belgian COVID-19 epidemic using a stochastic compartmental model and studying its implied future trajectories. MedRXiv 2020. [Google Scholar] [CrossRef]
- Pellis, L.; Scarabel, F.; Stage, H.B.; Overton, C.E.; Chappell, L.H.; Lythgoe, K.A.; Fearon, E.; Bennett, E.; Curran-Sebastian, J.; Das, R.; et al. Challenges in control of Covid-19: Short doubling time and long delay to effect of interventions. arXiv 2020, arXiv:2004.00117. [Google Scholar]
- Kraemer, M.U.G.; Yang, C.; Gutierrez, B.; Wu, C.; Klein, B.; Pigott, D.M.; du Plessis, L.; Faria, N.R.; Li, R.; Hanage, W.P.; et al. The effect of human mobility and control measures on the COVID-19 epidemic in china. Science 2020, 368, 493–497. [Google Scholar] [CrossRef] [PubMed]
- Ferguson, N.M.; Laydon, D.; Nedjati-Gilani, G.; Imai, N.; Ainslie, K.; Baguelin, M.; Bhatia, S.; Boonyasiri, A.; Cucunuba, Z.; Cuomo-Dannenburg, G.; et al. Impact of nonpharmaceutical interventions (NPIs) to reduce COVID-19 mortality and healthcare demand. In Imperial College London COVID-19 Response Team (2020); 2020; pp. 1–20. [Google Scholar] [CrossRef]
- Rees, E.M.; Nightingale, E.S.; Jafari, Y.; Waterlow, N.R.; Cliffor, S.; Pearson, C.A.B.; CMMID Working Group; Jombart, T.; Procter, S.R.; Knight, G.M. COVID-19 length of hospital stay: A systematic review and data synthesis. BMC Med. 2020, 18, 270. [Google Scholar] [CrossRef] [PubMed]
- Yang, X.; Yu, Y.; Xu, J.; Shu, H.; Xia, J.; Liu, H.; Wu, Y.; Zhang, L.; Yu, Z.; Fang, M.; et al. Clinical course and outcomes of critically ill patients with SARS-CoV-2 pneumonia in Wuhan, China: A single-centered, retrospective, observational study. Lancet Respir. Med. 2020. [Google Scholar] [CrossRef]
| Est | s.e. | Est | s.e. | |
|---|---|---|---|---|
| Symptom onset—hospitalization | ||||
| (Intercept) | 1.218 | 0.044 *** | 1.208 | 0.036 *** |
| Male | 0.032 | 0.020 | −0.076 | 0.017 *** |
| Age | −0.535 | 0.104 *** | 0.033 | 0.084 |
| Age 20–60 | 0.618 | 0.034 *** | −0.490 | 0.028 *** |
| Age 60–80 | 0.433 | 0.035 *** | −0.251 | 0.029 *** |
| Nursing home: No | −0.452 | 0.044 *** | 0.250 | 0.039 *** |
| Nursing home: Unknown | −0.046 | 0.021 * | 0.143 | 0.019 *** |
| Period 21 March to 30 March | 0.234 | 0.033 *** | −0.100 | 0.028 *** |
| Period 31 March to 18 April | 0.187 | 0.035 *** | 0.137 | 0.030 *** |
| Period 19 April to 12 June | 0.028 | 0.047 | 0.495 | 0.039 *** |
| Symptom onset—diagnosis | ||||
| (Intercept) | 1.527 | 0.042 *** | 1.232 | 0.035 *** |
| Male | 0.040 | 0.019 * | −0.098 | 0.016 *** |
| Age | −0.400 | 0.081 *** | −0.196 | 0.059 *** |
| Age 20–60 | 0.383 | 0.031 *** | −0.389 | 0.025 *** |
| Age 60–80 | 0.284 | 0.031 *** | −0.201 | 0.026 *** |
| Nursing home: No | −0.480 | 0.038 *** | 0.062 | 0.031 * |
| Nursing home: Unknown | 0.022 | 0.019 | −0.004 | 0.016 |
| Period 21 March to 30 March | 0.181 | 0.034 *** | −0.187 | 0.030 *** |
| Period 31 March to 18 April | 0.029 | 0.036 | 0.097 | 0.032 ** |
| Period 19 April to 12 June | −0.297 | 0.047 *** | 0.545 | 0.042 *** |
| Est | s.e. | Est | s.e. | |
|---|---|---|---|---|
| Length of stay in hospital | ||||
| (Intercept) | 2.480 | 0.035 *** | 0.913 | 0.024 *** |
| Male | 0.091 | 0.019 *** | / | / |
| Age | −1.143 | 0.067 *** | / | / |
| Age 20–60 | −0.553 | 0.024 *** | / | / |
| Age 60–80 | −0.087 | 0.023 *** | / | / |
| Period 21 March to 30 March | −0.242 | 0.034 *** | −0.008 | 0.027 |
| Period 31 March to 18 April | −0.270 | 0.034 *** | 0.017 | 0.027 |
| Period 19 April to 12 June | −0.359 | 0.038 *** | 0.087 | 0.030 ** |
| Length of stay in ICU | ||||
| (Intercept) | 2.183 | 0.152 *** | 1.052 | 0.029 *** |
| Age | −0.443 | 0.401 | / | / |
| Age 20–60 | 0.098 | 0.126 | / | / |
| Age 60–80 | 0.273 | 0.122 * | / | / |
| Nursing home: No | −0.282 | 0.147 | / | / |
| Nursing home: Unknown | −0.170 | 0.072 * | / | / |
| Period 21 March to 30 March | −0.135 | 0.112 | / | / |
| Period 31 March to 18 April | −0.186 | 0.115 | / | / |
| Period 19 April to 12 June | −0.418 | 0.151 ** | / | / |
| Length of stay in hospital (reason out of hospital = recovered) | ||||
|---|---|---|---|---|
| Est | s.e. | Est | s.e. | |
| (Intercept) | 2.724 | 0.044 *** | 0.720 | 0.024 *** |
| Male | 0.077 | 0.022 *** | / | / |
| Age | −1.074 | 0.074 *** | / | / |
| Age 20–60 | −0.625 | 0.032 *** | / | / |
| Age 60–80 | −0.231 | 0.031 *** | / | / |
| Nursing home: No | 0.261 | 0.038 *** | 0.008 | 0.031 |
| Nursing home: Unknown | 0.012 | 0.0245 | 0.099 | 0.018 *** |
| Period 21 March to 30 March | −0.307 | 0.040 *** | 0.034 | 0.027 |
| Period 31 March to 18 April | −0.326 | 0.039 *** | 0.007 | 0.027 |
| Period 19 April to 12 June | −0.388 | 0.045 *** | 0.097 | 0.031 ** |
| Length of stay in hospital (reason out of hospital = death) | ||||
| Est | s.e. | Est | s.e. | |
| (Intercept) | 2.573 | 0.070 *** | 0.842 | 0.014 *** |
| Age 20–60 | 0.372 | 0.084 *** | / | / |
| Age 60–80 | 0.162 | 0.040 *** | / | / |
| Nursing home: No | −0.383 | 0.048 *** | / | / |
| Nursing home: Unknown | −0.160 | 0.047 ** | / | / |
| Period 21 March to 30 March | −0.142 | 0.069 | / | / |
| Period 31 March to 18 April | −0.156 | 0.069 * | / | / |
| Period 19 April to 12 June | −0.189 | 0.079 * | / | / |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Faes, C.; Abrams, S.; Van Beckhoven, D.; Meyfroidt, G.; Vlieghe, E.; Hens, N.; Belgian Collaborative Group on COVID-19 Hospital Surveillance. Time between Symptom Onset, Hospitalisation and Recovery or Death: Statistical Analysis of Belgian COVID-19 Patients. Int. J. Environ. Res. Public Health 2020, 17, 7560. https://doi.org/10.3390/ijerph17207560
Faes C, Abrams S, Van Beckhoven D, Meyfroidt G, Vlieghe E, Hens N, Belgian Collaborative Group on COVID-19 Hospital Surveillance. Time between Symptom Onset, Hospitalisation and Recovery or Death: Statistical Analysis of Belgian COVID-19 Patients. International Journal of Environmental Research and Public Health. 2020; 17(20):7560. https://doi.org/10.3390/ijerph17207560
Chicago/Turabian StyleFaes, Christel, Steven Abrams, Dominique Van Beckhoven, Geert Meyfroidt, Erika Vlieghe, Niel Hens, and Belgian Collaborative Group on COVID-19 Hospital Surveillance. 2020. "Time between Symptom Onset, Hospitalisation and Recovery or Death: Statistical Analysis of Belgian COVID-19 Patients" International Journal of Environmental Research and Public Health 17, no. 20: 7560. https://doi.org/10.3390/ijerph17207560
APA StyleFaes, C., Abrams, S., Van Beckhoven, D., Meyfroidt, G., Vlieghe, E., Hens, N., & Belgian Collaborative Group on COVID-19 Hospital Surveillance. (2020). Time between Symptom Onset, Hospitalisation and Recovery or Death: Statistical Analysis of Belgian COVID-19 Patients. International Journal of Environmental Research and Public Health, 17(20), 7560. https://doi.org/10.3390/ijerph17207560





