Resilience Assessment of Complex Urban Public Spaces
Abstract
1. Introduction
2. Literature Review
2.1. Resilience
2.2. Resilience Assessment Indicator System
2.3. Resilience Assessment Approach
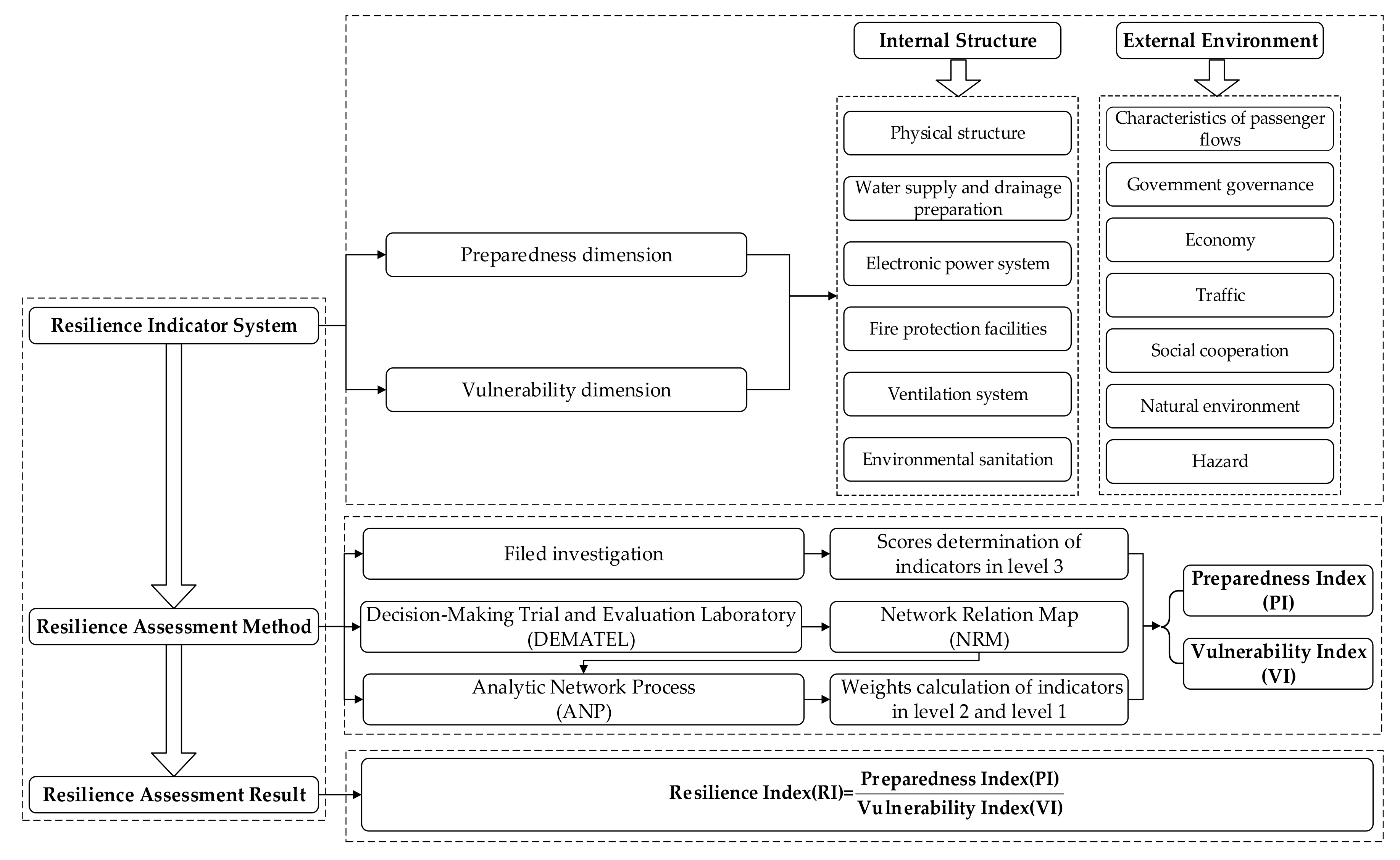
3. Resilience Assessment Framework of CUPSs
3.1. A Two-Dimension Practical Indicator System
3.1.1. Preparedness Dimension
3.1.2. Vulnerability Dimension
3.2. Indicator Adaption to the CUPSs
- (1)
- Physical structure. CUPSs are characterized by multidimensional spaces and multi-layer structures, and several functions are integrated into the space. For instance, the traffic transfer hub integrates various transfer modes, including metro, bus, taxi, railway, etc. However, numerous random and intentional events are threatening CUPSs due to their characteristics of high spatial integration, large underground space, and crowded passengers. Therefore, the four main indicators in level 2 for analyzing preparedness and vulnerability can be identified as the multi-layer structure, internal spatial layout, underground spatial layout, and multi-function. Furthermore, the indicators in level 3 have been determined;
- (2)
- Water supply and drainage preparation. This indicator is used to demonstrate the ability to prevent and respond to disasters such as fires and flooding. This dimension includes only one indicator in level 2, namely “water supply and drainage facilities”. The number of emergency water supply and drainage facilities is considered in level 3;
- (3)
- Electronic power system. The electronic power system plays the backbone role in the normal operation of CUPSs. Indicators in the sub-level include emergency power supply equipment and the power condition;
- (4)
- Fire protection facilities. Fire-fighting equipment is a general emergency tool for dealing with fire. Besides, the automatic alarm system can also remind passengers of emergency evacuation effectively and rapidly. The above two aspects are considered in the sub-level;
- (5)
- Ventilation system. The ventilation system is associated with the air environment in CUPSs. In general, ventilation in three-dimensional space mainly depends on the air shaft and air conditioning system;
- (6)
- Environmental sanitation. Environmental sanitation is related to the physical structure, ventilation system, characteristics of passenger flow, etc. Health protection measures should be considered as the main content, including post-disaster disease prevention and epidemic prevention. Disease and epidemic transmission can cause the expansion of accidents and even more serious losses. Post-disaster disease prevention is crucial and directly related to the recovery efficiency of the system. Accordingly, indicators in level 3 include “the number of cleaners” and “the number of sanitation and epidemic prevention personnel”.
- (1)
- Characteristics of passenger flows. In CUPSs, crowd clusters exist at every layer, which is a vulnerable point to be struck by risk events. Therefore, passenger flow characteristics should be considered for emergency preparation and a rapid response. The sub-indicators in this dimension comprise statistics of passenger flows, spatial and temporal distribution of passenger flows, and security protection for crowd clusters;
- (2)
- Government governance. In this dimension, the three sub-indicators are multi-stakeholder cooperation, disaster emergency plan, and disaster management plan. Multi-stakeholder cooperation represents the relationship between multi-government departments and enterprises, which is necessary for daily operations and the emergency response during a disaster. The disaster emergency plan aims to rapidly respond to risk events and reduce losses through pre-disaster planning and preparation. The disaster management plan includes security measures, such as disaster prevention propaganda, police security protection, and security facilities setting;
- (3)
- Economy. Economic strength has some impacts on the emergency response speed during risk events. The level of economic development is relevant to the resilience of CUPSs. Therefore, the financial support and rescue material reserve offered by the government are considered. In addition, indicators reflecting regional economic development are also added;
- (4)
- Traffic. Traffic condition is closely related to post-disaster emergency rescue. Traffic accessibility is an important indicator that can be demonstrated through the number of connected roads and traffic operation. High traffic accessibility facilitates rescuers and emergency vehicles;
- (5)
- Social cooperation. Social cooperation includes social preparedness and social service from passengers, volunteers, and non-governmental organizations (NGOs). The mutual and close cooperation between professional rescuers and the public is conducive to disasters. The coverage of emergency vehicles and medical services is also considered;
- (6)
- Natural environment. The natural environment is used to explain disaster preparedness. The statistics of multi-category natural disaster is considered to help further predict and prevent natural disasters;
- (7)
- Hazard. CUPSs are exposed to the natural environment and subject to various disturbances. Hazards occurring in the CUPSs can be described in terms of variety, characteristics, and severity.
4. Methods
4.1. Preparedness and Vulnerability Score Calculation Methods
4.2. Indicator Weights Determination Methods
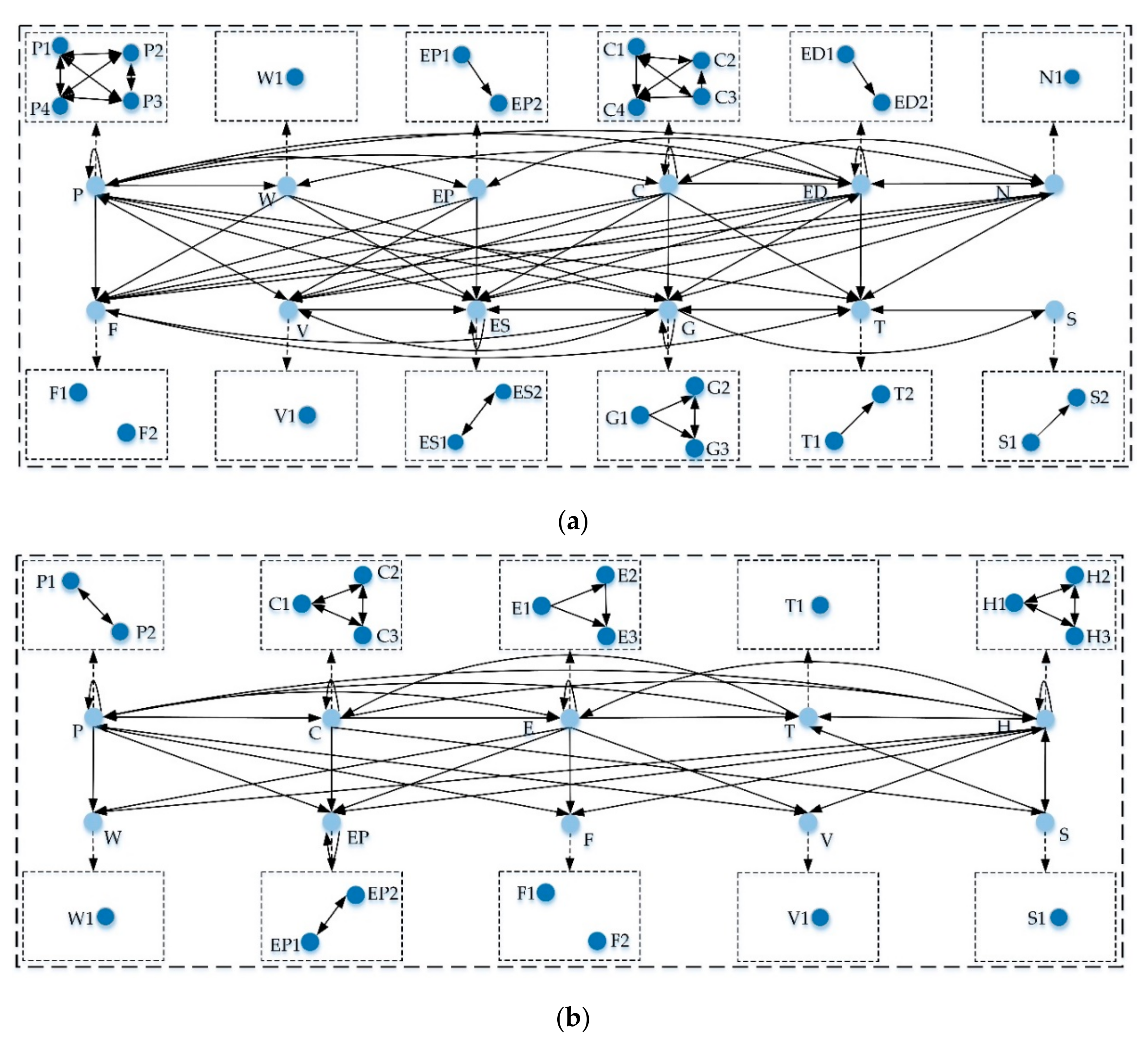
4.2.1. DEMATEL
4.2.2. ANP
5. Results
5.1. The Chongqing West Railway Station and Lianglukou Rail Transit Station
5.2. Data Collection
5.3. Evaluation Results
5.3.1. Score Determination of Indicators in Level 3
5.3.2. Weight Calculation of Indicators in Level 2
5.3.3. Resilience Evaluation Score
6. Results Analysis
6.1. Results Analysis of “Preparedness”
6.2. Results Analysis of “Vulnerability”
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Xu, H.; Xue, B. Key indicators for the resilience of complex urban public spaces. J. Build. Eng. 2017, 12, 306–313. [Google Scholar] [CrossRef]
- Holling, C.S. Resilience and stability of ecological systems. Annu. Rev. Ecol. Syst. 1973, 4, 1–23. [Google Scholar] [CrossRef]
- López-Cuevas, A.; Ramírez-Márquez, J.; Sanchez-Ante, G.; Barker, K. A community perspective on resilience analytics: A visual analysis of community mood. Risk Anal. 2017, 37, 1566–1579. [Google Scholar] [CrossRef]
- Torabi, E.; Dedekorkut-Howes, A.; Howes, M. Adapting or maladapting: Building resilience to climate-related disasters in coastal cities. Cities 2018, 72, 295–309. [Google Scholar] [CrossRef]
- Yang, Y.; Ng, S.T.; Zhou, S.; Xu, F.J.; Li, H. A physics-based framework for analyzing the resilience of interdependent civil infrastructure systems: A climatic extreme event case in Hong Kong. Sustain. Cities Soc. 2019, 47, 101485. [Google Scholar] [CrossRef]
- Alexander, D.E. Resilience and disaster risk reduction: An etymological journey. Nat. Hazards Earth Syst. Sci. 2013, 13, 2707–2716. [Google Scholar] [CrossRef]
- Hosseini, S.; Barker, K.; Ramirez-Marquez, J.E. A review of definitions and measures of system resilience. Reliab. Eng. Syst. Saf. 2016, 145, 47–61. [Google Scholar] [CrossRef]
- US Department of Homeland Security. National Infrastructure Protection Plan: Partnering to Enhance Protection and Resiliency. 2009. Available online: https://www.dhs.gov/sites/default/files/publications/national-infrastructure-protection-plan-2009-508.pdf (accessed on 19 July 2019).
- Kusumastuti, R.D.; Viverita; Husodo, Z.A.; Suardi, L.; Danarsari, D.N. Developing a resilience index towards natural disasters in Indonesia. Int. J. Disaster Risk Reduct. 2014, 10, 327–340. [Google Scholar] [CrossRef]
- Simpson, D.M.; Katirai, M. Indicator Issues and Proposed Framework for a Disaster Preparedness Index (DPi), Draft Version 1.0. 2006. Available online: http://www.fritzinstitute.org/PDFs/WhitePaper/DaveSimpson IndicatorsRepor.pdf (accessed on 19 July 2019).
- Renschler, C.S.; Frazier, A.E.; Arendt, L.A.; Cimellaro, G.P.; Reinhorn, A.M.; Bruneau, M. A Framework for Defining and Measuring Resilience at the Community Scale: The PEOPLES Resilience Framework, 1st ed.; Multidisciplinary Center for Earthquake Engineering Research: Buffalo, NY, USA, 2010; pp. 1–110. [Google Scholar]
- Cariolet, J.M.; Vuillet, M.; Diab, Y. Mapping urban resilience to disasters-a review. Sustain. Cities Soc. 2019, 51, 101746. [Google Scholar] [CrossRef]
- United Nations International Strategy for Disaster Reduction. Hyogo Framework for Action 2005–2015: Building the Resilience of Nations and Communities to Disasters. In The World Conference on Disaster Reduction(A/CONF.206/6); United Nations International Strategy for Disaster Reduction: Kobe, Japan, 2005; pp. 1–34. [Google Scholar]
- United Nations Office for Disaster Risk Reduction. The Sendai Framework for Disaster Risk Reduction 2015–2030. In The Third UN World Conference on Disaster Risk Reduction; United Nations Office for Disaster Risk Reduction: Sendai, Japan, 2015; pp. 1–37. [Google Scholar]
- Zhang, M.; Chen, W.; Cai, K.; Gao, X.; Zhang, X.; Liu, J.; Wang, Z.; Li, D. Analysis of the spatial distribution characteristics of urban resilience and its influencing factors: A case study of 56 cities in China. Int. J. Environ. Res. Public Health 2019, 16, 4442. [Google Scholar] [CrossRef]
- Schoch-Spana, M.; Gill, K.; Hosangadi, D.; Slemp, C.; Burhans, R.; Zeis, J.; Carbone, E.G.; Links, J. The COPEWELL rubric: A self-assessment toolkit to strengthen community resilience to disasters. Int. J. Environ. Res. Public Health 2019, 16, 2372. [Google Scholar] [CrossRef]
- Tiernan, A.; Drennan, L.; Nalau, J.; Onyango, E.; Morrissey, L.; Mackey, B. A review of themes in disaster resilience literature and international practice since 2012. Policy Des. Pract. 2019, 2, 53–74. [Google Scholar] [CrossRef]
- Adger, W.N. Vulnerability. Glob. Environ. Chang. 2006, 16, 268–281. [Google Scholar] [CrossRef]
- Salas, J.; Yepes, V. Urban vulnerability assessment: Advances from the strategic planning outlook. J. Clean. Prod. 2018, 179, 544–558. [Google Scholar] [CrossRef]
- Szewrański, S.; Świader, M.; Kazak, J.K.; Tokarczyk-Dorociak, K.; van Hoof, J. Socio-environmental vulnerability mapping for environmental and flood resilience assessment: The case of ageing and poverty in the city of Wrocław, Poland. Integr. Environ. Assess. Manag. 2018, 14, 592–597. [Google Scholar] [CrossRef]
- Cutter, S.L.; Barnes, L.; Berry, M.; Burton, C.; Evans, E.; Tate, E.; Webb, J. A place-based model for understanding community resilience to natural disasters. Glob. Environ. Chang. 2008, 18, 598–606. [Google Scholar] [CrossRef]
- Cutter, S.L.; Burton, C.G.; Emrich, C.T. Disaster resilience indicators for benchmarking baseline conditions. J. Homel. Secur. Emerg. Manag. 2010, 7, 1–24. [Google Scholar] [CrossRef]
- Sherrieb, K.; Norris, F.H.; Galea, S. Measuring capacities for community resilience. Soc. Indic. Res. 2010, 99, 227–247. [Google Scholar] [CrossRef]
- Frazier, T.G.; Thompson, C.M.; Dezzani, R.J.; Butsick, D. Spatial and temporal quantification of resilience at the community scale. Appl. Geogr. 2013, 42, 95–107. [Google Scholar] [CrossRef]
- Pfefferbaum, R.L.; Pfefferbaum, B.; Van Horn, R.L.; Klomp, R.W.; Norris, F.H.; Reissman, D.B. The communities advancing resilience toolkit (CART): An intervention to build community resilience to disasters. J. Public Health Manag. Pract. 2013, 19, 250–258. [Google Scholar] [CrossRef]
- Cutter, S.L.; Ash, K.D.; Emrich, C.T. The geographies of community disaster resilience. Glob. Environ. Chang. 2014, 29, 65–77. [Google Scholar] [CrossRef]
- Burton, C.G. A validation of metrics for community resilience to natural hazards and disasters using the recovery from Hurricane Katrina as a case study. Ann. Assoc. Am. Geogr. 2015, 105, 67–86. [Google Scholar] [CrossRef]
- Cimellaro, G.P.; Renschler, C.; Reinhorn, A.M. PEOPLES: A framework for evaluating resilience. J. Struct. Eng. 2016, 142, 04016063. [Google Scholar] [CrossRef]
- Suárez, M.; Gómez-Baggethun, E.; Benayas, J.; Tilbury, D. Towards an urban resilience index: A case study in 50 Spanish cities. Sustainability 2016, 8, 774. [Google Scholar] [CrossRef]
- Wang, L.; Xue, X.; Wang, Z.; Zhang, L. A unified assessment approach for urban infrastructure sustainability and resilience. Adv. Civ. Eng. 2018, 2018, 2073968. [Google Scholar] [CrossRef]
- Sharifi, A.; Yamagata, Y. Urban resilience assessment: Multiple dimensions, criteria, and indicators. In Urban Resilience; Yamagata, Y., Maruyama, H., Eds.; Springer International Publishing: Cham, Switzerland, 2016; pp. 259–276. [Google Scholar]
- Bruneau, M.; Reinhorn, A. Exploring the concept of seismic resilience for acute care facilities. Earthq. Spectra 2007, 23, 41–62. [Google Scholar] [CrossRef]
- Cimellaro, G.P.; Reinhorn, A.M.; Bruneau, M. Framework for analytical quantification of disaster resilience. Eng. Struct. 2010, 32, 3639–3649. [Google Scholar] [CrossRef]
- Henry, D.; Emmanuel Ramirez-Marquez, J. Generic metrics and quantitative approaches for system resilience as a function of time. Reliab. Eng. Syst. Saf. 2012, 99, 114–122. [Google Scholar] [CrossRef]
- United Nations International Strategy for Disaster Reduction. UNISDR Terminology on Disaster Risk Reduction. 2009. Available online: https://www.preventionweb.net/files/50683_oiewgreportenglish.pdf (accessed on 28 July 2019).
- European Civil Protection and Humanitarian Aid Operations. Disaster Preparedness. 2019. Available online: https://ec.europa.eu/echo/printpdf/what/humanitarian-aid/disaster_preparedness_en (accessed on 2 August 2019).
- Allen, K.M. Community-based disaster preparedness and climate adaptation: Local capacity-building in the Philippines. Disasters 2006, 30, 81–101. [Google Scholar] [CrossRef]
- Miceli, R.; Sotgiu, I.; Settanni, M. Disaster preparedness and perception of flood risk: A study in an alpine valley in Italy. J. Environ. Psychol. 2008, 28, 164–173. [Google Scholar] [CrossRef]
- Khademi, N.; Balaei, B.; Shahri, M.; Mirzaei, M.; Sarrafi, B.; Zahabiun, M.; Mohaymany, A.S. Transportation network vulnerability analysis for the case of a catastrophic earthquake. Int. J. Disaster Risk Reduct. 2015, 12, 234–254. [Google Scholar] [CrossRef]
- Thomas, L.S.; Vargas, L.G. Decision Making with the Analytic Network Process: Economics, Political, Social and Technological Application with Benefits, Opportunities, Costs and Risks, 2nd ed.; Springer: Heidelberg, Germany, 1980; pp. 1–370. [Google Scholar]
- Yang, Y.P.O.; Shieh, H.M.; Der Leu, J.; Tzeng, G.H. A novel hybrid MCDM model combined with DEMATEL and ANP with applications. Int. J. Oper. Res. 2008, 5, 160–168. [Google Scholar]
- Gabus, A.; Fontela, E. World Problems, an Invitation to Further Thought within the Framework of DEMATEL; Battelle Geneva Research Center: Geneva, Switzerland, 1972; pp. 5–57. [Google Scholar]
- Hsu, C.H.; Wang, F.K.; Tzeng, G.H. The best vendor selection for conducting the recycled material based on a hybrid MCDM model combining DANP with VIKOR. Resour. Conserv. Recycl. 2012, 66, 95–111. [Google Scholar] [CrossRef]
- Li, C.W.; Tzeng, G.H. Identification of a threshold value for the DEMATEL method using the maximum mean de-entropy algorithm to find critical services provided by a semiconductor intellectual property mall. Expert Syst. Appl. 2009, 36, 9891–9898. [Google Scholar] [CrossRef]
- Büyüközkan, G.; Güleryüz, S. An integrated DEMATEL-ANP approach for renewable energy resources selection in Turkey. Int. J. Prod. Econ. 2016, 182, 435–448. [Google Scholar] [CrossRef]
- Tsai, W.H.; Chou, W.C. Selecting management systems for sustainable development in SMEs: A novel hybrid model based on DEMATEL, ANP, and ZOGP. Expert Syst. Appl. 2009, 36, 1444–1458. [Google Scholar] [CrossRef]
- Gigović, L.; Pamučar, D.; Božanić, D.; Ljubojević, S. Application of the GIS-DANP-MABAC multi-criteria model for selecting the location of wind farms: A case study of Vojvodina, Serbia. Renew. Energy 2017, 103, 501–521. [Google Scholar] [CrossRef]
- Wang, Y.L.; Tzeng, G.H. Brand marketing for creating brand value based on a MCDM model combining DEMATEL with ANP and VIKOR methods. Expert Syst. Appl. 2012, 39, 5600–5615. [Google Scholar] [CrossRef]
- District Management Committee of the Chongqing West Railway Station. The Introduction of the Chongqing West Railway Station. 2018. Available online: http://www.cqxizhan.com/xzzk.html (accessed on 7 September 2019).
- Chongqing Municipal People’s Government. The Chongqing Medium- and Long-Term Railway Network Planning (2016–2030). 2017. Available online: http://www.cq.gov.cn/publicinfon/web/views/Show!detail.action?sid=4308529 (accessed on 10 September 2019).
| References | Objects | Indicator Categories |
|---|---|---|
| Cutter et al. [21] | community | social, economic, institutional, infrastructure, ecological, community competence |
| Cutter et al. [22] | community | social, economic, institutional, infrastructure, community capital |
| Sherrieb et al. [23] | community | social capital, economic development |
| Frazier et al. [24] | community | social, economic, institutional, infrastructure, community capital, regulatory, ecological, temporal, spatial |
| Pfefferbaum et al. [25] | community | connection and caring, resources, transformative potential, disaster management, information and communication |
| Cutter et al. [26] | community | social, economic, institutional, infrastructure, community capital, environmental |
| Kusumastuti et al. [9] | community | social, economic, institutional, infrastructure, community capacity, hazard |
| Burton [27] | community | social, economic, institutional, infrastructure, community capital, environmental systems |
| Cimellaro et al. [28] | community | social-cultural capital, economic development, organized governmental services, physical infrastructures, population and demographics, environmental and ecosystem, lifestyle and community competence |
| Suárez et al. [29] | urban system | self-sufficiency, business diversity, land use diversity, food diversity, spaces for citizen participation |
| Xu and Xue [1] | complex urban public spaces | economy development, government governance, physical structure, crowd cluster, natural environment, traffic accessibility, |
| Wang et al. [30] | infrastructure | demand, status, influence, resource, measure |
| Sharifi and Yamagata [31] | urban system | society and well-being, economy, governance and institution, built environment and infrastructure, materials and environmental resources |
| Level 1 | Weight | Score | Score | Level 2 | Weight | Score | Score | Level 3 | Score | Score |
|---|---|---|---|---|---|---|---|---|---|---|
| (W) | (L) | (W) | (L) | (W) | (L) | |||||
| Physical structure (P) | 0.098 | 0.290 | 0.241 | P1: Multi-layer structure | 0.011 | 1.750 | 2.250 | P1.1: The number of layers of CUPSs | 2 | 1 |
| P1.2: The height of the atrium | 2 | 4 | ||||||||
| P1.3: The number of layers of underground spaces | 1 | 2 | ||||||||
| P1.4: The height of each layer of CUPSs | 2 | 2 | ||||||||
| P2: Internal spatial layout | 0.035 | 3.500 | 2.833 | P2.1: The total number of escalators | 2 | 4 | ||||
| P2.2: The total number of elevators | 4 | 2 | ||||||||
| P2.3: The total number of emergency passages | 4 | 2 | ||||||||
| P2.4: The number of security checkpoints | 4 | 2 | ||||||||
| P2.5: The number of entrances and exits | 4 | 4 | ||||||||
| P2.6: The number of columns in the space | 3 | 3 | ||||||||
| P3: Underground spatial layout | 0.032 | 4.000 | 2.000 | P3.1: The coverage of the pedestrian passage | 4 | 2 | ||||
| P3.2: The coverage of the business zone | 4 | 2 | ||||||||
| P4: Multi-function | 0.020 | 1.000 | 2.667 | P4.1: The number of the function | 1 | 3 | ||||
| P4.2: The category of the function | 1 | 3 | ||||||||
| P4.3: The connection of the function | 1 | 2 | ||||||||
| Water supply and drainage preparation (W) | 0.048 | 0.144 | 0.144 | W1: Water supply and drainage facilities | 0.048 | 3.000 | 3.000 | W1.1: The number of emergency water supply facilities | 3 | 3 |
| W1.2: The number of emergency water drainage facilities | 3 | 3 | ||||||||
| Electronic power system (EP) | 0.058 | 0.232 | 0.193 | EP1: Emergency power supply equipment | 0.039 | 4.000 | 3.000 | EP1.1: The category of emergency power supply equipment | 4 | 3 |
| EP1.2: The amount of emergency power supply equipment | 4 | 3 | ||||||||
| EP2: Power condition | 0.019 | 4.000 | 4.000 | EP2.1: Voltage qualification rate | 4 | 4 | ||||
| EP2.2: Emergency lighting distribution rate | 4 | 4 | ||||||||
| Fire protection facilities (F) | 0.106 | 0.285 | 0.387 | F1: Fire-fighting equipment | 0.055 | 3.333 | 3.333 | F1.1: The amount of fire-fighting equipment | 3 | 4 |
| F1.2: The category of fire-fighting equipment | 4 | 2 | ||||||||
| F1.3: The amount of fire-fighting equipment in each layer of the CUPSs | 3 | 4 | ||||||||
| F2: Automatic alarm system | 0.051 | 2.000 | 4.000 | F2.1: The number of automatic fire alarm systems | 2 | 4 | ||||
| F2.2: The number of automatic fire alarm systems in each layer of the CUPSs | 2 | 4 | ||||||||
| Ventilation system (V) | 0.072 | 0.216 | 0.144 | V1: Ventilation facilities and equipment | 0.072 | 3.000 | 2.000 | V1.1: The number of air shafts | 3 | 2 |
| V1.2: Installation of the air conditioning system | 3 | 2 | ||||||||
| Environmental sanitation (ES) | 0.107 | 0.365 | 0.241 | ES1: Indoor environment of the CUPSs | 0.060 | 3.333 | 1.667 | ES1.1: Indoor temperature and humidity | 4 | 2 |
| ES1.2: Indoor volume decibel | 3 | 1 | ||||||||
| ES1.3: The cleanliness of the indoor environment | 3 | 2 | ||||||||
| ES2: Health protection measures | 0.047 | 3.500 | 3.000 | ES2.1: The number of cleaners in the CUPSs | 3 | 2 | ||||
| ES2.2: The number of sanitation and epidemic prevention personnel | 4 | 4 | ||||||||
| Characteristics of passenger flows (C) | 0.066 | 0.239 | 0.156 | C1: Statistics of passenger flows | 0.010 | 3.000 | 1.333 | C1.1: The designed capacity of the CUPSs | 2 | 2 |
| C1.2: The average daily volume of inbound passenger flows | 4 | 1 | ||||||||
| C1.3: The average daily volume of outbound passenger flows | 3 | 1 | ||||||||
| C2: Spatial distribution of passenger flows | 0.014 | 2.000 | 1.500 | C2.1: The maximum density of passenger volume | 1 | 1 | ||||
| C2.2: The distribution of passenger flows in each layer of the CUPSs | 3 | 2 | ||||||||
| C3: Temporal distribution of passenger flows | 0.004 | 2.500 | 2.000 | C3.1: Daily distribution of passenger flows | 3 | 1 | ||||
| C3.2: Annual distribution of passenger flows | 2 | 3 | ||||||||
| C4: Security protection for crowd clusters | 0.038 | 4.500 | 3.000 | C4.1: The average number of policemen for every crowd cluster | 5 | 3 | ||||
| C4.2: The amount of equipment and number of facilities for every crowd cluster | 4 | 3 | ||||||||
| Government governance (G) | 0.151 | 0.574 | 0.489 | G1: Multi-stakeholder cooperation | 0.017 | 3.500 | 4.000 | G1.1: The number of governance departments in the CUPSs | 4 | 4 |
| G1.2: Closeness of cooperation among different departments | 3 | 4 | ||||||||
| G1.3: The time period of multi-stakeholder cooperation | 3 | 4 | ||||||||
| G1.4: The degree of effectiveness of multi-stakeholder cooperation | 4 | 4 | ||||||||
| G2: Disaster emergency plan | 0.065 | 3.667 | 3.500 | G2.1: The number of overall emergency plans | 4 | 4 | ||||
| G2.2: The number of special emergency plans | 3 | 3 | ||||||||
| G2.3: The frequency of emergency drills | 4 | 3 | ||||||||
| G2.4: The number of professional rescuers | 4 | 4 | ||||||||
| G2.5: Professional rescuers’ training | 3 | 3 | ||||||||
| G2.6: The number of rescue material reserves | 4 | 4 | ||||||||
| G3: Disaster management plan | 0.069 | 4.000 | 2.800 | G3.1: The number of risk assessment measures | 4 | 3 | ||||
| G3.2: The number of risk mitigation plans | 3 | 3 | ||||||||
| G3.3: Strength of propaganda on risk event prevention | 4 | 3 | ||||||||
| G3.4: The number of evacuation signs in the CUPSs | 4 | 3 | ||||||||
| G3.5: The number of evacuation signs in each layer of the CUPSs | 4 | 3 | ||||||||
| G3.6: The number of emergency escape routes | 4 | 2 | ||||||||
| G3.7: The number of security policemen | 5 | 2 | ||||||||
| G3.8: The category and number of security facilities and equipment | 5 | 2 | ||||||||
| G3.9: The proportion of floating population exposed to disaster management education | 4 | 4 | ||||||||
| G3.10: The number of disaster management education activities per year | 3 | 3 | ||||||||
| Economic development (ED) | 0.096 | 0.358 | 0.369 | ED1: Economic support | 0.044 | 4.000 | 4.250 | ED1.1: Regional gross domestic product | 3 | 5 |
| ED1.2: Financial allocation to the CUPSs | 5 | 4 | ||||||||
| ED1.3: Financial reserves for the emergency rescue after risk events | 4 | 4 | ||||||||
| ED1.4: Financial reserves for the post-disaster reconstruction | 4 | 4 | ||||||||
| ED2: Prepared rescue materials | 0.052 | 3.500 | 3.500 | ED2.1: The number of prepared rescue materials | 4 | 4 | ||||
| ED2.2: The degree and category that the rescue materials could respond to | 3 | 3 | ||||||||
| Traffic accessibility (T) | 0.117 | 0.257 | 0.309 | T1: Traffic condition | 0.019 | 1.500 | 2.500 | T1.1: The number of connected roads | 2 | 3 |
| T1.2: Traffic flow operation status | 1 | 2 | ||||||||
| T2: Emergency rescue | 0.098 | 2.333 | 2.667 | T2.1: The unimpeded nature of special emergency routes | 2 | 2 | ||||
| T2.2: Emergency rescue vehicles’ accessibility | 2 | 3 | ||||||||
| T2.3: Rescuers’ accessibility | 3 | 3 | ||||||||
| Social cooperation (S) | 0.049 | 0.172 | 0.147 | S1: Social preparedness | 0.024 | 3.000 | 3.000 | S1.1: The proportion of floating population with emergency vehicles | 3 | 3 |
| S1.2: The proportion of floating population covered by medical services | 3 | 3 | ||||||||
| S2: Social service | 0.025 | 4.000 | 3.000 | S2.1: The number of emergency volunteers | 4 | 3 | ||||
| S2.2: The number of emergency nongovernmental organizations | 4 | 3 | ||||||||
| Natural environment (N) | 0.054 | 0.162 | 0.162 | N1: The statistics of multi-category natural disaster | 0.054 | 3.000 | 3.000 | N1.1: The statistics of strength for natural disasters | 3 | 3 |
| N1.2: The statistics of incidence for natural disasters | 3 | 3 |
| Level 1 | Weight | Score | Score | Level 2 | Weight | Score | Score | Level 3 | Score | Score |
|---|---|---|---|---|---|---|---|---|---|---|
| (W) | (L) | (W) | (L) | (W) | (L) | |||||
| Physical structure (P) | 0.131 | 0.368 | 0.580 | P1: Multi-layer structure | 0.020 | 4.500 | 4.000 | P1.1: The complexity of topography in the CUPSs | 5 | 4 |
| P1.2: The number of layers of the CUPSs | 4 | 4 | ||||||||
| P2: Internal spatial layout | 0.111 | 2.500 | 4.500 | P2.1: The load of escalators | 2 | 5 | ||||
| P2.2: The load of elevators | 3 | 4 | ||||||||
| P2.3: The number of emergency passage distributions | 1 | 4 | ||||||||
| P2.4: The volume of passenger flow at security checkpoints | 4 | 5 | ||||||||
| Water supply and drainage preparation (W) | 0.080 | 0.120 | 0.160 | W1: Water supply and drainage facilities | 0.080 | 1.500 | 2.000 | W1.1: The failure rate of the emergency water supply facilities | 2 | 2 |
| W1.2: The failure rate of the emergency water drainage facilities | 1 | 2 | ||||||||
| Electronic power system (EP) | 0.124 | 0.141 | 0.248 | EP1: Emergency power supply equipment | 0.073 | 1.000 | 2.000 | EP1.1: The failure rate of the emergency power supply equipment | 1 | 2 |
| EP2: Power condition | 0.051 | 1.333 | 2.000 | EP2.1: Voltage disqualification rate | 2 | 2 | ||||
| EP2.2: The frequency of average interruption | 1 | 2 | ||||||||
| EP2.3: The average interruption duration | 1 | 2 | ||||||||
| Fire protection facilities (F) | 0.103 | 0.235 | 0.384 | F1: Fire-fighting equipment | 0.057 | 2.500 | 3.500 | F1.1: The obsolete rate of fire-fighting equipment | 3 | 4 |
| F1.2: The failure rate of fire-fighting equipment | 2 | 3 | ||||||||
| F2: Automatic alarm system | 0.046 | 2.000 | 4.000 | F2.1: The failure rate of the automatic alarm systems | 2 | 4 | ||||
| Ventilation system (V) | 0.097 | 0.194 | 0.388 | V1: Ventilation facilities and equipment | 0.097 | 2.000 | 4.000 | V1.1: The failure rate of the air conditioning system | 2 | 4 |
| Characteristics of internal vulnerability (C) | 0.090 | 0.262 | 0.404 | C1: Crowd cluster statistics | 0.032 | 2.000 | 4.000 | C1.1: The frequency of passenger traffic overload | 2 | 4 |
| C2: Spatial distribution of crowd cluster | 0.030 | 3.333 | 5.000 | C2.1: The number of crowd clusters | 3 | 5 | ||||
| C2.2: The location of crowd clusters | 3 | 5 | ||||||||
| C2.3: The crowd cluster density of population in each layer | 4 | 5 | ||||||||
| C3: Temporal distribution of crowd cluster | 0.028 | 3.500 | 4.500 | C3.1: Daily distribution of crowd clusters | 3 | 5 | ||||
| C3.2: Annual distribution of crowd clusters | 4 | 4 | ||||||||
| Economy (E) | 0.084 | 0.200 | 0.241 | E1: Regional economic condition | 0.016 | 4.000 | 3.000 | E1.1: Regional average expense | 4 | 3 |
| E1.2: Portion of regional expense for daily needs | 4 | 3 | ||||||||
| E2: Financial reserves | 0.023 | 2.000 | 2.500 | E2.1: The financial reserves for post-disaster emergency rescue | 2 | 2 | ||||
| E2.2: The financial reserves for post-disaster reconstruction | 2 | 3 | ||||||||
| E3: Rescue material reserves | 0.045 | 2.000 | 3.000 | E3.1: The reserves for post-disaster rescue material | 2 | 3 | ||||
| Traffic (T) | 0.068 | 0.204 | 0.238 | T1: Traffic condition | 0.068 | 3.000 | 3.500 | T1.1: Traffic accessibility | 4 | 3 |
| T1.2: Public transportation service capacity | 2 | 4 | ||||||||
| Social cooperation (S) | 0.062 | 0.186 | 0.186 | S1: Social circumstance | 0.062 | 3.000 | 3.000 | S1.1: The coverage of emergency vehicles | 3 | 3 |
| S1.2: The coverage of medical services | 3 | 3 | ||||||||
| Hazard (H) | 0.174 | 0.352 | 0.435 | H1: Variety | 0.037 | 2.750 | 2.500 | H1.1: The number of natural disasters | 2 | 1 |
| H1.2: The number of accident disasters | 2 | 3 | ||||||||
| H1.3: The number of public health accidents | 3 | 2 | ||||||||
| H1.4: The number of social security accidents | 4 | 4 | ||||||||
| H2: Characteristics | 0.045 | 2.500 | 2.500 | H2.1: The strength of emergencies | 3 | 2 | ||||
| H2.2: The frequency of emergencies | 2 | 3 | ||||||||
| H3: Severity | 0.092 | 1.500 | 2.500 | H3.1: The degree of loss in the CUPSs | 1 | 3 | ||||
| H3.2: Disaster-prone areas of the CUPSs | 2 | 4 | ||||||||
| H3.3: The number of injured casualties in the CUPSs’ disaster area | 1 | 1 | ||||||||
| H3.4: The loss caused by disasters per year | 2 | 2 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, H.; Li, Y.; Wang, L. Resilience Assessment of Complex Urban Public Spaces. Int. J. Environ. Res. Public Health 2020, 17, 524. https://doi.org/10.3390/ijerph17020524
Xu H, Li Y, Wang L. Resilience Assessment of Complex Urban Public Spaces. International Journal of Environmental Research and Public Health. 2020; 17(2):524. https://doi.org/10.3390/ijerph17020524
Chicago/Turabian StyleXu, Hui, Yang Li, and Lin Wang. 2020. "Resilience Assessment of Complex Urban Public Spaces" International Journal of Environmental Research and Public Health 17, no. 2: 524. https://doi.org/10.3390/ijerph17020524
APA StyleXu, H., Li, Y., & Wang, L. (2020). Resilience Assessment of Complex Urban Public Spaces. International Journal of Environmental Research and Public Health, 17(2), 524. https://doi.org/10.3390/ijerph17020524






