Effects of Data Aggregation on Time Series Analysis of Seasonal Infections
Abstract
1. Introduction
2. Case Study Data
3. Building the Time Series
4. Assessing Data Irregularities
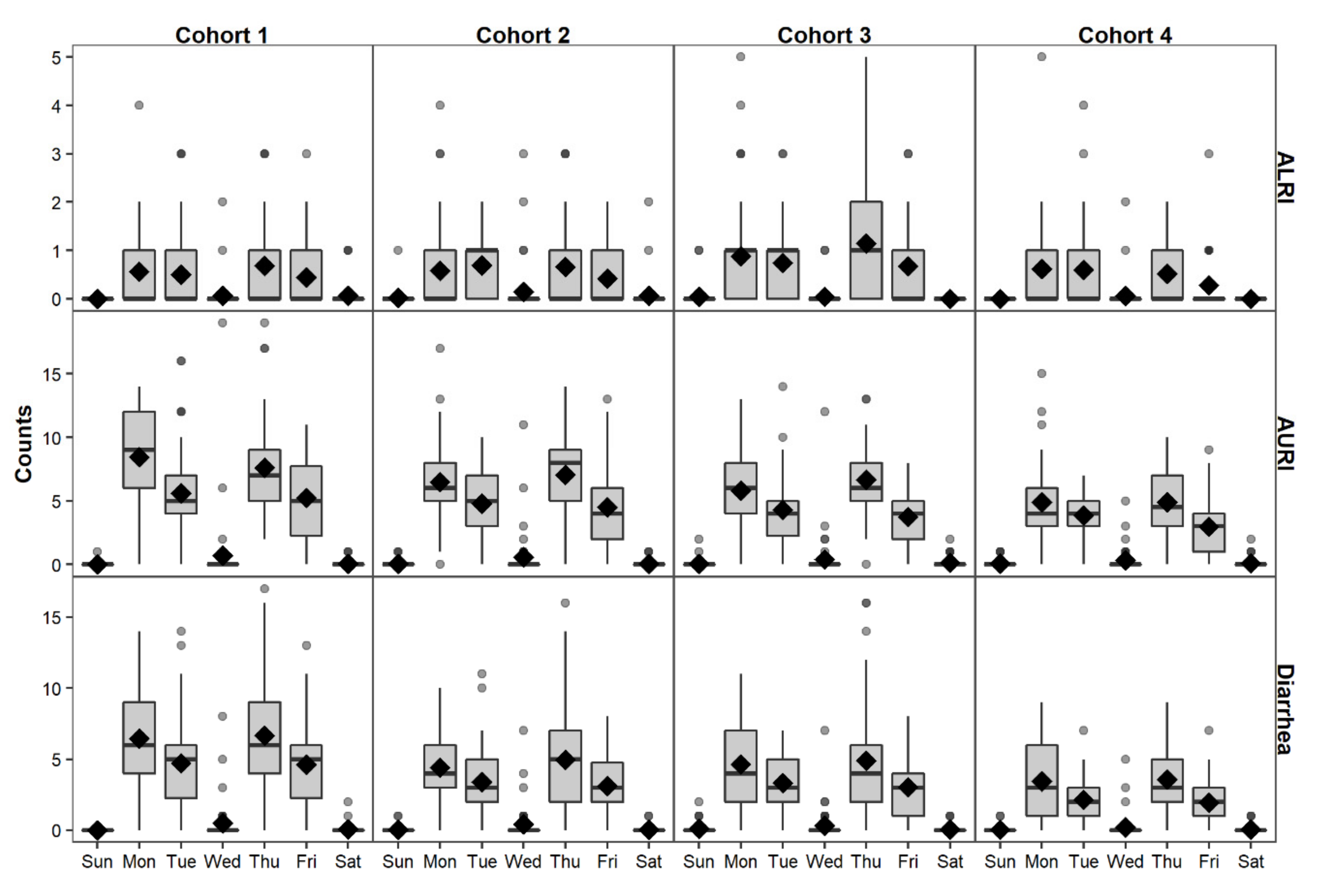
4.1. Calendar Effects for Daily Data
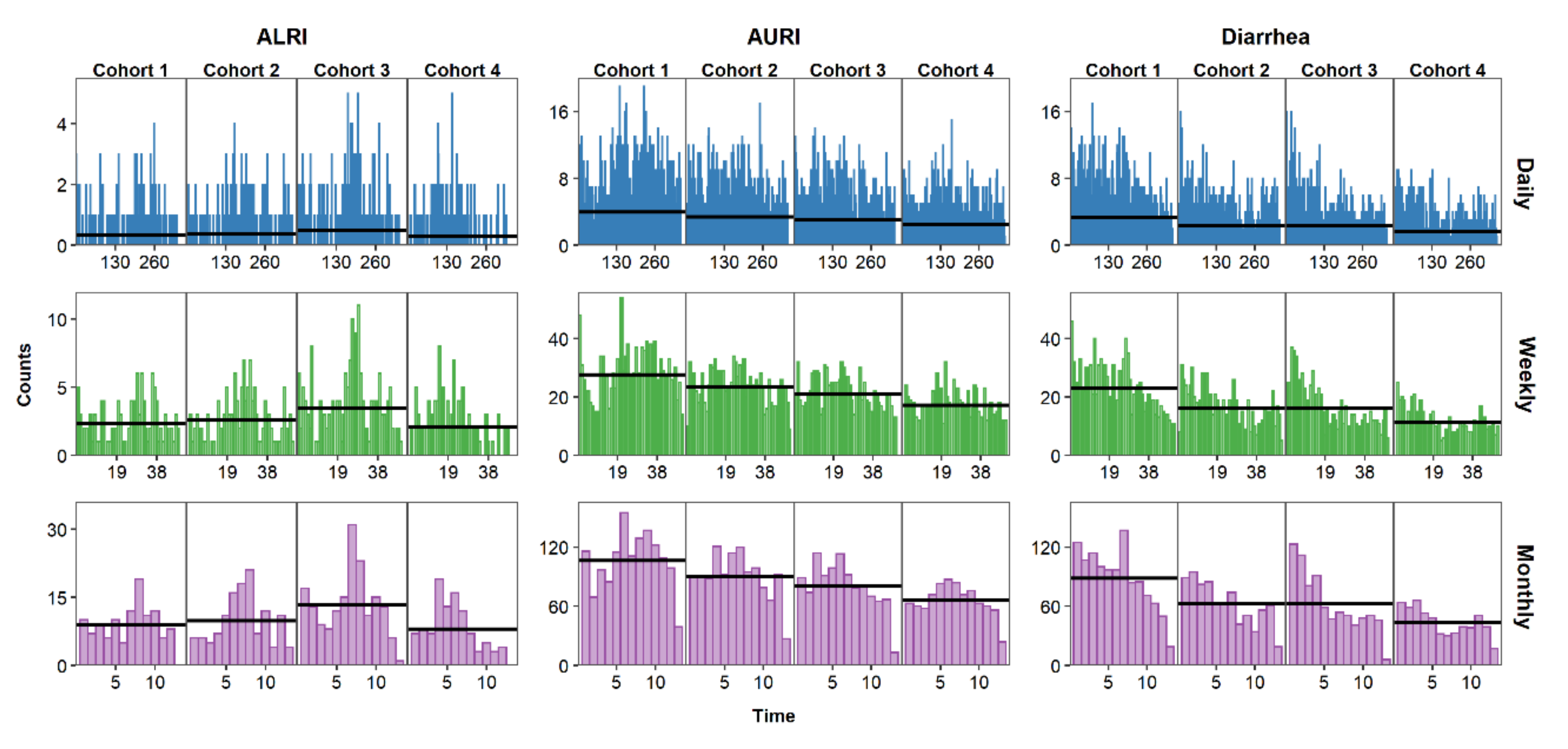
4.2. Aggregation Irregularities for Weekly and Monthly Data
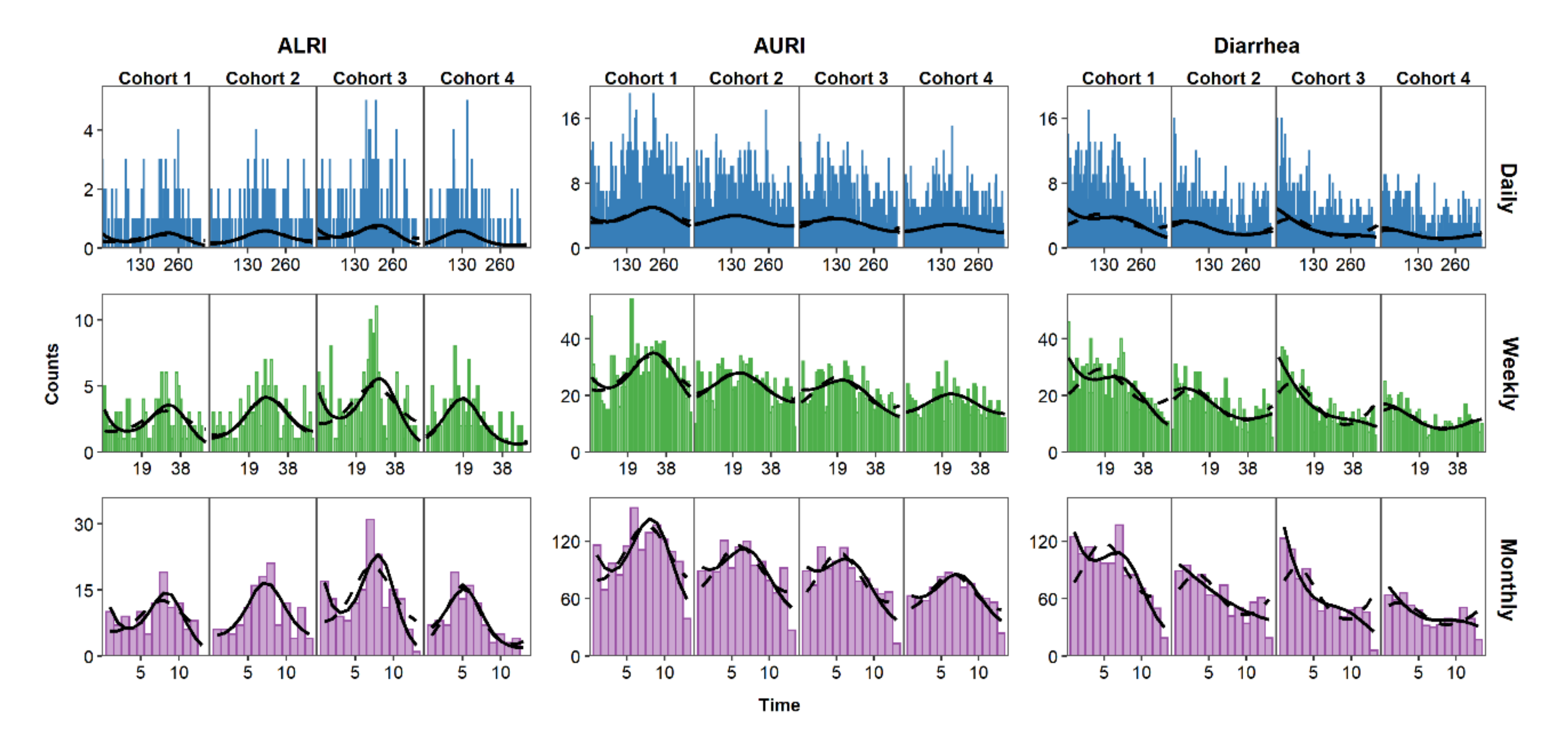
5. Visualizing the Time Series
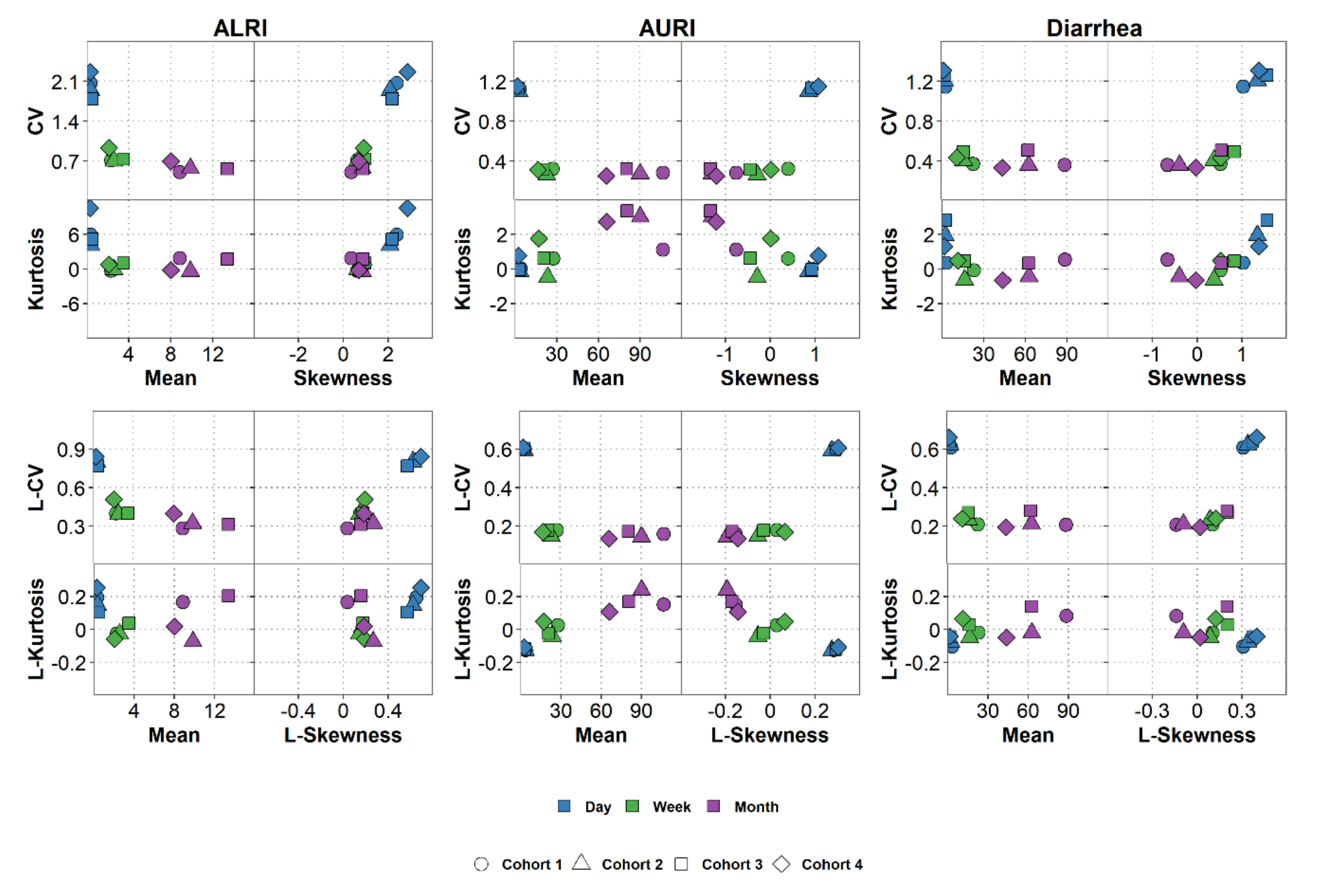
6. Characterizing the Data Distribution
7. Modeling Time Series
7.1. Selecting a Model
7.2. Assessing Model Fit
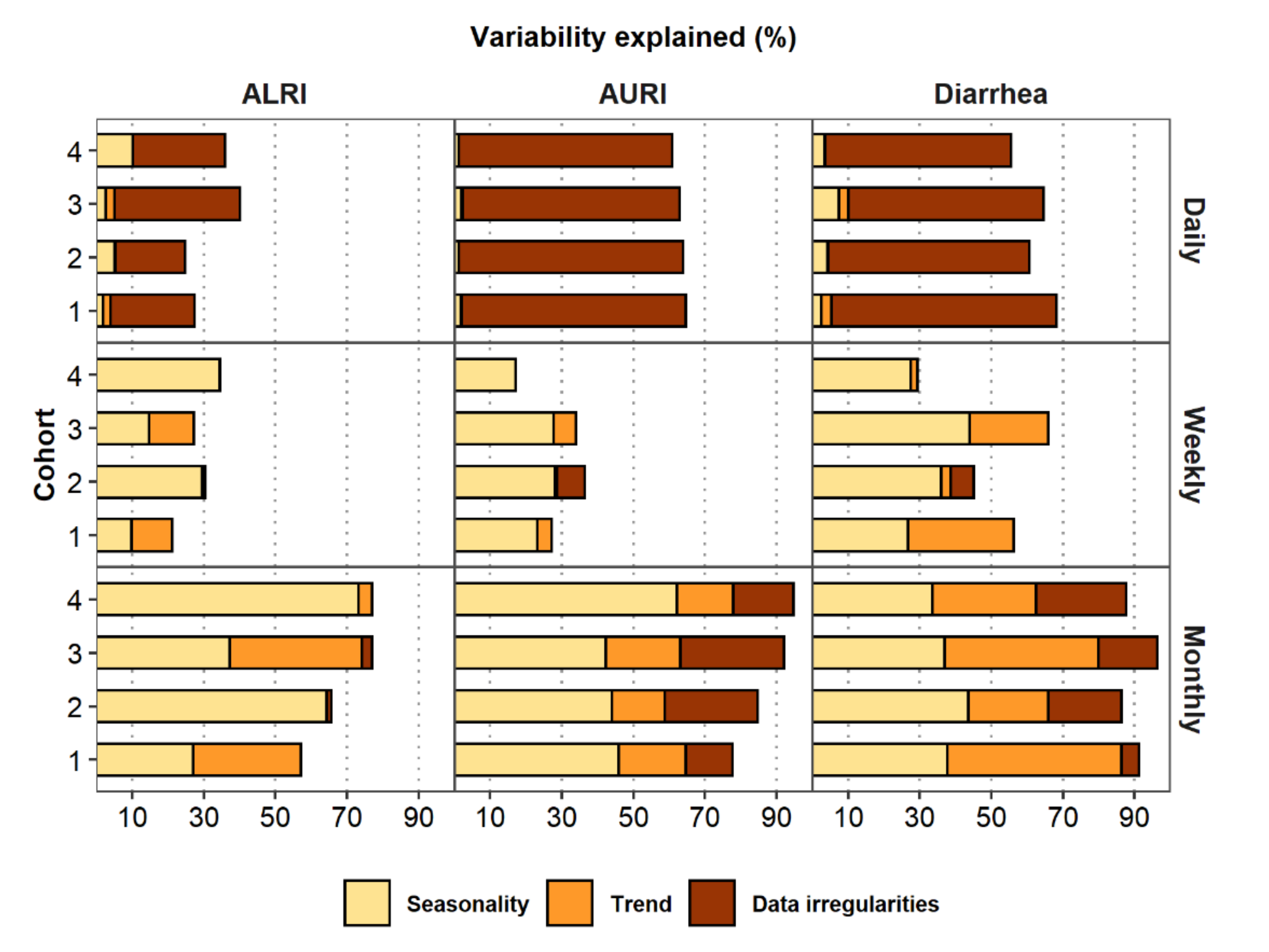
7.3. Modeling Seasonality, Trend, and Data Irregularities
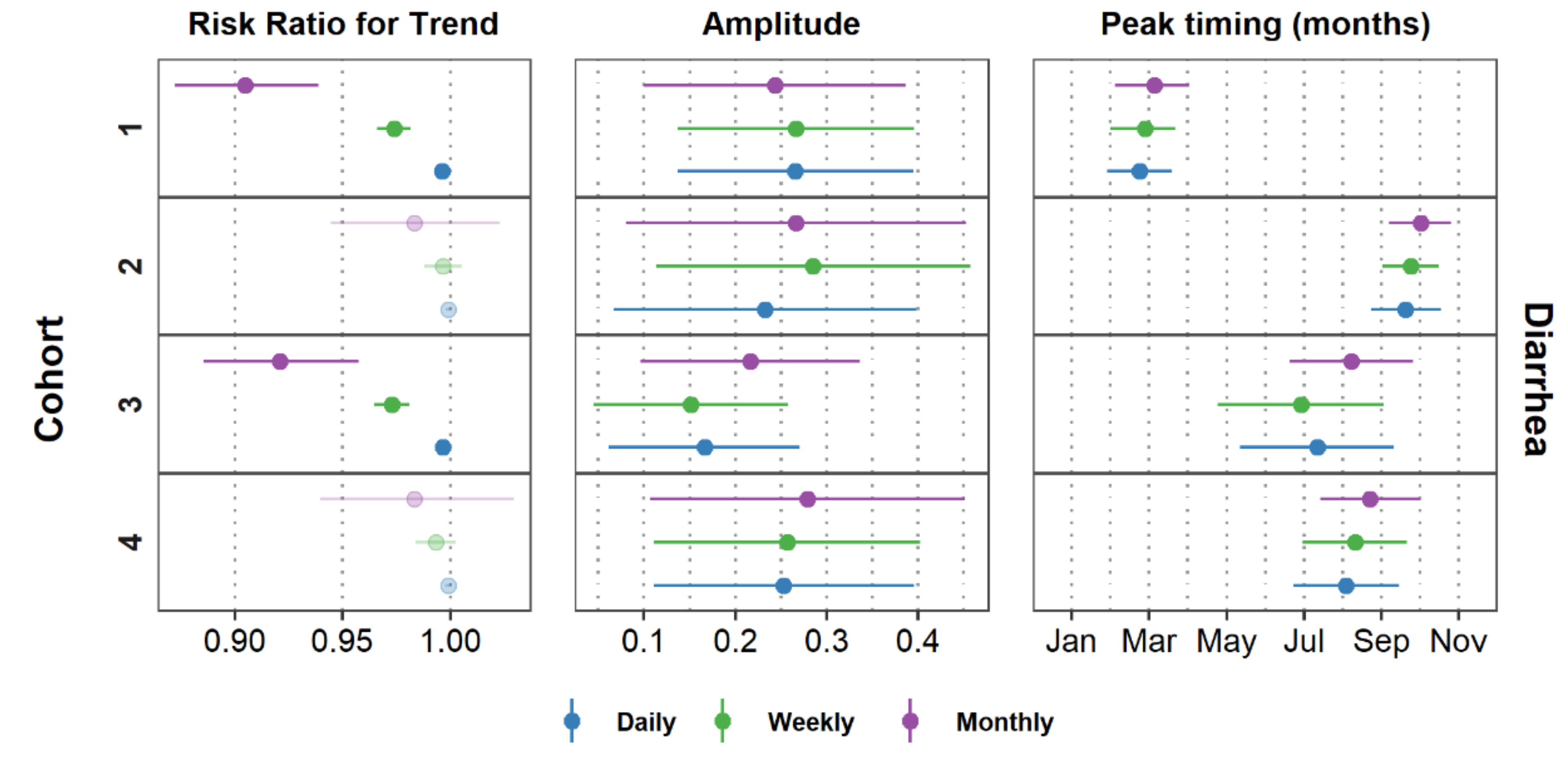
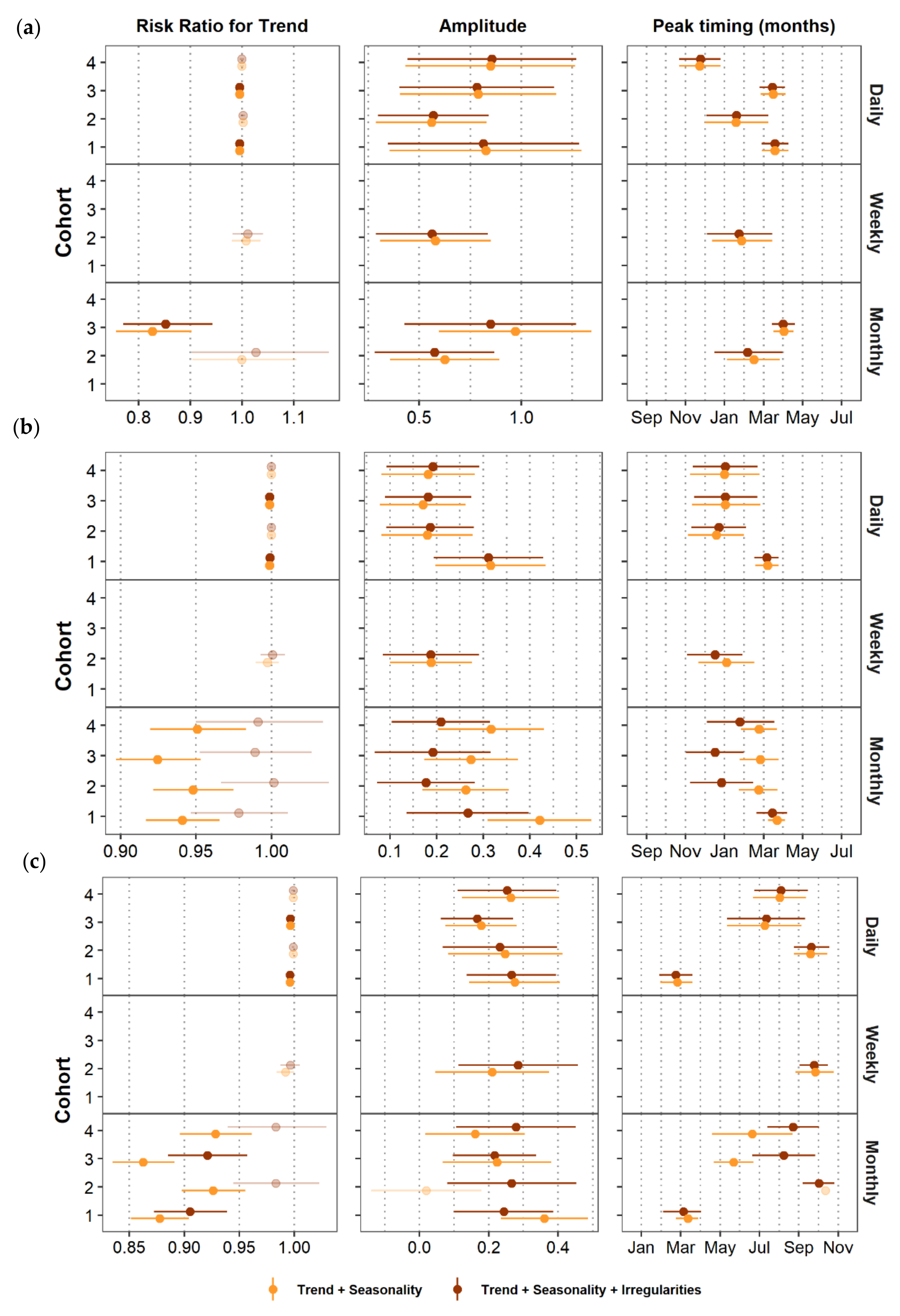
7.4. Characterizing Amplitude and Peak Timing
8. Comparing Model Results
9. Further Considerations
10. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A

References
- Stratton, M.D.; Ehrlich, H.Y.; Mor, S.M.; Naumova, E.N. A comparative analysis of three vector-borne diseases across Australia using seasonal and meteorological models. Sci. Rep. 2017, 7, 40186. [Google Scholar] [CrossRef]
- Altizer, S.; Dobson, A.; Hosseini, P.; Hudson, P.; Pascual, M.; Rohani, P. Seasonality and the dynamics of infectious diseases. Ecol. Lett. 2006, 9, 467–484. [Google Scholar] [CrossRef]
- Ureña-Castro, K.; Ávila, S.; Gutierrez, M.; Naumova, E.N.; Ulloa-Gutierrez, R.; Mora-Guevara, A. Seasonality of Rotavirus Hospitalizations at Costa Rica’ s National Children’ s Hospital in 2010–2015. Int. J. Environ. Res. Publ. Health 2019, 16, 1–13. [Google Scholar] [CrossRef]
- Sarkar, R.; Kang, G.; Naumova, E.N. Rotavirus Seasonality and Age Effects in a Birth Cohort Study of Southern India. PLoS ONE 2013, 8, e71616. [Google Scholar]
- Phin, N.; Parry-Ford, F.; Harrison, T.; Stagg, H.R.; Zhang, N.; Kumar, K.; Lortholary, O.; Zumla, A.; Abubakar, I. Epidemiology and clinical management of Legionnaires’ disease. Lancet Infect. Dis. 2014, 14, 1011–1021. [Google Scholar] [CrossRef]
- Naumova, E.N.; Jagai, J.S.; Matyas, B.; DeMaria, A.; MacNeill, I.B.; Griffiths, J.K. Seasonality in six enterically transmitted diseases and ambient temperature. Epidemiol. Infect. 2007, 135, 281–292. [Google Scholar] [CrossRef]
- Lal, A.; Hales, S.; French, N.; Baker, M.G. Seasonality in Human Zoonotic Enteric Diseases: A Systematic Review. PLoS ONE 2012, 7, e31883. [Google Scholar] [CrossRef]
- Naumova, E.N.; Christodouleas, J.; Hunter, P.R.; Syed, Q. Effect of precipitation on seasonal variability in cryptosporidiosis recorded by the North West England surveillance system in 1990–1999. J. Water Health 2005, 3, 185–196. [Google Scholar]
- Naumova, E.N.; MacNeill, I.B. Seasonality assessment for biosurveillance systems. In Advances in Statistical Methods for the Health Sciences; Auget, J.-L., Balakrishnan, N., Mesbah, M., Molenberghs, G., Eds.; Birkhauser: Boston, MA, USA, 2006; pp. 437–450. [Google Scholar]
- Bhaskaran, K.; Gasparrini, A.; Hajat, S.; Smeeth, L.; Armstrong, B. Time series regression studies in environmental epidemiology. Int. J. Epidemiol. 2013, 42, 1187–1195. [Google Scholar] [CrossRef]
- Chatfield, C. The Analysis of Time Series: An Introduction, 6th ed.; Chapman & Hall: New York, NY, USA; CRC: Boca Raton, FL, USA, 2003; p. 352. [Google Scholar]
- Zeger, S.L.; Irizarry, R.; Peng, R.D. On time series analysis of public health and biomedical data. Annu. Rev. Publ. Health 2006, 27, 57–79. [Google Scholar]
- Lopez Bernal, J.; Cummins, S.; Gasparrini, A. Interrupted time series regression for the evaluation of public health interventions: A tutorial. Int. J. Epidemiol. 2016, 46, 348–355. [Google Scholar] [CrossRef]
- Barnett, A.G.; Dobson, A.J. Analysing Seasonal Health Data; Springer: Berlin, Germany, 2010. [Google Scholar]
- Stashevsky, P.S.; Yakovina, I.N.; Alarcon Falconi, T.M.; Naumova, E.N. Agglomerative Clustering of Enteric Infections and Weather Parameters to Identify Seasonal Outbreaks in Cold Climates. Int. J. Environ. Res. Publ. Health 2019, 16, 2083. [Google Scholar] [CrossRef]
- Alarcon Falconi, T.M.; Cruz, M.S.; Naumova, E.N. The shift in seasonality of legionellosis in the USA. Epidemiol. Infect. 2018, 146, 1824–1833. [Google Scholar] [CrossRef]
- Centers for Disease Control and Prevention (CDC). Legionellosis—United States, 2000–2009. Morb. Mortal. Wkl. Rep. 2011, 60, 1083–1086. [Google Scholar]
- Ontario Agency for Health Protection and Promotion (Public Health Ontario). Epidemiology of Legionellosis in Ontario, 2013. Surveillance Period: January 1, 2013 to December 31, 2013; Public Health Ontario: Toronto, ON, Canada, 2014. [Google Scholar]
- European Centre for Disease Prevention and Control. Legionnaires’ Disease in Europe, 2014; European Centre for Disease Prevention and Control: Stockholm, Sweden, 2016. [Google Scholar]
- Alonso, W.J.; Cile Viboud, C.; Simonsen, L.; Hirano, E.W.; Daufenbach, L.Z.; Miller, M.A. Original Contribution Seasonality of Influenza in Brazil: A Traveling Wave from the Amazon to the Subtropics. Am. J. Epidemiol. 2007, 165, 1434–1442. [Google Scholar] [CrossRef]
- Chui, K.K.; Webb, P.; Russell, R.M.; Naumova, E.N. Geographic variations and temporal trends of Salmonella-associated hospitalization in the U.S. elderly, 1991–2004: A time series analysis of the impact of HACCP regulation. BMC Publ. Health 2009, 9, 447. [Google Scholar] [CrossRef]
- Adegboye, O.A.; Al-Saghir, M.; Leung, D.H.Y. Joint spatial time-series epidemiological analysis of malaria and cutaneous leishmaniasis infection. Epidemiol. Infect. 2017, 145, 685–700. [Google Scholar] [CrossRef] [PubMed]
- Burkom, H.S.; Elbert, Y.; Feldman, A.; Lin, J. Role of data aggregation in biosurveillance detection strategies with applications from ESSENCE. Morbid. Mortal. Wkl. Rep. 2004, 53, 67–73. [Google Scholar]
- Cherrie, M.P.C.; Nichols, G.; Iacono, G.L.; Sarran, C.; Hajat, S.; Fleming, L.E. Pathogen seasonality and links with weather in England and Wales: A big data time series analysis. BMC Publ. Health 2018, 18, 1067. [Google Scholar] [CrossRef]
- Centers for Disease Control and Prevention. National Notifiable Diseases Surveillance System, Weekly Tables of Infectious Disease Data. Atlanta, GA, USA. Available online: https://www.cdc.gov/nndss/infectious-tables.html (accessed on 17 June 2020).
- Fefferman, N.H.; O’Neil, E.A.; Naumova, E.N. Confidentiality and Confidence: Is Data Aggregation a Means to Achieve Both? J. Publ. Health Policy 2005, 26, 430–449. [Google Scholar] [CrossRef]
- Wei, W.W.S. Some Consequences of Temporal Aggregation in Seasonal Time Series Models. In Seasonal Analysis of Economic Time Series National Bureau of Economic Research; Zellner, A., Ed.; National Bureau of Economic Research: Washington, DC, USA, 1978; pp. 433–448. [Google Scholar]
- Simpson, R.B.; Alarcon Falconi, T.M.; Venkat, A.; Chui, K.H.H.; Navidad, J.; Naumov, Y.N.; Gorski, J.; Bhattacharyya, S.; Naumova, E.N. Incorporating calendar effects to predict influenza seasonality in Milwaukee, Wisconsin. Epidemiol. Infect. 2019, 147, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Cheng, T.; Adepeju, M. Modifiable Temporal Unit Problem (MTUP) and Its Effect on Space-Time Cluster Detection. PLoS ONE 2014, 9, e100465. [Google Scholar] [CrossRef] [PubMed]
- Cleveland, W.S.; Devlin, S.J. Calendar Effects in Monthly Time Series: Detection by Spectrum Analysis and Graphical Methods. J. Am. Stat. Assoc. 1980, 75, 487–496. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2018. [Google Scholar]
- Team Rs. RStudio: Integrated Development for R; RStudio, Inc.: Boston, MA, USA, 2006. [Google Scholar]
- Walter, S.D. Calendar Effects in the Analysis of Seasonal Data. Am. J. Epidemiol. 1994, 140, 649–657. [Google Scholar] [CrossRef]
- Cleveland, W.S.; Devlin, S.J. Calendar effects in monthly time series: Modeling and adjustment. J. Am. Stat. Assoc. 1982, 77, 520–528. [Google Scholar]
- Simon, A.K.; Hollander, G.A.; McMichael, A. Evolution of the immune system in humans from infancy to old age. Proc. Royal Soc. B 2015, 282. [Google Scholar] [CrossRef]
- Hosking, J.R.M. L-Moments: Analysis and Estimation of Distributions Using Linear Combinations of Order Statistics. J. Royal Stat. Soc. Ser. B Methodol. 1990, 52, 105–124. [Google Scholar]
- Ver Hoef, J.M.; Boveng, P.L. Quasi-Poisson vs. Negative Binomial Regression: How Should We Model Overdispersed Count Data? Ecology 2007, 88, 2766–2772. [Google Scholar] [CrossRef]
- Openshaw, S. Ecological fallacies and the analysis of areal census data (UK, Italy). Environ. Plan. A 1984, 16, 17–31. [Google Scholar] [CrossRef]
- Dark, S.J.; Bram, D. The modifiable areal unit problem (MAUP) in physical geography. Prog. Phys. Geogr. 2007, 31, 471–479. [Google Scholar]
- Kang, H. The prevention and handling of the missing data. Korean J. Anesthesiol. 2013, 64, 402–406. [Google Scholar] [CrossRef] [PubMed]
- Dilmaghani, S.; Henry, I.C.; Soonthornnonda, P.; Christensen, E.R.; Henry, R.C. Harmonic analysis of environmental time series with missing data or irregular sample spacing. Environ. Sci. Technol. 2007, 41, 7030–7038. [Google Scholar] [CrossRef] [PubMed]
- Ramanathan, K.; Thenmozhi, M.; George, S.; Anandan, S.; Veeraraghavan, B.; Naumova, E.N.; Jeyaseelan, L. Assessing Seasonality Variation with Harmonic Regression: Accommodations for Sharp Peaks. Int. J. Environ. Res. Publ. Health 2020, 17, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Naumova, E.N.; Yepes, H.; Griffiths, J.K.; Sempértegui, F.; Khurana, G.; Jagai, J.S.; Játiva, E.; Estrella, B. Emergency room visits for respiratory conditions in children increased after Guagua Pichincha volcanic eruptions in April 2000 in Quito, Ecuador observational study: Time series analysis. Environ. Health Glob. Access Sci. Source 2007, 6, 21. [Google Scholar] [CrossRef] [PubMed]



| Date | Day of the Week | Day | Counts of Diarrhea | |||||
|---|---|---|---|---|---|---|---|---|
| Daily | Weekly | Monthly | ||||||
| Calendar | Study | Calendar | Study | Calendar | Study | |||
| 7/16/2000 | Sun. | 1 | 25 | … | ||||
| 7/17/2000 | Mon. | 2 | 72 | |||||
| 7/18/2000 | Tue. | 3 | ||||||
| 7/19/2000 | Wed. | 4 | ||||||
| 7/20/2000 | Thu. | 5 | 1 | 16 | 46 | 125 | ||
| 7/21/2000 | Fri. | 6 | 2 | 9 | ||||
| 7/22/2000 | Sat. | 7 | 3 | 0 | ||||
| 7/23/2000 | Sun. | 8 | 4 | 0 | 36 | |||
| 7/24/2000 | Mon. | 9 | 5 | 14 | ||||
| 7/25/2000 | Tue. | 10 | 6 | 7 | ||||
| 7/26/2000 | Wed. | 11 | 7 | 0 | ||||
| 7/27/2000 | Thu. | 12 | 8 | 9 | 32 | |||
| 7/28/2000 | Fri. | 13 | 9 | 6 | ||||
| 7/29/2000 | Sat. | 14 | 10 | 0 | ||||
| 7/30/2000 | Sun. | 15 | 11 | 0 | 30 | |||
| 7/31/2000 | Mon. | 16 | 12 | 11 | ||||
| 8/1/2000 | Tue. | 17 | 13 | 6 | ||||
| 8/2/2000 | Wed. | 18 | 14 | 0 | ||||
| 8/3/2000 | Thu. | 19 | 15 | 9 | 25 | |||
| 8/4/2000 | Fri. | 20 | 16 | 4 | ||||
| 8/5/2000 | Sat. | 21 | 17 | 0 | ||||
| 8/6/2000 | Sun. | 22 | 18 | 0 | 19 | |||
| 8/7/2000 | Mon. | 23 | 19 | 7 | ||||
| 8/8/2000 | Tue. | 24 | 20 | 5 | ||||
| 8/9/2000 | Wed. | 25 | 21 | 0 | ||||
| 8/10/2000 | Thu. | 26 | 22 | 5 | 22 | |||
| 8/11/2000 | Fri. | 27 | 23 | 2 | ||||
| 8/12/2000 | Sat. | 28 | 24 | 0 | ||||
| 8/13/2000 | Sun. | 29 | 25 | 0 | ||||
| 8/14/2000 | Mon. | 30 | 26 | 6 | ||||
| 8/15/2000 | Tue. | 31 | 27 | 9 | ||||
| 8/16/2000 | Wed. | 32 | 28 | 0 | 30 | 116 | ||
| … | …. | … | … | … | … | … | … | … |
| Cohort | Effective Length | Actual Length | Missing Data | Aggregation Irregularities |
|---|---|---|---|---|
| NE | N | ID (%) | n (%) | |
| Daily Aggregation | ||||
| 1 | 350 | 348 | 2 (0.6) | -- |
| 2 | 350 | 345 | 5 (1.4) | -- |
| 3 | 350 | 344 | 6 (1.7) | -- |
| 4 | 350 | 348 | 2 (0.6) | -- |
| Weekly Aggregation | ||||
| 1 | 50 | 50 | 0 (0.0) | 0 (0.0) |
| 2 | 50 | 50 | 0 (0.0) | 1 (2.0) |
| 3 | 50 | 50 | 0 (0.0) | 1 (2.0) |
| 4 | 50 | 50 | 0 (0.0) | 0 (0.0) |
| Monthly Aggregation | ||||
| 1 | 13 | 13 | 0 (0.0) | 1 (7.7) |
| 2 | 13 | 13 | 0 (0.0) | 1 (7.7) |
| 3 | 13 | 13 | 0 (0.0) | 1 (7.7) |
| 4 | 13 | 13 | 0 (0.0) | 1 (7.7) |
| Cohort | Time | Missing Days (%) | Aggregation Standard | Time Units with Aggregation Irregularities | ||
|---|---|---|---|---|---|---|
| Non-Working | Working | Total | ||||
| Weekly Aggregation | ||||||
| 1 | 28 | 1 (33.3) | -- | 1 (14.3) | Complete | 0 |
| 50 | 1 (33.3) | -- | 1 (14.3) | Complete | ||
| 2 | 10 | 2 (66.7) | -- | 2 (28.6) | Complete | 1 |
| 48 | 1 (33.3) | -- | 1 (14.3) | Complete | ||
| 50 | 1 (33.3) | 1 (25.0) | 2 (28.6) | Incomplete | ||
| 3 | 9 | 1 (33.3) | -- | 1 (14.3) | Complete | 1 |
| 50 | 3 (100.0) | 2 (50.0) | 5 (71.4) | Incomplete | ||
| 4 | 50 | 2 (66.7) | -- | 2 (28.6) | Complete | 0 |
| Monthly Aggregation | ||||||
| 1 | 7 | 1 (8.3) | -- | 1 (3.3) | Complete | 1 |
| 13 | 5 (50.0) | 6 (42.9) | 11 (36.7) | Incomplete | ||
| 2 | 3 | 2 (16.7) | -- | 2 (6.7) | Complete | 1 |
| 12 | 1 (8.3) | -- | 1 (3.3) | Complete | ||
| 13 | 5 (50.0) | 7 (50.0) | 12 (40.0) | Incomplete | ||
| 3 | 3 | 1 (8.3) | -- | 1 (3.3) | Complete | 1 |
| 13 | 7 (70.0) | 8 (57.1) | 15 (50.0) | Incomplete | ||
| 4 | 13 | 6 (60.0) | 6 (42.9) | 12 (40.0) | Incomplete | 1 |
| Cohort | N | Aggregation Irregularities (n) | ALRI | AURI | Diarrhea | |||
|---|---|---|---|---|---|---|---|---|
| Time with No Cases (%) | Time with No Cases (%) | Time with No Cases (%) | ||||||
| Incomplete | Complete | Incomplete | Complete | Incomplete | Complete | |||
| Weekly aggregation | ||||||||
| 1 | 50 | 0 | -- | 6 (12) | -- | 0 (0) | -- | 0 (0) |
| 2 | 50 | 1 | 0 (0) | 5 (10) | 0 (0) | 0 (0) | 0 (0) | 0 (0) |
| 3 | 50 | 1 | 1 (100)* | 4 (8) | 1 (100)* | 0 (0) | 1 (100)* | 0 (0) |
| 4 | 50 | 0 | -- | 15 (30) | -- | 1 (2) | -- | 1 (2) |
| Monthly aggregation | ||||||||
| 1 | 13 | 1 | 1 (100)* | 0 (0) | 0 (0) | 0 (0) | 0 (0) | 0 (0) |
| 2 | 13 | 1 | 0 (0) | 0 (0) | 0 (0) | 0 (0) | 0 (0) | 0 (0) |
| 3 | 13 | 1 | 0 (0) | 0 (0) | 0 (0) | 0 (0) | 0 (0) | 0 (0) |
| 4 | 13 | 1 | 1 (100)* | 0 (0) | 0 (0) | 0 (0) | 0 (0) | 0 (0) |
| Cohort | Total Cases | Time with No Cases (%) | Minimum | Maximum | Median | Mean | Sd | Variance | CV | Skewness | Kurtosis | L-CV | L-Skewness | L-Kurtosis |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Daily Aggregation | ||||||||||||||
| 1 | 115 | 266 (76.4) | 0 | 4 | 0 | 0.330 | 0.685 | 0.470 | 2.074 | 2.384 | 5.956 | 0.818 | 0.652 | 0.194 |
| 2 | 128 | 257 (74.5) | 0 | 4 | 0 | 0.371 | 0.720 | 0.519 | 1.942 | 2.078 | 4.111 | 0.803 | 0.622 | 0.147 |
| 3 | 174 | 235 (68.3) | 0 | 5 | 0 | 0.506 | 0.907 | 0.822 | 1.793 | 2.178 | 5.167 | 0.770 | 0.573 | 0.104 |
| 4 | 104 | 276 (79.3) | 0 | 5 | 0 | 0.299 | 0.677 | 0.458 | 2.264 | 2.864 | 10.562 | 0.841 | 0.694 | 0.254 |
| Weekly Aggregation | ||||||||||||||
| 1 | 115 | 6 (12.0) | 0 | 6 | 2 | 2.300 | 1.644 | 2.704 | 0.715 | 0.614 | −0.256 | 0.399 | 0.148 | −0.025 |
| 2 | 128 | 5 (10.0) | 0 | 7 | 2 | 2.560 | 1.798 | 3.231 | 0.702 | 0.634 | −0.092 | 0.393 | 0.143 | −0.029 |
| 3 | 174 | 5 (10.0) | 0 | 11 | 3 | 3.480 | 2.549 | 6.500 | 0.733 | 0.967 | 1.007 | 0.401 | 0.174 | 0.037 |
| 4 | 104 | 15 (30.0) | 0 | 8 | 2 | 2.080 | 1.936 | 3.749 | 0.931 | 0.902 | 0.758 | 0.509 | 0.191 | −0.058 |
| Monthly Aggregation | ||||||||||||||
| 1 | 115 | 1 (7.7) | 0 | 19 | 9 | 8.846 | 4.506 | 20.308 | 0.509 | 0.345 | 1.870 | 0.284 | 0.036 | 0.167 |
| 2 | 128 | 0 (0.0) | 4 | 21 | 7 | 9.846 | 5.580 | 31.141 | 0.567 | 0.852 | −0.399 | 0.323 | 0.266 | −0.074 |
| 3 | 174 | 0 (0.0) | 1 | 31 | 13 | 13.385 | 7.556 | 57.090 | 0.565 | 0.879 | 1.689 | 0.314 | 0.155 | 0.203 |
| 4 | 104 | 1 (7.7) | 0 | 19 | 7 | 8.000 | 5.538 | 30.667 | 0.692 | 0.682 | −0.217 | 0.399 | 0.185 | 0.018 |
| Quadrant | Peak Timing |
|---|---|
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alarcon Falconi, T.M.; Estrella, B.; Sempértegui, F.; Naumova, E.N. Effects of Data Aggregation on Time Series Analysis of Seasonal Infections. Int. J. Environ. Res. Public Health 2020, 17, 5887. https://doi.org/10.3390/ijerph17165887
Alarcon Falconi TM, Estrella B, Sempértegui F, Naumova EN. Effects of Data Aggregation on Time Series Analysis of Seasonal Infections. International Journal of Environmental Research and Public Health. 2020; 17(16):5887. https://doi.org/10.3390/ijerph17165887
Chicago/Turabian StyleAlarcon Falconi, Tania M., Bertha Estrella, Fernando Sempértegui, and Elena N. Naumova. 2020. "Effects of Data Aggregation on Time Series Analysis of Seasonal Infections" International Journal of Environmental Research and Public Health 17, no. 16: 5887. https://doi.org/10.3390/ijerph17165887
APA StyleAlarcon Falconi, T. M., Estrella, B., Sempértegui, F., & Naumova, E. N. (2020). Effects of Data Aggregation on Time Series Analysis of Seasonal Infections. International Journal of Environmental Research and Public Health, 17(16), 5887. https://doi.org/10.3390/ijerph17165887





