Abstract
Diarrhea is responsible for killing around 525,000 children every year, even though it is preventable and treatable. This research focuses on both houseflies’ roles and humans’ roles in carrying pathogens causing diarrhea as multiple disease carriers. Both human and fly compartmental models are simulated with five diseases control strategies in order to identify the epidemic dynamics. The framework considers the life cycle of flies modeled into eggs, larvae, pupae, susceptible flies, and carrier flies, while the human system follows a compartment model as susceptible, infected, recovered, and back to susceptible again (SIRS). The relationships are modeled into an ordinary differential equation-based compartmental system. Then, the control parameters of the compartmental framework are analyzed. In order to propose effective control methods, five control strategies are considered: (1) elimination of flies’ breeding site, (2) sanitation, (3) installation of UV light trap, (4) good personal and food hygiene, and (5) water purification. Then, overall, ten control scenarios using the five control strategies are analyzed. Among them, effective control solutions considering various dynamic epidemiology are provided with the simulations and analyses. The proposed framework contributes to an effective control strategy in reducing the number of both flies and infected humans, since it minimizes the spread of the disease and considers cost-effectiveness.
1. Introduction
Infectious diarrhea, a disease causing fluid loss and dehydration, is the eighth leading cause of death, responsible for around 525,000 children deaths globally every year [1], mostly children in developing countries. Diarrhea is caused by infectious organisms, including viral and bacterial pathogens [2]. These are typically transmitted from the stool of one individual. This means the pathogen spreads through contaminated food and water or from an infectious person to a healthy person as a result of poor hygiene. Although diarrhea is both preventable and treatable, it is still fatal. This is due to several reasons, including a lack of awareness and shortages of existing lifesaving interventions.
Several existing studies showed that bacteria causing diarrhea are carried by houseflies [3,4] mainly. The house fly, Musca domestica L., is known to carry pathogens including bacteria, viruses, fungi, and parasites which cause life threatening diseases in humans and animals [5,6]. Houseflies breed in human feces [7] and the existing studies [8,9,10,11,12] have shown increased incidences of diarrhea during the periods of high fly density. Most importantly, several existing studies [8,13,14,15] have shown that a reduction in housefly density may affect the reduction in diarrhea incidence as well.
Mathematical models [16] are widely used to convert the real case into mathematical epidemiologic representations and predict the dynamics of infectious disease transmission so that they have vital roles in developing public health strategies for disease control and prevention. The formulation process of diarrhea considers multiple carriers (e.g., houseflies and infected humans). Then, the mathematical model is used for relevant disease control. Effective disease control has become an important part of computational epidemiology [17] that can provide useful guidelines for designing effective disease intervention strategies while balancing the costs of the control measures.
The objective of this paper is to understand and to formulate diarrhea’s dynamic epidemiology through a set of differential equation-based mathematical models and to predict the possible future for the effectiveness of disease control strategies not only for reducing the infected population, but also decreasing or even eliminating fly population as principal carriers of the disease as well.
The following section presents the relevant epidemiologic network of diarrhea and its mathematical models along with multiple controls and their theoretical solutions. Then, the effectiveness of the proposed framework and simulation results are analyzed in Section 3 and Section 4. In order to show the influence of each intervention towards the spreading of the disease, numerical simulations under several control scenarios are provided in Section 5.
2. Background and Epidemiologic Network Model
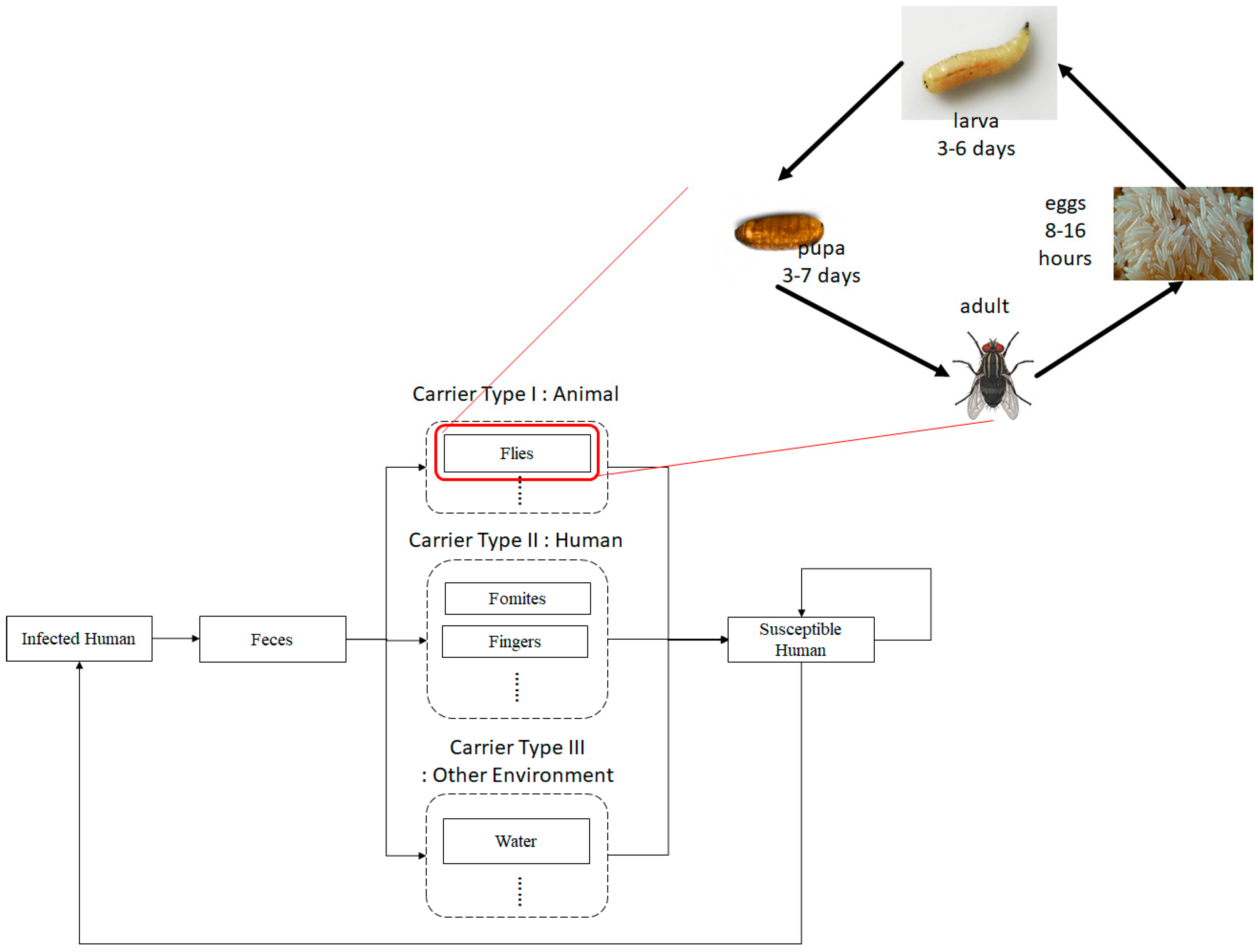
Figure 1 shows a flow diagram of diarrhea transmission through multiple carriers, including humans, flies and other environmental carriers. The system contains humans’ and flies’ epidemiologic systems, which are transformed into both (human and flies) compartmental models. As shown in Figure 1, the flies system shows the lifecycle of flies from egg stage , larva , pupa , until adult flies, which divides into susceptible , and carrier flies . A carrier means an agent that carries a pathogen causing the disease but it does not show any symptoms of illness.
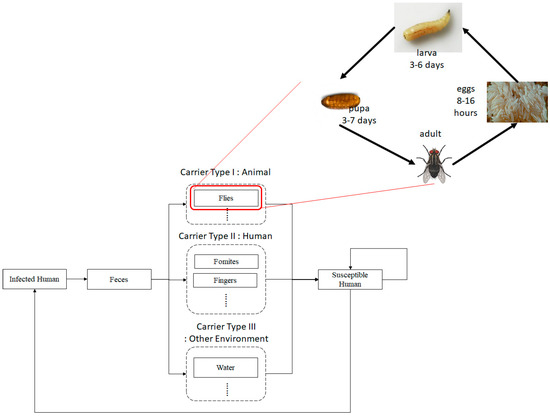
Figure 1.
Flow diagram of disease transmission through multiple carriers and a life cycle of a fly as a principal disease carrier.
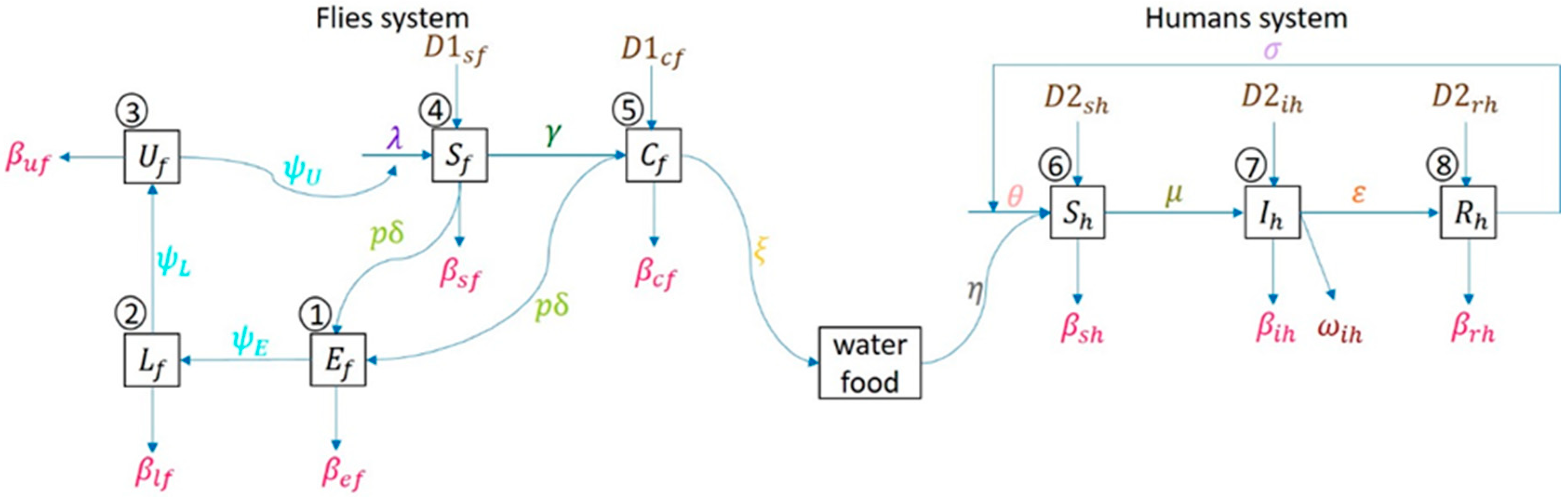
The human system follows susceptible human , infectious , recovered , and back to susceptible again, since no one has immunity against diarrhea. Figure 2 shows an epidemiologic network where human can be infected by the disease by consuming contaminated food or water due to carrier flies laying pathogens on it.
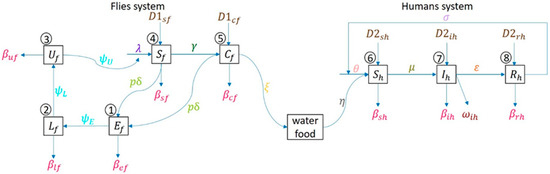
Figure 2.
Network model of flies’ life cycle (egg-larva-pupa-adult) and human as susceptible-infected-recovered in compartmental model.
As shown in Figure 2, a set of mathematical models are derived from the fly-human compartmental model. The model parameters in Figure 2 are provided in Table 1.

Table 1.
Notations of variables and parameters.
Table 2 shows the differential equation-based transition models with respect to the lifecycle of the fly and the epidemiologic processes of a human. Humans are classified with the Susceptible-Infected-Recovered-Susceptible (SIRS) reaction-diffusion compartmental model. The ordinary differential equations (ODE) are generated based on each of states in the network. The time unit is “day” in this research.

Table 2.
Ordinary differential equations (ODE) considering both the fly and the human system.
The solutions of the compartment models, as shown in Table 2, have to be non-negative (positiveness) and exist (boundedness). The below conditions show the positiveness and boundedness of the compartment model.
Let the initial dataset be and . is positive and bounded interval for all time .
Consider the Inequality (1) at time .
Inequality (1) proves that the solution set is positive for all time . The same rule can be applied for Inequality (2) until Inequality (6) at time .
3. Epidemic Model Dynamics
The dynamics of the models provided in Table 2 depend on the basic reproduction number, which is defined as the average number of secondary infections of an infectious human [18,19].
The basic reproduction number is denoted by as the number of secondary infections caused by an infected individual. If the value of , then the disease dies out. While the value of , then the number of infectious individuals increases and the disease invades the population. Let be the number of individuals in each compartment where the first compartments contain infected individuals. The disease-free equilibrium (DFE) is given by (S,E,I,R) = (). The terms S, E, I and R mean Susceptible, Exposed, Infected, and Recovered, respectively. In this model dynamics, it is assumed that the DFE exists and is stable in the absence of disease. Consider those equations written in the form for where, is the rate of appearance of new infections in compartment i and is the rate of other transitions between compartment i and other infected compartments. F () is entry wise non-negative and V () is a non-singular matrix for . denotes a vector of new infection rates (flows from X to Y) and is a vector of all other rates. For each compartment, an inflow in V is negative and an outflow in V is positive. It is assumed that and . is called the next generation matrix where the spectral radius of it is equal to , which is the largest eigenvalue of . is derived using Equations (7)–(10).
Then, is determined as the basic reproduction number using .
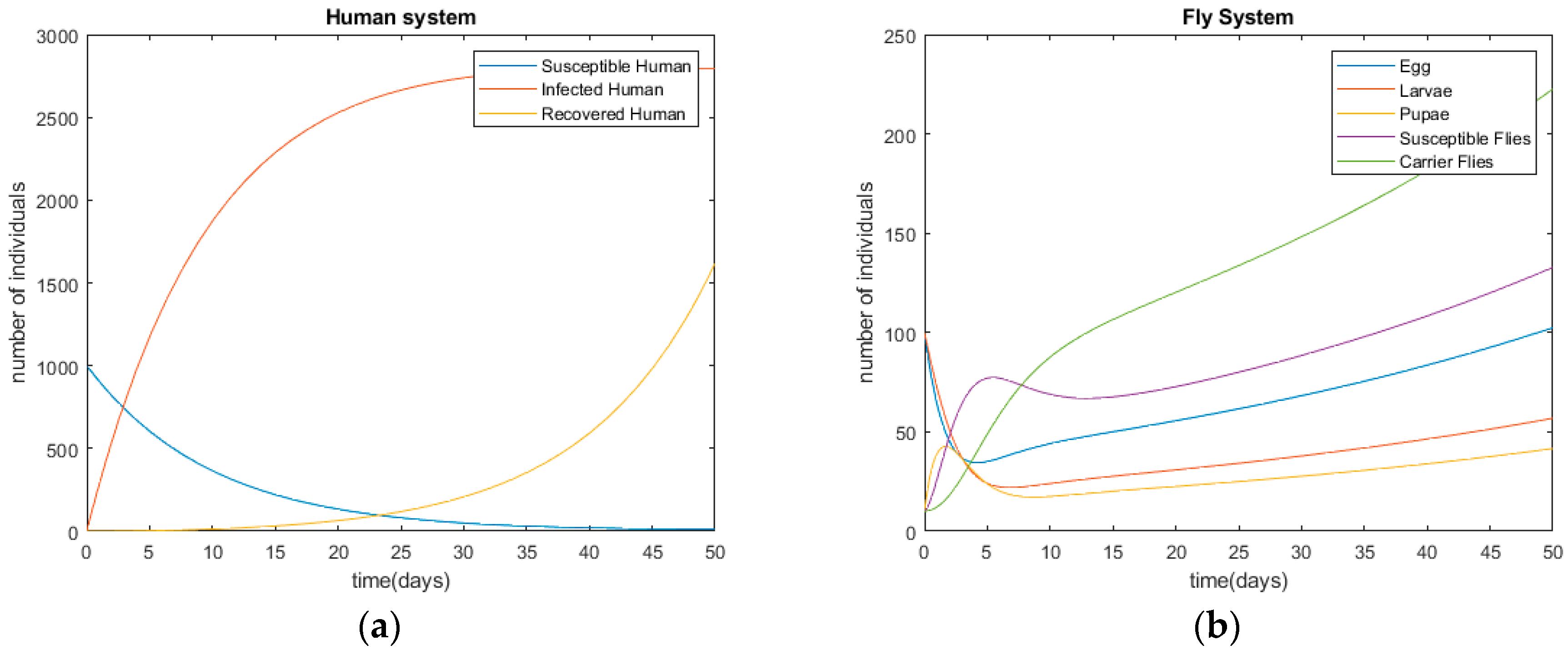
After modeling the infection processes of diarrhea provided in Section 2 and Section 3, the derived differential equations are solved with the initial conditions of ; ; ; ; ; ; ; . The initial parameters are supposed with real-world examples. Figure 3 shows the disease’s infection simulations without any control method, in terms of humans’ and flies’ status. The simulation is performed using Matlab©. According to Figure 3, the disease starts with an outbreak at t = 0 and, the number of infected people is around 2700 at t = 20. The time unit is day in this research.
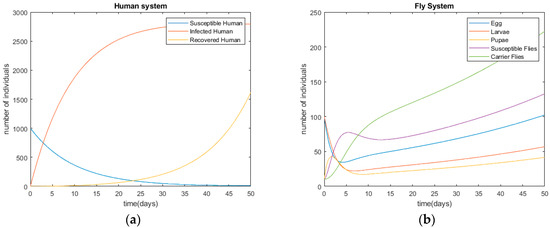
Figure 3.
Diseases’ infection trends of diarrhea without control methods. (a) Human system; (b) fly system.
The provided ODE-based compartment model is used to check the epidemiologic processes of diarrhea and the effectiveness of control methods, which are provided in the following section.
4. Effective Control Framework Considering Multiple Disease Carriers
In this section, the previous fundamental infection model is extended with several control strategies on the spread of the disease. The term “effectiveness” is evaluated with the blocks of additional infections and a cost-effective concept. This consideration may help to block the spread of SARS-2 or COIVID-19. The cost-effective criteria are determined using Pontryagin’s [20] maximum principle on five variations of control methods. Pontryagin [20,21] introduced the idea of adjoint functions which has a similar purpose as Lagrange multipliers, to append the differential equation to the objective function.
This section focuses on effective control frameworks to prevent additional infections of humans. In order to control additional spreads of diarrhea, five control methods are considered: (1) elimination of fly’s breeding site, (2) sanitation-related investment, (3) installation of UV light traps for killing flies, (4) good personal and food hygiene, and (5) water purification. In general, these methods intend to prevent additional infections among humans or to remove one of primary disease carriers—flies.
As the first control method, “Elimination of flies’ breeding site” is considered. As flies feed on garbage, food waste, and animal feces, therefore one way to prevent additional infections is to keep the places clean, and to spray pesticide on prone areas. This intervention could reduce or even eliminate the maturation rate of fly eggs, larva, and pupa, which eventually impacts the number of adult flies. Let denote the level of a breeding site elimination strategy (). The effect of breeding site elimination will decrease the maturation rate of eggs, larvae, and pupae, which is modelled as and , respectively.
The second control option is sanitation efforts [22], which include the sterilization of cooking utensils, washing, and drinking water by boiling it properly. The parameter () denotes the level of sanitation strategy. The effect of sanitation is to decrease the number of pathogens, which is modelled as a reduction in the rate of the carrier fly population by the term .
The third control method is to install light traps. When flies see ultra-violet (UV) light, they are naturally lured in the direction of the source of the UV rays. This strategy is more desirable than spray for indoor fly control as it keeps the surroundings clean. denotes the effectiveness of the installation of UV light trap strategy. The effect of this effort is to decrease the number of susceptible and carrier flies by the terms and .
The next consideration is to keep good personal and food hygiene. Good personal and food hygiene can be defined as handling, preparing, and storing food in a way that reduces the risk of becoming contaminated. Let be the good personal and food hygiene effort. The effect of this effort is to suppress the number of infected people by the term .
The final option is to purify water. Chlorine is often a choice for water purification, since it effectively inactivates the bacteria causing diarrhea, leaves residual protection, has low cost and is easy to transport and use. There are two chlorine-based options [23] used in diarrhea outbreaks, such as tablets and liquid. denotes the level of water purification strategy. The effect of water purification is to inactivate pathogens, which is modelled as a reduction in the disease transmission rate by the term Table 3 explains each control parameter for each control option.

Table 3.
Control parameters.
Based on the control parameters shown in Table 3, the initial transmission models are modified with additional terms to Equations (12)–(17). The additional term is underlined in each equation.
In this research, an effective control model is considered as a cost-effective control method within a controllable infection size. The objective function that aims to minimize cost in the control strategy is obtained by Equation (18). In Equation (18), the parameter denotes the cost for elimination of breeding site, is the cost for sanitation-based works, is the cost for installing UV light trap, is the cost for isolation of infected person, and is the cost of water purification. Each denotes each control parameter-based cost.
where , , and .
Due to the fact that the cost function is nonlinear with the infection trends, time and other conditions, the mathematical programming belongs to the differential equation-based nonlinear mathematical programming. When denoting the prices associated with their respective classes by , the nonlinear mathematical programming is solved using Pontryagin’s maximum principle and the derivation of necessary conditions. As explained in [24,25], the existence of an optimal control is a sequence of the convexity of the integrand with respect to ; a priori boundedness of the state variables, and the Lipschitz property of the state system with respect to the state variables. The differential equations are obtained by differentiating the Hamiltonian function, as shown in Appendix A. Finally, optimal control values are obtained as shown in Appendix B.
Therefore, it can be concluded by the standard control arguments involving the bounds on the controls in Table 4 as follows:

Table 4.
The optimal control parameter of each strategy.
5. Simulation and Analysis of Control Model Considering Multiple Disease Carriers
With the provided optimal control frameworks, numerical simulations are performed using the parameter values given in Table 1 and Table 3. Several control scenarios are considered with combinations of intervention strategies for non-adult flies, adult flies, and infected humans, as summarized in Table 5. Table 5 shows the highest number of flies and humans using 50 days’ of simulation.

Table 5.
Scenarios with combinations of control strategies.
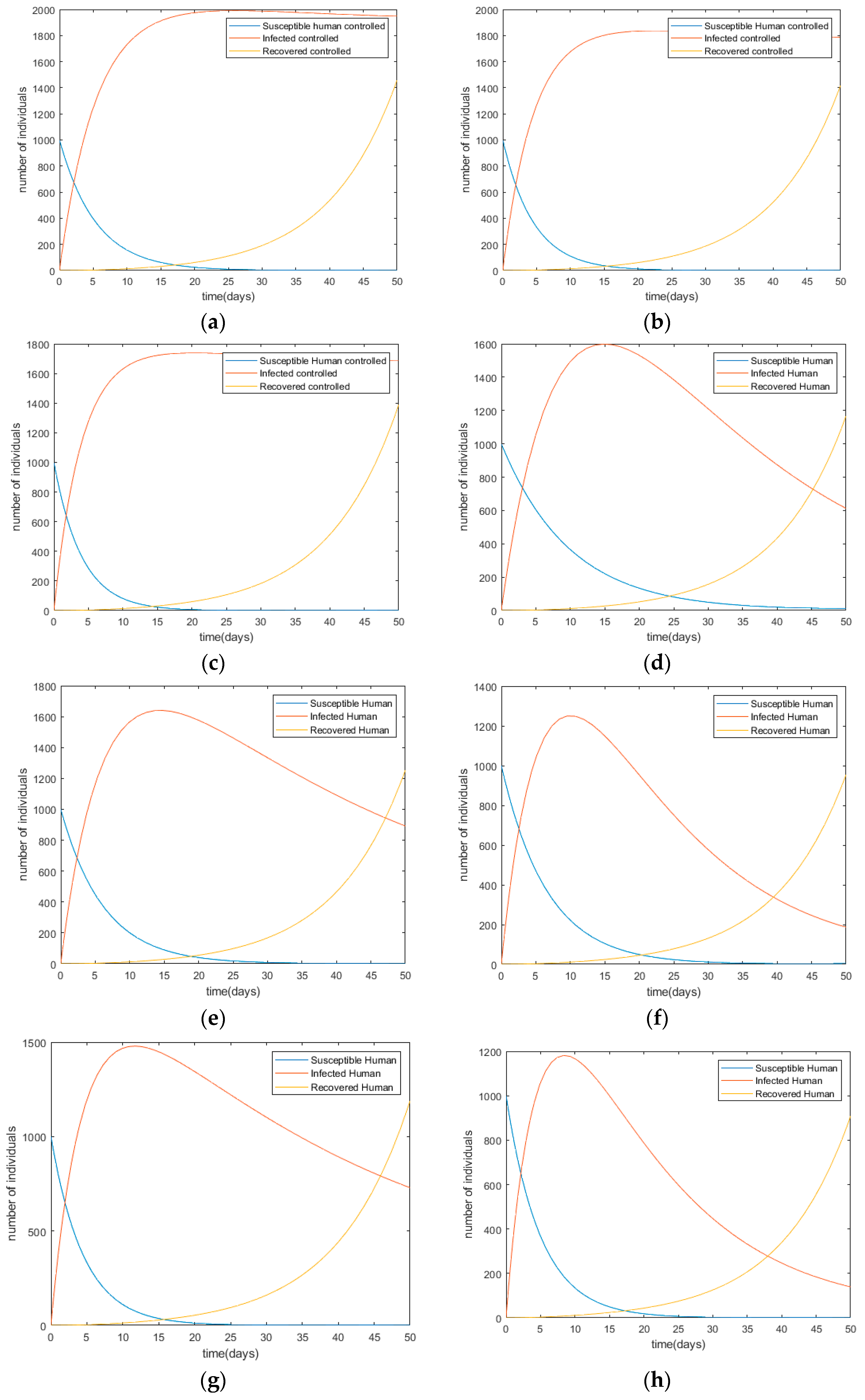
Each control is applied and is combined with more than one control to examine the impact on the human population. The simulation results are shown in Figure 4.
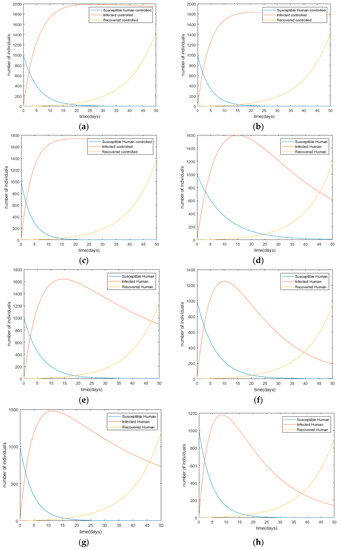
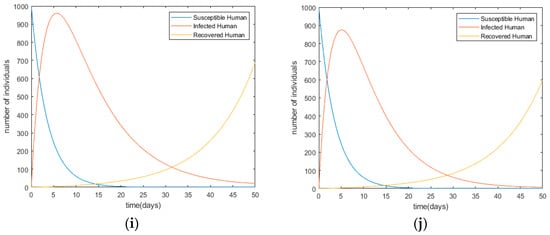
Figure 4.
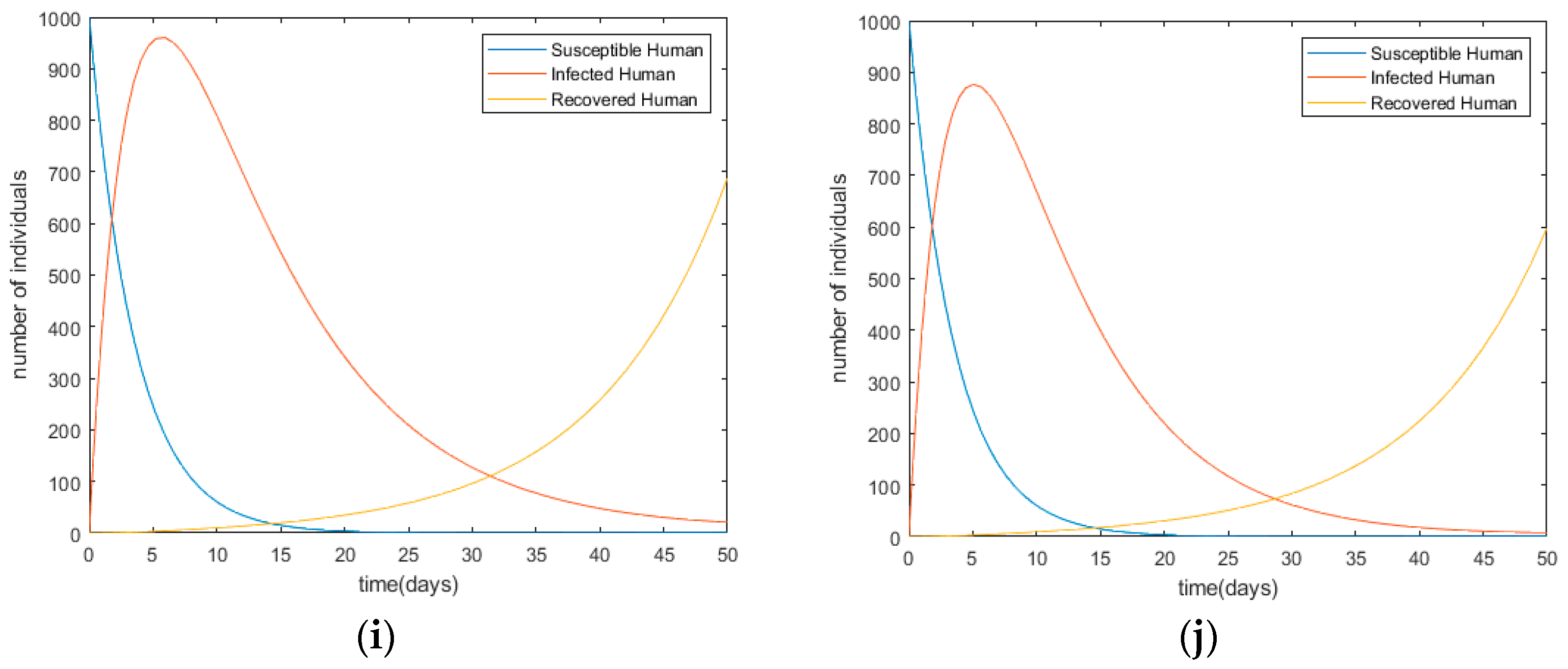
Changes in infection trends toward the human population with each control scenario (a) Scenario I; (b) Scenario II; (c) Scenario III; (d) Scenario IV; (e) Scenario V; (f) Scenario VI; (g) Scenario VII; (h) Scenario VIII; (i) Scenario IX; (j) Scenario X.
Table 6 shows the assumed control costs and medical treatment costs. The costs are assigned with the consideration of existing relevant literatures [26,27,28,29,30].

Table 6.
Cost values for control simulations.
After comparing all of those ten scenarios, the most effective strategy is considered Scenario X, which combines all control method under the assumptions. Table 7 shows the simulation result for each control scenario I to scenario X.

Table 7.
Result of control scenario.
In terms of cost and the number of infected persons, Scenario X shows the best performance. This indicates that the overall control methods are required for effective disease control and their portions influence its performance. It also denotes the significant reduction in number of infected people from 2795 to 877 as a result of the decreasing number of disease carriers. It means there is a 65.7% reduction in the number of infected people compared to the simulation without applying any control.
The provided framework can be used to check the effectiveness with different assumptions and numerical simulations considering multiple disease carriers.
6. Conclusions
This paper presents the ordinary differential equation-based epidemiologic models to understand diarrhea’s infection dynamics and with the consideration of multiple carriers. Numerical simulation and mathematical analyses were performed to identify the relationship and the status of flies and humans when the disease outbreaks.
Then, each control strategy is applied, as shown in Scenarios I to V, and is combined in some combinations of these strategies to obtain the optimal condition, as shown in Scenarios VI to X. Under a certain simulation scenario, Scenario X, which combines all control methods, is proven to be the most effective strategy in reducing both of the number of flies and the infected population, as it minimizes the spread of the disease.
In the future, further study about broader conditions such as the effect of temperature on the transmission of a disease is required, as the population of housefly reaches its peak when the temperature is warmer.
The proposed framework is considered an effective disease control considering multiple carriers with epidemiologic dynamics and the relevant parameters.
Author Contributions
F.R. and H.L. conceptualized the framework and developed the methodologies. F.R. implemented and validated the framework. H.L. supervised the overall research processes. F.R. wrote the manuscript. And H.L. reviewed and edited it. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by The Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education, S. Korea, grant number NRF-2018R1D1A3B07047113.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
Consider the objective function to investigate the optimal strategy needed to control the spreading of diarrhea provided in Equation, where represent the weight constants of the eggs, larva, pupa, susceptible flies, carrier flies, susceptible human, infected human, and recovered human.
The Hamiltonian is provided with and the ODEs, where are the co-state variables given by the system:
Appendix B
Optimal control values are obtained using the Hamiltonian function shown in Appendix A. Then, the nonlinear mathematical programming is solved using Pontryagin’s Maximum Principle and the derivation of necessary conditions.
References
- GBD 2016 Causes of Death Collaborators. Global, regional, and national age-sex specific mortality for 264 causes of death, 1980–2016: A systematic analysis for the Global Burden of Disease Study 2016. Lancet 2017, 390, 1151–1210. [Google Scholar] [CrossRef]
- InformedHealth.org. Cologne, Germany: Institute for Quality and Efficiency in Health Care (IQWiG). 2006. Acute infectious Diarrhea: Common Germs and Routes of Infection. 4 May 2016. Available online: https://www.ncbi.nlm.nih.gov/books/NBK373086/ (accessed on 13 June 2019).
- Olsen, A.R.; Hammack, T.S. Isolation of Salmonella spp. from the housefly, Musca domestica L., and the dump fly, Hydrotaea aenescens (Wiedemann) (Diptera: Muscidae), at caged-layer houses. J. Food Prot. 2000, 63, 958–960. [Google Scholar] [CrossRef] [PubMed]
- Hosseini, S.M.; Zeyni, B.; Rastyani, S.; Jafari, R.; Shamloo, F.; Tabar, Z.K.; Rabestani, M.R. Presence of virulence factors and antibiotic resistances in Enterococcus sp collected from dairy products and meat. Der Pharm. Lett. 2016, 8, 138–145. [Google Scholar]
- Tsagaan, A.; Kanuka, I.; Okado, K. Study of pathogenic bacteria detected in fly samples using universal primer-multiplex PCR. Mong. J. Agric. Sci. 2015, 15, 27–32. [Google Scholar] [CrossRef]
- Nassiri, H.; Zarrin, M.; Veys-Behbahani, R.; Faramarzi, S.; Nasiri, A. Isolation and identification of pathogenic filamentous fungi and yeasts from adult house fly (Diptera: Muscidae) captured from the hospital environments in Alivaz city, Southwestern Iran. J. Med. Entomol. 2015, 52, 1351–1356. [Google Scholar]
- Peffly, R.L. A summary of recent studies on house flies in Egypt. J. Egypt. Public Health Assoc. 1953, 28, 55–74. [Google Scholar]
- Chavasse, D.C.; Shier, R.P.; Murphy, O.A.; Huttly, S.R.; Cousens, S.N.; Akhtar, A. Impact of fly control on childhood diarrhea in Pakistan: Community randomized trial. Lancet 1999, 353, 22–25. [Google Scholar] [CrossRef]
- Echeverria, P.; Harrison, B.A.; Tirapat, C.; McFarland, A. Flies as a source of enteric pathogens in a rural village in Thailand. Appl. Environ. Microbiol. 1983, 46, 32–36. [Google Scholar] [CrossRef]
- Nash, J.T. House flies as carriers of disease. J. Hyg. (Lond.) 1909, 9, 141–169. [Google Scholar] [CrossRef][Green Version]
- Collinet-Adler, S.; Babji, S.; Francis, M.; Kattula, D.; Premkumar, P.S.; Sarkar, R.; Mohan, V.R.; Ward, H.; Kang, G.; Balraj, V.; et al. Environmental Factors Associated with High Fly Densities and Diarrhea in Vellore, India. Appl. Environ. Microbiol. 2015, 81, 6053–6058. [Google Scholar] [CrossRef]
- Das, J.K.; Hadi, Y.B.; Salam, R.A.; Hoda, M.; Lassi, Z.S.; Bhutta, Z.A. Fly control to prevent diarrhea in children. Cochrane Database Syst. Rev. 2018, 12, CD011654. [Google Scholar] [PubMed]
- Cohen, D.; Green, M.; Block, C.; Slepon, R.; Ambar, R.; Wasserman, S.S.; Levine, M.M. Reduction of transmission of shigellosis by control of houseflies (Musca domestica). Lancet 1991, 337, 993–997. [Google Scholar] [CrossRef]
- Lindsay, D.; Stewart, W.; Watt, J. Effect of fly control on diarrhea in an area of moderate morbidity. Public Health Rep. 1953, 68, 361–367. [Google Scholar] [CrossRef] [PubMed]
- Watt, J.; Lindsay, D.R. Diarrhea control studies; effect of fly control in a high morbidity area. Public Health Rep. 1948, 63, 1319–1333. [Google Scholar] [CrossRef] [PubMed]
- Hartemink, N.; Vanwambeke, S.O.; Heesterbeek, H.; Rogers, D.; Morley, D.; Pesson, B.; Davies, C.; Mahamdallie, S.; Ready, P. Integrated mapping of establishment risk for emerging vector-borne infections: A case study of canine leishmaniasis in southwest France. PLoS ONE 2011, 6, e20817. [Google Scholar] [CrossRef] [PubMed]
- Lenhart, S.; Workman, J.T. Optimal Control Applied to Biological Models; Chapman and Hall/CRC: London, UK, 2007. [Google Scholar]
- Heffernan, J.; Smith, R.; Wahl, L. Perspectives on the basic reproductive ratio. J. R. Soc. Interface 2005, 2, 281–293. [Google Scholar] [CrossRef]
- Diekmann, O.; Heesterbeek, J.; Metz, J.A. On the definition and the computation of the basic reproduction ratio R0 in models for infectious diseases in heterogeneous populations. J. Math. Biol. 1990, 28, 365–382. [Google Scholar] [CrossRef]
- Pontryagin, L.S. Mathematical Theory of Optimal Processes; Routledge: London, UK, 2018. [Google Scholar]
- Getachew, T.T.; Oluwole, D.M.; David, M. Modelling and optimal control of pneumonia disease with cost-effective strategies. J. Biol. Dyn. 2017, 11 (Suppl. 2), 400–426. [Google Scholar]
- Cairncross, S.; Hunt, C.; Boisson, S.; Bostoen, K.; Curtis, V.; Fung, I.C.H.; Schmidt, W.-P. Water, sanitation and hygiene for the prevention of diarrhea. Int. J. Epidemiol. 2010, 39 (Suppl. 1), i193–i205. [Google Scholar] [CrossRef]
- Branz, A.; Levine, M.; Lehmann, L.; Bastable, A.; Ali, S.I.; Kadir, K.; Yates, T.; Bloom, D.; Lantagne, D. Chlorination of drinking water in emergencies: A review of knowledge, recommendations for implementation, and research needed. Waterlines 2017, 36, 4–39. [Google Scholar] [CrossRef]
- Okosun, K.O.; Rachid, O.; Marcus, N. Optimal control strategies and cost-effectiveness analysis of a malaria model. BioSystems 2013, 111, 83–101. [Google Scholar] [CrossRef] [PubMed]
- Fleming, W.H.; Rishel, R.W. Deterministic and Stochastic Optimal Control; Springer: New York, NY, USA, 2017. [Google Scholar]
- How Much Does It Cost to Get Rid Of Flies? Available online: https://www.kompareit.com/homeandgarden/home-services-compare-fly-exterminator-cost.html (accessed on 3 August 2020).
- Sandy, C.; Vivian, V. Water supply, sanitation and hygiene promotion. In Disease Control Priorities in Developing Countries; Oxford University Press: New York, NY, USA, 2006. [Google Scholar]
- Golan, E.H.; Vogel, S.J.; Frenzen, P.D.; Ralston, K.L. Tracing the Costs and Benefits of Improvements in Food Safety: The Case of the Hazard Analysis and Critical Control Point Program for Meat and Poultry; Agricultural Economic Report Number 791; United States Department of Agriculture: Washington, DC, USA, 2000. [Google Scholar]
- Ephrem, T.S.; Sirak, R.; Helmut, K.; Bezatu, M. Effect of household water treatment with chlorine on diarrhea among children under the age of five years in rural areas of Dire Dawa, eastern Ethiopia: A cluster randomized controlled trial. Infect. Dis. Poverty 2020. [Google Scholar] [CrossRef]
- Van, M.H.; Tuan, A.T.; Anh, D.H.; Viet, H.N. Cos of hospitalization for foodborne diarrhea: A case study from Vietnam. J. Korean Med. Sci. 2015. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).