Risk Interactions of Coronavirus Infection across Age Groups after the Peak of COVID-19 Epidemic
Abstract
1. Introduction
2. Materials and Methods
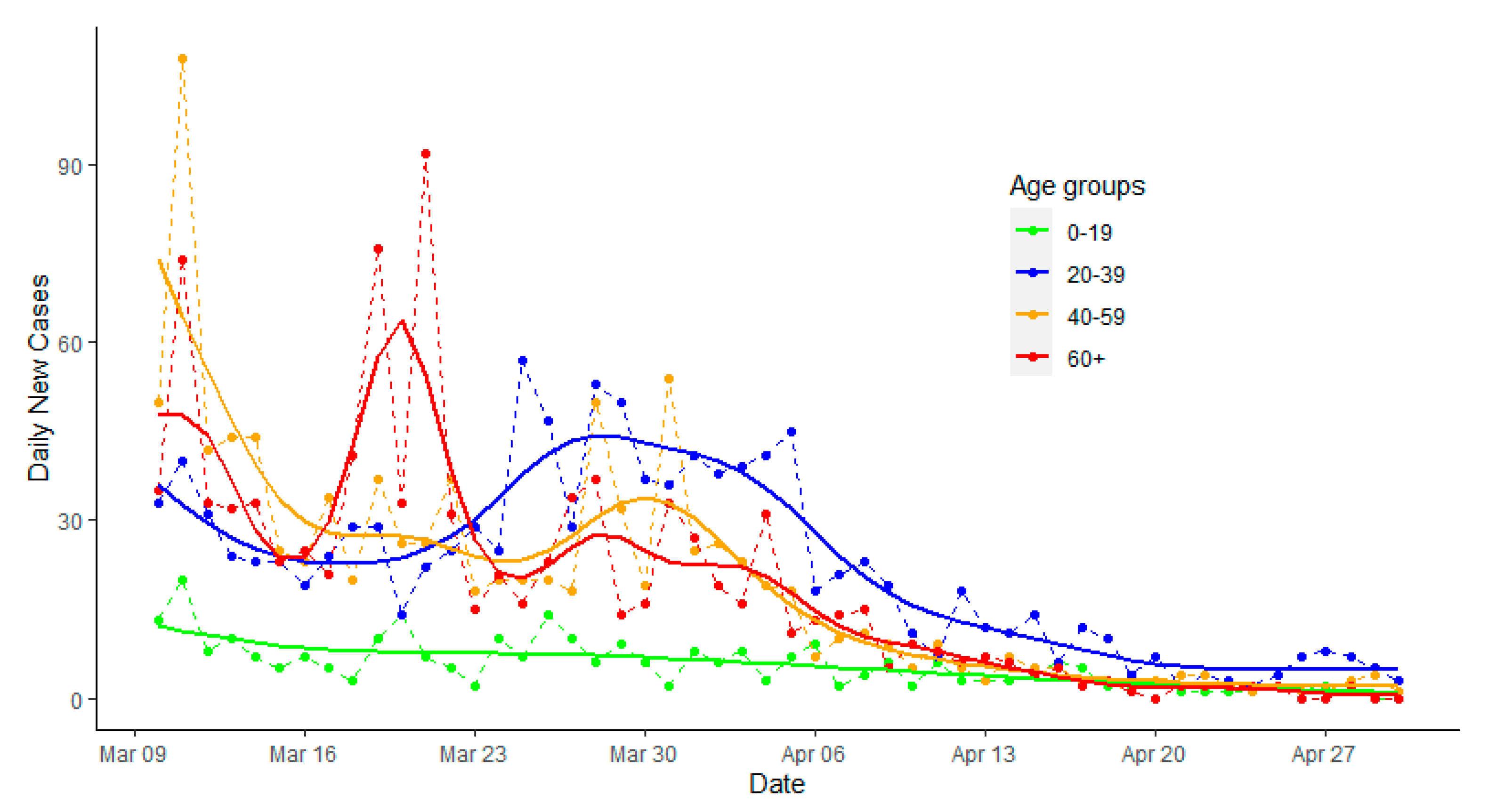
3. Results
4. Discussion
5. Conclusions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| SARS-CoV-2 | severe acute respiratory syndrome coronavirus 2 |
| COVID-19 | coronavirus infectious disease 2019 |
| GAM | generalized additive model |
| VAR | vector autoregressive regression |
| NB | negative binomial model |
| REML | restricted maximum likelihood |
| PMF | probability mass function |
Appendix A
Appendix A.1. Obtained Smoothed Predicted Daily Cases with Generalized Additive Model (GAM)
Appendix A.2. Model Setups and Comparisons
Appendix B. Additional Table
| Model Outcomes | Predictors | Lags of Predictors | ||||
|---|---|---|---|---|---|---|
| Lag 1 | Lag 2 | Lag 3 | Lag 4 | Lag 5 | ||
| Aged 60 or above | ||||||
| 60 or above | 1.93 (1.14–3.19) * | 1.09 (0.66–1.80) | 1.02 (0.61–1.82) | 0.99 (0.57–1.67) | 1.11 (0.68–1.87) | |
| 40–59 | 1.03 (0.53–2.02) | 1.66 (0.83–3.01) | 0.69 (0.36–1.46) | 1.26 (0.72–2.25) | 1.00 (0.57–1.71) | |
| 20–39 | 0.94 (0.54–1.69) | 1.30 (0.66–2.42) | 1.42 (0.73–2.68) | 0.50 (0.25–1.01) | 1.21 (0.63–2.37) | |
| 0–19 | 1.10 (0.72–1.78) | 1.29 (0.79–1.98) | 0.85 (0.51–1.35) | 0.62 (0.40–0.98) # | 1.52 (0.88–2.55) | |
| Aged 40–59 | ||||||
| 60 or above | 1.64 (1.12–2.41) * | 0.75 (0.50–1.09) | 0.97 (0.67–1.49) | 1.01 (0.69–1.53) | 1.02 (0.69–1.53) | |
| 40–59 | 1.15 (0.68–1.96) | 1.55 (0.92–2.46) | 1.14 (0.64–2.24) | 0.90 (0.54–1.39) | 0.95 (0.63–1.47) | |
| 20–39 | 1.10 (0.59–1.73) | 1.13 (0.70–1.81) | 1.54 (0.95–2.47) | 0.63 (0.37–1.27) | 0.89 (0.44–1.56) | |
| 0–19 | 1.09 (0.77–1.53) | 1.23 (0.87–1.78) | 1.16 (0.82–1.64) | 1.16 (0.82–1.60) | 1.15 (0.79–1.68) | |
| Aged 20–39 | ||||||
| 60 or above | 1.00 (0.71–1.44) | 0.93 (0.65–1.39) | 1.00 (0.69–1.48) | 1.58 (1.10–2.26) * | 0.90 (0.64–1.29) | |
| 40–59 | 1.12 (0.69–1.86) | 1.09 (0.67–1.72) | 0.96 (0.58–1.53) | 0.97 (0.65–1.44) | 1.08 (0.72–1.61) | |
| 20–39 | 1.63 (1.09–2.48) * | 1.04 (0.66–1.64) | 1.35 (0.86–2.11) | 0.99 (0.58–1.56) | 0.96 (0.60–1.56) | |
| 0–19 | 1.04 (0.74–1.44) | 0.95 (0.69–1.29) | 0.89 (0.63–1.23) | 0.95 (0.67–1.40) | 0.73 (0.51–1.04) | |
| Aged 0–19 | ||||||
| 60 or above | 1.77 (1.17–2.76) * | 1.35 (0.82–2.14) | 1.00 (0.62–1.61) | 0.81 (0.50–1.32) | 1.52 (0.97–2.44) | |
| 40–59 | 0.76 (0.39–1.42) | 0.71 (0.39–1.27) | 0.86 (0.43–1.64) | 0.94 (0.53–1.66) | 0.96 (0.58–1.60) | |
| 20–39 | 1.53 (0.87–2.72) | 1.46 (0.82–2.69) | 1.05 (0.57–1.92) | 0.78 (0.41–1.41) | 0.90 (0.49–1.74) | |
| 0–19 | 0.94 (0.63–1.44) | 0.83 (0.57–1.25) | 0.88 (0.58–1.33) | 0.92 (0.59–1.44) | 1.52 (0.95–2.42) | |
References
- Zhu, N.; Zhang, D.; Wang, W.; Li, X.; Yang, B.; Song, J.; Zhao, X.; Huang, B.; Shi, W.; Lu, R.; et al. A Novel Coronavirus from Patients with Pneumonia in China, 2019. N. Engl. J. Med. 2020, 382, 727–733. [Google Scholar] [CrossRef] [PubMed]
- Li, Q.; Guan, X.; Wu, P.; Wang, X.; Zhou, L.; Tong, Y.; Ren, R.; Leung, K.S.M.; Lau, E.H.Y.; Wong, J.Y.; et al. Early Transmission Dynamics in Wuhan, China, of Novel Coronavirus-Infected Pneumonia. N. Engl. J. Med. 2020, 382, 1199–1207. [Google Scholar] [CrossRef] [PubMed]
- Guan, W.J.; Ni, Z.Y.; Hu, Y.; Liang, W.H.; Ou, C.Q.; He, J.X.; Liu, L.; Shan, H.; Lei, C.L.; Hui, D.S.C.; et al. Clinical Characteristics of Coronavirus Disease 2019 in China. N. Engl. J. Med. 2020. [Google Scholar] [CrossRef] [PubMed]
- Richardson, S.; Hirsch, J.S.; Narasimhan, M.; Crawford, J.M.; McGinn, T.; Davidson, K.W.; Barnaby, D.P.; Becker, L.B.; Chelico, J.D.; Cohen, S.L.; et al. Presenting Characteristics, Comorbidities, and Outcomes Among 5700 Patients Hospitalized With COVID-19 in the New York City Area. JAMA 2020. [Google Scholar] [CrossRef] [PubMed]
- Wu, Z.; McGoogan, J.M. Characteristics of and Important Lessons From the Coronavirus Disease 2019 (COVID-19) Outbreak in China: Summary of a Report of 72314 Cases From the Chinese Center for Disease Control and Prevention. JAMA 2020. [Google Scholar] [CrossRef]
- Garg, S.; Kim, L.; Whitaker, M.; O’Halloran, A.; Cummings, C.; Holstein, R.; Prill, M.; Chai, S.J.; Kirley, P.D.; Alden, N.B.; et al. Hospitalization Rates and Characteristics of Patients Hospitalized with Laboratory-Confirmed Coronavirus Disease 2019—COVID-NET, 14 States, March 1–30, 2020. Mmwr Morb Mortal Wkly. Rep. 2020, 69, 458–464. [Google Scholar] [CrossRef]
- Yu, X. Urban-rural inequalities during the COVID-19 pandemic among elderly people in Florida, US. medRxiv 2020. [Google Scholar] [CrossRef]
- Hay, J.A.; Haw, D.J.; Hanage, W.P.; Metcalf, C.J.E.; Mina, M.J. Implications of the Age Profile of the Novel Coronavirus. Available online: https://dash.harvard.edu/handle/1/42639493 (accessed on 4 July 2020).
- Chavan, P.; Kedia, S.; Yu, X. Physical and Functional Limitations in US Older Cancer Survivors. J. Palliat. Care Med. 2017. [Google Scholar] [CrossRef]
- Ward, B.W.; Schiller, J.S.; Goodman, R.A. Multiple chronic conditions among US adults: A 2012 update. Prev. Chronic Dis. 2014, 11, E62. [Google Scholar] [CrossRef]
- CDC. Severe Outcomes Among Patients with Coronavirus Disease 2019 (COVID-19)—United States, February 12–March 16, 2020. MMWR Morb Mortal Wkly. Rep. 2020, 343–346. [Google Scholar]
- Imai, N.; Cori, A.; Dorigatti, I.; Baguelin, M.; Donnelly, C.A.; Riley, S.; Ferguson, N.M. Report 3: Transmissibility of 2019-nCoV; Imperial College of London: London, UK, 2020. [Google Scholar]
- Lv, H.; Wu, N.C.; Tsang, O.T.-Y.; Yuan, M.; Perera, R.A.P.M.; Leung, W.S.; So, R.T.Y.; Chan, J.M.C.; Yip, G.K.; Chik, T.S.H.; et al. Cross-reactive Antibody Response between SARS-CoV-2 and SARS-CoV Infections. Cell Rep. 2020, 31, 107725. [Google Scholar] [CrossRef] [PubMed]
- Lipsitch, M.; Swerdlow, D.L.; Finelli, L. Defining the Epidemiology of Covid-19—Studies Needed. N. Engl. J. Med. 2020, 382, 1194–1196. [Google Scholar] [CrossRef]
- Shim, E.; Tariq, A.; Choi, W.; Lee, Y.; Chowell, G. Transmission potential and severity of COVID-19 in South Korea. Int. J. Infect. Dis 2020, 93, 339–344. [Google Scholar] [CrossRef]
- Park, S.Y.; Kim, Y.M.; Yi, S.; Lee, S.; Na, B.J.; Kim, C.B.; Kim, J.I.; Kim, H.S.; Kim, Y.B.; Park, Y.; et al. Coronavirus Disease Outbreak in Call Center, South Korea. Emerg. Infect. Dis. 2020, 26. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.; Castro, M.C. Spatiotemporal pattern of COVID-19 and government response in South Korea (as of May 31, 2020). Int. Ernational J. Infect. Dis. 2020. [Google Scholar] [CrossRef] [PubMed]
- Yu, X.; Duan, J.; Jiang, Y.; Zhang, H. Distinctive trajectories of COVID-19 epidemic by age and gender: A retrospective modeling of the epidemic in South Korea. Int.Ernational J. Infect. Dis. 2020. [Google Scholar] [CrossRef]
- Chowell, G.; Mizumoto, K. The COVID-19 pandemic in the USA: What might we expect? Lancet 2020, 395, 1093–1094. [Google Scholar] [CrossRef]
- Kissler, S.M.; Tedijanto, C.; Goldstein, E.; Grad, Y.H.; Lipsitch, M. Projecting the transmission dynamics of SARS-CoV-2 through the postpandemic period. Science 2020. [Google Scholar] [CrossRef]
- Anderson, R.M.; Heesterbeek, H.; Klinkenberg, D.; Hollingsworth, T.D. How will country-based mitigation measures influence the course of the COVID-19 epidemic? Lancet 2020, 395, 931–934. [Google Scholar] [CrossRef]
- Kim, Y.J.; Seo, M.H.; Yeom, H.E. Estimating a breakpoint in the spread pattern of COVID-19 in South Korea. Int. J. Infect. Dis. 2020. [Google Scholar] [CrossRef]
- Wood, S.N. Generalized Additive Models: An Int.roduction with R, 2nd ed.; Chapman and Hall/CRC: Boca Raton, FL, USA, 2017. [Google Scholar]
- Brandt, P.T.; Sandler, T. A bayesian Poisson vector autoregressive model. Political Anal. 2012, 20, 23. [Google Scholar] [CrossRef][Green Version]
- Yang, Z.; Hardin, J.W.; Addy, C.L.; Vuong, Q.H. Testing approaches for overdispersion in poisson regression versus the generalized poisson model. Biom. J. 2007, 49, 565–584. [Google Scholar] [CrossRef] [PubMed]
- Lauer, S.A.; Grantz, K.H.; Bi, Q.; Jones, F.K.; Zheng, Q.; Meredith, H.R.; Azman, A.S.; Reich, N.G.; Lessler, J. The Incubation Period of Coronavirus Disease 2019 (COVID-19) From Publicly Reported Confirmed Cases: Estimation and Application. Ann. Int. Ern. Med. 2020. [Google Scholar] [CrossRef] [PubMed]
- Hilbe, J.M. Modeling Count Data; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- Carpenter, B.; Gelman, A.; Hoffman, M.D.; Lee, D.; Goodrich, B.; Betancourt, M.; Brubaker, M.; Guo, J.; Li, P.; Riddell, A. Stan: A probabilistic programming language. J. Stat. Softw. 2017, 76. [Google Scholar] [CrossRef]
- Davies, N.G.; Klepac, P.; Liu, Y.; Prem, K.; Jit, M.; Eggo, R.M. Age-dependent effects in the transmission and control of COVID-19 epidemics. medRxiv 2020. [Google Scholar] [CrossRef]
- Zhang, J.; Litvinova, M.; Liang, Y.; Wang, Y.; Wang, W.; Zhao, S.; Wu, Q.; Merler, S.; Viboud, C.; Vespignani, A.; et al. Changes in contact patterns shape the dynamics of the COVID-19 outbreak in China. Science 2020. [Google Scholar] [CrossRef]
- Mossong, J.; Hens, N.; Jit, M.; Beutels, P.; Auranen, K.; Mikolajczyk, R.; Massari, M.; Salmaso, S.; Tomba, G.S.; Wallinga, J.; et al. Social contacts and mixing patterns relevant to the spread of infectious diseases. PLoS Med. 2008, 5, e74. [Google Scholar] [CrossRef]
- Tenforde, M.W.; Billig Rose, E.; Lindsell, C.J.; Shapiro, N.I.; Files, D.C.; Gibbs, K.W.; Prekker, M.E.; Steingrub, J.S.; Smithline, H.A.; Gong, M.N.; et al. Characteristics of Adult Outpatients and Inpatients with COVID-19-11 Academic Medical Centers, United States, March-May 2020. MMWR Morb Mortal Wkly. Rep. 2020, 69, 841–846. [Google Scholar] [CrossRef]
- Cowling, B.J.; Ho, L.M.; Leung, G.M. Effectiveness of control measures during the SARS epidemic in Beijing: A comparison of the Rt curve and the epidemic curve. Epidemiol Infect. 2008, 136, 562–566. [Google Scholar] [CrossRef]
- Gostic, K.; Gomez, A.C.; Mummah, R.O.; Kucharski, A.J.; Lloyd-Smith, J.O. Estimated effectiveness of symptom and risk screening to prevent the spread of COVID-19. Elife 2020, 9. [Google Scholar] [CrossRef]
- Pan, A.; Liu, L.; Wang, C.; Guo, H.; Hao, X.; Wang, Q.; Huang, J.; He, N.; Yu, H.; Lin, X.; et al. Association of Public Health Interventions With the Epidemiology of the COVID-19 Outbreak in Wuhan, China. JAMA 2020. [Google Scholar] [CrossRef] [PubMed]
- Yu, X. Modeling Return of the Epidemic: Impact of Population Structure, Asymptomatic Infection, Case Importation and Personal Contacts. medRxiv 2020. [Google Scholar] [CrossRef]
- Bai, Y.; Yao, L.; Wei, T.; Tian, F.; Jin, D.Y.; Chen, L.; Wang, M. Presumed Asymptomatic Carrier Transmission of COVID-19. JAMA 2020. [Google Scholar] [CrossRef]
- Li, C.; Ji, F.; Wang, L.; Wang, L.; Hao, J.; Dai, M.; Liu, Y.; Pan, X.; Fu, J.; Li, L.; et al. Asymptomatic and Human-to-Human Transmission of SARS-CoV-2 in a 2-Family Cluster, Xuzhou, China. Emerg. Infect. Dis. 2020, 26. [Google Scholar] [CrossRef]
- Li, G.; Li, W.; He, X.; Cao, Y. Asymptomatic and Presymptomatic Infectors: Hidden Sources of COVID-19 Disease. Clin. Infect. Dis. 2020. [Google Scholar] [CrossRef]
- Kucharski, A.J.; Russell, T.W.; Diamond, C.; Liu, Y.; Edmunds, J.; Funk, S.; Eggo, R.M. Centre for Mathematical Modelling of Infectious Diseases, C.-w.g. Early dynamics of transmission and control of COVID-19: A mathematical modelling study. Lancet Infect. Dis. 2020. [Google Scholar] [CrossRef]
- IHME. Forecasting COVID-19 impact on hospital bed-days, ICU-days, ventilatordays and deaths by US state in the next 4 months. IHME COVID-19 health service utilization forecasting team. MMWR Morb Mortal Wkly. Rep. 2020, 69, 343–346. [Google Scholar]
- Woody, S.; Garcia Tec, M.; Dahan, M.; Gaither, K.; Lachmann, M.; Fox, S.; Meyers, L.A.; Scott, J.G. Projections for first-wave COVID-19 deaths across the US using social-distancing measures derived from mobile phones. medRxiv 2020. [Google Scholar] [CrossRef]
- Consul, P. Generalized Poisson Distribution: Properties and Applications; Marcel Decker: New York, NY, USA, 1989. [Google Scholar]
| Model Outcomes | Predictors | Lags of Predictors | ||||
|---|---|---|---|---|---|---|
| Lag 1 | Lag 2 | Lag 3 | Lag 4 | Lag 5 | ||
| Aged 60 or above | ||||||
| 60 or above | 2.09 (1.28–3.17) * | 1.21 (0.78–1.80) | 0.90 (0.60–1.39) | 1.03 (0.60–1.67) | 0.96 (0.63–1.53) | |
| 40–59 | 0.95 (0.49–1.84) | 1.81 (0.98–3.29) | 0.59 (0.30–1.18) | 1.37 (0.85–2.23) | 1.03 (0.61–1.70) | |
| 20–39 | 0.89 (0.53–1.46) | 2.02 (1.12–3.47) * | 1.28 (0.72–2.31) | 0.41 (0.22–0.78) # | 1.11 (0.58–2.22) | |
| 0–19 | 0.90 (0.61–1.43) | 1.36 (0.95–1.95) | 0.82 (0.57–1.19) | 0.61 (0.44–0.85) # | 1.64 (1.03–2.58) * | |
| Aged 40–59 | ||||||
| 60 or above | 1.66 (1.19–2.29) * | 0.79 (0.55–1.12) | 0.89 (0.64–1.23) | 0.98 (0.70–1.40) | 1.02 (0.71–1.40) | |
| 40–59 | 1.01 (0.62–1.63) | 1.76 (1.16–2.66) * | 1.23 (0.76–1.96) | 0.89 (0.62–1.29) | 0.88 (0.62–1.28) | |
| 20–39 | 1.13 (0.75–1.73) | 1.12 (0.76–1.67) | 1.59 (1.03–2.50) * | 0.60 (0.37–0.95) | 0.88 (0.53–1.48) | |
| 0–19 | 1.04 (0.79–1.37) | 1.28 (0.97–1.68) | 1.17 (0.88–1.57) | 1.14 (0.88–1.49) | 1.17 (0.84–1.62) | |
| Aged 20–39 | ||||||
| 60 or above | 0.95 (0.69–1.29) | 0.89 (0.65–1.23) | 1.01 (0.72–1.39) | 1.54 (1.11–2.12) * | 0.97 (0.69–1.31) | |
| 40–59 | 1.17 (0.73–1.88) | 1.18 (0.78–1.78) | 0.98 (0.60–1.52) | 0.90 (0.64–1.26) | 1.04 (0.75–1.47) | |
| 20–39 | 1.56 (1.05–2.36) * | 1.02 (0.68–1.55) | 1.45 (0.96–2.24) | 1.06 (0.68–1.64) | 0.85 (0.55–1.32) | |
| 0–19 | 1.04 (0.79–1.37) | 0.96 (0.75–1.27) | 0.88 (0.66–1.20) | 0.97 (0.75–1.26) | 0.74 (0.54–1.00) | |
| Aged 0–19 | ||||||
| 60 or above | 1.78 (1.23–2.61) * | 1.34 (0.86–2.06) | 0.99 (0.67–1.51) | 0.82 (0.52–1.25) | 1.55 (1.02–2.30) * | |
| 40–59 | 0.76 (0.41–1.38) | 0.71 (0.42–1.18) | 0.85 (0.47–1.56) | 0.91 (0.55–1.57) | 0.97 (0.62–1.54) | |
| 20–39 | 1.51 (0.92–2.55) | 1.50 (0.85–2.57) | 1.04 (0.61–1.80) | 0.78 (0.44–1.38) | 0.91 (0.51–1.62) | |
| 0–19 | 0.93 (0.64–1.36) | 0.85 (0.60–1.21) | 0.85 (0.60–1.27) | 0.92 (0.62–1.38) | 1.51 (0.99–2.31) | |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, X. Risk Interactions of Coronavirus Infection across Age Groups after the Peak of COVID-19 Epidemic. Int. J. Environ. Res. Public Health 2020, 17, 5246. https://doi.org/10.3390/ijerph17145246
Yu X. Risk Interactions of Coronavirus Infection across Age Groups after the Peak of COVID-19 Epidemic. International Journal of Environmental Research and Public Health. 2020; 17(14):5246. https://doi.org/10.3390/ijerph17145246
Chicago/Turabian StyleYu, Xinhua. 2020. "Risk Interactions of Coronavirus Infection across Age Groups after the Peak of COVID-19 Epidemic" International Journal of Environmental Research and Public Health 17, no. 14: 5246. https://doi.org/10.3390/ijerph17145246
APA StyleYu, X. (2020). Risk Interactions of Coronavirus Infection across Age Groups after the Peak of COVID-19 Epidemic. International Journal of Environmental Research and Public Health, 17(14), 5246. https://doi.org/10.3390/ijerph17145246





