An Optimal Pollution Control Model for Environmental Protection Cooperation between Developing and Developed Countries
Abstract
1. Introduction
2. Literature Review
3. The Theoretical Model
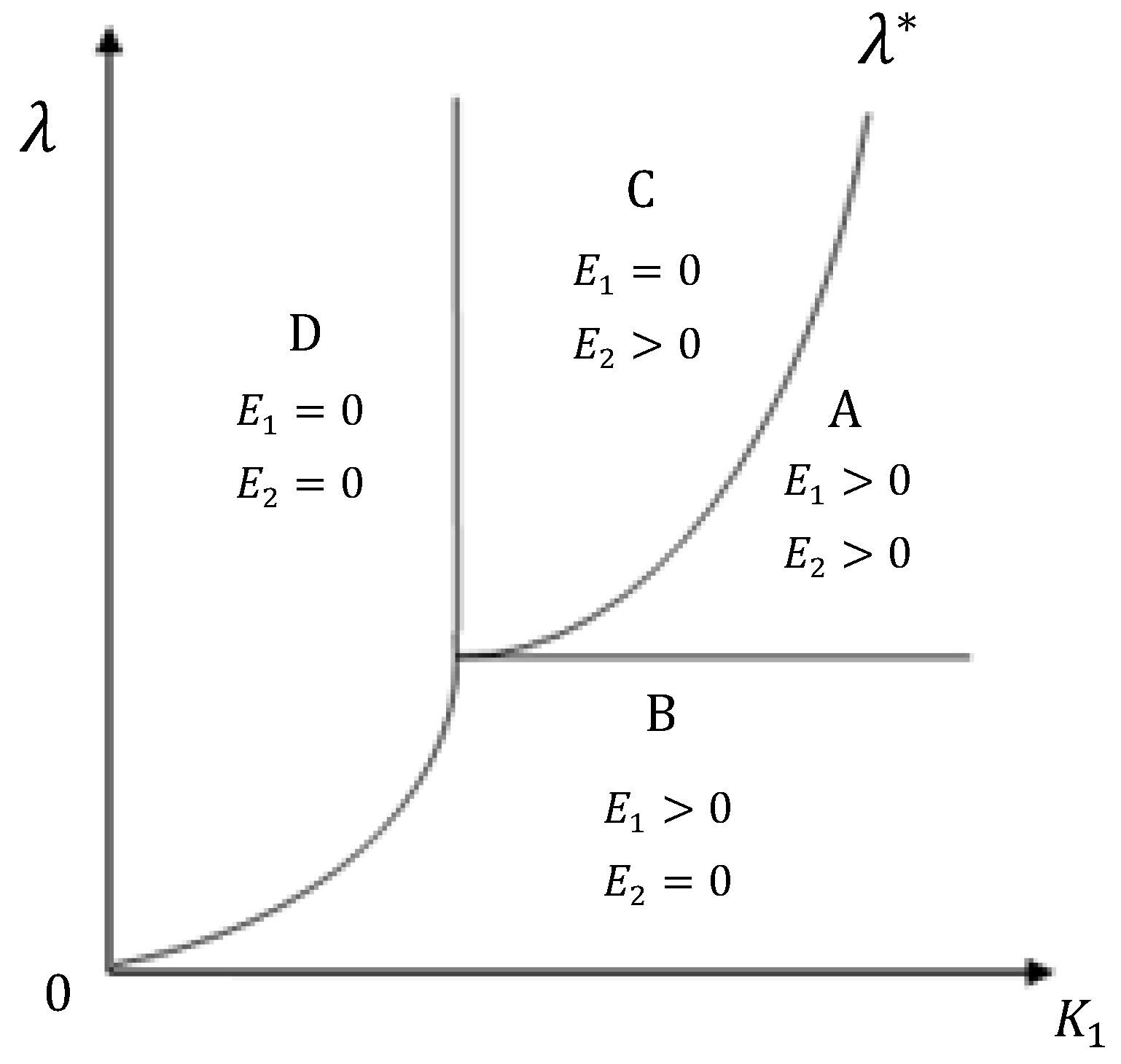
4. Four Regions of Environmental Investment
4.1. Region A
4.2. Region B
4.3. Region C
4.4. Region D
4.5. Boundaries of the Four Regions
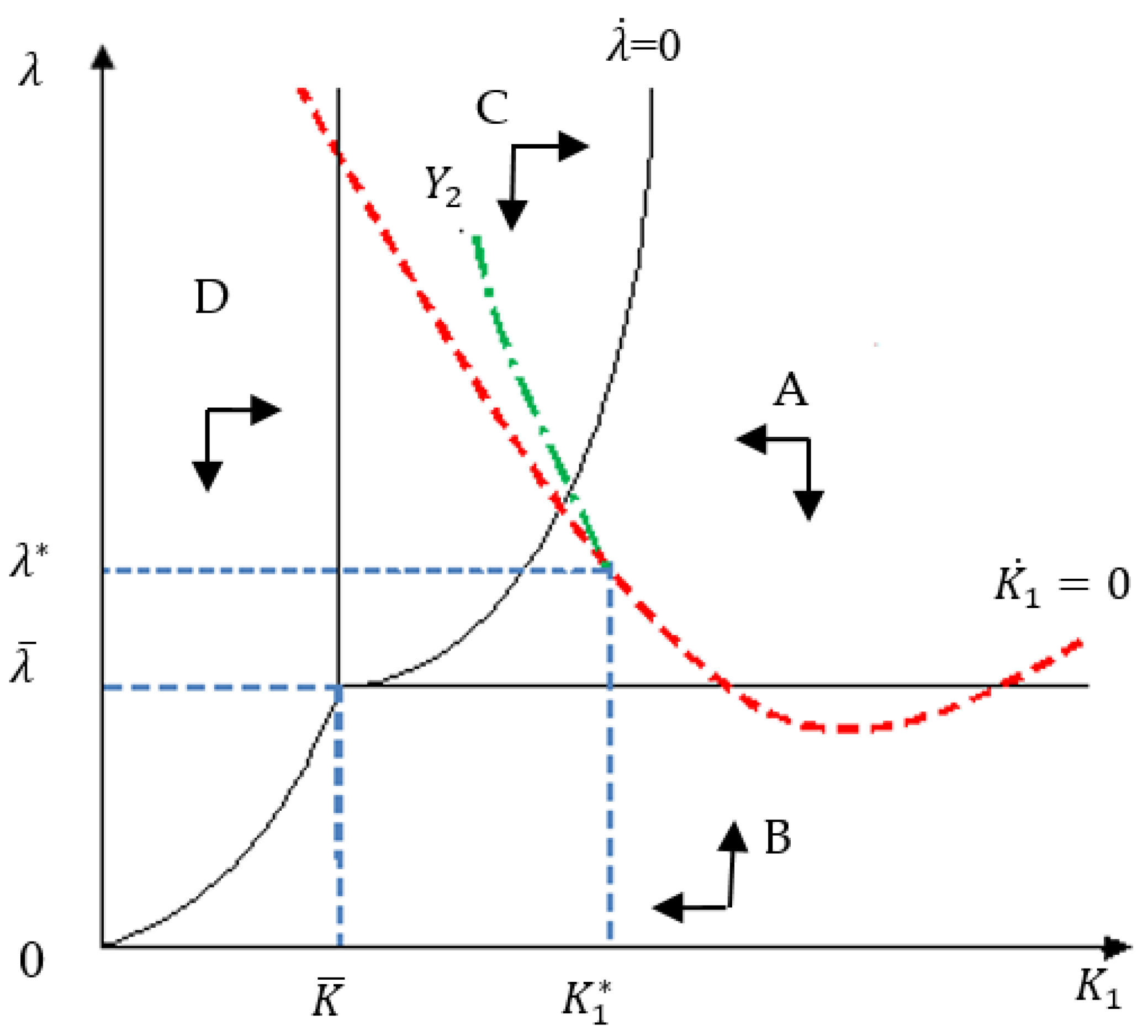
5. An Optimal Pollution Control Model
5.1. The Optimal Equilibrium
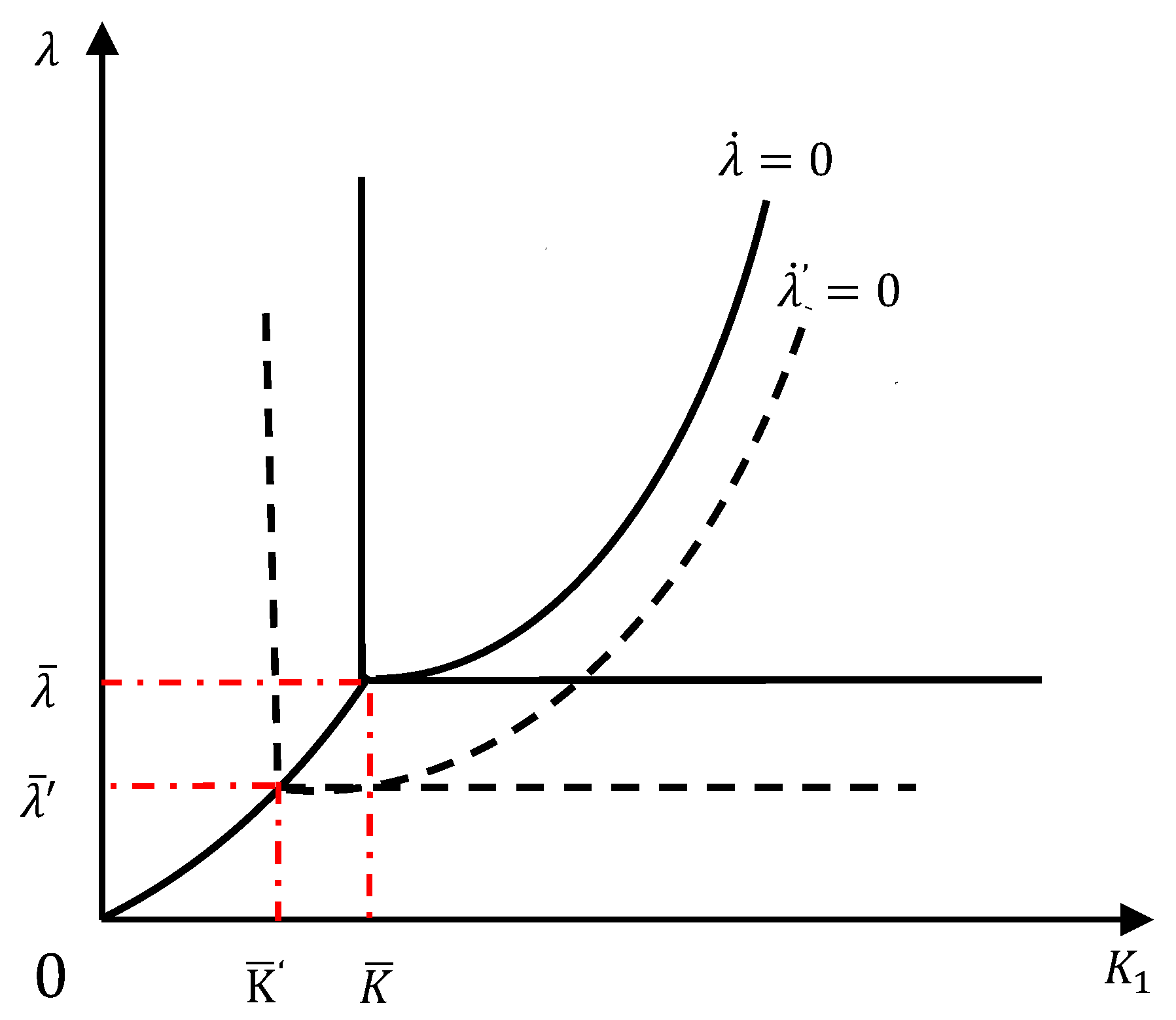
5.2. Discusion and Insights
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Daniel, C. Legal Consequences of Peremptory Norms in International Law; Cambridge University Press: Cambridge, UK, 2017. [Google Scholar]
- Climate Action Summit 2019. Global Climate Action NAZCA. United Nations. Archived from the original on 2019-10-17. Retrieved 2019-10-06. Available online: www.un.org/en/climatechange/ (accessed on 20 December 2019).
- Chakraborty, B. Paris Agreement on Climate Change: US Withdraw as Trump Calls it ‘Unfair’. Fox News. Archived from the original on 31 July 2017. Retrieved 25 July 2017. Available online: www.foxnews.com/politics/paris-agreement-on-climate-change-us-withdraws-as-trump-calls-it-unfair (accessed on 20 December 2019).
- Fiona, H. Progress and Problems as UN Climate Change Talks End with a Deal. The Guardian, 15 December 2018. Available online: www.theguardian.com/environment/2018/dec/15 (accessed on 15 December 2018).
- Fiona, H. What Was Agreed at COP24 in Poland and Why Did it Take So Long? The Guardian, 16 December 2018. Available online: www.theguardian.com/environment/2018/dec/16 (accessed on 16 December 2018).
- Farand, C. What is the UN Climate Action Summit? Climate Home News. Archived from the original on 2019-09-22. Available online: www.climatechangenews.com/2019/09/16/un-climate-action-summit/ (accessed on 16 September 2019).
- Rosane, O. What to Expect from Today’s UN Climate Action Summit. Ecowatch. Archived from the original on 2019-09-23. Retrieved 2019-09-23. Available online: www.ecowatch.com/climate-action-summit-2019-2640522348.html (accessed on 23 September 2019).
- Rosane, O. UN Climate Action Summit Falls ‘Woefully Short’ of Expectations. Ecowatch. Archived from the original on 2019-09-25. Retrieved 2019-09-25. Available online: www.ecowatch.com/un-climate-action-summit-2640575796.html (accessed on 24 September 2019).
- Somini, S. U.N. Climate Talks End with Few Commitments and a ‘Lost’ Opportunity. The New York Times, 15 December 2019. Available online: www.nytimes.com/2019/12/15/climate/cop25-un-climate-talks-madrid.html (accessed on 15 December 2019).
- Record-Long UN Climate Talks End with No Deal on Carbon Markets. The Times of Israel, 15 December 2019. Available online: www.timesofisrael.com/record-long-un-climate-talks-end-with-no-deal-on-carbon-markets/ (accessed on 23 September 2019).
- Marlowe, H. Five Reasons COP25 Climate Talks Failed. Phys.org, 25 December 2019. Available online: https://phys.org/news/2019-12-cop25-climate.html (accessed on 25 December 2019).
- Post, S.; Kleinen-von Königslöw, K.; Schäfer, M.S. Between Guilt and Obligation: Debating the Responsibility for Climate Change and Climate Politics in the Media. Environ. Commun. 2019, 6, 723–739. [Google Scholar] [CrossRef]
- Patrícia, G.F. ‘Common but Differentiated Responsibilities’ in the National Courts: Lessons from Urgenda v. The Netherlands. Transnatl. Environ. Law 2016, 5, 329–351. [Google Scholar] [CrossRef]
- Gupta, J. A history of international climate change policy. Wiley Interdiscip. Rev. Clim. Chang. 2010, 1, 636–653. [Google Scholar]
- Hallding, K.; Jürisoo, M.; Carson, M.; Atteridge, A. Rising powers: The evolving role of BASIC countries. Clim. Policy 2013, 13, 608–631. [Google Scholar] [CrossRef]
- Schmidt, A.; Schäfer, M.S. Constructions of climate justice in German, Indian and US media. Clim. Chang. 2015, 133, 535–549. [Google Scholar] [CrossRef]
- Klein, D.; Pia, M. The Paris Agreement on Climate Change: Analysis and Commentary; Oxford University Press: Oxford, UK, 2017; pp. 84–98. [Google Scholar]
- Bodansky, D. The Copenhagen Climate Change Conference: A Post-Mortem. Am. J. Int. Law 2010, 104, 230–240. [Google Scholar]
- “Putting the ‘Enhanced Transparency Framework’ into Action: Priorities for a Key Pillar of the Paris Agreement”. POLICY BRIEF, Stockholm Environment Institute. Archived (PDF) from the original on 19 November 2016. Available online: www.sei-international.org/publications?pid=3033 (accessed on 20 December 2019).
- Tian, F.; Sošić, G.; Debo, L. Manufacturers’ Competition and Cooperation in Sustainability: Stable Recycling Alliances. Manag. Sci. 2019, 65, 4733–4753. [Google Scholar] [CrossRef]
- Castro, P. Common but Differentiated Responsibilities Beyond the Nation State: How Is Differential Treatment Addressed in Transnational Climate Governance Initiatives? Transnatl. Environ. Law 2016, 5, 379–400. [Google Scholar]
- Zhang, X.; Valerie, J. Karplusb Carbon emissions in China: How far can new efforts bend the curve? Energy Econ. 2016, 54, 388–395. [Google Scholar]
- Conconi, P. Green lobbies and transboundary pollution in large open economies. J. Int. Econ. 2003, 59, 399–422. [Google Scholar] [CrossRef]
- Hoel, M. The triple inefficiency of uncoordinated environmental policies. Scand. J. Econ. 2005, 107, 157–173. [Google Scholar] [CrossRef]
- Bhagwati, J.A. Global Warming Fund Could Succeed Where Kyoto Failed. Financ. Times 2006, 32, 644–654. [Google Scholar]
- Eyckmans, J.; Finus, M. Measures to enhance the success of global climate treaties. Int. Environ. Agreem. Politics Law Econ. 2007, 7, 73–97. [Google Scholar]
- Fünfgelt, J.; Schulze, G.G. Endogenous environmental policy when pollution is transboundary. SSRN Electron. J. 2011. [Google Scholar] [CrossRef]
- He, J.; Zhang, P. Evaluating the Coordination of Industrial-Economic Development Based on Anthropogenic Carbon Emissions in Henan Province, China. Int. J. Environ. Res. Public Health 2018, 15, 1815. [Google Scholar] [CrossRef]
- Gong, X.; Mi, J.; Wei, C.; Yang, R. Measuring Environmental and Economic Performance of Air Pollution Control for Province-Level Areas in China. Int. J. Environ. Res. Public Health 2019, 16, 1378. [Google Scholar] [CrossRef]
- Jørgensen, S.; Martín-Herrán, G.; Zaccour, G. Dynamic Games in the Economics and Management of Pollution. Environ. Modeling Assess. 2010, 15, 433–467. [Google Scholar]
- Rubio, S.; Casino, B. Self-enforcing international environmental agreements with a stock pollutant. Span. Econ. Rev. 2005, 7, 89–109. [Google Scholar] [CrossRef]
- Missfeldt, F. Game-theoretic modelling of transboundary pollution. J. Econ. Surv. 1999, 13, 287–321. [Google Scholar]
- Jørgensen, S.; Zaccour, G. Time consistent side payments in a dynamic game of downstream pollution. J. Econo. Dyn. Control 2001, 25, 1973–1987. [Google Scholar] [CrossRef]
- Cabo, F.; Martín-Herrán, G. North-south transfers vs. biodiversity conservation: A trade differential game. Ann. Reg. Sci. 2006, 40, 249–278. [Google Scholar]
- Martin, D.; Meyer, M. Pathways to a Resource-Efficient and Low-Carbon Europe. Ecol. Econ. 2019, 155, 88–104. [Google Scholar]
- Zagonari, F. International pollution problems: Unilateral initiatives by environmental groups in one country. J. Environ. Econ. Manag. 1998, 36, 46–69. [Google Scholar] [CrossRef]
- Breton, M.; Sbragia, L.; Zaccour, G. Dynamic models for international environmental agreements. Environ. Resour. Econ. 2010. [Google Scholar] [CrossRef]
- Bian, J.; Liao, Y.; Wang, Y.Y.; Tao, F. Analysis of Firm CSR Strategies. Eur. J. Operat. Res. 2020, in press. [Google Scholar] [CrossRef]
- Li, J.; Yi, L.; Shi, V.; Chen, X. Supplier encroachment strategy in the presence of retail strategic inventory: Centralization or decentralization? Omega 2020, 102213, in press. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, L.; Zhu, J.; Zhang, Y.; Chen, X. An Optimal Pollution Control Model for Environmental Protection Cooperation between Developing and Developed Countries. Int. J. Environ. Res. Public Health 2020, 17, 3868. https://doi.org/10.3390/ijerph17113868
Liu L, Zhu J, Zhang Y, Chen X. An Optimal Pollution Control Model for Environmental Protection Cooperation between Developing and Developed Countries. International Journal of Environmental Research and Public Health. 2020; 17(11):3868. https://doi.org/10.3390/ijerph17113868
Chicago/Turabian StyleLiu, Liyuan, Jing Zhu, Yibin Zhang, and Xiding Chen. 2020. "An Optimal Pollution Control Model for Environmental Protection Cooperation between Developing and Developed Countries" International Journal of Environmental Research and Public Health 17, no. 11: 3868. https://doi.org/10.3390/ijerph17113868
APA StyleLiu, L., Zhu, J., Zhang, Y., & Chen, X. (2020). An Optimal Pollution Control Model for Environmental Protection Cooperation between Developing and Developed Countries. International Journal of Environmental Research and Public Health, 17(11), 3868. https://doi.org/10.3390/ijerph17113868




