An Interval Two-Stage Stochastic Programming Model for Flood Resources Allocation under Ecological Benefits as a Constraint Combined with Ecological Compensation Concept
Abstract
:1. Introduction
2. Case Descriptions
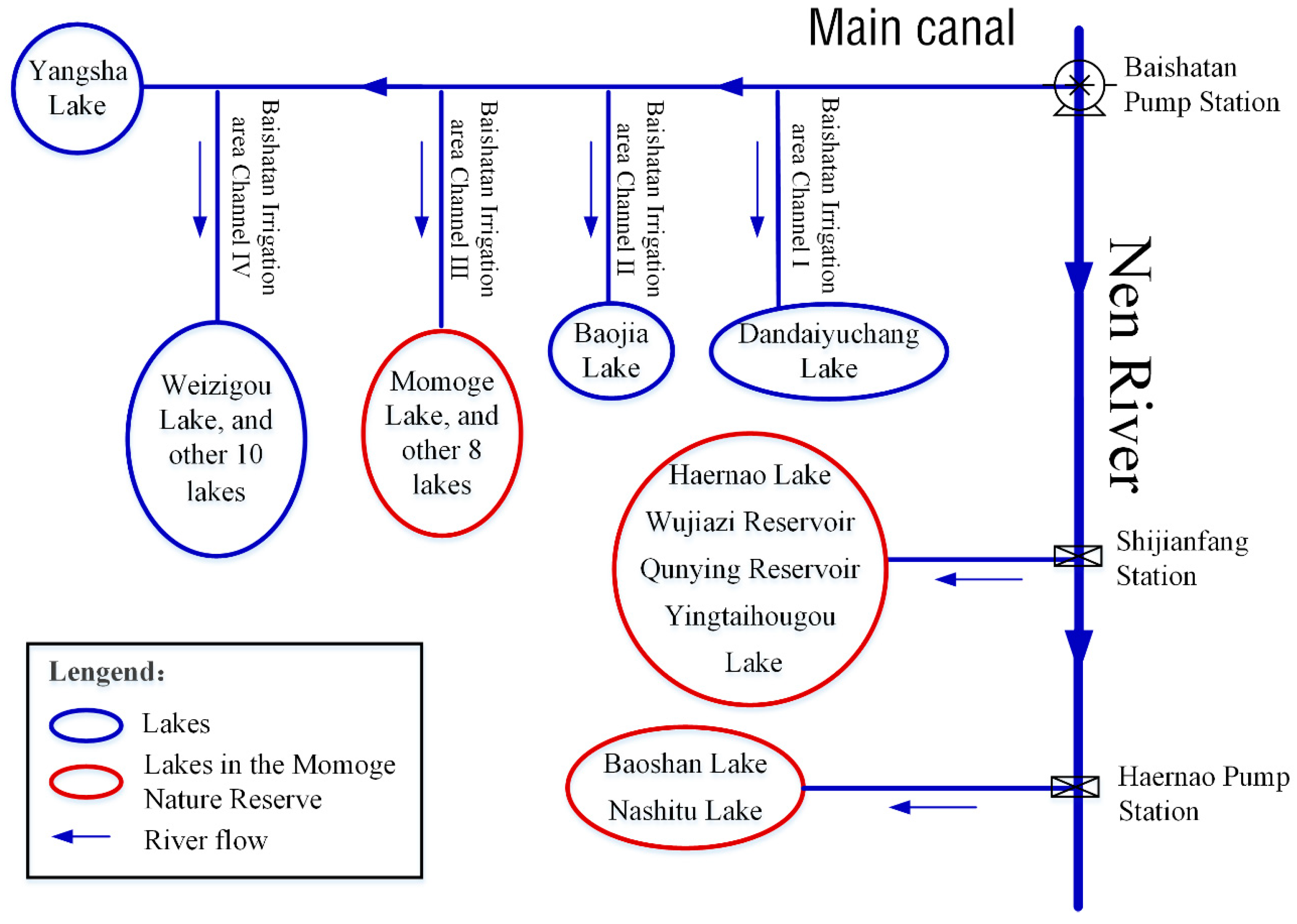
2.1. Project Overview
2.2. Ecological Benefits Evaluation Index System
3. Interval Two-Stage Flood Resources Allocation Model
3.1. Model Formulation
3.2. Model Solution
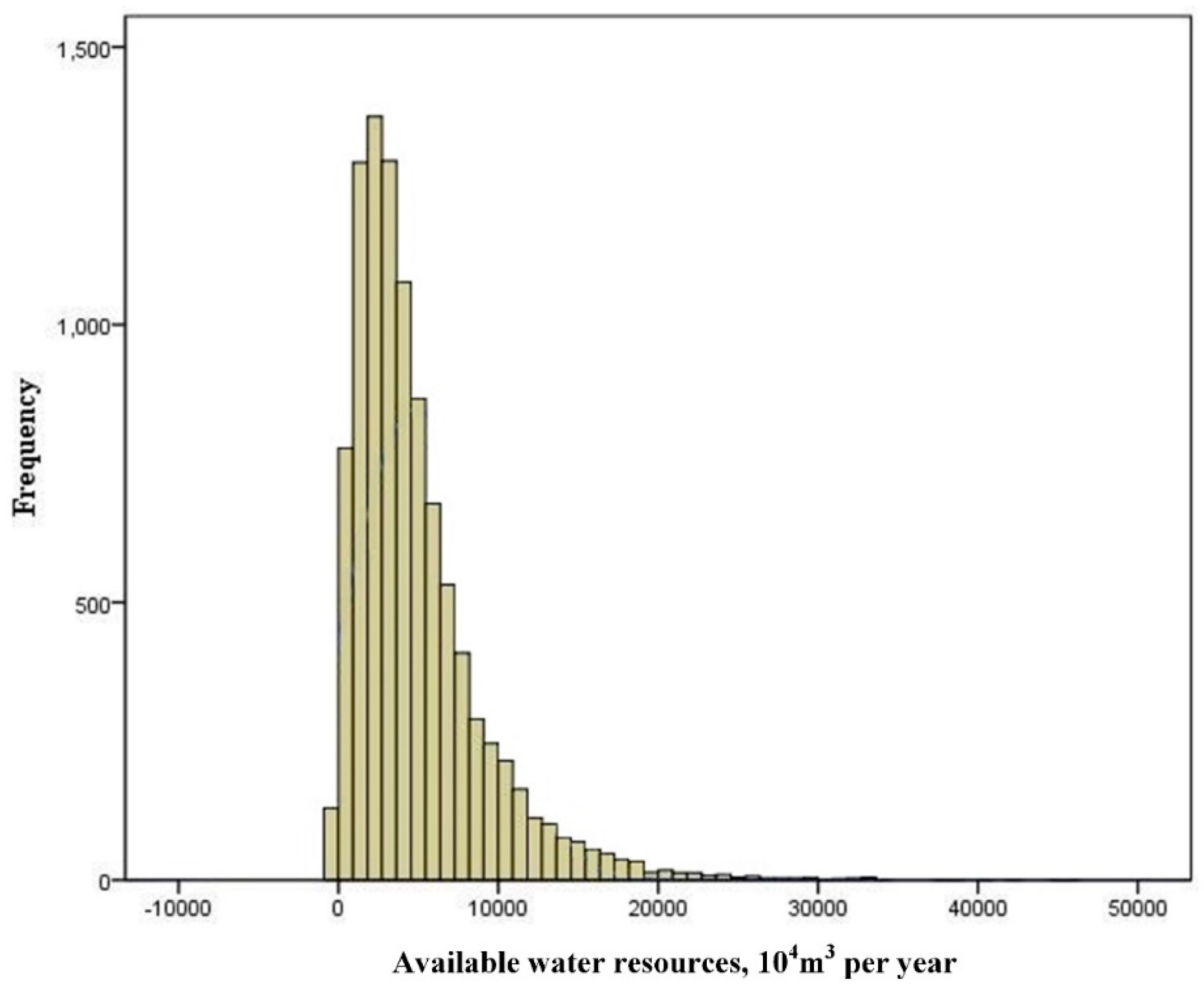
3.3. Model Parameters and Data Description
4. Results Analysis and Discussion
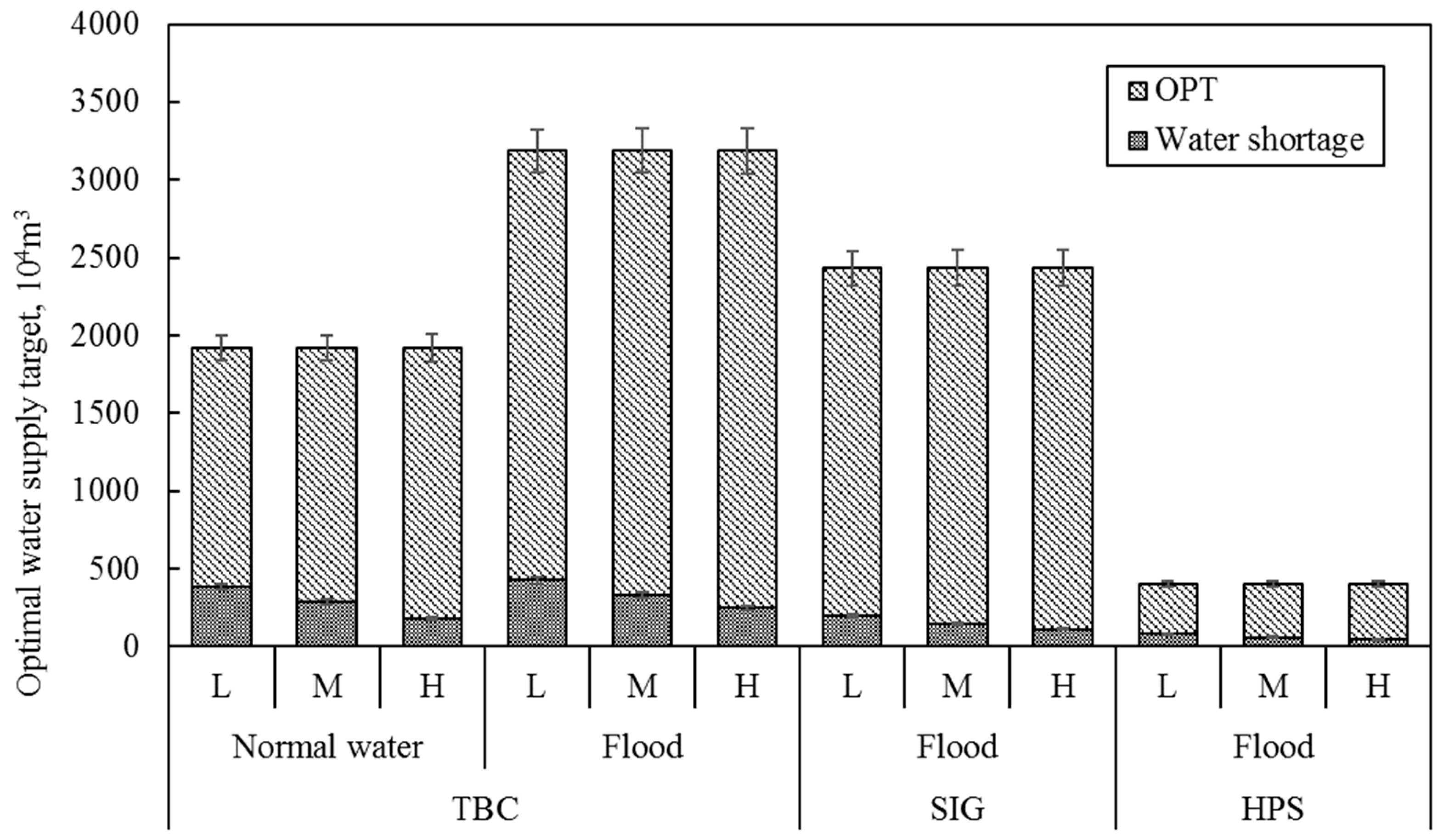
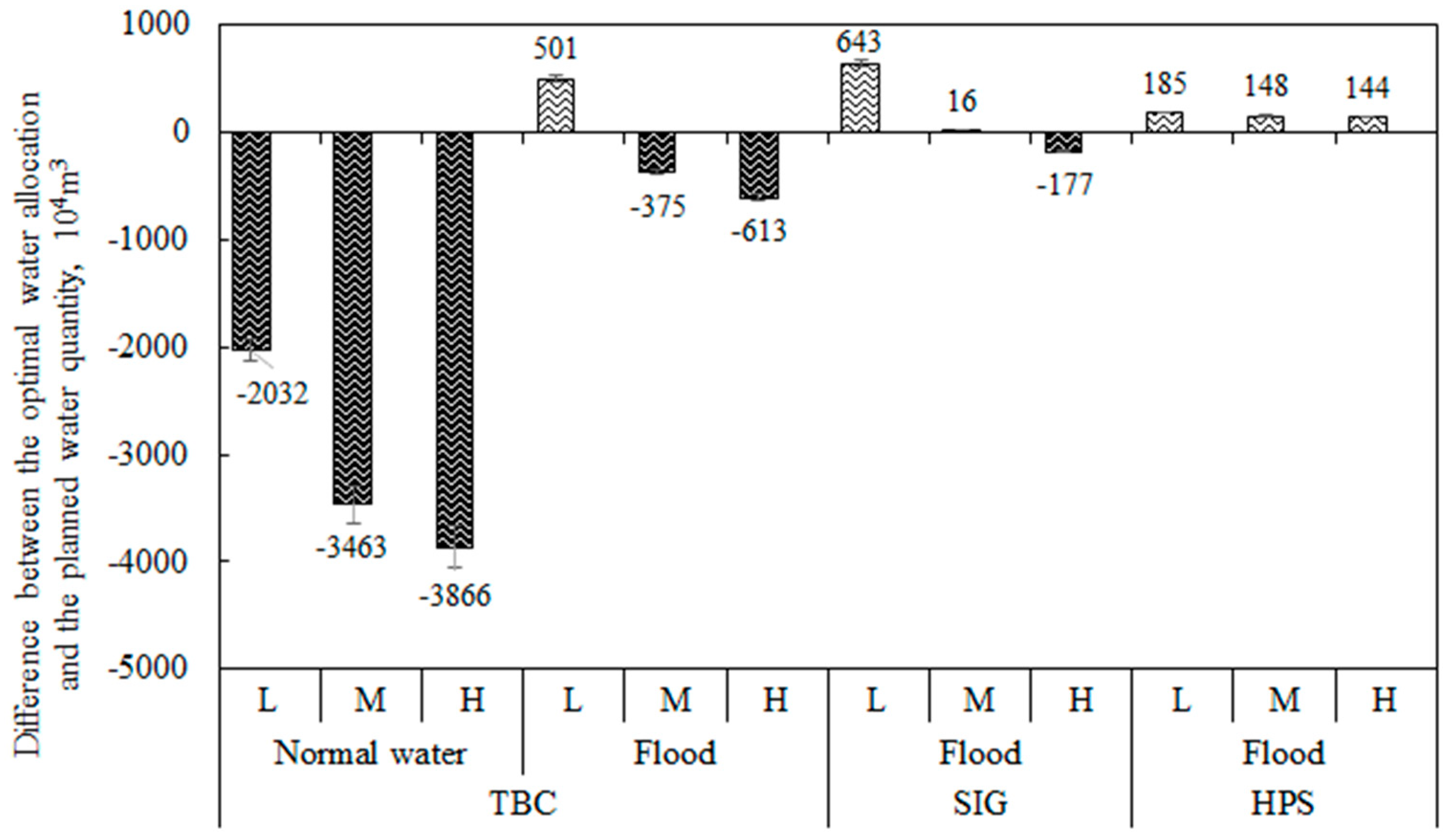
4.1. Water Supply Allocation Scheme
4.2. Ecological Benefits Analysis of the Water Replenishment Scheme in Momoge National Nature Reserve (MNNR)
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Cao, Y.; Ni, G.; Hu, H.; Yin, J. Optimization dispatching theory and its application of floodwater utilization. J. Hydroelectr. Eng. 2005, 5, 1721–1725. [Google Scholar] [CrossRef]
- Decision of the Central Committee of the Communist Party of China on Accelerating the Reform and Development of Water Conservancy [EB/OL]. Available online: http://www.gov.cn/gongbao/content/2011/content_1803158.htm (accessed on 18 February 2019).
- Cheng, X.T.; Wu, Y.C.; Wang, Y.Y. Research on the New Concept Flood Management Flood Protection Safety System; China Water Conservancy and Hydropower Press: Beijing, China, 2004; pp. 125–136. [Google Scholar]
- Peng, J.; Luo, H.; Ma, W.; Xiang, L.Y. Water pollution risk analysis on flood resource utilization in Haihe River detention areas. J. China Inst. Water 2007, 29, 1–2. [Google Scholar] [CrossRef]
- Huang, F.; Yan, B.; Zhang, X.; Zhao, D.; Guo, L.; Wang, Y.; Xia, Z. Water Regime Evolution of Large Seasonal Lakes: Indicators for Characterization and an Application in Poyang Lake, China. Int. J. Environ. Res. Public Health 2018, 15, 2598. [Google Scholar] [CrossRef]
- Yuan, Z.; Xu, J.; Wang, Y. Projection of Future Extreme Precipitation and Flood Changes of the Jinsha River Basin in China Based on CMIP5 Climate Models. Int. J. Environ. Res. Public Health 2018, 15, 2491. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Cong, Z. Trends of precipitation intensity and frequency in hydrological regions of China from 1956 to 2005. Glob. Planet. Chang. 2014, 117, 40–51. [Google Scholar] [CrossRef]
- Ward, F.A. Economic impacts on irrigated agriculture of water conservation programs in drought. J. Hydrol. 2014, 508, 114–127. [Google Scholar] [CrossRef]
- Jiang, B.; Chen, Y.; Xiao, Y. Evaluation of the economic value of final ecosystem services from the Baiyangdian wetland. Acta Ecol. Sin. 2017, 37, 2497–2505. [Google Scholar] [CrossRef]
- Xiang, L.Y.; Wei, Z.M. Flood resource utilization—Concept, way and strategy. Water Resour. Dev. Res. 2005, 7, 24–29. [Google Scholar] [CrossRef]
- Plate, E.J. Flood risk and flood management. J. Hydrol. 2002, 267, 2–11. [Google Scholar] [CrossRef]
- Li, C.A. Possible floodwater utilization of the Yangtze River. Earth Sci. J. China Univ. Geosci. 2003, 28, 461–465. [Google Scholar] [CrossRef]
- Liu, K.L.; Wang, Y.T.; Hu, S.Y. Comparative study on application of quantitative analysis methods to division of flood seasonal phases for reservoir. Water Res. Hydropower Eng. 2006, 3, 76–78. [Google Scholar] [CrossRef]
- Luo, Q.; Fang, G.H.; Huang, X.F.; Yan, K.; Zhou, J.; Zhuang, J. Study on the Utilization Potential of Rainwater Resources in the Water Shortage Areas in the Lower Reaches. Int. J. Hydroelectr. Energy 2011, 29, 5–7. [Google Scholar] [CrossRef]
- Fang, G.; Yang, Y.; Yuan, Y.; Huang, X.; Wen, X. Risk decision analysis of floodwater resource utilization based on adjusting flood limited water level of reservoir. Fresenius Environ. Bull. 2017, 26, 5745–5753. [Google Scholar]
- Afzal, J.; Noble, D.H.; Weatherhead, E.K. Optimization Model for Alternative Use of Different Quality Irrigation Waters. J. Irrig. Drain. Eng. 1992, 118, 218–228. [Google Scholar] [CrossRef]
- Dudley, N.J. Irrigation planning: 4. Optimal interseasonal water allocation. Water Resour. Res. 1972, 8, 586–594. [Google Scholar] [CrossRef]
- Kumar, A.M.; Vijya, K. Fuzzy optimization model for water quality management of a river system. J. Water Resour. Plan. Manag. 1999, 125, 179–180. [Google Scholar] [CrossRef]
- Lu, H.W.; Huang, G.H.; Zeng, G.M.; Maqsood, I.; He, L. An Inexact Two-stage Fuzzy-stochastic Programming Model for Water Resources Management. Water Resour. Manag. 2008, 22, 991–1016. [Google Scholar] [CrossRef]
- Cardwell, H.; Ellis, H. Stochastic dynamic programming models for water quality management. Water Resour. Res. 2010, 29, 803–813. [Google Scholar] [CrossRef]
- Xie, Y.L.; Li, Y.P.; Huang, G.H.; Li, Y.F.; Chen, L.R. An inexact chance-constrained programming model for water quality management in Binhai New Area of Tianjin, China. Sci. Total. Environ. 2011, 409, 1757–1773. [Google Scholar] [CrossRef]
- Meng, C.; Wang, X.L.; Li, Y. An Optimization Model for Waste Load Allocation under Water Carrying Capacity Improvement Management, A Case Study of the Yitong River, Northeast China. Water 2017, 9, 573. [Google Scholar] [CrossRef]
- Fu, Y.H.; Guo, P.; Fang, S.Q.; Li, M. Optimal allocation of water resources in irrigation district based on two-stage stochastic programming method. Trans. Chin. Soc. Agric. Eng. 2014, 30, 73–81. [Google Scholar] [CrossRef]
- Wang, H.Y.; Gao, T.Z.; Gao, J.; Huang, Q. Optimal Allocation of Water Resources in the Middle Route of South-to-North Water Transfer Project Based on AHP-LP Method: A Case Study of Water Receiving Area in Hebei Province. Resour. Environ. Yangtze Basin 2007, 16, 588–592. [Google Scholar] [CrossRef]
- Liu, Y. Study on the Interval Optimization Model of Momoge Wetland Replenishment Scheme under the Constraint of Ecological Benefit. Master’s Dissertation, Changchun Institute of Technology, Jilin, China, December 2017. [Google Scholar]
- Alcamo, J.; Robert, T.; Zakri, A.H. Ecosystems and Human Well-Being: A Framework for Assessment; Sarukhán, J., Whyte, A., Eds.; Island Press: Washington, DC, USA, 2003. [Google Scholar]
- Raffaelli, D.; White, P.C.L. Ecosystems and Their Services in a Changing World. Adv. Ecol. Res. 2013, 48, 1–70. [Google Scholar] [CrossRef]
- Zhao, T.Q.; Ouyang, Z.Y.; Wang, X.K.; Miao, H.; Wei, Y. Service Function of Land Surface Water Ecosystem in China and Its Eco-economic Value Evaluation. J. Nat. Resour. 2003, 18, 443–452. [Google Scholar] [CrossRef]
- Yang, F.; Li, X.; Liu, X. Use patterns of ecological agriculture and biological carbon sinking extension in marsh wetland. Trans. Chin. Soc. Agric. Eng. 2012, 28, 156–162. [Google Scholar] [CrossRef]
- Cai, B.; Meng, C.; Wang, X.; Li, Y. Application of a Fuzzy Two-Stage Chance Constrained Stochastic Programming Model for Optimization of the Ecological Services Value of the Interconnected River System Network Project in the Western Jilin Province, China. Water 2019, 11, 68. [Google Scholar] [CrossRef]
- Fu, Q.; Liu, Y.F.; Liu, D.; Li, T.F.; Liu, W.; Osman, A. Optimal allocation of multiple water sources in irrigation district based on interval multi-stage stochastic programming model. Trans. Chin. Soc. Agric. Eng. 2016, 32, 132–139. [Google Scholar] [CrossRef]
- Cui, B.S.; Yang, Z.F. Classification of wetland ecological environment water demand grade and case analysis. Resour. Sci. 2003, 25, 21–28. [Google Scholar] [CrossRef]
- Zhao, B.; Wang, T.L.; Zhou, L.F.; Yang, P.Q. Summary of the Calculation Method of Eco-environmental Water Demand and Application in Estuarine Wetland. J. Anhui Agric. Sci. 2007, 35, 5532–5534. [Google Scholar] [CrossRef]

| Target Layer | Criteria Layers | Indicator Layers |
|---|---|---|
| Total benefits of ecological water transfer project | Ecosystem material production | Food production value |
| Raw material production value | ||
| Ecosystem environmental regulation | Carbon sequestration value | |
| Oxygen release value | ||
| Flood storage value | ||
| Microclimate regulation value | ||
| Plant adsorption value | ||
| Biodiversity value | ||
| Humanities and social services | Scientific research value | |
| Tourism value | ||
| Landscape value |
| Water Intake | Water Flow Level | Normal Water (104 m3 per Year) | Flood (104 m3 per Year) | ||
|---|---|---|---|---|---|
| Lower Bound | Upper Bound | Lower Bound | Upper Bound | ||
| TBC | L (P1 = 0.4) | 2060 | 4634 | 1306 | 2938 |
| M (P2 = 0.5) | 4291 | 6437 | 2720 | 4080 | |
| H (P3 = 0.1) | 5149 | 10621 | 3264 | 7344 | |
| SIG | L (P1 = 0.4) | 0 | 0 | 918 | 2065 |
| M (P2 = 0.5) | 0 | 0 | 1912 | 2868 | |
| H (P3 = 0.1) | 0 | 0 | 2294 | 5162 | |
| HPS | L (P1 = 0.4) | 0 | 0 | 79 | 178 |
| M (P2 = 0.5) | 0 | 0 | 165 | 247 | |
| H (P3 = 0.1) | 0 | 0 | 198 | 445 | |
| Water intake | Lakes | Fish Pond | Crab Pond | Reed Wetland | Marsh | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Lower Bound | Upper Bound | Lower Bound | Upper Bound | Lower Bound | Upper Bound | Lower Bound | Upper Bound | |||
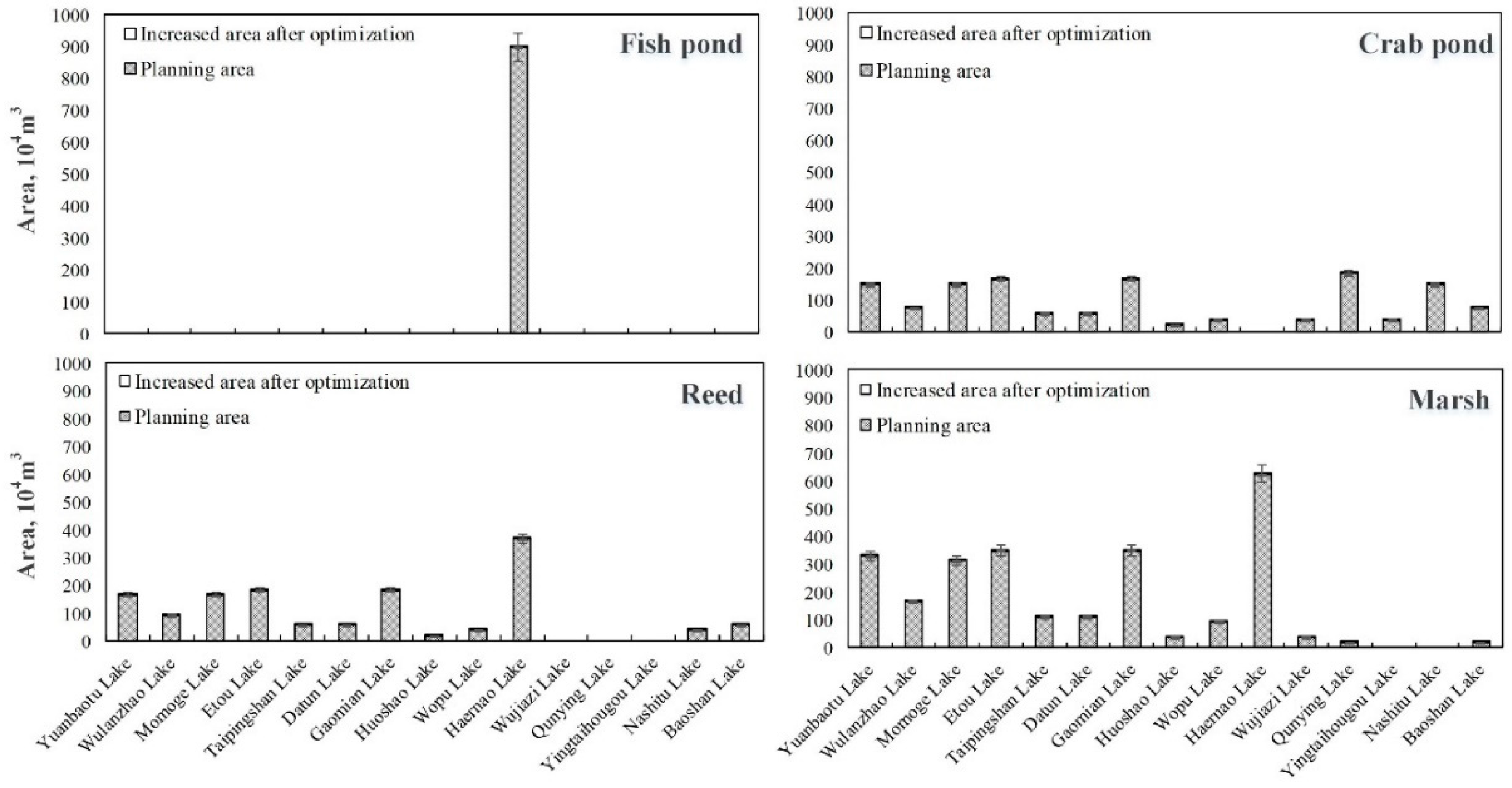
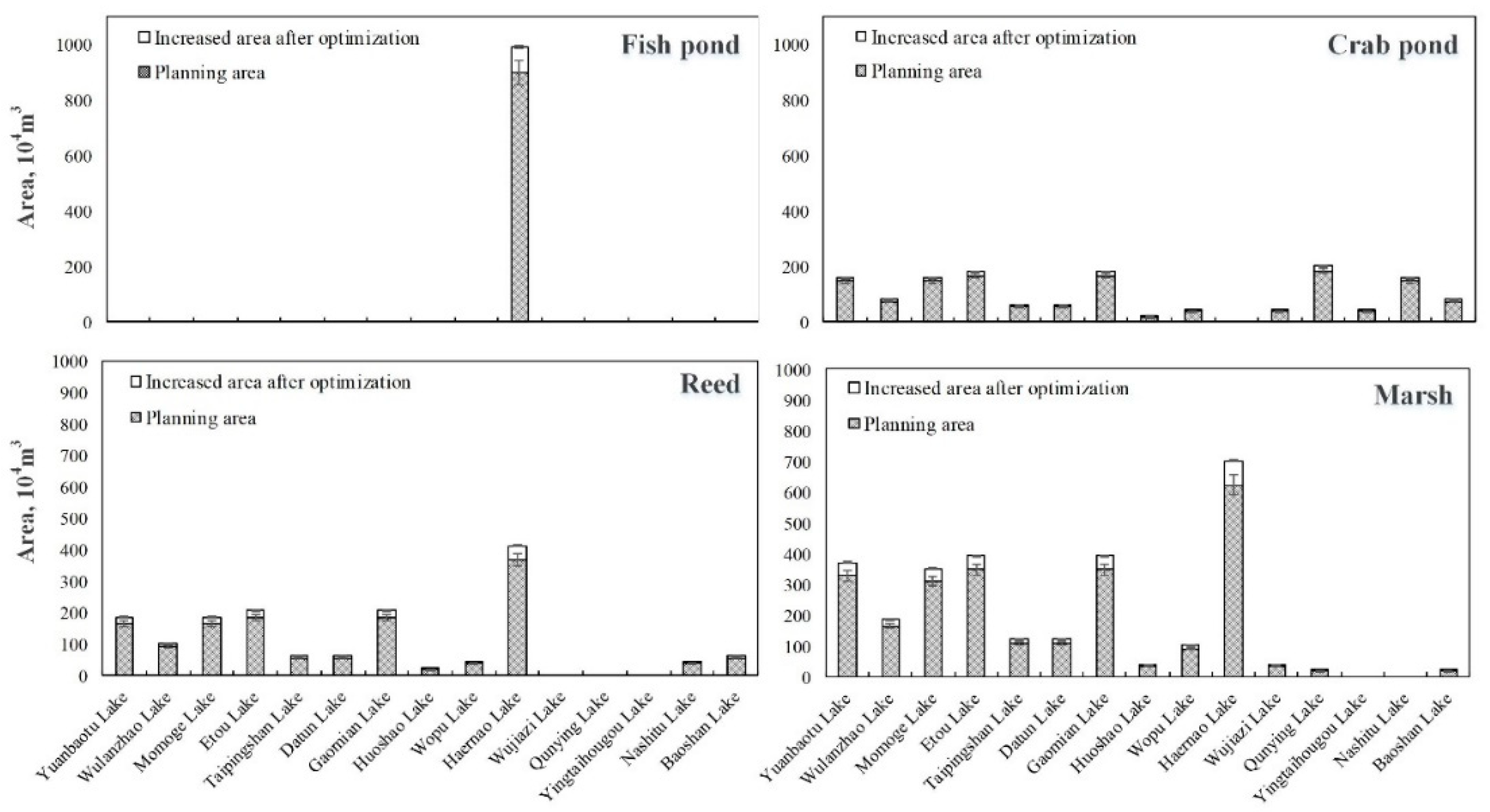
| Ecological function planning area (104 m2) | TBC | Yuanbaotu Lake | - | - | 120 | 147 | 135 | 165 | 270 | 330 |
| Wulanzhao Lake | - | - | 60 | 73 | 75 | 92 | 135 | 165 | ||
| Momoge Lake | - | - | 120 | 147 | 135 | 165 | 255 | 312 | ||
| Etou Lake | - | - | 135 | 165 | 150 | 183 | 285 | 348 | ||
| Taipingshan Lake | - | - | 45 | 55 | 45 | 55 | 90 | 110 | ||
| Datun Lake | - | - | 45 | 55 | 45 | 55 | 90 | 110 | ||
| Gaomian Lake | - | - | 135 | 165 | 150 | 183 | 285 | 348 | ||
| Huoshao Lake | - | - | 15 | 18 | 15 | 18 | 30 | 37 | ||
| Wopu Lake | - | - | 30 | 37 | 30 | 37 | 75 | 92 | ||
| SIG | Haernao Lake | 735 | 898 | - | - | 300 | 367 | 510 | 623 | |
| Wujiazi Lake | - | - | 30 | 37 | - | - | 30 | 37 | ||
| Qunying Lake | - | - | 150 | 183 | - | - | 15 | 18 | ||
| Yingtaihougou Lake | - | - | 30 | 37 | - | - | - | - | ||
| HPS | Nashitu Lake | - | - | 120 | 147 | 30 | 37 | - | ||
| Baoshan Lake | - | - | 60 | 73 | 45 | 55 | 15 | 18 | ||
| Water demand per unit area (m3/m2) | 0.5 | 0.6 | 0.5 | 0.6 | 1.7 | 2.9 | 0.7 | 1.1 | ||
| Ecological benefits per unit area (Yuan/m2) | 0.04 | 2.40 | 0.04 | 3.60 | 0.04 | 3.64 | 0.04 | 3.64 | ||
| Fish Pond | Crab Pond | Reed | Marsh | |
|---|---|---|---|---|
| Food production (Fish) | 1 | 0 | 0 | 0 |
| Food production (Crab) | 0 | 1 | 0 | 0 |
| Raw material production (Reed) | 0 | 0 | 1 | 0 |
| Carbon sequestration | 0 | 0 | 1 | 1 |
| Oxygen release | 0 | 0 | 1 | 1 |
| Flood storage | 1 | 1 | 1 | 1 |
| Microclimate regulation | 1 | 1 | 1 | 1 |
| Plant adsorption | 0 | 0 | 1 | 1 |
| Biodiversity | 1 | 1 | 1 | 1 |
| Scientific research | 1 | 1 | 1 | 1 |
| Tourism | 1 | 1 | 1 | 1 |
| Landscape | 1 | 1 | 1 | 1 |
| Water Intake | Type of Water Resources | Cost (Yuan/m3) | Water Shortage Penalty Coefficient (Yuan/m3) | |
|---|---|---|---|---|
| Lower Bound | Upper Bound | |||
| TBC | Normal water | 0.18 | 0.04 | 3.64 |
| Flood | 0.11 | 0.04 | 3.64 | |
| SIG | Normal water | 0.18 | 0 | 0 |
| Flood | 0.11 | 0.04 | 3.64 | |
| HPS | Normal water | 0.18 | 0 | 0 |
| Flood | 0.11 | 0.04 | 3.64 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qiu, Y.; Liu, Y.; Liu, Y.; Chen, Y.; Li, Y. An Interval Two-Stage Stochastic Programming Model for Flood Resources Allocation under Ecological Benefits as a Constraint Combined with Ecological Compensation Concept. Int. J. Environ. Res. Public Health 2019, 16, 1033. https://doi.org/10.3390/ijerph16061033
Qiu Y, Liu Y, Liu Y, Chen Y, Li Y. An Interval Two-Stage Stochastic Programming Model for Flood Resources Allocation under Ecological Benefits as a Constraint Combined with Ecological Compensation Concept. International Journal of Environmental Research and Public Health. 2019; 16(6):1033. https://doi.org/10.3390/ijerph16061033
Chicago/Turabian StyleQiu, Yu, Yuan Liu, Yang Liu, Yingzi Chen, and Yu Li. 2019. "An Interval Two-Stage Stochastic Programming Model for Flood Resources Allocation under Ecological Benefits as a Constraint Combined with Ecological Compensation Concept" International Journal of Environmental Research and Public Health 16, no. 6: 1033. https://doi.org/10.3390/ijerph16061033
APA StyleQiu, Y., Liu, Y., Liu, Y., Chen, Y., & Li, Y. (2019). An Interval Two-Stage Stochastic Programming Model for Flood Resources Allocation under Ecological Benefits as a Constraint Combined with Ecological Compensation Concept. International Journal of Environmental Research and Public Health, 16(6), 1033. https://doi.org/10.3390/ijerph16061033




