The Role of Vertical Transmission in the Control of Dengue Fever
Abstract
1. Introduction
2. A Two-Strain Dengue Model with Control
3. An Optimal Control Problem
4. Numerical Results
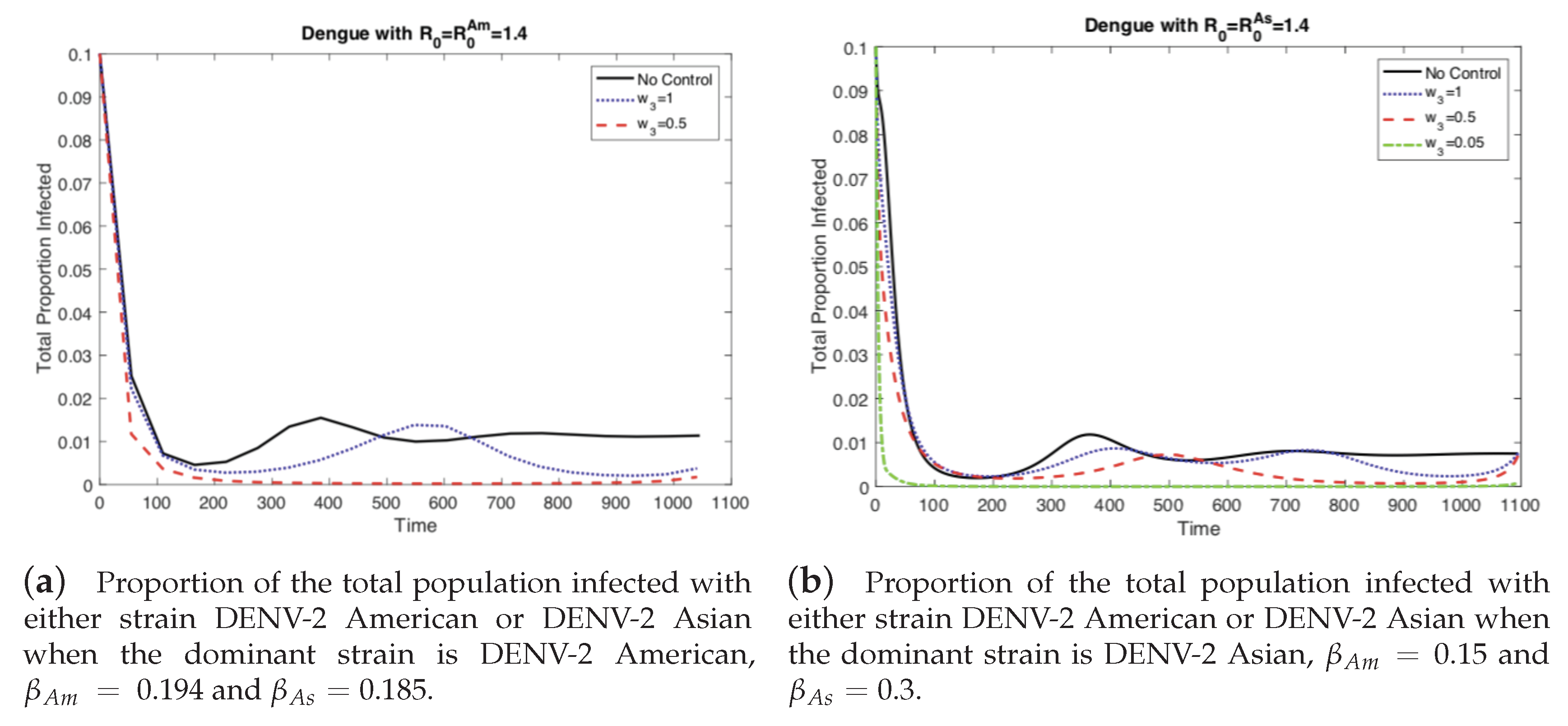
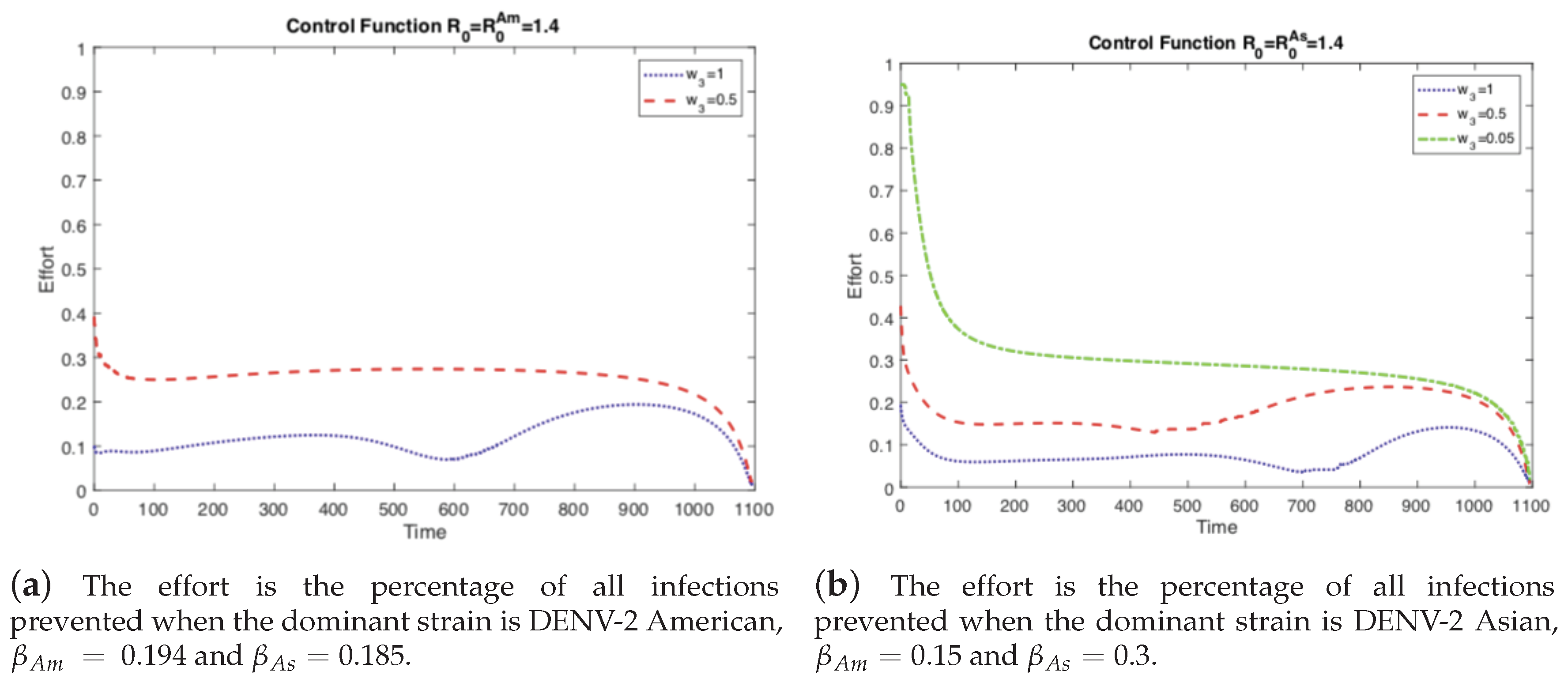
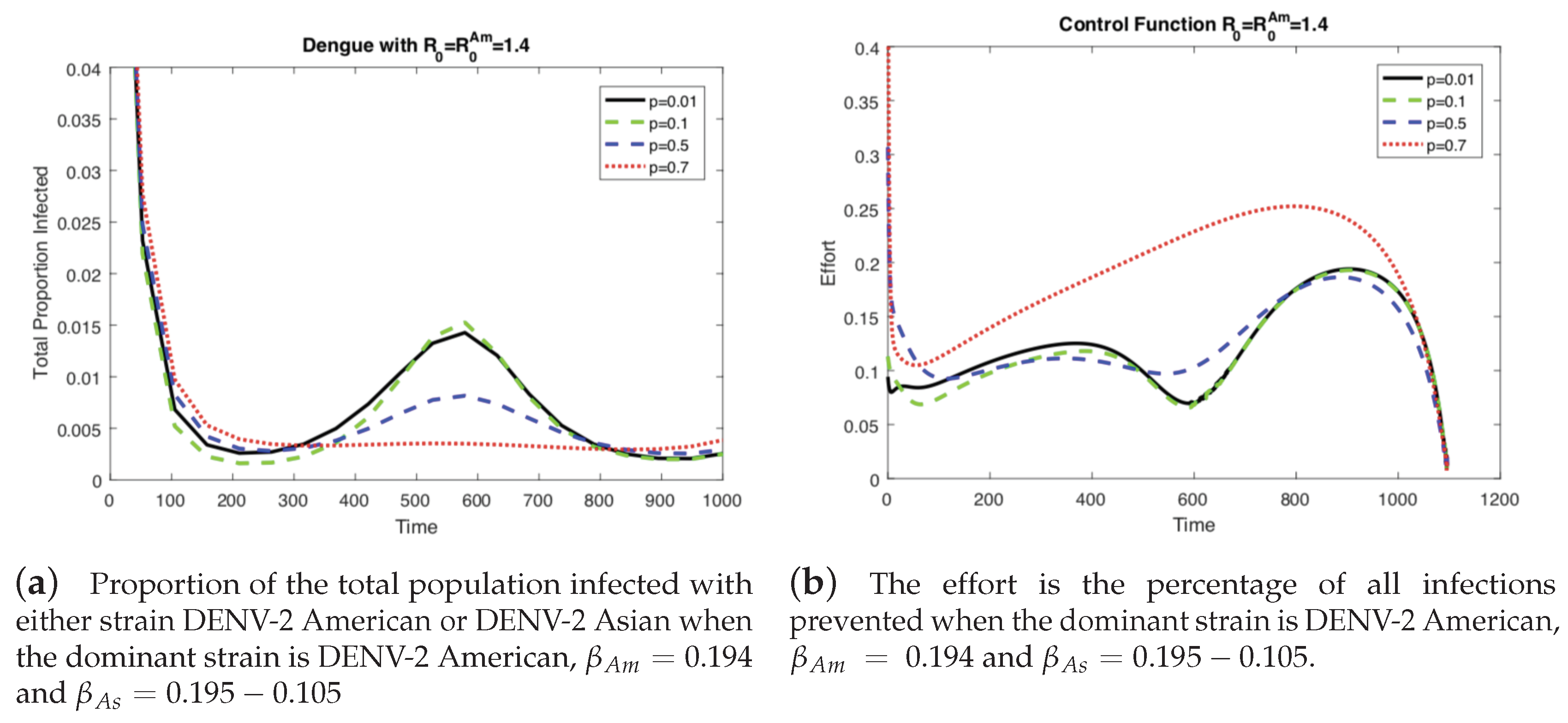
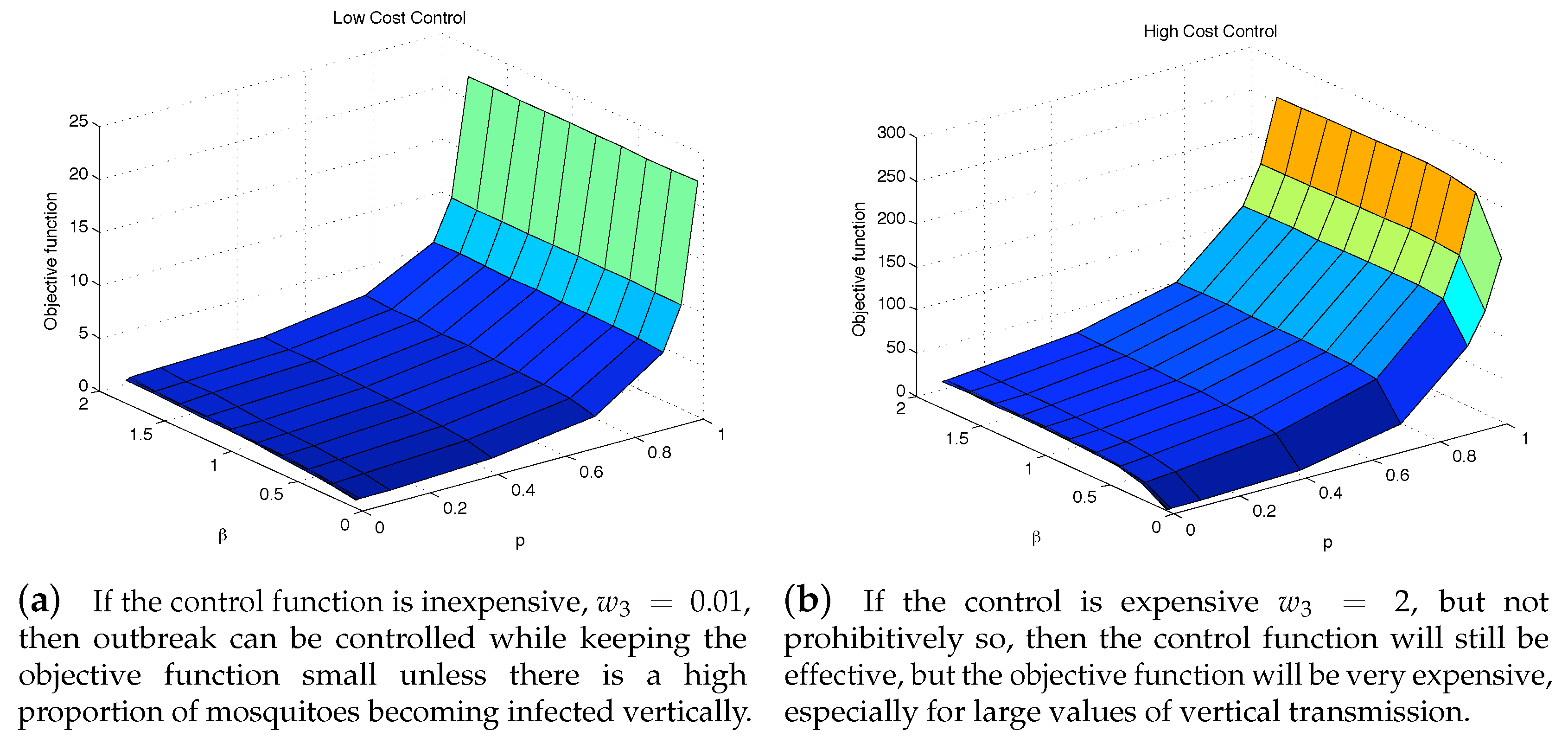
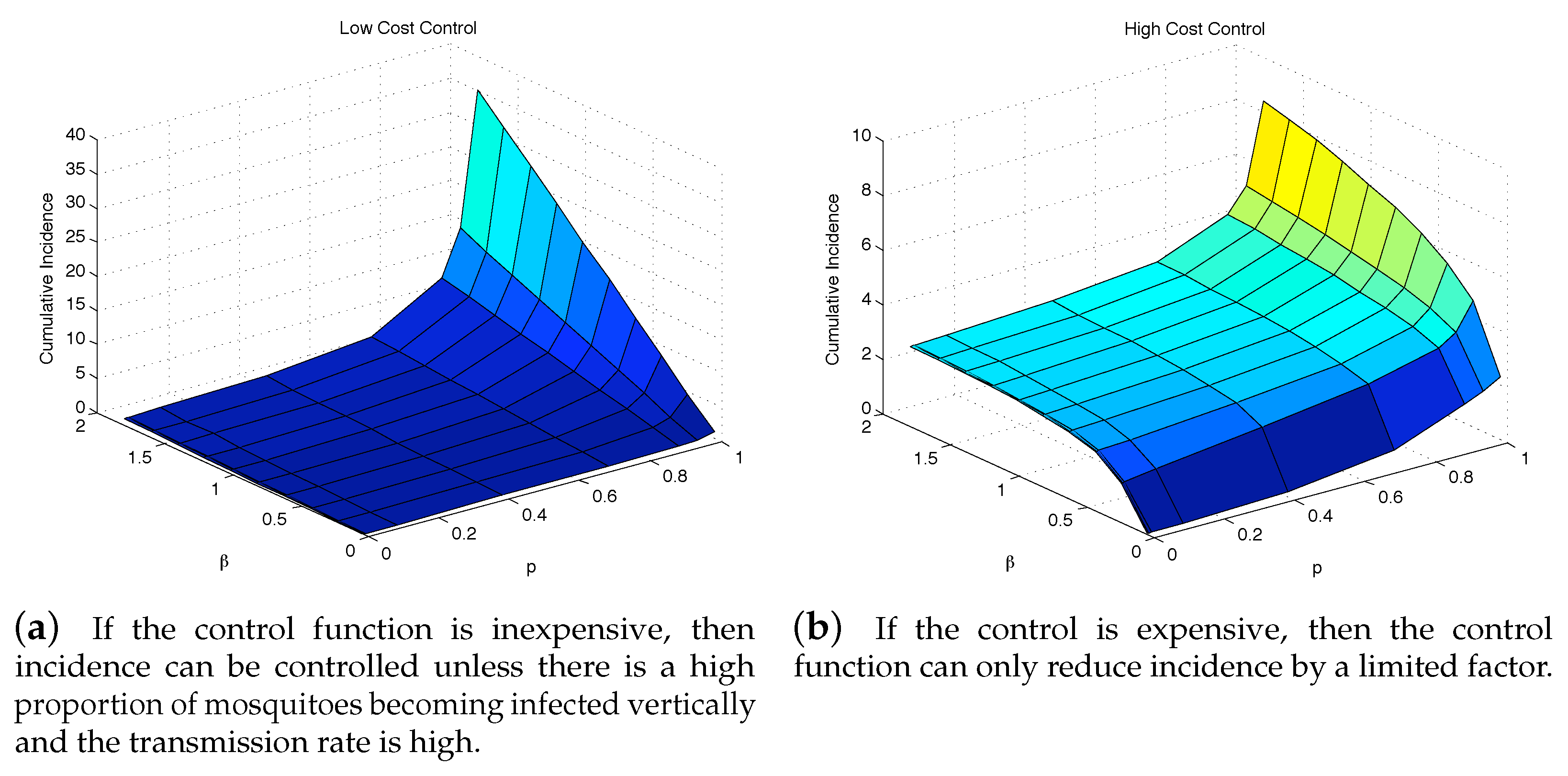
4.1. The Impact of the Relative Cost on the Controlled Dengue Dynamics
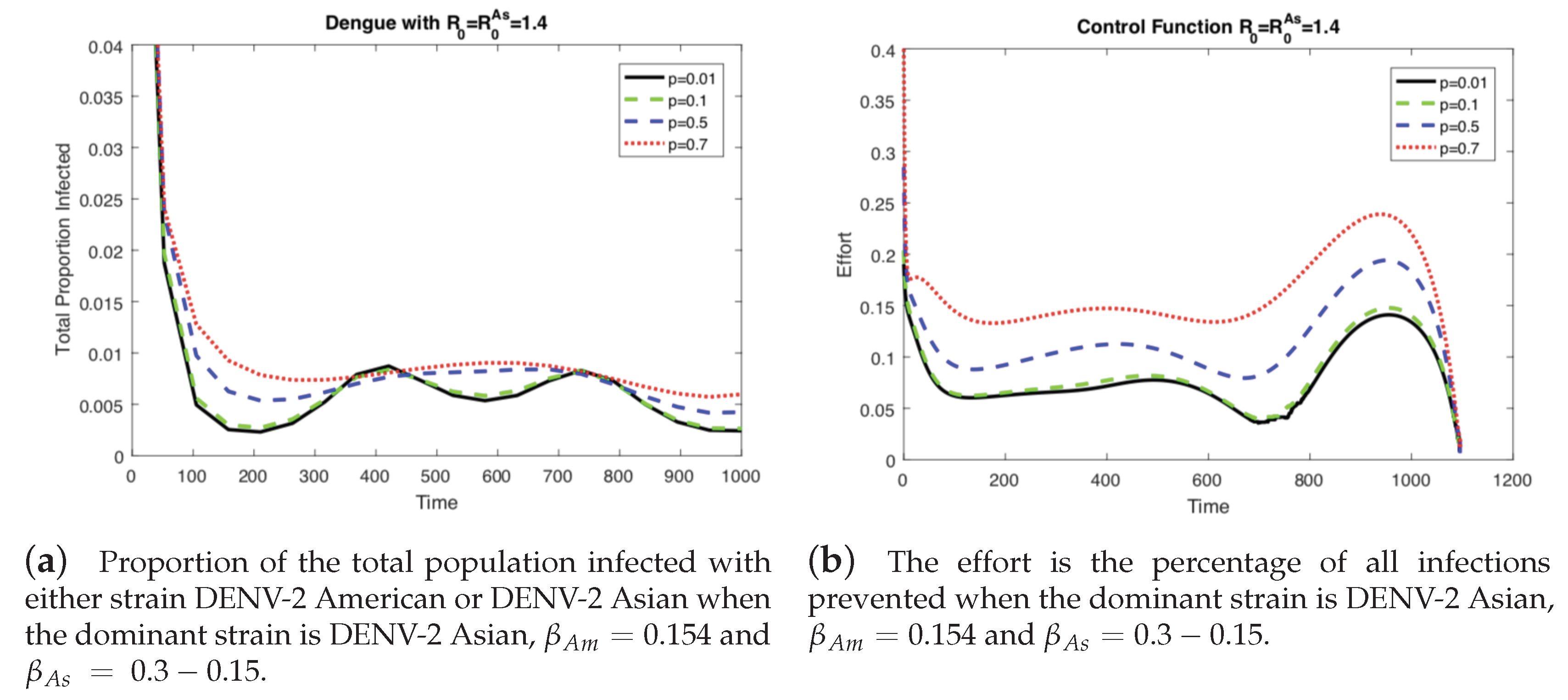
4.2. The Impact of Vertical Transmission on the Controlled Dengue Dynamics
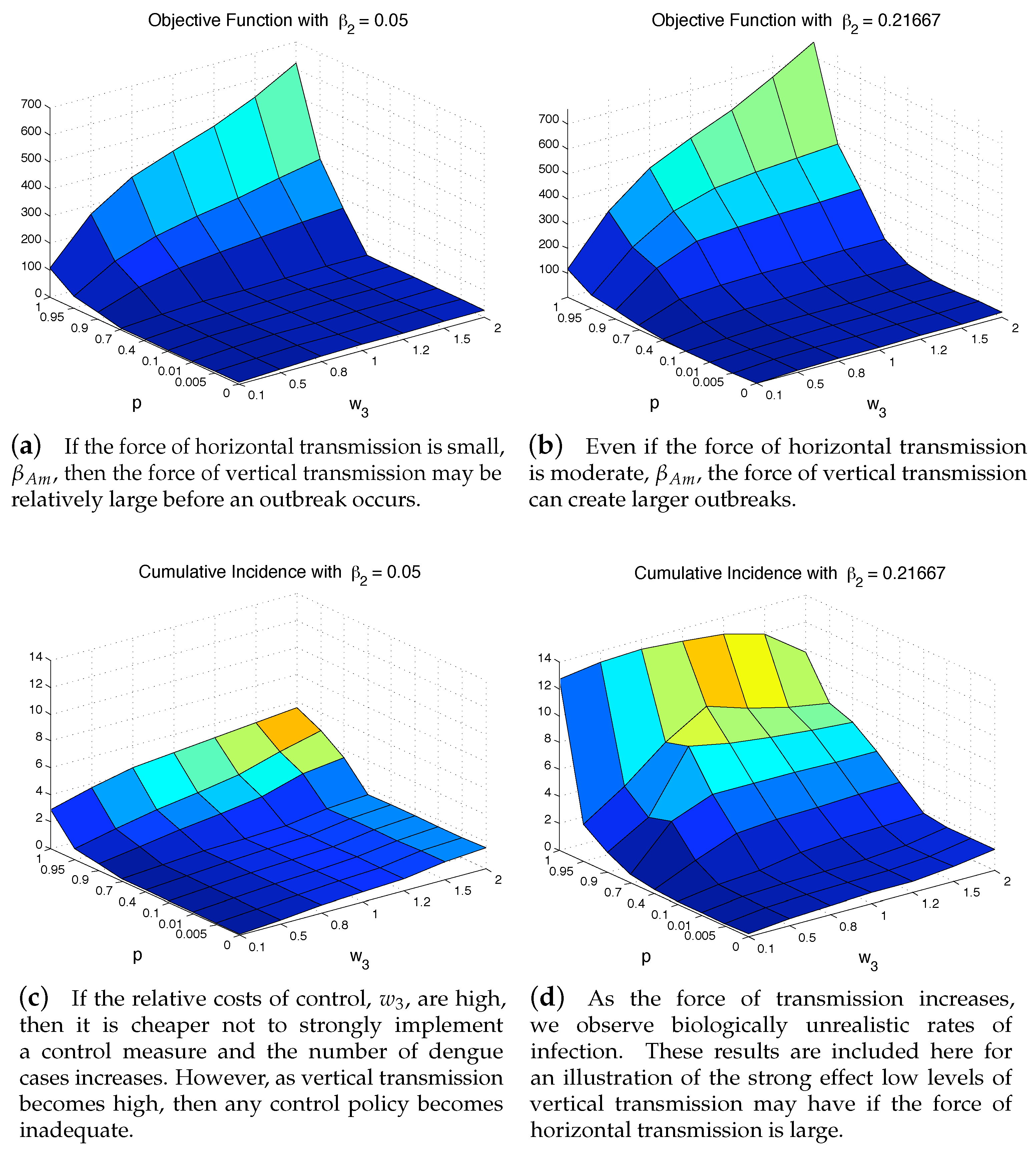
4.3. The Impact of Vertical Transmission on the Objective Function
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Existence of Optimal Control
- The set of controls and corresponding state variables is non-empty.
- The control set, is convex and closed.
- The right hand side of system (2) is bounded by a linear function in the state and control.
- The integrand of the objective functional is convex and bounded below by and the Lipschitz condition is satisfied.
- The payoff function is continuous.
- If we consider the vector of state variables , then we can write our system of equations asSince we know our state variables are bounded in the positive orthant, the particular form of our system of equations dictates that is bounded. Thus there exists a unique solution to our system given suitable initial conditions.
- By the construction of , this condition is clearly met.
- The total population for both the host and vector systems is constant, thus all solutions are bounded. The control function is also bounded, thus the right-hand side can be bounded by a linear function in the state and control.
- The integrand is linear in the state variable and quadratic in the control function, and thus clearly convex. Furthermore, the Lipschitz is condition is clearly satisfied as the integrand is bounded below since both the state and control are non-negative.
- The payoff function is clearly continuous by construction.
References
- WHO. Dengue and Severe Dengue; Fact Sheet; WHO: Geneva, Switzerland, 2017. [Google Scholar]
- Harrington, L.C.; Scott, T.W.; Lerdthusnee, K.; Coleman, R.C.; Costero, A.; Clark, G.G.; Jones, J.J.; Kitthawee, S.; Kittayapong, P.; Sithiprasasna, R.; et al. Dispersal of the dengue vector Aedes aegypti within and between rural communities. Am. J. Trop. Med. Hyg. 2005, 72, 209. [Google Scholar] [CrossRef] [PubMed]
- Gómez-Dantés, H.; Willoquet, J.R. Dengue in the Americas: Challenges for prevention and control. Cad. Saúde Púb. 2009, 25, 19–31. [Google Scholar] [CrossRef]
- Farrar, J.; Focks, D.; Gubler, D.; Barrera, R.; Guzman, M.G.; Simmons, C.; Kalayanarooj, S.; Lum, L.; McCall, P.J.; Lloyd, L.; et al. Editorial: Towards a global dengue research agenda. Trop. Med. Int. Health 2007, 12, 695–699. [Google Scholar] [CrossRef] [PubMed]
- Bhatt, S.; Gething, P.W.; Brady, O.J.; Messina, J.P.; Farlow, A.W.; Moyes, C.L.; Drake, J.M.; Brownstein, J.S.; Hoen, A.G.; Sankoh, O.; et al. The global distribution and burden of dengue. Nature 2013, 496, 504. [Google Scholar] [CrossRef] [PubMed]
- WHO. Dengue Control: The Mosquito; WHO: Geneva, Switzerland, 2018. [Google Scholar]
- UN. UN Lauds International Cooperation in Eradicating Deadly Cattle Plague; UN: New York, NY, USA, 2011. [Google Scholar]
- Anderson, R.; May, R. Vaccination and herd immunity to infectious diseases. Nature 1985, 318, 323–329. [Google Scholar] [CrossRef] [PubMed]
- Reiter, P.; Gubler, D.J. Surveillance and control of urban dengue vectors. In Dengue and Dengue Hemorragic Fever; CAB International: New York, NY, USA, 1997; pp. 45–60. [Google Scholar]
- Amanna, I.; Slifka, M. Public fear of vaccination: Separating fact from fiction. Viral Immun. 2005, 18, 307–315. [Google Scholar] [CrossRef] [PubMed]
- WHO. Dengue Vaccine Research; WHO: Geneva, Switzerland, 2015. [Google Scholar]
- Ceballos, G.; Ehrlich, P. Mammal population losses and the extinction crisis. Science 2002, 296, 904. [Google Scholar] [CrossRef] [PubMed]
- Sodhi, N.; Brook, B.; Bradshaw, C. Causes and consequences of species extinctions. Princet. Guide Ecol. 2009, 1, 514–520. [Google Scholar]
- Govindarajan, M.; Mathivanan, T.; Elumalai, K.; Krishnappa, K.; Anandan, A. Mosquito larvicidal, ovicidal, and repellent properties of botanical extracts against Anopheles stephensi, Aedes aegypti, and Culex quinquefasciatus (Diptera: Culicidae). Parasit. Res. 2011, 109, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Koodalingam, A.; Mullainadhan, P.; Arumugam, M. Effects of extract of soapnut Sapindus emarginatus on esterases and phosphatases of the vector mosquito, Aedes aegypti (Diptera: Culicidae). Acta Trop. 2011, 118, 27–36. [Google Scholar] [CrossRef] [PubMed]
- Yakob, L.; Funk, S.; Camacho, A.; Brady, O.; Edmunds, W.J. Aedes aegypti control through modernized, integrated vector management. PLoS Curr. 2017, 9. [Google Scholar] [CrossRef] [PubMed]
- Gubler, D.J.; Kuno, G. Dengue and Dengue Hemorrhagic Fever; CABI: Wallingford, UK, 1997. [Google Scholar]
- Goh, K. Dengue-a re-emerging infectious disease in Singapore. Dengue Singap. 1998, 26, 33–49. [Google Scholar]
- Halstead, S.; Lan, N.; Myint, T.; Shwe, T.; Nisalak, A.; Kalyanarooj, S.; Nimmannitya, S.; Soegijanto, S.; Vaughn, D.; Endy, T. Dengue hemorrhagic fever in infants: Research opportunities ignored. Emerg. Infect. Dis. 2002, 8, 1474. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, H.; Nguyen, L.; Lei, H.; Lin, Y.; Lien, L.; Huang, K.; Lin, C.; Do, Q.; Vo, H.; Lam, M.; et al. Volume replacement in infants with dengue hemorrhagic fever/dengue shock syndrome. Am. J. Trop. Med. Hyg. 2006, 74, 684. [Google Scholar] [PubMed]
- Joshi, V.; Mourya, D.; Sharma, R. Persistence of dengue-3 virus through transovarial transmission passage in successive generations of Aedes aegypti mosquitoes. Am. J. Trop. Med. Hyg. 2002, 67, 158. [Google Scholar] [CrossRef] [PubMed]
- Adams, B.; Boots, M. How important is vertical transmission in mosquitoes for the persistence of dengue? Insights from a mathematical model. Epidemics 2010, 2, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Haddow, A.D.; Guzman, H.; Popov, V.L.; Wood, T.G.; Widen, S.G.; Haddow, A.D.; Tesh, R.B.; Weaver, S.C. First isolation of Aedes flavivirus in the Western Hemisphere and evidence of vertical transmission in the mosquito Aedes (Stegomyia) albopictus (Diptera: Culicidae). Virology 2013, 440, 134–139. [Google Scholar] [CrossRef] [PubMed]
- Arunachalam, N.; Tewari, S.; Thenmozhi, V.; Rajendran, R.; Paramasivan, R.; Manavalan, R.; Ayanar, K.; Tyagi, B. Natural vertical transmission of dengue viruses by Aedes aegypti in Chennai, Tamil Nadu, India. Indian J. Med. Res. 2008, 127, 395–397. [Google Scholar] [PubMed]
- Rosen, L.; Shroyer, D.; Tesh, R.; Freier, J.; Lien, J. Transovarial transmission of dengue viruses by mosquitoes: Aedes albopictus and Aedes aegypti. Am. J. Trop. Med. Hyg. 1983, 32, 1108–1119. [Google Scholar] [CrossRef] [PubMed]
- Bosio, C.; Thomas, R.; Grimstad, P.; Rai, K. Variation in the efficiency of vertical transmission of dengue-1 virus by strains of Aedes albopictus (Diptera: Culicidae). J. Med. Entomol. 1992, 29, 985–989. [Google Scholar] [CrossRef] [PubMed]
- Kow, C.; Koon, L.; Yin, P. Detection of dengue viruses in field caught male Aedes aegypti and Aedes albopictus (Diptera: Culicidae) in Singapore by type-specific PCR. J. Med. Entomol. 2001, 38, 475–479. [Google Scholar] [CrossRef] [PubMed]
- Gunther, J.; Martínez-Muñoz, J.; Pérez-Ishiwara, D.; Salas-Benito, J. Evidence of vertical transmission of dengue virus in two endemic localities in the state of Oaxaca, Mexico. Intervirology 2007, 50, 347–352. [Google Scholar] [CrossRef] [PubMed]
- Vilela, A.; Figueiredo, L.; dos Santos, J.; Eiras, Á.; Bonjardim, C.; Ferreira, P.; Kroon, E. Dengue virus 3 genotype I in Aedes aegypti mosquitoes and eggs, Brazil, 2005–2006. Emerg. Infect. Dis. 2010, 16, 989–992. [Google Scholar] [CrossRef] [PubMed]
- Khin, M.; Than, K. Transovarial transmission of dengue 2 virus by Aedes aegypti in nature. Am. J. Trop. Med. Hyg. 1983, 32, 590. [Google Scholar] [CrossRef] [PubMed]
- Ferreira-de Lima, V.H.; Lima-Camara, T.N. Natural vertical transmission of dengue virus in Aedes aegypti and Aedes albopictus: A systematic review. Parasit. Vectors 2018, 11, 77. [Google Scholar] [CrossRef] [PubMed]
- Ross, R. The Prevention of Malaria; Dutton: New York, NY, USA, 1910. [Google Scholar]
- Reiner, R.C., Jr.; Perkins, T.A.; Barker, C.M.; Niu, T.; Chaves, L.F.; Ellis, A.M.; George, D.B.; Le Menach, A.; Pulliam, J.R.; Bisanzio, D.; et al. A systematic review of mathematical models of mosquito-borne pathogen transmission: 1970–2010. J. R. Soc. Interface 2013, 10, 20120921. [Google Scholar] [CrossRef] [PubMed]
- Gubler, D.J. Dengue, urbanization and globalization: The unholy trinity of the 21st century. Trop. Med. Health 2011, 39, S3–S11. [Google Scholar] [CrossRef] [PubMed]
- Nishiura, H. Mathematical and statistical analyses of the spread of dengue. Dengue Bull. 2006, 30, 51. [Google Scholar]
- Andraud, M.; Hens, N.; Marais, C.; Beutels, P. Dynamic epidemiological models for dengue transmission: A systematic review of structural approaches. PLoS ONE 2012, 7, e49085. [Google Scholar] [CrossRef] [PubMed]
- Esteva, L.; Vargas, C. Influence of vertical and mechanical transmission on the dynamics of dengue disease. Math. Biosci. 2000, 167, 51–64. [Google Scholar] [CrossRef]
- Murillo, D.; Holechek, S.A.; Murillo, A.L.; Sanchez, F.; Castillo-Chavez, C. Vertical transmission in a two-strain model of dengue fever. Let. Biomath. 2014, 1, 249–271. [Google Scholar] [CrossRef]
- Akbar, M.; Agoes, R.; Djatie, T.; Kodyat, S. PCR detection of dengue transovarial transmissibility in Aedes aegypti in Bandung, Indonesia. Proc. ASEAN Congr. Trop. Med. Parasitol. 2008, 3, 84–89. [Google Scholar]
- Armstrong, P.M.; Rico-Hesse, R. Efficiency of dengue serotype 2 virus strains to infect and disseminate in Aedes aegypti. Am. J. Trop. Med. Hyg. 2003, 68, 539–544. [Google Scholar] [CrossRef] [PubMed]
- Kochel, T.; Watts, D.; Halstead, S.; Hayes, C.; Espinoza, A.; Felices, V.; Caceda, R.; Bautista, C.; Montoya, Y.; Douglas, S.; et al. Effect of dengue-1 antibodies on American dengue-2 viral infection and dengue haemorrhagic fever. Lancet 2002, 360, 310–312. [Google Scholar] [CrossRef]
- Montoya, Y.; Holechek, S.; Cáceres, O.; Palacios, A.; Burans, J.; Guevara, C.; Quintana, F.; Herrera, V.; Pozo, E.; Anaya, E.; et al. Circulation of dengue viruses in North-Western Peru, 2000–2001. Dengue Bull. 2003, 27, 52–62. [Google Scholar]
- Rico-Hesse, R.; Harrison, L.; Salas, R.; Tovar, D.; Nisalak, A.; Ramos, C.; Boshell, J.; de Mesa, M.; Nogueira, R.; Rosa, A. Origins of dengue type 2 viruses associated with increased pathogenicity in the Americas. Virology 1997, 230, 244–251. [Google Scholar] [CrossRef] [PubMed]
- Knowlton, K.; Solomon, G.; Rotkin-Ellman, M. Fever Pitch: Mosquito-Borne Dengue Fever Threat Spreading in the Americas; NRDC, Issue Paper, July 2009. Available online: http://www.nrdc.org/health/dengue/files/dengue.pdf (accessed on 1 February 2011).
- Brauer, F.; Castillo-Chavez, C. Mathematical Models in Population Biology and Epidemiology; Springer: Berlin, Germany, 2001. [Google Scholar]
- Lenhart, S.; Workman, J. Optimal Control Applied to Biological Models; CRC Press: New York, NY, USA, 2007. [Google Scholar]
- Pontryagin, L.; Boltyanskii, V.; Gamkrelidze, R.; Mishchenko, E. The Mathematical Theory of Optimal Control Processes; Routledge: New York, NY, USA, 2018. [Google Scholar]
- Blayneh, K.; Cao, Y.; Kwon, H. Optimal control of vector-borne diseases: Treatment and prevention. Discret. Contin. Dyn. Syst. 2009, 11, 587–611. [Google Scholar] [CrossRef]
- Lee, S.; Chowell, G.; Castillo-Chavez, C. Optimal control of influenza pandemics: The role of antiviral treatment and isolation. J. Theor. Biol. 2010, 265, 136–150. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.; Jung, E.; Castillo-Chávez, C. Optimal control intervention strategies in low- and high-risk problem drinking populations. Soc.-Econ. Plan. Sci. 2010, 44, 258–265. [Google Scholar] [CrossRef]
- Lee, S.; Morales, R.; Castillo-Chávez, C. A note on the use of influenza vaccination strategies when supply is limited. Math. Biosci. Eng. 2011, 8, 172–182. [Google Scholar]
- Watts, D.M.; Porter, K.R.; Putvatana, P.; Vasquez, B.; Calampa, C.; Hayes, C.G.; Halstead, S.B. Failure of secondary infection with American genotype dengue 2 to cause dengue haemorrhagic fever. Lancet 1999, 354, 1431–1434. [Google Scholar] [CrossRef]
- Rodhain, F.; Rosen, L. Mosquito vectors and dengue virus-vector relationships. Dengue Dengue Hemorrhagic Fever 1997, 45–60, 112–134. [Google Scholar]
- Aldila, D.; Götz, T.; Soewono, E. An optimal control problem arising from a dengue disease transmission model. Math. Biosci. 2013, 242, 9–16. [Google Scholar] [CrossRef] [PubMed]
- Rodrigues, H.S.; Monteiro, M.T.T.; Torres, D.F. Vaccination models and optimal control strategies to dengue. Math. Biosci. 2014, 247, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Agusto, F.; Khan, M. Optimal control strategies for dengue transmission in Pakistan. Math. Biosci. 2018, 305, 102–121. [Google Scholar] [CrossRef] [PubMed]
- Shepard, D.S.; Coudeville, L.; Halasa, Y.A.; Zambrano, B.; Dayan, G.H. Economic impact of dengue illness in the Americas. Am. J. Trop. Med. Hyg. 2011, 84, 200–207. [Google Scholar] [CrossRef] [PubMed]
- Godói, I.P.; Da Silva, L.V.D.; Sarker, A.R.; Megiddo, I.; Morton, A.; Godman, B.; Alvarez-Madrazo, S.; Bennie, M.; Guerra-Junior, A.A. Economic and epidemiological impact of dengue illness over 16 years from a public health system perspective in Brazil to inform future health policies including the adoption of a dengue vaccine. Expert Rev. Vaccines 2018, 17, 1123–1133. [Google Scholar] [CrossRef] [PubMed]
- Mourya, D.; Gokhale, M.; Basu, A.; Barde, P.; Sapkal, G.; Padbidri, V.; Gore, M. Horizontal and vertical transmission of dengue virus type 2 in highly and lowly susceptible strains of Aedes aegypti mosquitoes. Acta Virol. 2001, 45, 67–72. [Google Scholar] [PubMed]
- Fleming, W.; Rishel, R. Deterministic and Stochastic Optimal Control; Springer: New York, NY, USA, 1975. [Google Scholar]
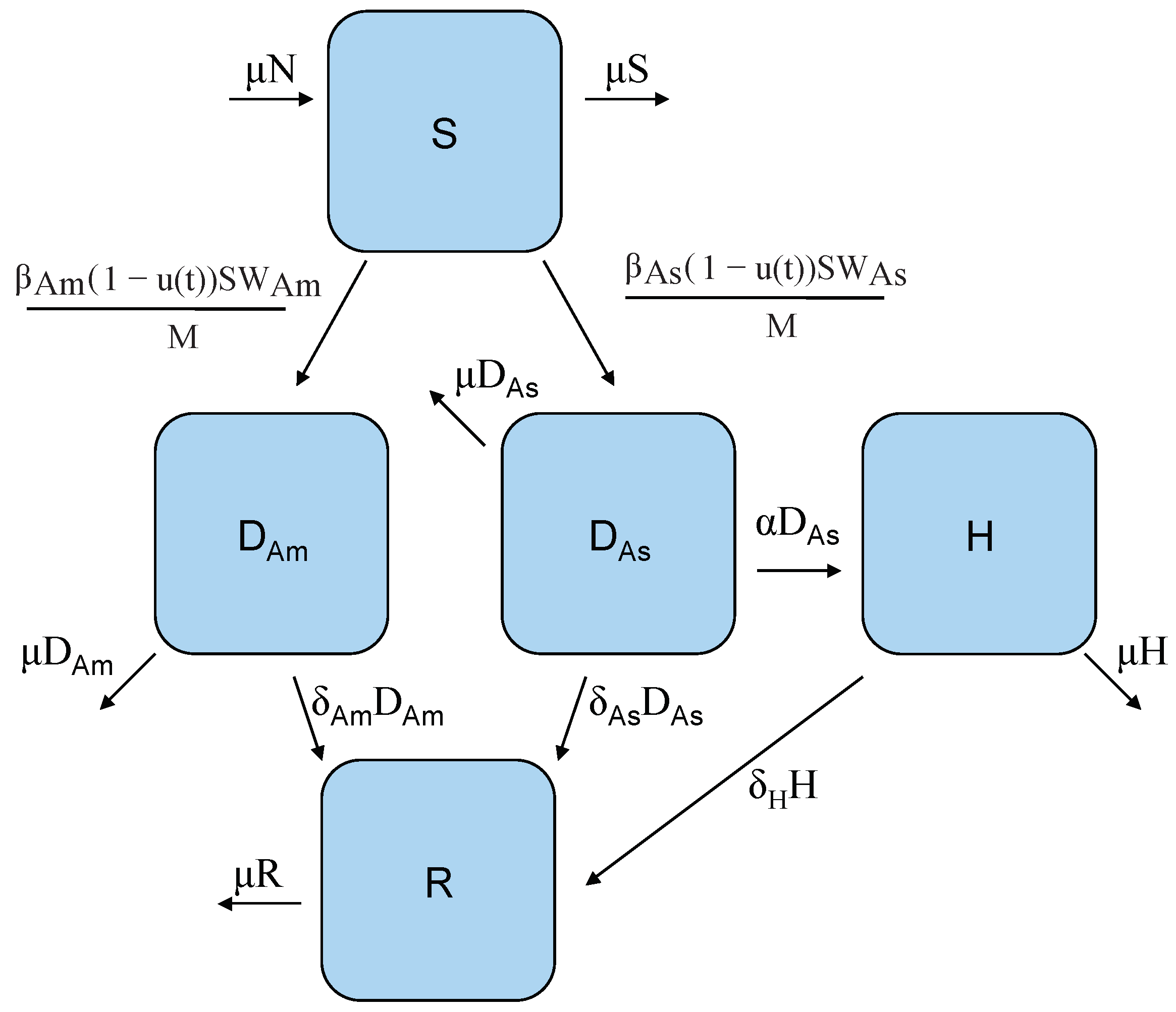

| Parameter | Default Value | Units | Source |
|---|---|---|---|
| M | 1 | per day | [52] |
| N | 1 | per day | [52] |
| 0.113 | per day | [52] | |
| 0.0958 | per day | [53] | |
| p | 0–1 | proportion | [27] |
| 0.00038 | per day | estimated | |
| 0.28 | per day | estimated | |
| 0.28 | per day | estimated | |
| 0.01–0.2 | per day | estimated | |
| 0.01–0.2 | per day | estimated | |
| 0.2 | per day | estimated |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Murillo, D.; Murillo, A.; Lee, S. The Role of Vertical Transmission in the Control of Dengue Fever. Int. J. Environ. Res. Public Health 2019, 16, 803. https://doi.org/10.3390/ijerph16050803
Murillo D, Murillo A, Lee S. The Role of Vertical Transmission in the Control of Dengue Fever. International Journal of Environmental Research and Public Health. 2019; 16(5):803. https://doi.org/10.3390/ijerph16050803
Chicago/Turabian StyleMurillo, David, Anarina Murillo, and Sunmi Lee. 2019. "The Role of Vertical Transmission in the Control of Dengue Fever" International Journal of Environmental Research and Public Health 16, no. 5: 803. https://doi.org/10.3390/ijerph16050803
APA StyleMurillo, D., Murillo, A., & Lee, S. (2019). The Role of Vertical Transmission in the Control of Dengue Fever. International Journal of Environmental Research and Public Health, 16(5), 803. https://doi.org/10.3390/ijerph16050803






