Pythagorean 2-Tuple Linguistic Taxonomy Method for Supplier Selection in Medical Instrument Industries
1
School of Business, Sichuan Normal University, Chengdu 610101, China
2
School of Statistics, Southwestern University of Finance and Economics, Chengdu 611130, China
3
School of Economics and Management, Chongqing University of Arts and Sciences, Chongqing 402160, China
*
Authors to whom correspondence should be addressed.
Int. J. Environ. Res. Public Health 2019, 16(23), 4875; https://doi.org/10.3390/ijerph16234875
Received: 28 October 2019 / Revised: 26 November 2019 / Accepted: 27 November 2019 / Published: 3 December 2019
(This article belongs to the Special Issue Network Analytics in Healthcare Decision Making)
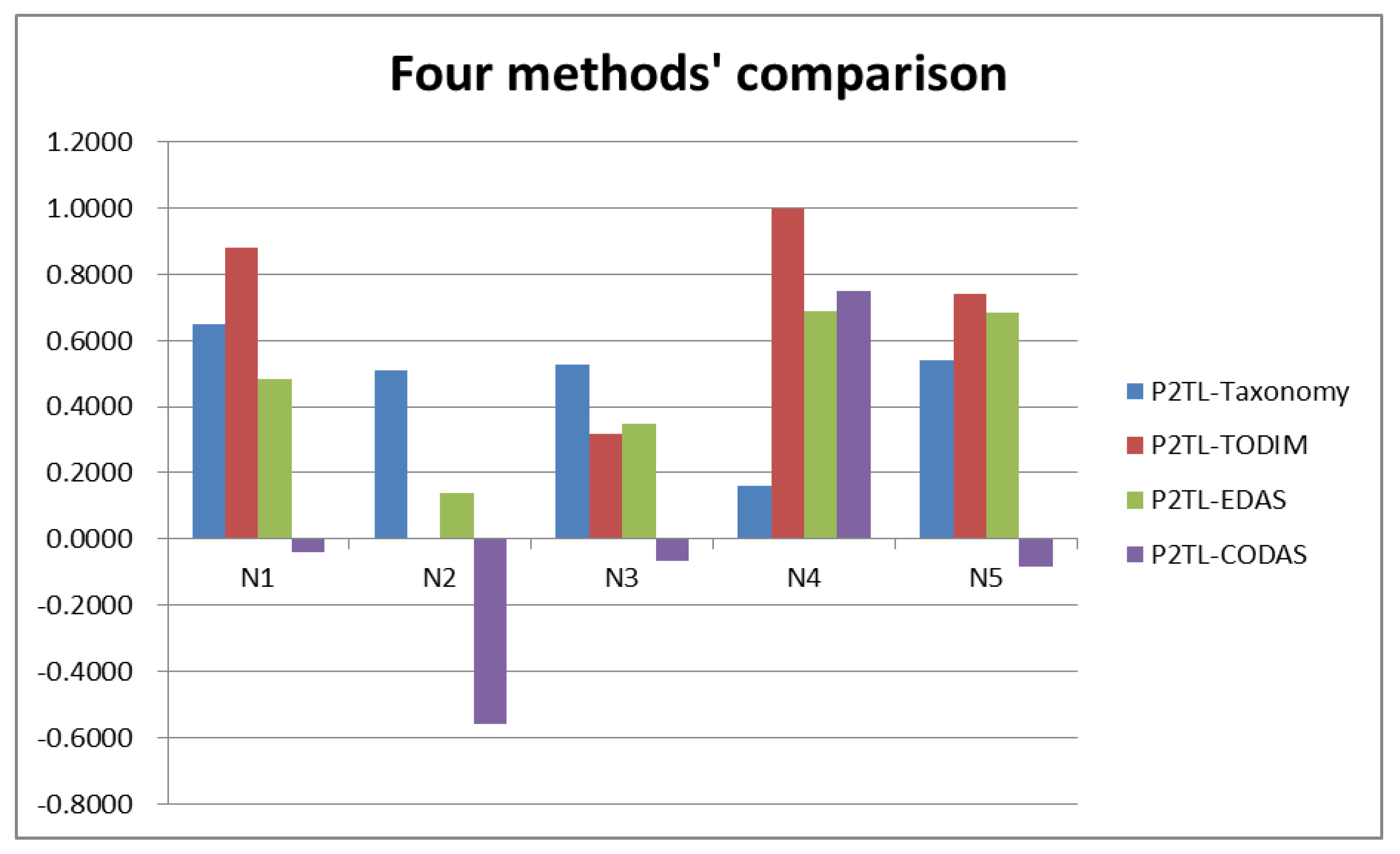
Supplier selection in medical instrument industries is a classical multiple attribute group decision making (MAGDM) problem. The Pythagorean 2-tuple linguistic sets (P2TLSs) can reflect uncertain or fuzzy information well and solve the supplier selection in medical instrument industries, and the original Taxonomy is very appropriate for comparing different alternatives with respect to their advantages from studied attributes. In this study, we present an algorithm that combines Pythagorean 2-tuple linguistic numbers (P2TLNs) with the Taxonomy method, where P2TLNs are applied to express the evaluation of decision makers on alternatives. Relying on the Pythagorean 2-tuple linguistic weighted average (P2TLWA) operator or Pythagorean 2-tuple linguistic weighted geometric (P2TLWG) operator to fuse P2TLNs, the new general framework is established for Pythagorean 2-tuple linguistic multiple attribute group decision making (MAGDM) under the classical Taxonomy method. Ultimately, an application case for supplier selection in medical instrument industries is designed to test the novel method’s applicability and practicality and a comparative analysis with three other methods is used to elaborate further.
View Full-Text
Keywords:
multiple attribute group decision making (MAGDM); Pythagorean 2-tuple linguistic numbers (P2TLNs); Taxonomy method; supplier selection; medical instrument industries
▼
Show Figures
Figure 1
This is an open access article distributed under the Creative Commons Attribution License which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited
MDPI and ACS Style
He, T.; Wei, G.; Lu, J.; Wei, C.; Lin, R. Pythagorean 2-Tuple Linguistic Taxonomy Method for Supplier Selection in Medical Instrument Industries. Int. J. Environ. Res. Public Health 2019, 16, 4875.
Show more citation formats
Note that from the first issue of 2016, MDPI journals use article numbers instead of page numbers. See further details here.
