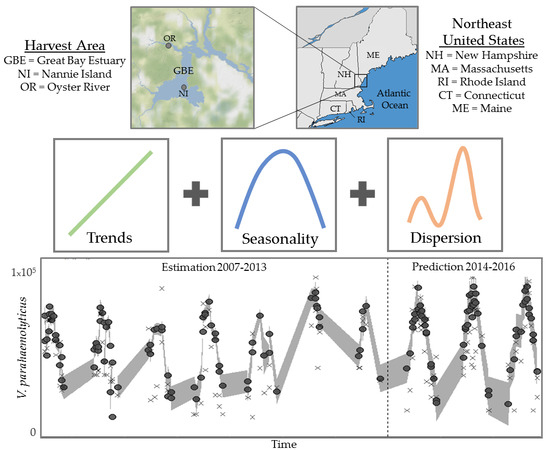
Forecasting Seasonal Vibrio parahaemolyticus Concentrations in New England Shellfish
Abstract
1. Introduction
2. Materials and Methods
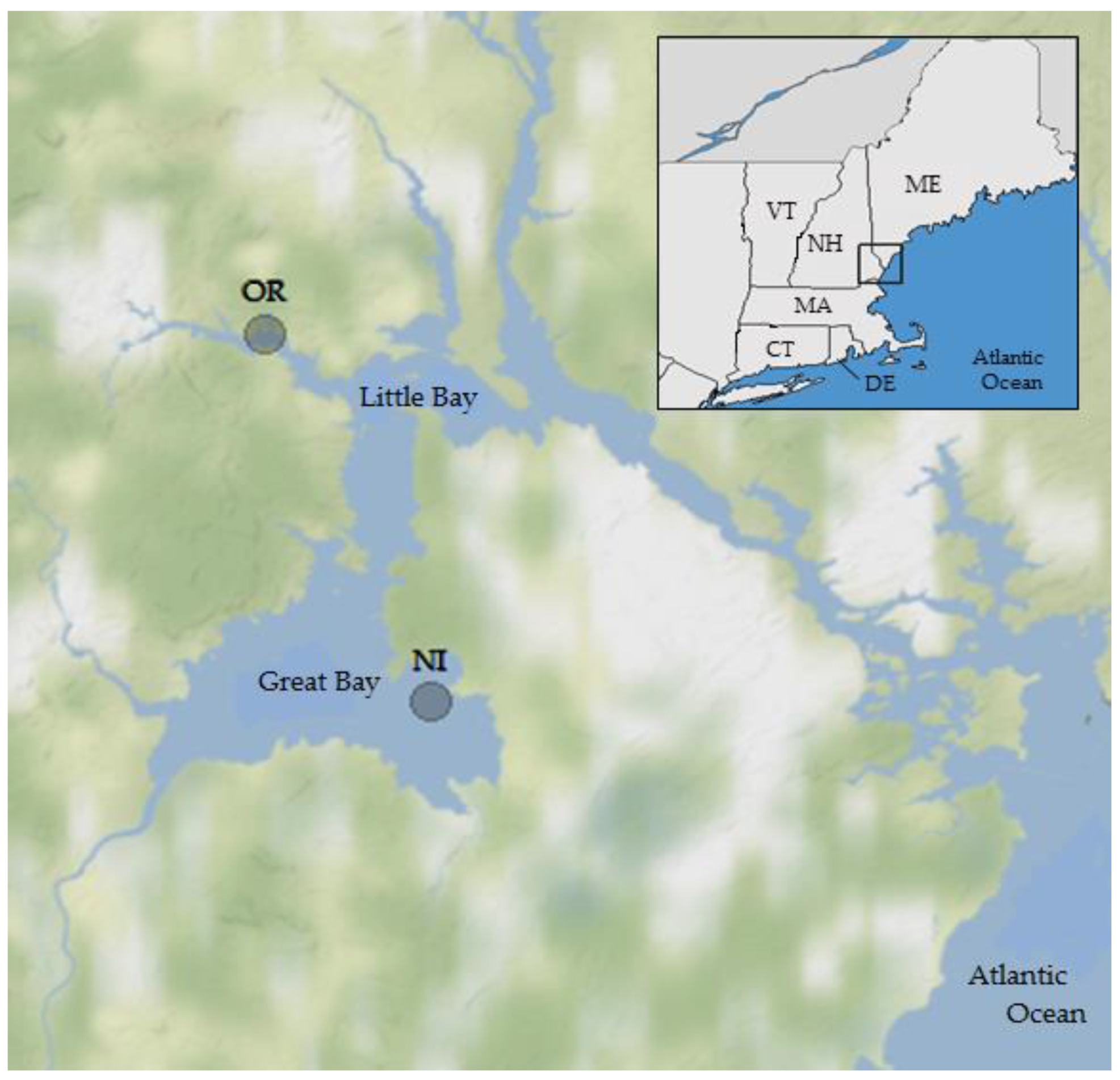
2.1. Study Sites, Environmental Sampling and Bacterial Analysis
2.2. Oyster Sample Collection and Processing
2.3. Statistical Analysis
2.3.1. Model Development Strategy
2.3.2. Seasonality and Trend Analysis
2.3.3. Extreme Value Trend Analysis
2.3.4. Variable Selection and Non-Linearity Assessment
2.3.5. Model Building
2.4. Assessment of Model Forecasting Ability
3. Results
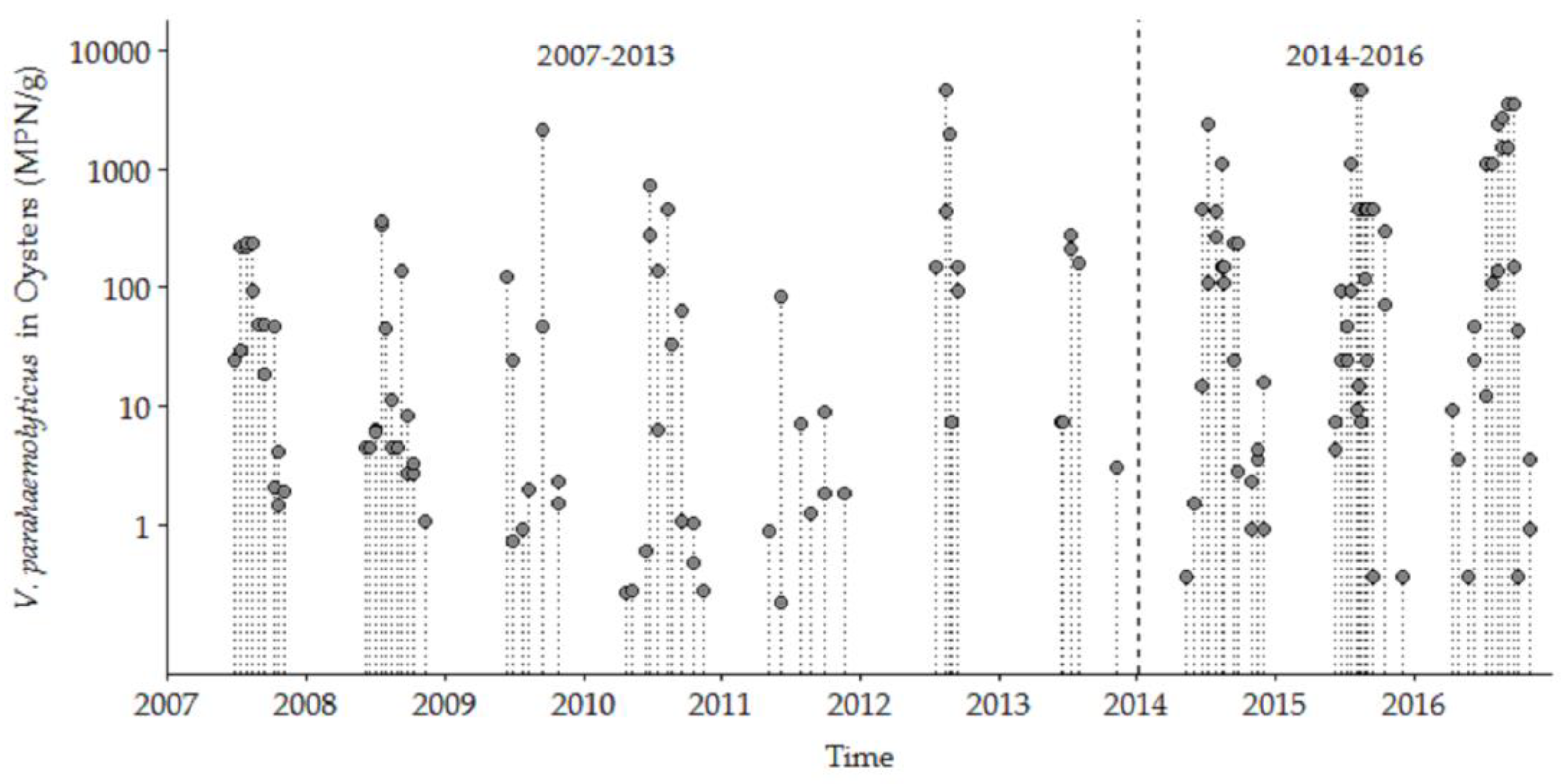
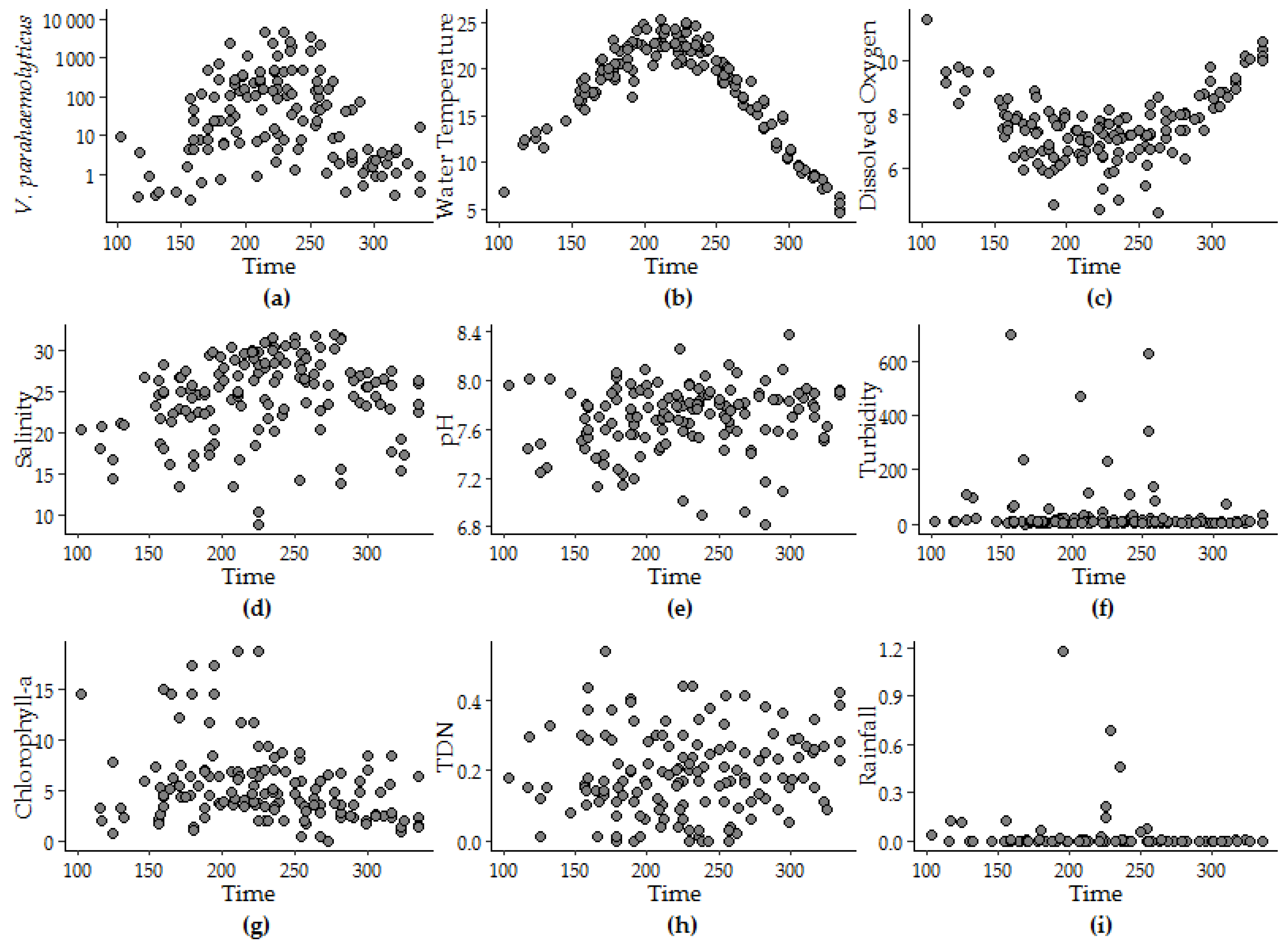
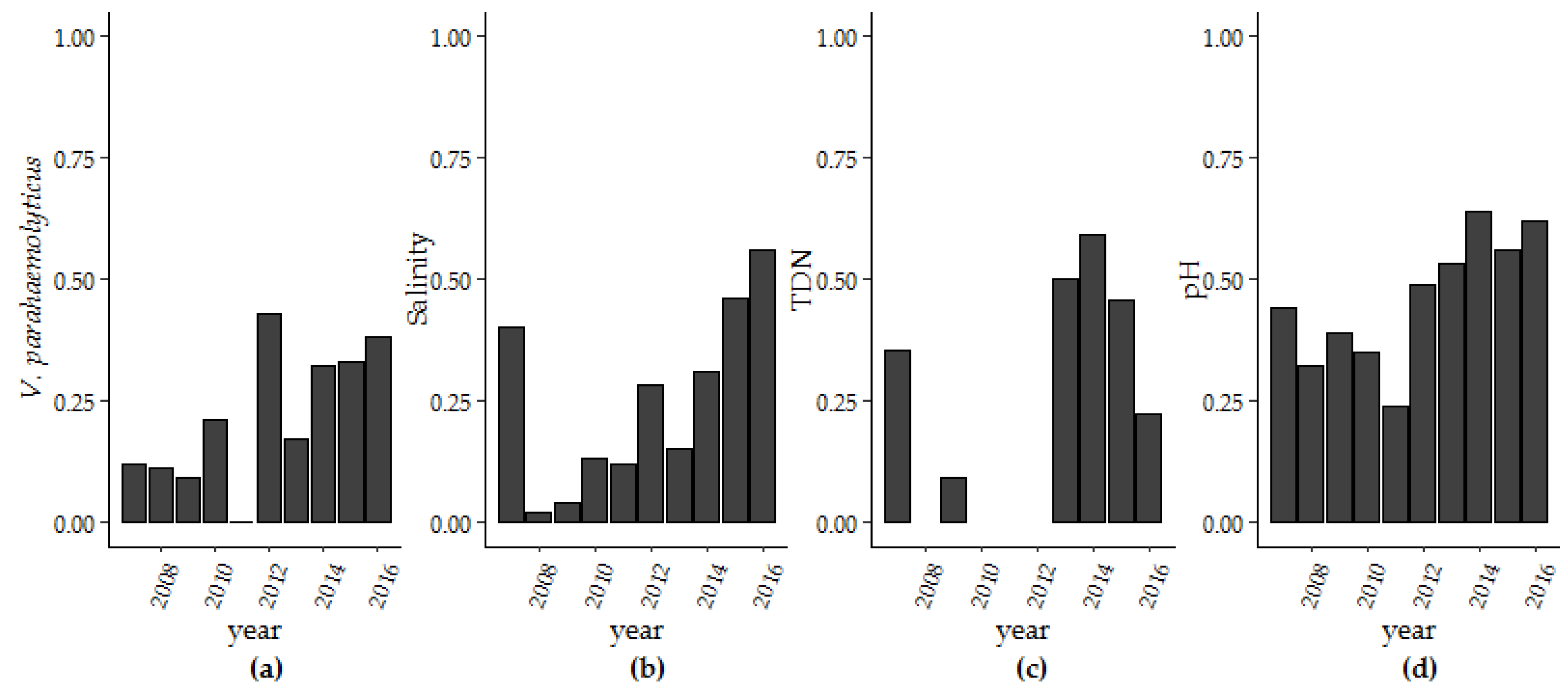
3.1. V. parahaemolyticus Concentrations in the GBE, 2007–2016
3.1.1. Trends and Seasonality
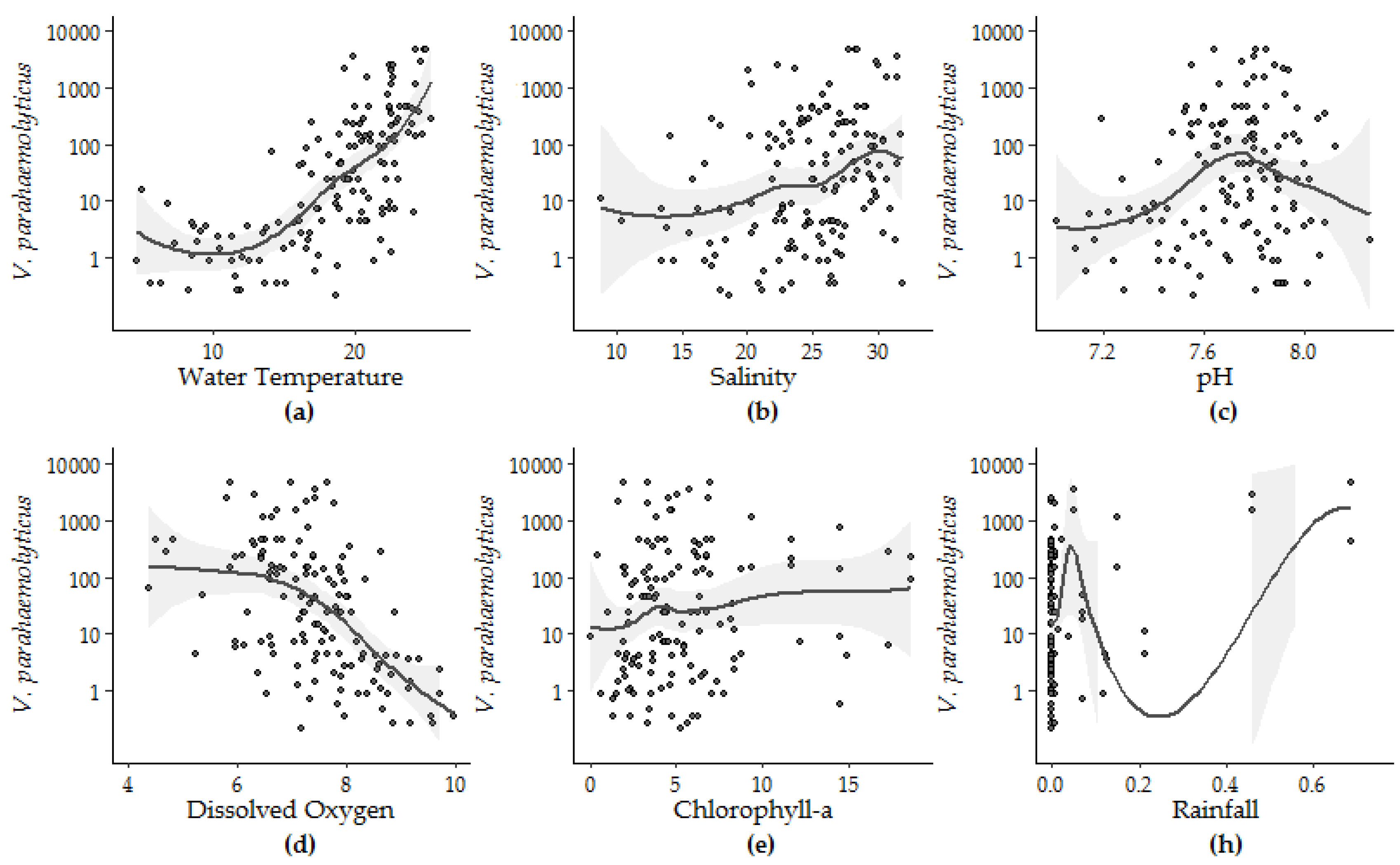
3.1.2. Univariate Regression
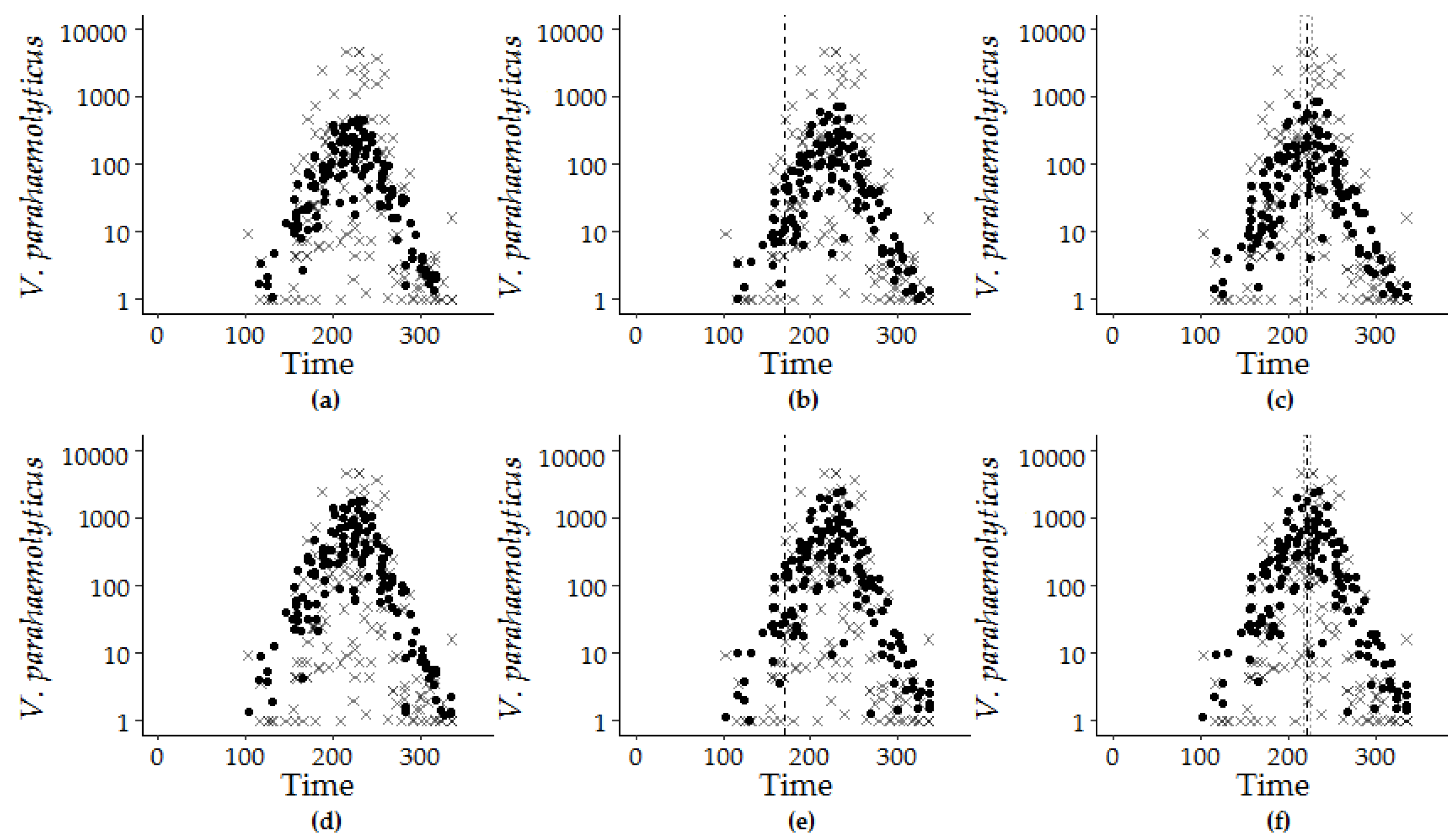
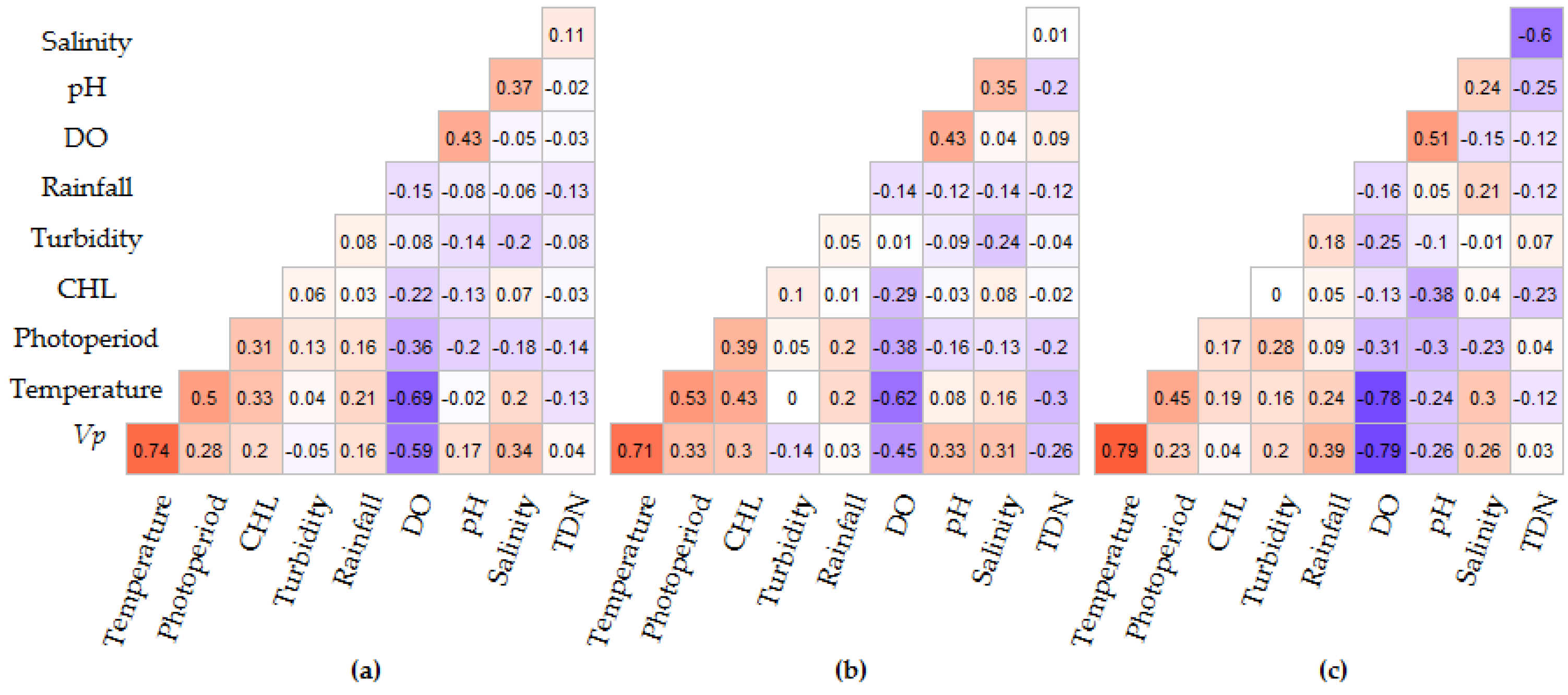
3.2. Sequential Model Building
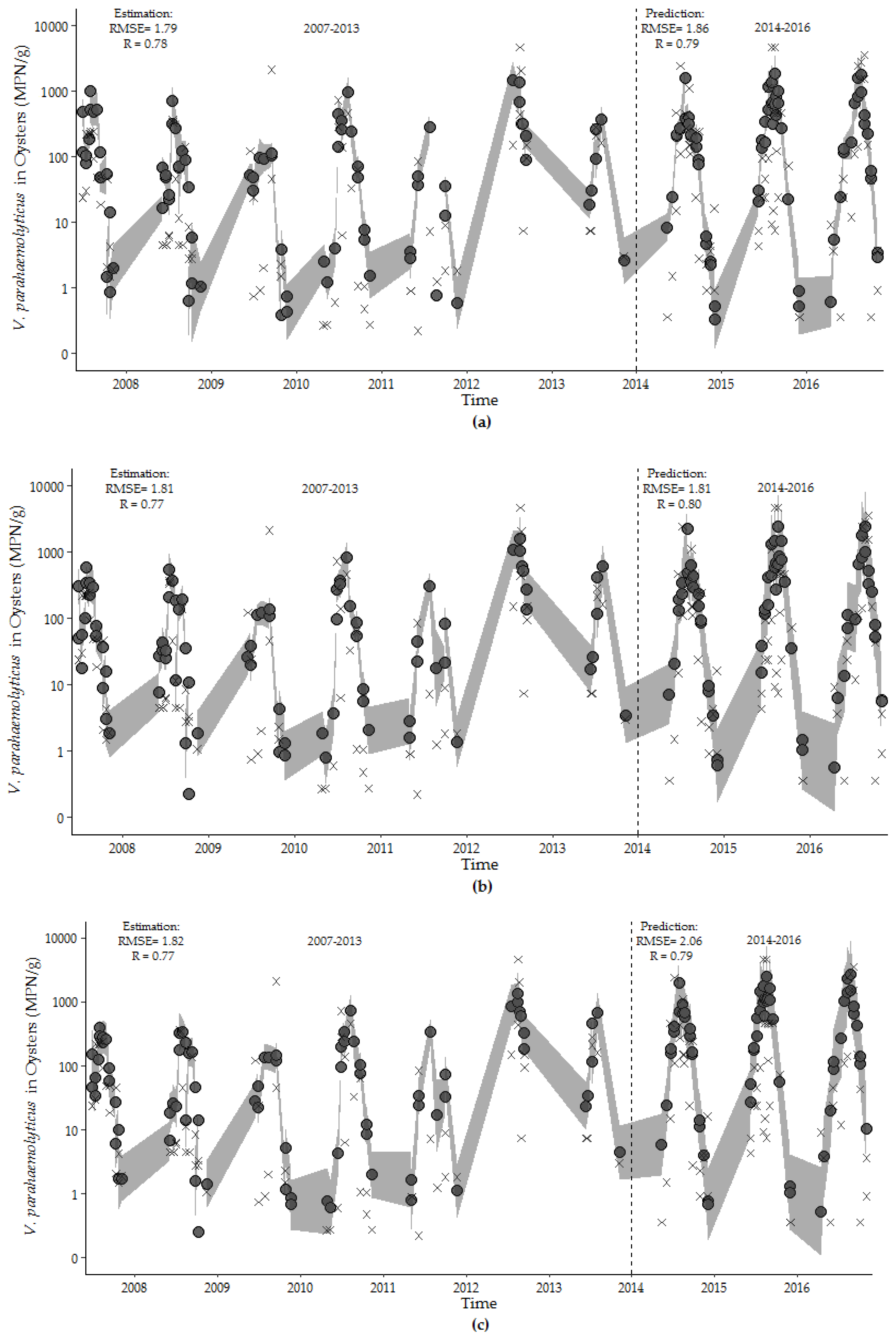
3.3. Model Performance Prediction
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- CDC. Foodborne Diseases Active Surveillance Network (FoodNet): FoodNet 2015 Surveillance Report (Final Data); U.S. Department of Health and Human Services, CDC: Atlanta, GA, USA, 2017.
- Nilsson, W.B.; Paranjpye, R.N.; Hamel, O.S.; Hard, C.; Strom, M.S. Vibrio parahaemolyticus risk assessment in the Pacific Northwest: It’s not what’s in the water. FEMS Microbiol. Ecol. 2019, 95, fiz027. [Google Scholar] [CrossRef] [PubMed]
- Newton, A.; Garrett, N.; Stroika, S.; Halpin, J.; Turnsek, M.; Mody, R. Notes from the field: Increase in Vibrio parahaemolyticus infections associated with consumption of Atlantic coast shellfish—2013. Morb. Mortal. Wkly. Rep. (MMWR) 2014, 63, 335–336. [Google Scholar] [PubMed]
- Ceccarelli, D.; Hasan, N.A.; Huq, A.; Colwell, R.R. Distribution and dynamics of epidemic and pandemic Vibrio parahaemolyticus virulence factors. Front. Cell. Infect. Microbiol. 2013, 3, 97. [Google Scholar] [CrossRef] [PubMed]
- López-Hernández, K.M.; Pardío-Sedas, V.T.; Lizárraga-Partida, L.; Williams, J.D.J.; Martínez-Herrera, D.; Flores-Primo, A.; Uscanga-Serrano, R.; Rendón-Castro, K. Environmental parameters influence on the dynamics of total and pathogenic Vibrio parahaemolyticus densities in Crassostrea virginica harvested from Mexico’s Gulf coast. Mar. Pollut. Bull. 2015, 91, 317–329. [Google Scholar] [CrossRef] [PubMed]
- Vezzulli, L.; Colwell, R.R.; Pruzzo, C. Ocean warming and spread of pathogenic Vibrios in the aquatic environment. Microb. Ecol. 2013, 65, 817–825. [Google Scholar] [CrossRef]
- Baker-Austin, C.; Trinanes, J.A.; Taylor, N.G.; Hartnell, R.; Siitonen, A.; Martinez-Urtaza, J. Emerging Vibrio risk at high latitudes in response to ocean warming. Nat. Clim. Chang. 2013, 3, 73. [Google Scholar] [CrossRef]
- Baker-Austin, C.; Trinanes, J.; Gonzalez-Escalona, N.; Martinez-Urtaza, J. Non-cholera vibrios: The microbial barometer of climate change. Trends Microbiol. 2017, 25, 76–84. [Google Scholar] [CrossRef]
- Centers for Disease Control and Prevention (CDC). Increase in Vibrio parahaemolyticus Illnesses Associated with Consumption of Shellfish from Several Atlantic Coast Harvest Areas, United States, 2013. Available online: https://www.cdc.gov/vibrio/investigations/ (accessed on 1 November 2019).
- Jones, S.H. Microbial Pathogens and Biotoxins: State of the Gulf of Maine Report. Gulf of Maine Council on the Marine Environment. Available online: http://www.gulfofmaine.org/2/sogom-homepage/ (accessed on 1 November 2019).
- Martinez-Urtaza, J.; Baker-Austin, C.; Jones, J.; Newton, A.; DePaola, A. Spread of Pacific Northwest Vibrio parahaemolyticus strain. N. Engl. J. Med. 2013, 369, 1573–1574. [Google Scholar] [CrossRef]
- McLaughlin, J.B.; DePaola, A.; Bopp, C.A.; Martinek, K.A.; Napolilli, N.P.; Allison, C.G.; Murray, S.L.; Thompson, E.C.; Bird, M.M.; Middaugh, J.P. Outbreak of Vibrio parahaemolyticus gastroenteritis associated with Alaskan oysters. N. Engl. J. Med. 2005, 353, 1463–1470. [Google Scholar] [CrossRef]
- Xu, F.; Ilyas, S.; Hall, J.A.; Jones, S.H.; Cooper, V.S.; Whistler, C.A. Genetic characterization of clinical and environmental Vibrio parahaemolyticus from the Northeast USA reveals emerging resident and non-indigenous pathogen lineages. Front. Microbiol. 2015, 6, 272. [Google Scholar] [CrossRef]
- Xu, F.; Gonzalez-Escalona, N.; Drees, K.P.; Sebra, R.P.; Cooper, V.S.; Jones, S.H.; Whistler, C.A. Parallel evolution of two clades of an Atlantic-endemic pathogenic lineage of Vibrio parahaemolyticus by independent acquisition of related pathogenicity islands. Appl. Environ. Microbiol. 2017, 83, e01168-17. [Google Scholar] [CrossRef]
- Lipp, E.K.; Huq, A.; Colwell, R.R. Effects of global climate on infectious disease: The cholera model. Clin. Microbiol. Rev. 2002, 15, 757–770. [Google Scholar] [CrossRef] [PubMed]
- Lovell, C.R. Ecological fitness and virulence features of Vibrio parahaemolyticus in estuarine environments. Appl. Microbiol. Biotechnol. 2017, 101, 1781–1794. [Google Scholar] [CrossRef] [PubMed]
- Martinez-Urtaza, J.; Blanco-Abad, V.; Rodriguez-Castro, A.; Ansede-Bermejo, J.; Miranda, A.; Rodriguez-Alvarez, M.X. Ecological determinants of the occurrence and dynamics of Vibrio parahaemolyticus in offshore areas. ISME J. 2012, 6, 994–1006. [Google Scholar] [CrossRef] [PubMed]
- Urquhart, E.A.; Zaitchik, B.F.; Guikema, S.D.; Haley, B.J.; Taviani, E.; Chen, A.; Brown, M.E.; Huq, A.; Colwell, R.R. Use of Environmental Parameters to Model Pathogenic Vibrios in Chesapeake Bay. J. Environ. Inf. 2016, 26, 1–13. [Google Scholar] [CrossRef]
- Whistler, C.A.; Hall, J.A.; Xu, F.; Ilyas, S.; Siwakoti, P.; Cooper, V.S.; Jones, S.H. Use of whole-genome phylogeny and comparisons for development of a multiplex PCR assay to identify sequence type 36 Vibrio parahaemolyticus. J. Clin. Microbiol. 2015, 53, 1864–1872. [Google Scholar] [CrossRef]
- Blackwell, K.D.; Oliver, J.D. The ecology of Vibrio vulnificus, Vibrio cholerae, and Vibrio parahaemolyticus in North Carolina estuaries. J. Microbiol. 2008, 46, 146–153. [Google Scholar] [CrossRef]
- Caburlotto, G.; Haley, B.J.; Lleò, M.M.; Huq, A.; Colwell, R.R. Serodiversity and ecological distribution of Vibrio parahaemolyticus in the Venetian Lagoon, Northeast Italy. Environ. Microbiol. Rep. 2010, 2, 151–157. [Google Scholar] [CrossRef]
- Cook, D.W.; Bowers, J.C.; DePaola, A. Density of total and pathogenic (tdh+) Vibrio parahaemolyticus in Atlantic and Gulf Coast molluscan shellfish at harvest. J. Food Prot. 2002, 65, 1873–1880. [Google Scholar] [CrossRef]
- Froelich, B.A.; Ayrapetyan, M.; Fowler, P.; Oliver, J.D.; Noble, R.T. Development of a matrix tool for the prediction of Vibrio species in oysters harvested from North Carolina. Appl. Environ. Microbiol. 2015, 81, 1111–1119. [Google Scholar] [CrossRef]
- Johnson, C.N.; Flowers, A.R.; Noriea, N.F.; Zimmerman, A.M.; Bowers, J.C.; DePaola, A.; Grimes, D.J. Relationships between environmental factors and pathogenic vibrios in the northern Gulf of Mexico. Appl. Environ. Microbiol. 2010, 76, 7076–7084. [Google Scholar] [CrossRef] [PubMed]
- Johnson, C.N.; Bowers, J.C.; Griffitt, K.J.; Molina, V.; Clostio, R.W.; Pei, S.; Laws, E.; Paranjpye, R.N.; Strom, M.S.; Chen, A.; et al. Ecology of Vibrio parahaemolyticus and Vibrio vulnificus in the coastal and estuarine waters of Louisiana, Maryland, Mississippi, and Washington (United States). Appl. Environ. Microbiol. 2012, 78, 7249–7257. [Google Scholar] [CrossRef] [PubMed]
- Julie, D.; Solen, L.; Antoine, V. Ecology of pathogenic and non-pathogenic Vibrio parahaemolyticus on the French Atlantic coast. Effects of temperature, salinity, turbidity and chlorophyll a. Environ. Microbiol. 2010, 12, 929–937. [Google Scholar] [CrossRef] [PubMed]
- Kaneko, T.; Colwell, R.R. Ecology of Vibrio parahaemolyticus in Chesapeake Bay. J. Bacteriol. 1973, 113, 24–32. [Google Scholar]
- Paranjpye, R.N.; Nilsson, W.B.; Liermann, M.; Hilborn, E.D.; George, B.J.; Li, Q.; Bill, B.D.; Trainer, V.L.; Strom, M.S.; Sandifer, P.A. Environmental influences on the seasonal distribution of Vibrio parahaemolyticus in the Pacific Northwest of the USA. FEMS Microbiol. Ecol. 2015, 91, 121. [Google Scholar] [CrossRef]
- Parveen, S.; Hettiarachchi, K.A.; Bowers, J.C.; Jones, J.L.; Tamplin, M.L.; McKay, R.; Beatty, W.; Brohawn, K.; DaSilva, L.V.; DePaola, A. Seasonal distribution of total and pathogenic Vibrio parahaemolyticus in Chesapeake Bay oysters and waters. Int. J. Food Microbiol. 2008, 128, 354–361. [Google Scholar] [CrossRef]
- Parveen, S.; DaSilva, L.; DePaola, A.; Bowers, J.; White, C.; Munasinghe, K.A.; Brohawn, K.; Mudoh, M.; Tamplin, M.L. Development and validation of a predictive model for the growth of Vibrio parahaemolyticus in post-harvest shellstock oysters. Int. J. Microbiol. 2013, 161, 1–6. [Google Scholar] [CrossRef]
- Takemura, A.; Chien, D.; Polz, M. Associations and dynamics of Vibrionaceae in the environment, from the genus to the population level. Front. Microbiol. 2014, 5. [Google Scholar] [CrossRef]
- Froelich, B.A.; Noble, R.T. Vibrio bacteria in raw oysters: Managing risks to human health. Philos. Trans. R. Soc. B Biol. Sci. 2016, 371, 20150209. [Google Scholar] [CrossRef]
- Crystal, E.N.; Schuster, B.M.; Striplin, M.J.; Jones, S.H.; Whistler, C.A.; Cooper, V.S. Influence of seasonality on the genetic diversity of Vibrio parahaemolyticus in New Hampshire shellfish waters as determined by multilocus sequence analysis. Appl. Environ. Microbiol. 2012, 78, 3778–3782. [Google Scholar]
- Mahoney, J.C.; Gerding, M.J.; Jones, S.H.; Whistler, C.A. Comparison of the pathogenic potentials of environmental and clinical Vibrio parahaemolyticus strains indicates a role for temperature regulation in virulence. Appl. Environ. Microbiol. 2010, 76, 7459–7465. [Google Scholar] [CrossRef] [PubMed]
- Schuster, B.M.; Tyzik, A.L.; Donner, R.A.; Striplin, M.J.; Almagro-Moreno, S.; Jones, S.H.; Cooper, V.S.; Whistler, C.A. Ecology and genetic structure of a northern temperate Vibrio cholerae population related to toxigenic isolates. Appl. Environ. Microbiol. 2011, 77, 7568–7575. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Urquhart, E.A.; Jones, S.H.; Jong, W.Y.; Schuster, B.M.; Marcinkiewicz, A.L.; Whistler, C.A.; Cooper, V.S. Environmental conditions associated with elevated Vibrio parahaemolyticus concentrations in Great Bay Estuary, New Hampshire. PLoS ONE 2016, 11, e0155018. [Google Scholar] [CrossRef] [PubMed]
- Bartley, C.H.; Slanetz, L.W. Occurrence of Vibrio parahaemolyticus in Estuarine Waters and Oysters of New Hampshire. Appl. Environ. Microbiol. 1971, 21, 965–966. [Google Scholar]
- Jones, S.; Summer-Brason, B. Incidence and detection of pathogenic Vibrio spp. in a northern New England estuary, USA. J. Shellfish Res. 1998, 17, 1665–1669. [Google Scholar]
- O’Neill, K.; Jones, S.; Grimes, D. Incidence of Vibrio vulnificus in northern New England water and shellfish. FEMS Microbiol. Lett. 1990, 72, 163–167. [Google Scholar] [CrossRef]
- Nash, C.; Dejadon, B. New Hampshire Vibrio Parahaemolyticus Risk Evaluation; New Hampshire Department of Environmental Services, Shellfish Program: Portsmouth, NH, USA, 2019.
- National Estuarine Research Reserve System-Centrialized Data Management Office. Available online: https://cdmo.baruch.sc.edu/dges/. (accessed on 2 October 2019).
- Kaysner, C.; DePaola, A. Chapter 9: Vibrio. In Bacteriological Analytical Manual Online; US Food and Drug Administration: Silver Spring, MD, USA, 2004. Available online: https://www.fda.gov/food/laboratory-methods-food/bam-vibrio (accessed on 17 June 2019).
- Panicker, G.; Call, D.R.; Krug, M.J.; Bej, A.K. Detection of pathogenic Vibrio spp. in shellfish by using multiplex PCR and DNA microarrays. Appl. Environ. Microbiol. 2004, 70, 7436–7444. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria; Available online: https://www.R-project.org/ (accessed on 1 November 2019).
- Faraway, J.J. Extending the Linear Model with R: Generalized Linear, Mixed Effects and Nonparametric Regression Models; Chapman and Hall/CRC: Boca Raton, FL, USA, 2016. [Google Scholar]
- Wickham, H. Ggplot2: Elegant Graphics for Data Analysis; Springer-Verlag: New York, NY, USA, 2016. [Google Scholar]
- Hastie, T.; Tibshirani, R. Generalized Additive Models; CRC Press: Boca Raton, FL, USA, 1990; Volume 43. [Google Scholar]
- Wood, S.N. Generalized Additive Models: An Introduction with R, 2nd ed.; Chapman and Hall/CRC: Boca Raton, FL, USA, 2017. [Google Scholar]
- Ruckstuhl, A. Introduction to Nonlinear Regression. In IDP Institut fur Datenanalyse und Prozessdesign, Zurcher Hochschule fur Angewandte Wissenschaften. 2010, p. 365. Available online: https://stat.ethz.ch/~stahel/courses/cheming/nlreg10E.pdf (accessed on 14 July 2019).
- Akaike, H. A New Look at the Statistical Model Identification. In Selected Papers of Hirotugu Akaike; Springer: New York, NY, USA, 1974; pp. 215–222. [Google Scholar]
- Naumova, E.N.; MacNeill, I.B. Seasonality Assessment for Biosurveillance. In Advances in Statistical Methods for the Health Sciences; Auget, J.L., Balakrishnan, N., Mesbah, M., Molenberghs, G., Eds.; Birkhauser: Basel, Switzerland, 2007; pp. 437–450. [Google Scholar]
- Alarcon Falconi, T.M.; Cruz, M.; Naumova, E.N. The shift in seasonality of legionellosis in the U.S. Epidemiol. Infect. 2018, 146, 1824–1833. [Google Scholar] [CrossRef]
- Cox, A.; Gomez-Chiarri, M. Vibrio parahaemolyticus in Rhode Island coastal ponds and the estuarine environment of Narragansett Bay. Appl. Environ. Microbiol. 2012, 78, 2996–2999. [Google Scholar] [CrossRef]
- DePaola, A.; Hopkins, L.H.; Peeler, J.T.; Wentz, B.; McPhearson, R.M. Incidence of Vibrio parahaemolyticus in US coastal waters and oysters. Appl. Environ. Microbiol. 1990, 56, 2299–2302. [Google Scholar]
- Deepanjali, A.; Kumar, H.S.; Karunasagar, I. Seasonal variation in abundance of total and pathogenic Vibrio parahaemolyticus bacteria in oysters along the southwest coast of India. Appl. Environ. Microbiol. 2005, 71, 3575–3580. [Google Scholar] [CrossRef] [PubMed]
- Kaneko, T.; Colwell, R.R. The annual cycle of Vibrio parahaemolyticus in Chesapeake Bay. Microb. Ecol. 1997, 4, 135–155. [Google Scholar] [CrossRef] [PubMed]
- Oberbeckmann, S.; Wichels, A.; Wiltshire, K.H.; Gerdts, G. Occurrence of Vibrio parahaemolyticus and Vibrio alginolyticus in the German Bight over a seasonal cycle. Antonie Van Leeuwenhoek 2011, 100, 291–307. [Google Scholar] [CrossRef] [PubMed]
- Su, Y.C.; Liu, C. Vibrio parahaemolyticus: A concern of seafood safety. Food Microbiol. 2007, 24, 549–558. [Google Scholar] [CrossRef] [PubMed]
- Turner, J.W.; Malayil, L.; Guadagnoli, D.; Cole, D.; Lipp, E.K. Detection of Vibrio parahaemolyticus, Vibrio vulnificus and Vibrio cholerae with respect to seasonal fluctuations in temperature and plankton abundance. Environ. Microbiol. 2014, 16, 1019–1028. [Google Scholar] [CrossRef]
- Oberbeckmann, S.; Fuchs, B.M.; Meiners, M.; Wichels, A.; Wiltshire, K.H.; Gerdts, G. Seasonal dynamics and modeling of a Vibrio community in coastal waters of the North Sea. Microb. Ecol. 2012, 63, 543–551. [Google Scholar] [CrossRef]
- Davis, B.J.; Jacobs, J.M.; Davis, M.F.; Schwab, K.J.; DePaola, A.; Curriero, F.C. Environmental determinants of Vibrio parahaemolyticus in the Chesapeake Bay. Appl. Environ. Microbiol. 2017, 83, e01147-17. [Google Scholar] [CrossRef]
- Vezzulli, L.; Pezzati, E.; Moreno, M.; Fabiano, M.; Pane, L.; Pruzzo, C.; VibrioSea Consortium. Benthic ecology of Vibrio spp. and pathogenic Vibrio species in a coastal Mediterranean environment (La Spezia Gulf, Italy). Microb. Ecol. 2009, 58, 808–818. [Google Scholar] [CrossRef]
- Froelich, B.; Bowen, J.; Gonzalez, R.; Snedeker, A.; Noble, R. Mechanistic and statistical models of total Vibrio abundance in the Neuse River Estuary. Water Res. 2013, 47, 5783–5793. [Google Scholar] [CrossRef]
- Hsieh, J.; Fries, J.; Noble, R. Dynamics and predictive modelling of Vibrio spp. in the Neuse River Estuary, North Carolina, USA. Environ. Microbiol. 2008, 10, 57–64. [Google Scholar] [CrossRef]
- Tonkin, J.D.; Bogan, M.T.; Bonada, N.; Rios-Touma, B.; Lytle, D.A. Seasonality and predictability shape temporal species diversity. Ecology 2017, 98, 1201–1216. [Google Scholar] [CrossRef] [PubMed]
- Shmueli, G. To explain or to predict? Stat. Sci. 2010, 25, 289–310. [Google Scholar] [CrossRef]
- DePaola, A.; Nordstrom, J.L.; Bowers, J.C.; Wells, J.G.; Cook, D.W. Seasonal abundance of total and pathogenic Vibrio parahaemolyticus in Alabama oysters. Appl. Environ. Microbiol. 2003, 69, 1521–1526. [Google Scholar] [CrossRef] [PubMed]
- Young, I.; Gropp, K.; Fazil, A.; Smith, B.A. Knowledge synthesis to support risk assessment of climate change impacts on food and water safety: A case study of the effects of water temperature and salinity on Vibrio parahaemolyticus in raw oysters and harvest waters. Food Res. Int. 2015, 68, 86–93. [Google Scholar] [CrossRef]
- Parveen, S.; Jahncke, M.; Elmahdi, S.; Crocker, H.; Bowers, J.; White, C.; Gray, S.; Morris, A.C.; Brohawn, K. High salinity relaying to reduce Vibrio parahaemolyticus and Vibrio vulnificus in Chesapeake Bay oysters (Crassostrea virginica). J. Food Sci. 2017, 82, 484–491. [Google Scholar] [CrossRef] [PubMed]
- Turner, J.W.; Good, B.; Cole, D.; Lipp, E.K. Plankton composition and environmental factors contribute to Vibrio seasonality. ISME J. 2009, 3, 1082. [Google Scholar] [CrossRef]
- Wong, H.C.; Wang, P. Induction of viable but nonculturable state in Vibrio parahaemolyticus and its susceptibility to environmental stresses. J. Appl. Microbiol. 2004, 96, 359–366. [Google Scholar] [CrossRef] [PubMed]
- Wong, H.C.; Peng, P.Y.; Han, J.M.; Chang, C.Y.; Lan, S.L. Effect of mild acid treatment on the survival, enteropathogenicity, and protein production in Vibrio parahaemolyticus. Infect. Immun. 2015, 66, 3066–3071. [Google Scholar]
- Main, C.R.; Salvitti, L.R.; Whereat, E.B.; Coyne, K.J. Community-level and species-specific associations between phytoplankton and particle-associated Vibrio species in Delaware’s inland bays. Appl. Environ. Microbiol. 2015, 81, 5703–5713. [Google Scholar] [CrossRef]
- Grimes, D.J.; Ford, T.E.; Colwell, R.R.; Baker-Austin, C.; Martinez-Urtaza, J.; Subramaniam, A.; Capone, D.G. Viewing marine bacteria, their activity and response to environmental drivers from orbit: Satellite remote sensing of bacteria. Microb. Ecol. 2014, 67, 489–500. [Google Scholar] [CrossRef]
- Hartwick, M.; Jones, S.H. Vibrio parahaemolyticus Population Dynamics Within an Estuarine Microbial Community. Int. Symp. Microb. Ecol. 2016. Poster presentation. [Google Scholar]
- Hartwick, M.; Berenson, A.; Whistler, C.A.; Cooper, V.S.; Jones, S.H. Seasonal Plankton Communities and Plankton-Associated Vibrio parahaemolyticus Improve the Estimation of Vibrio parahaemolyticus Concentration in Oysters in the Great Bay Estuary. In preparation.
- Gilbert, J.A.; Steele, J.A.; Caporaso, J.G.; Steinbrück, L.; Reeder, J.; Temperton, B.; Huse, S.; McHardy, A.C.; Knight, R.; Joint, I.; et al. Defining seasonal marine microbial community dynamics. ISME J. 2012, 6, 298. [Google Scholar] [CrossRef] [PubMed]
- Rehnstam-Holm, A.; Godhe, A.; Härnström, K.; Raghunath, P.; Saravanan, V.; Collin, B.; Karunasagar, I.; Karunasagar, I. Association between phytoplankton and Vibrio spp. along the southwest coast of India: A mesocosm experiment. Aquat. Microb. Ecol. 2010, 58, 127–139. [Google Scholar]
- Davis, B.J.; Jacobs, J.M.; Zaitchik, B.; DePaola, A.; Curriero, F.C. Vibrio parahaemolyticus in the Chesapeake Bay: Operational in situ prediction and forecast models can benefit from inclusion of lagged water quality measurements. Appl. Environ. Microbiol. 2019, 85, e01007-19. [Google Scholar] [CrossRef] [PubMed]
- Schillaci, C. Vibrioparahaemolyticus (Vp) Illness in Massachusetts and Impact on the Cape and Island’s Shellfish Industry. In Proceedings of the 4th Annual Cape Coastal Conference, Hyannis, MA, USA, 6–7 December 2016; Available online: http://www.waquoitbayreserve.org/wp-content/uploads/CC4_Schillaci_Vibrio.pdf (accessed on 2 October 2019).
- Semenza, J.C.; Trinanes, J.; Lohr, W.; Sudre, B.; Löfdahl, M.; Martinez-Urtaza, J.; Nichols, G.L.; Rocklöv, J. Environmental suitability of Vibrio infections in a warming climate: An early warning system. Environ. Health Perspect. 2017, 125, 107004. [Google Scholar] [CrossRef] [PubMed]
- Vezzulli, L.; Grande, C.; Reid, P.C.; Hélaouët, P.; Edwards, M.; Höfle, M.G.; Brettar, I.; Colwell, R.R.; Pruzzo, C. Climate influence on Vibrio and associated human diseases during the past half-century in the coastal North Atlantic. Proc. Natl. Acad. Sci. USA 2016, 113, E5062–E5071. [Google Scholar] [CrossRef]
- Vezzulli, L.; Pezzati, E.; Brettar, I.; Höfle, M.; Pruzzo, C. Effects of global warming on vibrio ecology. Microbiol. Spectr. 2015, 3. [Google Scholar] [CrossRef]
| Variable a | Coefficients b | Standard Error | r2 | Deviance | AIC | Peak Timing c | ||
|---|---|---|---|---|---|---|---|---|
| Trend | Seasonality | Trend | Seasonality | |||||
| Vp (MPN/g) | 0.0005 *** | 0.57 *** | 0.0001 | 0.11 | 0.19 | 0.21 | 673.4 | |
| 0.0006 *** | −2.87 *** −3.66 *** | 0.0001 | 0.34 0.33 | 0.50 | 0.51 | 597.4 | 222 ± 5 | |
| Water Temperature (°C) | <0.001 | 2.01 *** | <0.001 | 0.15 | 0.53 | 0.54 | 774.1 | |
| 0.002 * | −5.81 *** −10.22 *** | <0.001 | 0.24 0.23 | 0.93 | 0.93 | 497.9 | 213 ± 2 | |
| Dissolved Oxygen (mg/L) | <0.001 | −0.31 *** | <0.001 | 0.05 | 0.22 | 0.23 | 441.5 | |
| <0.001 | 1.45 *** 1.91 *** | <0.001 | 0.15 0.14 | 0.58 | 0.59 | 352.0 | 220 ± 6 | |
| Salinity (ppt) | 0.001 *** | −0.19 | 0.0003 | 0.20 | 0.12 | 0.13 | 849.4 | |
| 0.002 *** | −4.06 *** −1.77 ** | 0.0003 | 0.76 0.72 | 0.26 | 0.28 | 825.5 | 251 ± 18 | |
| pH | <0.001 *** | −0.02 * | <0.001 | 0.01 | 0.08 | 0.10 | 19.9 | |
| <0.001 *** | −0.06 0.03 | 0.006 | 0.05 0.05 | 0.09 | 0.11 | 20.9 | 298 ± 98 | |
| Turbidity (NTU) | −0.02 *** | 3.93 | 0.007 | 4.10 | 0.06 | 0.09 | 1723.6 | |
| −0.02 *** | −6.34 −9.83 | 0.007 | 16.77 15.87 | 0.06 | 0.08 | 1716.5 | 135 ± 111 | |
| Chlorophyll-a (µg/L) | −0.0002 | 0.62 *** | 0.005 | 0.0002 | 0.09 | 0.10 | 775.3 | |
| <0.001 | 0.11 −2.02 *** | <0.001 | 0.65 0.61 | 0.09 | 0.10 | 778.2 | 180 ± 37 | |
| Total Dissolved Nitrogen (mg/L) | <0.001 *** | −0.008 * | <0.001 | 0.005 | 0.15 | 0.16 | −229.0 | |
| <0.001 *** | 0.02 0.04 * | <0.001 | 0.02 0.02 | 0.15 | 0.17 | −228.2 | 206 ± 45 | |
| Rainfall (mm) | <0.001 | 0.01 * | <0.001 | <0.001 | 0.01 | 0.02 | −76.7 | |
| <0.001 | −0.03 −0.07 ** | <0.001 | 0.001 <0.001 | 0.01 | 0.04 | −74.6 | 209 ± 38 | |
| Year | V. Parahaemolyticus | Salinity | TDN | pH | ||||
|---|---|---|---|---|---|---|---|---|
| 75th Percentile | 25th and 75th Percentile | |||||||
| 220 MPN/g | 27 ppt | 0.27 mg/L | 7.56–7.88 | |||||
| n | % | n | % | n | % | n | % | |
| 2007 | 2/17 | 11.8% | 196/488 | 40.2% | 6/17 | 35.3% | 215/488 | 44.1% |
| 2008 | 2/18 | 11.1% | 10/465 | 2.2% | 0/18 | 0.0% | 148/465 | 31.8% |
| 2009 | 1/11 | 9.1% | 18/463 | 3.9% | 1/11 | 9.0% | 173/449 | 38.5% |
| 2010 | 3/14 | 21.4% | 58/451 | 12.9% | 0/14 | 0.0% | 157/451 | 34.8% |
| 2011 | 0/9 | 0.0% | 46/377 | 12.2% | 0/9 | 0.0% | 102/430 | 23.7% |
| 2012 | 3/7 | 42.9% | 135/475 | 28.4% | 0/7 | 0.0% | 217/447 | 48.5% |
| 2013 | 1/6 | 16.7% | 65/438 | 14.8% | 3/6 | 50.0% | 231/438 | 52.7% |
| 2014 | 7/22 | 31.8% | 135/432 | 31.3% | 13/22 | 59.1% | 277/432 | 64.1% |
| 2015 | 8/24 | 33.3% | 205/443 | 46.3% | 10/22 | 45.5% | 230/408 | 56.3% |
| 2016 | 8/21 | 38.1% | 266/479 | 55.5% | 4/18 | 22.2% | 289/465 | 62.1% |
| Variable | Model 5 | Model 6 | Model 6–Model 5 | ||
|---|---|---|---|---|---|
| p-Value | p-Value | Deviance | AIC | ||
| Water Temperature (°C) | <0.001 | <0.001 | 0.03 | 0.03 | 8.27 |
| Dissolved Oxygen (mg/L) | <0.001 | <0.001 | 0.04 | 0.05 | 7.28 |
| Salinity (ppt) | <0.001 | <0.001 | −0.01 | 0.0 | 0.0 |
| pH | 0.009 | 0.002 | 0.14 | 0.08 | 8.48 |
| Chlorophyll a (µg/L) | 0.05 | 0.09 | 0.01 | 0.29 | 0.11 |
| Rainfall (mm) | 0.03 | 0.02 | 0.04 | 0.04 | −6.31 |
| Turbidity (NTU) | 0.27 | 0.48 | 0.01 | 0.25 | 0.43 |
| Total Dissolved Nitrogen (mg/L) | 0.38 | 0.31 | 0.02 | 0.03 | 3.20 |
| Model Composition a | Coefficients | St. Error | Deviance | AIC | Coefficients | St. Error | Deviance | AIC |
|---|---|---|---|---|---|---|---|---|
| Model 7 GLM-G | GLM-NB | |||||||
| 1. Temperature Salinity | 0.34 *** 0.12 ** | 0.03 0.03 | 0.54 | 586.9 | 0.34 *** 0.13 *** | 0.03 0.03 | 0.48 | 1533.4 |
| 2. Temperature C-pH b | 0.37 *** −4.73 *** | 0.03 0.94 | 0.57 | 583.1 | 0.41 *** −5.52 *** | 0.03 0.91 | 0.51 | 1521.6 |
| 3. Temperature C-pH Salinity | 0.35 *** −3.93 *** 0.07 ** | 0.03 0.99 0.03 | 0.59 | 572.5 | 0.34 *** −4.38 *** 0.07 ** | 0.02 0.93 0.02 | 0.53 | 1518.3 |
| 4. Temperature C-pH Salinity C-pH*Salinity | 0.35 *** 4.61 0.11 *** −0.41 *** | 0.02 3.35 0.04 0.16 | 0.61 | 567.8 | 0.34 *** 5.52 * 0.10 ** −0.53 ** | 0.02 0.03 2.97 0.14 | 0.57 | 1507.1 |
| Model 8 GLM-G | GLM-NB | |||||||
| 1. Trend Photoperiod Temperature C-pH | 0.0003 ** −0.35 ** 0.46 *** −3.77 *** | 0.0001 0.11 0.04 0.95 | 0.62 | 564.4 | 0.0003 *** −0.32 *** 0.43 *** −4.52 *** | 0.0001 0.09 0.03 0.86 | 0.58 | 1501.9 |
| 2. Trend Photoperiod Temperature C-pH Salinity | 0.0002 ** −0.32 ** 0.44 *** −3.77 *** 0.02 | 0.001 0.11 0.04 0.99 0.06 | 0.62 | 565.9 | 0.0003 *** −0.32 *** 0.43 *** −4.48 *** −0.004 | 0.0001 0.13 0.04 0.89 0.03 | 0.58 | 1503.9 |
| Model 9 GLM-G | GLM-NB | |||||||
| 1. Trend Sin(.) Cos(.) Temperature C-pH | 0.0003 ** 0.07 1.47 0.50 *** −3.78 *** | 0.0001 0.69 1.12 0.11 0.96 | 0.62 | 566.3 | 0.0003 *** −0.28 0.79 0.41 *** −4.49 *** | 0.0001 0.56 0.91 0.09 0.87 | 0.58 | 1504.2 |
| 2. Trend Sin(.) Cos(.) Temp C-pH Salinity | 0.0003 ** 0.15 1.47 0.49 *** −3.60 *** 0.03 | 0.0001 0.69 1.12 0.11 0.99 0.04 | 0.62 | 567.7 | 0.0003 *** −0.31 0.77 0.41 *** −4.61 *** −0.006 | 0.0001 0.57 0.91 0.09 0.89 0.03 | 0.58 | 1506.2 |
| Model | Variable a | Time Interval | ||
|---|---|---|---|---|
| P1 | P2 | P3 | ||
| Model 7.4 | Coefficient: Temperature | 0.34 *** | 0.37 *** | 0.31 *** |
| Salinity | 0.10 *** | 0.08 ** | 0.24 ** | |
| C-pH | 5.51 * | 5.12 | 266.01 *** | |
| Salinity*C-pH | −0.53 *** | −0.53 *** | −11.01 *** | |
| r2 | 0.54 | 0.58 | 0.57 | |
| Deviance | 0.57 | 0.58 | 0.54 | |
| RMSE | 1.91 | 1.79 | 1.96 | |
| Model 8.1 | Coefficient: Trend | 0.0003 *** | 0.0003 | 0.0007 |
| Photoperiod | −0.31 *** | −0.28 ** | −0.48 ** | |
| Temperature | 0.43 *** | 0.45 *** | 0.44 *** | |
| C-pH | −4.51 *** | −4.32 *** | -5.10 | |
| r2 | 0.61 | 0.57 | 0.61 | |
| Deviance | 0.58 | 0.59 | 0.53 | |
| RMSE | 1.85 | 1.81 | 1.92 | |
| Model 9.1 | Coefficient: Trend | 0.0004 *** | 0.0004 * | 0.0008 |
| Sin(.) | −0.41 | −1.88 * | 1.72 * | |
| Cos(.) | 0.63 | −1.54 | 4.66 ** | |
| Temperature | 0.40 *** | 0.29 ** | 0.74 *** | |
| C-pH | −4.30 *** | −4.20 *** | 1.60 | |
| r2 | 0.61 | 0.55 | 0.63 | |
| Deviance | 0.58 | 0.60 | 0.54 | |
| RMSE | 1.81 | 1.82 | 1.83 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hartwick, M.A.; Urquhart, E.A.; Whistler, C.A.; Cooper, V.S.; Naumova, E.N.; Jones, S.H. Forecasting Seasonal Vibrio parahaemolyticus Concentrations in New England Shellfish. Int. J. Environ. Res. Public Health 2019, 16, 4341. https://doi.org/10.3390/ijerph16224341
Hartwick MA, Urquhart EA, Whistler CA, Cooper VS, Naumova EN, Jones SH. Forecasting Seasonal Vibrio parahaemolyticus Concentrations in New England Shellfish. International Journal of Environmental Research and Public Health. 2019; 16(22):4341. https://doi.org/10.3390/ijerph16224341
Chicago/Turabian StyleHartwick, Meghan A., Erin A. Urquhart, Cheryl A. Whistler, Vaughn S. Cooper, Elena N. Naumova, and Stephen H. Jones. 2019. "Forecasting Seasonal Vibrio parahaemolyticus Concentrations in New England Shellfish" International Journal of Environmental Research and Public Health 16, no. 22: 4341. https://doi.org/10.3390/ijerph16224341
APA StyleHartwick, M. A., Urquhart, E. A., Whistler, C. A., Cooper, V. S., Naumova, E. N., & Jones, S. H. (2019). Forecasting Seasonal Vibrio parahaemolyticus Concentrations in New England Shellfish. International Journal of Environmental Research and Public Health, 16(22), 4341. https://doi.org/10.3390/ijerph16224341