Potential for Hydroclimatically Driven Shifts in Infectious Disease Outbreaks: The Case of Tularemia in High-Latitude Regions
Abstract
1. Introduction
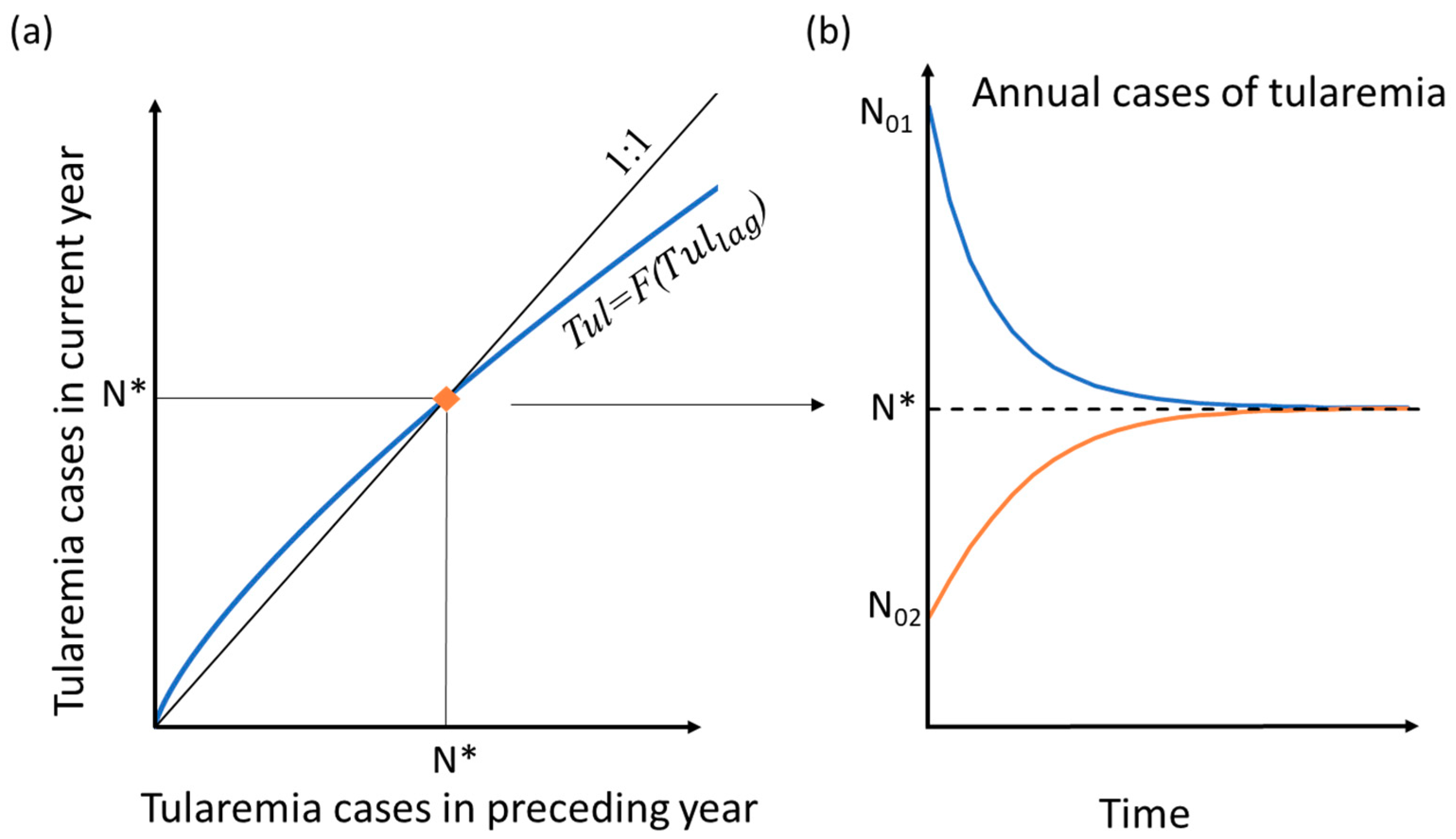
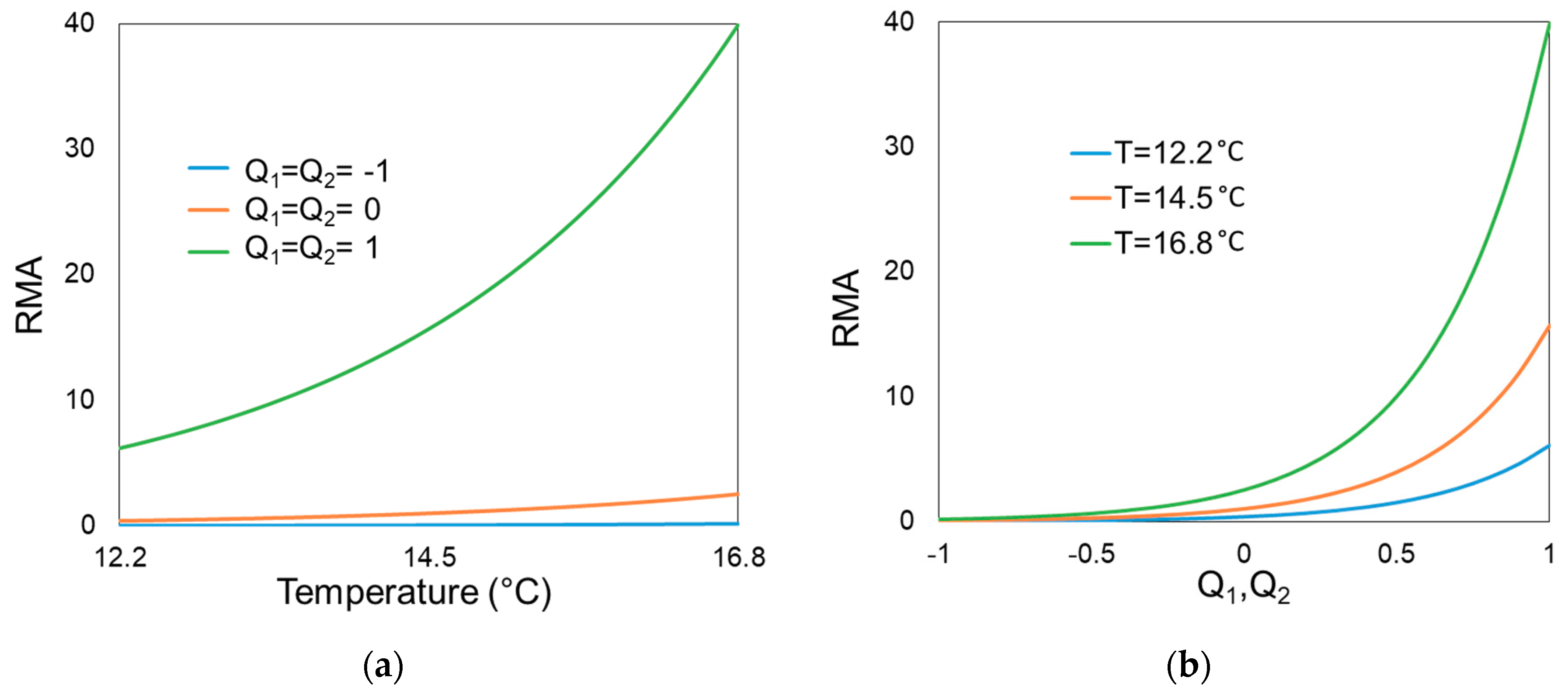
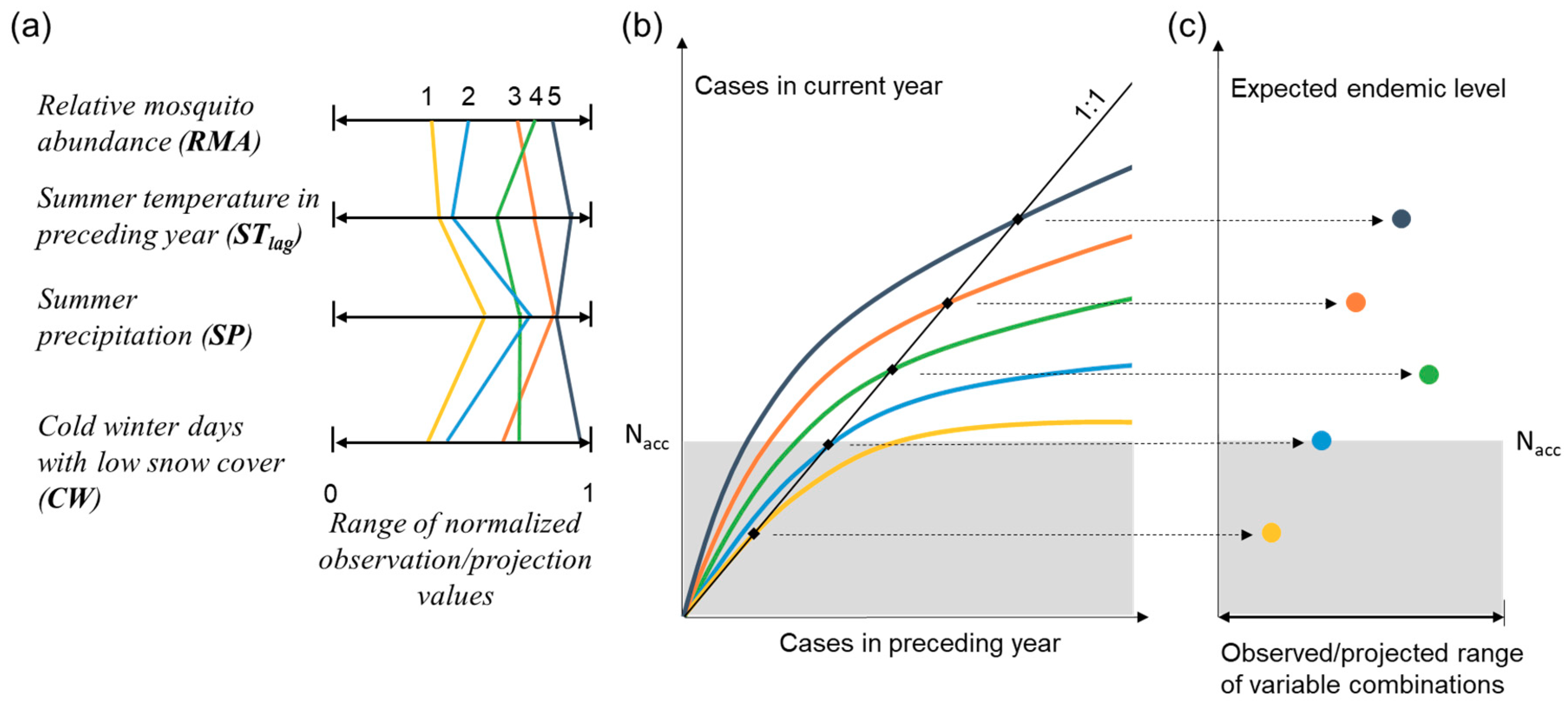
2. Methods with analytical solution development
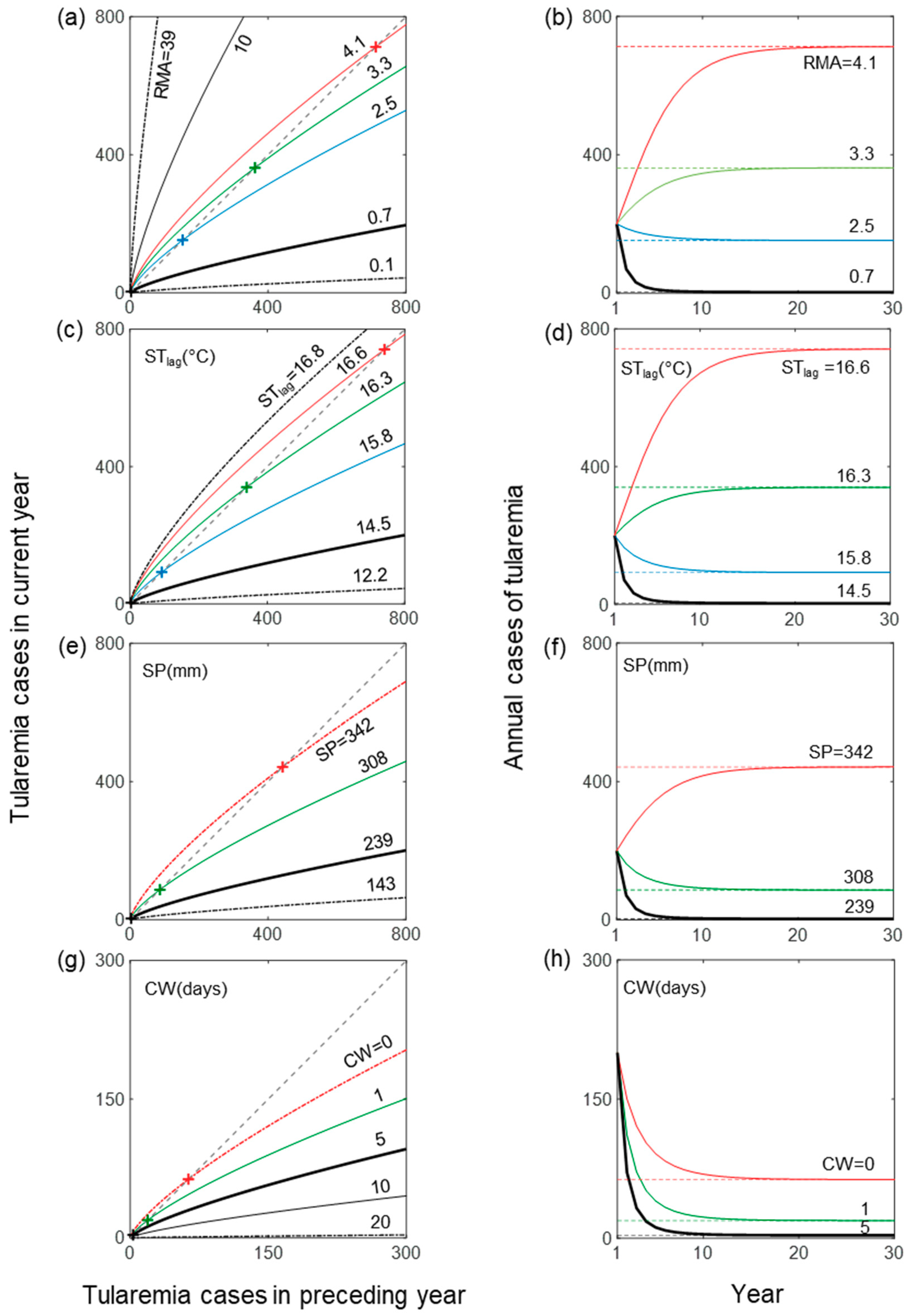
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Milly, P.C.D.; Dunne, K.A.; Vecchia, A.V. Global pattern of trends in streamflow and water availability in a changing climate. Nature 2005, 438, 347–350. [Google Scholar] [CrossRef] [PubMed]
- Jaramillo, F.; Destouni, G. Local flow regulation and irrigation raise global human water consumption and footprint. Science 2015, 350, 1248–1251. [Google Scholar] [CrossRef] [PubMed]
- Destouni, G.; Jaramillo, F.; Prieto, C. Hydroclimatic shifts driven by human water use for food and energy production. Nat. Clim. Chang. 2013, 3, 213–217. [Google Scholar] [CrossRef]
- Karlsson, J.M.; Jaramillo, F.; Destouni, G. Hydro-climatic and lake change patterns in Arctic permafrost and non-permafrost areas. J. Hydrol. 2015, 529, 134–145. [Google Scholar] [CrossRef]
- Garrett, K.A.; Dobson, A.D.M.; Kroschel, J.; Natarajan, B.; Orlandini, S.; Tonnang, H.E.Z.; Valdivia, C. The effects of climate variability and the color of weather time series on agricultural diseases and pests, and on decisions for their management. Agric. For. Meteorol. 2013, 170, 216–227. [Google Scholar] [CrossRef]
- Baker-Austin, C.; Trinanes, J.A.; Taylor, N.G.H.; Hartnell, R.; Siitonen, A.; Martinez-Urtaza, J. Emerging Vibrio risk at high latitudes in response to ocean warming. Nat. Clim. Chang. 2013, 3, 73–77. [Google Scholar] [CrossRef]
- Harvell, D.; Altizer, S.; Cattadori, I.M.; Harrington, L.; Weil, E. Climate change and wildlife diseases: When does the host matter the most? Ecology 2009, 90, 912–920. [Google Scholar] [CrossRef]
- Burge, C.A.; Mark Eakin, C.; Friedman, C.S.; Froelich, B.; Hershberger, P.K.; Hofmann, E.E.; Petes, L.E.; Prager, K.C.; Weil, E.; Willis, B.L.; et al. Climate change influences on marine infectious diseases: Implications for management and society. Ann. Rev. Mar. Sci. 2014, 6, 249–277. [Google Scholar] [CrossRef]
- Rodó, X.; Pascual, M.; Doblas-Reyes, F.J.; Gershunov, A.; Stone, D.I.; Giorgi, F.; Hudson, P.J.; Kinter, J.; Rodríguez-Arias, M.N.; Stenseth, N.C. Climate change and infectious diseases: Can we meet the needs for better prediction? Climatic Change 2013, 118, 625. [Google Scholar] [CrossRef]
- Rogers, D.J.; Randolph, S.E. Climate change and vector-borne diseases. Adv. Parasitol. 2006, 62, 345–381. [Google Scholar]
- Lowen, A.C.; Mubareka, S.; Steel, J.; Palese, P. Influenza virus transmission is dependent on relative humidity and temperature. PLoS Pathog. 2007, 3, 1470–1476. [Google Scholar] [CrossRef] [PubMed]
- Altizer, S.; Ostfeld, R.S.; Johnson, P.T.J.; Kutz, S.; Harvell, C.D. Climate Change and Infectious Diseases: From Evidence to a Predictive Framework. Science 2013, 341, 514–519. [Google Scholar] [CrossRef] [PubMed]
- Callaghan, T.V.; Björn, L.O.; Chernov, Y.; Chapin, T.; Christensen, T.R.; Huntley, B.; Ims, R.A.; Johansson, M.; Jolly, D.; Jonasson, S.; et al. Biodiversity, distributions and adaptations of Arctic species in the context of environmental change. Ambio 2004, 33, 404–417. [Google Scholar] [CrossRef] [PubMed]
- Foxman, E.F.; Storer, J.A.; Vanaja, K.; Levchenko, A.; Iwasaki, A. Two interferon-independent double-stranded RNA-induced host defense strategies suppress the common cold virus at warm temperature. Proc. Natl. Acad. Sci. USA 2016, 113, 8496–8501. [Google Scholar] [CrossRef] [PubMed]
- Reiner, R.C.; King, A.A.; Emch, M.; Yunus, M.; Faruque, A.S.G.; Pascual, M. Highly localized sensitivity to climate forcing drives endemic cholera in a megacity. Proc. Natl. Acad. Sci. USA 2012, 109, 2033–2036. [Google Scholar] [CrossRef] [PubMed]
- Selroos, J.-O.; Cheng, H.; Vidstrand, P.; Destouni, G. Permafrost Thaw with Thermokarst Wetland-Lake and Societal-Health Risks: Dependence on Local Soil Conditions under Large-Scale Warming. Water 2019, 11, 574. [Google Scholar] [CrossRef]
- Lehner, B.; Döll, P.; Alcamo, J.; Henrichs, T.; Kaspar, F. Estimating the Impact of Global Change on Flood and Drought Risks in Europe: A Continental, Integrated Analysis. Clim. Chang. 2006, 75, 273–299. [Google Scholar] [CrossRef]
- Hassol, S.; Assessment, A.C.I. Impacts of a Warming Arctic Arctic Climate Impact Assessment; Cambridge University Press: Cambridge, UK, 2004; ISBN 978-0-521-61778-9. [Google Scholar]
- Dyurgerov, M.; Bring, A.; Destouni, G. Integrated assessment of changes in freshwater inflow to the Arctic Ocean. J. Geophys. Res. Atmos. 2010, 115. [Google Scholar] [CrossRef]
- Azcárate, J.; Balfors, B.; Bring, A.; Destouni, G. Strategic environmental assessment and monitoring: Arctic key gaps and bridging pathways. Env. Res. Lett. 2013, 8, 044033. [Google Scholar] [CrossRef]
- Frampton, A.; Destouni, G. Impact of degrading permafrost on subsurface solute transport pathways and travel times. Water Resour. Res. 2015, 51, 7680–7701. [Google Scholar] [CrossRef]
- Revich, B.A.; Podolnaya, M.A. Thawing of permafrost may disturb historic cattle burial grounds in East Siberia. Glob Health Action 2011, 4. [Google Scholar] [CrossRef] [PubMed]
- Nilsson, L.M.; Destouni, G.; Berner, J.; Dudarev, A.A.; Mulvad, G.; Odland, J.O.; Parkinson, A.; Tikhonov, C.; Rautio, A.; Evengård, B. A call for urgent monitoring of food and water security based on relevant indicators for the Arctic. Ambio 2013, 42, 816–822. [Google Scholar] [CrossRef] [PubMed]
- Rydén, P.; Björk, R.; Schäfer, M.L.; Lundström, J.O.; Petersén, B.; Lindblom, A.; Forsman, M.; Sjöstedt, A.; Johansson, A. Outbreaks of Tularemia in a Boreal Forest Region Depends on Mosquito Prevalence. J. Infect. Dis. 2012, 205, 297–304. [Google Scholar] [CrossRef] [PubMed]
- Waits, A.; Emelyanova, A.; Oksanen, A.; Abass, K.; Rautio, A. Human infectious diseases and the changing climate in the Arctic. Environ. Int. 2018, 121, 703–713. [Google Scholar] [CrossRef] [PubMed]
- Malkhazova, S.; Mironova, V.; Shartova, N.; Orlov, D. Mapping Russia’s Natural Focal Diseases: History and Contemporary Approaches; Springer Nature: Basel, Switzerland, 2019. [Google Scholar]
- Olsufév, N.G. Results and perspectives of the study of natural foci of tularemia in USSR. Med. Parazitol. 1977, 46, 273–282. [Google Scholar]
- Tärnvik, A.; Priebe, H.; Grunow, R. Tularaemia in Europe: An Epidemiological Overview. Scand. J. Infect. Dis. 2004, 36, 350–355. [Google Scholar] [CrossRef] [PubMed]
- Revich, B.; Tokarevich, N.; Parkinson, A.J. Climate change and zoonotic infections in the Russian Arctic. Int. J. Circumpolar Health 2012, 71, 18792. [Google Scholar] [CrossRef] [PubMed]
- Nakazawa, Y.; Williams, R.; Peterson, A.T.; Mead, P.; Staples, E.; Gage, K.L. Climate Change Effects on Plague and Tularemia in the United States. Vector-Borne Zoonotic Dis. 2007, 7, 529–540. [Google Scholar] [CrossRef]
- Rydén, P.; Sjöstedt, A.; Johansson, A. Effects of climate change on tularaemia disease activity in Sweden. Glob. Health Action 2009, 2, 2063. [Google Scholar] [CrossRef]
- Palo, T.R.; Ahlm, C.; Tärnvik, A. Climate variability reveals complex events for tularaemia dynamics in man and mammals. Ecol. Soc. 2005, 10, 22. [Google Scholar] [CrossRef]
- Keim, P.; Johansson, A.; Wagner, D.M. Molecular Epidemiology, Evolution, and Ecology of Francisella. Ann. N. Y. Acad. Sci. 2007, 1105, 30–66. [Google Scholar] [CrossRef] [PubMed]
- Eisen, R.J.; Mead, P.S.; Meyer, A.M.; Pfaff, L.E.; Bradley, K.K.; Eisen, L. Ecoepidemiology of Tularemia in the Southcentral United States. Am. J. Trop. Med. Hyg. 2008, 78, 586–594. [Google Scholar] [CrossRef] [PubMed]
- Eliasson, H.; Lindbäck, J.; Nuorti, J.P.; Arneborn, M.; Giesecke, J.; Tegnell, A. The 2000 Tularemia Outbreak: A Case-Control Study of Risk Factors in Disease-Endemic and Emergent Areas, Sweden. Emerg. Infect. Dis. 2002, 8, 956–960. [Google Scholar] [CrossRef] [PubMed]
- World Health Organization & United Nations. Climate and Health Country Profiles 2015: A Global Overview; World Health Organization: Geneva, Switzerland, 2015. [Google Scholar]
- World Health Orgnization. Outbreak Surveillance and Response in Humanitarian Emergencies; World Health Orgnization: Geneva, Switzerland, 2012. [Google Scholar]
- Dirmeyer, P.A.; Wu, J.; Norton, H.E.; Dorigo, W.A.; Quiring, S.M.; Ford, T.W.; Santanello, J.A.; Bosilovich, M.G.; Ek, M.B.; Koster, R.D.; et al. Confronting Weather and Climate Models with Observational Data from Soil Moisture Networks over the United States. J. Hydrometeor. 2016, 17, 1049–1067. [Google Scholar] [CrossRef] [PubMed]
- Lloyd, S.; Kovats, R.; Armstrong, B. Global diarrhoea morbidity, weather and climate. Clim. Res. 2007, 34, 119–127. [Google Scholar] [CrossRef]
- Chou, W.-C.; Wu, J.-L.; Wang, Y.-C.; Huang, H.; Sung, F.-C.; Chuang, C.-Y. Modeling the impact of climate variability on diarrhea-associated diseases in Taiwan (1996–2007). Sci. Total Environ. 2010, 409, 43–51. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Rao, Y.; Wu, X.; Zhao, H.; Chen, J. A Method for Screening Climate Change-Sensitive Infectious Diseases. Int. J. Environ. Res. Public Health 2015, 12, 767–783. [Google Scholar] [CrossRef]
- Hales, S.; Kovats, S.; Lloyd, S.; Campbell-Lendrum, D.; World Health Organization; Health Security and Environment Cluster. Quantitative risk Assessment of the Effects of Climate Change on Selected Causes of Death, 2030s and 2050s; WHO: Geneva, Switzerland, 2014; ISBN 978-92-4-150769-1. [Google Scholar]
- Desvars-Larrive, A.; Liu, X.; Hjertqvist, M.; Sjöstedt, A.; Johansson, A.; Rydén, P. High-risk regions and outbreak modelling of tularemia in humans. Epidemiol. Infect. 2017, 145, 482–490. [Google Scholar] [CrossRef] [PubMed]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, Y.; Bring, A.; Kalantari, Z.; Destouni, G. Potential for Hydroclimatically Driven Shifts in Infectious Disease Outbreaks: The Case of Tularemia in High-Latitude Regions. Int. J. Environ. Res. Public Health 2019, 16, 3717. https://doi.org/10.3390/ijerph16193717
Ma Y, Bring A, Kalantari Z, Destouni G. Potential for Hydroclimatically Driven Shifts in Infectious Disease Outbreaks: The Case of Tularemia in High-Latitude Regions. International Journal of Environmental Research and Public Health. 2019; 16(19):3717. https://doi.org/10.3390/ijerph16193717
Chicago/Turabian StyleMa, Yan, Arvid Bring, Zahra Kalantari, and Georgia Destouni. 2019. "Potential for Hydroclimatically Driven Shifts in Infectious Disease Outbreaks: The Case of Tularemia in High-Latitude Regions" International Journal of Environmental Research and Public Health 16, no. 19: 3717. https://doi.org/10.3390/ijerph16193717
APA StyleMa, Y., Bring, A., Kalantari, Z., & Destouni, G. (2019). Potential for Hydroclimatically Driven Shifts in Infectious Disease Outbreaks: The Case of Tularemia in High-Latitude Regions. International Journal of Environmental Research and Public Health, 16(19), 3717. https://doi.org/10.3390/ijerph16193717






