1. Introduction
Soil magnetometry has frequently been used to detect and determine the potential soil pollution with Potentially Toxic Elements (PTE) emitted by industry, transportation, agriculture, households, and other types of anthropogenic sources. Due to the presence of magnetic particles in anthropogenic pollutants, soil magnetometry has been proposed as a fast and cheap alternative to expensive and time-consuming geochemical laboratory analyses. Numerous studies confirmed statistically significant correlation between industrial pollution and soil magnetic susceptibility [
1,
2,
3,
4].
Soil magnetometry is considered as one of the most innovative and promising methods in environmental research [
5,
6]. Recently, soil magnetometry was a subject of intense development as a method for the screening of soil polluted with toxic elements. Numerous studies were conducted [
7,
8,
9,
10] where the methodology of field and laboratory measurements was described and analyzed in detail. However, in addition to the measurement stage, the appropriate analysis of the measured values of magnetic susceptibility—leading to the accurate delineation of spatial distributions and the size of the potentially contaminated area—is an essential procedural requirement. When assessing the degree of soil contamination using soil magnetometry, various types of errors may occur. The first group of measurement errors is related to the apparatus used, the method of soil sampling, and the field measurements technique. These aspects were studied extensively, and numerous scientific papers have been published on this topic [
11,
12]. However, the biggest challenge is still the determination of the level of soil pollution in places where measurements were not taken, with the simultaneous assessment of the errors of these estimates. These errors may result from difficulties in proper assessment of the spatial variability of soil magnetic susceptibility as well as from other specific properties of the interpolation method [
13,
14]. Even the most advanced interpolation methods are characterized by the possibility of underestimating or overestimating the interpolated value. Therefore, it is important to estimate the uncertainty of estimated spatial distributions, as it may have a very significant impact on subsequent decisions regarding the classification of certain areas as contaminated or clean.
Simple interpolation methods do not allow the determination of the uncertainty of interpolated values. In the case of geostatistical methods, such as different types of kriging, it is possible to determine a spatial distribution of errors using kriging variance calculations [
15]. Such distribution already allows for some estimation of the uncertainty of the interpolated values of magnetic susceptibility of soil and related phenomena. The kriging variance, however, has some limitations arising from problems with assessing the proper model of spatial correlations of phenomena under study.
In this aspect, geostatistical simulations offer an advantage over estimations based on kriging. Geostatistical simulations are better at representing local variability because the small-scale variability is added back into the calculated spatial distributions [
16,
17,
18,
19,
20]. The averaging of simulated values from geostatistical simulations results in the kriging prediction because the variability added to the predicted value has a mean of zero. After calculating the number of realizations using Sequential Gaussian Simulations (SGS), it is possible to calculate numerous statistics of simulated values at each location within a study area or even calculate histograms or box-and-whisker plots.
Moreover, kriging is based on a local average of measured values and tends to produce smoothed spatial distributions where high-value areas are typically underestimated, while low-value areas are usually overestimated. Geostatistical simulations are better when reproducing high and low values. In soil magnetometry, it can be very important, especially in areas that are classified as hotspots where high values of soil magnetic susceptibility were measured.
This paper presents the analysis of a new approach to the assessment of uncertainty in soil magnetometry using geostatistical Gaussian simulation. More specifically, two of the most common schemes of field measurement of soil magnetic susceptibility were compared in terms of their magnitude of errors of the estimated spatial distributions. It is important to notice that the intention of this paper was not to introduce any new geostatistical modeling methods or updates to an existing one. The goal of this paper was to propose the use of a well-known method of geostatistical Gaussian simulation to be widely used in soil magnetometry studies of soil pollution. The goal was to show the benefits and advantages of using geostatistical simulation, specifically in the soil magnetometry method. This was dictated by the fact that, despite the significant development of soil magnetometry, most of the work focused on the advance in measurement and analytical methods. A very important part of the analysis of the results of field measurements has been neglected to some extent.
In the selected study area, a large number of measurements of soil magnetic susceptibility was made, and several tens of spatial distributions of soil, κ, were simulated and later used to calculate the mean, median, minimum, and maximum of these realizations. As a measure of uncertainty of the simulated values of soil magnetic susceptibility, we have presented spatial distributions of the coefficient of variation of simulated κ, calculated as the standard deviation of simulated values of soil magnetic susceptibility divided by means of simulated values of κ.
Next, simulated and measured values of κ were compared using classic statistics as well as analysis of spatial correlations. The parameters of spatial correlations of κ measured in the study area were determined and compared with those calculated using simulated maps of average κ. The goal of this part of the analysis was to determine which of the data sets allows results that are characterized by parameters of spatial correlation as close as possible to those characterizing the measured κ values.
3. Results and Discussion
Before running the SGS, both data sets of measured values, κnon-avg and κavg, were tested for normality of their distributions. A Shapiro–Wilk test was performed with a significance level of 0.05. The results of this test suggested that for both sets of κnon-avg and κavg, it can be assumed that their distributions are close to normal distribution. On the basis of these results, it was concluded that the κnon-avg and κavg values could be used in further analyses, variogram calculation, and SGS simulation without data transformation.
As can be noticed in
Table 1, the data set that included all, non-averaged values, κ
non-avg, was much more frequent than the set of κ
avg. The average susceptibility values were similar for both sets of data and approximately equal to 65 × 10
−5 SI. More pronounced differences were observed in the case of quartiles and standard deviation values, where the averaging data resulted in a visible reduction in the spread of susceptibility values. For the κ
avg, the minimum and maximum susceptibility values were 31 × 10
−5 SI and 108 × 10
−5 SI, respectively, and for the set of κ
non-avg, 14 × 10
−5 SI and 149 × 10
−5 SI, respectively.
As can be observed in the
Figure 2, spatial distributions of κ
sim-avg simulated on the basis of two sets of data, κ
non-avg and κ
avg, did not differ significantly. Subareas with high and low values of κ
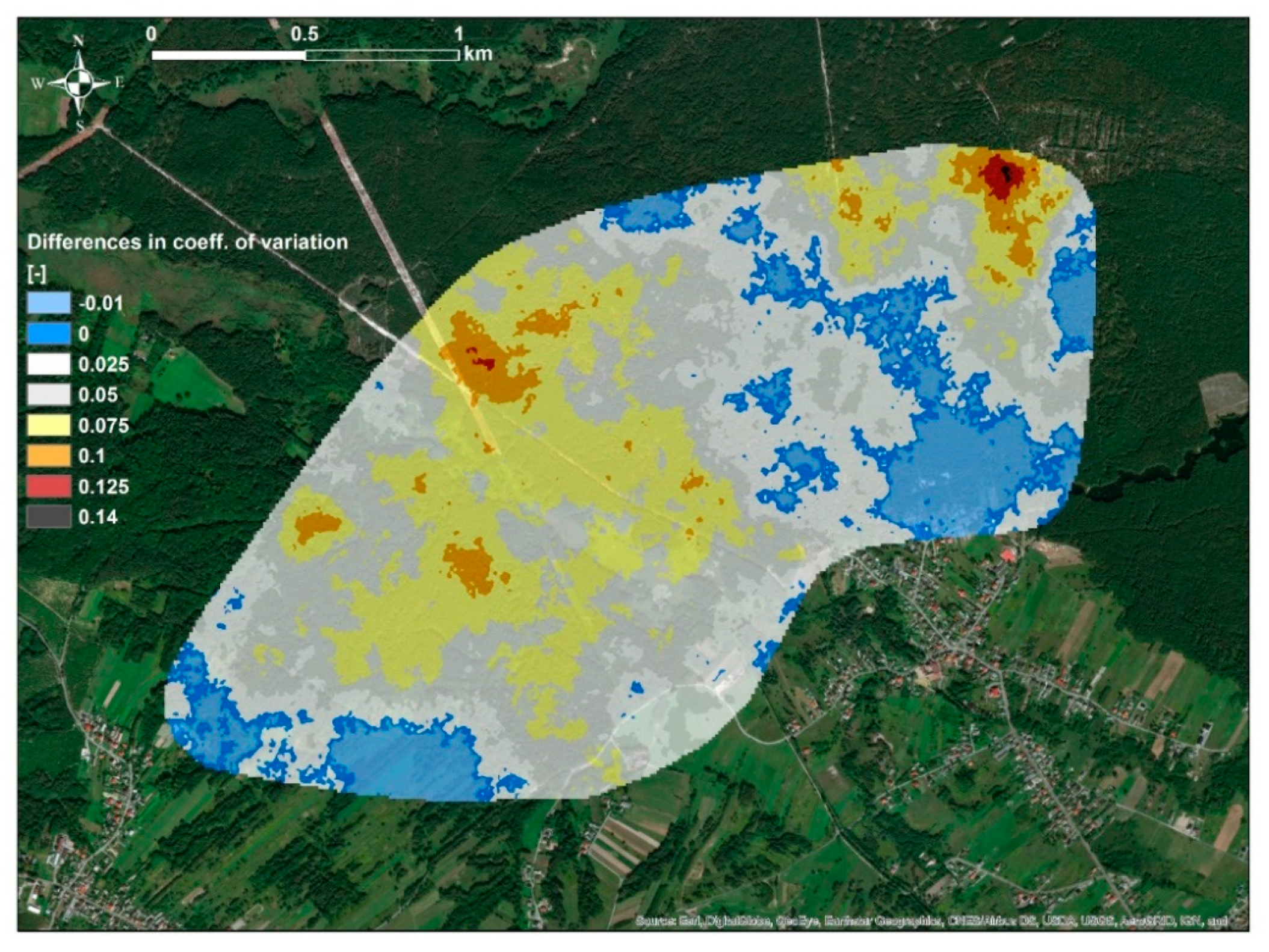
sim-avg were located in similar parts of the study area; in the Western and Eastern parts, respectively. Further analysis of the differences between these distributions, using differential map (
Figure 3) between κ
sim-avg simulated using κ
non-avg and κ
sim-avg simulated using κ
avg showed that maximum variation between these distributions was in the range of 10 × 10
−5 SI. This was rather low values in comparison to the range of measured κ
non-avg and κ
avg values, which was over 100 × 10
−5 SI. Based on this observation, it might be assumed that the differences between simulated distributions of κ
sim-avg, which were simulated using data sets κ
non-avg and κ
avg, could be attributed to the specific sampling methodology.
Application of SGS made it possible to calculate, at each grid point, numerous realizations of κ values that have similar histograms and variograms as the input data, i.e., κ
non-avg and κ
avg data sets. Using these realizations, it was possible to assess the variability of the simulated values by calculating κ
sim-avg, κ
sim-min, κ
sim-max, and κ
sim-std. Firstly, standard deviations of simulated values κ
sim-std were calculated, and subsequently, the coefficients of variations, i.e., κ
sim-std divided by κ
sim-avg. As can be observed in
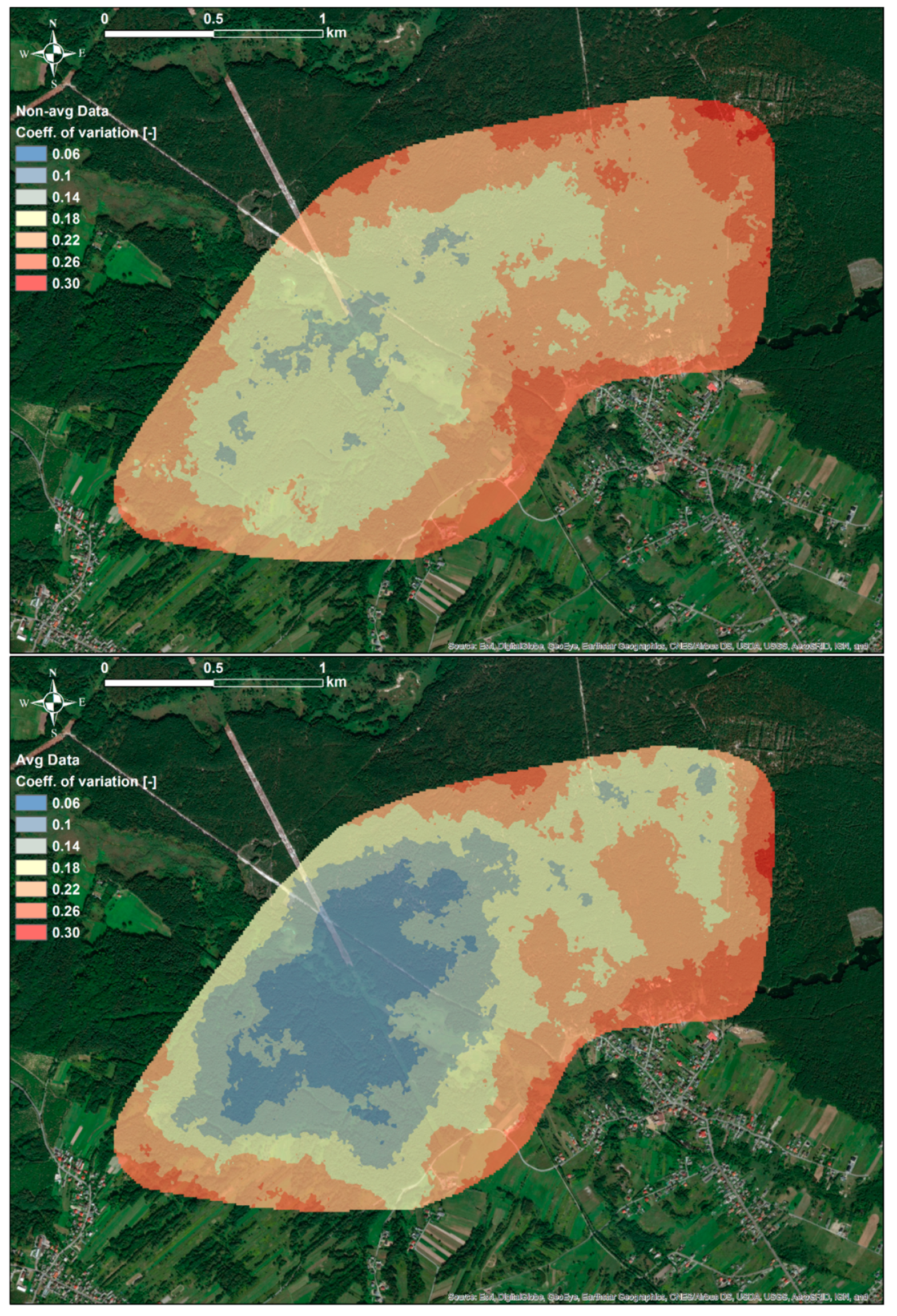
Figure 4 and
Figure 5, values of the coefficient of variation of κ were under 20% for the majority of the study area. It was also observed that slightly lower values of the coefficient of variation were observed for values simulated on the basis of the κ
avg data set. Such observations were due to the fact that the κ
avg data set was characterized by lower variability, which was reduced during the averaging of κ
non-avg values. As it was analyzed, distributions of measured susceptibility values, κ
non-avg, at sample points were characterized, in average, by standard deviation, and coefficient of variation equal to 18 × 10
−5 SI and 27%, respectively. Therefore, it was evident that the variability of simulated values of soil magnetic susceptibility at individual points was at a similar level to that of measured values.
In the next step, the characteristics of spatial correlations of κ were analyzed using measured κ
avg and κ
non-avg data sets, as well as simulated values of κ
sim-avg, κ
sim-min, κ
sim-max, and κ
sim-std. For this purpose, experimental variograms (
Figure 6) were calculated with 12 lags, and a lag distance equal to 200 m. Before the calculation of experimental variograms, input data were transformed using the normal-score transformation. After the experimental variograms of measured and simulated soil magnetic susceptibility were calculated, they were modeled using a spherical model with the nugget effect. The goal of this part of analysis was to investigate if the parameters of spatial correlations of simulated κ
sim-avg, κ
sim-min, κ
sim-max, and κ
sim-std were similar to those of measured κ
non-avg values.
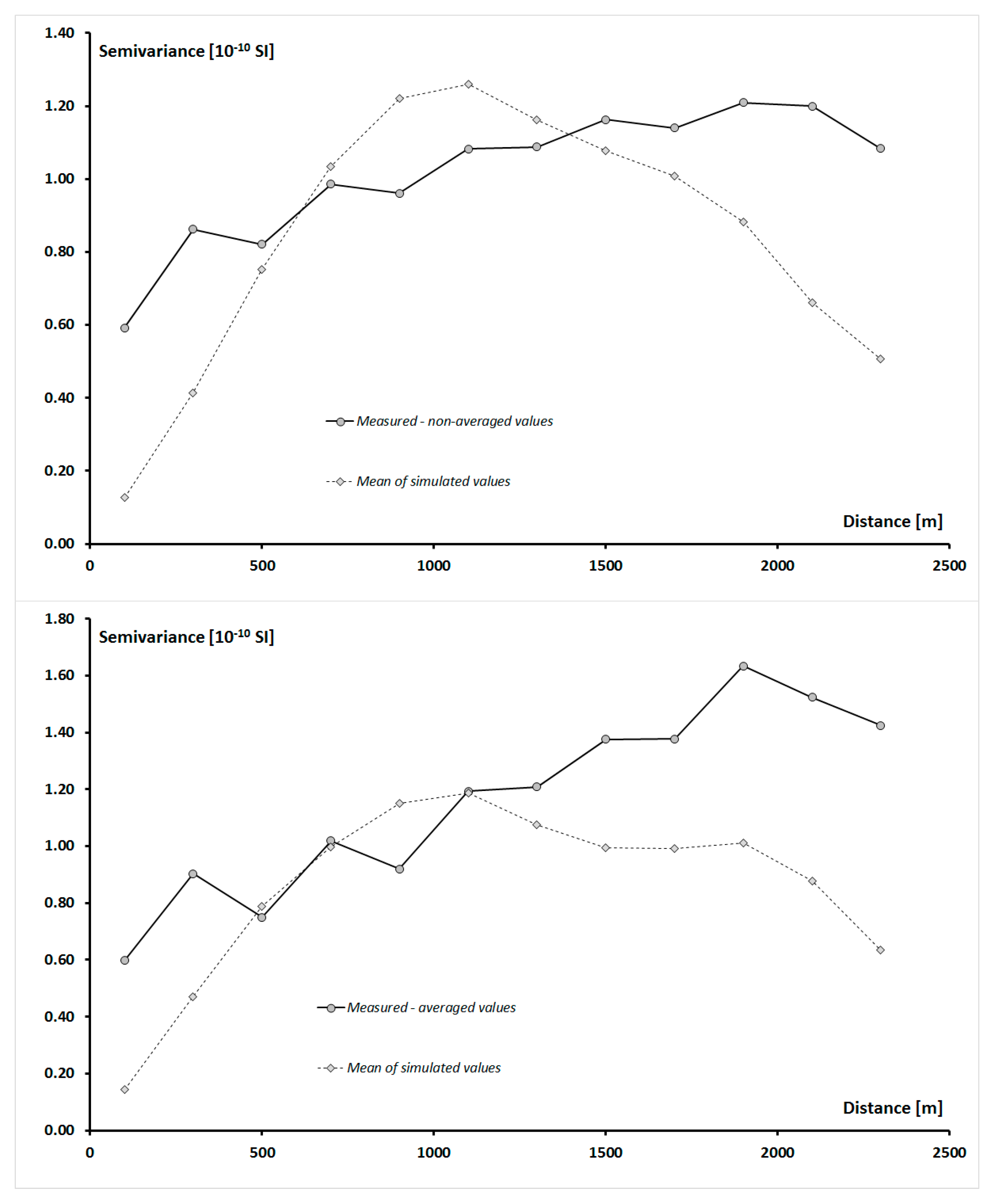
As can be observed in
Figure 6, experimental variograms of simulated κ
sim-avg had a similar shape to the variograms of measured κ
non-avg and κ
avg values, especially where they achieved sill. In order to investigate the similarities between spatial correlations of κ
sim-avg, κ
non-avg, and κ
avg more precisely, all variograms were modeled, and the parameters of these models were placed in
Table 2.
Comparison of the parameters of spherical models of measured and simulated values of soil magnetic susceptibility showed that the correlation range of κ
avg variogram was noticeable but not much longer than the correlation range of κ
non-avg variogram. As for the modeled nugget effect, it was lower for κ
avg variograms in comparison with κ
non-avg ones. Such observation could be explained by the fact that during the averaging of values of soil magnetic susceptibility, the impact of outliers was reduced. As can be observed in
Table 2, the sill of the spherical model of κ
avg was slightly higher as the sill of κ
non-avg. Referring these observed differences to the calculated experimental variograms, it can be noted that the differences in the sill values of spherical models of κ
non-avg and κ
avg concerned practically only distances above 1700 m. This distance was longer than the ranges of correlation of both κ
non-avg and κ
avg values. Differences in sill values could result mainly from a very large difference in the number of values of κ
non-avg and κ
avg, which were equal to 450 and 46, respectively. As a result, according to the Formula (1), on the basis of which the semivariance values were calculated, in the case of a variogram of κ
non-avg values, it was possible to find many more pairs of sample points. Due to the fact that the semivariance values of κ
non-avg were calculated on the basis of a much larger number of pairs of points than in the case κ
avg, the sill value of the spherical model of κ
non-avg was lower. However, it should be stated that the spatial characteristics of measured κ
non-avg and κ
avg values were rather similar, and the observed differences resulted from the sampling method.
In the next stage, the parameters of the variograms of measured κ
non-avg, κ
avg, and simulated κ
sim-avg values were compared. In each case, the variogram determined from the measured κ
non-avg or κ
avg values was used as the reference point. As can be noticed in
Table 2, the comparison was made separately for values simulated when the input data for SGS was set κ
non-avg and κ
avg.
As it was observed, values of nugget effect of variograms of simulated values κsim-avg were significantly lower than that of variograms of measured κnon-avg and κavg. Simultaneously, the comparison of the parameters of spherical models showed that variograms of simulated values, κsim-avg, were characterized by lower values of nugget effect than variograms of measured values of κnon-avg and κavg data. Such observations might suggest that SGS was quite effective in recreating the local variability of soil magnetic susceptibility, especially for distances shorter than a distance between sample points. Measured values of soil magnetic susceptibility were not available for such small distances, though they were available for simulated data sets, κsim-avg values were simulated for each simulation grid cell with a size of 10 m.
Sill values of variogram models of κ
sim-avg simulated using κ
non-avg and κ
avg data sets were comparable. It is important to underline here that a ratio of nugget effect to sill, which ranges from 0 to 1, is often recognized as a critical measure to define the spatial dependence of soil properties [
23,
24]. The closer this ratio is to zero, the stronger spatial correlations are observed. Precise assessment of this ratio is crucial to the quality of the results of geostatistical analyses in soil magnetometry. Usually, nugget effect is much more difficult to determine than sill. As it was observed, spherical models of simulated κ
sim-avg were characterized by a shorter range of correlation in comparison with variograms of measured κ
non-avg or κ
avg. As can be noticed in
Table 2, this difference was equal to about a few hundred meters. The explanation of such observations is related to the fact that values of simulated κ
sim-avg might be characterized by greater spatial variability at shorter distances. It is related to the fact that simulated data were much more numerous than the measured data and were available at all 60 thousand grid cells, so small-scale spatial variability of magnetic susceptibility was well reproduced.
4. Conclusions
The most pronounced differences between spatial distributions of the average soil magnetic susceptibility, simulated using non-averaged and averaged measurements, were found in places with a high and low level of magnetic susceptibility. In the parts of the study area where the lowest magnetic susceptibility was observed, values of soil magnetic susceptibility simulated using non-averaged data were higher than those simulated using averaged data. In the parts of the study area where soil magnetic susceptibility was the highest, the opposite situation was observed.
The spatial variation of soil magnetic susceptibility was distinctly higher in the case of simulations made on the basis of non-averaged measured data due to the considerable loss of information about the small-scale variability of soil magnetic susceptibility during data averaging. This resulted in the underestimation of the values of a nugget effect when using averaged data which, as a consequence, may lead to incorrect assessment of the level and extent of soil magnetic susceptibility distributions.
For longer distances, regardless of the measurement scheme used, reasonable reproducibility of the original semivariograms of soil magnetic susceptibility was achieved by simulated values. Variograms of the average of simulated values of soil magnetic susceptibility had similar sills and ranges of correlation to those of the variogram calculated from values measured in the study area. However, as before, the local variability of soil magnetic susceptibility was better reproduced when using non-averaged values than averaged ones, regardless of the fact whether the data is measured or simulated. This result confirms that it is favorable not to average magnetometric measurements for geostatistical analyses.
Thus, our study showed that the geostatistical Gaussian simulation provides deep insight into the variability and precision of soil magnetometry measurements at different distances, allowing for more efficient planning of soil field measurements.