Turbulent Aggregation and Deposition Mechanism of Respirable Dust Pollutants under Wet Dedusting using a Two-Fluid Model with the Population Balance Method
Abstract
:1. Introduction
2. The Numerical Model of Spray Dedusting
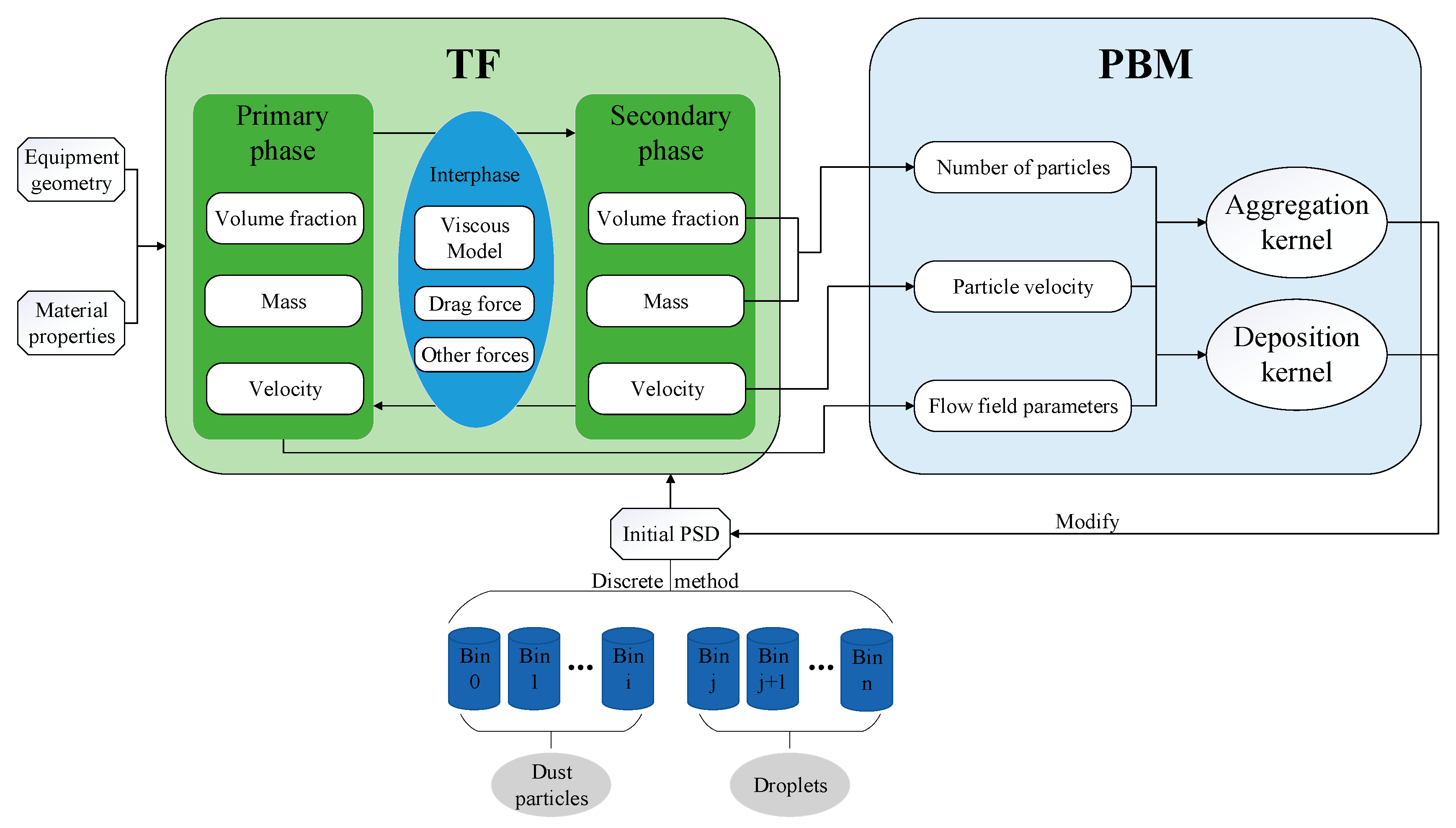
2.1. Two-Fluid (Euler–Euler) Model
2.2. Population Balance Model
2.3. Aggregation Kernel Model
2.4. Deposition Kernel Model
3. Model Validation
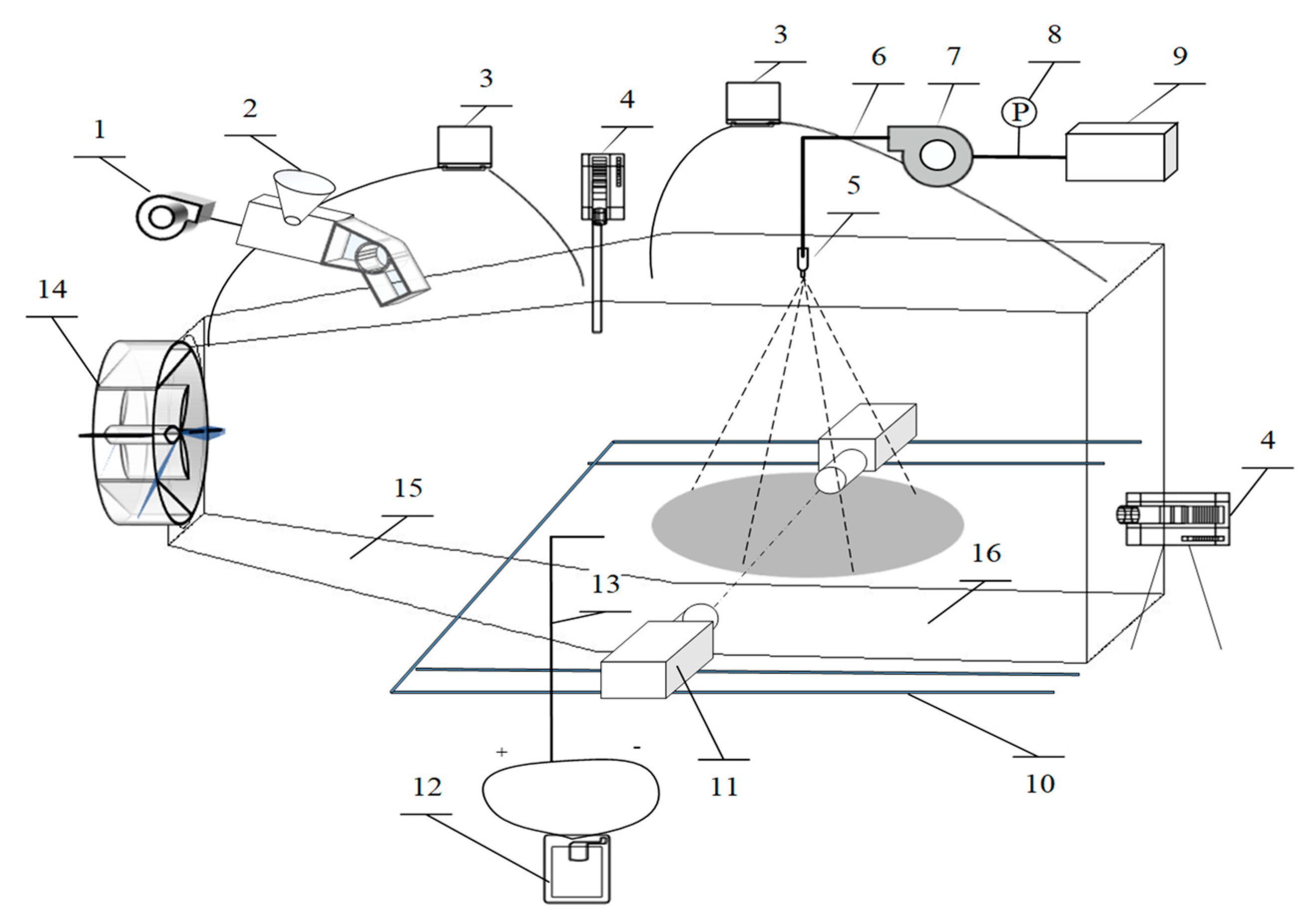
3.1. Experimental Set
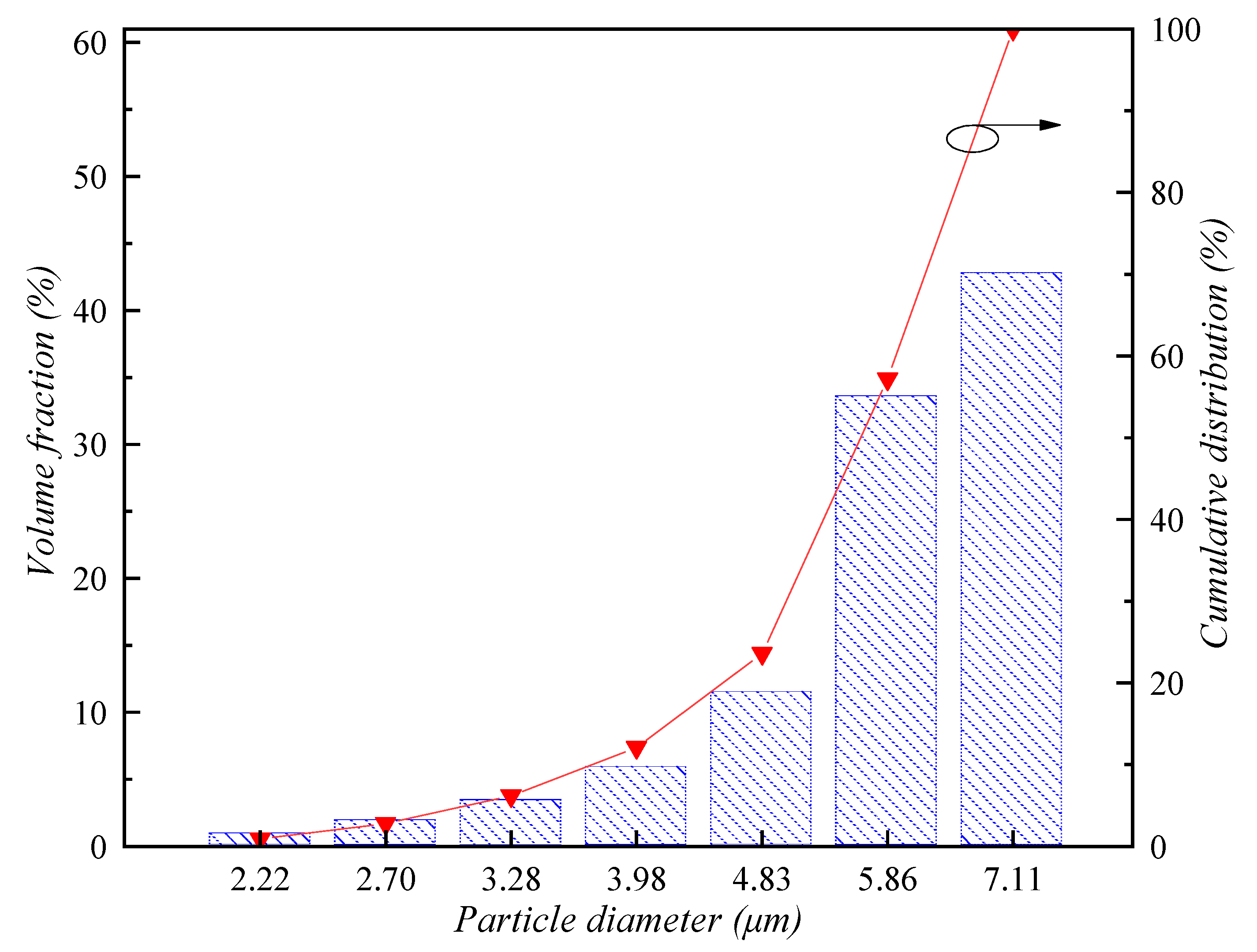
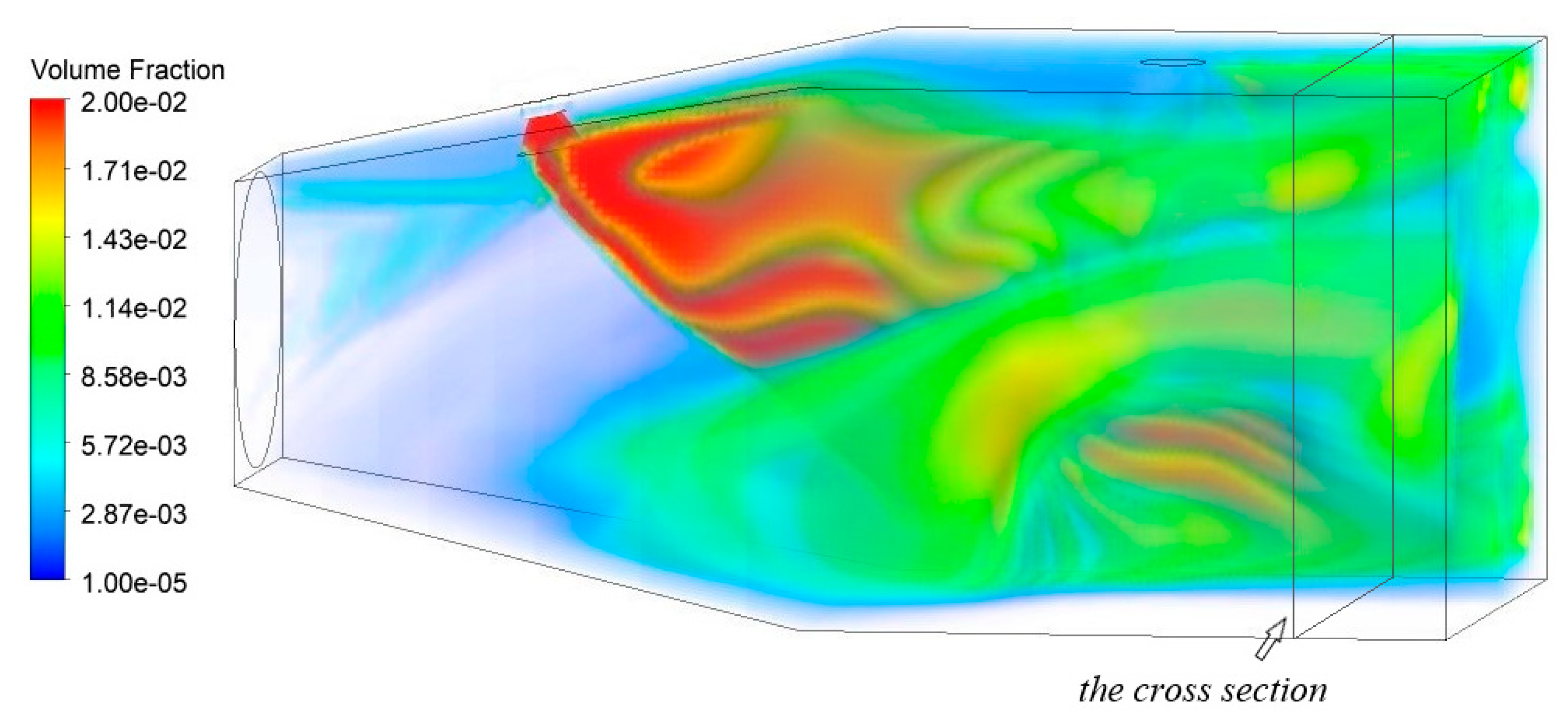
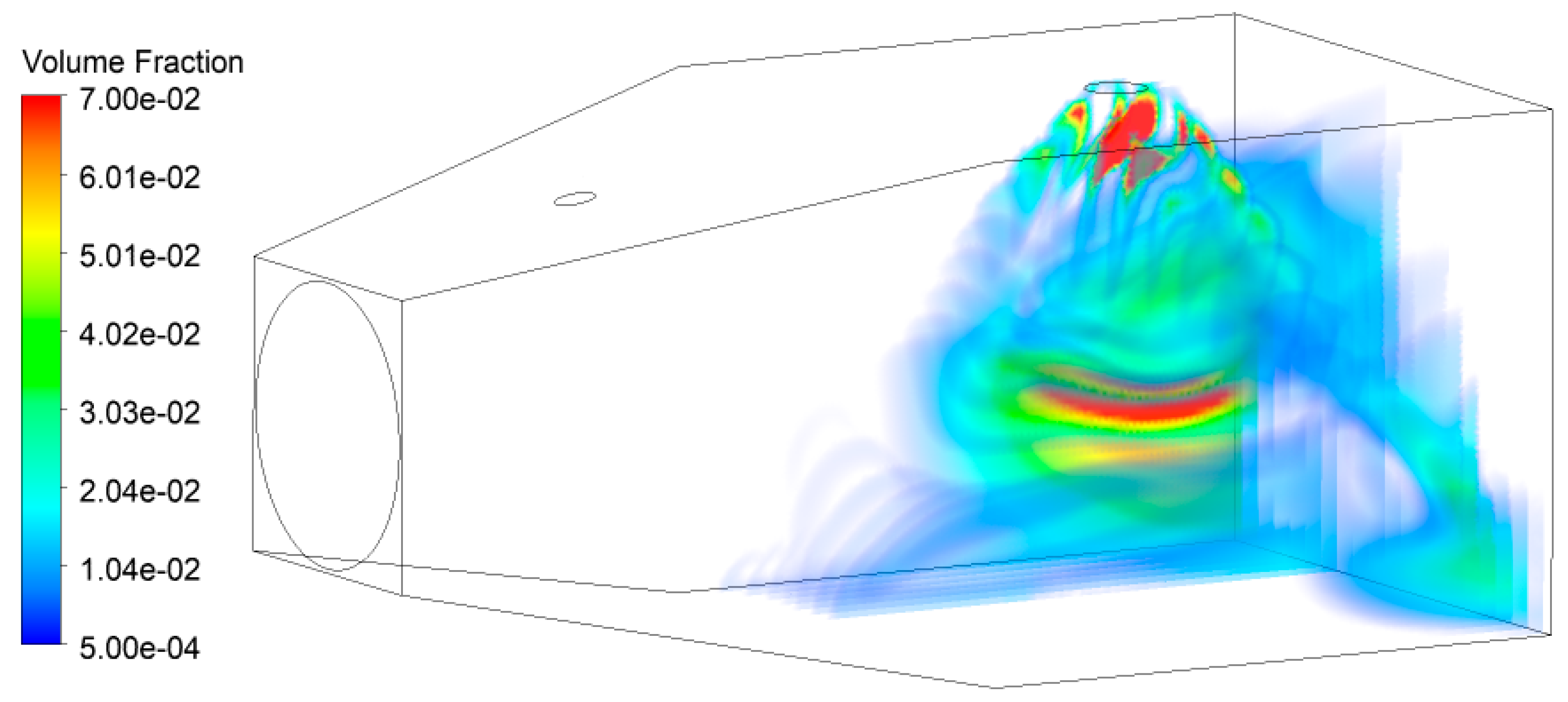
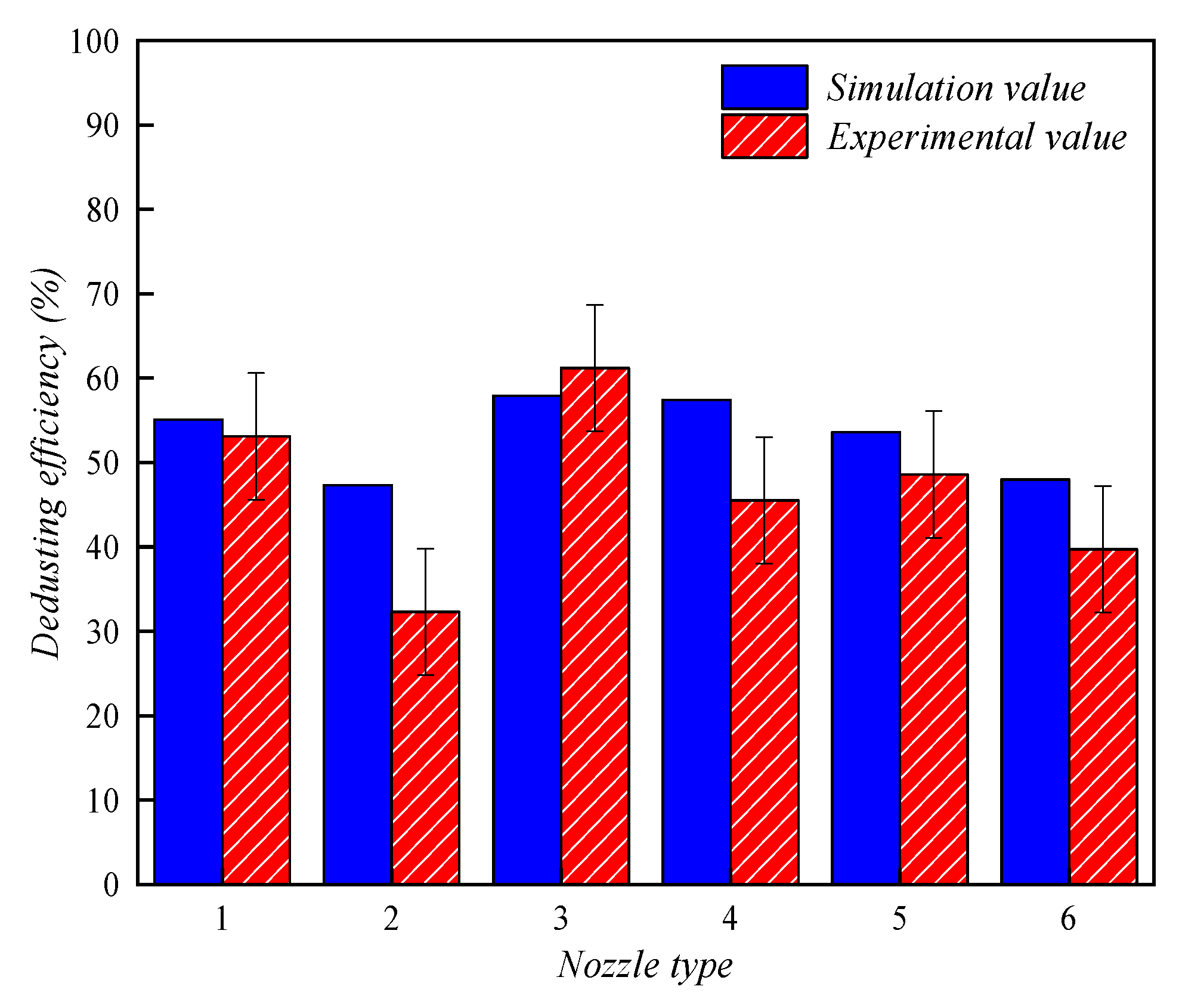
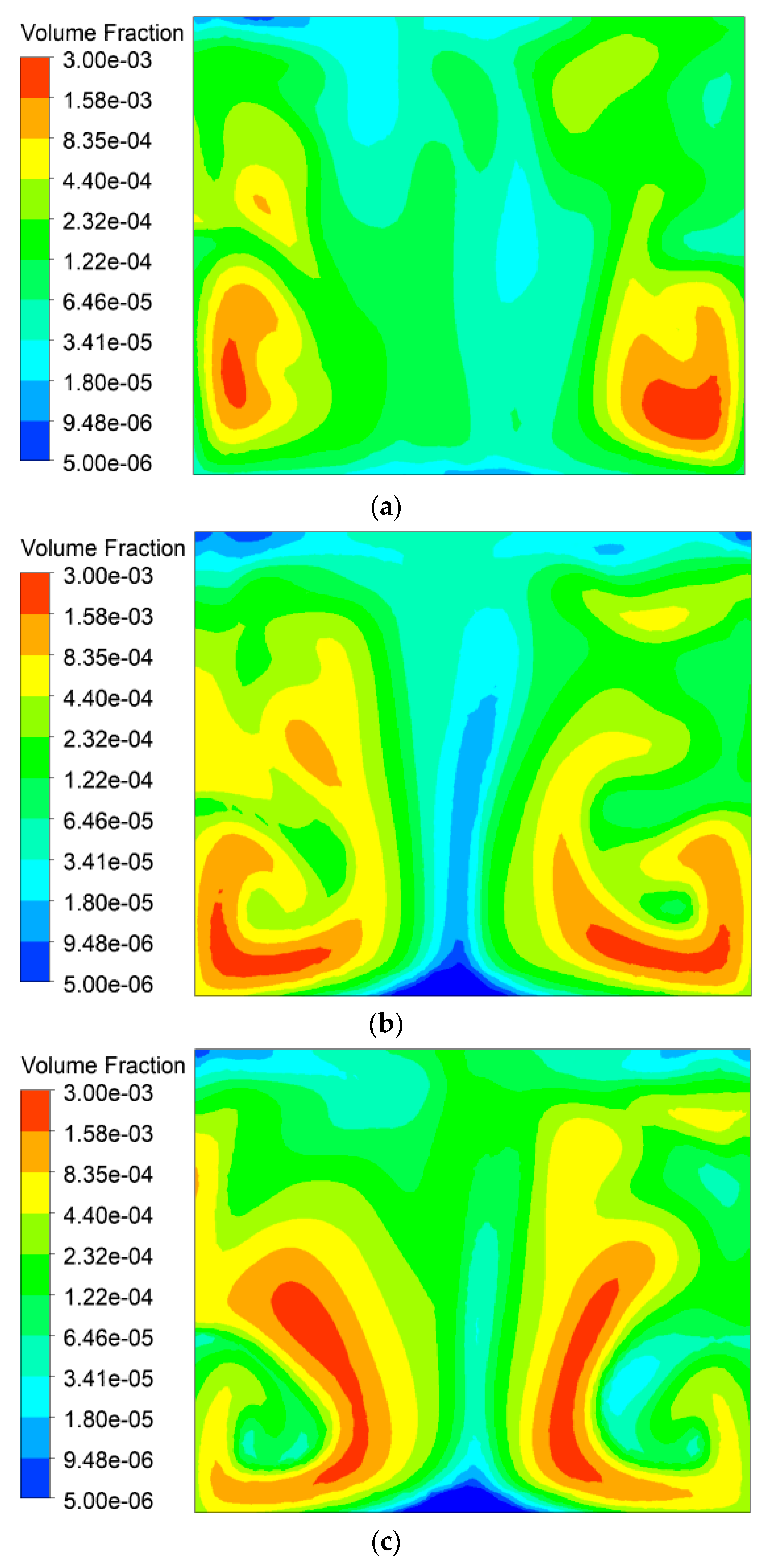
3.2. Results and Comparison
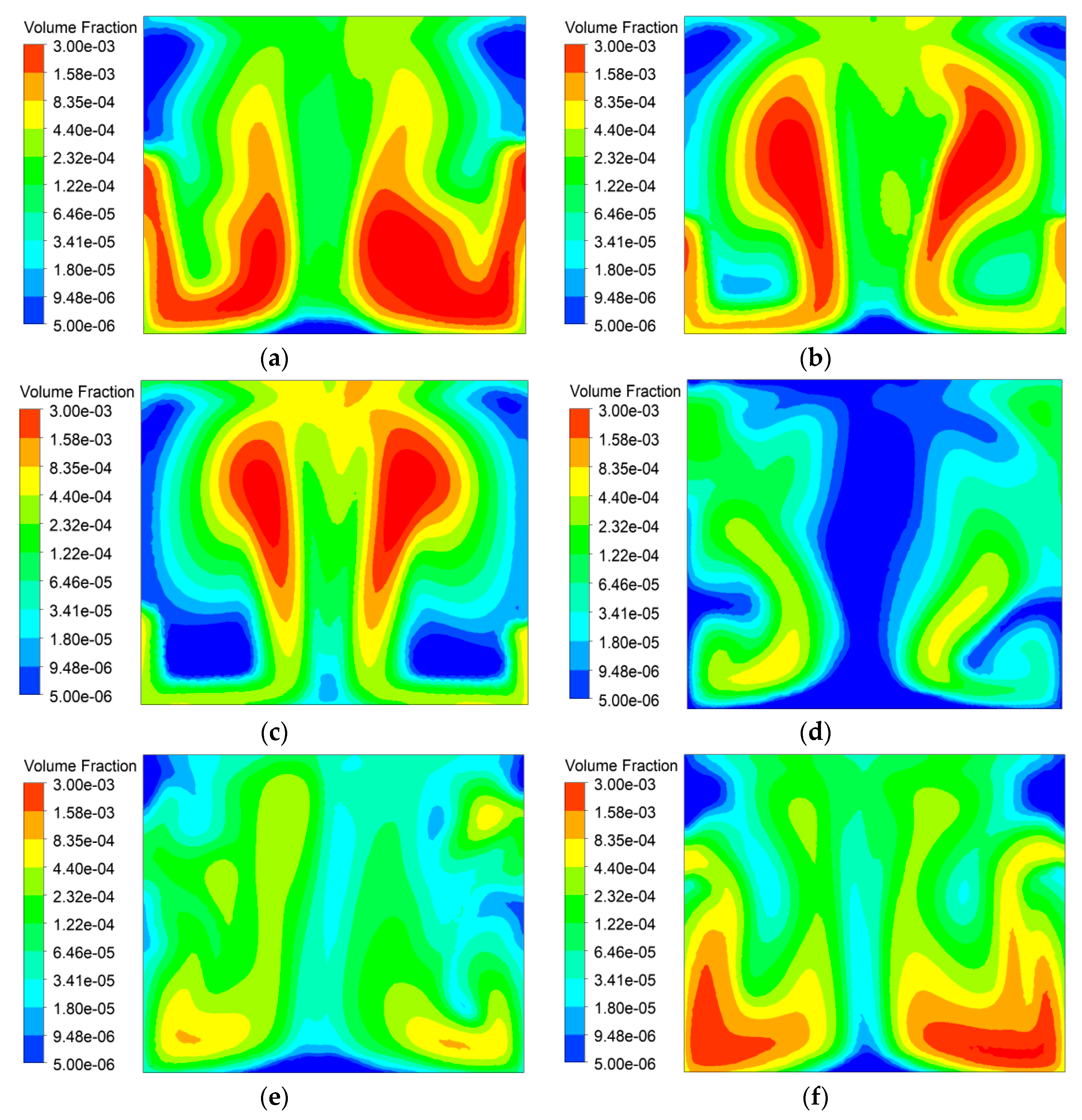
4. Discussion
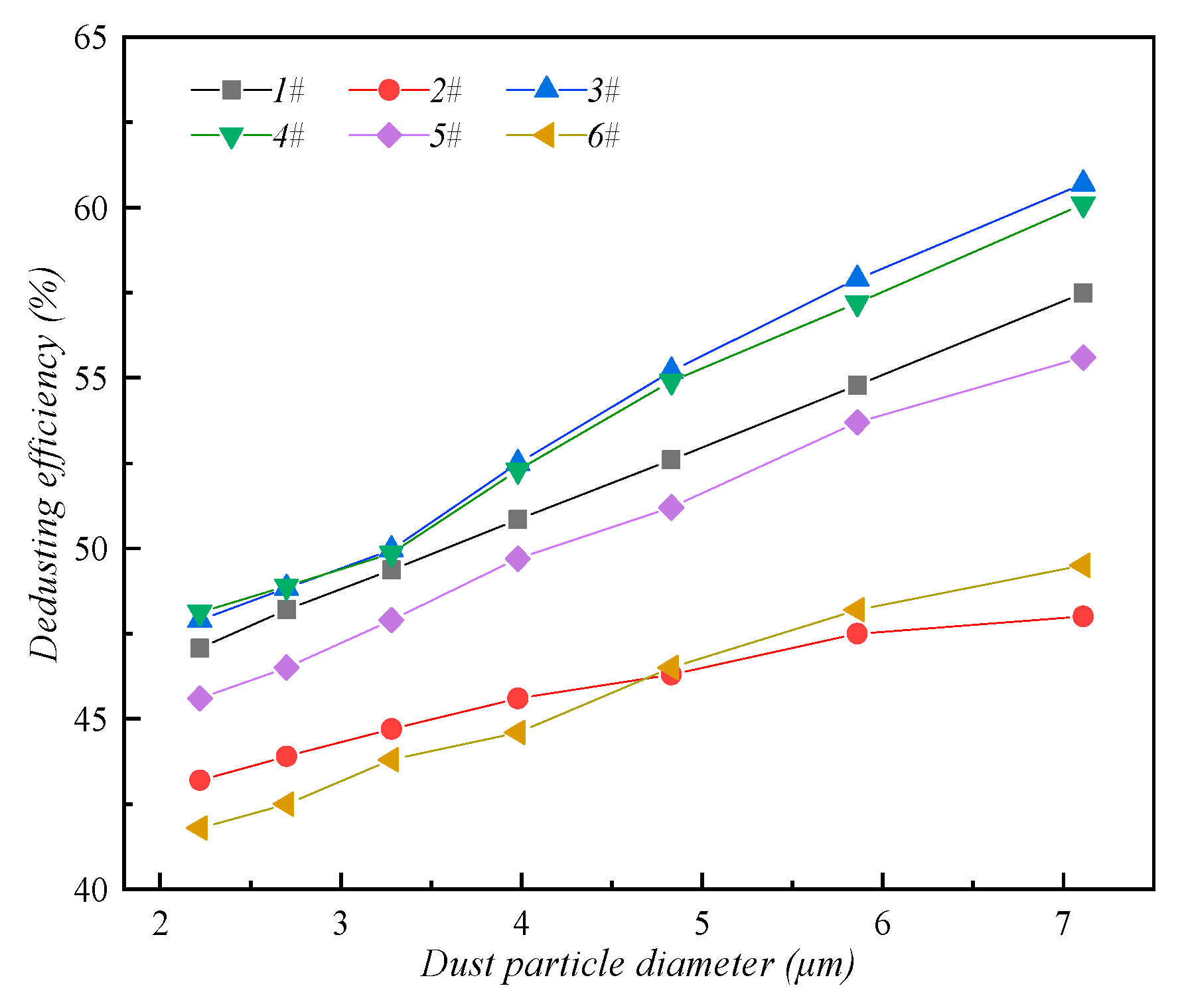
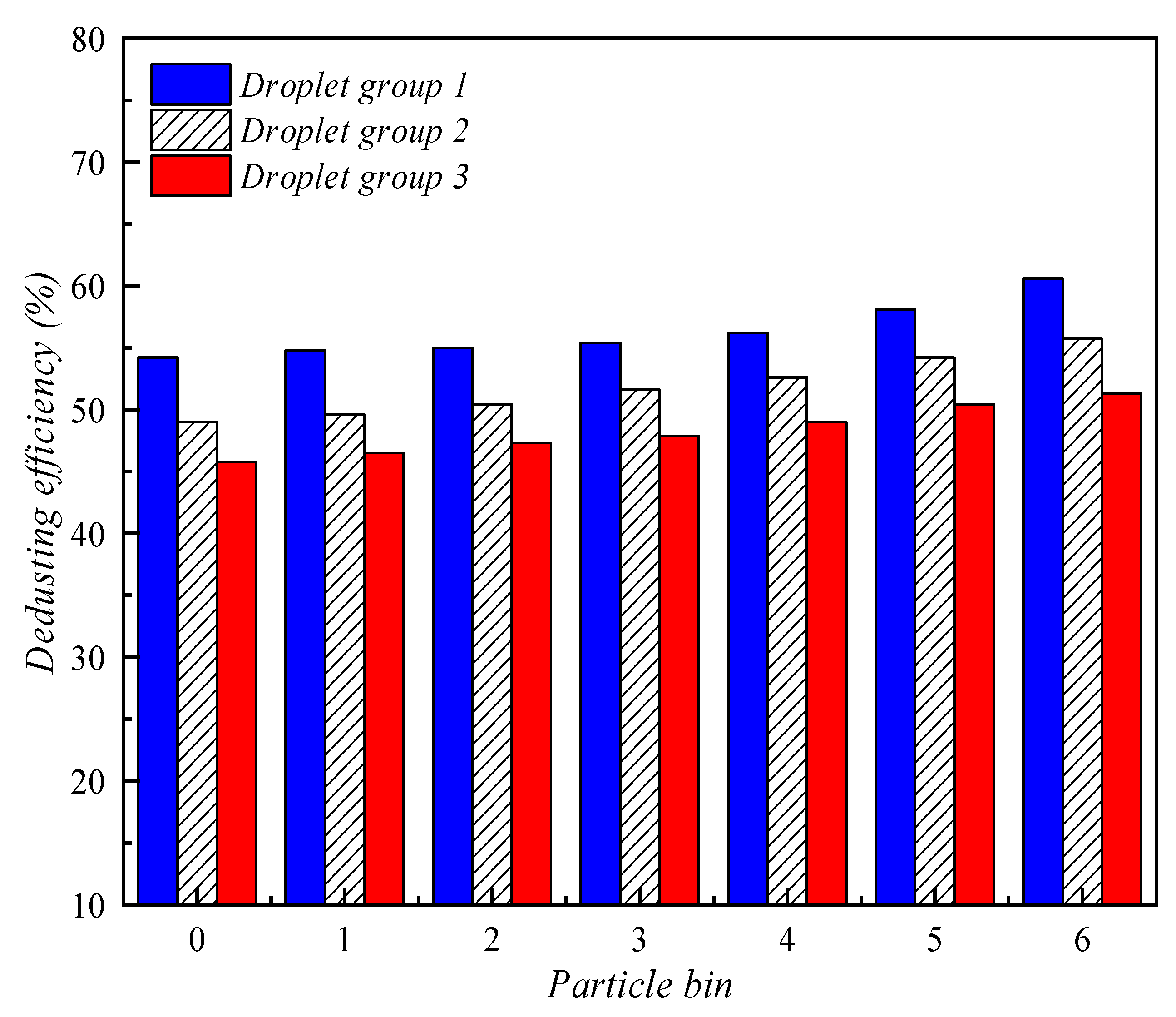
4.1. Effect of Droplet Size
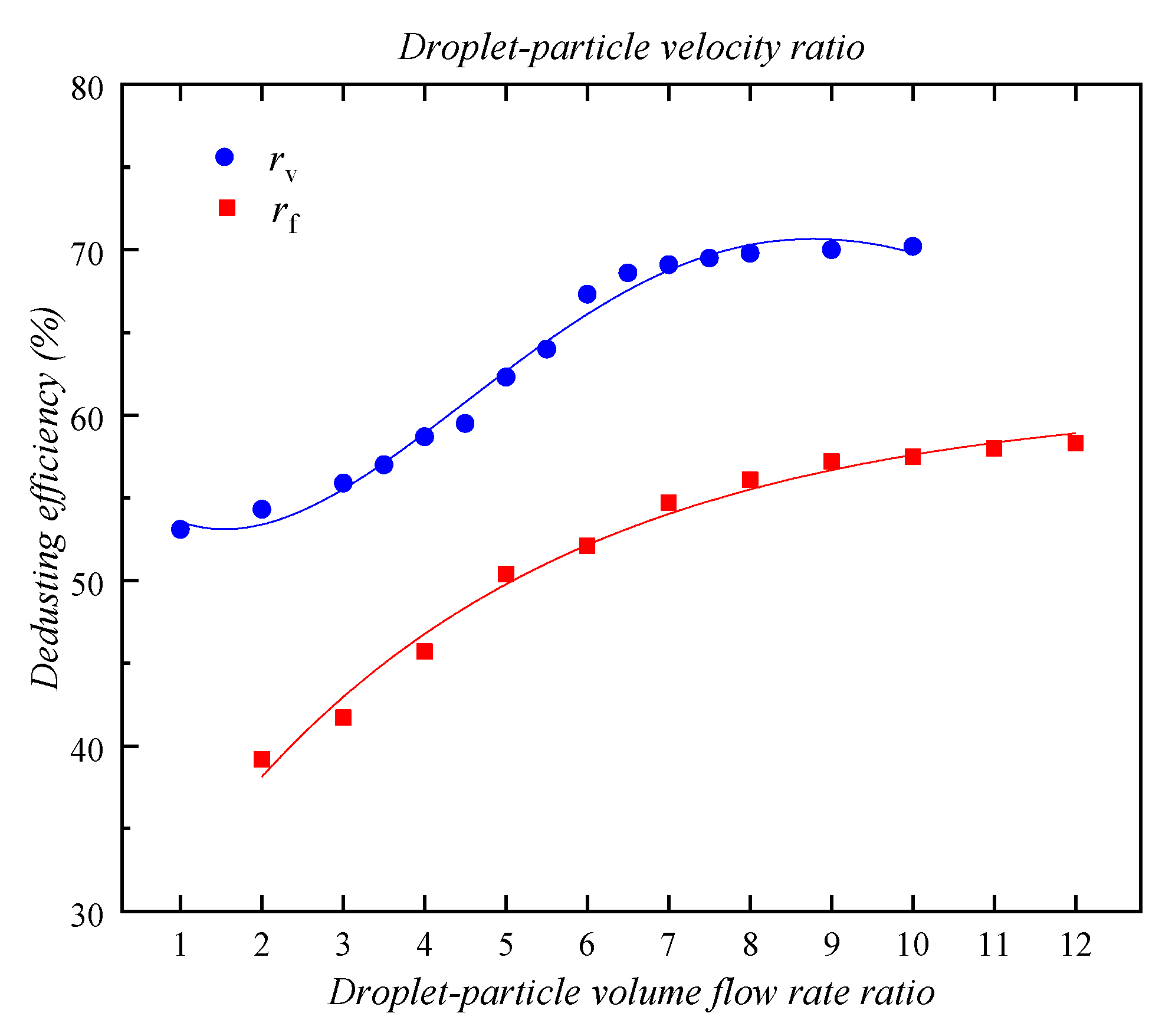
4.2. Effect of Droplet–Particle Volume Flow Rate Ratio
4.3. Effect of Droplet–Particle Velocity Ratio
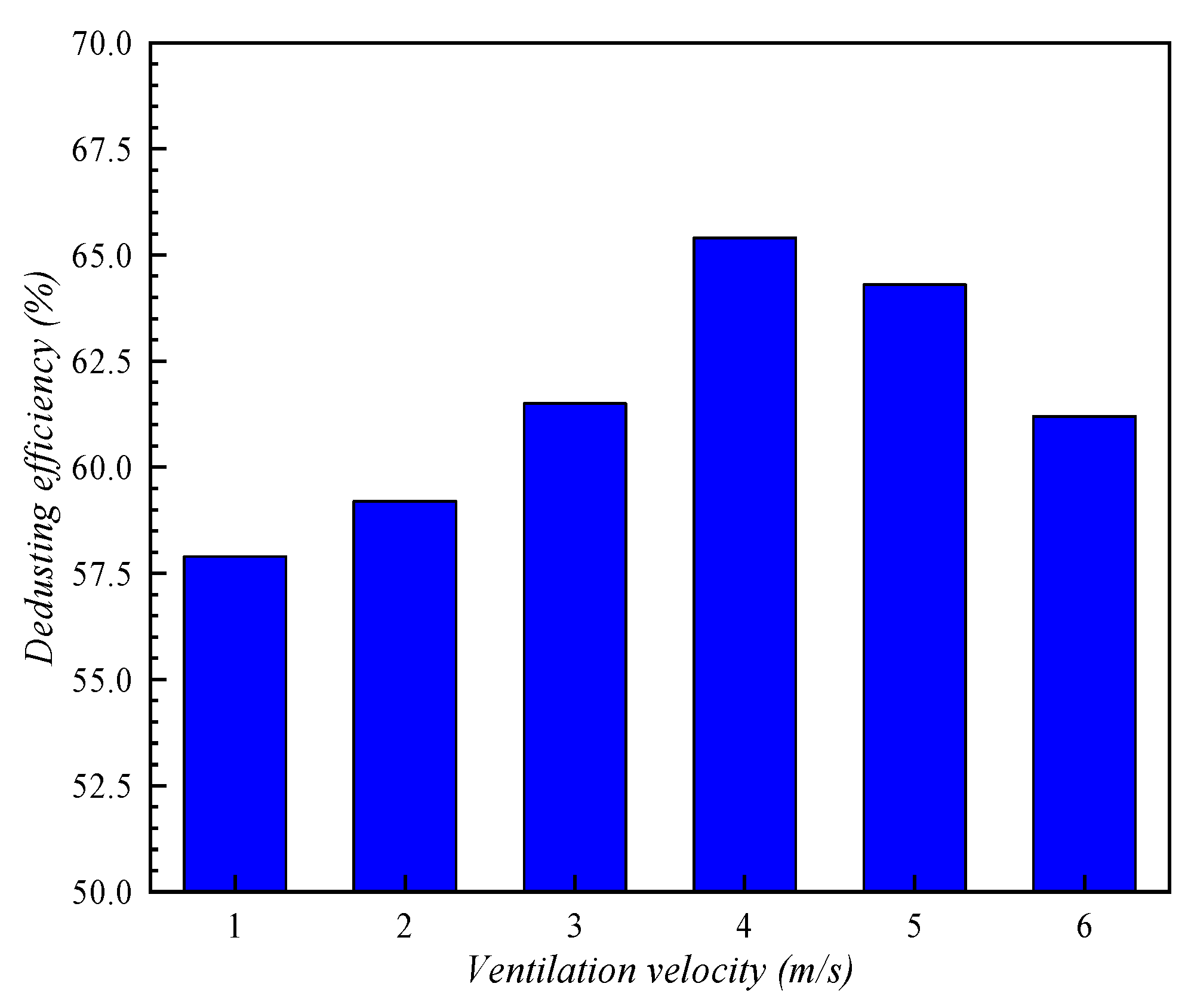
4.4. Effect of Ventilation Velocity
5. Conclusions
- The proposed mathematical model is well validated by the detailed experimental results for spray dedusting in the existing literature, and the numerical results of dedusting efficiency agree well with the experimental values. The turbulent aggregation kernel and the deposition kernel proposed in this paper are accurate enough to describe the wet dedusting process dominated by respirable dust capture and deposition.
- Key parameters analysis shows that the smaller the droplet diameter of the water mist formed by the atomizing device, the higher the capture efficiency of respirable dust. In other words, in practical application the dedusting efficiency of the respirable dust can be increased by ensuring that the water mist diameter is between 15 μm and 70 μm. The volume–flow rate ratio rf and velocity ratio of droplets to dust rv also have great influence on dedusting efficiency.
- When rf increases from 2 to 12, the dedusting efficiency increases from 39.2% to 54.7%. However, when this value continues to increase, the dedusting efficiency is not significantly improved. The fitting formula is given as ηf = 11.846ln(rf) + 30.375, R2 = 0.9745.
- When rv increases 10 times, the dedusting efficiency increases from 53.1% to 70.2%. Increasing the ratio clearly has little effect on dedusting efficiency. The fitting formula is ηv = −0.0819rv3 + 1.2102rv2 − 2.4142rv + 54.451, R2 = 0.9745.
- An optimized air distribution should be considered in the dedusting efficiency. Under the ventilation condition with 4 m/s inlet air, spray dedusting reaches the highest efficiency.
Author Contributions
Funding
Conflicts of Interest
References
- Nie, W.; Cheng, W.M. Regularity of Dust Distributing in Fully Mechanized Caving Face and Negative Pressure Spray Dust-Settling Technology. Appl. Mech. Mater. 2012, 246–247, 624–628. [Google Scholar] [CrossRef]
- Song, W.; Kan, J.; Wang, M.; Jiang, Z.A.; Tan, C. Study on Application of Gas-Water Spraying Dust Suppression System in Coal Mining Machines. Ind. Saf. Environ. Prot. 2015, 41, 60–62. [Google Scholar]
- Jiang, H.; Du, C.; Dong, J. Investigation of rock cutting dust formation and suppression using water jets during mining. Powder Technol. 2017, 307, 99–108. [Google Scholar] [CrossRef]
- Faschingleitner, J.; HöFlinger, W. Evaluation of primary and secondary fugitive dust suppression methods using enclosed water spraying systems at bulk solids handling. Adv. Powder Technol. 2011, 22, 236–244. [Google Scholar] [CrossRef]
- Wang, S.; Wang, Z.R. Numerical Analysis of Dedusting Effects of Harmful Dust in Confined Workplace. Appl. Mech. Mater. 2014, 556–562, 4103–4108. [Google Scholar] [CrossRef]
- Liang, A.C.; Jin, X.H.; Guo, S.J. Experimental study on Influencing Factors of combined dust removal effect of eddy current dust control system and wet cyclone dust removal system. Min. Saf. Environ. Prot. 2009, 36, 4–7. [Google Scholar]
- Nie, W.; Cheng, W.M.; Zhou, G.; Xie, J.; Cui, X.F. Experimental study on atomized particle size as affected by airflow disturbance at the heading face. J. China Univ. Min. Technol. 2012, 41, 378–383. [Google Scholar]
- Wang, P.F.; Liu, R.H.; Tang, M.; Zhang, W.; Gui, Z. Experimental study on Influence Factors of spray dustfall in coal mine. J. Saf. Environ. 2015, 15, 62–67. [Google Scholar]
- Nie, W.; Liu, Y.; Wang, H.; Wei, W.; Peng, H.; Cai, P.; Hua, Y.; Jin, H. The development and testing of a novel external-spraying injection dedusting device for the heading machine in a fully-mechanized excavation face. Process Saf. Environ. Prot. 2017, 109, 716–731. [Google Scholar] [CrossRef]
- Dubrovsky, V.V.; Podvysotsky, A.M.; Shraiber, A.A. Particle interaction in three-phase polydisperse flows. Int. J. Multiph. Flow 1992, 18, 337–352. [Google Scholar] [CrossRef]
- Mitra, S.; Doroodchi, E.; Pareek, V.; Joshi, J.B.; Evans, G.M. Collision behaviour of a smaller particle into a larger stationary droplet. Adv. Powder Technol. 2015, 26, 280–295. [Google Scholar] [CrossRef]
- Xie, Y.; Jiang, X. Dust removal technology with negative pressure and its application. J. China Univ. Min. Technol. 2003, 32, 567–570. [Google Scholar]
- Cousin, J.; Nuglisch, H.J. Modeling of Internal Flow in High pressure Swirl Injectors; Technical Paper; SAE: Warrendale, PA, USA, 2001. [Google Scholar]
- Chakraborty, S.N. Combating coal mine fire-application of high pressure water jet technology adopted by Goma Engineering Pvt. Ltd. J. Mines Met. Fuels 2009, 57, 398. [Google Scholar]
- Huang, J. Water Jet Dust Removal Technology; Xi’an Jiaotong University Press: Xi’an, China, 1993; pp. 108–125. [Google Scholar]
- Zhang, Z.; Jiang, Z.A.; Yan, P. Numerical simulation and application of spray and Dustfall in highway tunnel. Mod. Min. 2016, 1, 208–211. [Google Scholar]
- Wang, H.; Wang, C.; Wang, D. The influence of forced ventilation airflow on water spray for dust suppression on heading face in underground coal mine. Powder Technol. 2017, 320, 498–510. [Google Scholar] [CrossRef]
- Zhou, G.; Yin, W.J.; Feng, B. Simulation Analysis and Engineering Application of Dust-droplet Distribution Characteristics of Dust Source in Fully Mechanized Mining Face. J. China Coal Soc. 2018, 43, 173–183. [Google Scholar]
- Yu, H.; Cheng, W.; Peng, H.; Xie, Y. An investigation of the nozzle’s atomization dust suppression rules in a fully-mechanized excavation face based on the airflow-droplet-dust three-phase coupling model. Adv. Powder Technol. 2018, 29, 941–956. [Google Scholar] [CrossRef]
- Hong, K.; Liu, Z.; Wang, X.; Zhu, Z. Simulation of dust migration at working faces during drill-blasting construction of underground hydropower houses. J. Hydroelectr. Eng. 2016, 35, 124–130. [Google Scholar]
- Ramkrishna, D. Population Balances: Theory and Applications to Particulate Systems in Engineering; Elsevier: Amsterdam, The Netherlands, 2000. [Google Scholar]
- Hounslow, M.J.; Ryall, R.L.; Marshall, V.R. A Discretized Population Balance for Nucleation, Growth, and Aggregation. AIChE J. 1988, 34, 1821–1832. [Google Scholar] [CrossRef]
- Litster, J.D.; Smit, D.J.; Hounslow, M.J. Adjustable Discretization Population Balance for Growth and Aggregation. AIChE J. 1995, 41, 591–603. [Google Scholar] [CrossRef]
- Pietsch, W. Population Balances Theory and Applications to Particulate Systems Engineering. Chem. Eng. Prog. 2002, 98, 81. [Google Scholar]
- Corner, J.; Pendlebury, E.D. The coagulation and deposition of a stirred aerosol. Proc. Phys. Soc. Sect. B 1951, 64, 645. [Google Scholar] [CrossRef]
- Crump, J.G.; Seinfeld, J.H. Turbulent deposition and gravitational sedimentation of an aerosol in a vessel of arbitrary shape. J. Aerosol Sci. 1981, 12, 405–415. [Google Scholar] [CrossRef]
- Park, S.H.; Kim, H.O.; Han, Y.T.; Kwon, S.B.; Lee, K.W. Wall loss rate of polydispersed aerosols. Aerosol Sci. Technol. 2001, 35, 710–717. [Google Scholar] [CrossRef]
- Jung, C.H.; Lee, K.W. Filtration of Fine Particles by Multiple Liquid Droplet and Gas Bubble Systems. Aerosol Sci. Technol. 1998, 29, 389–401. [Google Scholar] [CrossRef]
- Barrasso, D.; Walia, S.; Ramachandran, R. Multi-component population balance modeling of continuous granulation processes: A parametric study and comparison with experimental trends. Powder Technol. 2013, 241, 85–97. [Google Scholar] [CrossRef]
- Akbari, V.; Borhani, T.N.; Shamiri, A.; Hamid, M.K. A CFD–PBM coupled model of hydrodynamics and mixing/segregation in an industrial gas-phase polymerization reactor. Chem. Eng. Res. Des. 2015, 96, 103–120. [Google Scholar] [CrossRef]
- Marchisio, D.L.; Vigil, R.D.; Fox, R.O. Implementation of the quadrature method of moments in CFD codes for aggregation–breakage problems. Chem. Eng. Sci. 2003, 58, 3337–3351. [Google Scholar] [CrossRef]
- Chen, A.; Wang, Z.; Sun, Z. Flotation bubble coalescence simulation based on phase group equilibrium model. J. Chem. Eng. 2015, 66, 4780–4787. [Google Scholar]
- Luo, H.; Svendsen, H.F. Theoretical model for drop and bubble breakup in turbulent dispersions. AIChE J. 1996, 42, 1225–1233. [Google Scholar] [CrossRef]
- Nie, W.; Liu, Y.H.; Ma, X.; Hu, X.M.; Peng, H.T.; Zhang, M.G. Particle size experiment of dust removal by high pressure spray between air flow disturbance supports. J. China Univ. Min. Technol. 2016, 45, 670–676. [Google Scholar]
- Smoluchowski, M. Versuch einer mathematischen Theorie der Koagulations Kinetis kolloider Lösungen. Z. Physik. Chem. 1917, 92, 129–168. [Google Scholar]
- Williams, M.M.R.; Loyalka, S.K. Aerosol Science Theory and Practice; Pergamon Press: New York, NY, USA, 1991. [Google Scholar]
- Saffman, P.G.; Turner, J.S. On the Collision of Droplets in Turbulent Clouds. J. Fluid Mech. 1956, 1, 16–30. [Google Scholar] [CrossRef]
- Alipchenkov, V.M.; Zaichik, L.I. Particle collision rate in turbulent flow. Fluid Dyn. 2001, 36, 608–618. [Google Scholar] [CrossRef]
- Zaichik, L.I.; Alipchenkov, V.M. Acceleration of heavy particles in isotropic turbulence. Int. J. Multiph. Flow 2008, 34, 865–868. [Google Scholar] [CrossRef]
- Wang, T.; Xia, Z.; Chen, C. Coupled CFD-PBM simulation of bubble size distribution in a 2D gas-solid bubbling fluidized bed with a bubble coalescence and breakup model. Chem. Eng. Sci. 2019, 202, 208–221. [Google Scholar] [CrossRef]
- Williams, Y.O.; Roas-Escalona, N.; Rodríguez-Lopez, G.; Villa-Torrealba, A.; Toro-Mendoza, J. Modeling droplet coalescence kinetics in microfluidic devices using population balances. Chem. Eng. Sci. 2019, 201, 475–483. [Google Scholar] [CrossRef]
- Wang, T.; Wang, J.; Yong, J. Theoretical prediction of flow regime transition in bubble columns by the population balance model. Chem. Eng. Sci. 2005, 60, 6199–6209. [Google Scholar] [CrossRef]
- Franklin, C.N.; Vaillancourt, P.A.; Yau, M.K.; Bartello, P. Collision rates of cloud droplets in turbulent flow. J. Atmos. Sci. 2005, 62, 2451–2466. [Google Scholar] [CrossRef]
- Abrahamson, J. Collision rates of small particles in a vigorously turbulent fluid. Chem. Eng. Sci. 1975, 30, 1371–1379. [Google Scholar] [CrossRef]
- Higashitani, K.; Yamauchi, K.; Matsuno, Y.; Hosokawa, G. Turbulent coagulation of particles dispersed in a viscous fluid. J. Chem. Eng. Jpn. 1983, 16, 299–304. [Google Scholar] [CrossRef]
- Park, S.H.; Lee, K.W. Lognormal size distribution theory for deposition of polydisperse aerosol particles. Nucl. Sci. Eng. 2000, 135, 288–295. [Google Scholar] [CrossRef]
- Schlichting, H.; Gersten, K. Boundary-Layer Theory; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Allen, M.D.; Raabe, O.G. Slip correction measurements of spherical solid aerosol particles in an improved Millikan apparatus. Aerosol Sci. Technol. 1985, 4, 269–286. [Google Scholar] [CrossRef]
- Zhou, G. Study on Theory and Technology of Spray Dust Reduction in Fully Mechanized Top Coal Caving Face; Shandong University of Science and Technology: Qingdao, China, 2009. [Google Scholar]
- Hirsch, C. Numerical Computation of Internal and External Flows, Volume 1 Fundamentals of Numerical Discretization. Int. J. Heat Fluid Flow 2007, 10, 371. [Google Scholar]
| Kernel | References | Expression | Comments |
|---|---|---|---|
| Free molecular aggregation | Smoluchowski (1917) [35] | Very small particles (up to 1 μm) aggregate because of collisions due to Brownian motions; the frequency of collision is size-dependent | |
| Coulomb aggregation | Williams and Loyalka (1991) [36] | The precondition is that the particle itself is already charged, no matter it is the same charge or different charge | |
| Turbulence aggregation | Saffman and Turner (1956) [37] Zaichik and Alipchenkov (2001,2008) [38,39] | For the viscous subrange: , for the inertial subrange: | In the turbulent flow field, aggregation can occur by two mechanisms: viscous subrange mechanism and inertial subrange mechanism |
| Bubble aggregation | Wang et al. (2019) [40] | Aggregation will occur during a collision of two bubbles provided that the contact time exceeds the aggregation time required for drainage of the liquid film between them to a critical rupture thickness | |
| Droplet aggregation | Williams et al. (2019) [41] | Droplet centers are assumed to move along streamlines, and aggregation occurs when the distance between the droplets is less than the sum of their radii |
| Nozzles | D10 (μm) | D50 (μm) | D90 (μm) | Q (L/min) | Dedusting Efficiency (%) |
|---|---|---|---|---|---|
| 1 | 34.93 | 70.62 | 117.67 | 6.46 | 53.1 |
| 2 | 41.10 | 70.62 | 109.22 | 7.92 | 32.3 |
| 3 | 38.57 | 74.67 | 122.81 | 7.36 | 61.2 |
| 4 | 32.94 | 65.15 | 112.39 | 8.15 | 45.5 |
| 5 | 37.01 | 69.03 | 118.36 | 5.63 | 48.6 |
| 6 | 40.03 | 75.14 | 123.85 | 4.30 | 39.7 |
| Droplet-Particle Volume Flow Rate Ratio | Dedusting Efficiency (%) | Droplet-Particle Volume Flow Rate Ratio | Dedusting Efficiency (%) |
|---|---|---|---|
| 2 | 39.2 | 8 | 56.1 |
| 3 | 41.7 | 9 | 57.2 |
| 4 | 45.7 | 10 | 57.5 |
| 5 | 50.4 | 11 | 58.0 |
| 6 | 52.1 | 12 | 58.3 |
| 7 | 54.7 | — | — |
| Droplet-Particle Velocity Ratio | Dedusting Efficiency (%) | Droplet-Particle Velocity Ratio | Dedusting Efficiency (%) |
|---|---|---|---|
| 1 | 53.1 | 6 | 67.3 |
| 2 | 54.3 | 6.5 | 68.6 |
| 3 | 55.9 | 7 | 69.1 |
| 3.5 | 57.0 | 7.5 | 69.5 |
| 4 | 58.7 | 8 | 69.8 |
| 4.5 | 59.5 | 9 | 70.0 |
| 5 | 62.3 | 10 | 70.2 |
| 5.5 | 64.0 | — | — |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, P.; Shen, S.; Zhou, L.; Liu, D. Turbulent Aggregation and Deposition Mechanism of Respirable Dust Pollutants under Wet Dedusting using a Two-Fluid Model with the Population Balance Method. Int. J. Environ. Res. Public Health 2019, 16, 3359. https://doi.org/10.3390/ijerph16183359
Wang P, Shen S, Zhou L, Liu D. Turbulent Aggregation and Deposition Mechanism of Respirable Dust Pollutants under Wet Dedusting using a Two-Fluid Model with the Population Balance Method. International Journal of Environmental Research and Public Health. 2019; 16(18):3359. https://doi.org/10.3390/ijerph16183359
Chicago/Turabian StyleWang, Pei, Shuai Shen, Ling Zhou, and Deyou Liu. 2019. "Turbulent Aggregation and Deposition Mechanism of Respirable Dust Pollutants under Wet Dedusting using a Two-Fluid Model with the Population Balance Method" International Journal of Environmental Research and Public Health 16, no. 18: 3359. https://doi.org/10.3390/ijerph16183359
APA StyleWang, P., Shen, S., Zhou, L., & Liu, D. (2019). Turbulent Aggregation and Deposition Mechanism of Respirable Dust Pollutants under Wet Dedusting using a Two-Fluid Model with the Population Balance Method. International Journal of Environmental Research and Public Health, 16(18), 3359. https://doi.org/10.3390/ijerph16183359





