Application of a Fusion Method for Gas and Particle Air Pollutants between Observational Data and Chemical Transport Model Simulations Over the Contiguous United States for 2005–2014
Abstract
1. Introduction
2. Materials and Methods
2.1. CMAQ Source
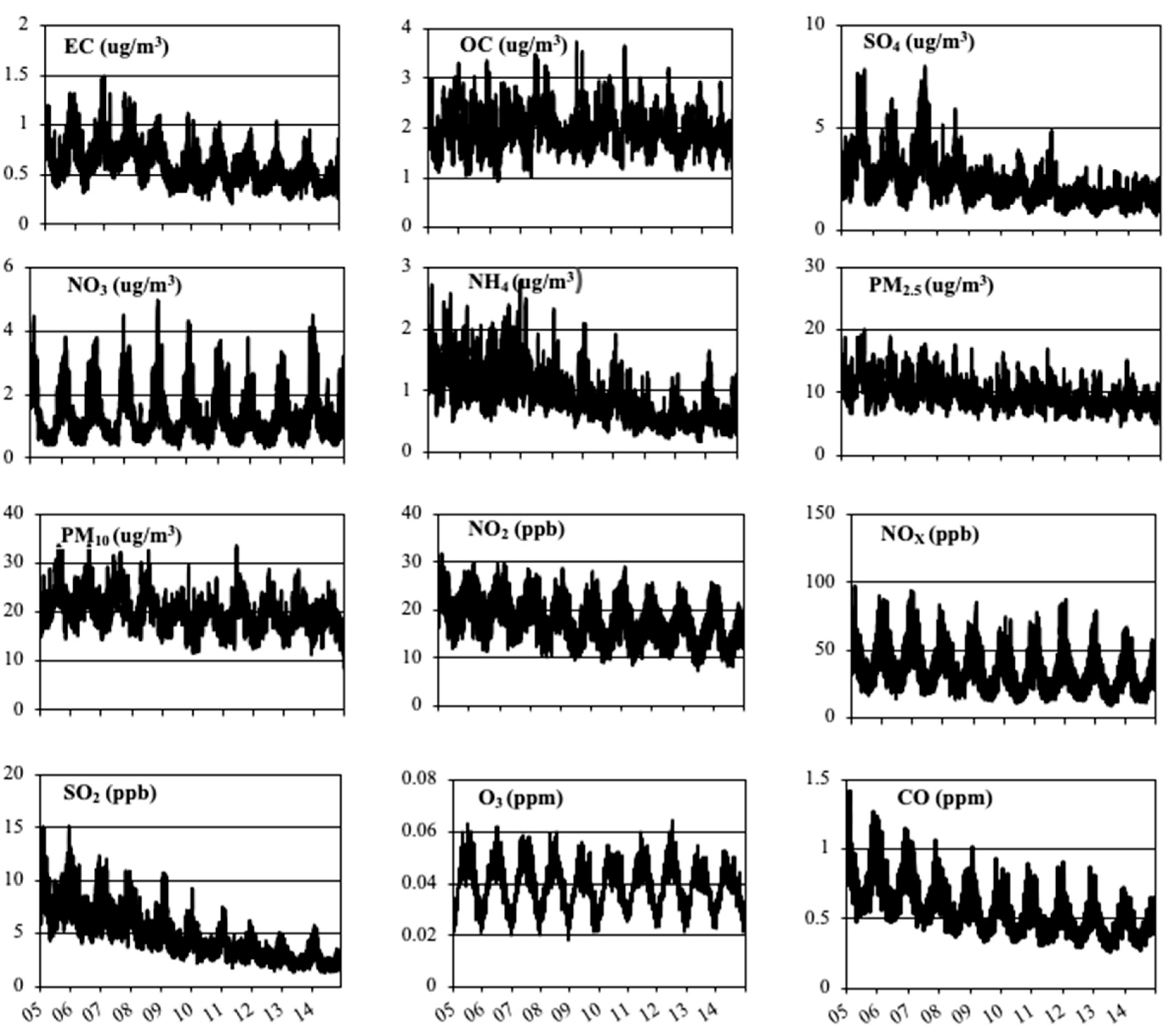
2.2. Monitoring Data
2.3. Data Fusion
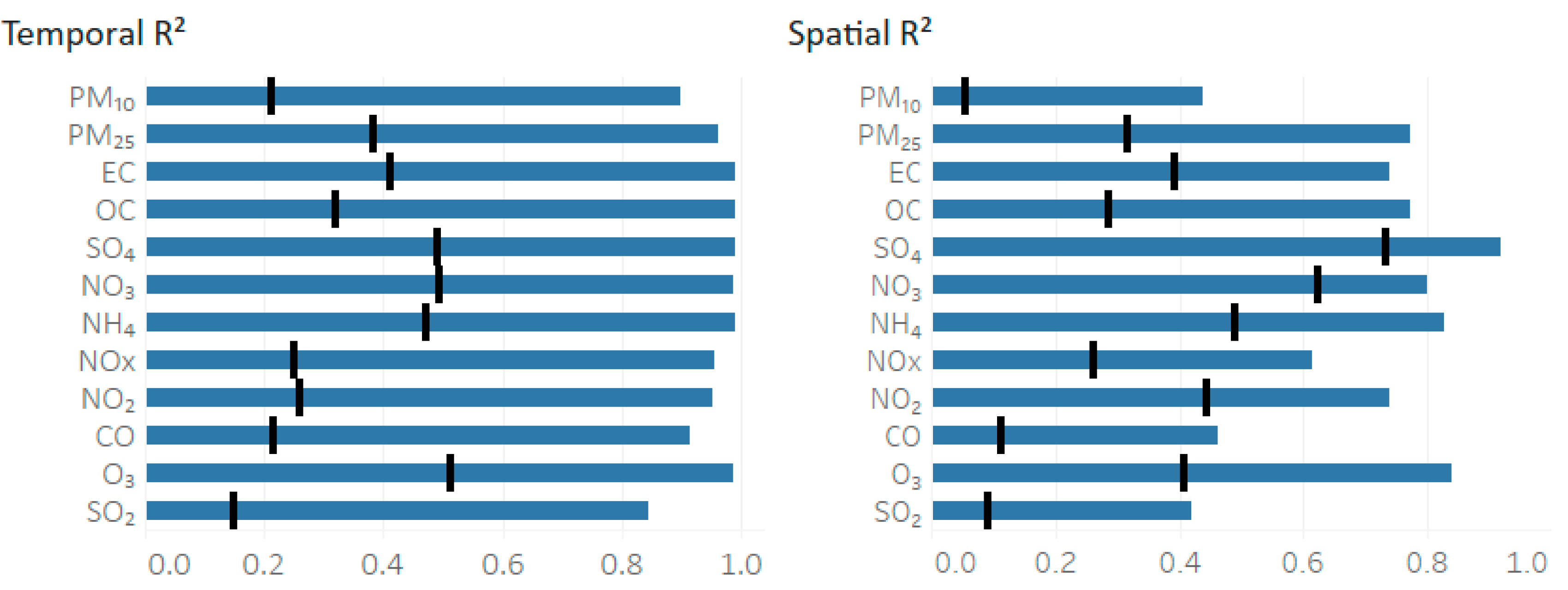
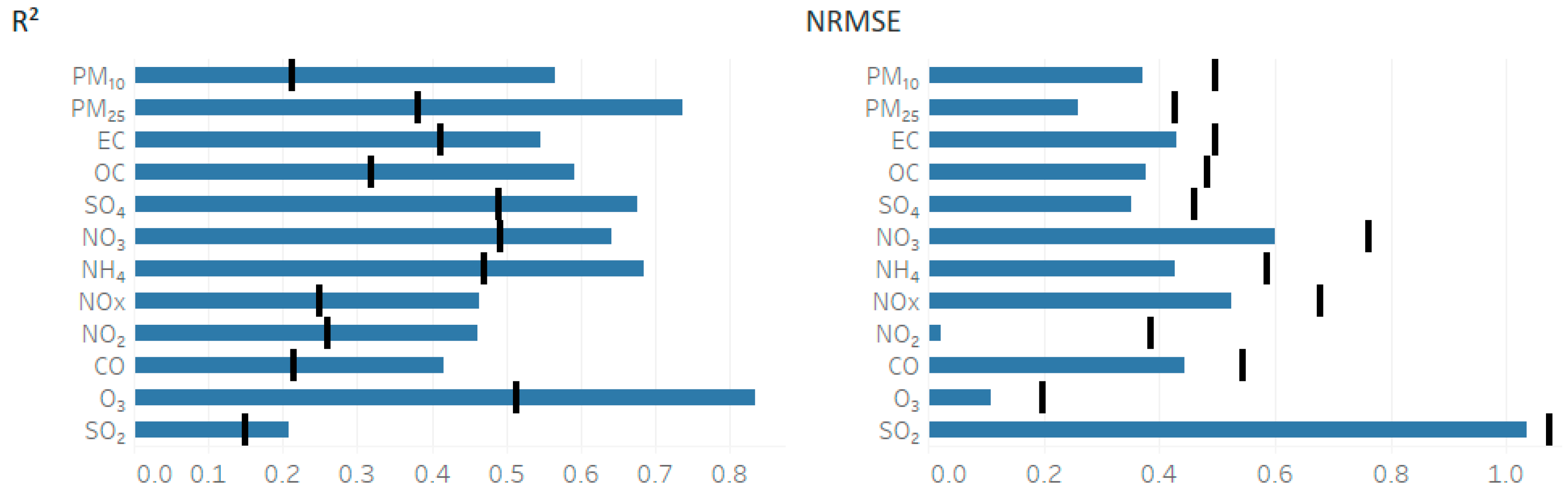
2.4. Model Performance Methods
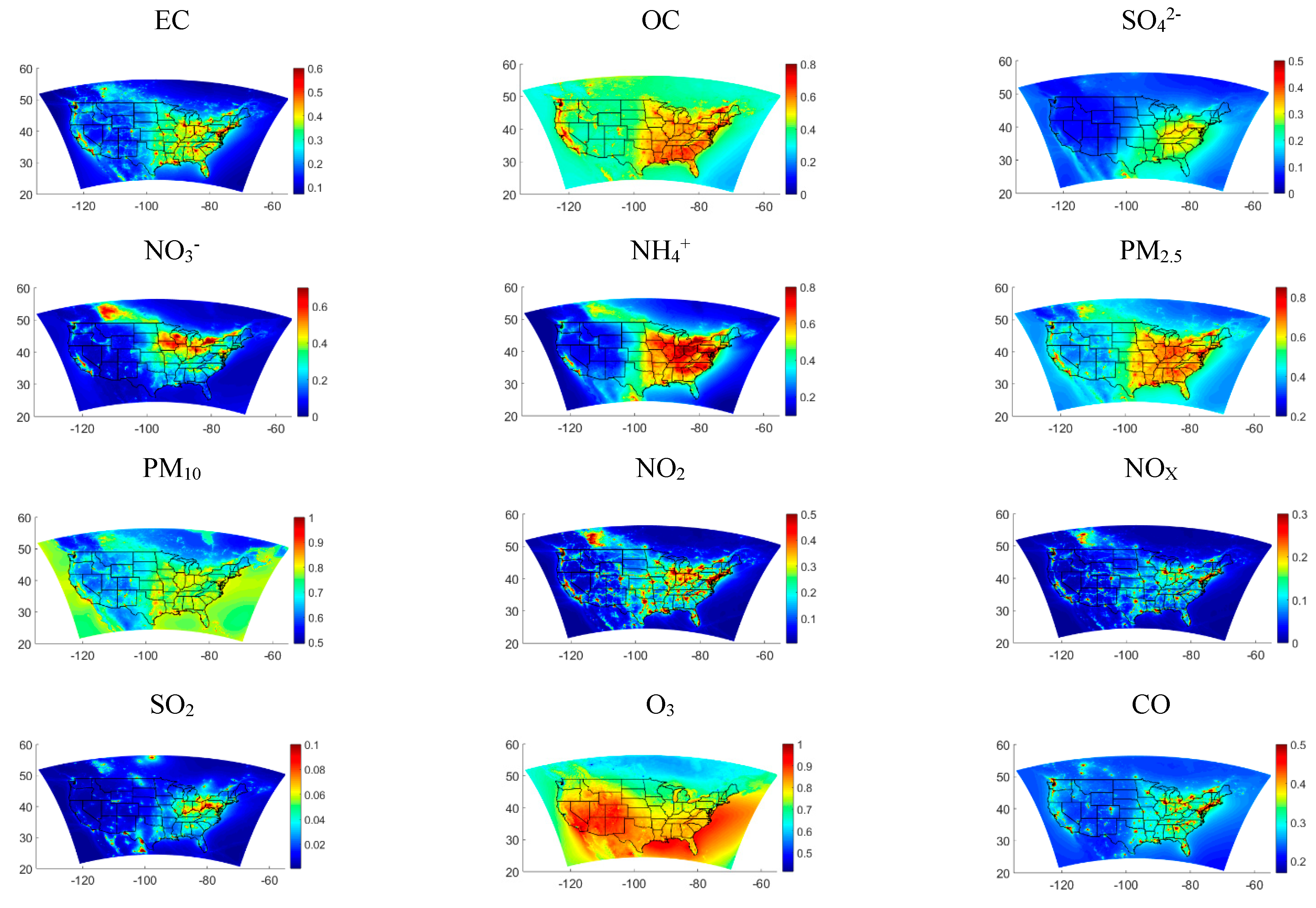
2.5. Spatial Plots
2.6. Model Evaluation Methods
2.7. Population Weighted Average Exposure
3. Results
4. Discussion
5. Conclusions
Supplementary Materials
Section S1. Metadata for 12km CMAQv5.0.2. Simulations
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Pope, C., III. Epidemiology of fine particulate air pollution and human health: Biologic mechanisms and who’s at risk? Environ. Health Perspect. 2000, 108 (Suppl. 4), 713–723. [Google Scholar] [CrossRef] [PubMed]
- Goldman, G.T.; Mulholland, J.A.; Russell, A.G.; Srivastava, A.; Strickland, M.J.; Klein, M.; Waller, L.A.; Tolbert, P.E.; Edgerton, E.S. Ambient air pollutant measurement error: Characterization and impacts in a time-series epidemiologic study in Atlanta. Environ. Sci. Technol. 2010, 44, 7692–7698. [Google Scholar] [CrossRef] [PubMed]
- Isakov, V.; Crooks, J.L.; Touma, J.; Valari, M. Development and evaluation of alternative metrics of ambient air pollution exposure for use in epidemiologic studies. In Air Pollution Modeling and Its Application XXI; Springer: Berlin/Heidelberg, Germany, 2011; pp. 681–686. [Google Scholar]
- Sarnat, S.E.; Sarnat, J.A.; Mulholland, J.; Isakov, V.; Özkaynak, H.; Chang, H.H.; Klein, M.; Tolbert, P.E. Application of alternative spatiotemporal metrics of ambient air pollution exposure in a time-series epidemiological study in Atlanta. J. Expo. Sci. Environ. Epidemiol. 2013, 23, 593–605. [Google Scholar] [CrossRef] [PubMed]
- Bell, M.L. The use of ambient air quality modeling to estimate individual and population exposure for human health research: A case study of ozone in the Northern Georgia Region of the United States. Environ. Int. 2006, 32, 586–593. [Google Scholar] [CrossRef] [PubMed]
- Tolbert, P.E.; Klein, M.; Peel, J.L.; Sarnat, S.E.; Sarnat, J.A. Multipollutant modeling issues in a study of ambient air quality and emergency department visits in Atlanta. J. Expo. Sci. Environ. Epidemiol. 2007, 17, S29–S35. [Google Scholar] [CrossRef] [PubMed]
- Peel, J.L.; Tolbert, P.E.; Klein, M.; Metzger, K.B.; Flanders, W.D.; Todd, K.; Mulholland, J.A.; Ryan, P.B.; Frumkin, H. Ambient air pollution and respiratory emergency department visits. Epidemiology 2005, 16, 164–174. [Google Scholar] [CrossRef] [PubMed]
- Baxter, L.K.; Dionisio, K.L.; Burke, J.; Sarnat, S.E.; Sarnat, J.A.; Hodas, N.; Rich, D.Q.; Turpin, B.J.; Jones, R.R.; Mannshardt, E.; et al. Exposure prediction approaches used in air pollution epidemiology studies: Key findings and future recommendations. J. Expo. Sci. Environ. Epidemiol. 2013, 23, 654–659. [Google Scholar] [CrossRef]
- Marshall, J.D.; Nethery, E.; Brauer, M. Within-urban variability in ambient air pollution: Comparison of estimation methods. Atmos. Environ. 2008, 42, 1359–1369. [Google Scholar] [CrossRef]
- Appel, K.W.; Gilliland, A.B.; Sarwar, G.; Gilliama, R.C. Evaluation of the Community Multiscale Air Quality (CMAQ) model version 4.5: Sensitivities impacting model performance: Part I—Ozone. Atmos. Environ. 2007, 41, 9603–9615. [Google Scholar] [CrossRef]
- Appel, K.W.; Bhave, P.V.; Gilliland, A.B.; Sarwar, G.; Roselle, S.J. Evaluation of the community multiscale air quality (CMAQ) model version 4.5: Sensitivities impacting model performance: Part II—Particulate matter. Atmos. Environ. 2008, 42, 6057–6066. [Google Scholar] [CrossRef]
- Binkowski, F.S.; Roselle, S.J. Models-3 Community Multiscale Air Quality (CMAQ) model aerosol component 1. Model description. J. Geophys. Res. Space Phys. 2003, 108. [Google Scholar] [CrossRef]
- Hao, H.; Chang, H.H.; Holmes, H.A.; Mulholland, J.A.; Klein, M.; Darrow, L.A.; Strickland, M.J. Air pollution and preterm birth in the US State of Georgia (2002–2006): Associations with concentrations of 11 ambient air pollutants estimated by combining Community Multiscale Air Quality Model (CMAQ) simulations with stationary monitor measurements. Environ. Health Perspect. 2015, 124, 875–880. [Google Scholar] [CrossRef] [PubMed]
- Ivey, C.E.; Holmes, H.A.; Hu, Y.; Mulholland, J.A.; Russell, A.G. A method for quantifying bias in modeled concentrations and source impacts for secondary particulate matter. Front. Environ. Sci. Eng. 2016, 10, 14. [Google Scholar] [CrossRef]
- Baek, J.; Hu, Y.; Odman, M.T.; Russell, A.G. Modeling secondary organic aerosol in CMAQ using multigenerational oxidation of semi-volatile organic compounds. J. Geophys. Res. Space Phys. 2011, 116. [Google Scholar] [CrossRef]
- Appel, K.W.; Chemel, C.; Roselle, S.J.; Francis, X.V.; Hu, R.-M.; Sokhi, R.S.; Rao, S.; Galmarini, S. Examination of the Community Multiscale Air Quality (CMAQ) model performance over the North American and European domains. Atmos. Environ. 2012, 53, 142–155. [Google Scholar] [CrossRef]
- Canty, T.P.; Hembeck, L.; Vinciguerra, T.P.; Anderson, D.C.; Goldberg, D.L.; Carpenter, S.F.; Allen, D.J.; Loughner, C.; Salawitch, R.J.; Dickerson, R.R. Ozone and NOx chemistry in the eastern US: Evaluation of CMAQ/CB05 with satellite (OMI) data. Atmos. Chem. Phys. Discuss. 2015, 15, 4427–4461. [Google Scholar] [CrossRef]
- Zhang, H.; Chen, G.; Hu, J.; Chen, S.-H.; Wiedinmyer, C.; Kleeman, M.; Ying, Q. Evaluation of a seven-year air quality simulation using the Weather Research and Forecasting (WRF)/Community Multiscale Air Quality (CMAQ) models in the eastern United States. Sci. Total Environ. 2014, 473, 275–285. [Google Scholar] [CrossRef]
- Foley, K.M.; Roselle, S.J.; Appel, K.W.; Bhave, P.V.; Pleim, J.E.; Otte, T.L.; Mathur, R.; Sarwar, G.; Young, J.O.; Gilliam, R.C.; et al. Incremental testing of the Community Multiscale Air Quality (CMAQ) modeling system version 4.7. Geosci. Model Dev. 2010, 3, 205–226. [Google Scholar] [CrossRef]
- Friberg, M.D.; Zhai, X.D.; Holmes, H.; Chang, H.H.; Strickland, M.; Sarnat, S.E.; Tolbert, P.E.; Russell, A.G.; Mulholland, J.A. Method for Fusing Observational Data and Chemical Transport Model Simulations to Estimate Spatiotemporally-Resolved Ambient Air Pollution. Environ. Sci. Technol. 2016, 50, 3695–3705. [Google Scholar] [CrossRef]
- Huang, R.; Zhai, X.; Ivey, C.E.; Friberg, M.D.; Hu, X.; Liu, Y.; Di, Q.; Schwartz, J.; Mulholland, J.A.; Russell, A.G. Air pollutant exposure field modeling using air quality model-data fusion methods and comparison with satellite AOD-derived fields: Application over North Carolina, USA. Air Qual. Atmos. Health 2018, 11, 11–22. [Google Scholar] [CrossRef]
- Zhai, X.; Russell, A.G.; Sampath, P.; Mulholland, J.A.; Kim, B.-U.; Kim, Y.; D’Onofrio, D. Calibrating R-LINE model results with observational data to develop annual mobile source air pollutant fields at fine spatial resolution: Application in Atlanta. Atmos. Environ. 2016, 147, 446–457. [Google Scholar] [CrossRef]
- Shaddick, G.; Thomas, M.L.; Green, A.; Brauer, M.; Burnett, A.v.; Chang, H.H.; Cohen, A.; van Dingenen, R.; Dora, C. Data integration model for air quality: A hierarchical approach to the global estimation of exposures to ambient air pollution. J. R. Stat. Soc. Ser. C Appl. Stat. 2018, 67, 231–253. [Google Scholar] [CrossRef]
- Wang, Y.; Hu, X.; Chang, H.H.; Waller, L.A.; Belle, J.H.; Liu, Y. A Bayesian Downscaler Model to Estimate Daily PM2.5 Levels in the Conterminous US. Int. J. Environ. Res. Public Health 2018, 15, 1999. [Google Scholar] [CrossRef] [PubMed]
- Sampson, P.D.; Richards, M.; Szpiro, A.A.; Bergen, S.; Sheppard, L.; Larson, T.V.; Kaufman, J.D. A regionalized national universal kriging model using Partial Least Squares regression for estimating annual PM2.5 concentrations in epidemiology. Atmos. Environ. 2013, 75, 383–392. [Google Scholar] [CrossRef] [PubMed]
- Zhan, Y.; Luo, Y.; Deng, X.; Chen, H.; Grieneisen, M.L.; Shen, X.; Zhu, L.; Zhang, M. Spatiotemporal prediction of continuous daily PM 2.5 concentrations across China using a spatially explicit machine learning algorithm. Atmos. Environ. 2017, 155, 129–139. [Google Scholar] [CrossRef]
- Birant, D. Comparison of Decision Tree Algorithms for Predicting Potential Air Pollutant Emissions with Data Mining Models. J. Environ. Inform. 2011, 17, 46–53. [Google Scholar] [CrossRef]
- Yu, H.; Russell, A.; Mulholland, J.; Odman, T.; Hu, Y.; Chang, H.H.; Kumar, N.; Mullholland, J. Cross-comparison and evaluation of air pollution field estimation methods. Atmos. Environ. 2018, 179, 49–60. [Google Scholar] [CrossRef]
- Berrocal, V.J.; Gelfand, A.E.; Holland, D.M. Space-time data fusion under error in computer model output: An application to modeling air quality. Biometrics 2012, 68, 837–848. [Google Scholar] [CrossRef]
- Hu, X.; Belle, J.H.; Meng, X.; Wildani, A.; Waller, L.A.; Strickland, M.J.; Liu, Y. Estimating PM2.5 Concentrations in the Conterminous United States Using the Random Forest Approach. Environ. Sci. Technol. 2017, 51, 6936–6944. [Google Scholar] [CrossRef]
- Jinnagara Puttaswamy, S.; Nguyen, H.M.; Braverman, A.; Hu, X.; Liu, Y. Statistical data fusion of multi-sensor AOD over the continental United States. Geocarto Int. 2014, 29, 48–64. [Google Scholar] [CrossRef]
- Di, Q.; Kloog, I.; Koutrakis, P.; Lyapustin, A.; Wang, Y.; Schwartz, J. Assessing PM2.5 Exposures with High Spatiotemporal Resolution across the Continental United States. Environ. Sci. Technol. 2016, 50, 4712–4721. [Google Scholar] [CrossRef] [PubMed]
- Al-Saadi, J.; Szykman, J.; Pierce, R.B.; Kittaka, C.; Neil, D.; Chu, D.A.; Gumley, L.; Prins, E.; Weinstock, L.; Macdonald, C.; et al. Improving National Air Quality Forecasts with Satellite Aerosol Observations. Bull. Am. Meteorol. Soc. 2005, 86, 1249–1262. [Google Scholar] [CrossRef]
- Xue, T.; Zheng, Y.; Geng, G.; Zheng, B.; Jiang, X.; Zhang, Q.; He, K. Fusing Observational, Satellite Remote Sensing and Air Quality Model Simulated Data to Estimate Spatiotemporal Variations of PM2.5 Exposure in China. Remote Sens. 2017, 9, 221. [Google Scholar] [CrossRef]
- Friberg, M.D.; Kahn, R.A.; Holmes, H.A.; Chang, H.H.; Sarnat, S.E.; Tolbert, P.E.; Russell, A.G.; Mulholland, J.A. Daily ambient air pollution metrics for five cities: Evaluation of data-fusion-based estimates and uncertainties. Atmos. Environ. 2017, 158, 36–50. [Google Scholar] [CrossRef]
- Fuentes, M.; Song, H.-R.; Ghosh, S.K.; Holland, D.M.; Davis, J.M. Spatial Association between Speciated Fine Particles and Mortality. Biometrics 2006, 62, 855–863. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Foley, K.M.; Schwede, D.B.; Bash, J.O.; Pinto, J.P.; Dennis, R.L. A Measurement-Model Fusion Approach for Improved Wet Deposition Maps and Trends. J. Geophys. Res. Atmos. 2019, 124, 4237–4251. [Google Scholar] [CrossRef]
- US EPA Office of Research and Development. CMAQv5.0.2. Zenodo. 30 May 2014. Available online: http://doi.org/10.5281/zenodo.1079898 (accessed on 3 August 2017).
- US EPA. National Emissions Inventory (NEI), Facility-Level, US, 2005, 2008, 2011. Available online: https://www.epa.gov/air-emissions-inventories/national-emissions-inventory (accessed on 10 August 2019).
- US EPA. AirData Download Files Documentation. 2015. Available online: https://aqs.epa.gov/aqsweb/airdata/FileFormats.html (accessed on 3 August 2017).
- US EPA. NAAQS Table. Available online: https://www.epa.gov/criteria-air-pollutants/naaqs-table (accessed on 27 March 2019).
- US EPA. Air Quality System Database. Available online: http://www.epa.gov/ttn/airs/aqsdatamaty (accessed on 3 August 2017).
- Wong, D.W.; Yuan, L.; Perlin, S.A. Comparison of spatial interpolation methods for the estimation of air quality data. J. Expo. Sci. Environ. Epidemiol. 2004, 14, 404. [Google Scholar] [CrossRef]
- U.S. Census Bureau. Decennial Census of Population and Housing. Available online: https://www.census.gov/programs-surveys/decennial-census/data/tables.2010.html (accessed on 20 February 2019).
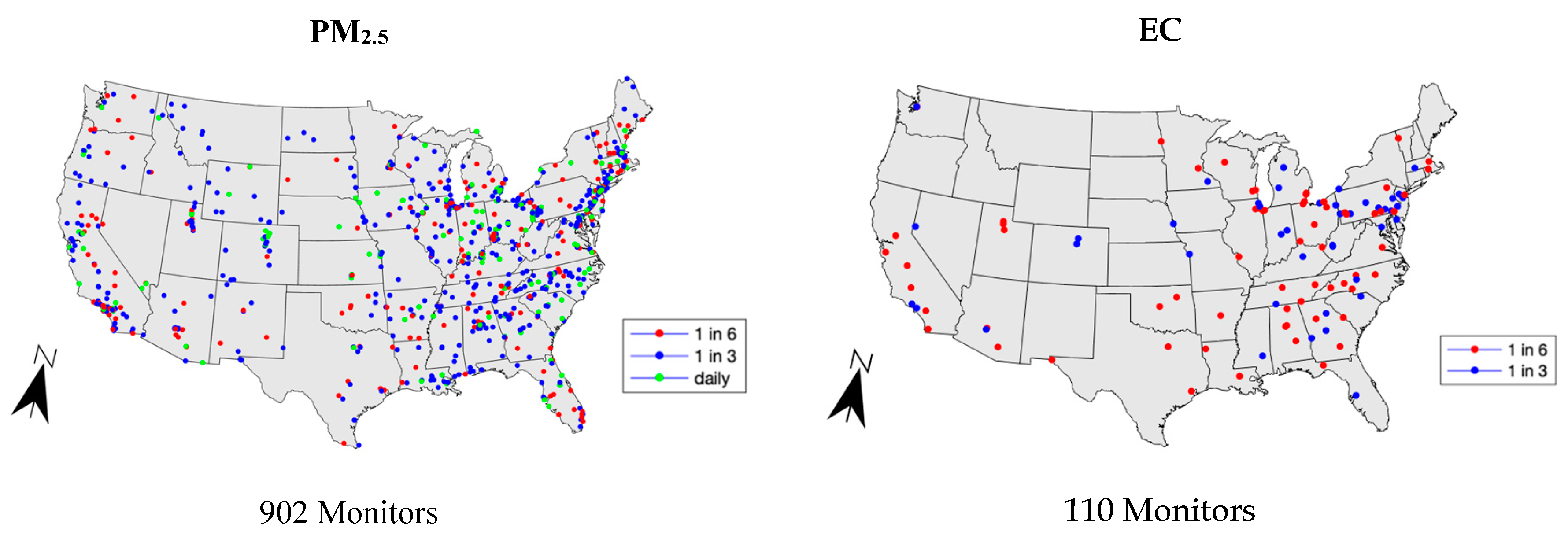
| Pollutant | Monitor Total | Daily | Total OBS | Completeness (%) | |
|---|---|---|---|---|---|
| Particulate Species | PM10 | 691–999 | 248–320 | 1,416,226 | 37–55 |
| PM2.5 | 768–1071 | 114–183 | 1,231,795 | 35–39 | |
| EC | 95–172 | 0 | 87,776 | 13–22 | |
| OC | 95–172 | 0 | 85,734 | 13–22 | |
| SO42− | 103–172 | 0 | 102,311 | 20–23 | |
| NO3− | 103–172 | 0 | 90,176 | 20–23 | |
| NH4+ | 102–172 | 0 | 94,332 | 19–22 | |
| Gases | NOx | 308–419 | 268–371 | 1,164,912 | 85–90 |
| NO2 | 300–400 | 270–389 | 1,373,569 | 87–90 | |
| CO | 303–418 | 278–393 | 1,257,734 | 87–90 | |
| O3 | 1182–1265 | 556–740 | 3,439,169 | 75–80 | |
| SO2 | 429–507 | 396–481 | 1,572,601 | 90–93 |
| R2 | ||||
|---|---|---|---|---|
| Particulate Species | PM10 | 11.67–15.64 | 0.10–0.23 | 0.03–0.14 |
| PM2.5 | 3.68–4.62 | 0.32–0.50 | 0.28–0.50 | |
| EC | 0.58–0.84 | 0.34–0.54 | 0.26–0.49 | |
| OC | 1.45–1.80 | 0.18–0.45 | 0.10–0.35 | |
| SO42− | 1.11–1.31 | 0.82–1.01 | 0.77–0.93 | |
| NO3− | 0.88–1.29 | 0.53–0.89 | 0.43–0.60 | |
| NH4+ | 0.74–1.45 | 0.46–0.76 | 0.24–0.78 | |
| Gases | NOx | 2.04–4.20 | 0.62–0.94 | 0.48–0.65 |
| NO2 | 1.66–2.21 | 0.68–0.76 | 0.63–0.71 | |
| CO | 0.82–1.09 | 0.43–0.67 | 0.16–0.36 | |
| O3 | 0.32–0.73 | 0.64–0.91 | 0.50–0.65 | |
| SO2 | 1.36–3.55 | 0.69–0.95 | 0.37–0.54 |
| 2005 | 2006 | 2007 | 2008 | 2009 | |||||||
| R2 | NRMSE | R2 | NRMSE | R2 | NRMSE | R2 | NRMSE | R2 | NRMSE | ||
| EC | 1 in 3 | 0.57 | 0.52 | 0.61 | 0.44 | 0.61 | 0.48 | 0.64 | 0.45 | 0.76 | 0.31 |
| 1 in 6 | 0.59 | 0.49 | 0.62 | 0.42 | 0.64 | 0.44 | 0.68 | 0.38 | 0.76 | 0.31 | |
| SO42− | 1 in 3 | 0.90 | 0.24 | 0.91 | 0.52 | 0.92 | 0.18 | 0.87 | 0.23 | 0.92 | 0.20 |
| 1 in 6 | 0.90 | 0.25 | 0.90 | 0.54 | 0.93 | 0.18 | 0.89 | 0.23 | 0.91 | 0.21 | |
| PM2.5 | 1 in 3 | 0.81 | 0.23 | 0.80 | 0.23 | 0.82 | 0.23 | 0.81 | 0.22 | 0.81 | 0.22 |
| 1 in 6 | 0.81 | 0.24 | 0.80 | 0.24 | 0.81 | 0.23 | 0.81 | 0.22 | 0.80 | 0.22 | |
| daily | 0.77 | 0.26 | 0.76 | 0.25 | 0.80 | 0.25 | 0.80 | 0.27 | 0.80 | 0.30 | |
| 2010 | 2011 | 2012 | 2013 | 2014 | |||||||
| R2 | NRMSE | R2 | NRMSE | R2 | NRMSE | R2 | NRMSE | R2 | NRMSE | ||
| EC | 1 in 3 | 0.70 | 0.38 | 0.71 | 0.34 | 0.69 | 0.37 | 0.76 | 0.34 | 0.69 | 0.36 |
| 1 in 6 | 0.68 | 0.41 | 0.72 | 0.32 | 0.72 | 0.31 | 0.76 | 0.33 | 0.71 | 0.33 | |
| SO42− | 1 in 3 | 0.85 | 0.31 | 0.91 | 0.19 | 0.90 | 0.21 | 0.89 | 0.20 | 0.87 | 0.24 |
| 1 in 6 | 0.84 | 0.30 | 0.91 | 0.18 | 0.89 | 0.21 | 0.90 | 0.20 | 0.88 | 0.24 | |
| PM2.5 | 1 in 3 | 0.79 | 0.23 | 0.81 | 0.22 | 0.74 | 0.25 | 0.77 | 0.26 | 0.73 | 0.27 |
| 1 in 6 | 0.78 | 0.23 | 0.81 | 0.22 | 0.74 | 0.26 | 0.76 | 0.26 | 0.74 | 0.28 | |
| daily | 0.78 | 0.24 | 0.78 | 0.24 | 0.74 | 0.26 | 0.75 | 0.26 | 0.72 | 0.27 | |
| 2005 | 2006 | 2007 | 2008 | 2009 | |||||||
| R2 | NRMSE | R2 | NRMSE | R2 | NRMSE | R2 | NRMSE | R2 | NRMSE | ||
| EC | Eastern | 0.51 | 0.42 | 0.56 | 0.40 | 0.38 | 0.52 | 0.45 | 0.47 | 0.67 | 0.36 |
| Western | 0.47 | 0.54 | 0.48 | 0.51 | 0.43 | 0.59 | 0.37 | 0.58 | 0.62 | 0.43 | |
| SO42− | Eastern | 0.81 | 0.32 | 0.76 | 0.32 | 0.79 | 0.31 | 0.74 | 0.33 | 0.71 | 0.31 |
| Western | 0.52 | 0.45 | 0.57 | 0.41 | 0.54 | 0.44 | 0.48 | 0.43 | 0.56 | 0.41 | |
| PM2.5 | Eastern | 0.75 | 0.24 | 0.76 | 0.23 | 0.82 | 0.23 | 0.80 | 0.23 | 0.79 | 0.23 |
| Western | 0.77 | 0.36 | 0.56 | 0.48 | 0.65 | 0.37 | 0.64 | 0.36 | 0.63 | 0.36 | |
| 2010 | 2011 | 2012 | 2013 | 2014 | |||||||
| R2 | NRMSE | R2 | NRMSE | R2 | NRMSE | R2 | NRMSE | R2 | NRMSE | ||
| EC | Eastern | 0.64 | 0.40 | 0.59 | 0.37 | 0.57 | 0.39 | 0.59 | 0.39 | 0.53 | 0.40 |
| Western | 0.59 | 0.45 | 0.56 | 0.48 | 0.58 | 0.45 | 0.63 | 0.44 | 0.61 | 0.44 | |
| SO42− | Eastern | 0.68 | 0.35 | 0.73 | 0.33 | 0.65 | 0.32 | 0.72 | 0.32 | 0.65 | 0.34 |
| Western | 0.42 | 0.51 | 0.58 | 0.40 | 0.58 | 0.37 | 0.61 | 0.39 | 0.54 | 0.46 | |
| PM2.5 | Eastern | 0.80 | 0.23 | 0.78 | 0.24 | 0.75 | 0.23 | 0.79 | 0.23 | 0.76 | 0.24 |
| Western | 0.60 | 0.38 | 0.65 | 0.37 | 0.63 | 0.37 | 0.64 | 0.38 | 0.60 | 0.41 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Senthilkumar, N.; Gilfether, M.; Metcalf, F.; Russell, A.G.; Mulholland, J.A.; Chang, H.H. Application of a Fusion Method for Gas and Particle Air Pollutants between Observational Data and Chemical Transport Model Simulations Over the Contiguous United States for 2005–2014. Int. J. Environ. Res. Public Health 2019, 16, 3314. https://doi.org/10.3390/ijerph16183314
Senthilkumar N, Gilfether M, Metcalf F, Russell AG, Mulholland JA, Chang HH. Application of a Fusion Method for Gas and Particle Air Pollutants between Observational Data and Chemical Transport Model Simulations Over the Contiguous United States for 2005–2014. International Journal of Environmental Research and Public Health. 2019; 16(18):3314. https://doi.org/10.3390/ijerph16183314
Chicago/Turabian StyleSenthilkumar, Niru, Mark Gilfether, Francesca Metcalf, Armistead G. Russell, James A. Mulholland, and Howard H. Chang. 2019. "Application of a Fusion Method for Gas and Particle Air Pollutants between Observational Data and Chemical Transport Model Simulations Over the Contiguous United States for 2005–2014" International Journal of Environmental Research and Public Health 16, no. 18: 3314. https://doi.org/10.3390/ijerph16183314
APA StyleSenthilkumar, N., Gilfether, M., Metcalf, F., Russell, A. G., Mulholland, J. A., & Chang, H. H. (2019). Application of a Fusion Method for Gas and Particle Air Pollutants between Observational Data and Chemical Transport Model Simulations Over the Contiguous United States for 2005–2014. International Journal of Environmental Research and Public Health, 16(18), 3314. https://doi.org/10.3390/ijerph16183314





