Acute Effects of a Speed Training Program on Sprinting Step Kinematics and Performance
Abstract
1. Introduction
2. Materials and Methods
2.1. Participants
2.2. Design
2.3. Testing Protocol
2.4. Assessment of Lower Extremity Explosive Power
2.5. Assessment of Sprint Performance
2.6. Statistical Analysis
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Charag, S.A.; Pal, R.; Yadav, S. Effect of plyometric training on muscular power and aerobic ability of the novice sprinters. Asian J. Phys. Educ. Comput. Sci. Sports 2011, 4, 77–81. [Google Scholar]
- Kukolj, M.; Ropret, R.; Ugarkovic, D.; Jaric, S. Anthropometric, strength, and power predictors of sprinting performance. J. Sports Med. Phys. Fit. 1999, 39, 120–122. [Google Scholar]
- Mackala, K.; Fostiak, M. Acute effects of plyometric intervention—Performance improvement and related changes in sprinting gait variability. J. Strength Cond. Res. 2015, 29, 1956–1965. [Google Scholar] [CrossRef] [PubMed]
- Marković, G.; Jukić, I.; Milanović, D.; Metikoš, D. Effects of sprint and plyometric training on muscle function and athletic performance. J. Strength Cond. Res. 2007, 21, 543–549. [Google Scholar] [PubMed]
- Rimmer, E.; Sleivert, G. Effects of plyometric intervention program on sprint performance. J. Strength Cond. Res. 2000, 14, 295–301. [Google Scholar]
- Coh, M.; Bačić, V.; Mackala, K. Biomechanical, neuromuscular and methodical aspects of running speed development. J. Hum. Kinet. 2010, 26, 73–81. [Google Scholar] [CrossRef]
- Bishop, D.J. Fatigue during intermittent-sprint exercise. Clin. Exp. Pharm. Physiol. 2012, 39, 836–841. [Google Scholar] [CrossRef]
- Billaut, F.; Basset, F.A. Effect of different recovery patterns on repeated-sprint ability and neuromuscular responses. J. Sports Sci. 2007, 25, 905–913. [Google Scholar] [CrossRef]
- Girard, O.; Mendez-Villanueva, A.; Bishop, D. Repeated-sprint ability: Part I. Factors contributing to fatigue. Sports Med. 2011, 41, 673–694. [Google Scholar] [CrossRef]
- Mendez-Villanueva, A.; Hamer, P.; Bishop, D. Fatigue in repeated sprint exercise is related to muscle power factors and reduced neuromuscular activity. Eur. J. Appl. Physiol. 2008, 103, 411–419. [Google Scholar] [CrossRef]
- Harrison, A.J.; Keane, S.P.; Coglan, J. Force-velocity relationship and stretch-shortening cycle function in sprint and endurance athletes. J. Strength Cond. Res. 2004, 18, 473–479. [Google Scholar] [PubMed]
- Hennessy, L.; Kilty, J. Relationship of the stretch-shortening cycle to sprint performance in trained female athletes. J. Strength Cond. Res. 2001, 15, 326–333. [Google Scholar] [PubMed]
- Johnson, M.D.; Buckley, J.G. Muscle power patterns in the mid-acceleration phase of Sprinting. J. Sports Sci. 2001, 19, 263–272. [Google Scholar] [CrossRef] [PubMed]
- Bezodis, I. Investigations of the step length-step frequency relationship in sprinting: Applied implications for performance. In Proceedings of the XXX International Conference on Biomechanics in Sports, Melbourne, Australia, 2–6 July 2012; pp. 43–49. [Google Scholar]
- Salo, A.; Bezodis, I.N.; Batterham, A.M.; Kerwin, D.G. Elite sprinting: Are athletes individually step-frequency or step-length reliant? Med. Sci. Sports Exerc. 2011, 43, 1055–1062. [Google Scholar] [CrossRef] [PubMed]
- Hunter, J.P.; Marshall, R.N.; McNair, P.J. Interaction of step length and step rate during sprint running. Med. Sci. Sports Exerc. 2004, 36, 261–271. [Google Scholar] [CrossRef] [PubMed]
- Coh, M.; Skof, B.; Kugovnik, O.; Dolenec, A. Kinematic-Dynamic Model of Maximal Speed of Young Sprinters. In Proceedings of the XII International Symposium on Biomechanics in Sports, Budapest, Hungary, 2–6 July 1994. [Google Scholar]
- Babić, V.; Coh, M.; Dizdar, D. Differences in kinematics parameters of athletes of different running quality. Biol. Sport 2011, 28, 15–121. [Google Scholar] [CrossRef]
- Bezodis, I.N.; Salo, A.I.T.; Kerwin, D.G. A longitudinal case study of step characteristics in a world class sprint athlete. In Proceedings of the XXVI International Conference on Biomechanics in Sports; Kwon, Y.H., J. Shim, J., Shim, J.K., Shin, I.S., Eds.; Rainbow Books: Seoul, Korea, 2008; pp. 537–540. [Google Scholar]
- Chatzilazaridis, I.; Panoutsakopoulos, V.; Papaiakovou, G.I. Stride characteristics progress in a 40-M sprinting test executed by male preadolescent, adolescent and adult athletes. Biol. Exerc. 2012, 8, 59–77. [Google Scholar] [CrossRef]
- Mackala, K.; Mero, A.A. Kinematic analysis of three best 100 m performance ever. J. Hum. Kinet. 2013, 36, 149–160. [Google Scholar]
- Gajer, B.; Thepaut-Mathieu, C.; Lehenaff, D. Evolution of stride and amplitude during course of the 100 m event in athletics. New Stud. Athl. 1999, 14, 43–50. [Google Scholar]
- Segers, V.; Lenoir, M.; Aerts, P.; De Clercq, D. Kinematics of the transition between walking and running when gradually changing speed. Gait Posture 2007, 26, 349–361. [Google Scholar] [CrossRef]
- Wilson, C.; Gittoes, M.; Heywood, P. The effect of pace on stride characteristics and variability in sprint running. In Proceedings of the XXVI International Symposium of Biomechanics in Sports (ISBS), Seoul, Korea, 14–18 July 2008; pp. 456–459. [Google Scholar]
- Kampmiller, T.; Vanderka, M.; Šelinger, P.; Šelingerová, M.; Čierna, D. Kinematic parameters of the running stride in 1- to 18-yeard-old youth. Kinesiol. Slov. 2011, 17, 63–75. [Google Scholar]
- Ozsu, I. Biomechanical structure of sprint start and effect of biological feedback methods on sprint start performance. Turk. J. Sport Exerc. 2014, 16, 72–79. [Google Scholar] [CrossRef]
- Kraemer, J.W.; Ratamess, A.N.; Volek, S.J.; Mazzetti, A.S.; Gomez, I.A. The effect of the Meridian Shoe on vertical jump and sprint performances following short-term combined plyometric/sprint and resistance training. J. Strength Cond. Res. 2000, 14, 228–238. [Google Scholar]
- Cormie, P.; McGuigan, M.R.; Newton, R.U. Developing maximal neuromuscular power: Part 1-biological basis of maximal power production. Sports Med. 2011, 41, 17–38. [Google Scholar] [CrossRef] [PubMed]
- Fatahi, A.; Sadeghi, H. Resistance, plyometrics and combined training in children and adolescents’ volleyball players: A review Study. J. Sci. Res. Rep. 2014, 20, 2584–2610. [Google Scholar] [CrossRef] [PubMed]
- Mehmet, K.; Alper, A.; Coskun, B.; Caner, A. Relationship among jumping performance and sprint parameters during maximum speed phase in sprinters. J. Strength Cond. Res. 2009, 23, 2272–2279. [Google Scholar]
- Wild, J.; Bezodis, N.; Blagrove, R.; Bezodis, I. Biomechanical comparison of accelerative and maximum velocity sprinting: Specific strength training consideration. U. K. Strength Cond. Assoc. 2011, 21, 23–36. [Google Scholar]
- Bruggemann, G.P.; Koszewski, D.; Muller, D. Biomechanical Research Project: Athens 1997; Final Report; Meyer & Meyer Sport: Oxford, UK, 1999; pp. 12–41. [Google Scholar]
- Shen, W. The effects of stride length and frequency on the speeds of elite sprinters in 100 meter dash. In Proceedings of the XVIII International Symposium of Biomechanics in Sports (ISBS), Hong-Kong, China, 25–30 June 2000; pp. 333–336. [Google Scholar]
- Mackala, K. Optimization of performance through kinematic analysis of the different phases of the 100 meters. New Stud. Athlet. 2007, 22, 7–16. [Google Scholar]
- Delecluse, C.H.; van Coppenolle, H.; Willems, R.; Diels, M.; Goris, M.; van Leempurte, M.; Vuylsteke, M. Analysis of 100 meter sprint performance as a multi-dimensional skill. J. Hum. Mov. Stud. 1995, 28, 87–101. [Google Scholar]
- Alcaraz, P.E.; Palao, J.M.; Elvira, J.L.L.; Linthorne, N.P. Effects of three types of resisted sprint training devices on the kinematics of sprinting at maximum velocity. J. Strength Cond. Res. 2008, 22, 890–897. [Google Scholar] [CrossRef]
- Hunter, J.P.; Marshall, R.N.; McNair, P.J. Relationships between ground reaction force impulse and kinematics of sprint-running acceleration. J. Appl. Biomech. 2001, 21, 31–43. [Google Scholar] [CrossRef]
- Coh, M.; Tomazin, K.; Stuhec, S. The biomechanical model of the sprint start and block acceleration. Facta Univ. Ser. Phys. Educ. Sport 2006, 4, 103–114. [Google Scholar]
| Type of Exercise Modality | Training Module | |
|---|---|---|
| 10-day Module | 12-day Module | |
| Number of Workouts (n) | ||
| Strength (combined with a short plyometrics session) | 3 | 2 |
| Plyometrics | − | 1 |
| Speed | 4 | 4 |
| Speed−endurance | 1 | 2 |
| Tempo | 2 | 1 |
| General fitness (supplementary session) | 4 | 4 |
| Recovery (swimming, massage, cryotherapy) | 5 | 5 |
| Day off (rest) | − | 1 |
| Testing | − | 1 |
| Total training workouts per module | 36 | |
| Exercises | Module 1 | Module 2 | ||||||
|---|---|---|---|---|---|---|---|---|
| 1st session | 2nd session | 3rd session | 4th session | 5th session | 6th session | 7th session | 8th session | |
| Sub−maximal speed (85–90%) | ||||||||
| 10 m skip A + 20 m acceleration | 2 rep. | 3 rep. | 2 rep. | 2 rep. | ||||
| 10 m skip C + 20 m acceleration | 2 rep. | 3 rep. | 2 rep. | 2 rep. | ||||
| 20 m sprint bounding + 20 m acceleration | 3 rep. | 3 rep. | 3 rep. | 4 rep. | ||||
| Falling start + 20 m build-up | 3 rep. | 2 rep. | 3 rep. | 2 rep. | ||||
| Block starts + 20 m build-up | 4 rep. | 4 rep. | 4 rep. | 4 rep. | ||||
| 40 m acceleration | 3 rep. | 4 rep. | 3 rep. | 6 rep. | ||||
| Total distance [m] | 540 | 600 | 540 | 640 | ||||
| Maximal speed (ca. 100%) | ||||||||
| Falling start + 20 m build up | 2 rep. | 2 rep. | 2 rep. | 2 rep. | ||||
| Block starts + 20 build up | 3 rep. | 4 rep. | 3 rep. | 4 rep. | ||||
| 30 m sprint | 3 rep. | 4 rep. | 3 rep. | 4 rep. | ||||
| 40 m sprint | 3 rep. | 4 rep. | 3 rep. | 4 rep. | ||||
| 50 m sprint | 1 rep. | 0 rep. | 1 rep. | 1 rep | ||||
| Total distance [m] | 360 | 400 | 360 | 450 | ||||
| Variables | Sub-Elite | Elite | t | p | ||
|---|---|---|---|---|---|---|
| x | SD | x | SD | |||
| Age (years) | 18.71 | 0.75 | 24.71 | 2.43 | −6.24 | 0.000043 |
| Height (cm) | 182.00 | 5.35 | 179.42 | 3.91 | 0.78 | 0.449165 |
| Body mass (kg) | 73.28 | 4.49 | 74.43 | 8.24 | −0.32 | 0.753007 |
| BMI (kg/m²) | 22.17 | 1.10 | 22.79 | 0.74 | −1.22 | 0.244110 |
| 60 m PB | 6.97 | 0.08 | 6.69 | 0.79 | 6.52 | 0.000028 |
| 100 m PB | 10.71 | 0.15 | 10.37 | 0.04 | 5.71 | 0.000097 |
| Variable | x | SD | x | SD | Δx | ΔxSD | t | p | Confidence −95.00% | Confidence +95.0% |
|---|---|---|---|---|---|---|---|---|---|---|
| Sub-elite | Pre−test | Post−test | ||||||||
| 60m–60m_t2 (s) | 7.10 | 0.09 | 7.02 | 0.05 | 0.08 | 0.04 | 4.77 | 0.0030 | 0.038 | 0.121 |
| 20m flying–20m flying_2t (s) | 2.21 | 0.08 | 2.13 | 0.05 | 0.07 | 0.05 | 3.57 | 0.0116 | 0.024 | 0.129 |
| 40m –40m_2t (s) | 4.37 | 0.04 | 4.32 | 0.03 | 0.06 | 0.01 | 7.94 | 0.0000 | 0.040 | 0.076 |
| SLJ–SLJ_2t (cm) | 2.91 | 0.06 | 2.99 | 0.07 | −0.08 | 0.04 | −4.81 | 0.0029 | −0.120 | −0.039 |
| STJ–STJ_2t (m) | 8.56 | 0.16 | 8.80 | 0.18 | −0.24 | 0.07 | −8.67 | 0.0001 | −.0313 | −0.175 |
| SFJ–SFJ_2t (m) | 14.90 | 0.62 | 15.56 | 0.53 | −0.66 | 0.13 | −13.66 | 0.0000 | −0.775 | −0.539 |
| CMJ –CMJ_2t (cm) | 76.43 | 4.89 | 82.71 | 5.34 | −6.29 | 1.70 | −9.76 | 0.0000 | −7.862 | −4.709 |
| Elite | Pre−test | Post−test | ||||||||
| 60m–60m_t2 (s) | 6.79 | 0.08 | 6.72 | 0.08 | 0.06 | 0.02 | 7.17 | 0.0003 | 0.040 | 0.082 |
| 20m flying–20m flying_2t (s) | 2.07 | 0.04 | 1.97 | 0.07 | 0.11 | 0.07 | 4.17 | 0.0058 | 0.047 | 0.179 |
| 40m –40m_2t (s) | 4.12 | 0.02 | 4.08 | 0.01 | 0.04 | 0.02 | 4.58 | 0.0037 | 0.018 | 0.061 |
| SLJ –SLJ_2t (m) | 3.15 | 0.10 | 3.23 | 0.11 | −0.07 | 0.05 | −3.92 | 0.0078 | −0.118 | −0.027 |
| STJ–STJ_2t (m) | 9.39 | 0.52 | 9.89 | 0.48 | −0.49 | 0.21 | −6.28 | 0.0007 | −0.693 | −0.304 |
| SFJ–SFJ_2t (m) | 15.81 | 0.44 | 16.59 | 0.57 | −0.78 | 0.50 | −4.11 | 0.0062 | −1.244 | −0.316 |
| CMJ –CMJ_2t (cm) | 81.57 | 2.57 | 87.86 | 1.07 | −6.28 | 2.06 | −8.08 | 0.0001 | −8.189 | −4.382 |
| Feature | Main Effect | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Group | ST | PT × Group | Step | Step × Group | ST × step | ST × step × group | ||||||||
| F | p | F | p | F | p | F | p | F | p | F | p | F | p | |
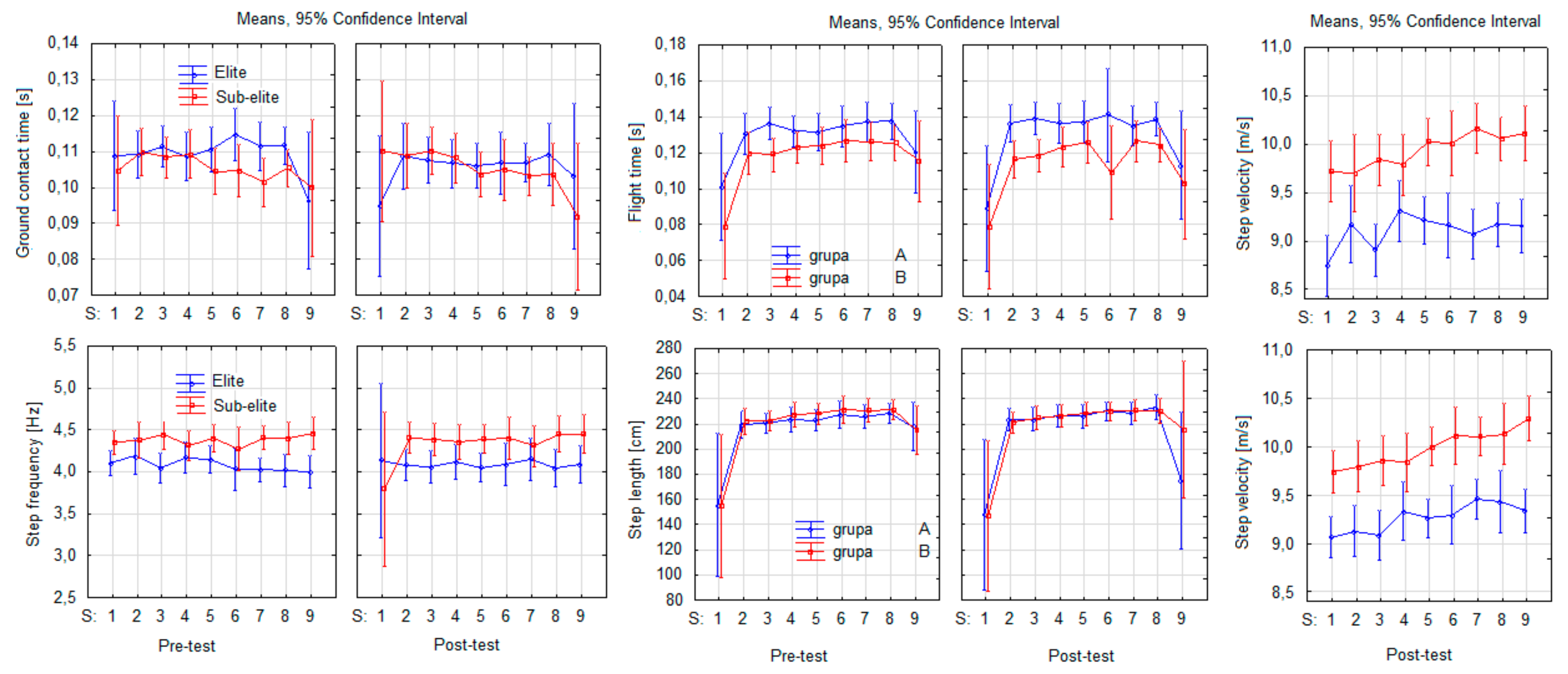
| CT | 0.27 | 0.6129 | 4.09 | 0.0660 | 2.79 | 0.1206 | 2.14 | 0.0388 | 0.74 | 0.6540 | 0.19 | 0.9918 | 2.34 | 0.0240 |
| FT | 9.05 | 0.0109 | 0.53 | 0.4789 | 0.85 | 0.3756 | 10.58 | 0.0000 | 0.24 | 0.9812 | 0.54 | 0.8220 | 0.57 | 0.8016 |
| SF | 4.91 | 0.0468 | 0.33 | 0.5763 | 0.73 | 0.4100 | 0.90 | 0.5167 | 1.68 | 0.1121 | 0.89 | 0.5247 | 1.13 | 0.3484 |
| SL | 0.61 | 0.4489 | 0.32 | 0.5841 | 0.08 | 0.7828 | 18.23 | 0.0000 | 0.25 | 0.9798 | 0.50 | 0.8503 | 0.50 | 0.8519 |
| SV | 56.64 | 0.0000 | 2.72 | 0.1249 | 0.74 | 0.4080 | 8.22 | 0.0000 | 2.06 | 0.0475 | 0.48 | 0.8703 | 0.80 | 0.6012 |
| Sub-Elite | Variable | Elite | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| [7] | [6] | [5] | [4] | [3] | [2] | [1] | [1] | [2] | [3] | [4] | [5] | [6] | [7] | |
| - | −0.77 | −0.76 | 0.85 | - | - | 60 m [1] | - | 0.81 | −0.76 | - | −0.87 * | - | - | |
| - | - | −0.76 * | 0.90 * | - | - | - | - | - | - | - | - | - | ||
| - | - | −0.85 * | - | - | - | - | 20 m flying start [2] | - | - | - | - | - | - | - |
| - | - | −0.76 * | - | - | - | - | 40 m [3] | - | - | - | - | - | - | - |
| −0.79 | 0.82 * | 0.79 * | - | - | - | - | SLJ [4] | - | - | - | - | - | 0.85 * | - |
| - | −0.90 | - | - | - | - | - | STJ [5] | - | - | - | - | - | 0.79 | - |
| - | 0.79 * | - | - | - | - | - | - | - | - | - | - | - | - | |
| - | - | - | - | - | - | - | SFJ [6] | - | - | - | - | - | - | - |
| CMJ [7] | ||||||||||||||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mackala, K.; Fostiak, M.; Schweyen, B.; Osik, T.; Coch, M. Acute Effects of a Speed Training Program on Sprinting Step Kinematics and Performance. Int. J. Environ. Res. Public Health 2019, 16, 3138. https://doi.org/10.3390/ijerph16173138
Mackala K, Fostiak M, Schweyen B, Osik T, Coch M. Acute Effects of a Speed Training Program on Sprinting Step Kinematics and Performance. International Journal of Environmental Research and Public Health. 2019; 16(17):3138. https://doi.org/10.3390/ijerph16173138
Chicago/Turabian StyleMackala, Krzysztof, Marek Fostiak, Brian Schweyen, Tadeusz Osik, and Milan Coch. 2019. "Acute Effects of a Speed Training Program on Sprinting Step Kinematics and Performance" International Journal of Environmental Research and Public Health 16, no. 17: 3138. https://doi.org/10.3390/ijerph16173138
APA StyleMackala, K., Fostiak, M., Schweyen, B., Osik, T., & Coch, M. (2019). Acute Effects of a Speed Training Program on Sprinting Step Kinematics and Performance. International Journal of Environmental Research and Public Health, 16(17), 3138. https://doi.org/10.3390/ijerph16173138





