An Effective Approach for the Multiobjective Regional Low-Carbon Location-Routing Problem
Abstract
1. Introduction
- We introduced a mixed-integer linear programming MOM for the RLCLRP. In the real-world logistics network, cost, service duration, and client satisfaction were considered the most significant performance indicators, and traveling cost incorporated FCCE cost.
- We developed an efficient MOHH to solve the MORLCLRP. For HLHs, we provided four selection strategies and three acceptance criteria to improve the performance of the MOHH framework and developed three MOEAs as the pool of LLHs.
- We conducted extensive computational experiments to assess the efficiency of the proposed algorithms and developed managerial implications by assessing problem parameters, such as client and depot locations, speed zone areas, and fleet composition. The model, algorithms and computational results can serve as a stepping-stone for further MORLCLRP research with cold chain logistics [6].
2. Literature Review
2.1. Research Considering Effecting Factors
2.2. Research about FCCE Models
2.3. Research Concerning LCLRP
- Mohammadi et al. [40] proposed a biobjective LCLRP by optimizing logistics costs and traveling distance (i.e., low carbon/green objective). Although traveling distance is a significant factor in FCCE, other parameters, especially vehicle-specific parameters and load, should be considered in the model;
- Govindan et al. [41] presented a more detailed model by combining traveling and fixed CE of depots and manufacturers, with several coefficient matrices (e.g., uniform distribution) used to consider the effect of vehicle and load. However, these coefficient matrices are generated with uniform distribution, which does not accurately reflect FCCE; This approach was also applied in Chen et al. [39] and Nakhjirkan and Rafiei [42];
- Validi et al. [43,44,45] used fuel efficiency and distance to calculate the FCCE, like Kuo et al. [17] and Poonthalir and Nadarajan [16]. Faraji and Afshar-Nadjafi [46] proposed a modified method considering the extra fuel consumption caused by carrying each extra loads. Tang et al. [47] applied the method to calculate routing CE by giving parameters for each edge, with the CE of depots/inventory also considered;
- Qazvini et al. [48] proposed a SOM considering the cost of fuel consumption as a constraint. Although this method is effective, it is more appropriate to view the FCCE cost as a traveling cost in the real world;
- Koc et al. [1] considered a city in which goods need to be delivered from a depot to clients located in nested zones characterized by different speed limits and used CMEM to estimate FCCE, which was considered a traveling cost. This followed Leng et al. [2], who studied an extensive version of the RLCLRP using a shared mechanism-based hyperheuristic. Leng et al. [4] also modeled a biobjective RLCLRP tackled by quantum-inspired MOHH;
- Toro et al. [50] deduced the FCCE model by analyzing the forces acting on a vehicle and found the model to be remarkably similar to the CMEM. In their MOM, they also looked at fuel consumption and total emissions associated with the fuel consumption model;
- Wang and Li [51] applied the FCR considering road slope as a FCCE model. However, in their MOM, somewhat confusingly, both objectives were cost objectives, and penalty and vehicle fixed costs were added with FCCE cost;
- Zhang et al. [3] applied the FCR model to calculate CE and used the quantum evolutionary algorithm to solve the proposed model. Wang et al. [30] subsequently developed an ant-based hyperheuristic to solve the model by Zhang et al. [3]. Leng et al. [28] proposed an extensive version of the model by Zhang et al. [3], and a quantum-inspired hyperheuristic to solve it. Zhao et al. [29] also developed an integrated model for the LCLRP by defining the FCCE cost, and developed an evolutionary hyperheuristic to solve it; Qian et al. [52] modified the model by Zhang et al. [3] with a biobjective model, and used tabu search-based MOHH to solve it;
- Wang et al. [27] developed a SOM using the FCR to estimate FCCE and as a part of costs.
2.4. Research about MOHH
3. Mathematical Model
3.1. Description and Assumption of MORLCLRP
3.2. Mathematical Model
3.3. Other Valid Constraints
4. Proposed Method
4.1. Domain Method
4.1.1. Chromosome Representation
4.1.2. Applied Operators
4.1.3. General Structure of MOEAs for MORLCLRP
| Algorithm 1 General framework of MOEAs for LCLRP |
| Input:Pop, maxgen, etc. |
| Output: child population (Pop) |
| 1: Generate corresponding parameters of meta-heuristics |
| //Main loop |
| 2: Repeat |
| 3: i:=i + 1 |
| 4: for each solution in Pop do |
| // Mutation |
| 5: if random < pm then |
| 6: Mu: randomly choose a mutational operator |
| 7: Obtain a child C |
| 8: end if |
| // Local search |
| 9: Local search: randomly select an operator from NDLS |
| 10: and DLS to optimize Child C/Parent P (if random > pm) |
| 11: Obtain a new solution CC |
| 12: end for |
| 13: Obtain child population CP |
| 14. Merge population: All = [Pop,CP] |
| 15: Update of solutions: apply the environmental selection of |
| meta-heuristic to generate the Pop into next generation |
| 16: Stopping criteria: if stopping criteria is satisfied, then |
| stop and output Pop. Otherwise go to Step 3. |
| 17: until i = maxgen |
4.2. Framework of MOHH
| Algorithm 2 General framework of MOHH |
| // Initialization |
| 1: Citer:=0 (Current iteration) |
| 2: Parameter setting: parameters in Hypervolume, Maxiter, N, etc. |
| 3: Generate population Pop |
| 4: Calculate the multiobjective fitness |
| // Main loop |
| 5: Cpop = Pop; Ppop = pop; ArPop = Ø; |
| 6: Repeat |
| 7: Citer:=Citer + 1 |
| 8: // High-level selection strategy |
| 9: Apply SR/MAB/CF/QS to select the promising LLH op |
| 10: // Low-level heuristics |
| 11: Apply the selected opth MOEA to generate Cpop |
| 12: // High-level acceptance criterion |
| 13: Apply the selected acceptance criterion (GDA, LA, and AM) |
| to determinate the Pop of next iteration |
| 14: // Archive population (if needed) |
| 15: Save all nondominated individuals into ArPop; |
| 16: if number of individuals in ArPop is larger than 5 × N then |
| 17: Apply environmental selection of NSGA-II to remove the |
| individuals with much more crowded |
| 18: end if |
| 19: until Citer = Maxiter |
| 20: if ArPop then |
| 21: Apply environmental selection of NSGA-II to remove the |
| 4 × N individuals with much more crowded |
| 22: Pop = ArPop |
| 23: end if |
| 24: return Pop |
4.3. Heuristic Selection Strategies
Simple Random
4.4. Fitness Rate Rank Based Multi-Armed Bandit (FRR-MAB)
4.4.1. Choice Function
4.4.2. Quantum-Inspired Selection
4.5. Move Acceptance Methods
5. Computational Evaluation
5.1. Implementation Aspects and Configuration of Parameters
5.2. Performance Metrics
5.3. Efficiency of MOHH
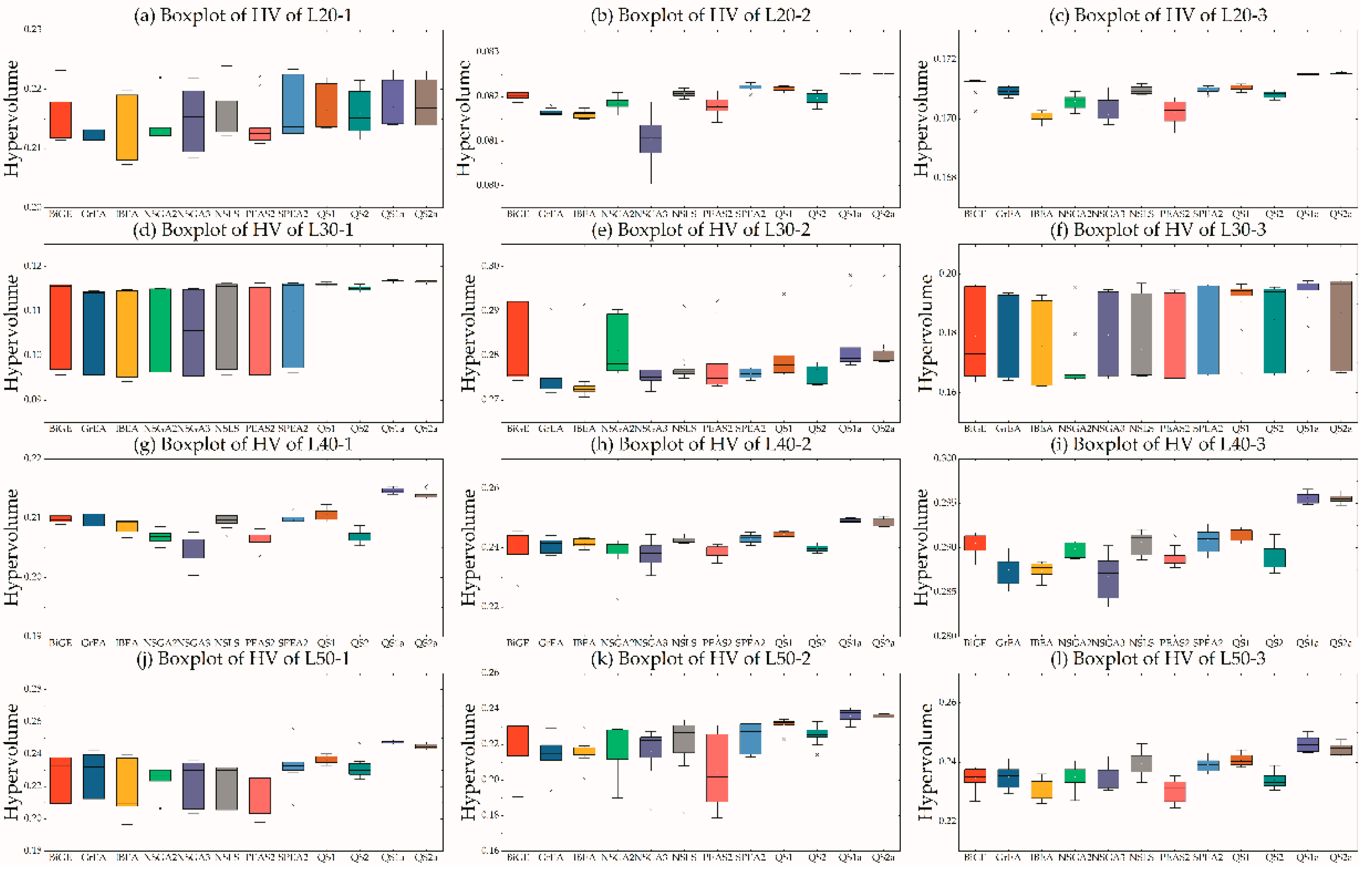
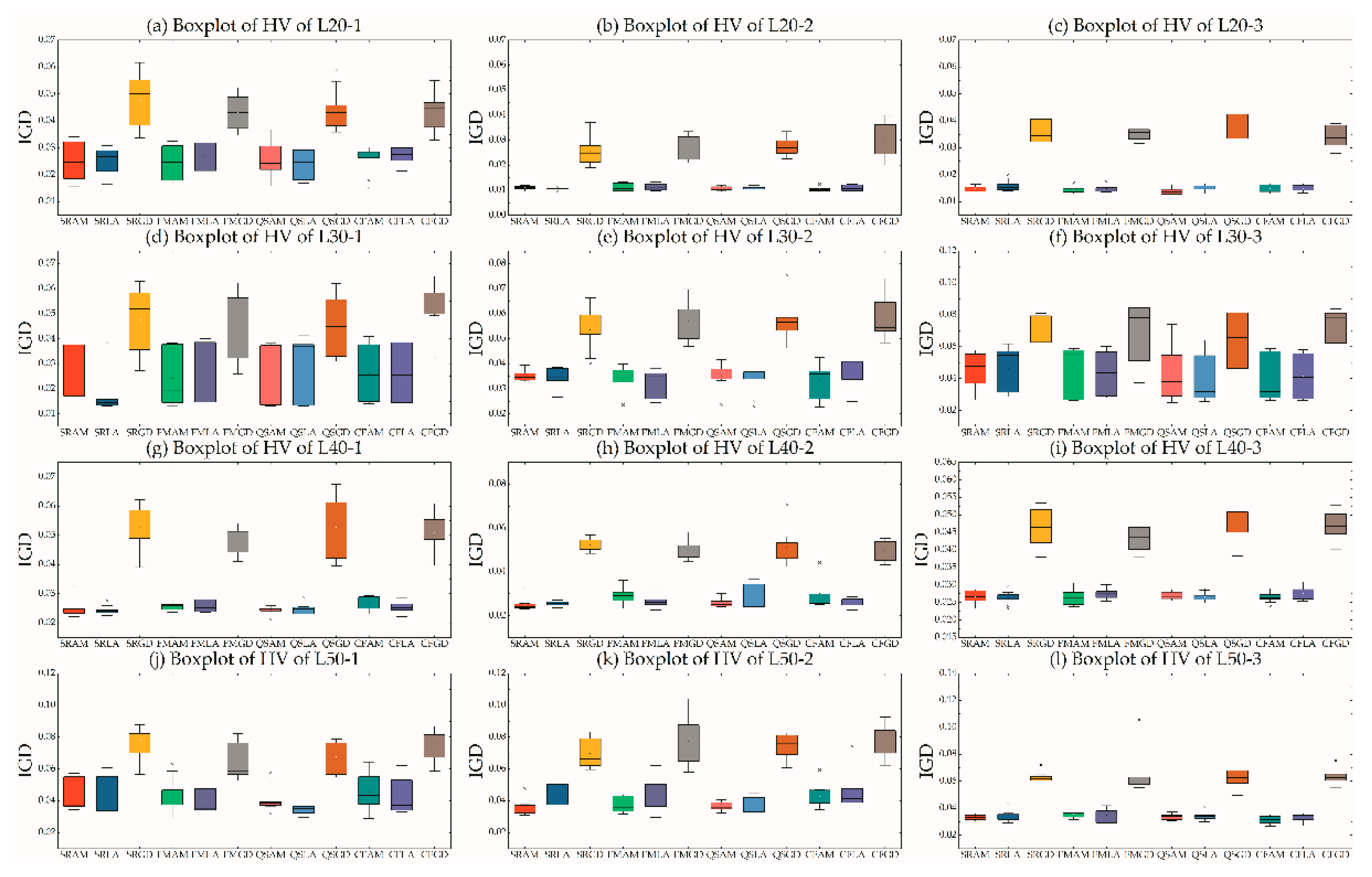
5.4. Efficiency of Pairs in MOHH
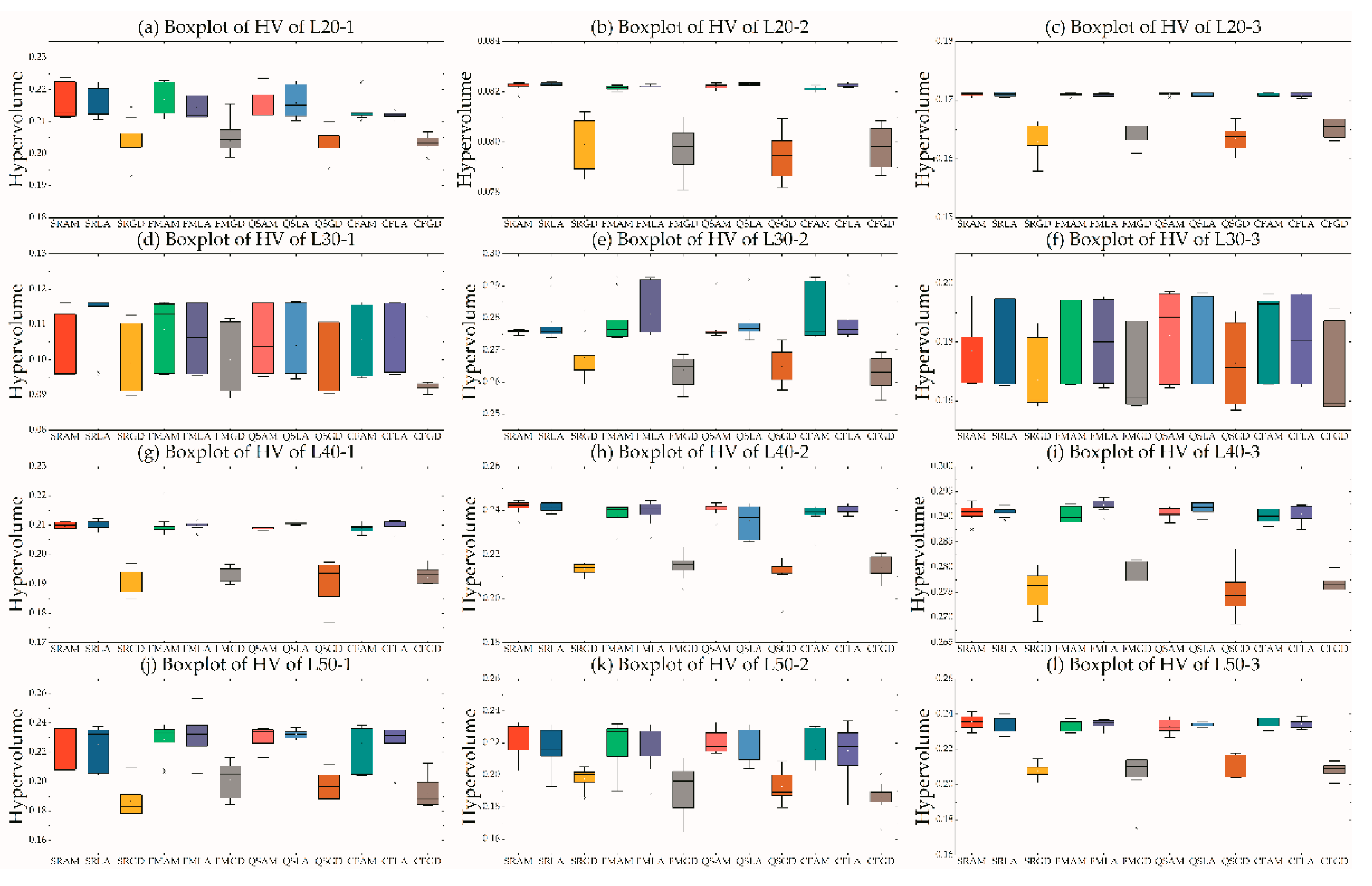
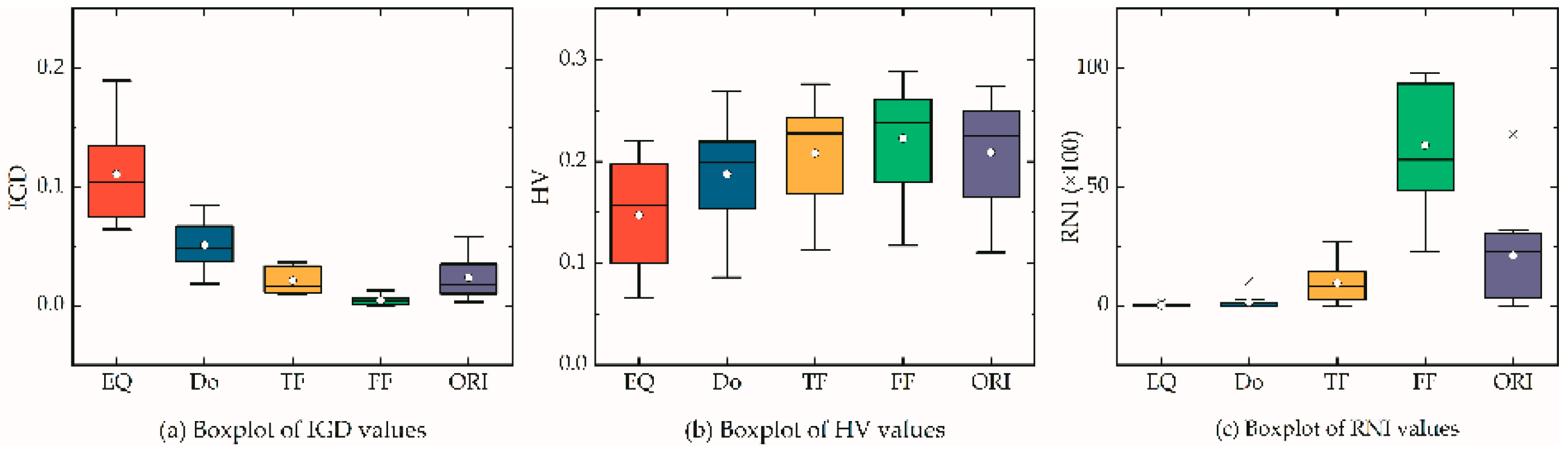
5.5. Effect of Clients and Depots Locations
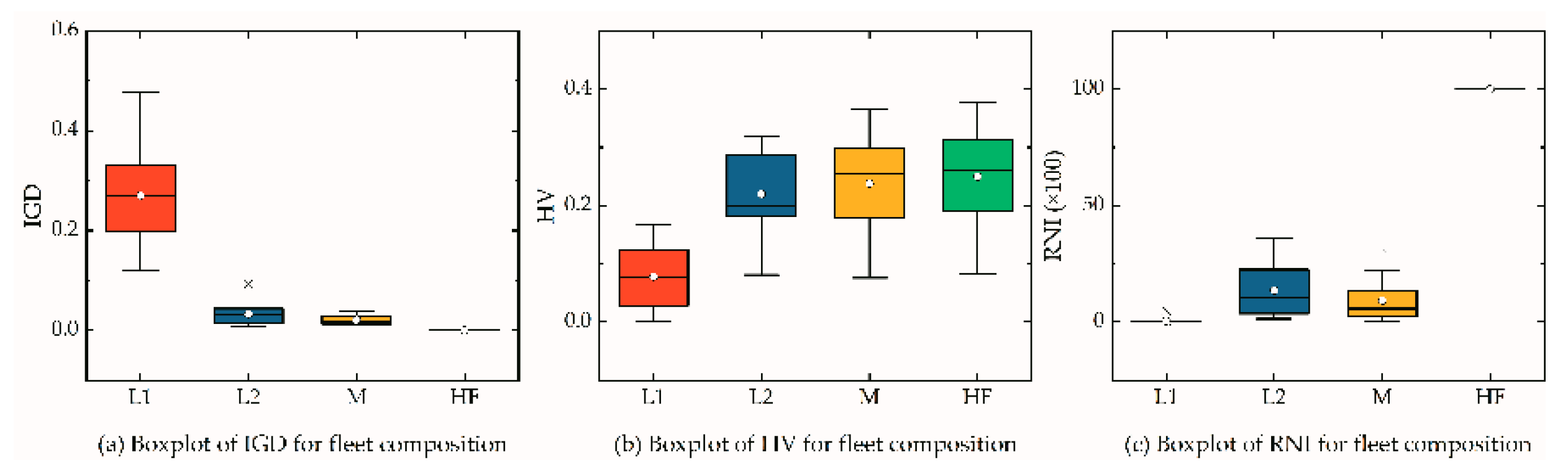
5.6. Effect of Fleet Composition
5.7. Effect of Zones Area
5.8. Management Implications
6. Conclusions
- Although method synthesis might promote the algorithm’s performance, the strategy is significant to choose and monitor the performance of each method. Moreover, the LLHs have strong ability in effecting the whole performance, therefore, the analysis should be conducted before constructing the pool of low-level heuristics;
- The HLHs are important for the algorithm’s performance, and the unmerited design may produce the poor performance than the simple random, such as FRR-MAB and GDA;
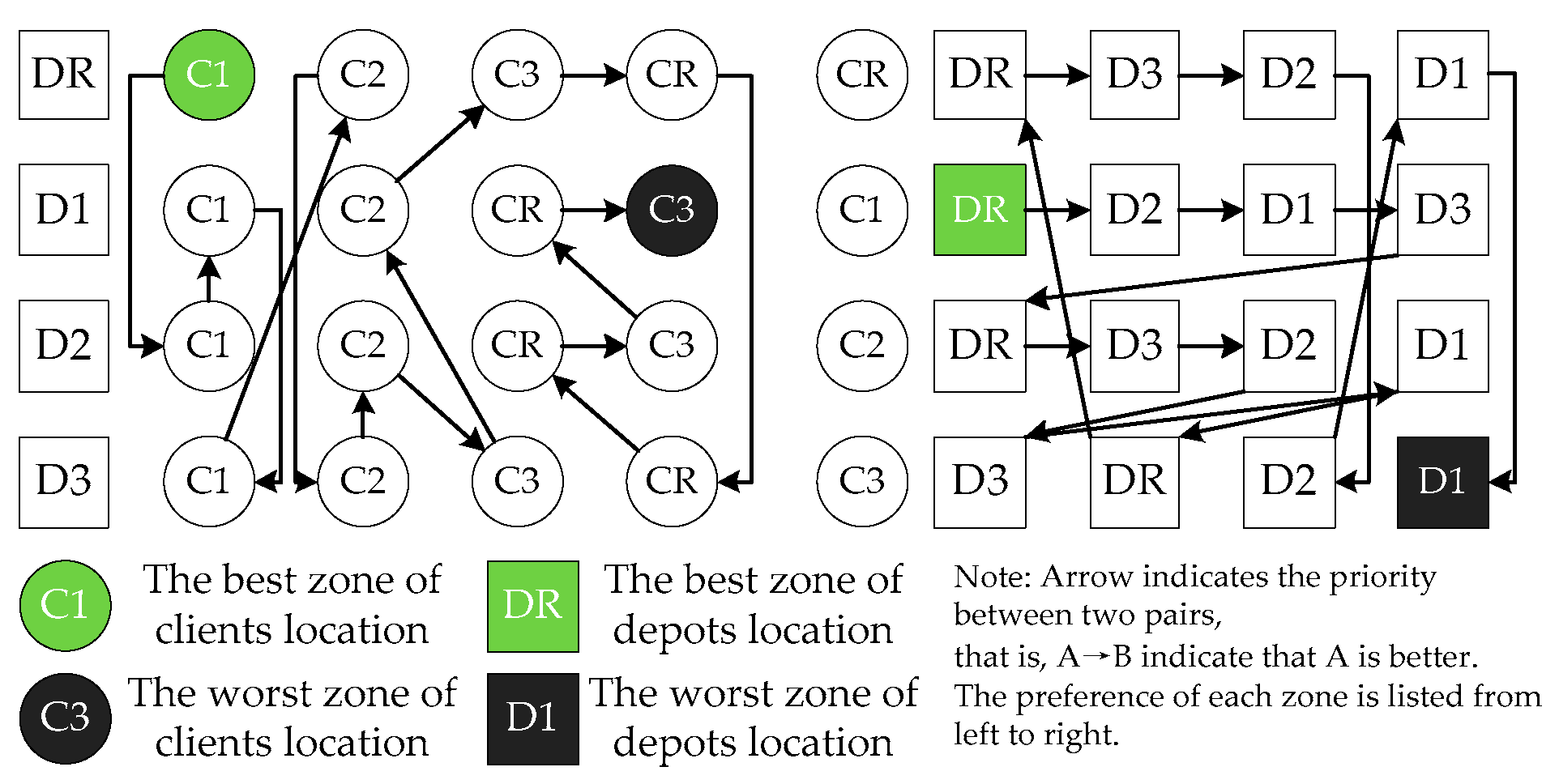
- The depot and client location has significant impacts on the logistics cost, client satisfaction, and service duration. Before determining the set of depots to open and the tracing of the routes, the joint effects of the depot and client location should be analyzed. In the context of this paper, the joint effect can be obtained: C1DR > C1D2 > C1D1 > C1D3 > C2DR > C2D3 > C2D2 > C3D3 > C2D1 > C3DR > CRDR > CRD3 > CRD2 > C3D2 > CRD1 > C3D1 (priority sequence). Moreover, we also analyzed the preference of client and depot in each speed zone, and we found that DR/D3 (C1→C2→C3→CR), D1/D2(C1→C2→CR→C3), CR/C2(DR→D3→D2→D1), C1(DR→D2→D1→D3), and C3(D3→DR→D2→D1), where A(B→C) indicates that the preference of A is B and C, and B is better than C;
- The fleet composition is another factor effecting the logistics network. From the perspectives of the results, the heterogonous fleet could always obtain better Pareto solutions;
- The zone area effects the depot and client location, and how to partition the speed zones (i.e., the best ratio of speed zones) and determine the depot and client location, to some extents, determine the logistics network. Therefore, the government and logistics companies should optimize the speed zone area for economic, environmental, and social effects.
Author Contributions
Funding
Conflicts of Interest
References
- Koc, C.; Bektas, T.; Jabali, O.; Laporte, G. The impact of depot location, fleet composition and routing on emission in city logistics. Transp. Res. Part B Methodol. 2016, 84, 81–102. [Google Scholar] [CrossRef]
- Leng, L.; Zhao, Y.; Wang, Z.; Wang, H.; Wang, W. Shared mechanism based self-adaptive hyperheuristic for regional low-carbon location-routing problem with time windows. Math. Probl. Eng. 2018, 2018, 8987402. [Google Scholar] [CrossRef]
- Zhang, C.M.; Zhao, Y.W.; Zhang, J.L.; Leng, L.L. Location and routing problem with minimizing carbon. Comp. Integr. Manuf. Syst. 2017, 23, 2768–2777. [Google Scholar] [CrossRef]
- Leng, L.; Zhao, Y.; Wang, Z.; Zhang, J.; Zhang, C. A novel hyper-heuristic for bi-objective regional low-carbon location-routing problem with multiple constraints. Sustainability 2019, 11, 1596. [Google Scholar] [CrossRef]
- Pourhejazy, P.; Kwon, O.K.; Lim, H. Integrating sustainability into the optimization of fuel logistics networks. KSCE J. Civ. Eng. 2019, 23, 1369–1383. [Google Scholar] [CrossRef]
- Qin, G.; Tao, F.; Li, L. A vehicle routing optimization problem for cold chain logistics considering customer satisfaction and carbon emissions. Int. J. Environ. Res. Public Health 2019, 16, 576. [Google Scholar] [CrossRef] [PubMed]
- Pourhejazy, P.; Kwon, O. The new generation of operations research methods in supply chain optimization: A review. Sustainability 2016, 8, 1033. [Google Scholar] [CrossRef]
- Drexl, M.; Schneider, M. A survey of variants and extensions of the location-routing problem. Eur. J. Oper. Res. 2015, 241, 283–308. [Google Scholar] [CrossRef]
- Ardekani, S.; Hauer, E.; Jamei, B. Traffic impact models. In The Traffic Flow Theory: A State-of-the Art Report; Federal Highway Administration Research and Technology: Washington DC, USA, 1996; Chapter 7; pp. 7–24. [Google Scholar]
- Bigazzi, A.; Bertini, R.L. Adding green performance metrics to a transportation data archive. Transp. Res. Rec. 2009, 2121, 30–40. [Google Scholar] [CrossRef]
- Alwakiel, H.N. Leveraging Weigh-in-Motion (WIM) Data to Estimate Link-Based Heavy-Vehicle Emissions. Ph.D. Thesis, Portland State University, Portland, OR, USA, 2011. [Google Scholar] [CrossRef]
- Lin, C.; Choy, K.L.; Chung, S.H.; Lam, H.Y. Survey of green vehicle routing problem: Past and future trends. Expert Syst. Appl. 2014, 41, 1118–1138. [Google Scholar] [CrossRef]
- Demir, E.; Bektas, T.; Laporte, G. A comparative analysis of several vehicle emission models for road freight transportation. Transp. Res. Part D Transp. Environ. 2011, 16, 347–357. [Google Scholar] [CrossRef]
- Demir, E.; Bektas, T.; Laporte, G. A review of recent research on green road freight transportation. Eur. J. Oper. Res. 2014, 237, 775–793. [Google Scholar] [CrossRef]
- Demir, E.; Bektas, T.; Laporte, G. The bi-objective pollution-routing problem. Eur. J. Oper. Res. 2014, 232, 464–478. [Google Scholar] [CrossRef]
- Poonthalir, G.; Nadarajan, R. A fuel efficient green vehicle routing problem with varying speed constraint (F-GVRP). Expert Syst. Appl. 2018, 100, 131–144. [Google Scholar] [CrossRef]
- Kuo, Y. Using simulated annealing to minimize fuel consumption for the time-dependent vehicle routing problem. Comput. Ind. Eng. 2010, 59, 157–165. [Google Scholar] [CrossRef]
- Kazemain, I.; Aref, S. A green perspective on capacitated time-dependent vehicle routing problem with time window. Int. J. Supply Chain Manag. 2017, 2, 20–38. [Google Scholar] [CrossRef]
- Mirmohammadi, S.H.; Tirkolaee, E.B.; Goli, A.; Dehnavi-Arani, S. The periodic green vehicle routing problem with considering of time-dependent urban traffic and time windows. Int. J. Opt. Civ. Eng. 2017, 7, 143–156. [Google Scholar]
- Andersson, H.; Hoff, A.; Christiansen, M.; Hasle, G.; Lokketanen, A. Industrial aspects and literature survey: Combined inventory management and routing. Comput. Oper. Res. 2010, 37, 1515–1536. [Google Scholar] [CrossRef]
- Koc, C.; Bektas, T.; Jabali, O. The fleet size and mix pollution-routing problem. Transp. Res. Part B Methodol. 2014, 70, 239–254. [Google Scholar] [CrossRef]
- Koc, C.; Bektas, T.; Jabali, O. The fleet size and mix location-routing time windows: Formulations and a heuristics algorithm. Eur. J. Oper. Res. 2016, 248, 33–51. [Google Scholar] [CrossRef]
- Pitera, K.; Sandoval, F.; Goodchild, A. Evaluation of emissions reduction in urban pickup systems heterogeneous fleet case study. Transp. Res. Rec. 2011, 2224, 8–16. [Google Scholar] [CrossRef]
- Xiao, Y.Y.; Konak, A. The heterogeneous green vehicle routing and scheduling problem with time-varying traffic congestion. Transp. Res. Part B Methodol. 2016, 88, 146–166. [Google Scholar] [CrossRef]
- Xiao, Y.Y.; Zhao, Q.H.; Falu, I. Development of a fuel consumption optimization model for the capacitated vehicle routing problem. Comput. Oper. Res. 2012, 39, 1419–1431. [Google Scholar] [CrossRef]
- Shen, L.; Tao, F.; Wang, S. Multi-depot open vehicle routing problem with time windows based on carbon trading. Int. J. Environ. Res. Public Health 2018, 15, 2025. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Tao, F.; Shi, Y. Optimization of location-routing problem for cold chain logistics considering carbon footprint. Int. J. Environ. Res. Public Health 2018, 15, 86. [Google Scholar] [CrossRef] [PubMed]
- Leng, L.; Zhao, Y.; Zhang, C.; Wang, S. Quantum-inspired hyper-heuristics for low-carbon location-routing problem with simultaneous pickup and delivery. Comp. Integr. Manuf. Syst. 2018, in press. [Google Scholar]
- Zhao, Y.; Leng, L.; Wang, S.; Zhang, C. Evolutionary hyper-heuristics for low-carbon location-routing problem with heterogeneous fleet. J. Control. Dec. 2018. [Google Scholar] [CrossRef]
- Wang, S.; Zhao, Y.; Leng, L.; Zhang, C. Research on low carbon location routing problem based on evolutionary hyper-heuristic algorithm of ant colony selection mechanism. Comp. Integr. Manuf. Syst. 2018, in press. [Google Scholar]
- Kan, Z.; Tang, L.; Kwan, M.P.; Zhang, X. Estimating vehicle fuel consumption and emissions using GPS big data. Int. J. Environ. Res. Public Health 2018, 15, 566. [Google Scholar] [CrossRef]
- Xiao, L.; Dridi, M.; Hassani, A.H.E.; Fei, H.; Lin, W. An improved cuckoo search for a patient transportation problem with consideration of reducing transport emissions. Sustainability 2018, 10, 793. [Google Scholar] [CrossRef]
- Lee, S.; Hwang, T. Estimating emissions from regional freight delivery under different urban development scenarios. Sustainability 2018, 10, 1188. [Google Scholar] [CrossRef]
- Hwang, T.; Ouyang, Y. Urban freight truck routing under stochastic congestion and emission considerations. Sustainability 2015, 7, 6610–6625. [Google Scholar] [CrossRef]
- Rakha, H.; Ahn, K.; Moran, K.; Saerens, B.; Van de Bulck, E. Simple comprehensive fuel consumption and CO2 emissions model based on instantaneous vehicle power. In Proceedings of the 90th Transportation Research Board Annual Meeting, Washington, DC, USA, 23–27 January 2011. [Google Scholar]
- Bandeira, J.; Carvalho, D.O.; Khattak, A.J.; Rouphail, N.M.; Coe; Coelho, M.C. A comparative empirical analysis of eco-friendly routes during peak and off-peak hours. In Proceedings of the Transportation Research Board 91st Annual Meeting, Washington, DC, USA, 22–26 January 2012. [Google Scholar]
- Bandeira, J.; Carvalho, D.O.; Khattak, A.J.; Rouphail, N.M.; Coelho, M.C. Generating emissions information for route selection: Experimental monitoring and routes characterization. J. Intell. Transport. Syst. 2013, 17, 3–17. [Google Scholar] [CrossRef]
- Japanese Government Website. Available online: http://www.mlit.go.jp/common/000037099.pdf (accessed on 18 March 2019).
- Chen, C.; Qiu, R.; Hu, X. The location-routing problem with full truckloads in low-carbon supply chain network designing. Math. Probl. Eng. 2018, 2018, 6315631. [Google Scholar] [CrossRef]
- Mohammadi, M.; Razmi, J.; Tavakkoli-Moghaddam, R. Multiobjective invasive weed optimization for stochastic green hub location routing problem with simultaneous pick-ups and deliveries. Econ. Comput. Econ. Cybern. Stud. 2013, 47, 247–266. [Google Scholar]
- Govindan, K.; Jafarian, A.; Khodaverdi, R.; Devika, K. Two-echelon multiple-vehicle location-routing problem with time windows for optimization of sustainable supply chain network of perishable food. Int. J. Prod. Econ. 2014, 152, 9–28. [Google Scholar] [CrossRef]
- Nakhjirkan, S.; Rafiei, F.M. An integrated multi-echelon supply chain network design considering stochastic demand: A genetic algorithm-based solution. Promet Traffic Transp. 2017, 29, 391–400. [Google Scholar] [CrossRef]
- Validi, S. Low-Carbon Multiobjective Location-Routing in Supply Chain Network Design. Ph.D. Thesis, Dublin City University Business School, Berlin, Germany, 2014. [Google Scholar]
- Validi, S.; Bhattacharya, A.; Byrne, P.J. Integrated low-carbon distribution system for the demand side of a product distribution supply chain: A DoE-guided MOPSO optimizer-based solution approach. Int. J. Prod. Res. 2014, 52, 3074–3096. [Google Scholar] [CrossRef]
- Validi, S.; Bhattacharya, A.; Byrne, P.J. A case analysis of a sustainable food supply chain distribution system-a multiobjective approach. Int. J. Prod. Econ. 2014, 152, 71–87. [Google Scholar] [CrossRef]
- Faraji, F.; Afshar-Nadjafi, B. A bi-objective green location-routing model and solving problem using a hybrid metaheuristic algorithm. Int. J. Logist. Syst. Manag. 2018, 30, 366–385. [Google Scholar] [CrossRef]
- Tang, J.; Ji, S.; Jiang, L. The design of a sustainable location-routing-inventory model considering consumer environmental behavior. Sustainability 2016, 8, 211. [Google Scholar] [CrossRef]
- Qazvini, Z.E.; Amalnick, M.S.; Mina, H. A green multi-depot location routing model with split-delivery and time window. Int. J. Manag. Concepts Philos. 2016, 9, 271–282. [Google Scholar] [CrossRef]
- Rabbani, M.; Davoudkhani, M.; Farrokhi-Asi, H. A new multiobjective green location routing problem with heterogeneous fleet of vehicles and fuel constraint. Int. J. Strateg. Decis. Sci. 2017, 8, 99–119. [Google Scholar] [CrossRef]
- Toro, E.M.; France, J.F.; Echeverri, M.G.; Guimarães, F. A multiobjective model for the green capacitated location-routing problem considering environmental impact. Comput. Ind. Eng. 2017, 110, 114–125. [Google Scholar] [CrossRef]
- Wang, X.; Li, X. Carbon reduction in the location routing problem with heterogeneous fleet, simultaneous pickup-delivery and time windows. In Proceedings of the 21st International Conference on Knowledge-Based and Intelligent Information and Engineering Systems (KES), Marseille, France, 6–8 September 2017; ZanniMerk, C., Frydman, C., Toro, C., Hicks, Y., Howlett, R.J., Jain, L.C., Eds.; Elsevier B.V.: Amsterdam, The Netherlands, 2017; Volume 112, pp. 1131–1140. [Google Scholar] [CrossRef]
- Qian, Z.; Zhao, Y.; Wang, S.; Leng, L.; Wang, W. A hyper heuristic algorithm for low carbon location routing problem. In Proceedings of the Advances in Neural Networks-ISNN 2018, 15th International Symposium on NeuralNetworks, Minsk, Belarus, 25–28 June 2018. [Google Scholar] [CrossRef]
- Ferreira, T.N.; Jackson, A.; Lima, P.; Strickler, A.; Kuk, J.N.; Vergilio, S.R.; Pozo, A. Hyper-heuristic-based product selection for software product line testing. IEEE Comput. Intell. Mag. 2017, 12, 34–45. [Google Scholar] [CrossRef]
- Strickler, A.; Lima, J.A.P.; Vergilio, S.R.; Pozo, A.T.R. Deriving products for variability test of feature models with a hyper-heuristic approach. Appl. Soft Comput. 2016, 49, 1232–1242. [Google Scholar] [CrossRef]
- Walker, J.D.; Ocha, G.; Gendreau, M.; Burke, E.K. Vehicle routing and adaptive iterated local search within the HyFlex hyper-heuristic framework. In Proceedings of the Learning and Intelligent Optimization 6th International Conference, Paris, France, 16–20 January 2012. [Google Scholar] [CrossRef]
- Denzinger, J.; Fuchs, M.; Fuchs, M. High performance ATP systems by combining several AI methods. In Proceedings of the International Joint Conference on Artificial Intelligence, Nagoya, Japan, 23–29 August 1997. [Google Scholar]
- Cowling, P.; Kendall, G.; Soubeiga, E. A hyper-heuristic approach to scheduling a sales summit. In Proceedings of the International Conference on the Practice and Theory of Automated Timetabling, Konstanz, Germany, 16–18 August 2000; Burke, E., Erben, W., Eds.; Springer: Berlin, Germany, 2000. [Google Scholar] [CrossRef]
- Burke, E.K.; Gendreau, M.; Hyde, M.; Kendall, G.; Ochoa, G.; Qu, R. Hyper-heuristics: A survey of the state of the art. J. Oper. Res. Soc. 2013, 64, 1695–1724. [Google Scholar] [CrossRef]
- Kumari, A.C.; Srinivas, K. Hyper-heuristic approach for multiobjective software module clustering. J. Syst. Softw. 2016, 117, 384–401. [Google Scholar] [CrossRef]
- Li, W.; Ozcan, E.; John, R. Multiobjective evolutionary algorithms and hyper-heuristics for wind farm layout optimization. Renew. Energy 2017, 105, 473–482. [Google Scholar] [CrossRef]
- Maashi, M.; Kendall, G.; Ozcan, E. Choice function based hyper-heuristics for multiobjective optimization. Appl. Soft Comput. 2015, 28, 312–326. [Google Scholar] [CrossRef]
- Chakhlevitch, K.; Cowling, P. Hyperheuristics: Recent developments. In Adaptive and Multilevel Metaheuristics; Springer: Berlin, Germany, 2008; pp. 3–29. [Google Scholar] [CrossRef]
- Burke, E.; Kendall, G.; Newall, J.; Hart, E.; Ross, P.; Schulenburg, S. Hyper-heuristics: An emerging direction in modern search technology. In Handbook of Metaheuristics; Springer: Boston, MA, USA, 2003; pp. 457–474. [Google Scholar] [CrossRef]
- Maashi, M.; Ozcan, E.; Kendall, G. A multiobjective hyper-heuristic based on choice function. Expert Syst. Appl. 2014, 41, 4475–7793. [Google Scholar] [CrossRef]
- Koulinas, G.; Kotsikas, L.; Anagnostopoulos, K. A particle swarm optimization based hyper-heuristic algorithm for the classic resource constrained project scheduling problem. Inf. Sci. 2014, 277, 680–693. [Google Scholar] [CrossRef]
- Kareb, D.E.; Fouquet, F.; Traon, Y.L.; Bourcier, J. Sputnik: Elitist Artificial Mutation Hyper-Heuristic for Runtime Usage of Multiobjective Evolutionary Algorithms. 2014. Available online: https://arxiv.org/abs/1402.4442v1 (accessed on 5 January 2019).
- Castro, O.R.; Pozo, A. A MOPSO based on hyper-heuristic to optimize many-objective problems. In Proceedings of the IEEE Symposium on Swarm Intelligence (SIS), Orlando, FL, USA, 9–12 December 2014; IEEE: New York, NY, USA, 2014; pp. 251–258. [Google Scholar] [CrossRef]
- Castro, O.R.; Pozo, A. Using hyper-heuristic to select leader and archiving methods for many-objective problems. In Proceedings of the 8th International Conference on Evolutionary Multi-Criterion Optimization (EMO), Guimaraes, Portugal, 29 March–1 April 2015; GasparCunha, A., Antunes, C.H., Coello, C.C., Eds.; Springer: Berlin, Germany, 2015; Volume 9018, pp. 109–123. [Google Scholar] [CrossRef]
- Goncalves, R.A.; Kuk, J.N.; Almeida, C.P.; Venske, S.M. MOEA/D-HH: A hyper-heuristic for multiobjective problems. In Lecture Notes in Computer Science, 8th International Conference on Evolutionary Multi-Criterion Optimization (EMO), Guimaraes, Portugal, 29 March–1 April 2015; GasparCunha, A., Antunes, C.H., Coello, C.C., Eds.; Springer: Berlin, Germany, 2015; Volume 9018, pp. 94–108. [Google Scholar] [CrossRef]
- Hitomi, N.; Selva, D. Experiments with human integration in asynchronous and sequential multi-agent frameworks for architecture optimization. In Procedia Computer Science, Conference on Systems Engineering Research, Hoboken, NJ, USA, 17–19 March 2015; Wade, J., Cloutier, R., Eds.; Elsevier: Amsterdam, The Netherlands, 2015; Volume 44, pp. 393–402. [Google Scholar] [CrossRef]
- Qian, C.; Tang, K.; Zhou, Z.H. Selection hyper-heuristics can provably be helpful in evolutionary multiobjective optimization. In Lecture Notes in Computer Science, 14th International Conference on Parallel Problem Solving from Nature (PPSN), Edinburgh, ENGLAND, 17–21 September 2016; Handl, J., Hart, E., Lewis, P.R., LopezIbanez, M., Ochoa, G., Paechter, B., Eds.; Springer: Cham, Switzerland, 2016; Volume 9921, pp. 835–846. [Google Scholar] [CrossRef]
- Freitag, M.; Hildebrandt, T. Automatic design of scheduling rules for complex manufacturing systems by multiobjective simulation-based optimization. CIRP Ann. Manuf. Technol. 2016, 65, 433–436. [Google Scholar] [CrossRef]
- Guizzo, G.; Vergilio, S.R.; Pozo, A.T.R.; Fritsche, G.M. A multiobjective and evolutionary hyper-heuristic applied to the integration and test order problem. Appl. Soft Comput. 2017, 56, 331–344. [Google Scholar] [CrossRef]
- Hitomi, H.; Selva, D.A. classification and comparison of credit assignment strategies in multiobjective adaptive operator selection. IEEE Trans. Evol. Comput. 2017, 21, 294–314. [Google Scholar] [CrossRef]
- Xu, C.; Liu, Y.; Li, P.; Yang, Y. Unified multiobjective mapping for network-on-chip using genetic-based hyper-heuristic algorithms. IET Comput. Digit. Tech. 2017, 12, 158–166. [Google Scholar] [CrossRef]
- Yao, Y.; Peng, Z.; Xiao, B. Parallel hyper-heuristic algorithm for multiobjective route planning in a smart city. IEEE Trans. Veh. Technol. 2018, 67, 10307–10318. [Google Scholar] [CrossRef]
- Almeida, C.; Goncalves, R.; Venske, S.; Luders, R.; Delgado, M. Multi-armed bandit based hyper-heuristics for the permutation flow shop problem. In Proceedings of the 7th Brazilian Conference on Intelligent Systems (BRACIS), Sao Paulo, Brazil, 22–25 October 2018; IEEE: New York, NY, USA, 2018; pp. 139–144. [Google Scholar] [CrossRef]
- Gomez, J.; Terashima-Marin, H. Evolutionary hyper-heuristics for tackling bi-objective 2D bin packing problems. Genet. Program. Evol. Mach. 2018, 19, 151–181. [Google Scholar] [CrossRef]
- Castro, O.R.; Fritsche, G.M.; Pozo, A. Evaluating selection methods on hyper-heuristic multiobjective particle swarm optimization. J. Heuristics 2018, 24, 581–616. [Google Scholar] [CrossRef]
- Zhang, Y.; Harman, M.; Ochoa, G.; Rule, G.; Brinkkemper, S. An empirical study of meta-and hyper-heuristic search for multiobjective release planning. ACM Trans. Softw. Eng. Methodol. 2018, 27, 3. [Google Scholar] [CrossRef]
- Zhou, Y.; Yang, J.; Zheng, L. Hyper-heuristic coevolution of machine assignment and job sequencing rules for multiobjective dynamic flexible job shop scheduling. IEEE Access 2019, 7, 68–88. [Google Scholar] [CrossRef]
- Chand, S.; Singh, H.; Ray, T. Evolving heuristics for the resource constrained project scheduling problem with dynamic resource disruptions. Swarm Evol. Comput. 2019, 44, 897–912. [Google Scholar] [CrossRef]
- Li, W.; Ozcan, E.; John, R. A learning automata-based multiobjective hyper-heuristic. IEEE Trans. Evol. Comput. 2019, 23, 59–72. [Google Scholar] [CrossRef]
- Krause, E.F. Taxicab Geometry: An Adventure in Non-Euclidean Geometry; Dover Publisher: New York, NY, USA, 2012. [Google Scholar]
- Karaoglan, I.; Altiparmak, F.; Kara, I.; Dengiz, B. A branch and cut algorithm for the location-routing problem with simultaneous pickup and delivery. Eur. J. Oper. Res. 2011, 211, 318–332. [Google Scholar] [CrossRef]
- Barreto, S.; Ferreira, C.; Paixao, J.; Santos, B.S. Using clustering analysis in a capacitated location-routing problem. Eur. J. Oper. Res. 2007, 179, 968–977. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Zitzler, E.; Laumanns, M.; Thiele, L. SPEA2: Improving the strength Pareto evolutionary algorithm. In Proceedings of the Evolutionary Methods for Design, Optimization and Control with Applications to Industrial Problems, Athens, Greece, 19–21 September 2001. [Google Scholar]
- Li, M.; Yang, S.; Liu, X. Bi-goal evolution for many-objective optimization problems. Artif. Intell. 2015, 228, 46–65. [Google Scholar] [CrossRef]
- Chen, B.; Zeng, W.; Lin, Y.; Zhang, D. A new local search-based multiobjective optimization algorithm. IEEE Trans. Evol. Comput. 2015, 19, 50–73. [Google Scholar] [CrossRef]
- Yang, S.; Li, M.; Liu, X.; Zheng, J. A grid-based evolutionary algorithm for many-objective optimization. IEEE Trans. Evol. Comput. 2013, 5, 721–736. [Google Scholar] [CrossRef]
- Zitzler, E.; Kunzli, S. Indicator-based selection in multiobjective search. In Proceedings of the Parallel Problem Solving from Nature-PPSN VIII, International Conference on Parallel Problem Solving from Nature, Birmingham, UK, 13–17 September 2004; Yao, X., Ed.; Springer: Berlin, Germany, 2004. [Google Scholar] [CrossRef]
- Deb, K.; Jain, H. An evolutionary many-objective optimization algorithm using reference-point based non-dominated sorting approach, Part I: Solving problems with box constraints. IEEE Trans. Evol. Comput. 2014, 4, 577–601. [Google Scholar] [CrossRef]
- Corne, D.W.; Jerram, N.R.; Knowles, J.D.; Oates, M.J. PESA-II: Region-based selection in evolutionary multiobjective optimization. In Proceedings of the Genetic and Evolutionary Computation Conference, New York, NY, USA, 9–13 July 2002. [Google Scholar]
- Zhang, Q.; Li, H. A multiobjective evolutionary algorithm based on decomposition. IEEE Trans. Evol. Comput. 2007, 11, 712–731. [Google Scholar] [CrossRef]
- Scoring System. Available online: http://www.asap.cs.nott.ac.uk/external/chesc2011/ (accessed on 12 February 2019).
- Nadizadeh, A.; Kafash, B. Routing problem with simultaneous pickup and delivery demands. Transp. Lett. 2019, 1, 1–19. [Google Scholar] [CrossRef]
- Yu, H.; Solvang, W.D. A carbon-constrained stochastic optimization model with augmented multi-criteria scenario-based risk-averse solution for reverse logistics network design under uncertainty. J. Clean. Prod. 2017, 164, 1248–1267. [Google Scholar] [CrossRef]
- Yu, H.; Solvang, W.D. Incorporating flexible capacity in the planning of a multi-product multi-echelon sustainable reverse logistics network under uncertainty. J. Clean. Prod. 2018, 198, 285–303. [Google Scholar] [CrossRef]
- Yu, H.; Solvang, W.D. An improved multiobjective programming with augmented ε-constraint method for hazardous waste location-routing problems. Int. J. Environ. Res. Public Health 2016, 13, 548. [Google Scholar] [CrossRef] [PubMed]
| Module | Characteristic | Example |
|---|---|---|
| Factor model (FM) | Only consider a few key factors, such as travel distance, vehicle load. | Fuel consumption rate (FCR) [3,6,25,26,27,28,29,30]; models by Pourhejazy et al. [5] |
| Macro view (Macro) | Average aggregate network parameters, factors don’t change over traveling time | Computer programs to calculate emissions from road transportation [31,32]; Methodology for calculating transportation emissions and energy consumption [33,34], etc. |
| Micro view (Micro) | More detailed information, second level, especially vehicle speed. | Comprehensive model emission model (CMEM) [1,2,4,13,15,21]; comprehensive power-based fuel consumption models [35]; vehicle specific power model [36,37] |
| Authors [Reference] (Year) | Domain-Problem | Main Characteristics/Component |
|---|---|---|
| Koulinas et al. [65] (2014) | Resource constrained project scheduling problem | Domain-LLH; particle swarm optimization |
| Kateb et al. [66] (2014) | Runtime usage of MOEAs | Artificial selection of mutation for NSGAII |
| Maashi et al. [64] (2014) | MOEAs benchmark (WFG test suite) | NSGAII, SPEA2, MOGA; choice function; All moves |
| Castro and Pozo [67,68] (2014&2015) | MOEAs benchmark (DTLZ test suite) | Using leader selection methods and archiving strategies as LLH; IE acceptance; R2 indicator |
| Goncalves et al. [69] (2015) | MOEAs benchmark (UF test suite) | Using DE operators as LLH; MOEA/D; Tchebycheff function |
| Hitomi and Selva [70] (2015) | Architecture optimization problems | Dynamic MAB; using heuristic agents as LLH |
| Maashi et al. [61] (2015) | MOEAs benchmark (WFG test suite) | Choice function; great deluge algorithm and late acceptance; NSGAII, SPEA2, and MOGA |
| Qian et al. [71] (2016) | Multiobjective optimization | Using selection mechanisms, mutation, acceptance strategies as LLH |
| Kumari and Srinivas [59] (2016) | software module clustering | Using crossover and mutation as LLH; NSGAII ranking mechanism; reinforcement learning strategy with adaptive weights |
| Strickler et al. [54] (2016) | variability test of feature models | Fitness rate rank-based MAB; NSGAII ranking mechanism; crossover and mutation operators |
| Freitag and Hildebrandt [72] (2016) | Scheduling rules for complex manufacturing systems | Using scheduling rules as LLH; simulation-based genetic programming; |
| Guizzo et al. [73] (2017) | Integration and test order problem | Choice function, MAB; crossover and mutation operators; reward based-Pareto dominance |
| Li et al. [60] (2017) | Wind farm layout problem | Random, fixed sequence, choice function; all moves, GDA, NSGAII ranking mechanism |
| Ferreira et al. [53] (2017) | Software Product Line Testing | Using crossover and mutation operators as LLH; HH-based MOEAs (IBEA, SPEA2, NSGAII, and MOEA/D-DRA), namely elitism selection strategy; random and upper confidence |
| Hitomi and Selva [74] (2017) | MOEAs benchmark (WFG, UF and DTLZ test suite) | HH-based MOEAs (IBEA, MOEA/D-DRA, NSGAII); multiple adaptive operator selections |
| Xu et al. [75] (2018) | Multiobjective mapping for network-on-chip | Genetic-based hyper-heuristic algorithm; using genetic operator as LLH; reinforcement learning strategy with adaptive weights |
| Yao et al. [76] (2018) | Multiobjective route planning in a smart city | Reinforcement learning mechanism; domain-LLH; |
| Almeida et al. [77] (2018) | Permutation flow shop problem | MOEA/D-DRA-based MOHH; MAB; crossover and mutation operators |
| Gomez and Terashima- Marin [78] (2018) | Bi-objective 2D bin packing problems | Evolutionary hyper-heuristics multiobjective framework; NSGAII, SPEA2 and GDE3 |
| Castro et al. [79] (2018) | MOEAs benchmark (DTLZ, WFG test suite) | Fitness rate rank-based MAB; using leader selection methods and archiving strategies as LLH; R2-based IE acceptance and reward |
| Zhang et al. [80] (2018) | Software release planning | Extreme value credit assignment; probability matching; domain-LLH |
| Qian et al. [52] (2018) | MOLCLRP | Tabu search; reinforcement learning method; NSGA-II ranking mechanism |
| Zhou et al. [81] (2019) | Flexible job shop scheduling | NSGA-II ranking mechanism; Pareto strength; genetic programming |
| Chand et al. [82] (2019) | resource constrained project scheduling problem | genetic programming hyperheuristic; NSGA-II ranking mechanism; using priority rules as LLH |
| Li et al. [83] (2019) | MOEAs benchmark | Learning automata; MOEAs as LLHs |
| Set | BiGE | GrEA | IBEA | NSGAII | NSGA-III | NSLS | PEAS-II | SPEA2 | QS1 | QS2 | QS1a | QS2a |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| L201 | 2.68 | 3.41 | 4.66 | 2.65 | 3.05 | 2.44 | 2.65 | 2.12 | 2.24 | 2.43 | 1.72 | 1.64 |
| L202 | 1.35 | 2.09 | 2.73 | 1.38 | 1.55 | 1.04 | 1.22 | 1.00 | 0.98 | 1.23 | 0.49 | 0.47 |
| L203 | 1.67 | 2.64 | 4.08 | 1.46 | 2.14 | 1.36 | 1.43 | 1.33 | 1.28 | 1.39 | 0.82 | 0.75 |
| L301 | 2.29 | 4.68 | 5.95 | 2.64 | 3.15 | 2.40 | 2.77 | 2.23 | 1.49 | 1.67 | 0.70 | 0.72 |
| L302 | 3.381 | 5.01 | 6.50 | 3.51 | 4.34 | 3.39 | 3.46 | 3.380 | 3.17 | 3.90 | 2.20 | 2.30 |
| L303 | 4.52 | 5.87 | 7.36 | 5.30 | 4.53 | 4.66 | 4.94 | 3.796 | 3.01 | 3.795 | 2.09 | 2.81 |
| L401 | 2.37 | 3.73 | 4.36 | 3.54 | 3.23 | 2.90 | 2.67 | 2.61 | 2.36 | 2.87 | 1.17 | 1.29 |
| L402 | 2.59 | 3.18 | 3.48 | 4.13 | 3.25 | 2.99 | 2.93 | 2.86 | 2.48 | 2.84 | 1.17 | 1.32 |
| L403 | 2.57 | 4.10 | 4.93 | 3.77 | 3.48 | 3.01 | 2.84 | 2.83 | 2.57 | 2.98 | 1.336 | 1.338 |
| L501 | 3.61 | 5.06 | 5.89 | 6.30 | 4.76 | 5.60 | 5.23 | 4.33 | 4.10 | 4.43 | 1.71 | 2.15 |
| L502 | 3.79 | 5.74 | 6.76 | 5.31 | 5.19 | 4.17 | 5.67 | 3.50 | 3.18 | 3.95 | 1.94 | 2.10 |
| L503 | 2.99 | 3.72 | 4.19 | 4.82 | 3.47 | 3.85 | 3.72 | 3.34 | 2.98 | 3.68 | 1.67 | 1.88 |
| f/s/t | 1/4/2 | 0/0/0 | 0/0/0 | 0/0/0 | 0/0/0 | 0/0/2 | 0/0/0 | 1/4/6 | 10/2/0 | 0/2/2 | 9 | 3 |
| Set | BiGE | GrEA | IBEA | NSGAII | NSGA-III | NSLS | PEAS-II | SPEA2 | QS1 | QS2 | QS1a | QS2a |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| L201 | 2.1467 | 2.1389 | 2.1199 | 2.1422 | 2.1520 | 2.1555 | 2.1401 | 2.1680 | 2.1647 | 2.1594 | 2.1699 | 2.1769 |
| L202 | 0.8204 | 0.8163 | 0.8161 | 0.8184 | 0.8105 | 0.8207 | 0.8180 | 0.8221 | 0.8218 | 0.8197 | 0.8251 | 0.8252 |
| L203 | 1.7113 | 1.7094 | 1.7007 | 1.7059 | 1.7016 | 1.7091 | 1.7021 | 1.7097 | 1.7105 | 1.7083 | 1.7151 | 1.7154 |
| L301 | 1.0995 | 1.0695 | 1.0670 | 1.0732 | 1.0519 | 1.0812 | 1.0555 | 1.0988 | 1.1603 | 1.1511 | 1.1678 | 1.1657 |
| L302 | 2.8058 | 2.7526 | 2.7432 | 2.8109 | 2.7704 | 2.7786 | 2.7822 | 2.7596 | 2.8053 | 2.7684 | 2.8287 | 2.8139 |
| L303 | 1.7902 | 1.7889 | 1.7584 | 1.6971 | 1.7939 | 1.7467 | 1.7393 | 1.8375 | 1.9062 | 1.8478 | 1.9222 | 1.8688 |
| L401 | 2.0993 | 2.0970 | 2.0870 | 2.0676 | 2.0394 | 2.0973 | 2.0661 | 2.0970 | 2.1067 | 2.0710 | 2.1468 | 2.1396 |
| L402 | 2.3967 | 2.4103 | 2.4153 | 2.3796 | 2.3799 | 2.4285 | 2.3836 | 2.4312 | 2.4457 | 2.3981 | 2.4919 | 2.4845 |
| L403 | 2.9053 | 2.8752 | 2.8740 | 2.8989 | 2.8676 | 2.9062 | 2.8898 | 2.9091 | 2.9145 | 2.8898 | 2.9560 | 2.9553 |
| L501 | 2.2779 | 2.2738 | 2.1761 | 2.2312 | 2.2345 | 2.2130 | 2.1681 | 2.3257 | 2.3613 | 2.3190 | 2.4770 | 2.4676 |
| L502 | 2.2264 | 2.1440 | 2.1580 | 2.1760 | 2.1605 | 2.2007 | 2.0440 | 2.2392 | 2.3101 | 2.2517 | 2.3589 | 2.3444 |
| L503 | 2.3465 | 2.3506 | 2.3081 | 2.3510 | 2.3456 | 2.3945 | 2.3042 | 2.3914 | 2.4076 | 2.3388 | 2.4609 | 2.4466 |
| f/s/t | 1/2/0 | 0/0/0 | 0/0/0 | 1/0/0 | 0/0/0 | 0/1/3 | 0/0/0 | 2/3/6 | 8/3/1 | 0/3/2 | 9 | 3 |
| SR | FRR-MAB | QS | CF | Total | |
|---|---|---|---|---|---|
| AM | 110 | 107 | 126 | 115 | 458 |
| LA | 130 | 116 | 133 | 99 | 478 |
| GDA | 0 | 0 | 0 | 0 | 0 |
| Total | 240 | 223 | 259 | 241 | NA |
| Set | CRDR | CRD1 | CRD2 | CRD3 | C1DR | C1D1 | C1D2 | C1D3 | C2DR | C2D1 | C2D2 | C2D3 | C3DR | C3D1 | C3D2 | C3D3 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| L201 | 17.6 | 23.6 | 16.3 | 12.5 | 4.8 | 9.2 | 6.5 | 8.3 | 3.6 | 10.6 | 5.0 | 3.7 | 17.0 | 36.3 | 24.4 | 16.2 |
| L202 | 36.0 | 41.0 | 36.1 | 34.8 | 4.4 | 8.5 | 5.8 | 9.2 | 13.3 | 19.4 | 16.5 | 15.4 | 25.2 | 29.7 | 25.5 | 22.7 |
| L203 | 22.1 | 23.1 | 27.4 | 21.4 | 4.5 | 7.2 | 6.8 | 12.6 | 13.9 | 13.3 | 11.2 | 12.2 | 19.1 | 21.5 | 17.3 | 16.0 |
| L204 | 14.4 | 22.8 | 17.0 | 16.6 | 2.7 | 6.9 | 5.9 | 7.4 | 6.6 | 12.4 | 7.5 | 10.0 | 12.6 | 21.7 | 15.5 | 14.0 |
| L301 | 13.8 | 19.6 | 20.6 | 14.6 | 4.5 | 4.2 | 4.3 | 8.7 | 4.8 | 7.8 | 5.9 | 10.0 | 11.4 | 32.1 | 20.5 | 11.2 |
| L302 | 17.2 | 40.5 | 17.6 | 17.9 | 3.2 | 7.3 | 4.4 | 7.2 | 11.7 | 14.8 | 10.1 | 13.1 | 27.8 | 26.9 | 21.1 | 16.7 |
| L303 | 16.7 | 19.1 | 16.1 | 16.3 | 4.9 | 6.4 | 4.8 | 7.2 | 7.9 | 10.9 | 8.5 | 9.5 | 11.0 | 14.8 | 10.7 | 11.0 |
| L304 | 31.4 | 36.2 | 29.4 | 26.7 | 4.0 | 6.6 | 4.3 | 11.1 | 13.1 | 16.0 | 11.5 | 13.0 | 32.2 | 36.0 | 31.4 | 27.7 |
| L401 | 9.4 | 24.3 | 13.4 | 10.9 | 4.5 | 10.2 | 4.7 | 9.2 | 5.2 | 14.3 | 8.8 | 9.8 | 7.2 | 21.5 | 12.9 | 6.2 |
| L402 | 11.6 | 22.6 | 13.6 | 8.8 | 3.3 | 6.3 | 7.1 | 6.2 | 6.2 | 14.1 | 7.1 | 7.2 | 10.3 | 20.2 | 9.9 | 7.1 |
| L403 | 11.1 | 23.8 | 14.0 | 11.6 | 3.0 | 4.3 | 4.7 | 10.1 | 4.1 | 16.1 | 8.7 | 7.6 | 12.6 | 25.7 | 13.4 | 7.8 |
| L404 | 9.8 | 21.2 | 9.4 | 12.1 | 5.1 | 2.5 | 7.3 | 5.5 | 10.6 | 10.3 | 12.1 | 9.8 | 11.4 | 15.0 | 15.3 | 10.4 |
| L501 | 19.7 | 26.0 | 19.9 | 20.0 | 3.2 | 1.9 | 7.3 | 11.3 | 10.5 | 14.4 | 9.7 | 10.9 | 17.4 | 31.2 | 19.3 | 11.8 |
| L502 | 10.6 | 29.4 | 17.4 | 10.8 | 2.2 | 12.8 | 7.1 | 7.9 | 3.1 | 7.0 | 7.6 | 5.8 | 10.8 | 28.6 | 17.8 | 14.0 |
| L503 | 14.2 | 25.8 | 16.8 | 13.1 | 4.5 | 1.6 | 3.3 | 8.6 | 5.7 | 17.8 | 9.4 | 8.7 | 13.5 | 29.3 | 17.1 | 13.8 |
| L504 | 19.2 | 34.5 | 22.8 | 16.9 | 2.2 | 2.8 | 8.0 | 6.4 | 11.0 | 22.8 | 14.4 | 11.2 | 15.2 | 31.4 | 22.2 | 15.0 |
| Set | CRDR | CRD1 | CRD2 | CRD3 | C1DR | C1D1 | C1D2 | C1D3 | C2DR | C2D1 | C2D2 | C2D3 | C3DR | C3D1 | C3D2 | C3D3 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| L201 | 15.0 | 12.7 | 17.6 | 19.9 | 25.2 | 23.0 | 25.1 | 23.5 | 27.4 | 22.3 | 25.9 | 27.4 | 16.3 | 6.8 | 12.4 | 16.9 |
| L202 | 9.6 | 7.0 | 9.4 | 10.8 | 32.8 | 27.6 | 30.7 | 31.9 | 24.2 | 19.5 | 22.6 | 24.5 | 15.4 | 12.1 | 14.5 | 17.2 |
| L203 | 10.9 | 9.8 | 7.0 | 11.4 | 25.7 | 24.0 | 25.7 | 21.2 | 14.3 | 14.6 | 17.1 | 16.4 | 12.8 | 11.0 | 13.2 | 14.6 |
| L204 | 18.8 | 12.9 | 17.2 | 18.6 | 32.4 | 28.5 | 29.4 | 29.9 | 28.4 | 23.2 | 27.2 | 28.3 | 22.4 | 16.2 | 20.5 | 23.8 |
| L301 | 19.6 | 14.9 | 15.5 | 19.4 | 28.3 | 29.5 | 28.2 | 25.7 | 31.1 | 27.9 | 30.5 | 26.6 | 23.0 | 12.1 | 17.4 | 23.8 |
| L302 | 19.1 | 8.2 | 17.7 | 17.6 | 32.5 | 29.1 | 32.2 | 30.1 | 22.2 | 20.9 | 23.7 | 21.4 | 12.6 | 12.7 | 16.1 | 19.7 |
| L303 | 18.2 | 16.2 | 18.1 | 20.3 | 30.6 | 29.6 | 31.1 | 32.4 | 25.2 | 22.7 | 25.2 | 27.2 | 23.6 | 20.6 | 22.9 | 25.2 |
| L304 | 0.8 | 0.5 | 1.6 | 2.1 | 17.1 | 15.0 | 16.6 | 16.5 | 7.1 | 5.7 | 7.0 | 7.2 | 0.2 | 0.0 | 0.1 | 0.9 |
| L401 | 24.8 | 14.1 | 21.2 | 23.7 | 34.0 | 25.6 | 31.4 | 33.4 | 29.1 | 21.5 | 25.0 | 30.4 | 27.9 | 16.7 | 22.3 | 30.1 |
| L402 | 24.5 | 17.1 | 23.0 | 28.0 | 35.4 | 30.3 | 29.1 | 32.4 | 28.4 | 21.9 | 27.0 | 29.1 | 24.9 | 17.6 | 25.7 | 28.6 |
| L403 | 22.2 | 15.0 | 20.3 | 22.5 | 31.9 | 31.1 | 32.3 | 28.4 | 29.4 | 19.8 | 24.3 | 28.9 | 22.0 | 13.6 | 21.6 | 26.2 |
| L404 | 33.0 | 22.9 | 32.1 | 33.9 | 40.0 | 40.1 | 35.6 | 42.3 | 31.8 | 30.7 | 29.0 | 34.6 | 32.3 | 27.8 | 27.0 | 33.1 |
| L501 | 16.6 | 12.4 | 15.7 | 16.5 | 29.5 | 29.0 | 23.1 | 22.9 | 20.8 | 17.7 | 20.9 | 22.8 | 16.1 | 9.2 | 15.7 | 20.9 |
| L502 | 18.9 | 9.6 | 14.4 | 18.3 | 27.9 | 19.8 | 22.6 | 23.7 | 25.3 | 22.4 | 22.1 | 23.4 | 18.4 | 10.3 | 14.9 | 16.5 |
| L503 | 20.8 | 14.2 | 19.2 | 22.1 | 30.0 | 31.8 | 32.0 | 30.7 | 28.6 | 19.4 | 25.2 | 27.1 | 21.6 | 12.6 | 19.4 | 22.0 |
| L504 | 22.2 | 12.9 | 19.1 | 24.1 | 37.8 | 34.5 | 30.8 | 32.7 | 27.7 | 19.2 | 24.1 | 28.1 | 25.1 | 14.4 | 19.8 | 25.4 |
| Instance | IGD | HV | RNI | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| L1 | L2 | M | HF | L1 | L2 | M | HF | L1 | L2 | M | HF | |
| L201 | 36.70 | 4.27 | 1.72 | 0 | 0.04 | 18.46 | 21.94 | 22.62 | 0 | 13.45 | 8.07 | 100 |
| L202 | 15.06 | 0.94 | 3.83 | 0 | 2.43 | 8.10 | 7.57 | 8.26 | 0 | 12.40 | 1.24 | 100 |
| L203 | 12.01 | 0.83 | 2.99 | 0 | 10.18 | 17.78 | 16.88 | 17.94 | 0 | 36.01 | 5.68 | 100 |
| L301 | 12.64 | 0.81 | 3.37 | 0 | 6.15 | 12.85 | 11.87 | 12.96 | 0 | 33.06 | 5.78 | 100 |
| L302 | 28.18 | 2.37 | 1.59 | 0 | 10.45 | 28.80 | 29.64 | 30.80 | 0 | 26.80 | 21.97 | 100 |
| L303 | 26.37 | 1.76 | 2.67 | 0 | 3.20 | 19.50 | 18.91 | 20.20 | 0 | 2.62 | 0.52 | 100 |
| L401 | 24.90 | 3.17 | 1.51 | 0 | 16.68 | 31.34 | 31.90 | 35.03 | 0.51 | 4.33 | 10.90 | 100 |
| L402 | 33.68 | 4.59 | 1.13 | 0 | 4.85 | 20.63 | 24.70 | 25.70 | 0 | 8.11 | 4.28 | 100 |
| L403 | 32.74 | 3.34 | 1.26 | 0 | 9.33 | 27.24 | 29.20 | 29.96 | 0 | 18.18 | 31.37 | 100 |
| L501 | 27.56 | 3.44 | 1.25 | 0 | 16.03 | 31.90 | 36.56 | 37.74 | 0.02 | 3.06 | 3.78 | 100 |
| L502 | 47.84 | 9.33 | 1.08 | 0 | 0 | 18.74 | 26.09 | 26.60 | 0 | 1.41 | 15.71 | 100 |
| L503 | 26.50 | 4.47 | 2.77 | 0 | 14.21 | 28.66 | 30.08 | 32.06 | 4.96 | 4.13 | 1.45 | 100 |
| Set | IGD | HV | RNI | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| EQ | Do | TF | FF | ORI | EQ | Do | TF | FF | ORI | EQ | Do | TF | FF | ORI | |
| L201 | 13.53 | 6.23 | 3.14 | 0.36 | 3.23 | 6.64 | 11.54 | 13.51 | 15.24 | 13.44 | 0 | 0 | 4.17 | 86.67 | 9.17 |
| L202 | 8.77 | 8.49 | 1.12 | 0.52 | 1.83 | 8.42 | 8.62 | 11.32 | 11.74 | 11.07 | 0.52 | 2.61 | 15.65 | 61.91 | 19.30 |
| L203 | 6.44 | 4.59 | 3.58 | 0.08 | 4.25 | 20.36 | 22.61 | 23.84 | 26.38 | 22.94 | 1.18 | 2.19 | 0 | 94.95 | 1.68 |
| L301 | 11.52 | 3.35 | 1.96 | 0.32 | 1.64 | 9.69 | 12.72 | 13.25 | 15.09 | 13.29 | 0 | 0 | 12.80 | 61.20 | 26.01 |
| L302 | 7.29 | 1.84 | 1.07 | 0.66 | 0.98 | 22.05 | 26.92 | 27.65 | 28.02 | 27.45 | 0.59 | 10.42 | 11.68 | 48.85 | 28.46 |
| L303 | 18.99 | 4.51 | 3.65 | 0.14 | 3.57 | 10.24 | 19.43 | 20.11 | 23.43 | 20.21 | 0 | 0 | 3.16 | 92.21 | 4.62 |
| L401 | 7.70 | 2.63 | 1.11 | 0.59 | 1.33 | 16.11 | 20.24 | 20.77 | 20.85 | 22.04 | 0 | 0.66 | 27.21 | 40.48 | 31.65 |
| L402 | 17.83 | 7.00 | 2.35 | 0.03 | 5.82 | 12.68 | 18.15 | 21.75 | 23.75 | 19.50 | 0 | 0 | 2.12 | 97.88 | 0 |
| L403 | 10.29 | 5.16 | 3.66 | 0.11 | 3.46 | 19.90 | 22.92 | 24.41 | 28.88 | 24.58 | 0 | 0 | 0.20 | 97.49 | 2.31 |
| L501 | 10.54 | 7.25 | 1.41 | 1.29 | 0.31 | 15.72 | 19.55 | 24.24 | 24.42 | 26.73 | 0 | 0 | 4.90 | 22.67 | 72.43 |
| L502 | 6.79 | 4.00 | 0.95 | 0.83 | 0.86 | 19.61 | 21.33 | 23.87 | 23.84 | 24.21 | 0.06 | 0.63 | 19.19 | 48.45 | 31.67 |
| L503 | 13.37 | 6.41 | 1.34 | 0.55 | 1.05 | 15.60 | 21.33 | 25.31 | 25.96 | 25.37 | 0 | 0 | 12.28 | 58.93 | 28.79 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Leng, L.; Zhao, Y.; Zhang, J.; Zhang, C. An Effective Approach for the Multiobjective Regional Low-Carbon Location-Routing Problem. Int. J. Environ. Res. Public Health 2019, 16, 2064. https://doi.org/10.3390/ijerph16112064
Leng L, Zhao Y, Zhang J, Zhang C. An Effective Approach for the Multiobjective Regional Low-Carbon Location-Routing Problem. International Journal of Environmental Research and Public Health. 2019; 16(11):2064. https://doi.org/10.3390/ijerph16112064
Chicago/Turabian StyleLeng, Longlong, Yanwei Zhao, Jingling Zhang, and Chunmiao Zhang. 2019. "An Effective Approach for the Multiobjective Regional Low-Carbon Location-Routing Problem" International Journal of Environmental Research and Public Health 16, no. 11: 2064. https://doi.org/10.3390/ijerph16112064
APA StyleLeng, L., Zhao, Y., Zhang, J., & Zhang, C. (2019). An Effective Approach for the Multiobjective Regional Low-Carbon Location-Routing Problem. International Journal of Environmental Research and Public Health, 16(11), 2064. https://doi.org/10.3390/ijerph16112064





