Modeling Skin Injury from Hot Rice Porridge Spills
Abstract
:1. Introduction
2. Heat Transport and Damage Integral
2.1. Heat Transport Modeling
2.2. Skin Damage Modeling
2.3. The Hot Porridge Spill Situations to be Analyzed
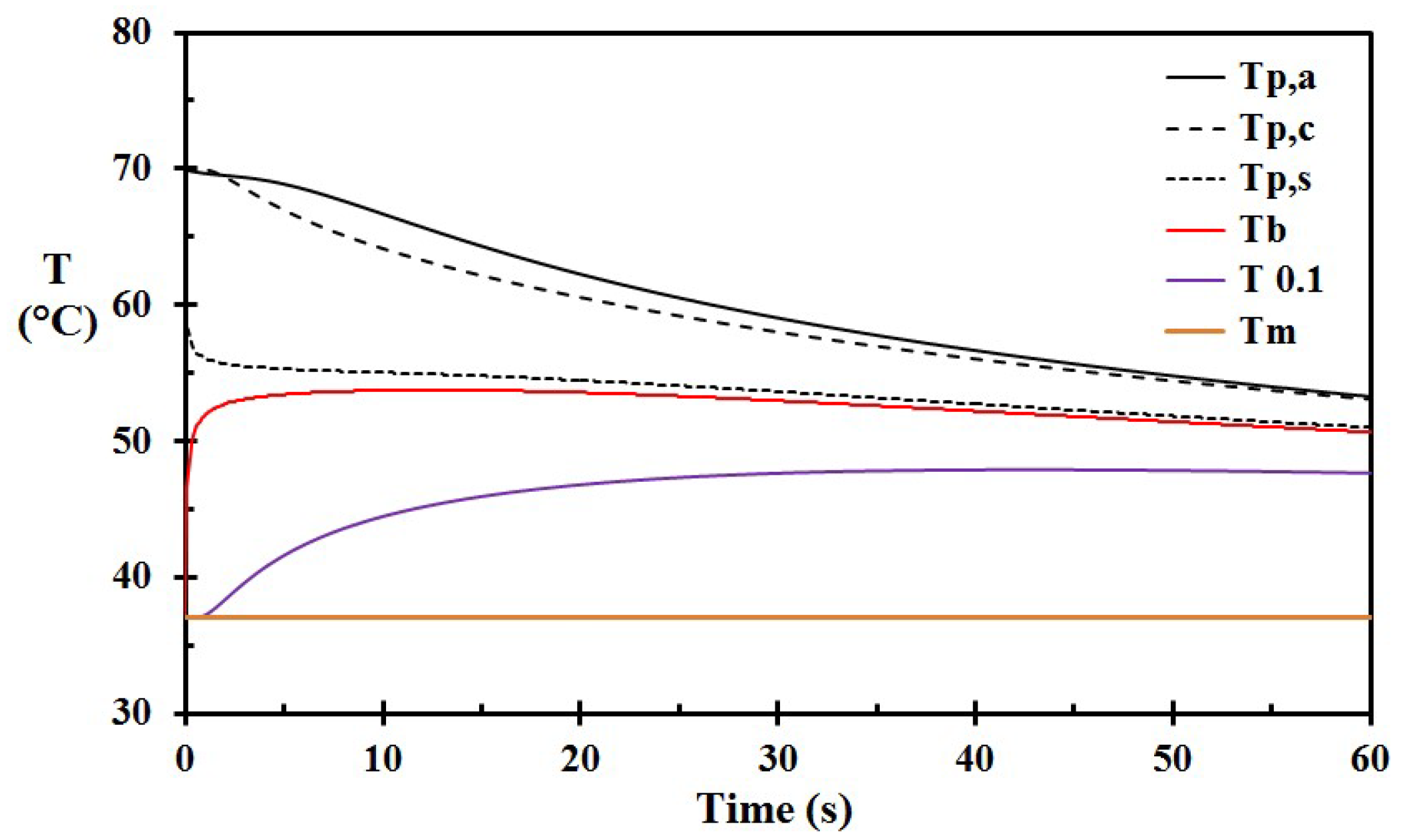
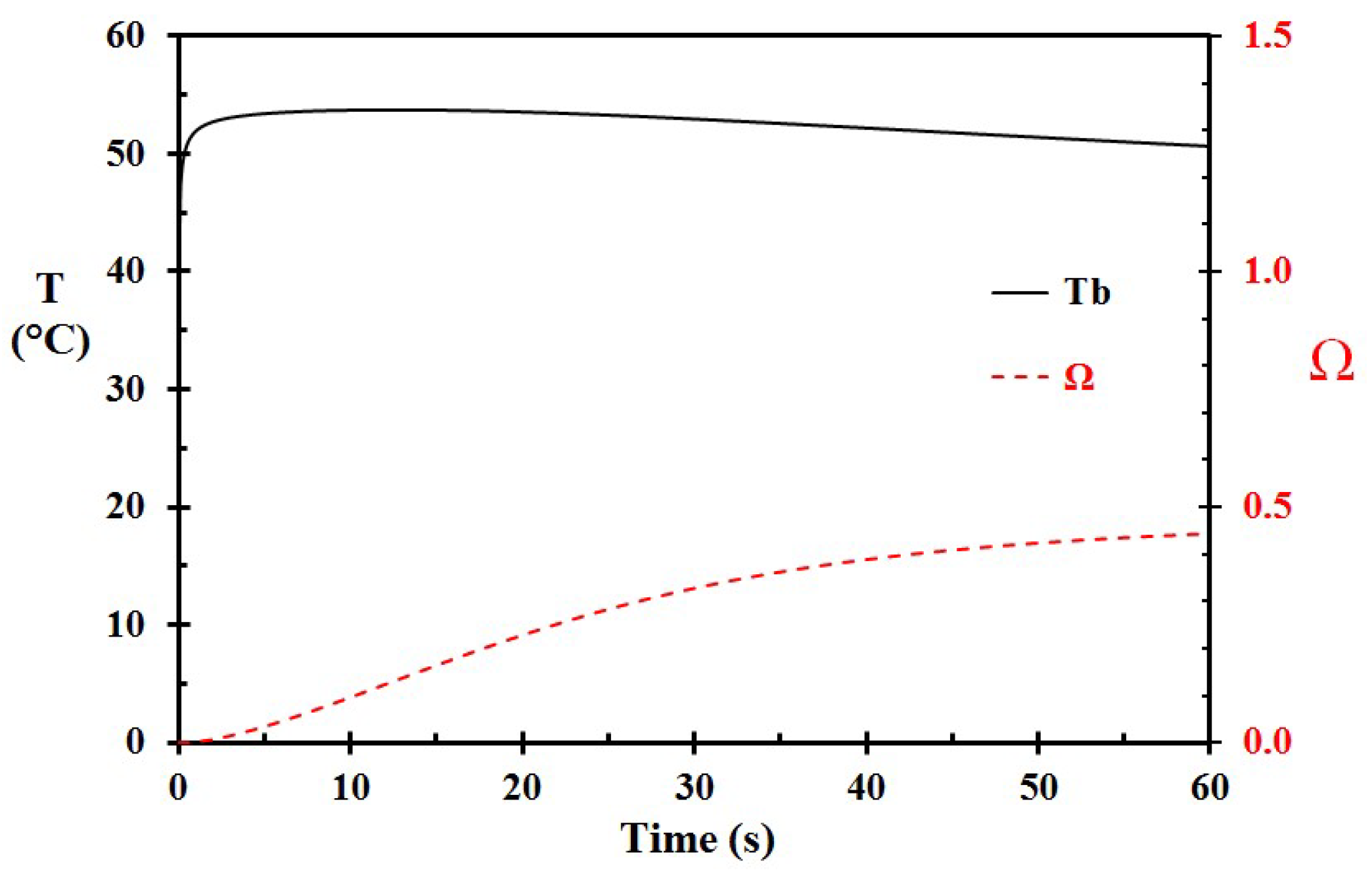
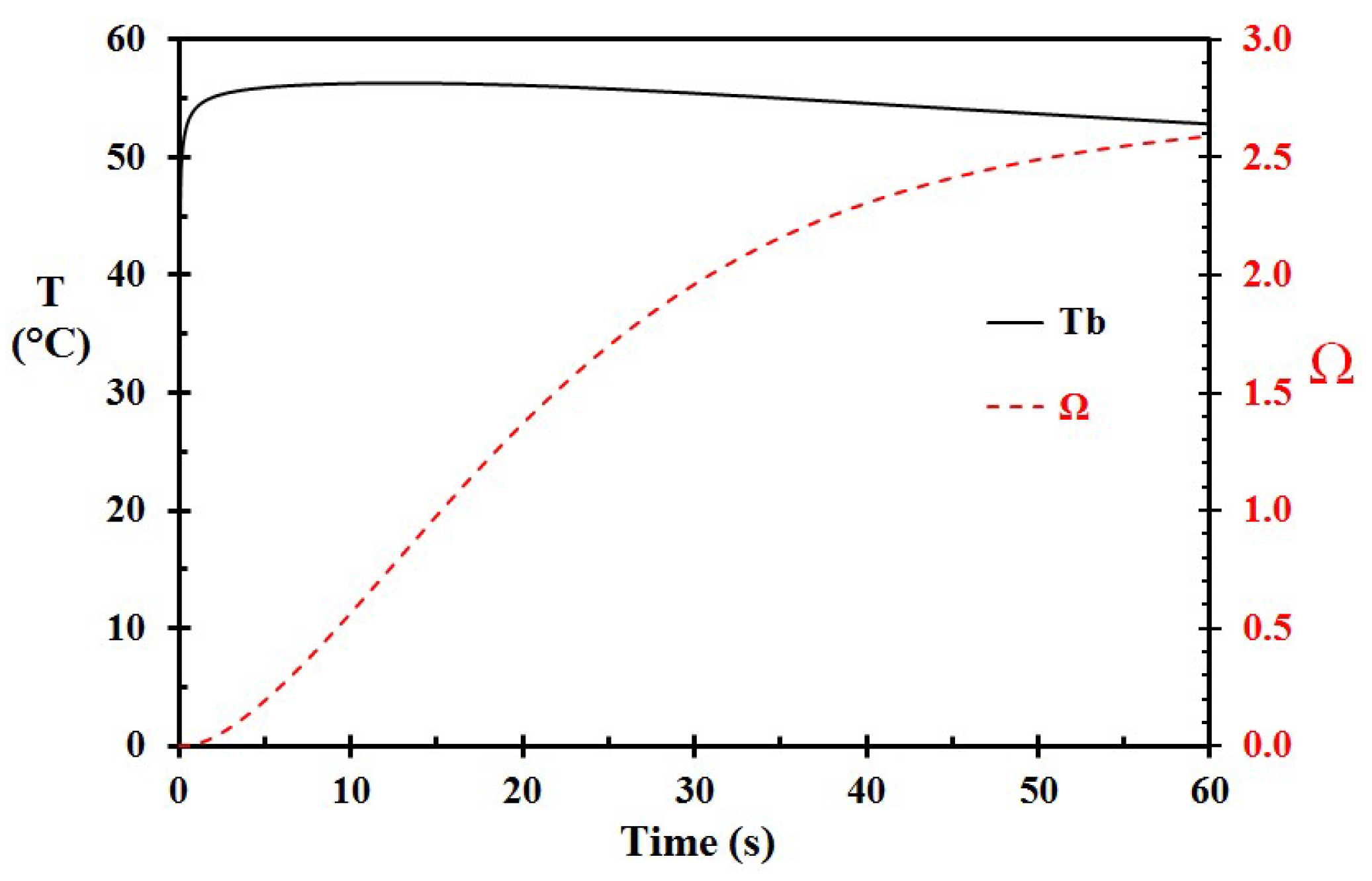
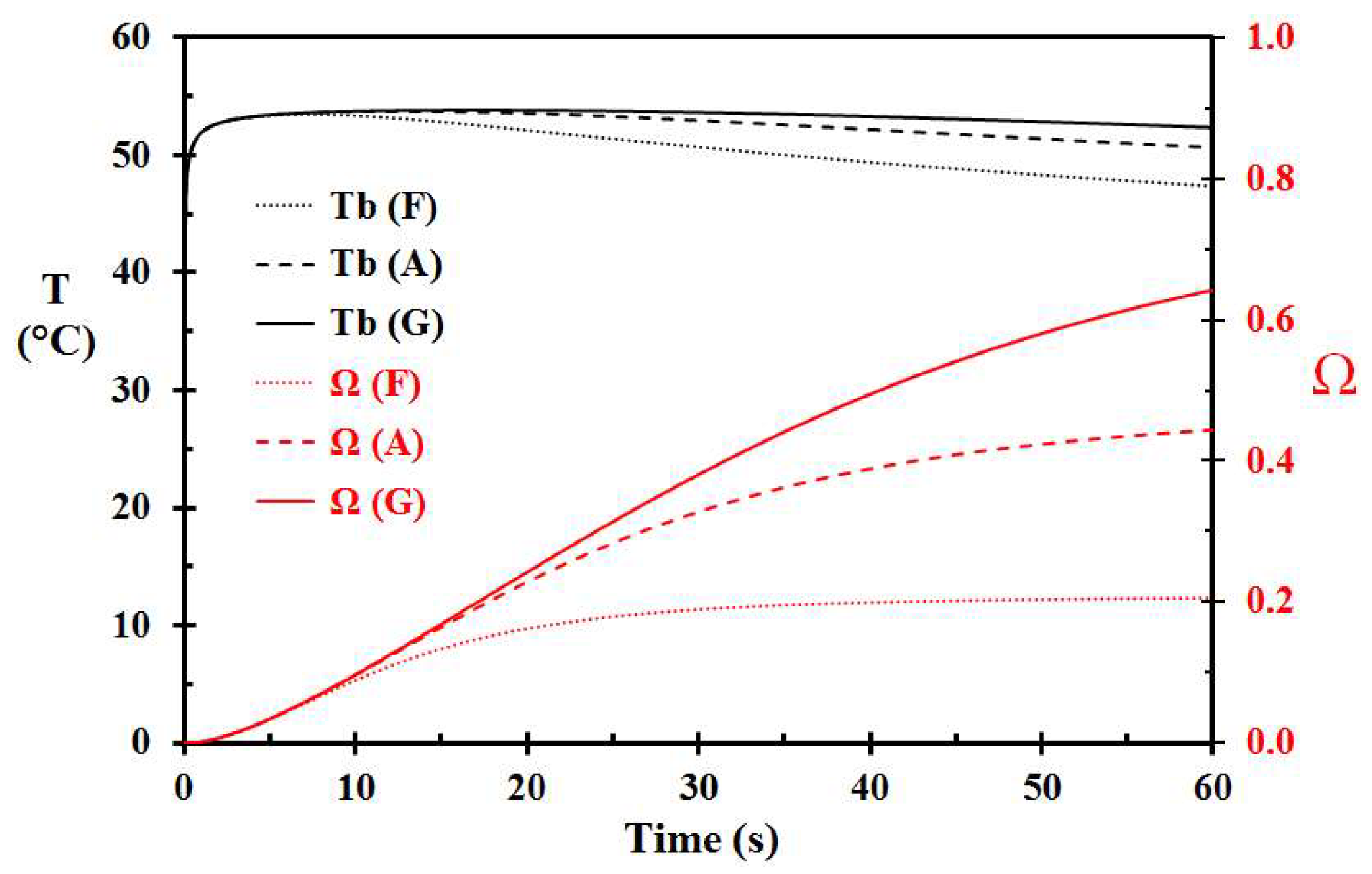
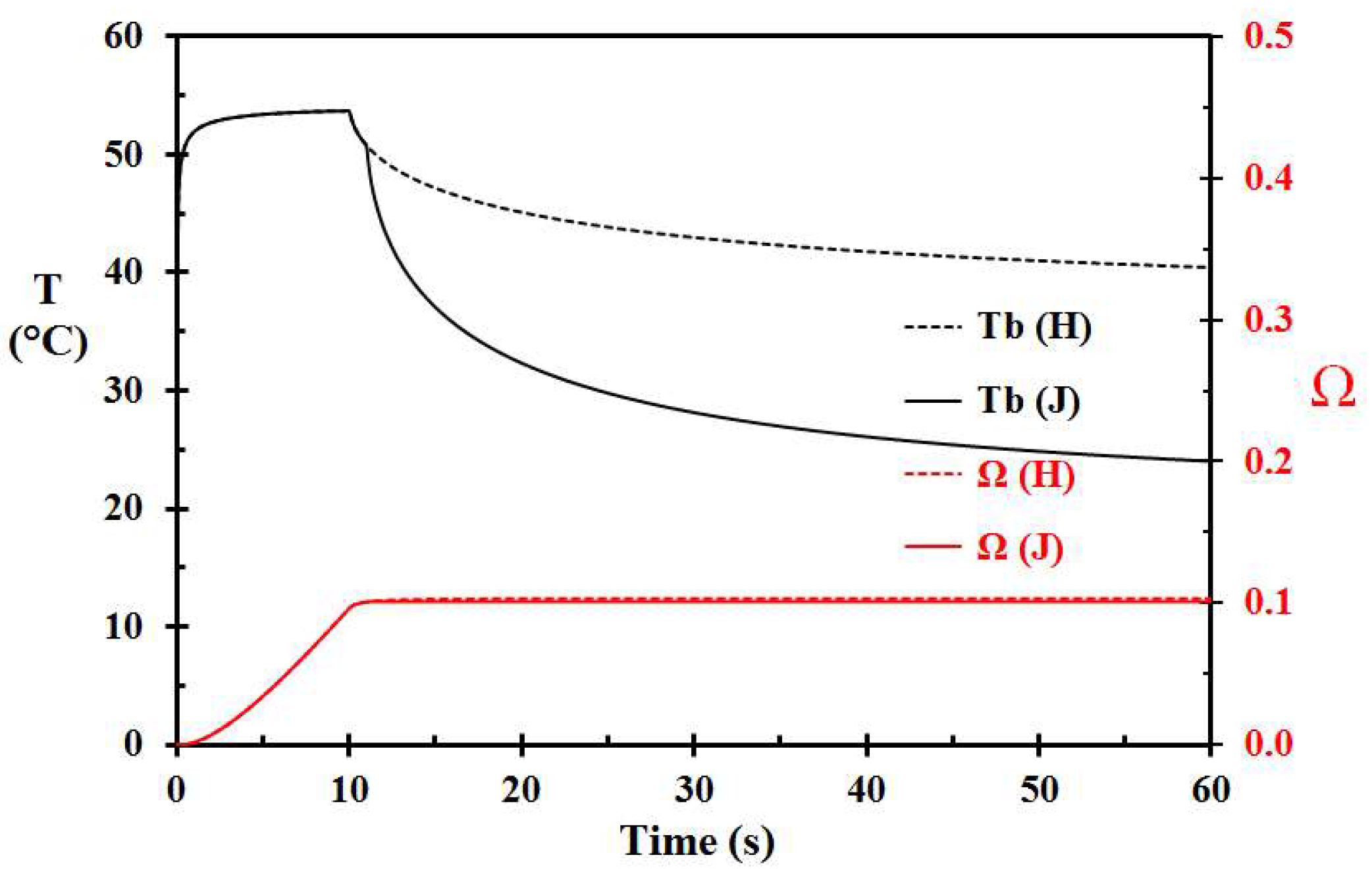
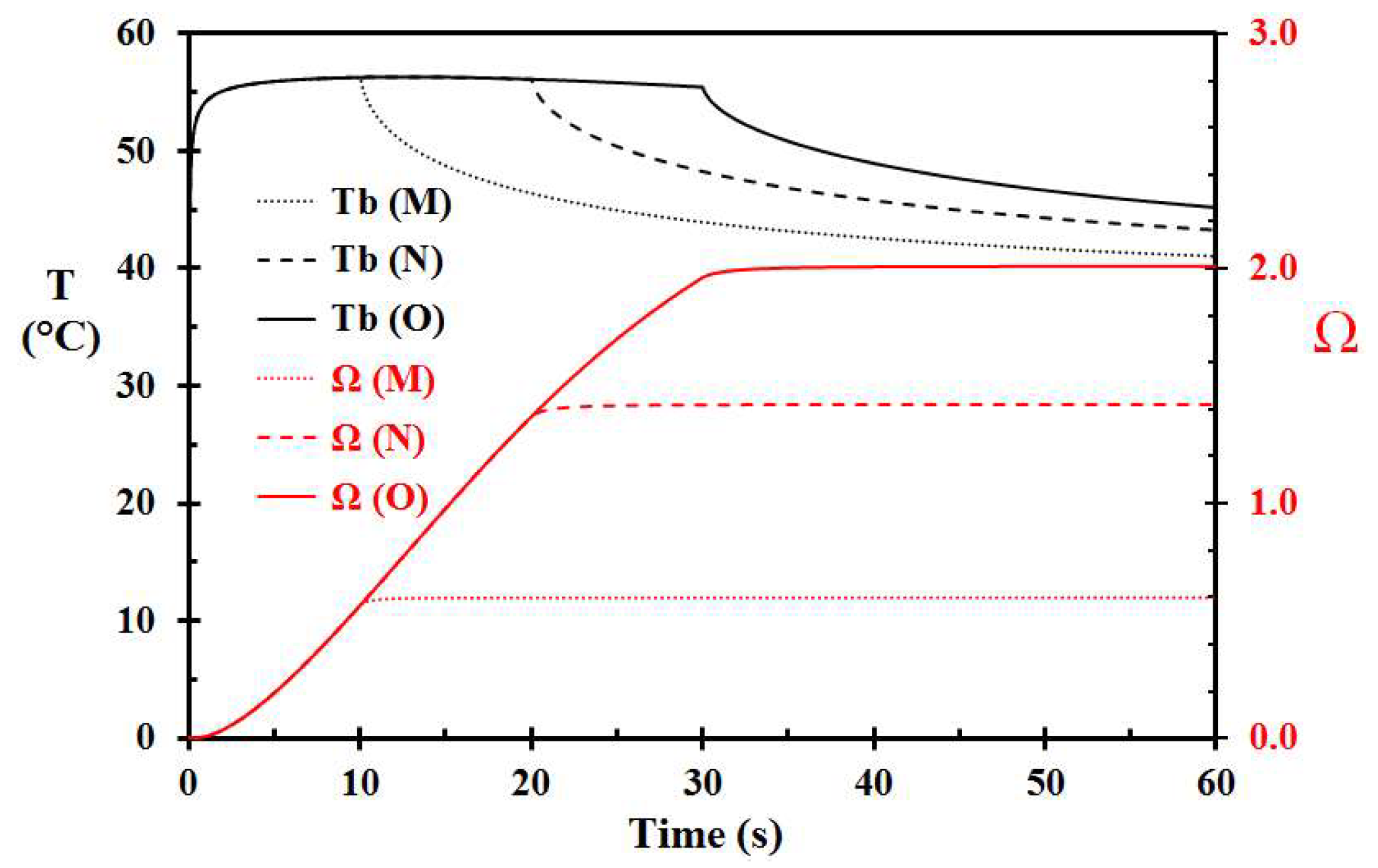
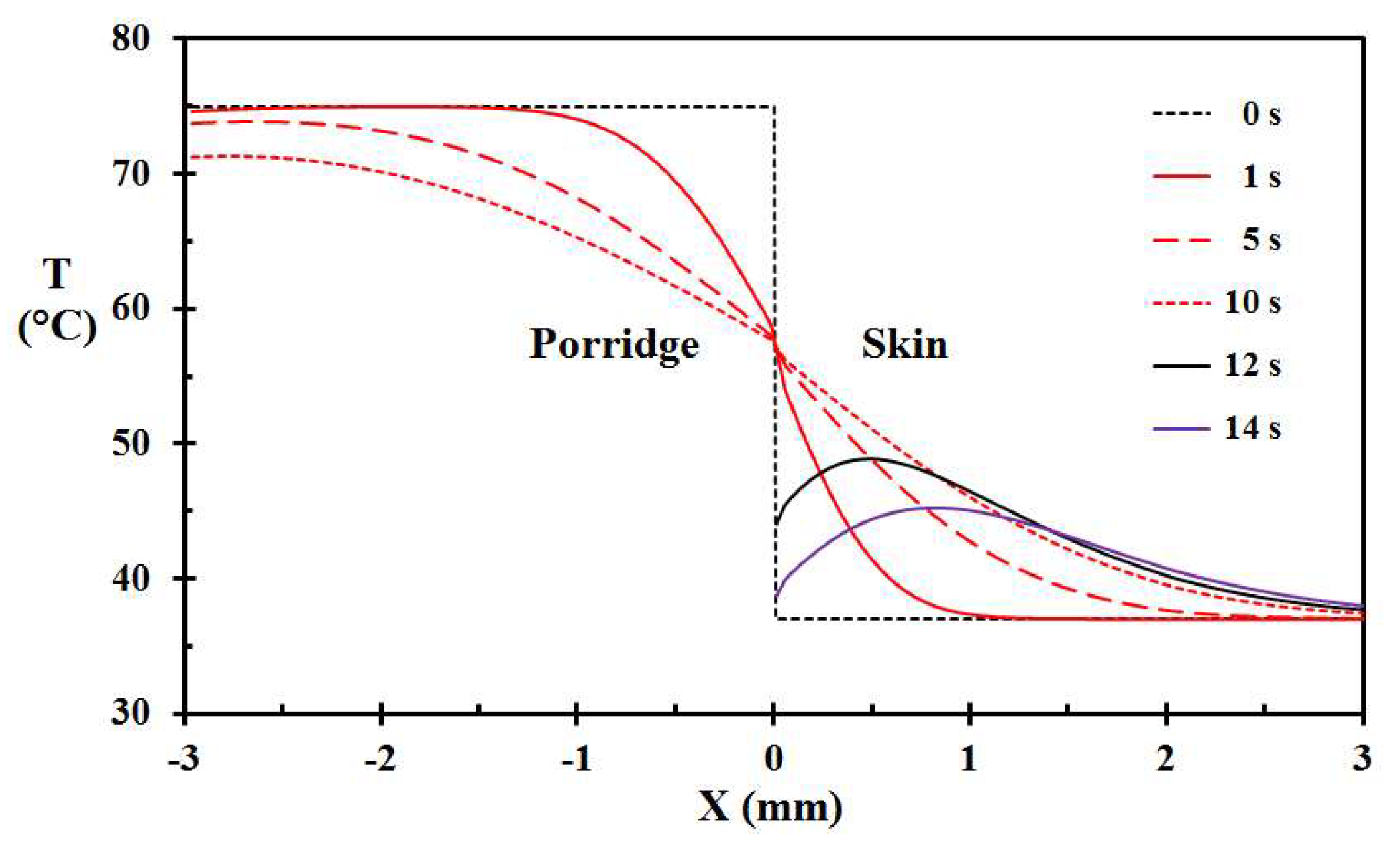
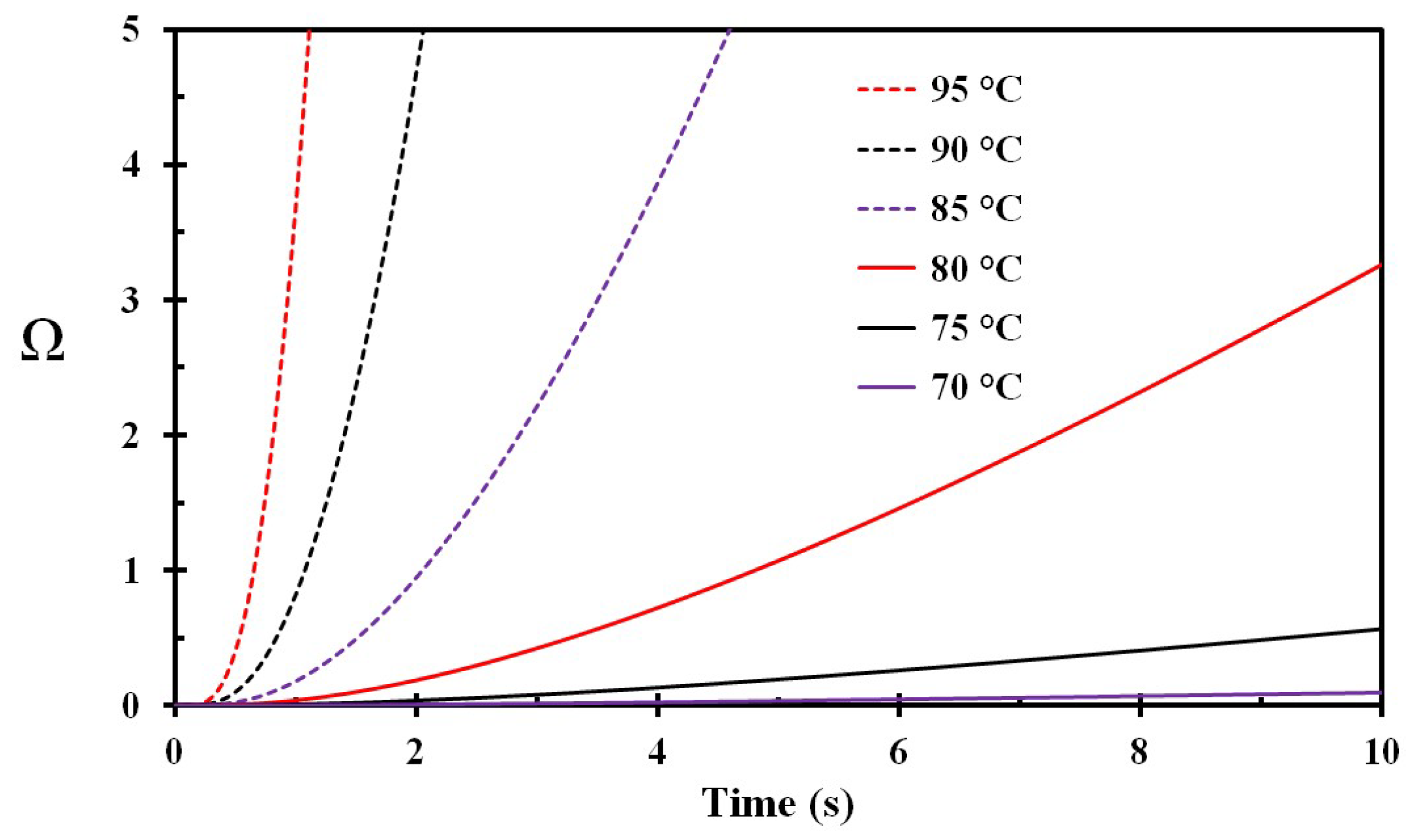
3. Results
4. Discussion
5. Conclusions
Acknowledgments
Conflicts of Interest
References
- He, S.; Alonge, O.; Agrawal, P.; Sharmin, S.; Islam, I.; Mashreky, S.R.; Arifeen, S.E. Epidemiology of burns in rural Bangladesh: An update. Int. J. Environ. Res. Public Health 2017, 14, 381. [Google Scholar] [CrossRef] [PubMed]
- Burn Incidence and Treatment in the United States: 2016. Available online: http://www.ameriburn.org/resources_factsheet.php (accessed on 30 September 2017).
- Guillory, A.N.; Clayton, R.P.; Herndon, D.N.; Finnerty, C.C. Cardiovascular dysfunction following burn injury: What we have learned from rat and mouse models. Int. J. Mol. Sci. 2016, 17, 53. [Google Scholar] [CrossRef] [PubMed]
- Killat, J.; Reimers, K.; Choi, C.Y.; Jahn, S.; Vogt, P.M.; Radtke, C. Cultivation of keratinocytes and fibroblasts in a three-dimensional bovine collagen-elastin matrix (Matriderm®) and application for full thickness wound coverage in vivo. Int. J. Mol. Sci. 2013, 14, 14460–14474. [Google Scholar] [CrossRef] [PubMed]
- Rigo, C.; Ferroni, L.; Tocco, I.; Roman, M.; Munivrana, I.; Gardin, C.; Cairns, W.R.L.; Vindigni, V.; Azzena, B.; Barbante, C.; et al. Active silver nanoparticles for wound healing. Int. J. Mol. Sci. 2013, 14, 4817–4840. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Henriques, F.C.; Moritz, A.R. Studies of thermal injury, I: The conduction of heat to and through skin and the temperatures attained therein: A theoretical and an experimental investigation. Am. J. Pathol. 1947, 23, 530–549. [Google Scholar] [PubMed]
- Moritz, A.; Henriques, F.C. Studies of thermal injury, II: The relative importance of time and surface temperature in the causation of cutaneous burns. Am. J. Pathol. 1947, 23, 695–720. [Google Scholar] [PubMed]
- Moritz, A.R. Studies of thermal injury, III: The pathology and pathogenesis of cutaneous burns: An experimental study. Am. J. Pathol. 1947, 23, 915–941. [Google Scholar] [PubMed]
- Fu, M.; Weng, W.G.; Yuan, H.Y. Numerical simulation of the effects of blood perfusion, water diffusion, and vaporization on the skin temperature and burn injuries. Numer. Heat Transf. Part A Appl. 2014, 65, 1187–1203. [Google Scholar] [CrossRef]
- Tobalem, M.; Harder, Y.; Tschanz, E.; Speidel, V.; Pittet-Cuénod, B.; Wettstein, R. First-aid with warm water delays burn progression and increases skin survival. J. Plast. Reconstr. Aesthet. Surg. 2013, 66, 260–266. [Google Scholar] [CrossRef] [PubMed]
- Johnson, N.N.; Abraham, J.P.; Helgeson, Z.I.; Minkowycz, W.J.; Sparrow, E.M. An archive of skin-layer thicknesses and properties and calculations of scald burns with comparisons to experimental observations. J. Therm. Sci. Eng. Appl. 2011, 3, 011003. [Google Scholar] [CrossRef]
- Monds, J.R.; McDonald, A.G. Determination of skin temperature distribution and heat flux during simulated fires using Green’s functions over finite-length scales. Appl. Therm. Eng. 2013, 50, 593–603. [Google Scholar] [CrossRef]
- Buettner, K. Effects of extreme heat and cold on human skin, II. Surface temperature, pain and heat conductivity in experiments with radiant heat. J. Appl. Physiol. 1951, 3, 703–713. [Google Scholar] [CrossRef] [PubMed]
- Lawrence, J.C.; Bull, J.P. Thermal conditions which cause skin burns. J. Eng. Med. 1976, 5, 61–63. [Google Scholar] [CrossRef]
- Lau, E.Y.K.; Tam, Y.-Y.M.; Chiu, T.W. Importance of clothing removal in scalds. Hong Kong Med. J. 2016, 22, 152–157. [Google Scholar] [CrossRef] [PubMed]
- Log, T. Skin temperatures of a pre-cooled wet person exposed to engulfing flames. Fire Saf. J. 2017, 89, 1–6. [Google Scholar] [CrossRef]
- Abraham, J.P.; Plourde, B.; Vallez, L.; Stark, J.; Diller, K.R. Estimating the time and temperature relationship for causation of deep-partial thickness skin burns. Burns 2015, 41, 1741–1747. [Google Scholar] [CrossRef] [PubMed]
- Abraham, J.P.; Nelson-Cheeseman, B.B.; Sparrow, E.; Wentz, J.E.; Gorman, J.M.; Wolf, S.E. Comprehensive method to predict and quantify scald burns from beverage spills. Int. J. Hyperth. 2016, 32, 900–910. [Google Scholar] [CrossRef] [PubMed]
- Abraham, J.P.; Hennessey, M.P.; Minkowycz, W.J. A simple algebraic model to predict burn depth and injury. Int. Commun. Heat Mass Transf. 2011, 38, 1169–1171. [Google Scholar] [CrossRef]
- Kadam, S.; Datta, A.K. Estimation of Thermal Properties and Heat Transfer Study during Continuous Processing of Rice in Milk. Chem. Eng. Commun. 2015, 202, 345–355. [Google Scholar] [CrossRef]
- Ng, E.Y.K.; Chua, L.T. Prediction of skin burn injury, Part 2: Parametric and sensitivity analysis. Proc. Inst. Mech. Eng. H 2002, 216, 171–183. [Google Scholar] [CrossRef] [PubMed]
- Lipkin, M.; Hardy, J.D. Measurement of some thermal properties of human tissues. J. Appl. Physiol. 1954, 7, 212–217. [Google Scholar] [CrossRef] [PubMed]
- Rai, K.N.; Rai, S.K. Heat transfer inside the tissues with a supplying vessel for the case when metabolic heat generation and blood perfusion are temperature dependent. Heat Mass Transf. 1999, 35, 345–350. [Google Scholar] [CrossRef]
- Log, T.; Gustafsson, S.E. Transient Plane Source (TPS) technique for measuring thermal transport properties of building materials. Fire Mater. 1995, 19, 43–49. [Google Scholar] [CrossRef]
- Millington, P.F.; Wilkinson, R. Skin; Cambridge University Press: New York, NY, USA, 1983. [Google Scholar]
- Viglianti, B.L.; Dewhirst, M.W.; Abraham, J.P.; Gorman, J.-M.; Sparrow, E.M. Rationalization of thermal injury quantification methods: Application to skin burns. Burns 2014, 40, 896–902. [Google Scholar] [CrossRef] [PubMed]
- Henriques, F.C.; Moritz, A. Studies of thermal injury, V: The predictability and the significance of thermal induced rate processes leading to irreversible epidermal injury. Arch. Pathol. 1947, 44, 489–502. [Google Scholar]
- Ye, H.; De, S. Thermal injury of skin and subcutaneous tissues: A review of experimental approaches and numerical models. Burns 2017, 43, 909–932. [Google Scholar] [CrossRef] [PubMed]
- Log, T. Modeling Skin Injury from Hot Spills on Clothing. Int. J. Environ. Res. Public Health. 2017, 14, 1374. [Google Scholar] [CrossRef] [PubMed]
- Vallez, L.J.; Plourde, B.D.; Wentz, J.E.; Nelson-Cheeseman, B.B.; Abraham, J.P. A review of scald burn injuries. Intern. Med. Rev. 2017, 3, 1–18. [Google Scholar]
- Bourdon, R.T.; Nelson-Cheeseman, B.B.; Abraham, J.P. Prediction, identification, and initial treatment guide for scald injuries. Aust. J. Emerg. Crit. Care Med. 2016, 3, 1043. [Google Scholar]
- Bourdon, R.T.; Nelson-Cheeseman, B.B.; Abraham, J.P. Review of the initial treatment and avoidance of scald injuries. World J. Dermatol. 2017, 6, 17–26. [Google Scholar] [CrossRef]
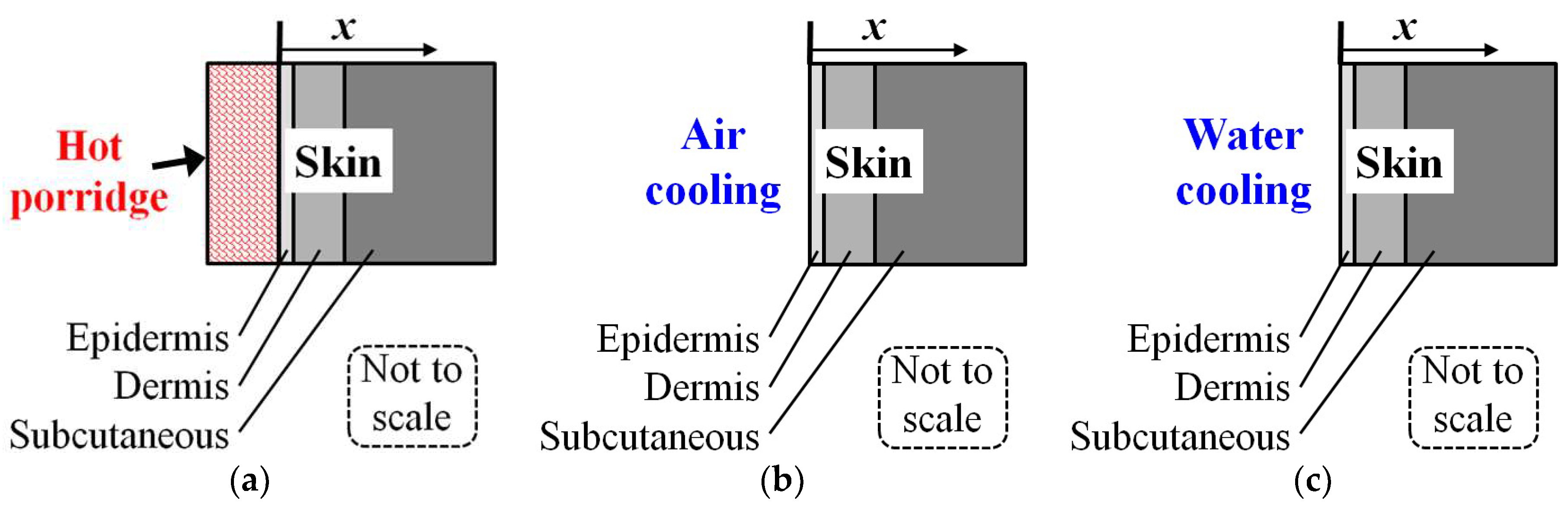
| Skin Layer | (W/m·K) | (kg/m3) | (J/kg·K) | (m2/s) | Thickness (μm) |
|---|---|---|---|---|---|
| Epidermis | 0.22 | 1200 | 3600 | 5.1 × 10−8 | 40, 50, 60, 80 |
| Dermis | 0.40 | 1200 | 3600 | 9.3 × 10−8 | 0.002 |
| Sub cutaneous | 0.20 | 1000 | 2500 | 8.0 × 10−8 | 0.010 |
| Muscle | 0.45 | 1000 | 3800 | 1.2 × 10−7 | 0.030 |
| Case | (μm) | (mm) | (°C) | (s) | (s) | Comments | |
|---|---|---|---|---|---|---|---|
| A | 60 | 3.0 | 70 | - | - | 0.444 | Base case, 60 μm epidermis, not removed |
| B | 60 | 3.0 | 75 | - | - | 2.591 | 5 °C warmer than the base case (A) |
| C | 60 | 3.0 | 65 | - | - | 0.075 | 5 °C colder than the base case (A) |
| D | 50 | 3.0 | 70 | - | - | 0.491 | 50 μm epidermis |
| E | 40 | 3.0 | 70 | - | - | 0.549 | 40 μm epidermis |
| F | 60 | 2.0 | 70 | - | - | 0.206 | 2.0 mm porridge layer |
| G | 60 | 4.0 | 70 | - | - | 0.642 | 4.0 mm porridge layer |
| H | 60 | 3.0 | 70 | 10 | - | 0.103 | Porridge removal at 10 s |
| I | 60 | 3.0 | 70 | 10 | 20 | 0.103 | Removal 10 s, water cooling t > 20 s |
| J | 60 | 3.0 | 70 | 10 | 11 | 0.101 | Removal 10 s, water cooling t > 11 s |
| K | 60 | 3.0 | 70 | 20 | - | 0.239 | Porridge removal at 20 s |
| L | 60 | 3.0 | 70 | 30 | - | 0.338 | Porridge removal at 30 s |
| M | 60 | 3.0 | 75 | 10 | - | 0.599 | 75 °C, porridge removal 10 s |
| N | 60 | 3.0 | 75 | 20 | - | 1.421 | 75 °C, porridge removal at 20 s |
| O | 60 | 3.0 | 75 | 30 | - | 2.009 | 75 °C, porridge removal at 30 s |
| P | 60 | 3.0 | 75 | 30 | - | 1.985 | 75 °C, removal at 30 s, water cooling t > 31 s |
| Q | 60 | 3.0 | 75 | 10 | 11 | 0.588 | 75 °C, removal at 10 s, water cooling t > 11 s |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Log, T. Modeling Skin Injury from Hot Rice Porridge Spills. Int. J. Environ. Res. Public Health 2018, 15, 808. https://doi.org/10.3390/ijerph15040808
Log T. Modeling Skin Injury from Hot Rice Porridge Spills. International Journal of Environmental Research and Public Health. 2018; 15(4):808. https://doi.org/10.3390/ijerph15040808
Chicago/Turabian StyleLog, Torgrim. 2018. "Modeling Skin Injury from Hot Rice Porridge Spills" International Journal of Environmental Research and Public Health 15, no. 4: 808. https://doi.org/10.3390/ijerph15040808
APA StyleLog, T. (2018). Modeling Skin Injury from Hot Rice Porridge Spills. International Journal of Environmental Research and Public Health, 15(4), 808. https://doi.org/10.3390/ijerph15040808





