A Decision-Making Method with Grey Multi-Source Heterogeneous Data and Its Application in Green Supplier Selection
Abstract
1. Introduction
- The fusion of different data types of grey information from multiple sources is processed by kernel and greyness degree which are the common information characteristics of grey multi-source heterogeneous data.
- In order to measure the proximity of a selected alternative to the ideal solution and the negative ideal solution comprehensively and accurately, a grey relational bi-directional projection method is proposed based on kernel and greyness degree.
- The Hierarchical Group-Decision Making Trial and Evaluation Laboratory (HG-DEMATEL) method is proposed based on analyzing the causalities between attributes. It can effectively use group decision-making information and determine the hierarchical attribute weights.
- The validity of the proposed method is verified in the practical decision problem of green supplier selection.
2. Literature Review
3. Preliminaries
- (1)
- If the probability distribution of is unknown, then ;
- (2)
- If the probability distribution of is known, then , where and are the probability and the kernel of interval grey number respectively, and the following conditions hold: , .
- (1)
- If the probability distribution of is unknown, then ;
- (2)
- If the probability distribution of is known, then , where is the probability of interval grey number , and conditions hold: , .
4. The Proposed Decision-Making Method
4.1. Problem Description
4.2. Grey Relational Bi-Directional Projection Ranking Method Based on Kernel and Greyness Degree
4.3. Determination of Hierarchical Attribute Weights Based on HG-DEMATEL
- (1)
- The difference value between aggregated matrix and original matrix is as small as possible.
- (2)
- The similarity degree value between aggregated matrix and original matrix is as big as possible.
4.4. The Decision-Making Steps
5. Case Study
5.1. Case Background
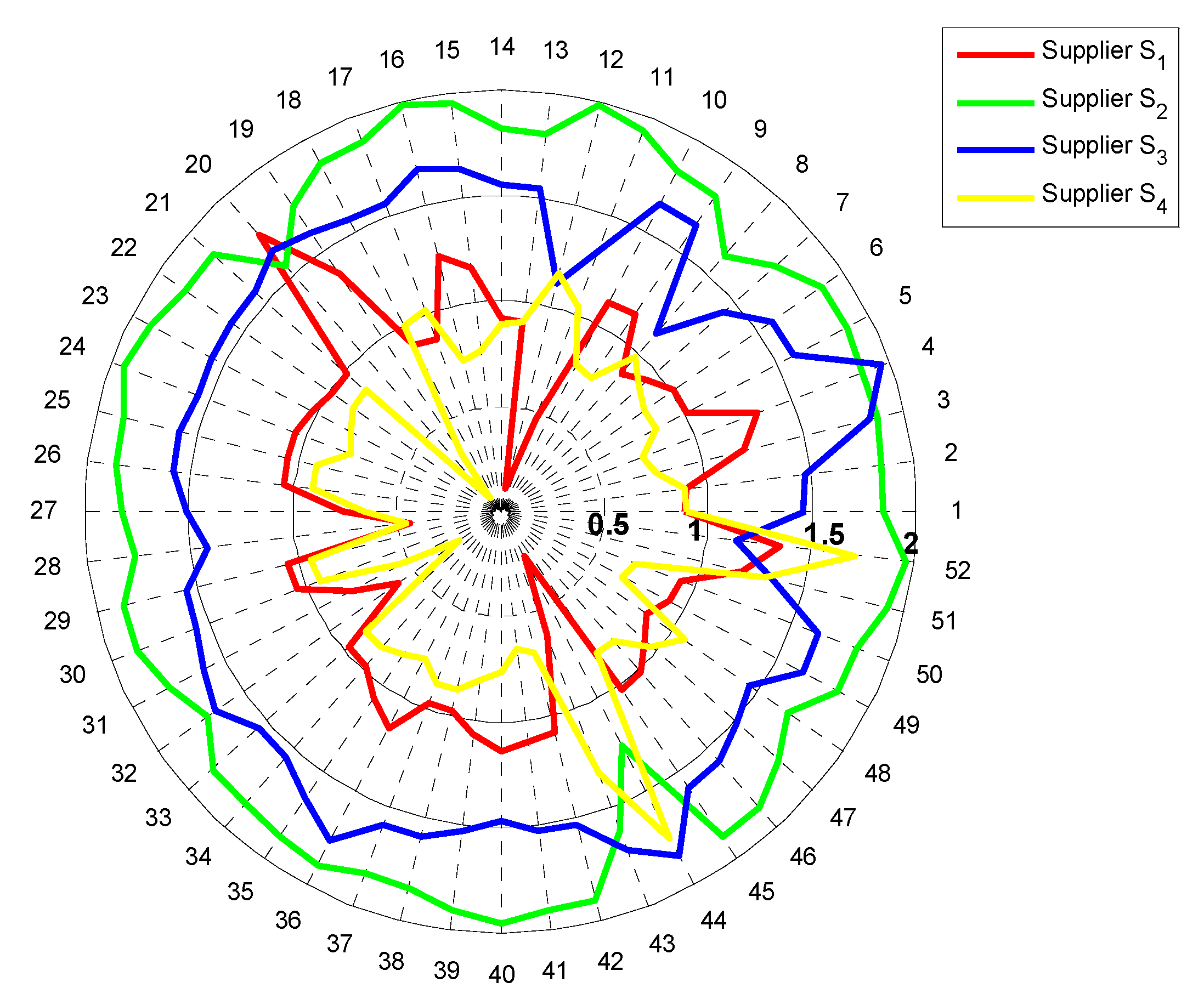
5.2. The Ranking of Alternatives
5.3. Discussion and Implications
6. Result Analysis
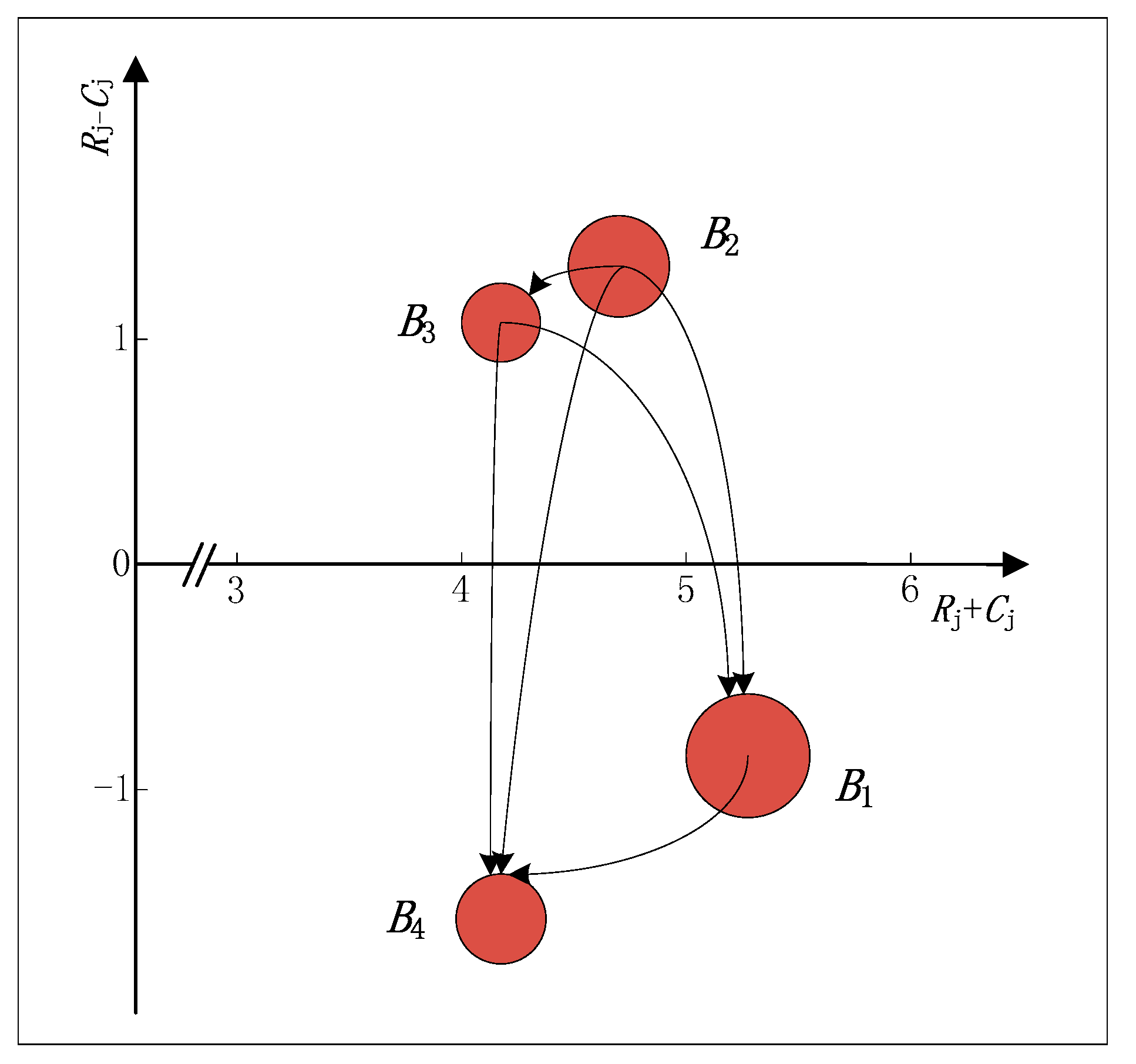
6.1. Causalities Analysis
- (1)
- With respect to the green level , the prominence and net effect of energy consumption are both highest, indicating that it is not only the most important sub-attribute, but also the cause of effecting . Only by reducing first it can well solve the ambient severities whose net effect is the lowest.
- (2)
- With respect to the product competitiveness , the prominence of product quality is highest, indicating that it is the most important sub-attribute in . Meanwhile, product price possesses the highest net effect and does so as the only positive net causer, which can affect the product quality and product performance . Therefore, we should give priority to the highest in net effect to improve the lowest in net effect.
- (3)
- With respect to the enterprise competitiveness , the prominence and net effect of management level are both highest, indicating that it is not only the most important sub-attribute, but also the cause of effecting . By improving the management level first it can well enhance the technical level , the staff quality , and especially the financial situation whose prominence and net effect are both lowest.
- (4)
- With respect to the cooperation support , the prominence and net effect of after-sale service capabilities are both highest. Meanwhile, customer satisfaction possesses the lowest net effect and does as the only negative net receiver. It indicates that the improvement in after-sale service capabilities can effectively increase customer satisfaction .
6.2. Sensitivity Analysis
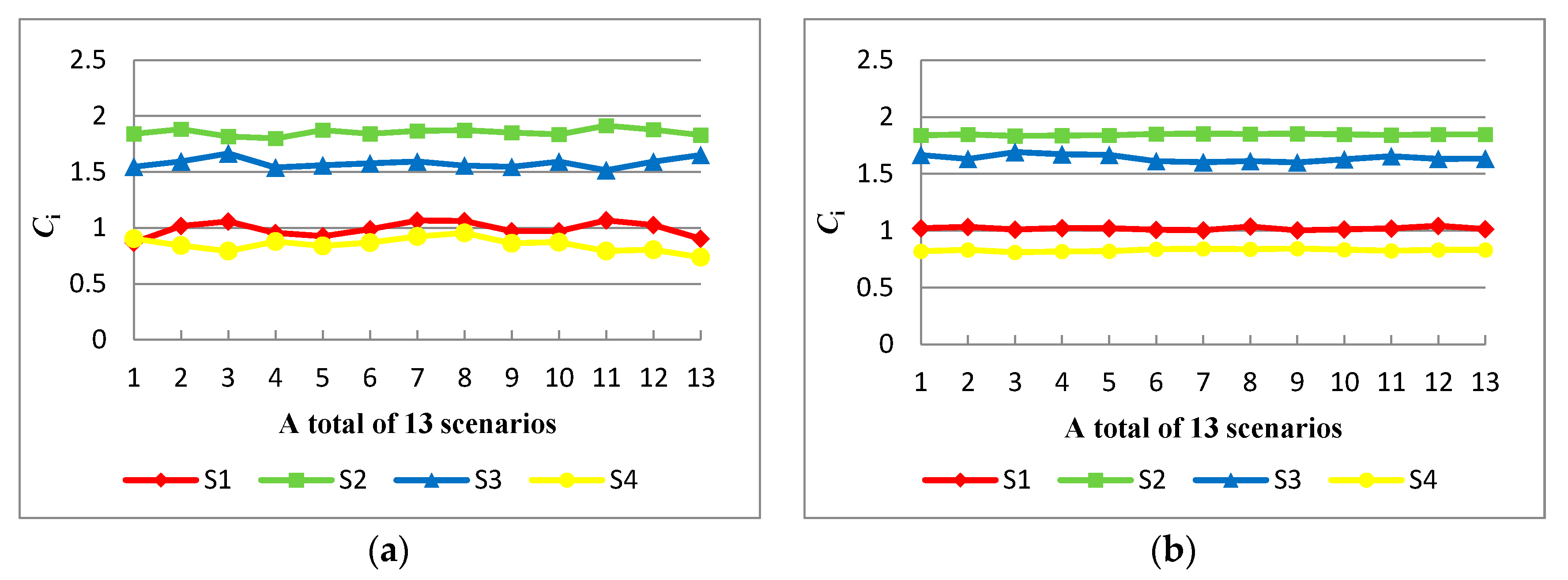
6.2.1. The Sensitivity Analysis for Variation of Attribute Weight
6.2.2. The Sensitivity Analysis for Variation of Attribute Number
6.3. Comparative Analysis
- (1)
- If we use the method in reference [51] to deal with the same problem in this paper, the value of relative kernel of each alternative can be calculated respectively: , , , , then we have .
- (2)
- If we use the method in reference [52] to deal with the same problem in this paper, the value of comprehensive correlation degree of each alternative can be obtained respectively:, , , , then we have .
- (3)
- If we use the classical GRA method to deal with the same problem in this paper, the value of grey relation degree of each alternative can be obtained respectively: , , , , then we have .
- (4)
- If we use the classical TOPSIS method to deal with the same problem in this paper, the value of relative closeness of each alternative can be obtained respectively: , , , , then we have .
- (1)
- A common method of solving hierarchical attribute weights, in which the causal relationships exist between attributes, is under consideration. The determination of the traditional objective attribute weights mainly depends on attribute values distribution, which assumes that attributes are independent. However, there usually exist causal relationships between attributes in the multi-hierarchical attribute system. The proposed HG-DEMATEL method may be a suitable way to solve this problem.
- (2)
- Different from the classical methods, such as TOPSIS, GRA, the proposed grey relational bi-directional projection method not only considers the measurement of distance proximity between alternatives and the ideal solution, but also takes the consistency of changing direction between them into account.
- (3)
- The decision-making information is usually the single homogeneous data in classical decision-making method, such as VIKOR, GRA, TOPSIS, while the proposed method can handle the composite decision-making information with two or more different types of grey information from multiple sources, which is more in line with the presentation of practical decision information.
7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Jamshidi-Zanjani, A.; Rezaei, M. Landfill site selection using combination of fuzzy logic and multi-attribute decision-making approach. Environ. Earth Sci. 2017, 76, 448. [Google Scholar] [CrossRef]
- Kou, G.; Peng, Y.; Wang, G.X. Evaluation of clustering algorithms for financial risk analysis using MCDM methods. Inf. Sci. 2014, 275, 1–12. [Google Scholar] [CrossRef]
- Yin, K.D.; Wang, P.Y.; Li, X.M. The Multi-Attribute Group Decision-Making Method Based on Interval Grey Trapezoid Fuzzy Linguistic Variables. Int. J. Environ. Res. Public Health 2017, 14, 1561. [Google Scholar] [CrossRef] [PubMed]
- Chuu, S.J. An investment evaluation of supply chain RFID technologies: A group decision-making model with multiple information sources. Knowl. Based Syst. 2014, 66, 210–220. [Google Scholar] [CrossRef]
- Kou, G.; Ergu, D.; Lin, C.S.; Chen, Y. Pairwise comparison matrix in multiple criteria decision making. Technol. Econ. Dev. Econ. 2016, 22, 738–765. [Google Scholar] [CrossRef]
- Kou, G.; Lu, Y.Q.; Peng, Y.; Shi, Y. Evaluation of classification algorithms using MCDM and rank correlation. Int. J. Inf. Technol. Decis. Mak. 2012, 11, 197–225. [Google Scholar] [CrossRef]
- Wu, W.S.; Kou, G. A group consensus model for evaluating real estate investment alternatives. Financ. Innov. 2016, 2, 8. [Google Scholar] [CrossRef]
- Liu, B.S.; Yang, X.D.; Huo, T.F.; Shen, G.Q.; Wang, X. A linguistic group decision-making framework for bid evaluation in mega public projects considering carbon dioxide emissions reduction. J. Clean. Prod. 2017, 148, 811–825. [Google Scholar] [CrossRef]
- Yan, S.L.; Liu, S.F.; Liu, J.F.; Wu, L.F. Dynamic grey target decision making method with grey numbers based on existing state and future development trend of alternatives. J. Intell. Fuzzy Syst. 2015, 28, 2159–2168. [Google Scholar] [CrossRef]
- Hu, M.L. Grey target decision model based on a new distance measure. J. Grey Syst. 2016, 28, 27–34. [Google Scholar]
- Zhou, H.; Wang, J.Q.; Zhang, H.Y. Grey stochastic multi-criteria decision-making based on regret theory and TOPSIS. Int. J. Mach. Learn. Cybern. 2017, 8, 651–664. [Google Scholar] [CrossRef]
- Lidinska, L.; Jablonsky, J. AHP model for performance evaluation of employees in a Czech management consulting company. Cent. Eur. J. Oper. Res. 2017, 26, 239–258. [Google Scholar] [CrossRef]
- Ji, P.; Zhang, H.Y.; Wang, J.Q. A projection-based TODIM method under multi-valued neutrosophic environments and its application in personnel selection. Neural Comput. Appl. 2017, 29, 221–234. [Google Scholar] [CrossRef]
- Hashemi, S.S.; Hajiagha, S.H.R.; Zavadskas, E.K.; Mahdiraji, H.A. Multicriteria group decision making with ELECTRE III method based on interval-valued intuitionistic fuzzy information. Appl. Math. Model. 2016, 40, 1554–1564. [Google Scholar] [CrossRef]
- Huang, Y.B.; Jiang, W. Extension of TOPSIS Method and its Application in Investment. Arab. J. Sci. Eng. 2017, 43, 693–705. [Google Scholar] [CrossRef]
- Zhou, W.; Yin, W.Y.; Peng, X.Q.; Liu, F.M.; Yang, F. Comprehensive evaluation of land reclamation and utilisation schemes based on a modified VIKOR method for surface mines. Int. J. Min. Reclam. Environ. 2016, 32, 93–108. [Google Scholar] [CrossRef]
- Deng, J.L. Introduction to grey system theory. J. Grey Syst. 1989, 1, 1–24. [Google Scholar]
- Kolhapure, R.; Shinde, V.; Kamble, V. Geometrical optimization of strain gauge force transducer using GRA method. Measurement 2017, 101, 111–117. [Google Scholar] [CrossRef]
- Kirubakaran, B.; Ilangkumaran, M. Selection of optimum maintenance strategy based on FAHP integrated with GRA–TOPSIS. Ann. Oper. Res. 2016, 245, 285–313. [Google Scholar] [CrossRef]
- Li, N.N.; Zhao, H.R. Performance evaluation of eco-industrial thermal power plants by using fuzzy GRA-VIKOR and combination weighting techniques. J. Clean. Prod. 2016, 135, 169–183. [Google Scholar] [CrossRef]
- Liu, J.; Guo, L.; Jiang, J.P.; Hao, L.L.; Liu, R.T.; Wang, P. Evaluation and selection of emergency treatment technology based on dynamic fuzzy GRA method for chemical contingency spills. J. Hazard. Mater. 2015, 299, 306–315. [Google Scholar] [CrossRef] [PubMed]
- Luo, D.; Wei, B.L.; Lin, P.Y. The Optimization of Several Grey Incidence Analysis Models. J. Grey Syst. 2015, 27, 1–11. [Google Scholar]
- Wang, P.; Zhu, Z.Q.; Wang, Y.H. A novel hybrid MCDM model combining the SAW, TOPSIS and GRA methods based on experimental design. Inf. Sci. 2016, 345, 27–45. [Google Scholar] [CrossRef]
- Tsaur, R.C.; Chen, I.F.; Chan, Y.S. TFT-LCD industry performance analysis and evaluation using GRA and DEA models. Int. J. Prod. Res. 2017, 55, 4378–4391. [Google Scholar] [CrossRef]
- Ho, T.C.; Chiu, R.H.; Chung, C.C.; Lee, H.S. Key influence factors for ocean freight forwarders selecting container shipping lines using the revised dematel approach. J. Mar. Sci. Technol. 2017, 25, 299–310. [Google Scholar] [CrossRef]
- Hsu, C.W.; Kuo, T.C.; Chen, S.H.; Hu, A.H. Using DEMATEL to develop a carbon management model of supplier selection in green supply chain management. J. Clean. Prod. 2013, 56, 164–172. [Google Scholar] [CrossRef]
- Su, C.M.; Horng, D.J.; Tseng, M.L.; Chiu, A.S.; Wu, K.J.; Chen, H.P. Improving sustainable supply chain management using a novel hierarchical grey-DEMATEL approach. J. Clean. Prod. 2016, 134, 469–481. [Google Scholar] [CrossRef]
- Luthra, S.; Govindan, K.; Mangla, S.K. Structural model for sustainable consumption and production adoption—A grey-DEMATEL based approach. Resour. Conserv. Recycl. 2017, 125, 198–207. [Google Scholar] [CrossRef]
- Seker, S.; Recal, F.; Basligil, H. A combined DEMATEL and grey system theory approach for analyzing occupational risks: A case study in Turkish shipbuilding industry. Hum. Ecol. Risk Assess. 2017, 23, 1340–1372. [Google Scholar] [CrossRef]
- Govindan, K.; Kaliyan, M.; Kannan, D.; Haq, A.N. Barriers analysis for green supply chain management implementation in Indian industries using analytic hierarchy process. Int. J. Prod. Econ. 2014, 147, 555–568. [Google Scholar] [CrossRef]
- Yu, Q.; Hou, F.J. An approach for green supplier selection in the automobile manufacturing industry. Kybernetes 2016, 45, 571–588. [Google Scholar] [CrossRef]
- Lin, C.H.; Madu, C.N.; Kuei, C.H.; Tsai, H.L.; Wang, K.N. Developing an assessment framework for managing sustainability programs. Expert Syst. Appl. 2015, 42, 2488–2501. [Google Scholar] [CrossRef]
- Govindan, K.; Kadziński, M.; Sivakumar, R. Application of a novel PROMETHEE-based method for construction of a group compromise ranking to prioritization of green suppliers in food supply chain. Omega 2017, 71, 129–145. [Google Scholar] [CrossRef]
- Roshandel, J.; Miri-Nargesi, S.S.; Hatami-Shirkouhi, L. Evaluating and selecting the supplier in detergent production industry using hierarchical fuzzy TOPSIS. Appl. Math. Model. 2013, 37, 10170–10181. [Google Scholar] [CrossRef]
- Azadi, M.; Jafarian, M.; Saen, R.F.; Mirhedayatian, S.M. A new fuzzy DEA model for evaluation of efficiency and effectiveness of suppliers in sustainable supply chain management context. Comput. Oper. Res. 2015, 54, 274–285. [Google Scholar] [CrossRef]
- Teresa, W.; Jennifer, B. Supplier evaluation and selection: An augmented DEA approach. Int. J. Prod. Res. 2009, 47, 4593–4608. [Google Scholar] [CrossRef]
- Ghayebloo, S.; Tarokh, M.J.; Venkatadri, U.; Diallo, C. Developing a bi-objective model of the closed-loop supply chain network with green supplier selection and disassembly of products: The impact of parts reliability and product greenness on the recovery network. J. Manuf. Syst. 2015, 36, 76–86. [Google Scholar] [CrossRef]
- Amin, S.H.; Zhang, G.Q. An integrated model for closed-loop supply chain configuration and supplier selection: Multi-objective approach. Expert Syst. Appl. 2012, 39, 6782–6791. [Google Scholar] [CrossRef]
- Stanujkic, D.; Dordjevic, B.; Dordjevic, M. Comparative analysis of some prominent MCDM methods: A case of ranking Serbian banks. Serb. J. Manag. 2013, 8, 213–241. [Google Scholar] [CrossRef]
- Qin, J.D.; Liu, X.W.; Pedrycz, W. An extended TODIM multi-criteria group decision making method for green supplier selection in interval type-2 fuzzy environment. Eur. J. Oper. Res. 2017, 258, 626–638. [Google Scholar] [CrossRef]
- Tsui, C.W.; Wen, U.P. A Hybrid Multiple Criteria Group Decision-Making Approach for Green Supplier Selection in the TFT-LCD Industry. Math. Probl. Eng. 2014, 2014, 1–13. [Google Scholar] [CrossRef]
- Hamdan, S.; Cheaitou, A. Supplier selection and order allocation with green criteria: An MCDM and multi-objective optimization approach. Comput. Oper. Res. 2017, 81, 282–304. [Google Scholar] [CrossRef]
- Bai, C.G.; Dhavale, D.; Sarkis, J. Complex investment decisions using rough set and fuzzy c-means: An example of investment in green supply chains. Eur. J. Oper. Res. 2016, 248, 507–521. [Google Scholar] [CrossRef]
- Luthra, S.; Govindan, K.; Kannan, D.; Mangla, S.K.; Garg, C.P. An integrated framework for sustainable supplier selection and evaluation in supply chains. J. Clean. Prod. 2017, 140, 1686–1698. [Google Scholar] [CrossRef]
- Liu, S.F.; Tao, L.Y.; Xie, N.M.; Yang, Y.J. On the new model system and framework of grey system theory. J. Grey Syst. 2016, 28, 1–15. [Google Scholar]
- Yang, Y.J. Extended grey numbers and their operations. In Proceedings of the 2007 IEEE International Conference on Fuzzy Systems and Intelligent Services, Man and Cybernetics, Montreal, QC, Canada, 7–10 October 2007; IEEE: Piscataway, NJ, USA, 2007; pp. 2181–2186. [Google Scholar]
- Wu, W.W.; Lee, Y.T. Developing global managers’ competencies using the fuzzy DEMATEL method. Expert Syst. Appl. 2007, 32, 499–507. [Google Scholar] [CrossRef]
- Altuntas, S.; Dereli, T. A novel approach based on DEMATEL method and patent citation analysis for prioritizing a portfolio of investment projects. Expert Syst. Appl. 2015, 42, 1003–1012. [Google Scholar] [CrossRef]
- Nie, W.B.; Liu, W.D.; Wang, J.D.; Zeng, T.; Hu, K. Evaluation approach in process failure risk analysis based on matrix similarity and evidence theory. Comput. Integr. Manuf. Syst. 2016, 22, 2602–2612. (In Chinese) [Google Scholar] [CrossRef]
- Kim, M.; Chai, S. Implementing Environmental Practices for Accomplishing Sustainable Green Supply Chain Management. Sustainability 2017, 9, 1192. [Google Scholar] [CrossRef]
- Guo, S.D.; Liu, S.F.; Fang, Z.G. Multi-attribute decision making model based on kernel and degree of greyness of interval grey numbers. Control Decision 2016, 31, 1042–1046. (In Chinese) [Google Scholar] [CrossRef]
- Liu, Z.X.; Liu, S.F.; Fang, Z.G. Decision making model of grey comprehensive correlation and relative close degree based on kernel and greyness degree. Control Decision 2017, 32, 1475–1480. (In Chinese) [Google Scholar] [CrossRef]
| Attribute | Sub-Attribute | Relevant Reference | Explanation |
|---|---|---|---|
| Green level (B1) | Resources recovery (b1) | [33,40,41] | The ratio of recovery to input |
| Ambient severities (b2) | [32,40] | The severity of affecting environment | |
| Energy consumption (b3) | [32,33,40] | The extent of energy consumption | |
| Product competitiveness (B2) | Product quality (b4) | [34,36,38] | The product qualified rate |
| Product price (b5) | [33,34,44] | The price of purchased product itself | |
| Product performance (b6) | [34,38] | The failure rate of the qualified product | |
| Enterprise competitiveness (B3) | Financial situation (b7) | [32,44] | The ability of fund raising and application |
| Technical level (b8) | [30,33,38] | The level of technical knowledge owned by an enterprise | |
| Staff quality (b9) | [38,39] | The proportion of middle or senior title within an enterprise | |
| Management level (b10) | [32,38,40] | The comprehensive management ability of an enterprise in the whole operation process | |
| Cooperation support (B4) | After-sale service capabilities (b11) | [38,41] | The capabilities of various services provided after the sale of a product |
| Customer satisfaction (b12) | [39,44] | The degree of satisfaction with products and related services | |
| Delivery on time (b13) | [33,36,38] | The ratio of the number of punctual deliveries to the number of total deliveries in a certain period of time |
| Potential Green Suppliers | |||||
|---|---|---|---|---|---|
| S1 | S2 | S3 | S4 | ||
| B1 | b1 | 33 | 35 | 36 | 31 |
| b2 | |||||
| b3 | |||||
| B2 | b4 | 91 | 98 | 95 | 88 |
| b5 | |||||
| b6 | 8.8 | 5.7 | 7.4 | 9.3 | |
| B3 | b7 | ||||
| b8 | |||||
| b9 | 27 | 32 | 33 | 23 | |
| b10 | |||||
| B4 | b11 | ||||
| b12 | |||||
| b13 | 91 | 95 | 86 | 95 | |
| Potential Green Suppliers | |||||
|---|---|---|---|---|---|
| S1 | S2 | S3 | S4 | ||
| B1 | b1 | 0.4 | 0.8 | 1 | 0 |
| b2 | |||||
| b3 | |||||
| B2 | b4 | 0.30 | 1.00 | 0.70 | 0.00 |
| b5 | |||||
| b6 | 0.14 | 1.00 | 0.53 | 0.00 | |
| B3 | b7 | ||||
| b8 | |||||
| b9 | 0.40 | 0.90 | 1.00 | 0.00 | |
| b10 | |||||
| B4 | b11 | ||||
| b12 | |||||
| b13 | 0.56 | 1.00 | 0.00 | 1.00 | |
| DM1 | DM2 | DM3 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Initial Direct Relation Matrix | Initial Direct Relation Matrix | Initial Direct Relation Matrix | ||||||||||
| B1 | B2 | B3 | B4 | B1 | B2 | B3 | B4 | B1 | B2 | B3 | B4 | |
| B1 | 0 | 2 | 1 | 1 | 0 | 2 | 1 | 2 | 0 | 1 | 3 | 2 |
| B2 | 4 | 0 | 0 | 3 | 4 | 0 | 1 | 2 | 3 | 0 | 2 | 3 |
| B3 | 2 | 1 | 0 | 2 | 2 | 2 | 0 | 3 | 1 | 1 | 0 | 4 |
| B4 | 1 | 0 | 1 | 0 | 2 | 0 | 1 | 0 | 2 | 1 | 0 | 0 |
| Attributes | R + C | R − C | Weights | Normalized Weights |
|---|---|---|---|---|
| B1 | 5.2942 | −0.7863 | 5.3523 | 0.2811 |
| B2 | 4.6655 | 1.2972 | 4.8425 | 0.2543 |
| B3 | 4.1847 | 1.1011 | 4.3272 | 0.2273 |
| B4 | 4.2221 | −1.6120 | 4.5193 | 0.2373 |
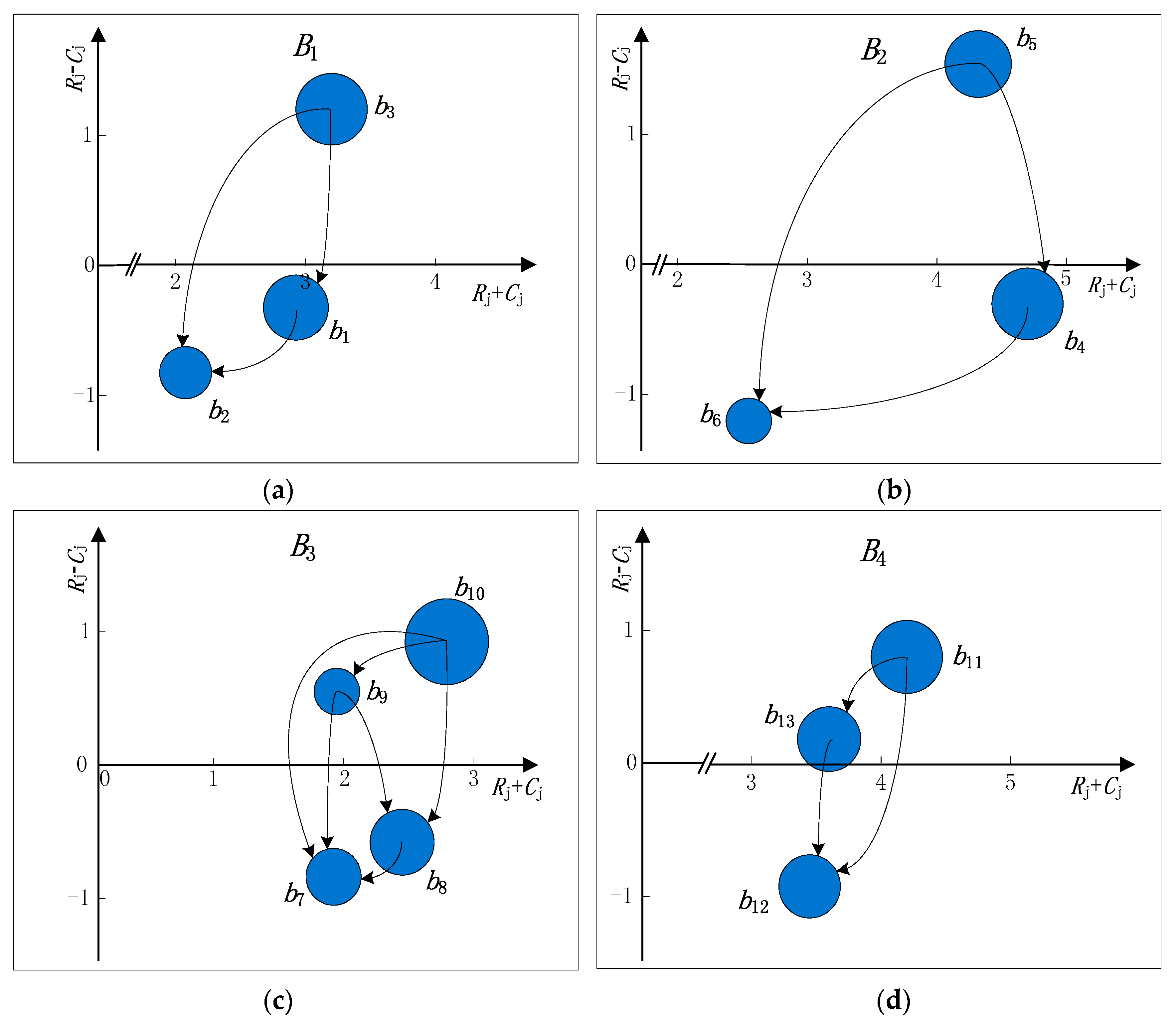
| Sub-Attributes | R + C | R − C | Normalized Sub-Attribute Weights | Overall Sub-Attribute Weights |
|---|---|---|---|---|
| b1 | 2.8913 | −0.3261 | 0.3422 | 0.0962 |
| b2 | 2.0761 | −0.8152 | 0.2623 | 0.0737 |
| b3 | 3.1630 | 1.1413 | 0.3955 | 0.1112 |
| b4 | 4.7123 | −0.2740 | 0.3906 | 0.0993 |
| b5 | 4.3014 | 1.5068 | 0.3772 | 0.0959 |
| b6 | 2.5205 | −1.2329 | 0.2322 | 0.0591 |
| b7 | 1.9130 | −0.8566 | 0.2208 | 0.0502 |
| b8 | 2.4013 | −0.5940 | 0.2606 | 0.0592 |
| b9 | 1.9307 | 0.5217 | 0.2107 | 0.0479 |
| b10 | 2.7714 | 0.9289 | 0.3079 | 0.0700 |
| b11 | 4.2338 | 0.7792 | 0.3755 | 0.0891 |
| b12 | 3.4545 | −0.9091 | 0.3116 | 0.0739 |
| b13 | 3.5844 | 0.1299 | 0.3129 | 0.0743 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, H.; Dang, Y.; Mao, W. A Decision-Making Method with Grey Multi-Source Heterogeneous Data and Its Application in Green Supplier Selection. Int. J. Environ. Res. Public Health 2018, 15, 446. https://doi.org/10.3390/ijerph15030446
Sun H, Dang Y, Mao W. A Decision-Making Method with Grey Multi-Source Heterogeneous Data and Its Application in Green Supplier Selection. International Journal of Environmental Research and Public Health. 2018; 15(3):446. https://doi.org/10.3390/ijerph15030446
Chicago/Turabian StyleSun, Huifang, Yaoguo Dang, and Wenxin Mao. 2018. "A Decision-Making Method with Grey Multi-Source Heterogeneous Data and Its Application in Green Supplier Selection" International Journal of Environmental Research and Public Health 15, no. 3: 446. https://doi.org/10.3390/ijerph15030446
APA StyleSun, H., Dang, Y., & Mao, W. (2018). A Decision-Making Method with Grey Multi-Source Heterogeneous Data and Its Application in Green Supplier Selection. International Journal of Environmental Research and Public Health, 15(3), 446. https://doi.org/10.3390/ijerph15030446





