Comparing Classic and Interval Analytical Hierarchy Process Methodologies for Measuring Area-Level Deprivation to Analyze Health Inequalities
Abstract
1. Introduction
2. Methods
2.1. The Multi-Criteria Deprivation Index for the City of Quito Using Traditional AHP
2.2. The Interval AHP: Applying the Interval Pairwise Comparison Matrix
2.3. Comparison and Validation of the MDIQ and I-MDIQ
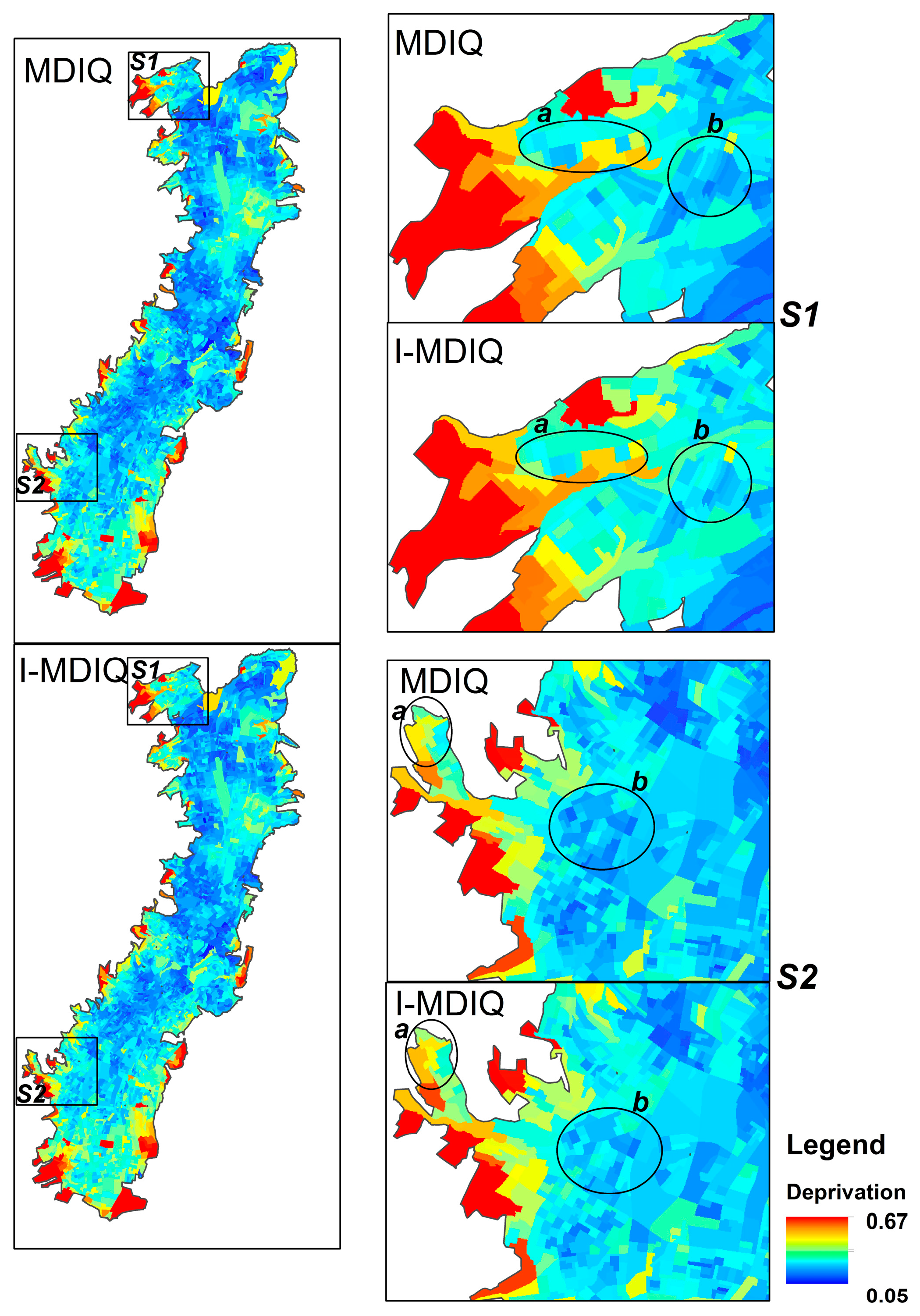
3. Results
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Cabrera-Barona, P.; Murphy, T.; Kienberger, S.; Blaschke, T. A multi-criteria spatial deprivation index to support health inequality analyses. Int. J. Health Geogr. 2015, 14, 11. [Google Scholar] [CrossRef] [PubMed]
- Niggebrugge, A.; Haynes, R.; Jones, A.; Lovett, A.; Harvey, I. The index of multiple deprivation 2000 access domain: A useful indicator for public health? Soc. Sci. Med. 2005, 60, 2743–2753. [Google Scholar] [CrossRef] [PubMed]
- Pampalon, R.; Hamel, D.; Gamache, P.; Raymond, G. A deprivation index for health planning in Canada. Chronic Dis. Can. 2009, 29, 178–191. [Google Scholar] [PubMed]
- Havard, S.; Deguen, S.; Bodin, J.; Louis, K.; Laurent, O.; Bard, D. A small-area index of socioeconomic deprivation to capture health inequalities in France. Soc. Sci. Med. 2008, 67, 2007–2016. [Google Scholar] [CrossRef] [PubMed]
- Townsend, P. Deprivation. J. Soc. Policy 1987, 16, 125–146. [Google Scholar] [CrossRef]
- Townsend, P.; Phillimore, P.; Beattie, A. Health and Deprivation. Inequality and the North; Routledge: London, UK, 1988. [Google Scholar]
- Carstairs, V.; Morris, R. Deprivation: Explaining differences in mortality between Scotland and England and Wales. Br. Med. J. 1989, 299, 886–889. [Google Scholar] [CrossRef]
- Jordan, H.; Roderick, P.; Martin, D. The Index of Multiple Deprivation 2000 and accessibility effects on health. J. Epidemiol. Community Health 2004, 58, 250–257. [Google Scholar] [CrossRef] [PubMed]
- Department of Environment, Transport and the Regions (DETR). Measuring Multiple Deprivation at the Small Area Level: The Indices of Deprivation 2000; DETR: London, UK, 2000.
- Lalloué, B.; Monnez, J.-M.; Padilla, C.; Kihal, W.; Le Meur, N.; Zmirou-Navier, D.; Deguen, S. A statistical procedure to create a neighborhood socioeconomic index for health inequalities analysis. Int. J. Equity Health 2013, 12, 21. [Google Scholar] [CrossRef]
- Cabrera-Barona, P.; Wei, C.; Hagenlocher, M. Multiscale evaluation of an urban deprivation index: Implications for quality of life and healthcare accessibility planning. Appl. Geogr. 2016, 70, 1–10. [Google Scholar] [CrossRef]
- Guillaume, E.; Pornet, C.; Dejardin, O.; Launay, L.; Lillini, R.; Vercelli, M.; Marí-Dell’Olmo, M.; Fernández Fontelo, A.; Borrell, C.; Ribeiro, A.I.; et al. Development of a cross-cultural deprivation index in five European countries. J. Epidemiol. Community Health 2016, 70, 493–499. [Google Scholar] [CrossRef] [PubMed]
- Bell, N.; Schuurman, N.; Hayes, M.V. Using GIS-based methods of multicriteria analysis to construct socio-economic deprivation indices. Int. J. Health Geogr. 2007, 6, 17. [Google Scholar] [CrossRef] [PubMed]
- Belhadj, B. New weighting scheme for the dimensions in multidimensional poverty indices. Econ. Lett. 2012, 116, 304–307. [Google Scholar] [CrossRef]
- Cabrera-Barona, P. Influence of Urban Multi-Criteria Deprivation and Spatial Accessibility to Healthcare on Self-Reported Health. Urban Sci. 2017, 1, 11. [Google Scholar] [CrossRef]
- Cabrera-Barona, P.; Blaschke, T.; Gaona, G. Deprivation, Healthcare Accessibility and Satisfaction: Geographical Context and Scale Implications. Appl. Spat. Anal. Policy 2017, 1–20. [Google Scholar] [CrossRef]
- Saaty, T.L. A Scaling Method for Priorities in Hierarchical Structures. J. Math. Psychol. 1977, 15, 234–281. [Google Scholar] [CrossRef]
- Feizizadeh, B.; Shadman Roodposhti, M.; Jankowski, P.; Blaschke, T. A GIS-based extended fuzzy multi-criteria evaluation for landslide susceptibility mapping. Comput. Geosci. 2014, 73, 208–221. [Google Scholar] [CrossRef] [PubMed]
- Boroushaki, S.; Malczewski, J. Measuring consensus for collaborative decision-making: A GIS-based approach. Comput. Environ. Urban Syst. 2010, 34, 322–332. [Google Scholar] [CrossRef]
- Ghorbanzadeh, O.; Pourmoradian, S.; Blaschke, T.; Feizizadeh, B. Nature Based Tourism Susceptibility Mapping by applying GIS-Decision Making Systems in East Azerbaijan Province, Iran. In Proceedings of the 1st International Conference of SilkGIS, Isfahan, Iran, 24–26 June 2017. [Google Scholar]
- Boroushaki, S.; Malczewski, J. Implementing an extension of the analytical hierarchy process using ordered weighted averaging operators with fuzzy quantifiers in ArcGIS. Comput. Geosci. 2008, 34, 399–410. [Google Scholar] [CrossRef]
- Saaty, R. The analytic hierarchy process—What it is and how it is used. Math. Model. 1987, 9, 161–176. [Google Scholar] [CrossRef]
- Ho, W. Integrated analytic hierarchy process and its applications—A literature review. Eur. J. Oper. Res. 2008, 186, 211–228. [Google Scholar] [CrossRef]
- Feizizadeh, B.; Ghorbanzadeh, O. GIS-based Interval Pairwise Comparison Matrices as a Novel Approach for Optimizing an Analytical Hierarchy Process and Multiple Criteria Weighting. In Proceedings of the GI_Forum 2017, Salzburg, Austria, 4–7 July 2017; pp. 27–35. [Google Scholar]
- Chen, Y.; Yu, J.; Khan, S. The spatial framework for weight sensitivity analysis in AHP-based multi-criteria decision making. Environ. Model. Softw. 2013, 48, 129–140. [Google Scholar] [CrossRef]
- Mideros, A. Ecuador: Defining and measuring multidimensional poverty. CEPAL Rev. 2006, 108, 49–67. [Google Scholar]
- Ramírez, R. La vida buena como riqueza de las naciones. Rev. Ciencias Soc. 2012, 237–249. (In Spanish) [Google Scholar] [CrossRef]
- Carstairs, V. Deprivation indices: Their interpretation and use in relation to health. J. Epidemiol. Community Health 1995, 49, S3–S8. [Google Scholar] [CrossRef] [PubMed]
- Bolloju, N. Aggregation of analytic hierarchy process models based on similarities in decision makers’ preferences. Eur. J. Oper. Res. 2001, 128, 499–508. [Google Scholar] [CrossRef]
- Sugihara, K.; Tanaka, H. Interval Evaluations in the Analytic Hierarchy Process by Possibility Analysis. Comput. Intell. 2001, 17, 567–579. [Google Scholar] [CrossRef]
- Liu, F. Acceptable consistency analysis of interval reciprocal comparison matrices. Fuzzy Sets Syst. 2009, 160, 2686–2700. [Google Scholar] [CrossRef]
- Jahanshahloo, G.; Hoseinzadeh, F.; Barzegarinegad, A.; Hatamaian, H. Weight gain for interval pairwise matrices in the AHP with area of confidence by DEA method. In Proceedings of the 4th National Conference of Data Envelopment Analysis, Babolsar, Iran, 13–14 June 2012; University of Mazandaran: Babolsar, Iran, 2012; pp. 1–3. [Google Scholar]
- Feizizadeh, B.; Jankowski, P.; Blaschke, T. A GIS based spatially-explicit sensitivity and uncertainty analysis approach for multi-criteria decision analysis. Comput. Geosci. 2014, 64, 81–95. [Google Scholar] [CrossRef] [PubMed]
- Lòpez-De Fede, A.; Stewart, J.E.; Hardin, J.W.; Mayfield-Smith, K. Comparison of small-area deprivation measures as predictors of chronic disease burden in a low-income population. Int. J. Equity Health 2016, 15, 89. [Google Scholar] [CrossRef]
- Doebler, S.; Glasgow, N. Relationships between Deprivation and the Self-Reported Health of Older People in Northern Ireland. J. Aging Health 2016, 29, 594–619. [Google Scholar] [CrossRef] [PubMed]
- Whynes, D.K. Deprivation and self-reported health: Are there “Scottish effects” in England and Wales? J. Public Health 2009, 31, 147–153. [Google Scholar] [CrossRef] [PubMed]
- Yamaguchi, A. Influences of Quality of Life on Health and Well-Being. Soc. Indic. Res. 2015, 123, 77–102. [Google Scholar] [CrossRef]
- Cabrera-Barona, P.; Blaschke, T.; Kienberger, S. Explaining Accessibility and Satisfaction Related to Healthcare: A Mixed-Methods Approach. Soc. Indic. Res. 2017, 133, 719–739. [Google Scholar] [CrossRef] [PubMed]
- Allik, M.; Brown, D.; Dundas, R.; Leyland, A.H. Developing a new small-area measure of deprivation using 2001 and 2011 census data from Scotland. Health Place 2016, 39, 122–130. [Google Scholar] [CrossRef] [PubMed]
- Carmone, F.J.; Kara, A.; Zanakis, S.H. A Monte Carlo investigation of incomplete pairwise comparison matrices in AHP. Eur. J. Oper. Res. 1997, 102, 538–553. [Google Scholar] [CrossRef]
- Miilunpalo, S.; Vuori, I.; Oja, P.; Pasanen, M.; Urponen, H. Self-rated health status as a health measure: The predictive value of self-reported health status on the use of physician services and on mortality in the working-age population. J. Clin. Epidemiol. 1997, 50, 517–528. [Google Scholar] [CrossRef]
- Bailis, D.S.; Segall, A.; Chipperfield, J.G. Two views of self-rated general health status. Soc. Sci. Med. 2003, 56, 203–217. [Google Scholar] [CrossRef]
| Indicators |
|---|
| A: % of the population that have a long-term disability |
| B: % of the population that does not have any level of formal education or instruction |
| C: % of the population that has no public social/health insurance |
| D: % of the population that work in unpaid jobs |
| E: % of households with four or more persons per dormitory |
| F: % of households without access to drinking water from the public system |
| G: % of households without access to a sewerage system |
| H: % of households without access to the public electricity grid |
| I: % of households without garbage collection service |
| J: distance (meters) to the nearest primary healthcare service |
| Indicator | A | B | C | D | E | F | G | H | I | J | Weights |
|---|---|---|---|---|---|---|---|---|---|---|---|
| A | 1 | 0.048 | |||||||||
| B | 3 | 1 | 0.067 | ||||||||
| C | 3 | 2 | 1 | 0.090 | |||||||
| D | 2 | 2 | 2 | 1 | 0.111 | ||||||
| E | 1 | 1 | 1/2 | 1/2 | 1 | 0.039 | |||||
| F | 4 | 4 | 3 | 3 | 6 | 1 | 0.228 | ||||
| G | 2 | 2 | 1 | 1 | 4 | 1/2 | 1 | 0.102 | |||
| H | 2 | 1 | 2 | 1 | 4 | 1/3 | 2 | 1 | 0.108 | ||
| I | 1 | 1 | 1 | 1/2 | 3 | 1/3 | 1 | 1 | 1 | 0.076 | |
| J | 2 | 2 | 1 | 1 | 3 | 1 | 1 | 2 | 2 | 1 | 0.131 |
| CR = 0.038 | |||||||||||
| Indicator | A | B | C | D | E | F | G | H | I | J | Weights |
|---|---|---|---|---|---|---|---|---|---|---|---|
| A | 1 | 0.0510 | |||||||||
| B | [3,5] | 1 | 0.0881 | ||||||||
| C | [3,5] | [2,3] | 1 | 0.1157 | |||||||
| D | [2,3] | [1,2] | [1,2] | 1 | 0.1080 | ||||||
| E | 1 | 1 | [1/2,1] | 1/2 | 1 | 0.0437 | |||||
| F | 4 | [3,4] | [2,3] | 3 | [5,6] | 1 | 0.2175 | ||||
| G | [1,2] | [1,2] | [1/2,1] | [1/2,1] | [3,4] | 1/2 | 1 | 0.0966 | |||
| H | 2 | [1/2,1] | [1,2] | 1 | 4 | 1/3 | 2 | 1 | 0.1052 | ||
| I | [1/2,1] | [1/3,1] | [1/2,1] | 1/2 | [2,3] | 1/3 | [1/2,1] | 1 | 1 | 0.0678 | |
| J | [1,2] | [1,2] | [1/2,1] | 1 | [2,3] | 1 | [1/2,1] | [1,2] | [1,2] | 1 | 0.1073 |
| CRB = 0.0482; CRC = 0.0474 | |||||||||||
| Slope Index of Inequality | t-Value | Variation Partition Coefficient | Likelihood Ratio Test | |
|---|---|---|---|---|
| MDIQ | 2.14 | 0.67 | 0.41 | 15.03 |
| I-MDIQ | 1.85 | 0.61 | 0.44 | 7.61 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cabrera-Barona, P.; Ghorbanzadeh, O. Comparing Classic and Interval Analytical Hierarchy Process Methodologies for Measuring Area-Level Deprivation to Analyze Health Inequalities. Int. J. Environ. Res. Public Health 2018, 15, 140. https://doi.org/10.3390/ijerph15010140
Cabrera-Barona P, Ghorbanzadeh O. Comparing Classic and Interval Analytical Hierarchy Process Methodologies for Measuring Area-Level Deprivation to Analyze Health Inequalities. International Journal of Environmental Research and Public Health. 2018; 15(1):140. https://doi.org/10.3390/ijerph15010140
Chicago/Turabian StyleCabrera-Barona, Pablo, and Omid Ghorbanzadeh. 2018. "Comparing Classic and Interval Analytical Hierarchy Process Methodologies for Measuring Area-Level Deprivation to Analyze Health Inequalities" International Journal of Environmental Research and Public Health 15, no. 1: 140. https://doi.org/10.3390/ijerph15010140
APA StyleCabrera-Barona, P., & Ghorbanzadeh, O. (2018). Comparing Classic and Interval Analytical Hierarchy Process Methodologies for Measuring Area-Level Deprivation to Analyze Health Inequalities. International Journal of Environmental Research and Public Health, 15(1), 140. https://doi.org/10.3390/ijerph15010140






