A Multivariate Dynamic Spatial Factor Model for Speciated Pollutants and Adverse Birth Outcomes
Abstract
1. Introduction
2. Data Description
2.1. National Birth Defects Data
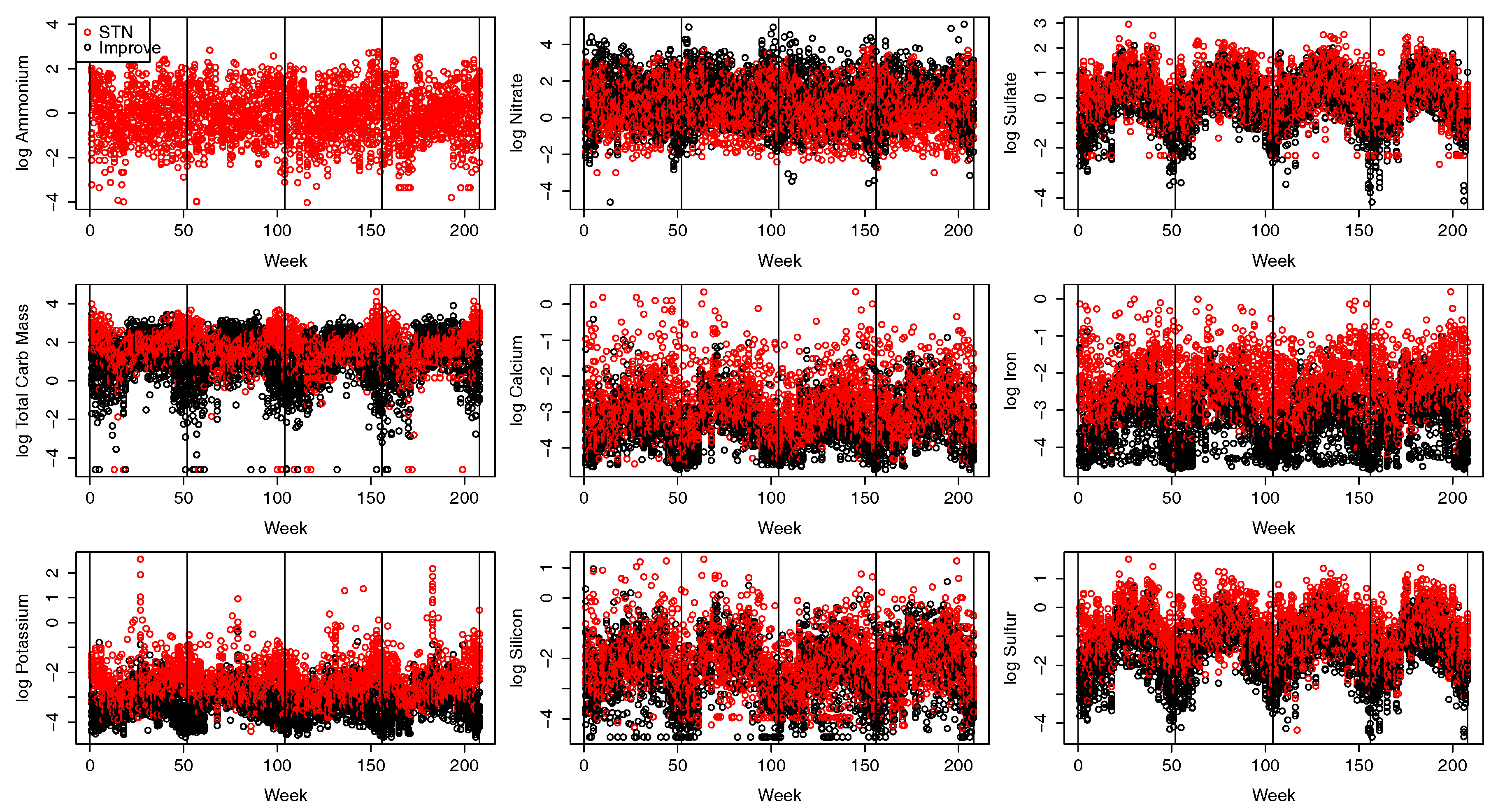
2.2. Pollution Data
3. Multivariate Spatio-Temporal Factor Model for Pollution
3.1. Factor Model for Speciated PM
3.2. Tailoring the Pollutant Model to CA Pollutant Data
3.3. Birth Defect Model
4. Results
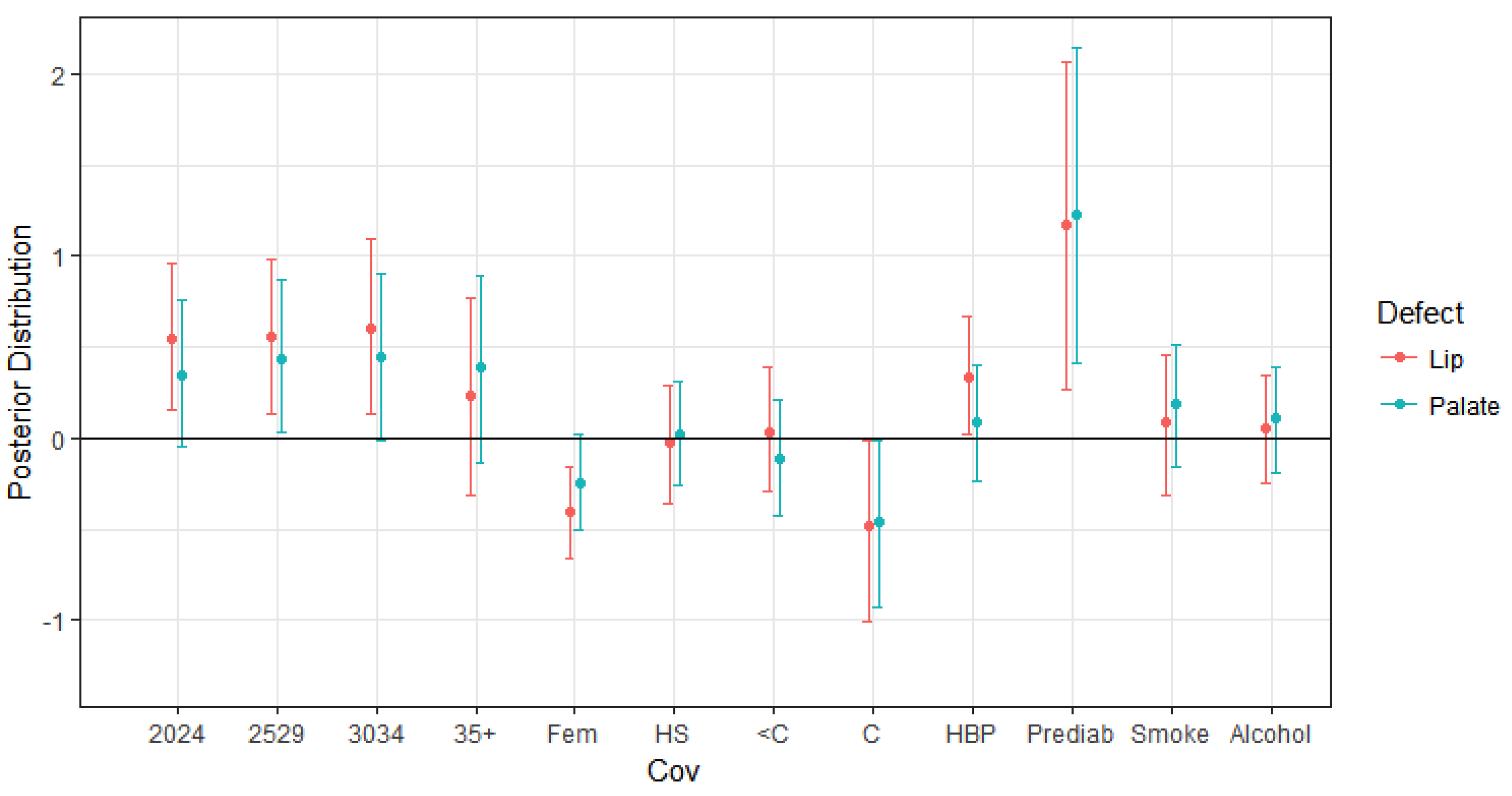
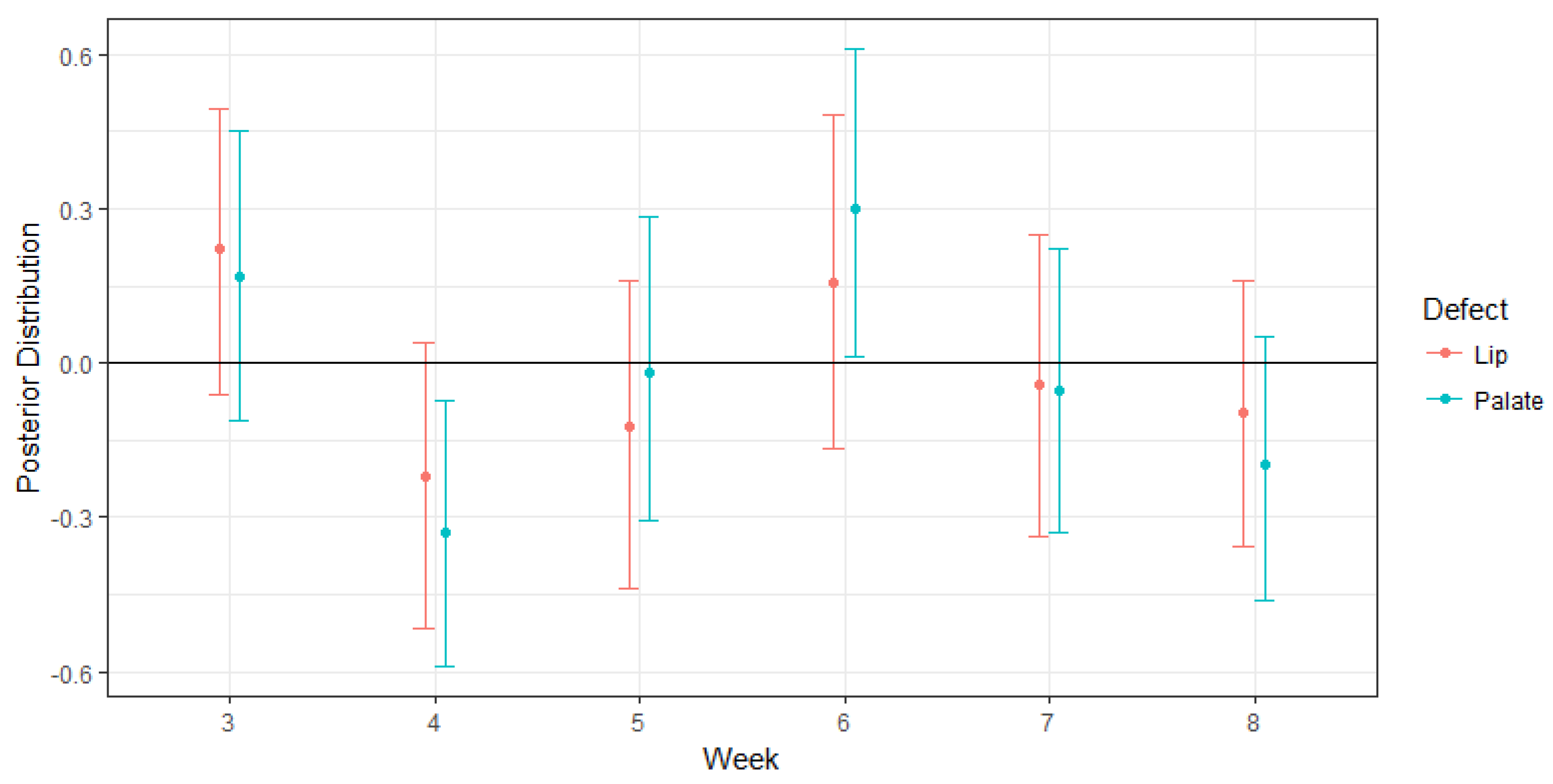
4.1. Impacts on Oral Cleft Risks
4.2. Model Comparison
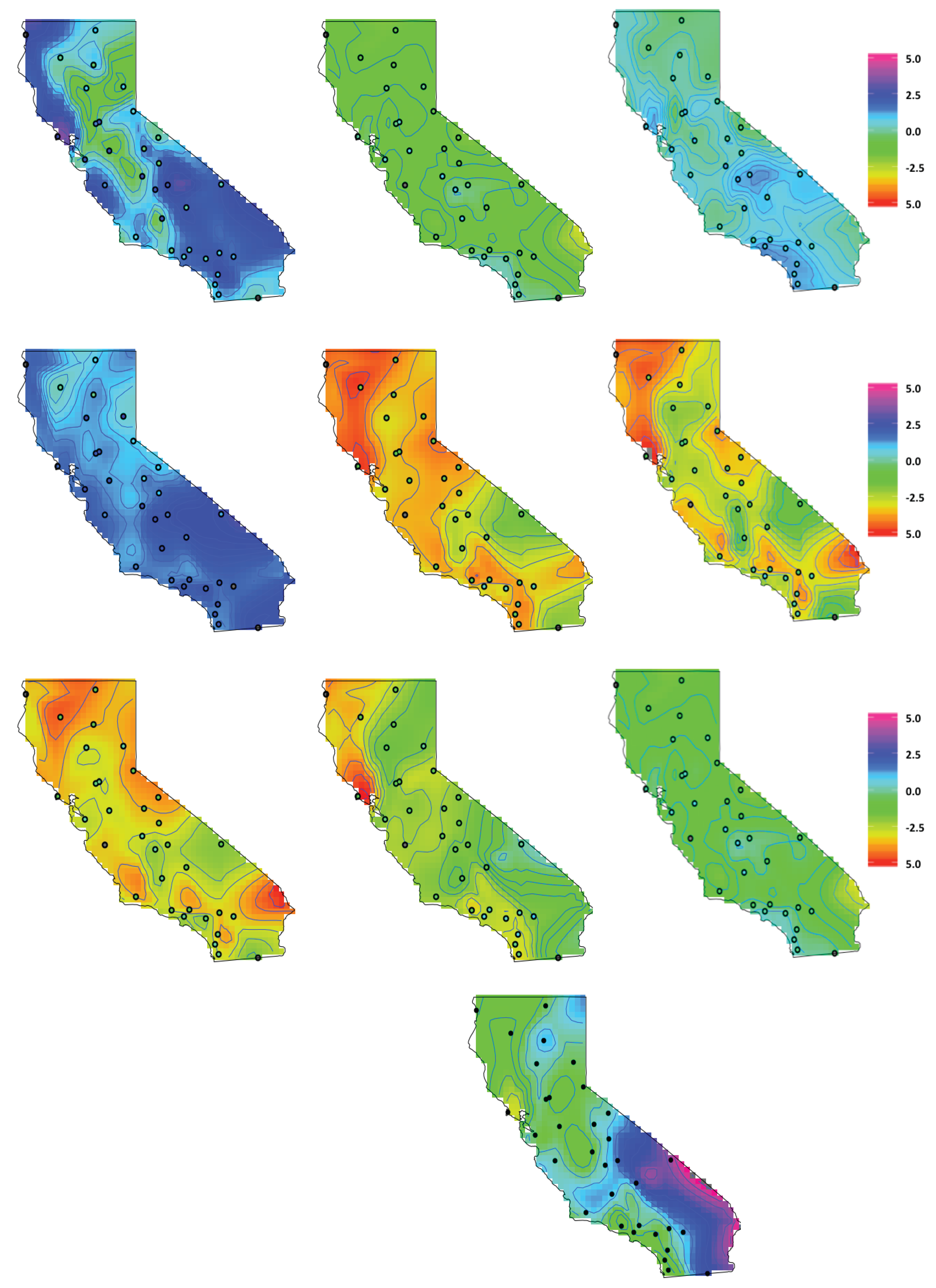
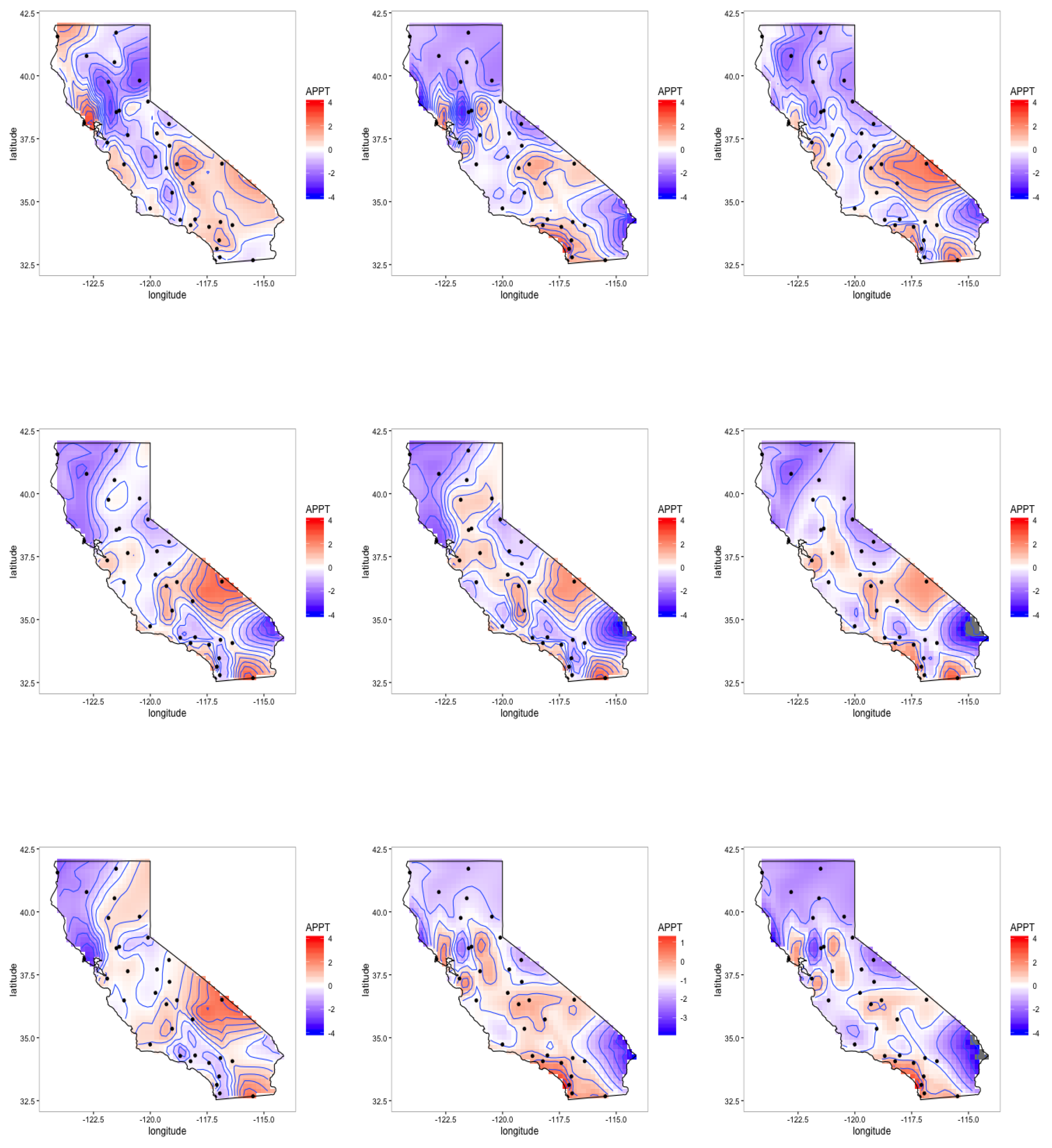
4.3. Latent Factor Results
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A. Factor Model Parameter Priors and Updates
- Forward Filtering: For , compute and , where , , , , and . Then, sample .
- Backwards Sampling: For sample where , , and .
References
- Zeiger, J.S.; Beaty, T.H. Is there a relationship between risk factors for oral clefts? Teratology 2002, 66, 205–208. [Google Scholar] [CrossRef] [PubMed]
- Garvey, D.J.; Longo, L.D. Chronic low level maternal carbon monoxide exposure and fetal growth and development. Biol. Reprod. 1978, 19, 8–14. [Google Scholar] [CrossRef] [PubMed]
- Longo, L.D. The biological effects of carbon monoxide on the pregnant woman, fetus, and newborn infant. Am. J. Obstet. Gynecol. 1977, 129, 69–103. [Google Scholar] [CrossRef]
- Ritz, B.; Yu, F.; Fruin, S.; Chapa, G.; Shaw, G.M.; Harris, J.A. Ambient air pollution and risk of birth defects in Southern California. Am. J. Epidemiol. 2002, 155, 17–25. [Google Scholar] [CrossRef] [PubMed]
- Gilboa, S.; Mendola, P.; Olshan, A.; Langlois, P.; Savitz, D.; Loomis, D.; Herring, A.; Fixler, D. Relation between ambient air quality and selected birth defects, seven county study, Texas, 1997–2000. Am. J. Epidemiol. 2005, 162, 238–252. [Google Scholar] [CrossRef] [PubMed]
- Hwang, B.F.; Jaakkola, J. Ozone and other air pollutants and the risk of oral clefts. Environ. Health Perspect. 2008, 116, 1411–1415. [Google Scholar] [CrossRef] [PubMed]
- Wang, W.; Guan, P.; Xu, W.; Zhou, B. Risk factors for oral clefts: A population-based case-control study in Shenyang, China. Paediatr. Perinat. Epidemiol. 2009, 23, 310–320. [Google Scholar] [CrossRef] [PubMed]
- Padula, A.M.; Tager, I.B.; Carmichael, S.L.; Hammond, S.K.; Lurmann, F.; Shaw, G.M. The association of ambient air pollution and traffic exposures with selected congenital anomalies in the San Joaquin Valley of California. Am. J. Epidemiol. 2013, 177, 1074–1085. [Google Scholar] [CrossRef] [PubMed]
- Fuentes, M.; Reich, B.J.; Huang, Y.N. Chapter in the Handbook of Environmental Statistics; Elsevier: Amsterdam, The Netherlands, 2017. [Google Scholar]
- Hansen, C.A.; Barnett, A.G.; Jalaludin, B.B.; Morgan, G.G. Ambient air pollution and birth defects in Brisbane, Australia. PLoS ONE 2009, 4, e5408. [Google Scholar] [CrossRef] [PubMed]
- Vrijheid, M.; Martinez, D.; Manzanares, S.; Dadvand, P.; Schembari, A.; Rankin, J.; Nieuwenhuijsen, M. Ambient air pollution and risk of congenital anomalies: A systematic review and meta-analysis. Environ. Health Perspect. 2011, 119, 599. [Google Scholar] [CrossRef] [PubMed]
- Richardson, D.B.; MacLehose, R.F.; Langholz, B.; Cole, S.R. Hierarchical latency models for dose-time-response associations. Am. J. Epidemiol. 2011, 173, 695–702. [Google Scholar] [CrossRef] [PubMed]
- Warren, J.; Fuentes, M.; Herring, A.; Langlois, P. Spatial-Temporal Modeling of the Association between Air Pollution Exposure and Preterm Birth: Identifying Critical Windows of Exposure. Biometrics 2012, 68, 1157–1167. [Google Scholar] [CrossRef] [PubMed]
- Chang, H.H.; Warren, J.L.; Darrow, L.A.; Reich, B.J.; Waller, L.A. Assessment of critical exposure and outcome windows in time-to-event analysis with application to air pollution and preterm birth study. Biostatistics 2015, 16, 509–521. [Google Scholar] [CrossRef] [PubMed]
- Lopes, H.F.; Salazar, E.; Gamerman, D. Spatial dynamic factor analysis. Bayesian Anal. 2008, 3, 759–792. [Google Scholar] [CrossRef]
- Neeley, E.; Christensen, W.; Sain, S. A Bayesian spatial factor analysis approach for combining climate model ensembles. Environmetrics 2014, 25, 483–497. [Google Scholar] [CrossRef]
- Jandarov, R.; Sheppard, L.; Sampson, P.; Szpiro, A. A Novel Dimension Reduction Approach for Spatially-Misaligned Multivariate Air Pollution Data. eprint arXiv, 2015; arXiv:1509.01171v1. [Google Scholar]
- Reefhuis, J.; Gilboa, S.M.; Anderka, M.; Browne, M.L.; Feldkamp, M.L.; Hobbs, C.A.; Jenkins, M.M.; Langlois, P.H.; Newsome, K.B.; Olshan, A.F.; et al. The national birth defects prevention study: A review of the methods. Birth Defects Res. A Clin. Mol. Teratol. 2015, 103, 656–669. [Google Scholar] [CrossRef] [PubMed]
- Stein, M.L. Prediction and inference for truncated spatial data. J. Comput. Graph. Stat. 1992, 1, 91–110. [Google Scholar]
- Spiegelhalter, D.J.; Best, N.G.; Carlin, B.P.; Van Der Linde, A. Bayesian measures of model complexity and fit. J. R. Stat. Soc. Ser. B (Stat. Methodol.) 2002, 64, 583–639. [Google Scholar] [CrossRef]
- Carter, C.K.; Kohn, R. On Gibbs sampling for state space models. Biometrika 1994, 81, 541–553. [Google Scholar] [CrossRef]
- Frühwirth-Schnatter, S. Data augmentation and dynamic linear models. J. Time Ser. Anal. 1994, 15, 183–202. [Google Scholar] [CrossRef]
- West, M.; Harrison, J. Bayesian Forecasting and Dynamic Models; Springer: New York, NY, USA, 1997; Volume 18. [Google Scholar]
| Variable | Levels | % Lip | % Palate | % Control |
|---|---|---|---|---|
| Age (Mother) | 19 and under | 26.3 | 33.3 | 40.4 |
| 20–24 | 30.9 | 29.7 | 39.4 | |
| 25–29 | 27.8 | 30.9 | 41.3 | |
| 30+ | 30.7 | 36.8 | 32.5 | |
| Education (Mother) | Less Than High School | 22.4 | 22.0 | 55.6 |
| High School | 21.8 | 25.9 | 52.3 | |
| Some College | 25.7 | 22.8 | 51.5 | |
| College Degree | 14.9 | 17.9 | 67.1 | |
| Fetal Sex | Male | 25.1 | 24.8 | 50.1 |
| Female | 22.0 | 21.7 | 56.3 | |
| High Blood Pressure (Mother) | No | 20.7 | 22.2 | 57.1 |
| Yes | 29.7 | 26.3 | 44.0 | |
| Smoker | No | 21.6 | 23.7 | 54.7 |
| Yes | 15.6 | 18.2 | 66.2 | |
| Alcohol Use | No | 21.7 | 23.7 | 54.6 |
| Yes | 22.6 | 25 | 52.4 |
| Nitrate | Sulfate | Total Carbon Mass | Calcium | Iron | Potassium | Silicon | Sulfur | |
|---|---|---|---|---|---|---|---|---|
| Sulfate | 0.41 | |||||||
| Total Carbon Mass | 0.38 | 0.05 | ||||||
| Calcium | 0.03 | 0.08 | 0.20 | |||||
| Iron | 0.19 | 0.11 | 0.48 | 0.77 | ||||
| Potassium | 0.07 | 0.17 | 0.08 | 0.16 | 0.12 | |||
| Silicon | 0.01 | 0.05 | 0.85 | 0.78 | 0.13 | |||
| Sulfur | 0.41 | 0.97 | 0.03 | 0.10 | 0.12 | 0.20 | 0.04 | |
| Ammonium | 0.96 | 0.60 | 0.34 | 0.05 | 0.19 | 0.06 | 0.59 |
| Mean | SD | 2.5% | 50% | 97.5% | |
|---|---|---|---|---|---|
| Maternal age 20–24 vs. 19 and under | 0.540 | 0.208 | 0.150 | 0.545 | 0.958 |
| Maternal age 25–29 vs. 19 and under | 0.556 | 0.222 | 0.128 | 0.562 | 0.976 |
| Maternal age 30–24 vs. 19 and under | 0.605 | 0.245 | 0.127 | 0.609 | 1.094 |
| Maternal age 35+ vs. 19 and under | 0.232 | 0.285 | −0.310 | 0.217 | 0.764 |
| Fetus Sex-Female | −0.405 | 0.134 | −0.664 | −0.407 | −0.157 |
| High school diploma vs. Less than high school | −0.021 | 0.164 | −0.354 | −0.019 | 0.290 |
| Some college vs. Less than high school | 0.032 | 0.173 | −0.296 | 0.027 | 0.388 |
| College graduate vs. Less than high school | −0.480 | 0.258 | −1.003 | −0.469 | −0.009 |
| High Blood Pressure | 0.332 | 0.165 | 0.017 | 0.330 | 0.671 |
| Maternal Prediabetes | 1.175 | 0.449 | 0.261 | 1.181 | 2.070 |
| Maternal Smoking | 0.089 | 0.192 | −0.310 | 0.091 | 0.454 |
| Maternal Alcohol Use | 0.049 | 0.149 | −0.243 | 0.052 | 0.348 |
| Maternal age 20–24 vs. 19 and under | 0.345 | 0.198 | −0.048 | 0.345 | 0.760 |
| Maternal age 25–29 vs. 19 and under | 0.439 | 0.208 | 0.027 | 0.437 | 0.866 |
| Maternal age 30–34 vs. 19 and under | 0.440 | 0.231 | −0.018 | 0.428 | 0.899 |
| Maternal age 35+ vs. 19 and under | 0.385 | 0.268 | −0.139 | 0.381 | 0.895 |
| Fetus Sex-Female | −0.247 | 0.133 | −0.503 | −0.246 | 0.021 |
| High School Education vs. Less than high school | 0.023 | 0.150 | −0.262 | 0.026 | 0.309 |
| Some college vs. Less than high school | −0.109 | 0.169 | −0.426 | −0.114 | 0.209 |
| College graduate vs. Less than high school | −0.430 | 0.167 | −0.943 | −0.412 | −0.001 |
| High Blood Pressure | 0.05 | 0.155 | −0.221 | 0.007 | 0.332 |
| Maternal Prediabetes | 1.214 | 0.431 | 0.391 | 1.196 | 2.072 |
| Maternal Smoking | 0.183 | 0.174 | −0.153 | 0.190 | 0.510 |
| Maternal Alcohol Use | 0.106 | 0.144 | −0.191 | 0.109 | 0.390 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kaufeld, K.A.; Fuentes, M.; Reich, B.J.; Herring, A.H.; Shaw, G.M.; Terres, M.A. A Multivariate Dynamic Spatial Factor Model for Speciated Pollutants and Adverse Birth Outcomes. Int. J. Environ. Res. Public Health 2017, 14, 1046. https://doi.org/10.3390/ijerph14091046
Kaufeld KA, Fuentes M, Reich BJ, Herring AH, Shaw GM, Terres MA. A Multivariate Dynamic Spatial Factor Model for Speciated Pollutants and Adverse Birth Outcomes. International Journal of Environmental Research and Public Health. 2017; 14(9):1046. https://doi.org/10.3390/ijerph14091046
Chicago/Turabian StyleKaufeld, Kimberly A., Montse Fuentes, Brian J. Reich, Amy H. Herring, Gary M. Shaw, and Maria A. Terres. 2017. "A Multivariate Dynamic Spatial Factor Model for Speciated Pollutants and Adverse Birth Outcomes" International Journal of Environmental Research and Public Health 14, no. 9: 1046. https://doi.org/10.3390/ijerph14091046
APA StyleKaufeld, K. A., Fuentes, M., Reich, B. J., Herring, A. H., Shaw, G. M., & Terres, M. A. (2017). A Multivariate Dynamic Spatial Factor Model for Speciated Pollutants and Adverse Birth Outcomes. International Journal of Environmental Research and Public Health, 14(9), 1046. https://doi.org/10.3390/ijerph14091046




