Structured Additive Quantile Regression for Assessing the Determinants of Childhood Anemia in Rwanda
Abstract
1. Introduction
2. Materials and Methods
2.1. Data Source
2.1.1. Dependent Variable
2.1.2. Independent Variables
2.2. Statistical Analysis
2.3. Model Selection
3. Results
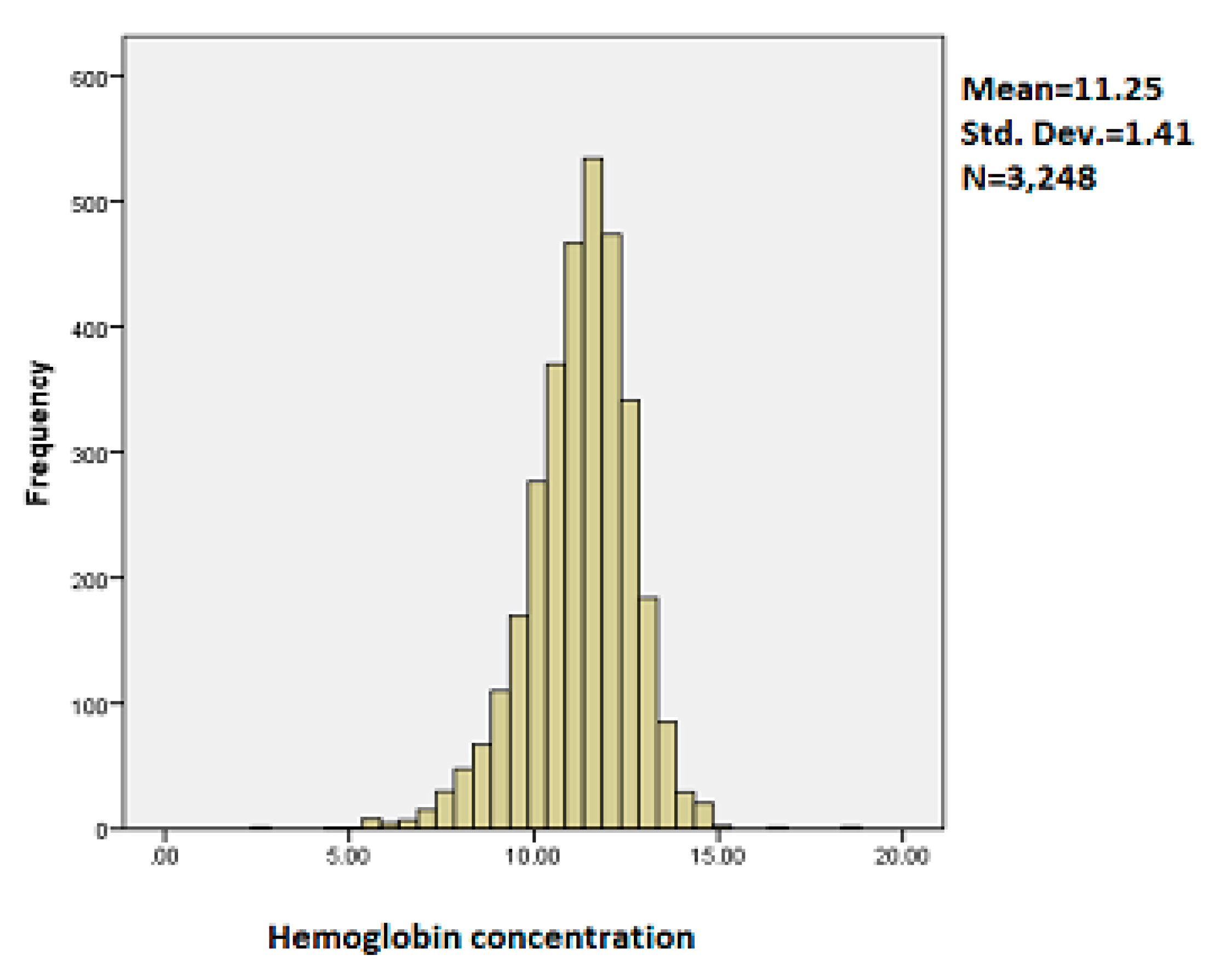
3.1. Exploratory Data Analysis
3.2. Results of Structured Additive Quantile Regression Analysis
3.2.1. Model Fit
3.2.2. Effects of Categorical Variables on Childhood Anemia
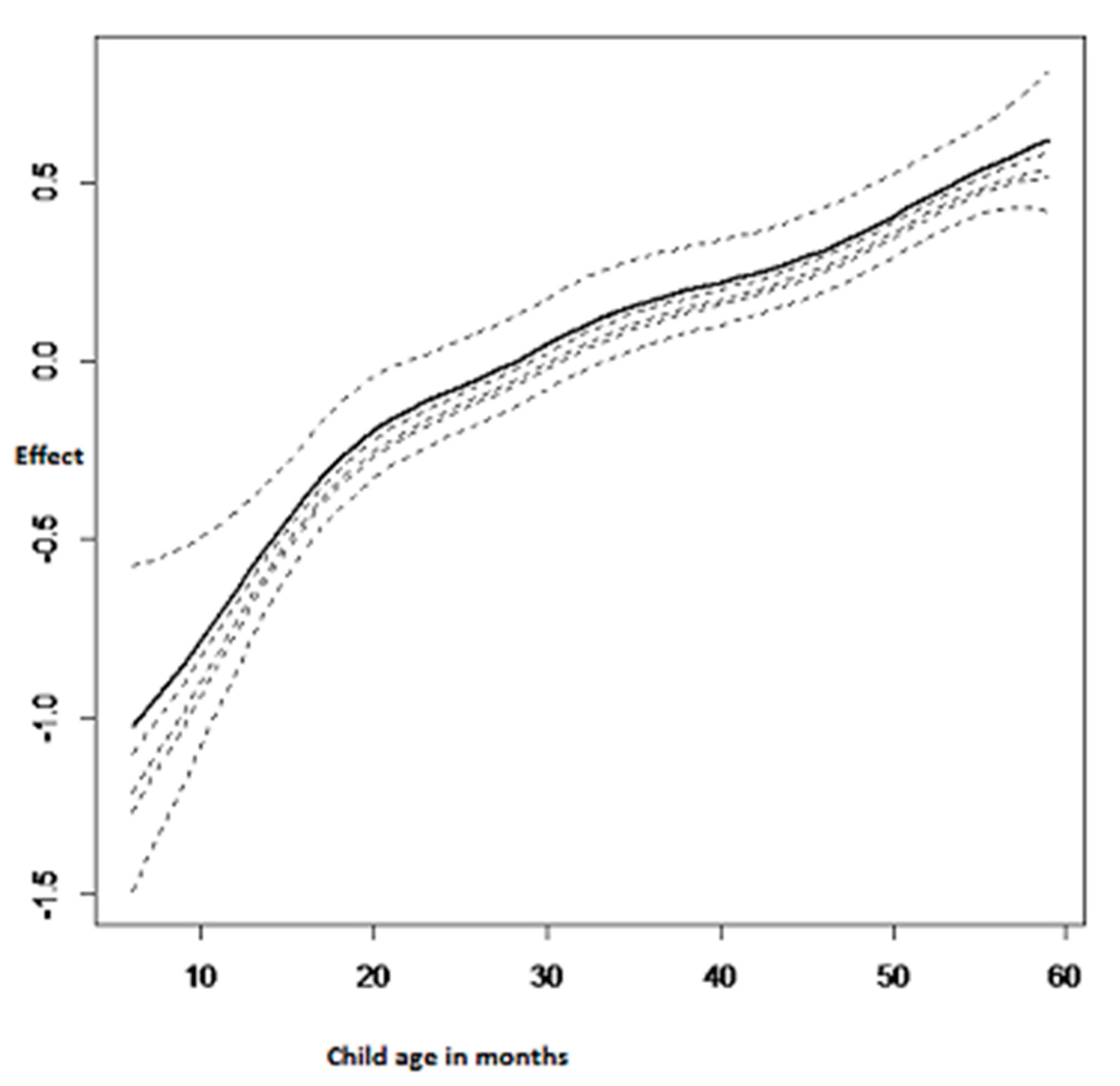
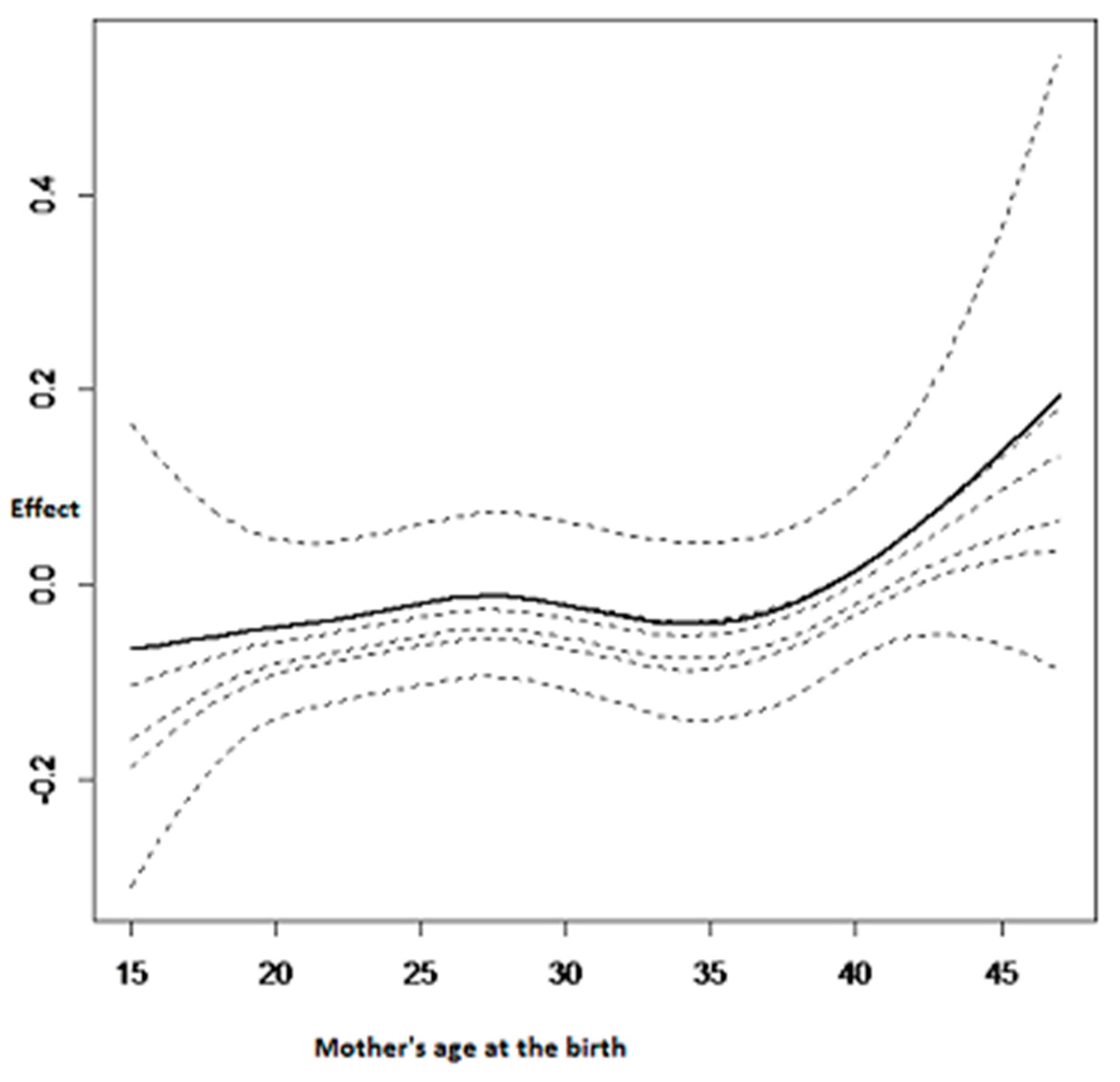
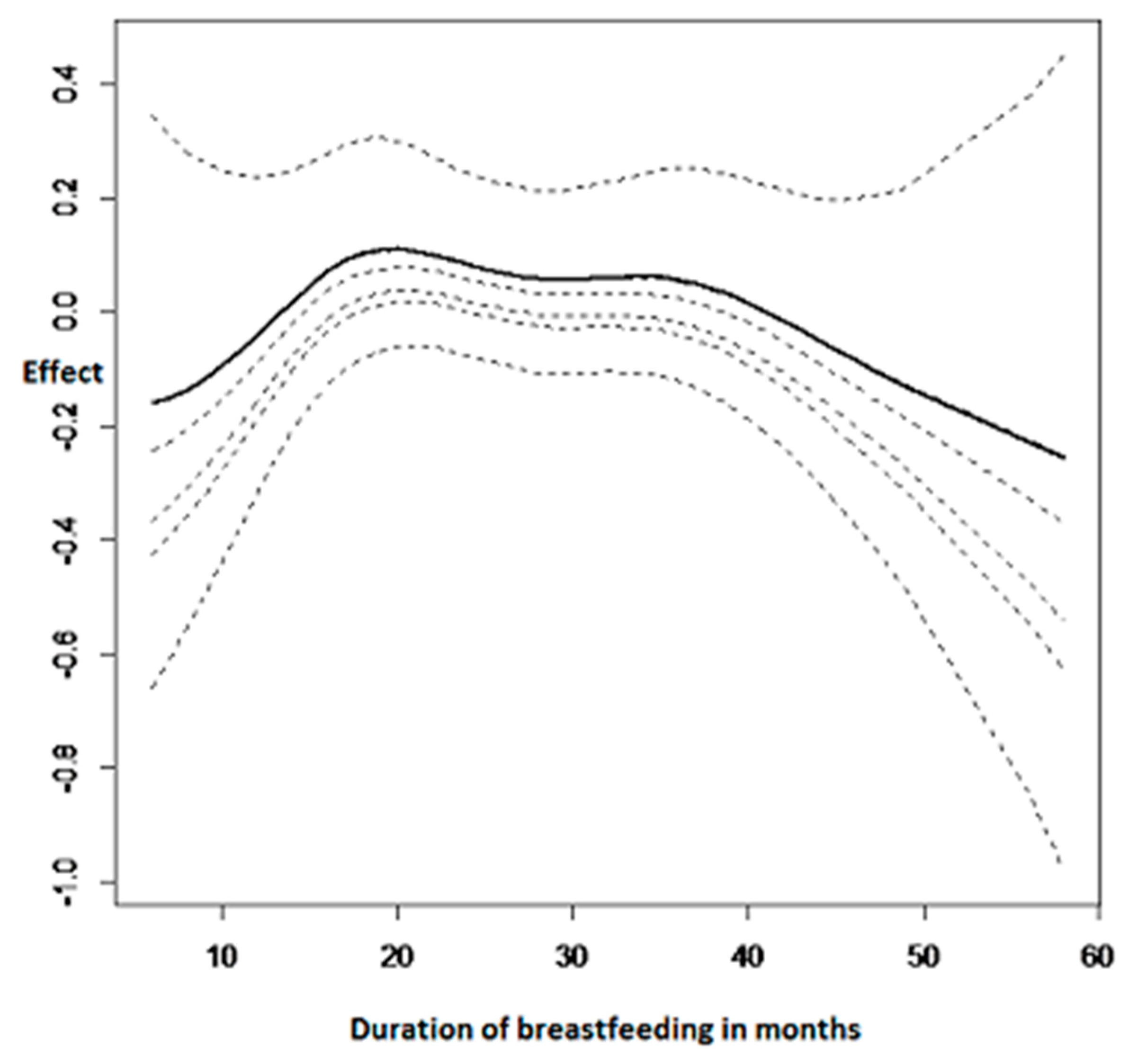
3.2.3. Nonlinear Effects on Childhood Anemia
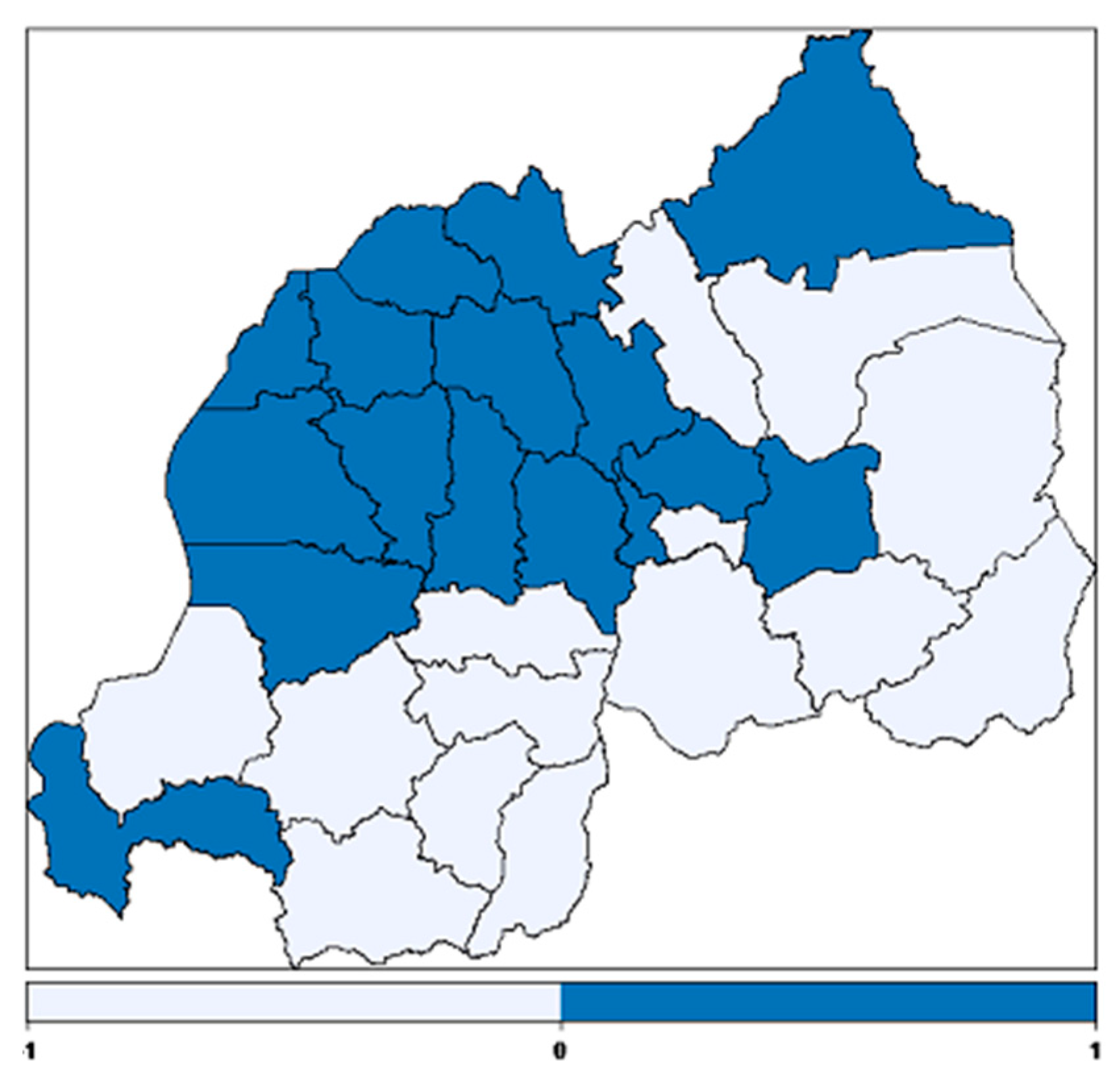
3.2.4. Spatial Effects
4. Discussion
5. Study Limitations
6. Recommendation
7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- De Benoist, B.; McLean, E.; Egll, L.; Cogswell, M. Worldwide prevalence of anaemia 1993–2005. In WHO Global Database on Anaemia; World Health Organization: Geneva, Switzerland, 2008. [Google Scholar]
- Pollitt, E.; Hathiral, P.; Kotchabhakd, N.J.; Missell, L.; Valvasevi, A. Iron deficiency and education achievement in Thailand. Am. J. Clin. Nutr. 1989, 50, 687–697. [Google Scholar] [PubMed]
- Woemantri, A.G.; Pollitt, E.; Kimm, I. Iron deficiency anaemias and educational achievement. Am. J. Clin. Nutr. 1985, 42, 1221–1228. [Google Scholar]
- World Health Organization. Iron deficiency anemia: Assessment, prevention, and control. In A Guide for Programme Managers; World Health Organization: Geneva, Switzerland, 2001. [Google Scholar]
- Crawley, S. Reducing the burden of anemia in infants and young children in malaria endemic countries of Africa: From evidence to action. Am. J. Trop. Med. Hyg. 2004, 71, 25–34. [Google Scholar] [PubMed]
- National Institute of Statistics of Rwanda (NISR) [Rwanda]; Ministry of Health (MOH) [Rwanda]; ICF International. Rwanda Demographic and Health Survey 2014–2015; NISR, MOH, and ICF International: Rockville, MD, USA, 2015. [Google Scholar]
- Uganda Bureau of Statistics (UBOS); ICF International Inc. Uganda Demographic and Health Survey 2011; UBOS: Kampala, Uganda; ICF international Inc.: Calverton, MD, USA, 2012. [Google Scholar]
- National Bureau of Statistics (NBS) [Tanzania]; ICF Macro. Tanzania Demographic and Health Survey 2010; NBS and ICF Macro: Der es Salaam, Tanzania, 2011. [Google Scholar]
- Institut de Statistique et d’études économiques du Burundi (ISTEEBU); Ministère de la santé publique et de lute contre le Sida [Burundi] (MSPLS); ICF International. Enquête Démographique et de Santé Burundi 2010; ISTEEBU, MSPLS, et ICF International: Bujumbura, Burundi, 2012. [Google Scholar]
- Konstantyner, T.; Oliveira, T.C.R.; Aguiar Carrazedo Taddei, J.A. Risk factors for anemia among Brasillian infants from the 2006 national demographic health survey. Anemia 2012, 2012, 7. [Google Scholar] [CrossRef] [PubMed]
- Kounnavong, S.; Sunahara, T.; Hashizume, M.; Okmumura, J.; Moji, K.; Boupha, B.; Yamamoto, T. Anemia and related factors in preschool children in southern rural Lao people’s Democratic Republic. Trop. Med. Health 2011, 39, 95–103. [Google Scholar] [CrossRef] [PubMed]
- Ngwira, A.; Kazembe, L.N. Bayesian random effects modelling with application to childhood anemia in Malawi. BMC Public Health 2015, 15, 161. [Google Scholar] [CrossRef]
- Gayawan, E.; Arogundade, E.D.; Adebayo, S.B. Possible determinants and spatial patterns of anaemia among young children in Nigeria: A Bayesian semi-parametric modeling. Int. Health 2014, 6, 35–45. [Google Scholar] [CrossRef] [PubMed]
- Kateera, F.; Ingabire, C.M.; Hakizimana, E.; Kalinda, P.; Mens, P.F.; Grobusch, M.P.; Mutesa, L.; Vugt, M. Malaria, anaemia and under-nutrition: Three frequently co-existing conditions among preschool children in rural Rwanda. Malar. J. 2015, 14, 440. [Google Scholar] [CrossRef] [PubMed]
- Ngwira, A.; Kazembe, N. Analysis of severity of childhood anemia in Malawi: A Bayesian ordered categories model. Open Access Med. Stat. 2016, 6, 9–20. [Google Scholar] [CrossRef]
- Dey, S.; Goswami, S.; Dey, T. Identifying predictors of childhood aneamia in North-East India. J. Health Popul. Nutr. 2013, 31, 462–470. [Google Scholar] [PubMed]
- Muchie, K.F. Determinants of severity levels of anemia among children aged 6–59 months in Ethiopia: Furheanalysis of the 2011 Ethiopian demographic and health survey. BMC Nutr. 2016, 2, 51. [Google Scholar] [CrossRef]
- Leal, L.P.; Batista Filho, M.; de Lira, P.I.C.; Figueiroa, J.N.; Osório, M.M. Prevalence of anemia and associated factors in children aged 6–59 months in Pernambuco, Northeastern Brazil. Rev. Saúde Públ. 2011, 45, 457–466. [Google Scholar] [CrossRef]
- Gebreegziabiher, G.; Etana, B.; Niggusie, D. Determinants of Anemia among Children Aged 6–59 Months Living in Kilte Awulaelo Woreda, Northern Ethiopia. Anemia 2014, 2014, 245870. [Google Scholar] [CrossRef] [PubMed]
- Gannoun, A.; Sarraco, J.; Yu, K. Nonparametric prediction by conditional median and quantile. J. Stat. Plan. Inference 2003, 117, 207–223. [Google Scholar] [CrossRef]
- Koenker, R.; Besset, G. Regression quantile. Econometrica 1978, 46, 33–50. [Google Scholar] [CrossRef]
- Koenker, R.; D’orey, V. Computing regression quantiles. Appl. Stat. 1993, 43, 410–414. [Google Scholar] [CrossRef]
- Yu, K.; Lu, Z.; Stander, J. Quantile regression: Applications and current research areas. Statistician 2003, 52, 331–350. [Google Scholar] [CrossRef]
- Koenker, R.; Hallock, A. Quantile Regression. An Introduction; University of Illinois, Urban-Campaign: Champaign, IL, USA, 2001. [Google Scholar]
- Yue, Y.R.; Rue, H. Bayesian inference for additive mixed quantile regression models. Comput. Stat. Data Anal. 2011, 55, 84–96. [Google Scholar] [CrossRef]
- Yu, K.; Zhang, J. A three-parameter asymmetric Laplace distribution and its extension. Commun. Stat. Theory Methods 2005, 34, 1867–1879. [Google Scholar] [CrossRef]
- Wecker, W.E.; Ansley, C.F. The signal extraction approach to nonlinear regression and spline smoothing. J. Am. Stat. Assoc. 1983, 78, 81–89. [Google Scholar] [CrossRef]
- Besag, J; York, J.; Mollie, A. Bayesian image restoration with two applications in spatial statistics (with discussion). Ann. Inst. Math. 1991, 43, 1–59. [Google Scholar] [CrossRef]
- Rue, H.; Martino, S. Approximate Bayesian inference for hierarchical Gaussian Markov random fields models. J. Stat. Plan. Inference 2007, 137, 3177–3192. [Google Scholar] [CrossRef]
- Rue, H.; Martino, S.; Chopin, N. Approximate Bayesian inference for latent Gaussian models by using integrated nested Laplace approximations. J. R. Stat. Soc. Ser. B (Stat. Methodol.) 2009, 71, 319–392. [Google Scholar] [CrossRef]
- Yu, Y.; Havard, R. Bayesian Inference for Structured Additive Quantile Regression Models. Available online: https://folk.ntnu.no/hrue/r-inla.org/papers/bay_qss.pdf (accessed on 16 June 2017).
- Spiergelhalter, D.J.; Best, N.G.; Carling, B.P.; van der Linde, A. Bayesian measures of model complexity and fit. J. R. Stat. Soc. Ser. B (Stat. Methodol.) 2002, 64, 583–639. [Google Scholar] [CrossRef]
- Souganidis, E.S.; Sun, K.; Pee, S.; Krammer, K; Rah, J.H.; PfannerRm Sari, M.; Bloem, M.W.; Semba, R.D. Relationship of maternal knowledge of anemia with maternal and child and health-related behaviors targeted at anemia among families in Indonesia. Matern. Child Health J. 2014, 16, 1913–1925. [Google Scholar] [CrossRef] [PubMed]
- Akindo, F.O.; Omoregie, R.; Mordi, R.; Okaka, C.E. Prevalence of Malaria and anemia among young children in a tertiary hospital in Benin city, Edo State, Nigeria. Fooyin. J. Health Sci. 2009, 1, 81–84. [Google Scholar] [CrossRef]
- Ngesa, O.; Mwambi, H. Prevalence and risk factors of anaemia among children aged 6 months and 14 years in Kenya. PLoS ONE 2014, 9, e113756. [Google Scholar] [CrossRef] [PubMed]
- Gebremedhim, S. Effect of a single high dose vitamin A supplementation on the hemoglobin status of children aged 6–59 months: Propensity score matched retrospective cohort study based on the data of Ethiopian Demographic and Health Survey 2011. BMC Pediatrics 2014, 14, 79. [Google Scholar] [CrossRef]
- Khan, J.R.; Awan, N.; Miso, F. Determinants of anemia among 6–59 months aged children in Bangladesh: Evidence from national representative data. BMC Pediatr. 2016, 16, 3. [Google Scholar] [CrossRef] [PubMed]
- Leite, M.S.; Cardoso, A.M.; Coimbra, C.E.; Welch, J.R.; Gugelmin, S.A.; Lira, P.C.I.; Horta, B.L.; Santos, R.V.; Escobar, A.L. Prevalence of anemia and associated factors among indigenous children in Brazil: Results from the First National Survey of Indigenous People’s Health and Nutrition. Nutr. J. 2013, 12, 69. [Google Scholar] [CrossRef] [PubMed]
- Cessie, S.; Verhoeff, F.H.; Mengistie, G.; Kazembe, P.; Broadhead, R.; Brabin, B.J. Changes in Haemoglobin levels in infant in Malawi: Effects of low birth weight and fetal anemia. Arch. Dis. Child. Fetal Neonat. Ed. 2002, 86, F182–F187. [Google Scholar] [CrossRef]
- Allen, L.H. Anemia and iron deficiency: Effects on pregnancy outcome. Am. J. Nutr. 2000, 71, 1280–1284. [Google Scholar]
- Wang, F.; Liu, H.; Wan, Y.; Li, J.; Chen, Y.; Zheng, J.; Huang, T.; Li, D. Prolonged Exclusive Breastfeeding Duration Is Positively Associated with Risk of Anemia in Infants Aged 12 Months. J. Nutr. 2016, 146, 1707–1713. [Google Scholar] [CrossRef]
- Müller, O.; Traoré, C.; Jahn, A.; Becher, H. Severe anaemia in west African children: Malaria or malnutrition? Lancet 2003, 361, 86–87. [Google Scholar] [CrossRef]
| Variable | Category | Anemic (%) | Not Anemic (%) | Pearson Chi-Square p-Value |
|---|---|---|---|---|
| Sex of the child | male | 607 (36.9%) | 1038 (63.1%) | 0.125 |
| female | 583 (36.4%) | 1020 (63.6%) | ||
| Birth order | 1st | 330 (35.6%) | 830 (64.4%) | 0.374 |
| 2–3 | 458 (35.7%) | 595 (64.3%) | ||
| 4–5 | 230 (38.9%) | 273 (61.1%) | ||
| 6+ | 172 (38.7%) | 361 (61.3%) | ||
| Did child eat meat, fish or poultry | yes | 35 (53.0%) | 31 (47.0%) | 0.097 |
| no | 736 (42.7%) | 987 (57.3%) | ||
| Had fever in the last two weeks | yes | 298 (44.4%) | 373 (55.6%) | <0.001 |
| no | 892 (34.6%) | 1685 (65.4%) | ||
| Had coughing in the last two weeks | yes | 372(39.0%) | 581(61.0%) | 0.068 |
| no | 818 (35.6%) | 1477 (64.4%) | ||
| Had diarrhea in the last two weeks | no | 993 (35.4%) | 1816 (64.6%) | <0.001 |
| yes | 197 (44.9%) | 242 (55.1%) | ||
| Stunted | no | 740(34.8%) | 1388 (65.2%) | 0.002 |
| yes | 451 (40.2%) | 670 (59.8%) | ||
| underweight | no | 1157 (36.3%) | 2034 (63.7%) | <0.001 |
| yes | 34 (58.6%) | 24 (41.4%) | ||
| Wasting | no | 992(35.1%) | 1838 (64.9%) | <0.001 |
| yes | 199 (47.5%) | 220 (52.5%) | ||
| Child’s birth weight in kg | Low (<2500 g) | 57 (38.3%) | 92(61.7%) | 0.643 |
| Higher (≥2500 g) | 1039 (36.5%) | 1817 (63.65) | ||
| Received Vitamin A | yes | 1005(35.5%) | 1840 (64.7%) | <0.001 |
| no | 185 (45.9%) | 218 (54.1%) | ||
| Had received drugs for intestinal worms | yes | 873 (33.1%) | 1766 (66.9%) | <0.001 |
| no | 317 (52.1%) | 292 (47.9%) | ||
| Mothers’ education level | No education | 189 (39.5%) | 289 (60.5%) | 0.153 |
| Primary | 857 (36.0%) | 1523 (64.0%) | ||
| Secondary a | 126(38.8%) | 199 (61.2%) | ||
| higher | 18(27.3%) | 48 (72.7%) | ||
| Mother’s anemia level | anemic | 279 (47.8%) | 305 (52.2%) | <0.001 |
| no | 912 (34.2%) | 1753 (65.8%) | ||
| Mother’s literacy | Yes | 877 (35.5%) | 1594(64.5%) | 0.016 |
| No | 313 (40.6%) | 464(59.7%) | ||
| Household size | 1–3 | 203 (38.6%) | 323 (61.4%) | 0.309 |
| 4 and more | 987 (36.3%) | 1735 (63.7%) | ||
| Place of residence | Urban | 156 (30.0%) | 364 (70.0%) | <0.001 |
| rural | 1034 (37.9%) | 1694 (62.1%) | ||
| Wealth index | Poor | 617 (40.4%) | 910 (59.6%) | <0.001 |
| Middle | 240 (37.0%) | 408 (63.0%) | ||
| Rich | 333 (31.0%) | 740 (69.0%) | ||
| Mother BMI | Less 18.5 | 58 (40.6%) | 85 (59.4%) | 0.183 |
| ≥18.5 | 1133 (36.5%) | 1973 (63.5%) | ||
| Slept with a mosquito-net | Yes | 1007 (36.3%) | 1770 (63.7%) | 0.280 |
| no | 183 (38.9%) | 288 (61.1%) | ||
| Household head | female | 235 (38.5%) | 375 (61.5%) | 0.288 |
| male | 956 (36.2%) | 1683 (63.8%) |
| Statistics | Model 1 | Model 2 | Model 3 | Model 4 | Model 5 |
|---|---|---|---|---|---|
| DIC | 10,757.44 | 10,750.7 | 10,707.7 | 10,996.9 | 10,629.84 |
| pD | 15.90 | 16.005 | 23.74 | 32.98 | 43.82 |
| D | 10,725.64 | 10,718.7 | 10,660.2 | 10,931 | 10,542.2 |
| Variable | Posterior Mean | Standard Deviation | 0.025 | 0.15 | 0.21 | 0.37 | 0.50 | 0.975 |
|---|---|---|---|---|---|---|---|---|
| Intercept | 11.1994 | 0.2253 | 10.7571 | 10.9657 | 11.0176 | 11.1247 | 11.1994 | 11.6414 |
| Sex of the child (female = ref) Male | 0.1194 | 0.0452 | 0.0307 | 0.0725 | 0.0829 | 0.1044 | 0.1194 | 0.2080 |
| Had fever (no = ref) Yes | −0.3511 | 0.0649 | −0.4785 | −0.4184 | −0.4035 | −0.3727 | −0.3511 | −0.2239 |
| Had cough (no = ref) Yes | −0.1359 | 0.0572 | −0.2483 | −0.1953 | −0.1821 | −0.1549 | −0.1359 | −0.0236 |
| Wasting (no = ref) Yes | −0.3214 | 0.0715 | −0.4618 | −0.3956 | −0.3791 | −0.3451 | −0.3214 | −0.1811 |
| Underweight (no = ref) Yes | −0.2421 | 0.1773 | −0.5902 | −0.4260 | −0.3851 | −0.3009 | −0.2421 | 0.1057 |
| Mother’s anemia (Yes = ref) No anemic | 0.4427 | 0.0600 | 0.3248 | 0.3804 | 0.3943 | 0.4228 | 0.4427 | 0.5605 |
| Mother’s literacy (yes = ref) No | −0.1736 | 0.0562 | −0.2839 | −0.2319 | −0.2189 | −0.1922 | −0.1736 | −0.0634 |
| Mother’s BMI (≥18.5 = ref) <18.5 | −0.0857 | 0.1115 | −0.3046 | −0.2014 | −0.1757 | −0.1227 | −0.0858 | 0.1329 |
| Wealth index (poor = ref) Middle | 0.0113 | 0.0624 | −0.1113 | −0.0535 | −0.0391 | −0.0094 | 0.0113 | 0.1337 |
| Rich | 0.2259 | 0.0568 | 0.1143 | 0.1669 | 0.1800 | 0.2070 | 0.2259 | 0.3374 |
| Received vitamin (no = ref) Yes | 0.1441 | 0.0732 | 0.0005 | 0.0682 | 0.0851 | 0.1199 | 0.1441 | 0.2877 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Habyarimana, F.; Zewotir, T.; Ramroop, S. Structured Additive Quantile Regression for Assessing the Determinants of Childhood Anemia in Rwanda. Int. J. Environ. Res. Public Health 2017, 14, 652. https://doi.org/10.3390/ijerph14060652
Habyarimana F, Zewotir T, Ramroop S. Structured Additive Quantile Regression for Assessing the Determinants of Childhood Anemia in Rwanda. International Journal of Environmental Research and Public Health. 2017; 14(6):652. https://doi.org/10.3390/ijerph14060652
Chicago/Turabian StyleHabyarimana, Faustin, Temesgen Zewotir, and Shaun Ramroop. 2017. "Structured Additive Quantile Regression for Assessing the Determinants of Childhood Anemia in Rwanda" International Journal of Environmental Research and Public Health 14, no. 6: 652. https://doi.org/10.3390/ijerph14060652
APA StyleHabyarimana, F., Zewotir, T., & Ramroop, S. (2017). Structured Additive Quantile Regression for Assessing the Determinants of Childhood Anemia in Rwanda. International Journal of Environmental Research and Public Health, 14(6), 652. https://doi.org/10.3390/ijerph14060652





