Extensions to Multivariate Space Time Mixture Modeling of Small Area Cancer Data
Abstract
:1. Introduction
2. Materials and Methods
2.1. Case Study
2.2. Statistical Methods
3. Results
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Conflicts of Interest
References
- Carroll, R.; Lawson, A.B.; Faes, C.; Kirby, R.S.; Aregay, M.; Watjou, K. Space-time variation of respiratory cancers in South Carolina: A flexible multivariate mixture modeling approach to risk estimation. Ann. Epidemiol. 2017, 27, 42–51. [Google Scholar] [CrossRef] [PubMed]
- Lawson, A.B.; Faes, C.; Kirby, R.S.; Aregay, M.; Watjou, K.; Carroll, R. Spatio-temporal multivariate mixture models for Bayesian model selection in disease mapping. Environmetrics 2017. Submitted. [Google Scholar]
- National Center for Health Statistics. International Classification of Disease, Ninth Revision (ICD-9); Centers for Disease Control: Atlanta, GA, USA, 1998.
- PDQ Adult Treatment Editorial Board. PDQ Lip and Oral Cavity Cancer Treatment. Available online: http://www.cancer.gov/types/head-and-neck/patient/lip-mouth-treatment-pdq (accessed on 27 May 2016).
- Ananthaswamy, H.N. Sunlight and skin cancer. J. Biomed. Biotechnol. 2001, 1, 49. [Google Scholar] [CrossRef] [PubMed]
- National Insitutes of Health. SEER Stat Fact Sheets: Lung and Bronchus Cancer; National Institutes of Health: Rockville, MD, USA, 2016.
- U.S. Cancer Statistics Working Group. United States Cancer Statistics: 1999–2012 Incidence and Mortality Web-Based Report; Department of Health and Human Services. Centers for Disease Control and Prevention and National Cancer Institute: Atlanta, GA, USA, 2015.
- Batista, N.E.; Oscar, A.A. Spatiotemporal analysis of lung cancer incidence and case fatality in Villa Clara Province, Cuba. MEDICC Rev. 2013, 15, 16–21. [Google Scholar] [PubMed]
- Hare, T.S. Space–Time Patterns of Respiratory Cancer Incidence and Mortality: Kentucky, 1969–2011. Pap. Appl. Geogr. 2015, 1, 333–341. [Google Scholar] [CrossRef]
- Kiberstis, P.A. Space, time, and the lung cancer genome. Science 2014, 346, 204. [Google Scholar] [CrossRef]
- Waller, L.A.; Carlin, B.P.; Xia, H.; Gelfand, A.E. Hierarchical Spatio-Temporal Mapping of Disease Rates. J. Am. Stat. Assoc. 1997, 92, 607–617. [Google Scholar] [CrossRef]
- Xia, H.; Carlin, B.P.; Waller, L.A. Hierarchical Models for Mapping Ohio Lung Cancer Rates. Environmetrics 1997, 8, 107–120. [Google Scholar] [CrossRef]
- Knorr-Held, L. Bayesian modelling of inseparable space-time variation in disease risk. Stat. Med. 2000, 19, 2555–2567. [Google Scholar] [CrossRef]
- Knorr-Held, L.; Besag, J. Modelling risk from a disease in time and space. Stat. Med. 1998, 17, 2045–2060. [Google Scholar] [CrossRef]
- Knorr-Held, L.; Best, N.G. A shared component model for detecting joint and selective clustering of two diseases. J. R. Stat. Soc. Ser. A 2001, 164, 73–85. [Google Scholar] [CrossRef]
- Lawson, A.B. Bayesian Disease Mapping: Hierarchical Modeling in Spatial Epidemiology, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- Lesaffre, E.; Lawson, A.B. Bayesian Biostatistics, 1st ed.; Wiley: West Sussex, UK, 2013; 534p. [Google Scholar]
- Lawson, A.B.; Banerjee, S.; Haining, R.; Ugarte, M.D. Handbook of Spatial Epidemiology; Fitzmaurice, G., Ed.; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- South Carolina Community Assessment Network. Cancer Incidence; Department of Health and Environental Control: Columbia, SC, USA, 2010.
- Breslow, N.E.; Day, N.E. The Design and Analysis of Cohort Studies; Oxford University Press: New York, NY, USA, 1987. [Google Scholar]
- National Insitutes of Health. SEER Stat Fact Sheets: Melanoma of the Skin; National Institutes of Health: Rockville, MD, USA, 2016.
- National Cancer Institute. General Information about Nasopharyneal Cancer: Key Points; Department of Health and Human Services. National Institutes of Health: Rockville, MD, USA.
- National Insitutes of Health. SEER Stat Fact Sheets: Oral Cavity and Pharynx Cancer; National Institutes of Health: Rockville, MD, USA.
- National Cancer Institute. Cancer Health Disparities; National Institutes of Health: Rockville, MD, USA, 2008.
- American Cancer Society. Cancer Facts & Figures 2015; American Cancer Society: Atlanta, GA, USA, 2015. [Google Scholar]
- American Cancer Society. Do We Know What Causes Melanoma Skin Cancer? American Cancer Society: Atlanta, GA, USA, 2015. [Google Scholar]
- Giovannucci, E. The epidemiology of vitamin D and cancer incidence and martality: A revew (United States). Cancer Causes Control 2005, 16, 83–95. [Google Scholar] [CrossRef] [PubMed]
- US Department of Health and Human Services. Area Health Resource Files (AHRF); US Department of Health and Human Services, Health Resources and Services Administration, Bureau of Health Workforce: Rockville, MD, USA, 2003.
- National Oceanic and Atmospheric Administration. Climate at a Glance; National Centers for Environmental Information: Ashville, NC, USA.
- South Carolina Department of Health and Environmental Control. Average in Home Radon Concentrations (pCi/L); South Carolina Department of Health and Environmental Control (SCDHEC): Columbia, SC, USA, 2014.
- North America Land Data Assimilation System (NLDAS). Daily Sunlight (Insolation) for Years 1979–2011 on CDC WONDER Online Database; Centers for Disease Control and Prevention: Atlanta, GA, USA, 2013.
- Lunn, D.; Jackson, C.; Best, N.; Thomas, A.; Spiegelhalter, D. The BUGS Book: A Practical Introduction to Bayesian Analysis, 1st ed.; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- Thomas, A.; Best, N.; Lunn, D.; Arnold, R.; Spiegelhalter, D. GeoBUGS User Manual 2014. Available online: http://www.openbugs.net/Manuals/GeoBUGS/Manual.html (accessed on 10 September 2011).
- Thomas, A.; O’hara, B.; Ligges, U.; Sturtz, S. Making BUGS Open. R News 2006, 6, 12–17. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2015. [Google Scholar]
- Carroll, R.; Lawson, A.B.; Faes, C.; Kirby, R.S.; Aregay, M.; Watjou, K. Spatio-temporal Bayesian model selection for disease mapping. Environmetrics 2016, 27, 466–478. [Google Scholar] [CrossRef] [PubMed]
- Besag, J.; Green, P.J. Spatial Statistics and Bayesian Computation. J. R. Stat. Soc. B 1993, 55, 25–37. [Google Scholar]
- Besag, J.; York, J.; Mollié, A. Bayesian image restoration, with two applications in spatial statistics. Ann. Inst. Stat. Math. 1991, 43, 1–20. [Google Scholar] [CrossRef]
- Watanabe, S. Asymptotic equivalence of Bayes cross validation and widely applicable information criterion in singular learning theory. J. Mach. Learn. Res. 2010, 11, 3571–3594. [Google Scholar]
- Gelman, A.; Hwang, J.; Vehtari, A. Understanding predictive information criteria for Bayesian models. Stat. Comput. 2013, 24, 997–1016. [Google Scholar] [CrossRef]
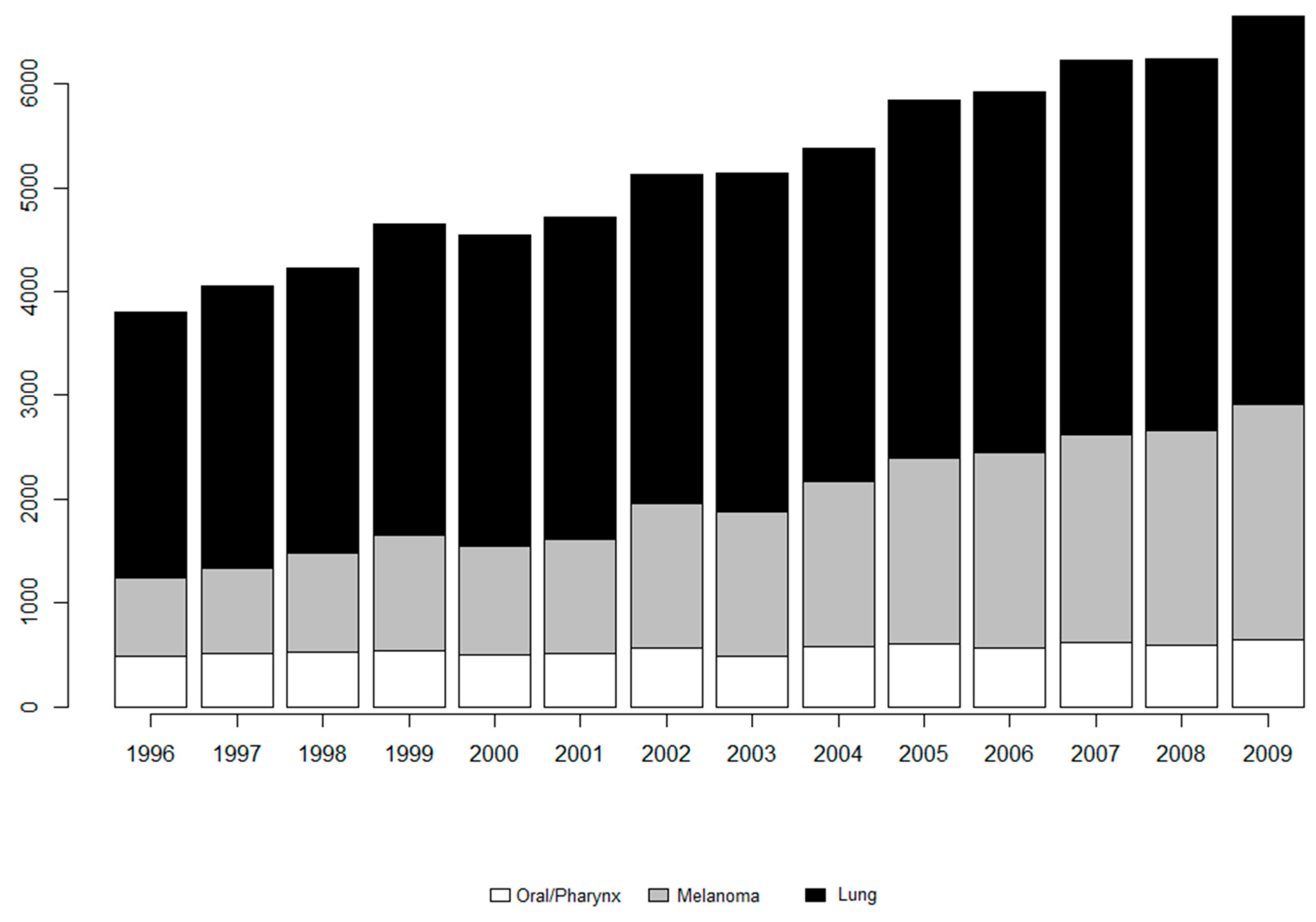

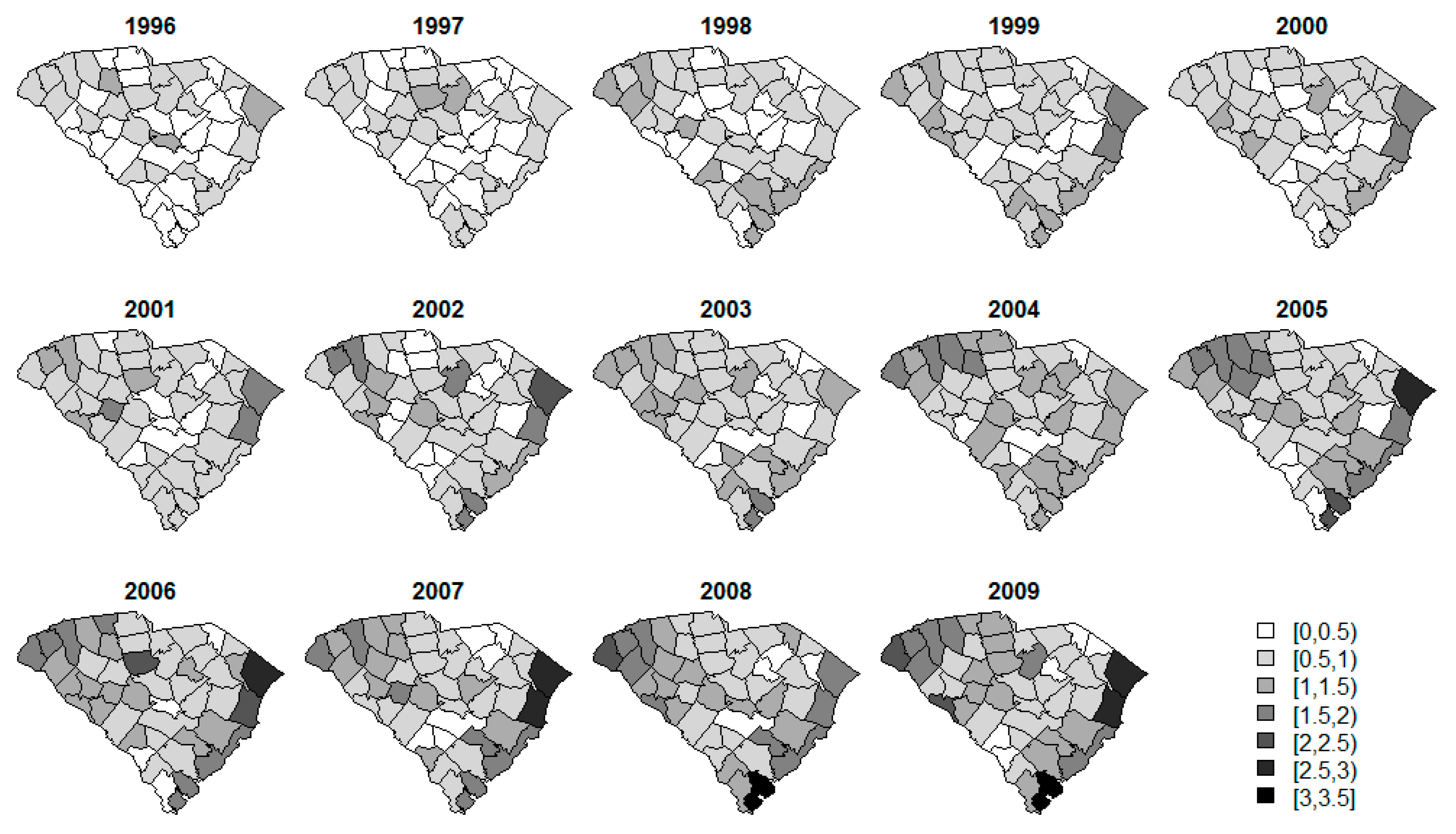

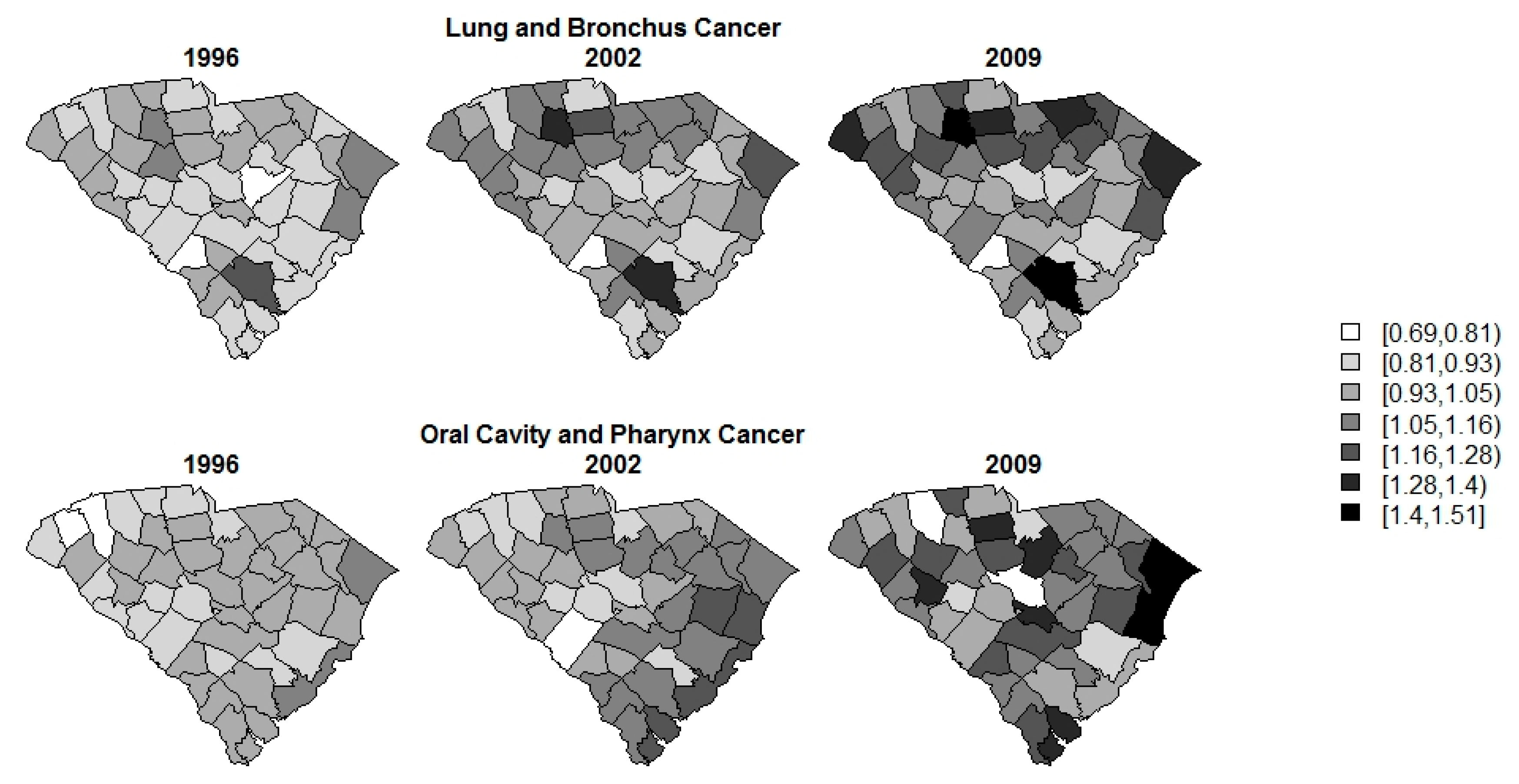
| Disease | Number (%) of Data in Each Threshold | ||
|---|---|---|---|
| 0 | 1–4 | 5–10 | |
| Oral/pharynx | 16 (2.5%) | 200 (31.1%) | 190 (29.5%) |
| Melanoma | 13 (2.0%) | 128 (19.9%) | 151 (23.4%) |
| Lung | 0 (0.0%) | 4 (0.6%) | 15 (2.3%) |
| Model | Spatial | Temporal | Spatio-Temporal | Mixture Parameter |
|---|---|---|---|---|
| Univariate | ||||
| F2PRED | - | |||
| Alt1 | - | |||
| Alt2 | ||||
| Bivariate/Multivariate 1 | ||||
| F2PRED | - | |||
| Alt1 | - | |||
| Alt2 | ||||
| Alt3a | - | |||
| Alt3b | - | |||
| Measure | Years | Univariate | Bivariate 2 | Multivariate 2 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| F2PRED | Alt1 | Alt2 | Alt1 | Alt2 | Alt3a | Alt3b | F2PRED | Alt1 | Alt2 | Alt3a | Alt3b | ||
| WAIC | ’96–‘09 | 3241.74 | 3239.09 | 4448.71 | 3196.02 | 3192.77 | 3194.97 | 3192.18 | 3431.50 | 3426.94 | 3520.64 | 3470.28 | 4184.67 |
| ’96–‘05 | 2298.34 | 2296.40 | 3130.11 | 2265.29 | 2265.94 | 2264.57 | 2262.46 | 2285.45 | 2479.40 | 2322.88 | 2473.00 | 2954.48 | |
| ’06–‘09 | 943.40 | 942.69 | 1318.60 | 930.73 | 926.83 | 930.40 | 929.72 | 1146.05 | 1000.37 | 1197.76 | 997.28 | 1230.20 | |
| pD | ’96–‘09 | 105.89 | 105.29 | 157.31 | 94.31 | 96.66 | 93.44 | 93.76 | 131.08 | 131.07 | 141.69 | 149.43 | 501.02 |
| ’96–‘05 | 75.39 | 74.35 | 96.14 | 65.53 | 68.85 | 66.34 | 65.84 | 74.29 | 103.97 | 73.92 | 106.24 | 344.19 | |
| ’06–‘09 | 30.50 | 30.94 | 61.17 | 28.79 | 27.80 | 27.09 | 27.92 | 56.78 | 42.40 | 67.78 | 43.18 | 156.83 | |
| MSPE | ’96–‘09 | 153.44 | 154.03 | 117.00 | 117.93 | 111.64 | 116.81 | 115.23 | 14,050.59 | 14,037.08 | 13,995.61 | 13,953.98 | 13,678.78 |
| ’96–‘05 | 103.93 | 103.75 | 84.43 | 84.53 | 80.58 | 82.13 | 82.00 | 73.51 | 71.79 | 79.94 | 74.44 | 73.05 | |
| ’06–‘09 | 49.51 | 50.28 | 32.57 | 33.40 | 31.06 | 34.68 | 33.22 | 13,977.08 | 13,965.29 | 13,915.67 | 13,879.53 | 13,605.73 | |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Carroll, R.; Lawson, A.B.; Faes, C.; Kirby, R.S.; Aregay, M.; Watjou, K. Extensions to Multivariate Space Time Mixture Modeling of Small Area Cancer Data. Int. J. Environ. Res. Public Health 2017, 14, 503. https://doi.org/10.3390/ijerph14050503
Carroll R, Lawson AB, Faes C, Kirby RS, Aregay M, Watjou K. Extensions to Multivariate Space Time Mixture Modeling of Small Area Cancer Data. International Journal of Environmental Research and Public Health. 2017; 14(5):503. https://doi.org/10.3390/ijerph14050503
Chicago/Turabian StyleCarroll, Rachel, Andrew B. Lawson, Christel Faes, Russell S. Kirby, Mehreteab Aregay, and Kevin Watjou. 2017. "Extensions to Multivariate Space Time Mixture Modeling of Small Area Cancer Data" International Journal of Environmental Research and Public Health 14, no. 5: 503. https://doi.org/10.3390/ijerph14050503
APA StyleCarroll, R., Lawson, A. B., Faes, C., Kirby, R. S., Aregay, M., & Watjou, K. (2017). Extensions to Multivariate Space Time Mixture Modeling of Small Area Cancer Data. International Journal of Environmental Research and Public Health, 14(5), 503. https://doi.org/10.3390/ijerph14050503







