Using Upper Extremity Skin Temperatures to Assess Thermal Comfort in Office Buildings in Changsha, China
Abstract
:1. Introduction
2. Research Methods
2.1. Time, Climate and Buildings
2.2. The Investigated Occupants and Sample Size
2.3. Physiological Measurements
2.4. Physical Measurements
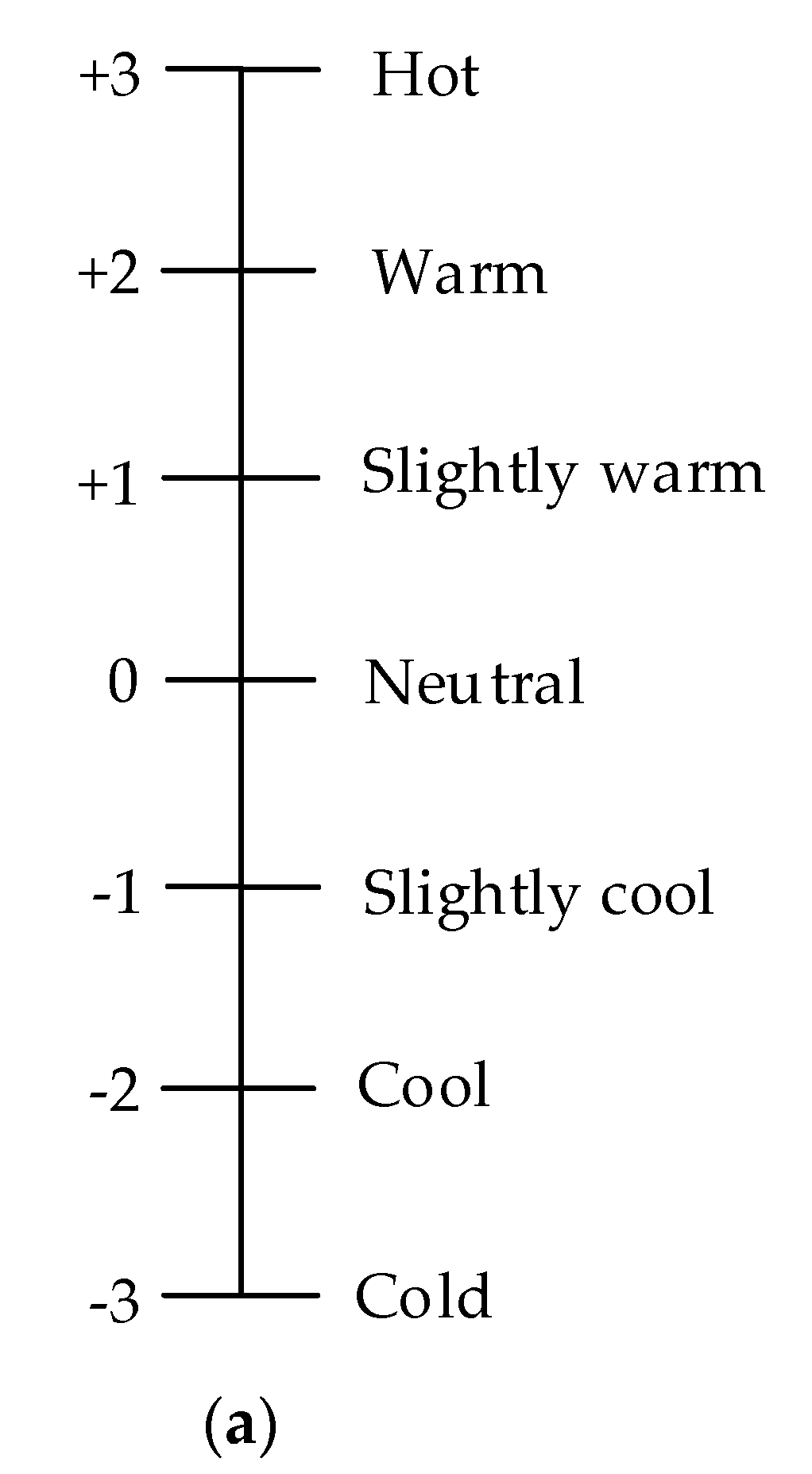
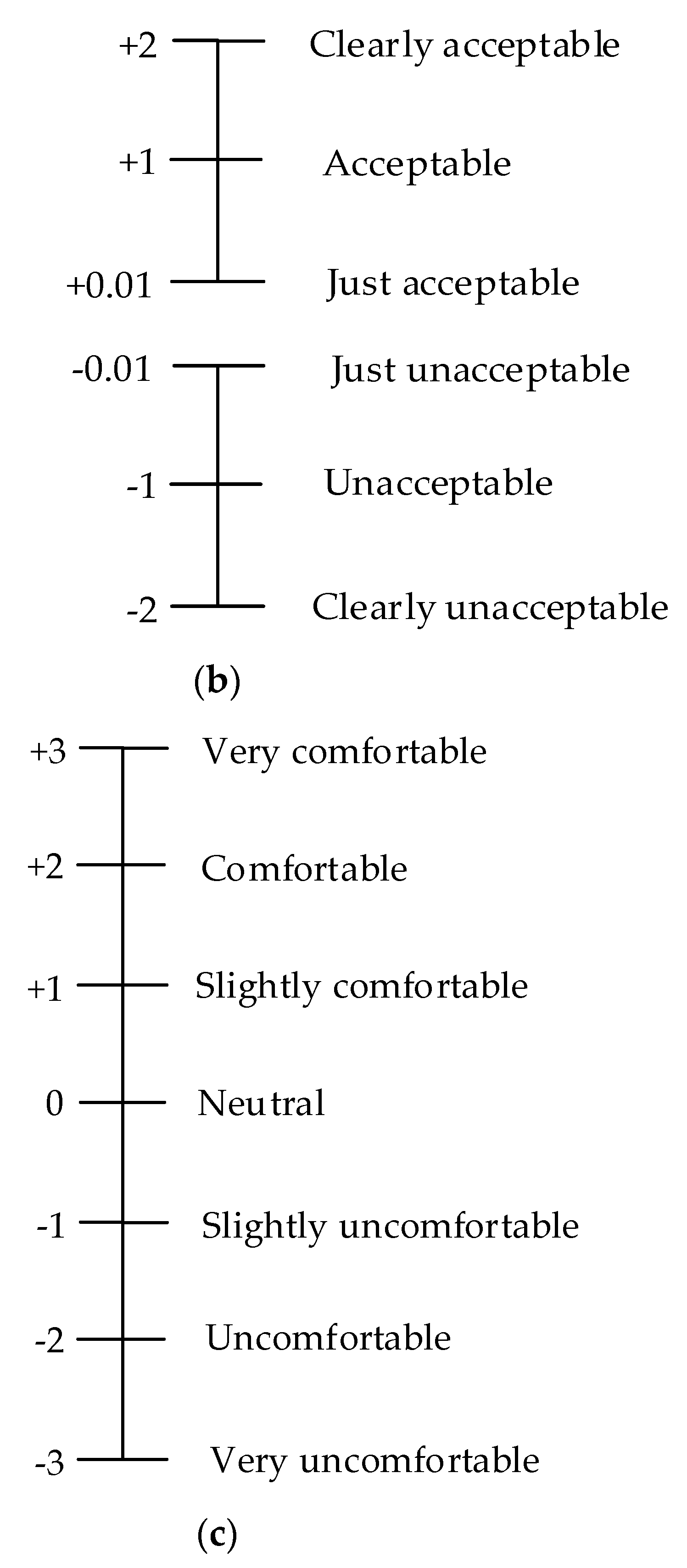
2.5. Thermal Comfort Survey
2.6. Statistic Analysis
3. Results
3.1. Thermal Environment
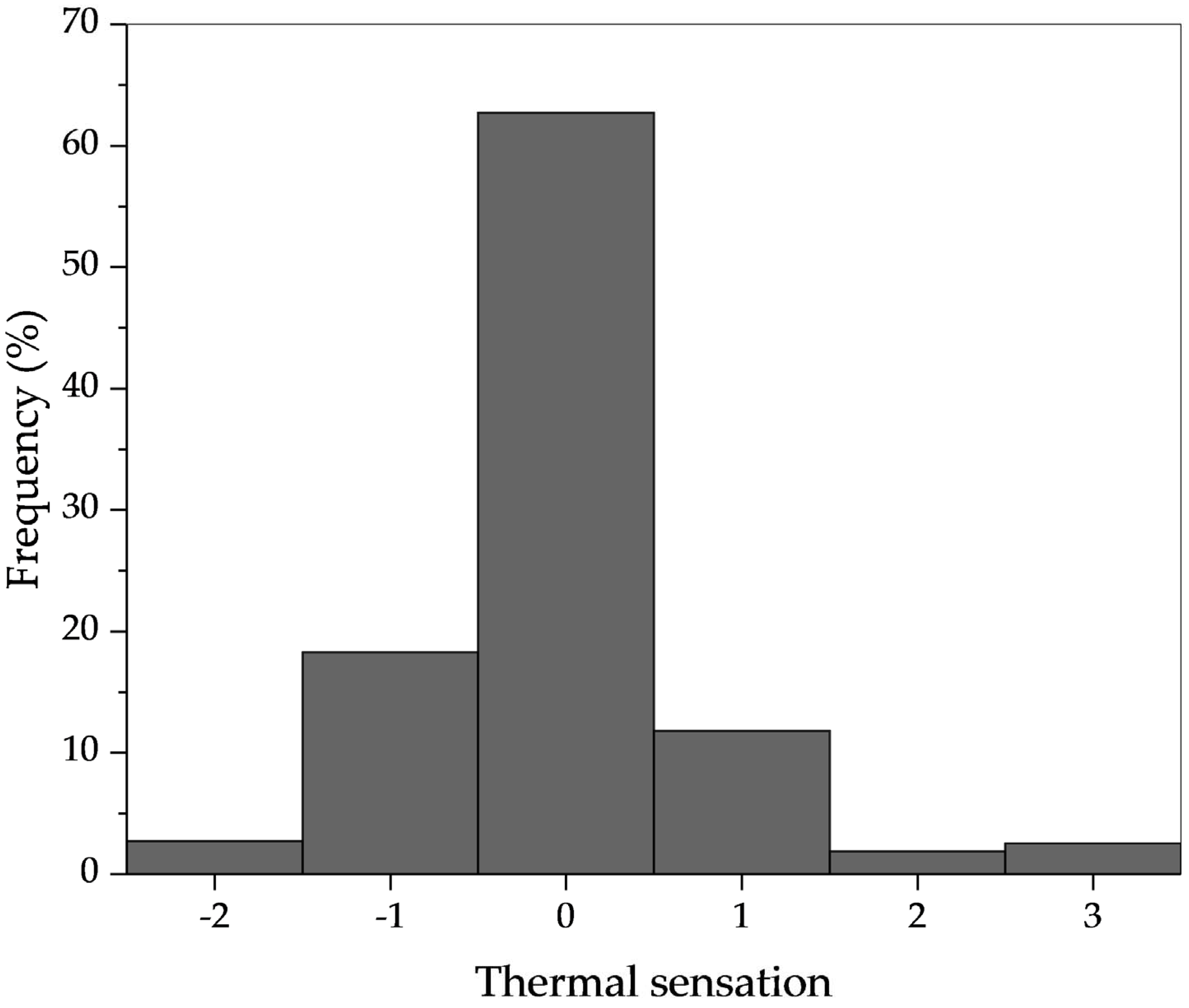
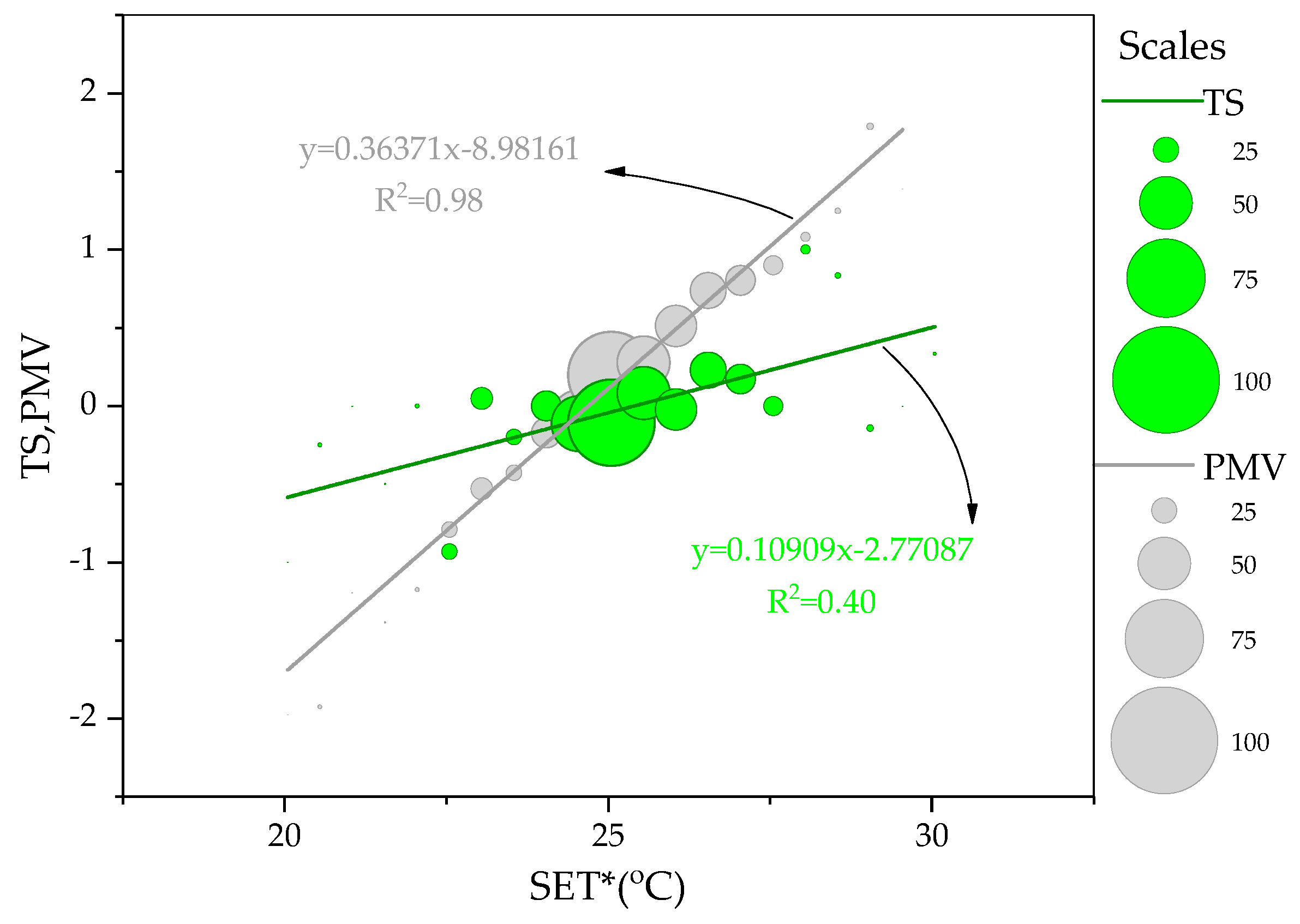
3.2. Relationship between Thermal Sensation and Thermal Environment
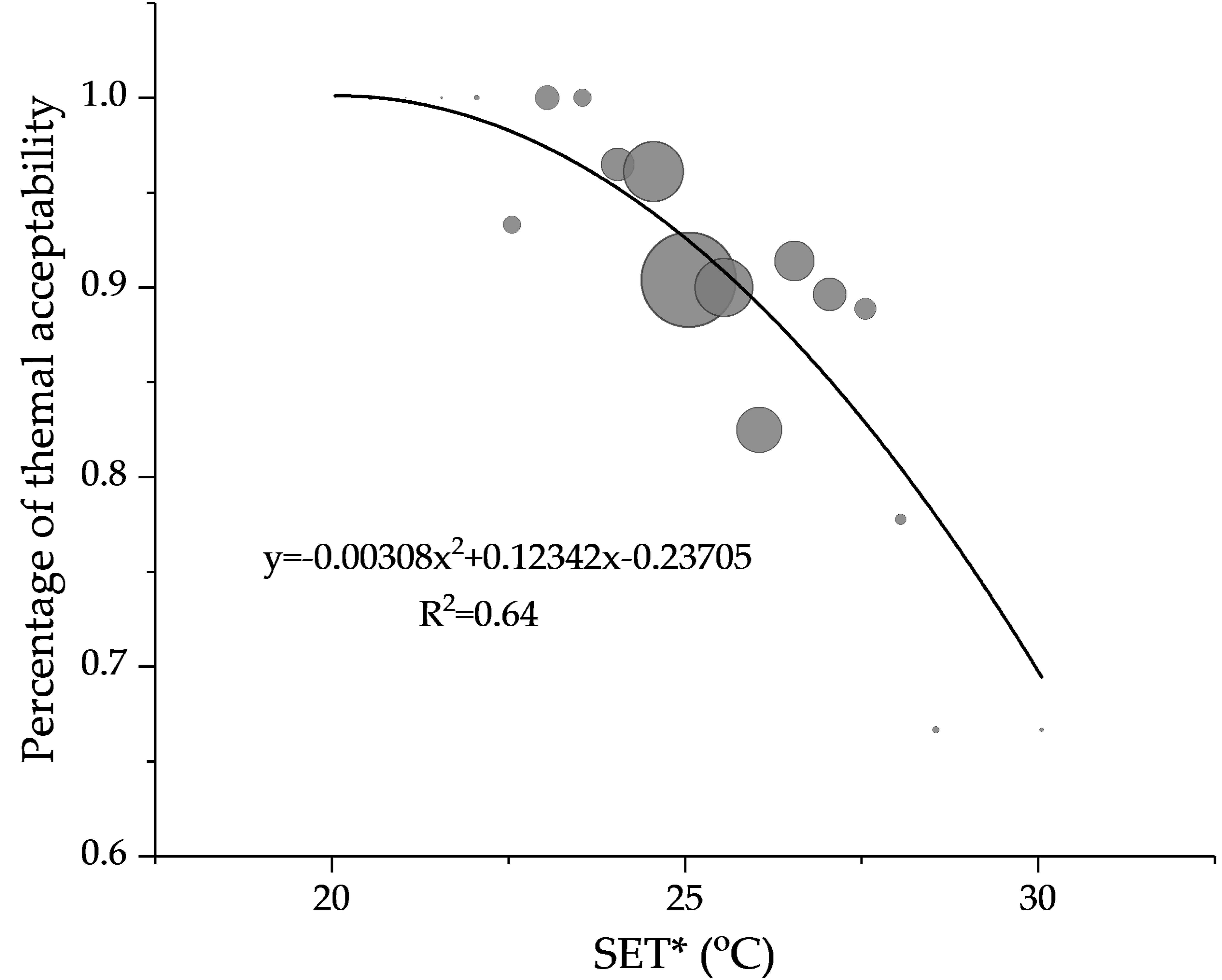
3.3. Thermal Acceptability
3.4. Overall Thermal Comfort and Physiological Responses
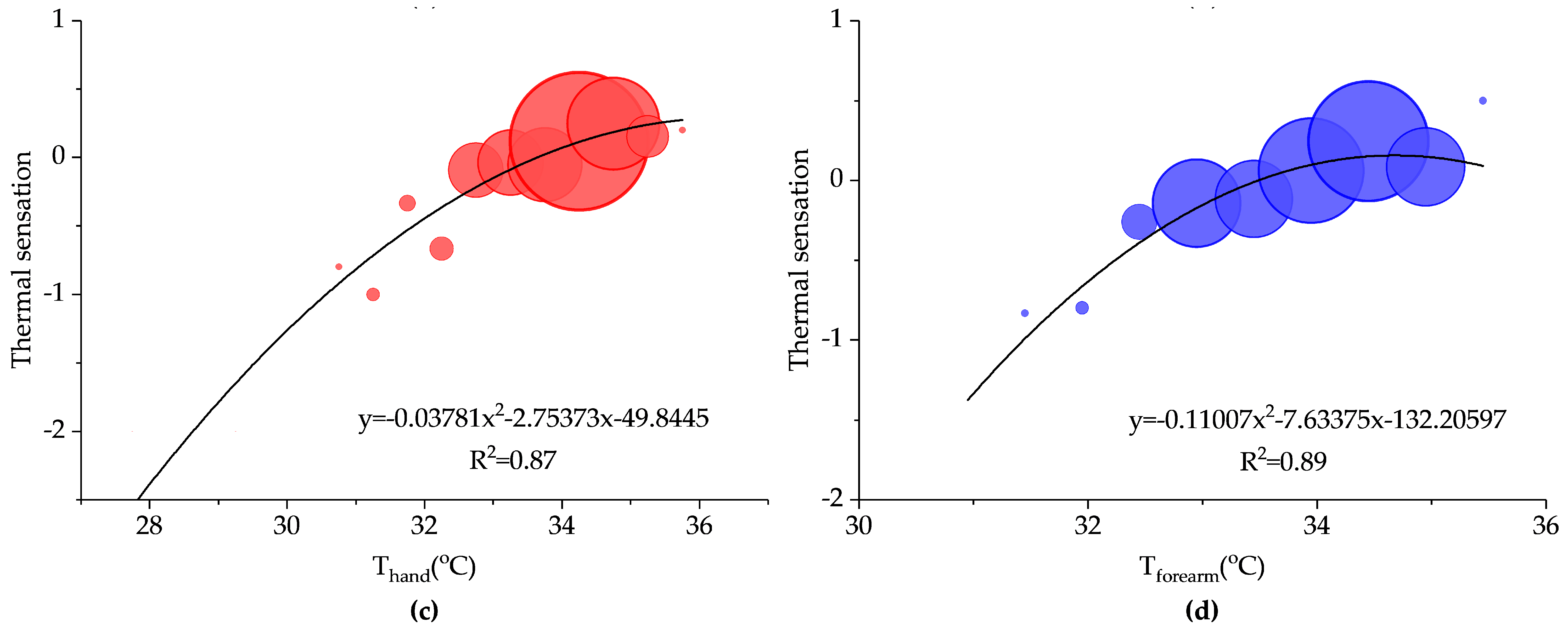
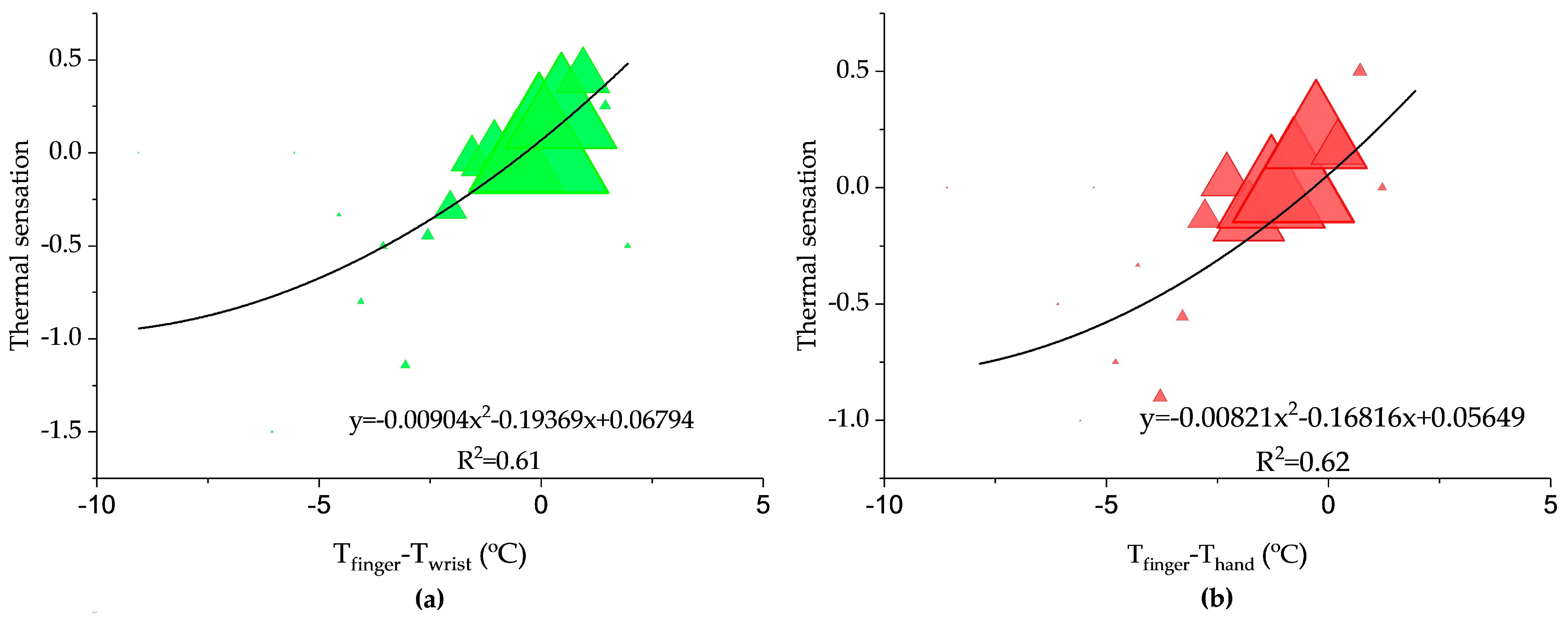
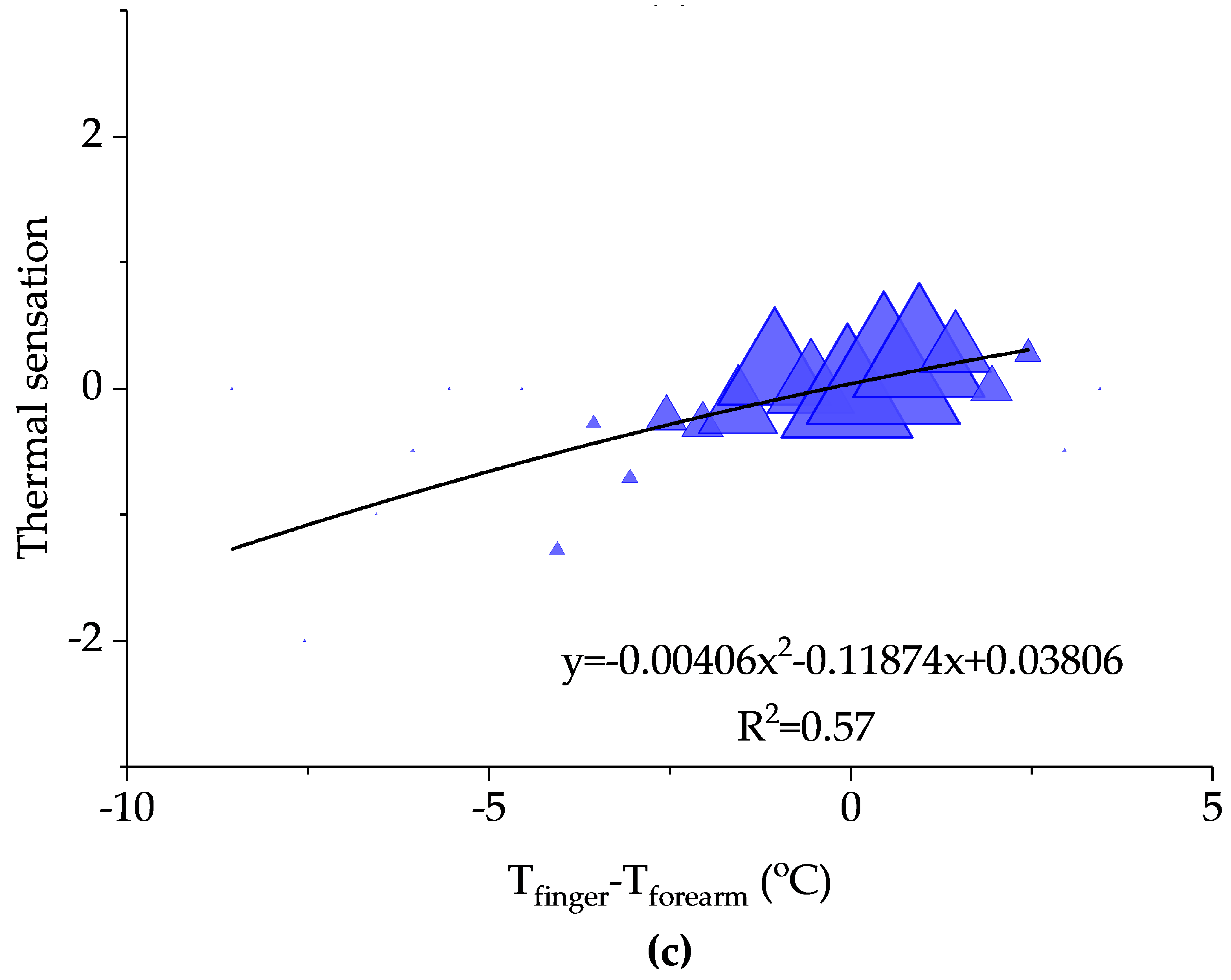
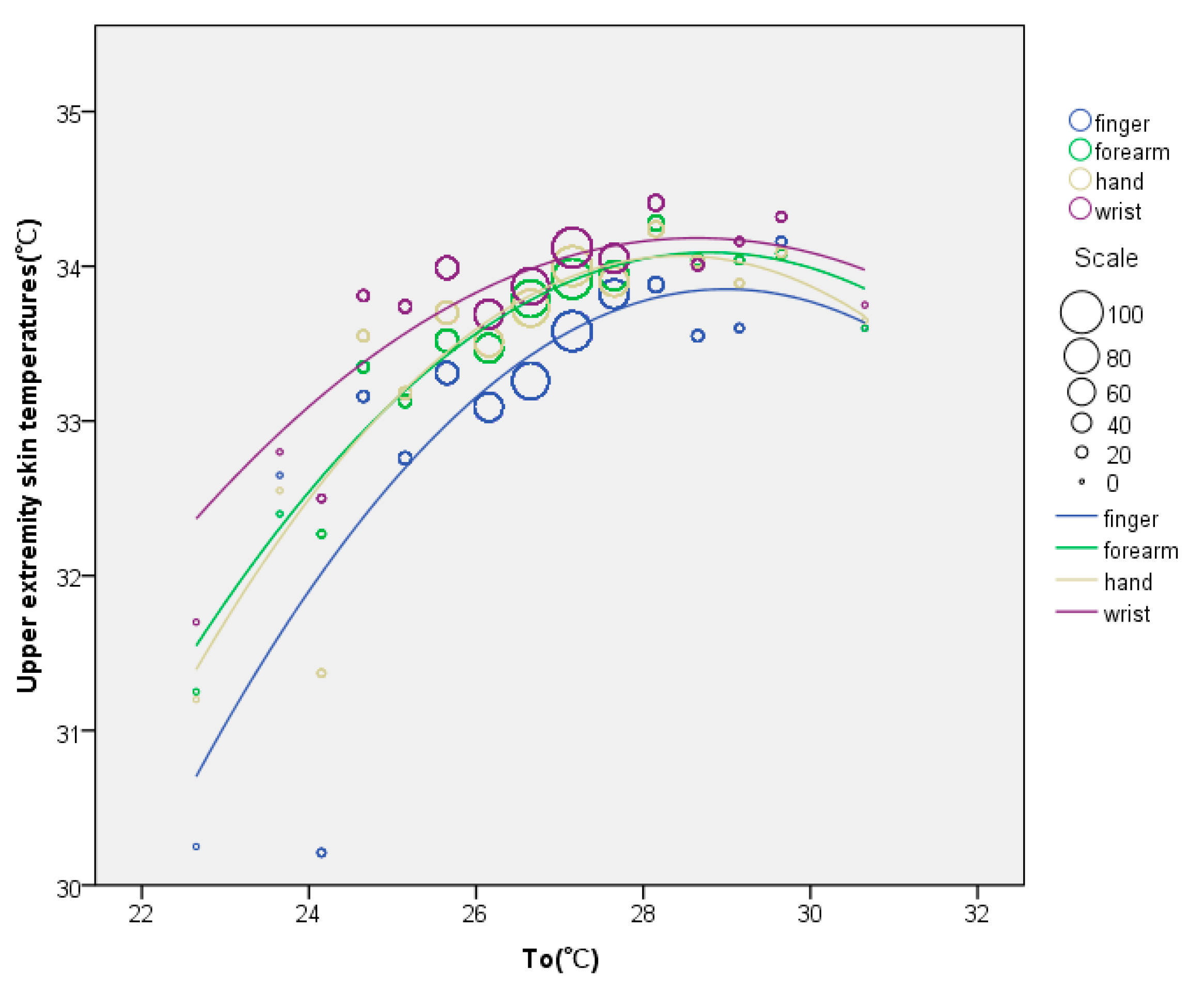
3.5. Relationships between Thermal Environment and Upper Extremity Skin Temperatures
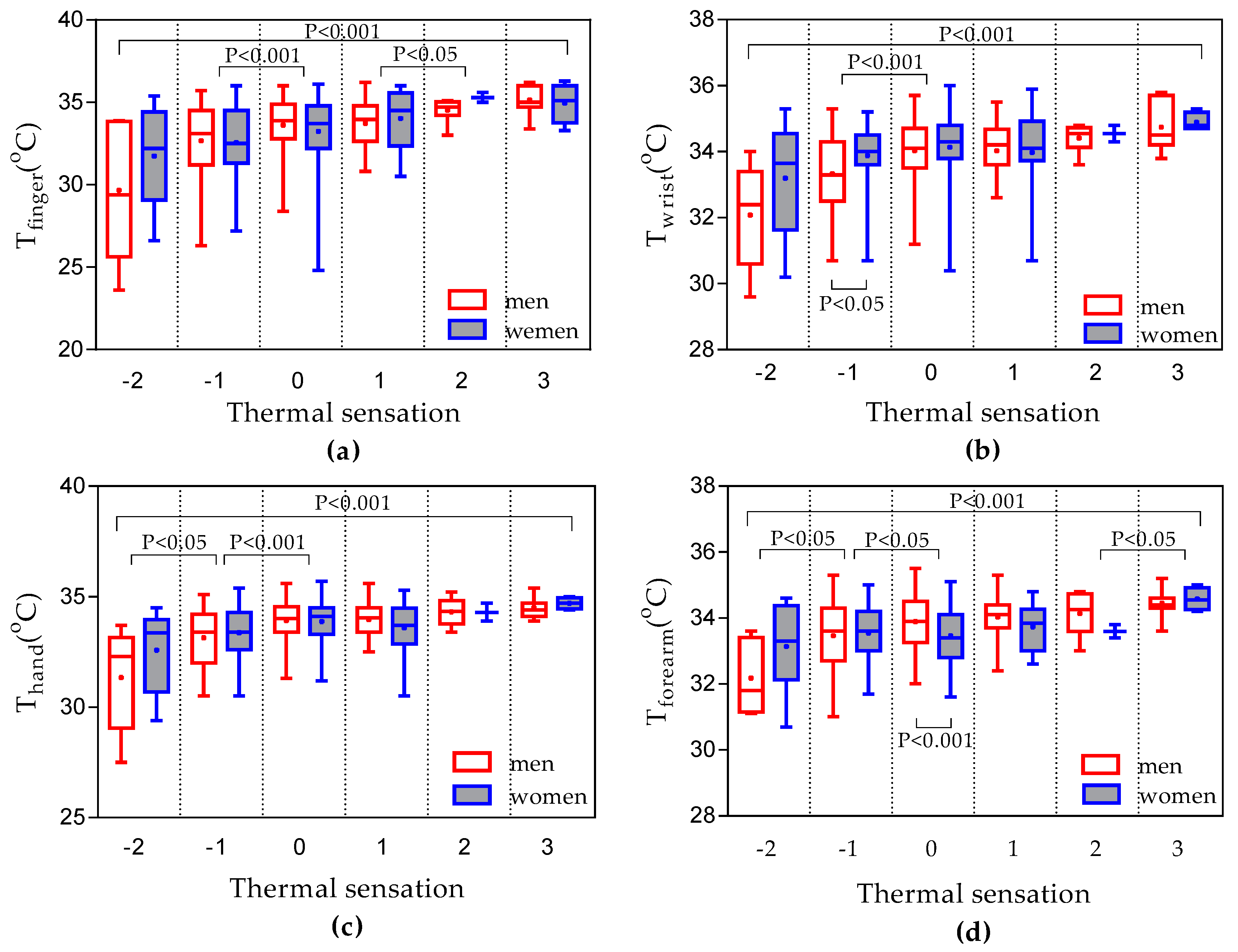
3.6. Sex Differences
4. Discussion
4.1. Predicted Mean Vote vs. Actual Thermal Sensation
4.2. Possible Thermal Comfort Indicators
4.3. Limitation and Future Challenges
5. Conclusions
- (1)
- The neutral temperature is 24.7 °C and the upper limit for 80% acceptability is 28.2 °C in SET*.
- (2)
- The high determination coefficient indicates that upper extremity skin temperatures may become potential physiological variables to evaluate thermal comfort of human beings. The forearm has the strongest relationship among the upper extremity.
- (3)
- The relationships between thermal sensation and the gradients between the finger and the rest upper extremity skin temperatures are also established through second-order polynomial functions. It is clear that when the upper extremities temperature gradients are zero, the corresponding thermal sensations are almost equal to the neutral thermal sensation. When people feel cold, there are negative gradients. The positive gradients imply warm sensation.
- (4)
- There are no significant differences in upper extremity skin temperatures between men and women except Tforearm.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- ASHRAE. ASHRAE Standard 55-2013—Thermal Environmental Conditions for Human Occupancy; ASHRAE: Atlanta, GA, USA, 2013. [Google Scholar]
- Chandel, S.; Sharma, V.; Marwah, B.M. Review of energy efficient features in vernacular architecture for improving indoor thermal comfort conditions. Renew. Sustain. Energy Rev. 2016, 65, 459–477. [Google Scholar] [CrossRef]
- Zhang, H.; Arens, E.; Taub, M.; Dickerhoff, D.; Bauman, F.; Fountain, M.; Pasut, W.; Fannon, D.; Zhai, Y.; Pigman, M. Using footwarmers in offices for thermal comfort and energy savings. Energy Build. 2015, 104, 233–243. [Google Scholar] [CrossRef]
- Sakellaris, I.; Saraga, D.; Mandin, C.; Roda, C.; Fossati, S.; de Kluizenaar, Y.; Carrer, P.; Dimitroulopoulou, S.; Mihucz, V.; Szigeti, T.; et al. Perceived Indoor Environment and Occupants’ Comfort in European “Modern” Office Buildings: The OFFICAIR Study. Int. J. Environ. Res. Public Health 2016, 13, 444. [Google Scholar] [CrossRef] [PubMed]
- Wu, C.-F.; Hsieh, Y.-F.; Ou, S.-J. Thermal Adaptation Methods of Urban Plaza Users in Asia’s Hot-Humid Regions: A Taiwan Case Study. Int. J. Environ. Res. Public Health 2015, 12, 13560–13586. [Google Scholar] [CrossRef] [PubMed]
- Fanger, P.O. Thermal Comfort. ANALYSIS and Applications in Environmental Engineering; Danish Technical Press: Copenhagen, Denmark, 1970. [Google Scholar]
- Fanger, P. Calculation of thermal comfort, Introduction of a basic comfort equation. ASHRAE Trans. 1967, 73, III4.1–III4.20. [Google Scholar]
- Nicol, F.; Humphreys, M.; Roaf, S. Adaptive Thermal Comfort: Principles and Practice; Routledge: London, UK, 2012. [Google Scholar]
- De Dear, R.J.; Brager, G.S.; Reardon, J.; Nicol, F. Developing an adaptive model of thermal comfort and preference/discussion. ASHRAE Trans. 1998, 104, 145. [Google Scholar]
- Gagge, A.P.; Fobelets, A.; Berglund, L. A standard predictive index of human response to the thermal environment. ASHRAE Trans. 1986, 92, 709–731. [Google Scholar]
- Gagge, A.P. An effective temperature scale based on a simple model of human physiological regulatory response. ASHRAE Trans. 1971, 77, 247–262. [Google Scholar]
- Gagge, A.P.; Nishi, Y. Heat exchange between human skin surface and thermal environment. Compr. Physiol. 2011. [Google Scholar] [CrossRef]
- Garcia-Souto, M. Temperature and Comfort Monitoring Systems for Humans. Ph.D. Thesis, Queen Mary, University of London, London, UK, 2012. [Google Scholar]
- Campero, M.; Serra, J.; Bostock, H.; Ochoa, J. Slowly conducting afferents activated by innocuous low temperature in human skin. J. Physiol. 2001, 535, 855–865. [Google Scholar] [CrossRef] [PubMed]
- Hensel, H. Neural processes in thermoregulation. Physiol. Rev. 1973, 53, 948–1017. [Google Scholar]
- Cabanac, M. Heat stress and behavior. Compr. Physiol. 2011. [Google Scholar] [CrossRef]
- Filingeri, D. Neurophysiology of skin thermal sensations. Compr. Physiol. 2016. [Google Scholar] [CrossRef]
- Hales, J. Skin Arteriovenous Anastomoses, Their Control and Role in Thermoregulation. In Cardiovascular Shunts. Alfred Benzon Symposium; Munksgaard: Copenhagen, Denmark, 1985; pp. 433–451. [Google Scholar]
- Sherman, J.L., Jr. Normal arteriovenous anastomoses. Medicine 1963, 42, 247–268. [Google Scholar] [CrossRef]
- Gagge, A.P.; Gonzalez, R.R. Mechanisms of heat exchange: Biophysics and physiology. Compr. Physiol. 2011. [Google Scholar] [CrossRef]
- Wang, Z.; He, Y.; Hou, J.; Jiang, L. Human skin temperature and thermal responses in asymmetrical cold radiation environments. Build. Environ. 2013, 67, 217–223. [Google Scholar] [CrossRef]
- Liu, W.; Lian, Z.; Deng, Q.; Liu, Y. Evaluation of calculation methods of mean skin temperature for use in thermal comfort study. Build. Environ. 2011, 46, 478–488. [Google Scholar] [CrossRef]
- Xiong, J.; Zhou, X.; Lian, Z.; You, J.; Lin, Y. Thermal perception and skin temperature in different transient thermal environments in summer. Energy Build. 2016, 128, 155–163. [Google Scholar] [CrossRef]
- Sakoi, T.; Tsuzuki, K.; Kato, S.; Ooka, R.; Song, D.; Zhu, S. Thermal comfort, skin temperature distribution, and sensible heat loss distribution in the sitting posture in various asymmetric radiant fields. Build. Environ. 2007, 42, 3984–3999. [Google Scholar] [CrossRef]
- Liu, H.; Liao, J.; Yang, D.; Du, X.; Hu, P.; Yang, Y.; Li, B. The response of human thermal perception and skin temperature to step-change transient thermal environments. Build. Environ. 2014, 73, 232–238. [Google Scholar] [CrossRef]
- Luo, M.; Ji, W.; Cao, B.; Ouyang, Q.; Zhu, Y. Indoor climate and thermal physiological adaptation: Evidences from migrants with different cold indoor exposures. Build. Environ. 2016, 98, 30–38. [Google Scholar] [CrossRef]
- Humphreys, M.; McCartney, K.; Nicol, J.; Raja, I. An analysis of some observations of the finger temperature and thermal comfort of office workers. Pollut. Indoor Air 1999, 602–607. [Google Scholar]
- Wang, D.; Zhang, H.; Arens, E.; Huizenga, C. Observations of upper-extremity skin temperature and corresponding overall-body thermal sensations and comfort. Build. Environ. 2007, 42, 3933–3943. [Google Scholar] [CrossRef]
- Nakayama, K.; Suzuki, T.; Kameyama, K. Estimation of thermal sensation using human peripheral skin temperature. In Proceedings of the IEEE International Conference on Systems Man Cybernet, San Antonio, TX, USA, 11–14 October 2009; pp. 2872–2877. [Google Scholar]
- Sim, S.Y.; Koh, M.J.; Joo, K.M.; Noh, S.; Park, S.; Kim, Y.H.; Park, K.S. Estimation of thermal sensation based on wrist skin temperatures. Sensors 2016, 16, 420. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y. Design criteria of built thermal environment for Hot Summer & Warm Winter zone of China. Build. Environ. 2015, 88, 97–105. [Google Scholar]
- WHO. Obesity: Preventing and Managing the Global Epidemic; WHO: Geneva, Switzerland, 2000. [Google Scholar]
- International Standard Organization. ISO 7726, Ergonomics of the Thermal Environment, Instruments for Measuring Physical Quantities; International Standard Organization: Geneva, Switzerland, 1998. [Google Scholar]
- Gagge, A.P.; Burton, A.C.; Bazett, H.C. A Practical System of Units for the Description of the Heat Exchange of Man with his Environment. Science 1941, 94, 428–430. [Google Scholar] [CrossRef] [PubMed]
- ASHRAE. ASHRAE Handbook–Fundamentals; ASHRAE: Atlanta, GA, USA, 2009. [Google Scholar]
- AQSIQ, GB/T 18977. Ergonomics of the Thermal Environment-Assessment of the Influence of the Thermal Environment Using Subjective Judgment Scales; AQSIQ: Beijing, China, 2003.
- Zhang, Y.; Chen, H.; Wang, J.; Meng, Q. Thermal comfort of people in the hot and humid area of China—impacts of season, climate, and thermal history. Indoor Air 2016, 26, 820–830. [Google Scholar] [CrossRef] [PubMed]
- Nie, C.; Gao, Y.; Li, B.; Tan, M. Research of summer comfortable temperature in Air-conditioning Room in Chongqing, China. In Proceedings of the 2011 International Conference on Remote Sensing, Environment and Transportation Engineering (RSETE), Nanjing, China, 24–26 June 2011; pp. 4318–4321. [Google Scholar]
- Rubinstein, E.H.; Sessler, D.I. Skin-surface temperature gradients correlate with fingertip blood flow in humans. Anesthesiology 1990, 73, 541–545. [Google Scholar] [CrossRef] [PubMed]
- Huizenga, C.; Zhang, H.; Arens, E.; Wang, D. Skin and core temperature response to partial-and whole-body heating and cooling. J. Thermal Biol. 2004, 29, 549–558. [Google Scholar] [CrossRef]
- Dedear, R.; Auliciems, A. Validation of the predicted mean vote model of thermal comfort in six Australian field studies. ASHRAE Trans. 1985, 91, 452–468. [Google Scholar]
- Fanger, P.O.; Toftum, J. Thermal Comfort in the Future-Excellence and Expectation; Oxford Brookes University: Oxford, UK, 2001. [Google Scholar]
- Schiller, G. A comparison of measured and predicted comfort in office buildings. ASHRAE Trans. 1990, 96, 609–622. [Google Scholar]
- Luo, M.; Cao, B.; Damiens, J.; Lin, B.; Zhu, Y. Evaluating thermal comfort in mixed-mode buildings: A field study in a subtropical climate. Build. Environ. 2015, 88, 46–54. [Google Scholar] [CrossRef]
- Yao, R.; Li, B.; Liu, J. A theoretical adaptive model of thermal comfort–Adaptive Predicted Mean Vote (aPMV). Build. Environ. 2009, 44, 2089–2096. [Google Scholar] [CrossRef]
- Kim, J.T.; Lim, J.H.; Cho, S.H.; Yun, G.Y. Development of the adaptive PMV model for improving prediction performances. Energy Build. 2015, 98, 100–105. [Google Scholar] [CrossRef]




| Gender | Number | Age | Height (cm) | Weight (kg) | BMI a (kg/m2) | Surface Area (m2) |
|---|---|---|---|---|---|---|
| Male | 298 | 26.0 ± 5.1 b | 172.1 ± 5.0 | 65.0 ± 7.9 | 21.9 ± 2.3 | 1.76 ± 0.11 |
| Female | 132 | 26.4 ± 6.2 | 160.9 ± 4.0 | 50.1 ± 5.2 | 19.3 ± 1.7 | 1.50 ± 0.08 |
| All | 430 | 26.1 ± 5.5 | 168.7 ± 7.0 | 60.4 ± 10.0 | 21.1 ± 2.4 | 1.68 ± 0.16 |
| Parameters | Instruments | Range | Accuracy | Resolution |
|---|---|---|---|---|
| Air temperature | Thermo recorder TR-72U | −10–60 °C | ±0.3 °C | 0.1 °C |
| Relative humidity | Thermo recorder TR-72U | 10–95% RH | ±5% RH | 1% RH |
| Globe temperature | HEART INDEX CHECKER 8778 | 0–50 °C | ±0.6 °C | 0.1 °C |
| WBGT-2009 | 0–80 °C | ±0.6 °C | 0.1 °C | |
| Air velocity | Testo 425 | 0–20 m/s | ±0.03 m/s | 0.01 m/s |
| Skin temperature | Testo 905-T2 | −50–350 °C | ±1.0 °C | 0.1 °C |
| Variables | Ta (°C) | Tg (°C) | RH (%) | Va (m/s) | To (°C) | Tr (°C) | SET* (°C) | INSUAL (clo) |
|---|---|---|---|---|---|---|---|---|
| 25th Percentile | 26.2 | 26.2 | 49.3 | 0.08 | 26.2 | 26.2 | 24.5 | 0.31 |
| 75th Percentile | 27.6 | 27.6 | 61 | 0.2 | 27.6 | 27.6 | 26.3 | 0.4 |
| Skewness | −6.63 | −7.36 | −0.45 | 2.84 | −7.28 | −7.47 | −0.89 | 0.71 |
| Kurtosis | 92.41 | 107.4 | 3.9 | 11.22 | 105.7 | 110.5 | 31.98 | 3.22 |
| Variables | Tfinger (°C) | Twrist (°C) | Thand (°C) | Tforearm (°C) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| M | F | M+F | M | F | M+F | M | F | M+F | M | F | M+F | |
| Mean | 33.5 | 33.2 | 33.4 | 33.9 | 33.5 | 33.7 | 33.9 | 34.0 | 33.9 | 33.8 | 33.7 | 33.7 |
| SD | 1.8 | 2.2 | 1.9 | 0.9 | 0.8 | 0.9 | 1.0 | 1.1 | 1.0 | 1.0 | 1.2 | 1.1 |
| Maxi | 36.2 | 36.3 | 36.3 | 35.5 | 35.1 | 35.5 | 35.8 | 36.3 | 36.0 | 35.6 | 35.7 | 35.7 |
| Mini | 23.6 | 24.8 | 23.6 | 31.0 | 30.7 | 30.7 | 29.6 | 30.2 | 29.6 | 27.5 | 29.4 | 27.5 |
| TS | −2 | −1 | 0 | 1 | 2 | 3 | All |
|---|---|---|---|---|---|---|---|
| Tfinger | |||||||
| M | 29.7 ± 4.4 | 32.7 ± 2.2 | 33.6 ± 1.5 | 33.7 ± 1.3 | 34.5 ± 0.4 | 35.1 ± 1.0 | 33.5 ± 1.8 |
| F | 31.7 ± 3.2 | 32.6 ± 2.1 | 33.3 ± 2.1 | 34.0 ± 1.8 | 35.3 ± 0.4 | 35.0 ± 1.2 | 33.2 ± 2.2 |
| M+F | 30.8 ± 3.7 | 32.6 ± 2.1 | 33.5 ± 1.7 | 33.8 ± 1.5 | 34.7 ± 0.8 | 35.1 ± 1.0 | 33.4 ± 1.9 |
| Twrist | |||||||
| M | 32.1 ± 1.6 | 33.3 ± 1.2 * | 34.0 ± 0.9 | 34.0 ± 0.8 | 34.4 ± 0.4 | 34.7 ± 0.8 | 33.9 ± 1.0 |
| F | 33.2 ± 1.8 | 33.9 ± 1.0 * | 34.1 ± 1.0 | 34.0 ± 1.3 | 34.6 ± 0.4 | 34.9 ± 0.3 | 34.0 ± 1.1 |
| M+F | 32.7 ± 1.8 | 33.6 ± 1.7 | 34.1 ± 0.9 | 34.0 ± 1.0 | 34.6 ± 0.4 | 34.8 ± 0.6 | 33.9 ± 1.0 |
| Thand | |||||||
| M | 31.3 ± 2.4 | 33.2 ± 1.3 | 33.9 ± 0.8 | 34.0 ± 0.8 | 34.3 ± 0.6 | 34.5 ± 0.5 | 33.8 ± 1.0 |
| F | 32.6 ± 1.9 | 33.4 ± 1.3 | 33.9 ± 1.0 | 33.6 ± 1.3 | 34.3 ± 0.6 | 34.7 ± 0.3 | 33.7 ± 1.2 |
| M+F | 32.0 ± 2.2 | 33.2 ± 1.3 | 33.9 ± 0.9 | 33.9 ± 0.9 | 34.3 ± 0.6 | 34.6 ± 0.4 | 33.7 ± 1.1 |
| Tforearm | |||||||
| M | 32.2 ± 1.2 | 33.5 ± 1.1 | 33.89 ± 0.78 *** | 34.0 ± 0.6 | 34.1 ± 0.7 | 34.4 ± 0.5 | 33.9 ± 0.9 *** |
| F | 33.1 ± 1.4 | 33.6 ± 0.8 | 33.47 ± 0.80 *** | 33.7 ± 0.7 | 33.6 ± 0.3 | 34.6 ± 0.4 | 33.5 ± 0.8 *** |
| M+F | 32.7 ± 1.3 | 33.5 ± 1.0 | 33.77 ± 0.81 | 34.0 ± 0.7 | 34.0 ± 0.6 | 34.5 ± 0.4 | 33.7 ± 0.9 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Z.; Li, N.; Cui, H.; Peng, J.; Chen, H.; Liu, P. Using Upper Extremity Skin Temperatures to Assess Thermal Comfort in Office Buildings in Changsha, China. Int. J. Environ. Res. Public Health 2017, 14, 1092. https://doi.org/10.3390/ijerph14101092
Wu Z, Li N, Cui H, Peng J, Chen H, Liu P. Using Upper Extremity Skin Temperatures to Assess Thermal Comfort in Office Buildings in Changsha, China. International Journal of Environmental Research and Public Health. 2017; 14(10):1092. https://doi.org/10.3390/ijerph14101092
Chicago/Turabian StyleWu, Zhibin, Nianping Li, Haijiao Cui, Jinqing Peng, Haowen Chen, and Penglong Liu. 2017. "Using Upper Extremity Skin Temperatures to Assess Thermal Comfort in Office Buildings in Changsha, China" International Journal of Environmental Research and Public Health 14, no. 10: 1092. https://doi.org/10.3390/ijerph14101092
APA StyleWu, Z., Li, N., Cui, H., Peng, J., Chen, H., & Liu, P. (2017). Using Upper Extremity Skin Temperatures to Assess Thermal Comfort in Office Buildings in Changsha, China. International Journal of Environmental Research and Public Health, 14(10), 1092. https://doi.org/10.3390/ijerph14101092







